The Characteristic Development of Micropores in Deep Coal and Its Relationship with Adsorption Capacity on the Eastern Margin of the Ordos Basin, China
Abstract
1. Introduction
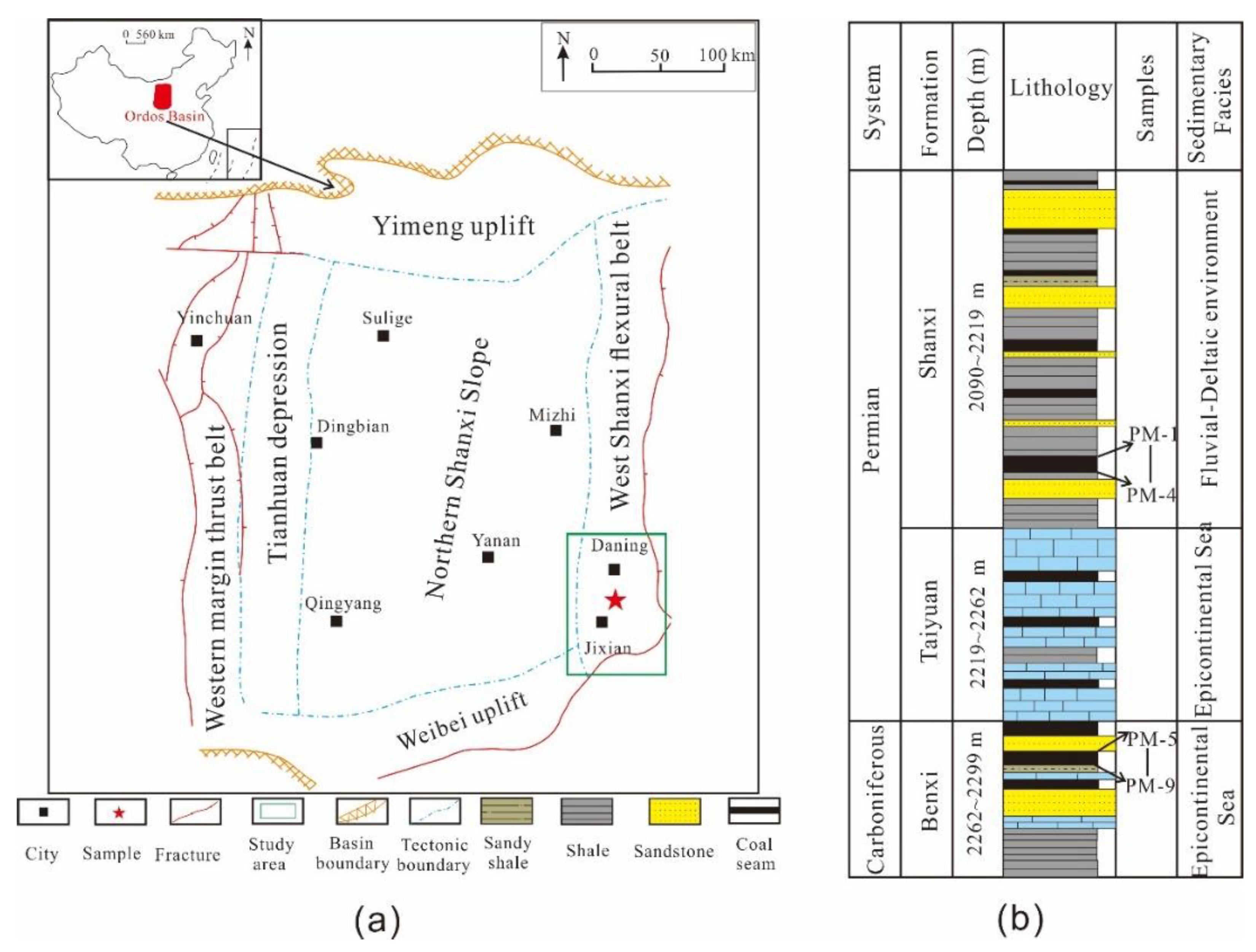
2. Geological Setting
3. Samples and Experimental Methods
4. Results
4.1. Coal Rock Coal Quality Characteristics
4.2. Pore Morphology Characteristics
4.3. Quantitative Analyses of Pore Structure
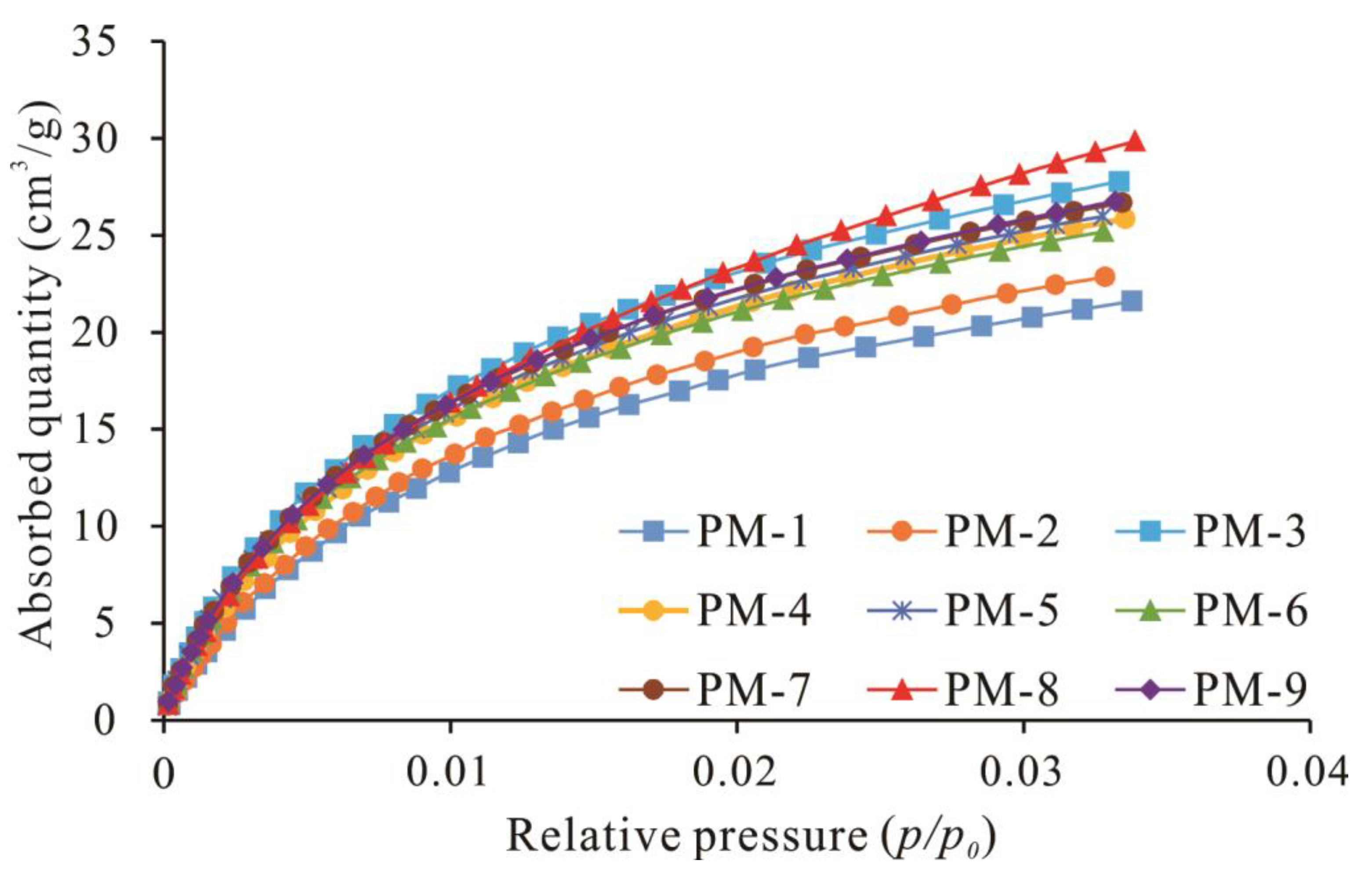
4.3.1. CO2 Adsorption Isotherms
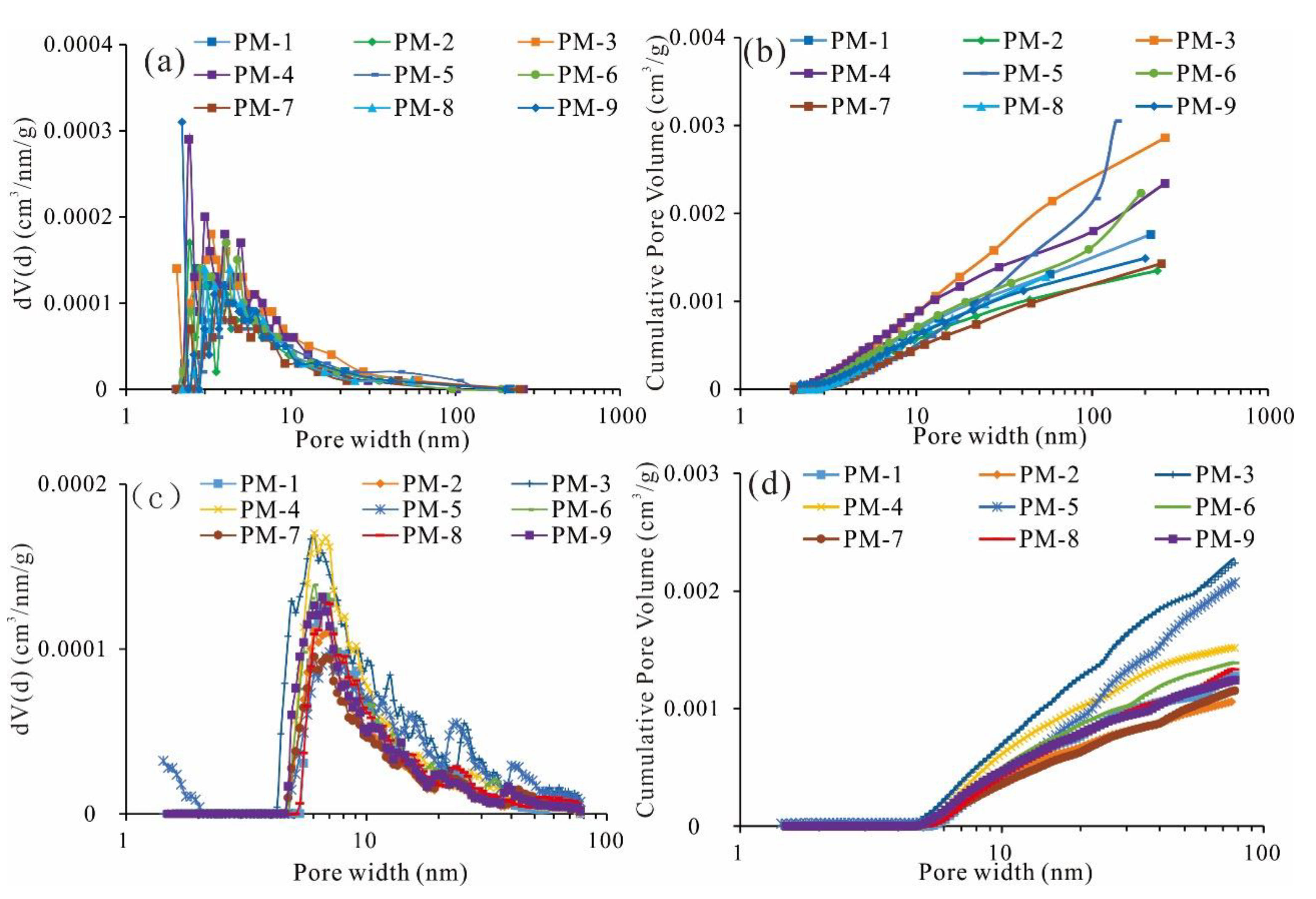
4.3.2. N2 Adsorption Isotherm
4.4. Pore Fractal Characteristics
4.5. Methane Adsorption Characteristics
5. Discussion
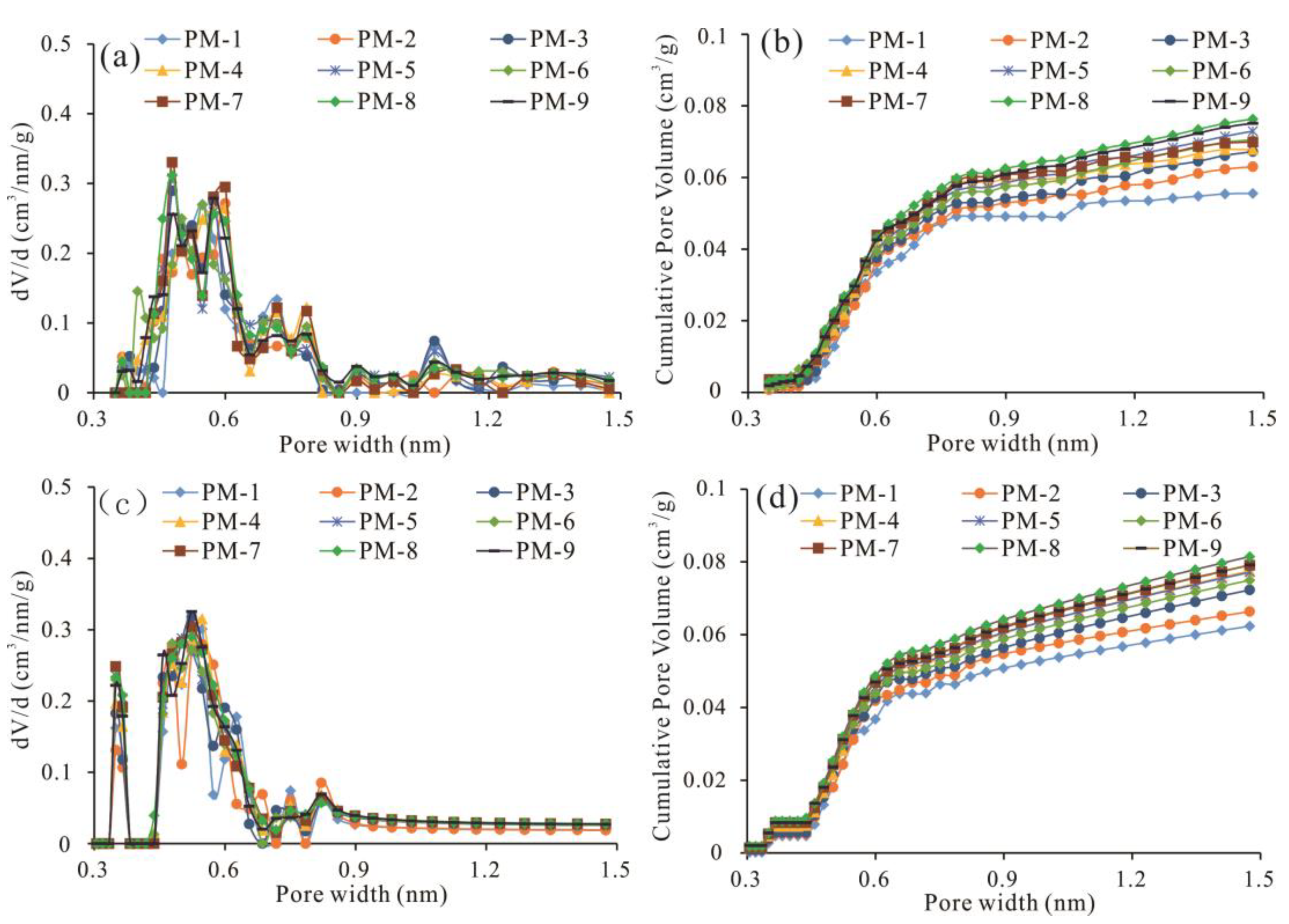
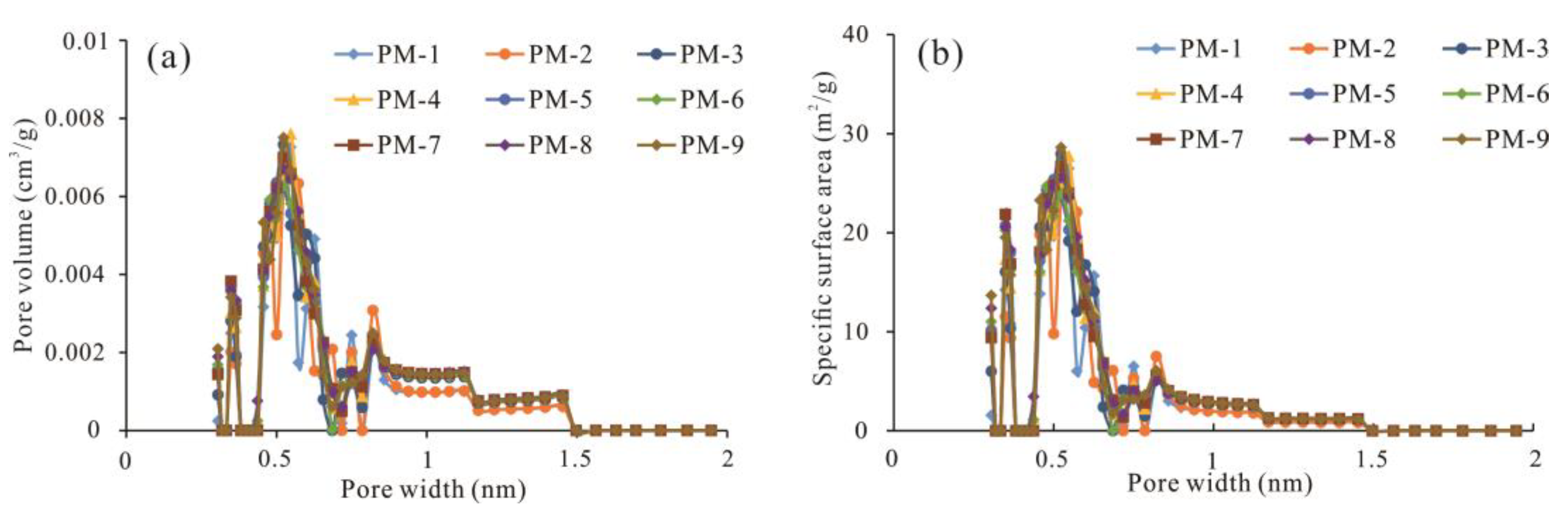
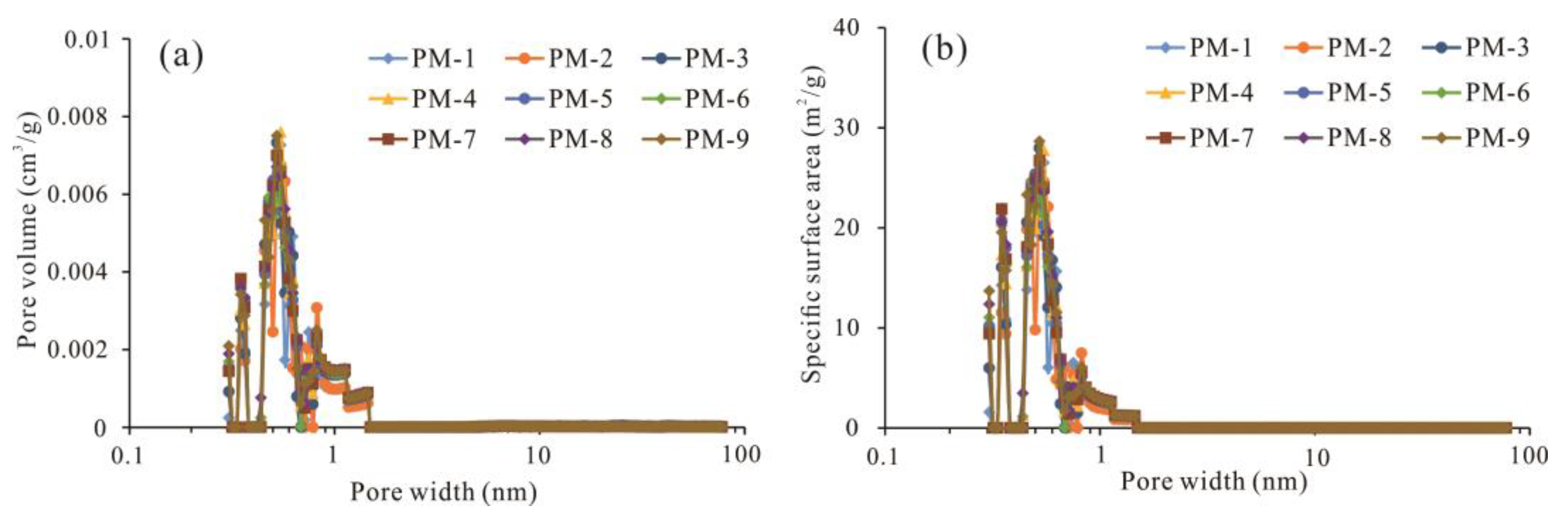
5.1. Development and Pore Size Distribution of Micropores
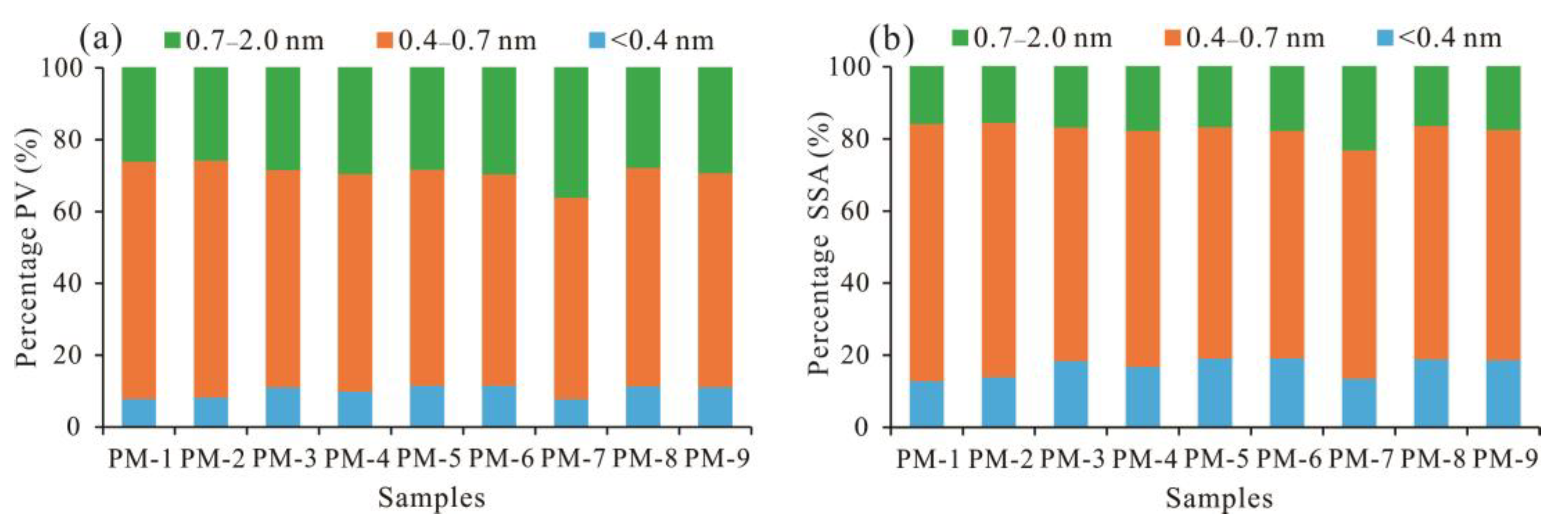
5.2. Proportion of Micropores in Total Pores
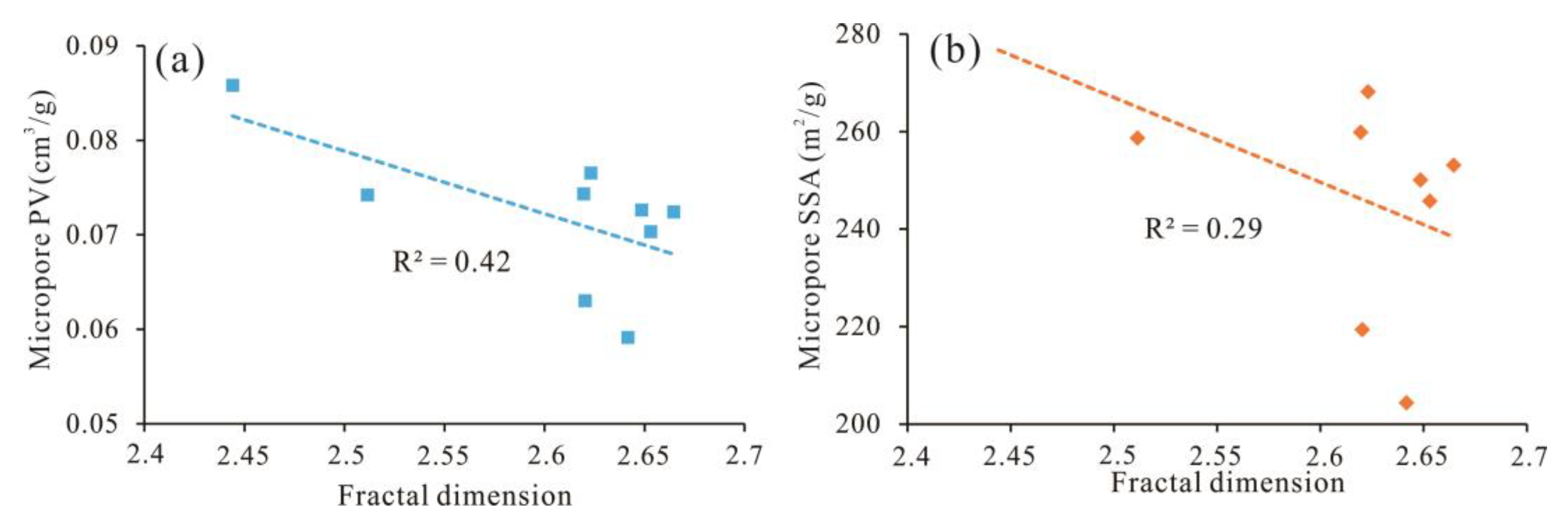
5.3. Pore Structural Parameters and Fractal Dimensions
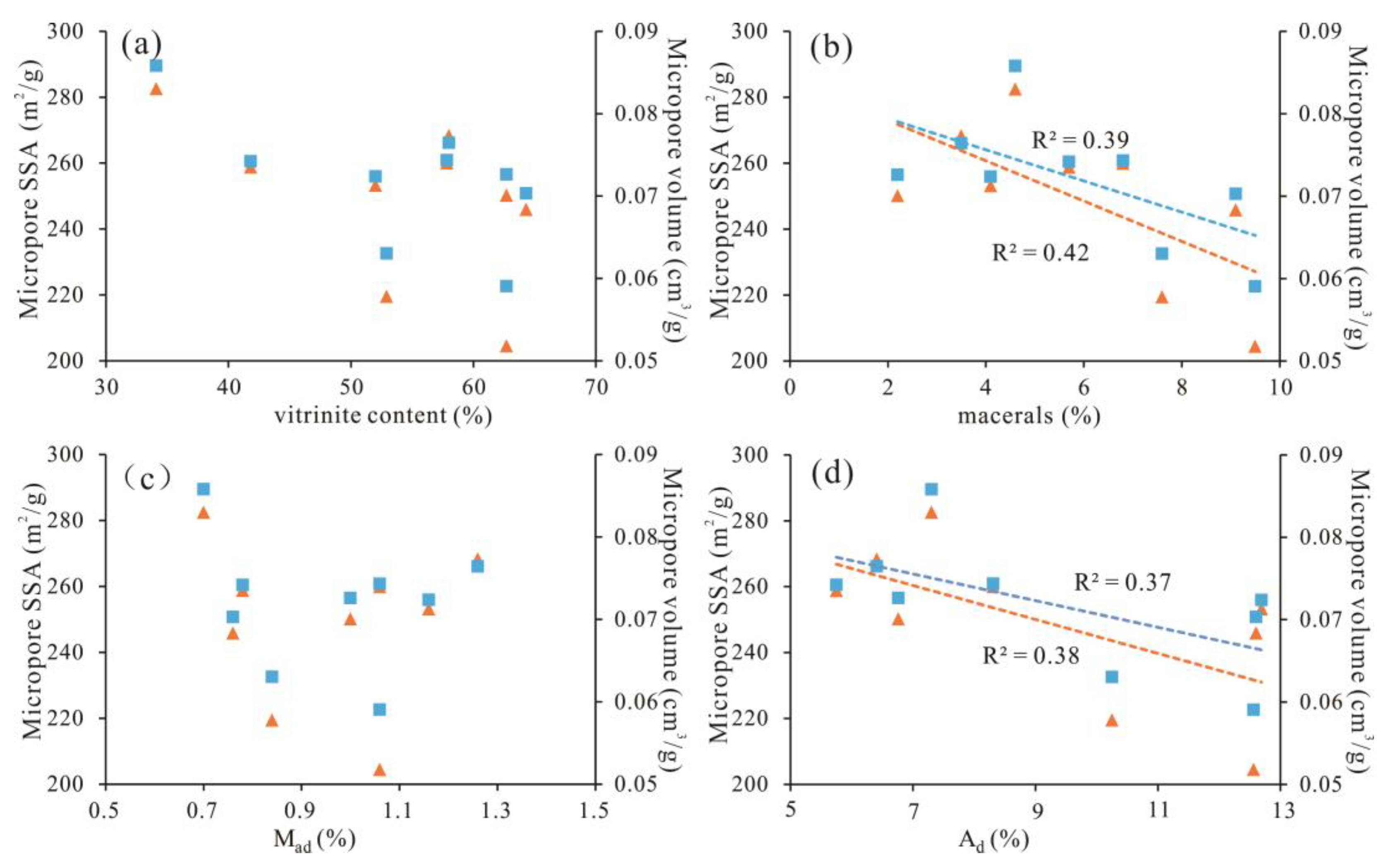
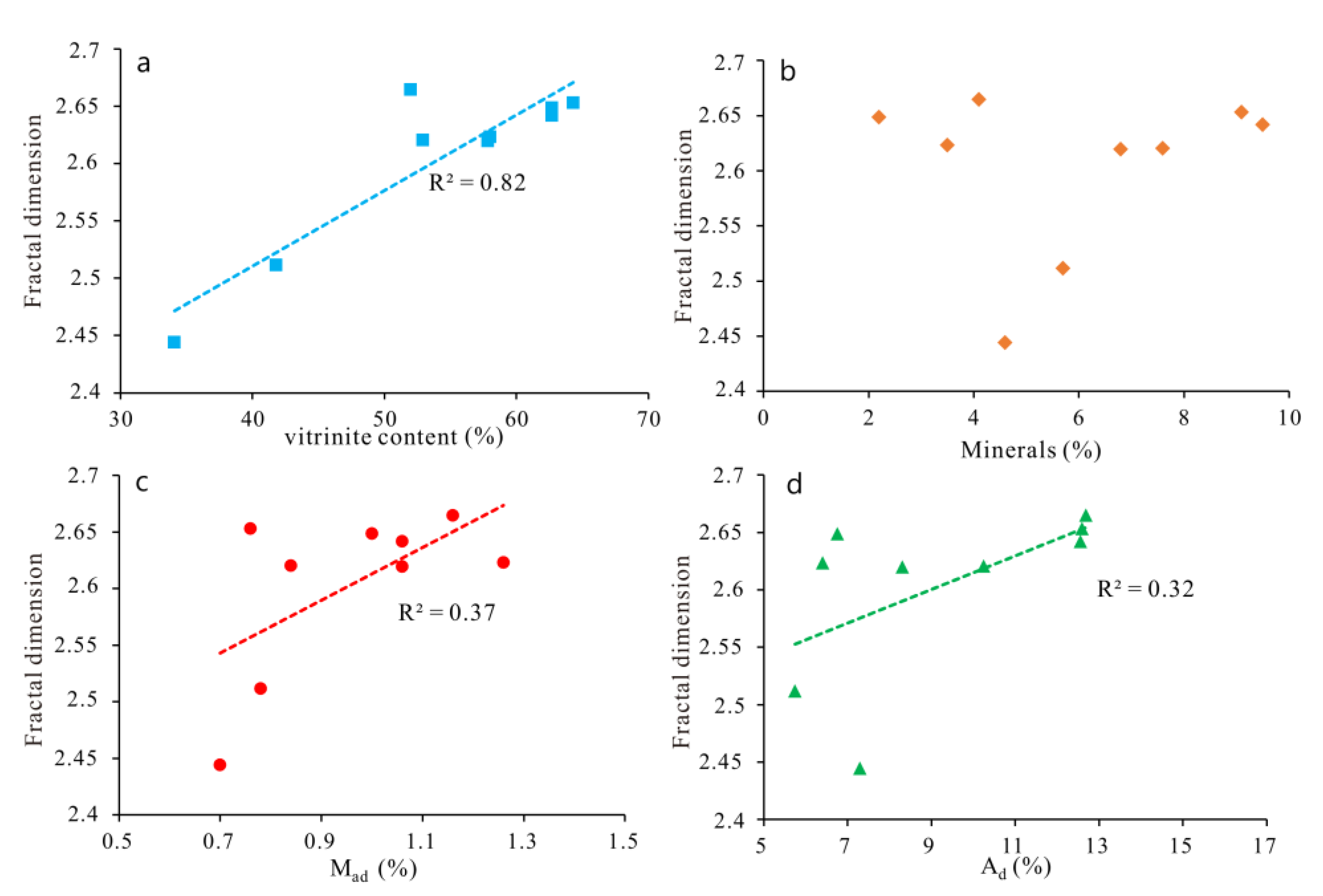
5.4. Influence on the Fractal Dimensions
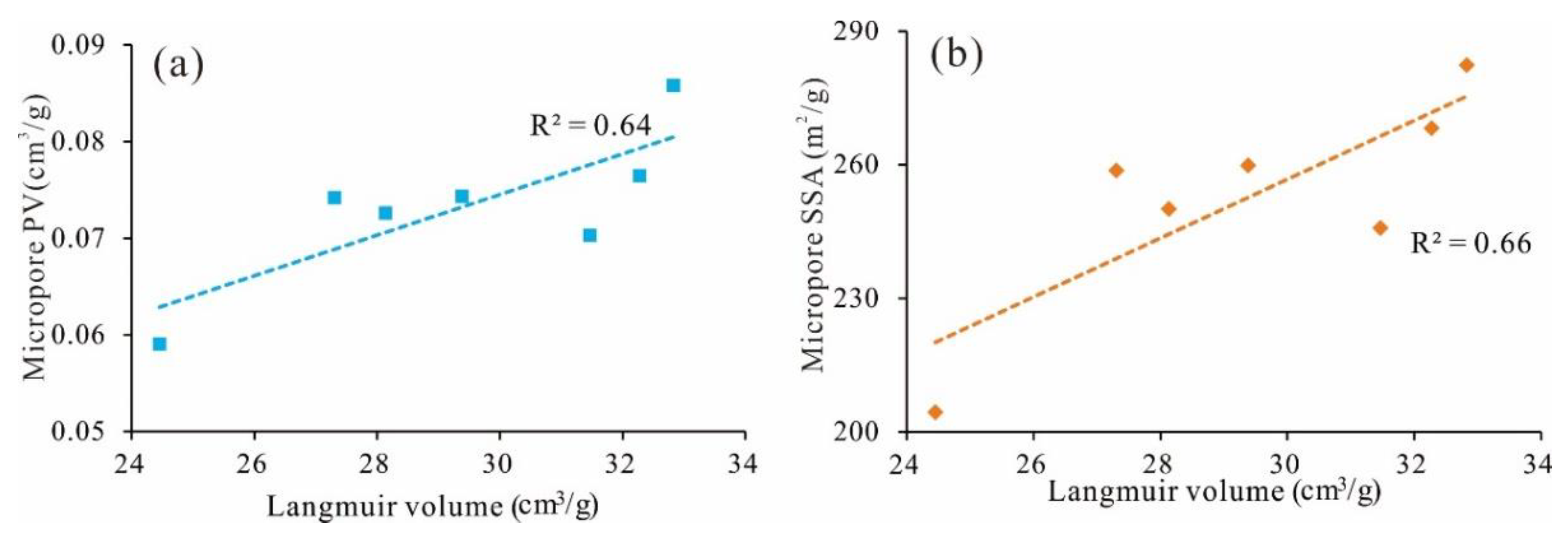
5.5. Adsorption Capacity of Micropores
6. Conclusions
- (1)
- The LPA method based on the NLDFT model is the best method to measure and calculate the PV, SSA and PSD corresponding to the pore size range from 0.3~1.5 nm, as validated by comparing the results of the LPA and LTA experiments and different calculation models. Combining the LPA method with the LTA method based on the NLDFT model, all micropores smaller than 2.0 nm can be measured.
- (2)
- The pores developed in deep coal rocks are mainly organic pores, InterP pores and microfractures, and the pore size distribution patterns of different coal samples have multiple peaks, among which micropores are the main contributors to the total PV and total SSA, with the micro-PV ranging from 0.059 to 0.086 cm3/g and the micro-SSA ranging from 204.380 to 282.415 m2/g.
- (3)
- Different coal samples in the study area have great differences in the degree of micropore development, but the pore distribution characteristics are basically the same. The PV and SSA of the 0.4–0.7 nm pore size range are the most developed, accounting for more than 60%. Micropore structure development is mainly affected by the maceral and mineral components. With increasing mineral content and Ad, micro-PV and micro-SSA decrease rapidly.
- (4)
- The micropore fractal dimension (D) is calculated based on LPA data. The D values range from 2.4441 to 2.6646, with an average of 2.603. The relationship between the D value and mineral content is not obvious, but D is positively correlated with vitrinite content, Mad and Ad.
- (5)
- The contribution rate of micro-SSA to total SSA of coal samples in the study area reaches 99%, and VL is linearly positively correlated with micro-SSA, which shows that the adsorption capacity of coal reservoir depends on the development degree of micro-SSA.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blacher, S.; Sahouli, B.; Heinrichs, B.; Lodewyckx, P.; Pirard, R.; Pirard, J.P. Micropore size distributions of activated carbons. Langmuir 2000, 16, 6754–6756. [Google Scholar] [CrossRef]
- Tao, S.; Chen, S.; Tang, D.; Zhao, X.; Xu, H.; Li, S. Material composition, pore structure and adsorption capacity of low-rank coals around the first coalification jump: A case of eastern Junggar Basin, China. Fuel 2018, 211, 804–815. [Google Scholar] [CrossRef]
- Sing, K.S.W.; Everett, D.H.; Haul, R.A.W. Reporting physisorption data for gas/solid systems with special reference to the determination of surface area and porosity. Pure Appl. Chem. 1985, 57, 603–619. [Google Scholar] [CrossRef]
- Cui, X.; Bustin, R.M.; Dipple, G. Selective transport of CO2, CH4, and N2 in coals: Insights from modeling of experimental gas adsorption data. Fuel 2004, 83, 293–303. [Google Scholar] [CrossRef]
- Groen, J.C.; Peffer, L.A.; Pérez-Ramıréz, J. Pore size determination in modified microand mesoporous materials. Pitfalls and limitations in gas adsorption data analysis. Microporous Mesoporous Mater. 2003, 60, 1–17. [Google Scholar] [CrossRef]
- Hou, S.; Wang, X.; Wang, X.; Yuan, Y.; Pan, S.; Wang, X. Pore structure characterization of low volatile bituminous coals with different particle size and tectonic deformation using low pressure gas adsorption. Int. J. Coal Geol. 2017, 183, 1–13. [Google Scholar] [CrossRef]
- Hu, B.; Cheng, Y.; He, X.; Wang, Z.; Wang, L.; Jiang, Z.; Wang, C.; Wei, L.; Wang, L. New insights into the CH4 adsorption capacity of coal based on microscopic pore properties. Fuel 2019, 262, 116675. [Google Scholar] [CrossRef]
- Li, C.; Jiang, B.; Ju, W.; Cheng, G.; Song, Y. Characteristics of tectonic deformation in the Daning-Jixian region, eastern Ordos Basin: Implications for the exploration and development of coalbed methane. Energy Explor. Exploit. 2019, 37, 907–921. [Google Scholar] [CrossRef]
- Song, D.; Ji, F.; Li, Y.; Zhao, H.; Song, B.; He, K. Heterogeneous development of micropores in medium-high rank coal and its relationship with adsorption capacity. Int. J. Coal Geol. 2020, 226, 103497. [Google Scholar] [CrossRef]
- Ma, X.; Guo, S.; Shi, D.; Zhou, Z.; Liu, G. Investigation of pore structure and fractal characteristics of marine-continental transitional shales from Longtan Formation using MICP, gas adsorption, and NMR (Guizhou, China). Mar. Pet. Geol. 2019, 107, 555–571. [Google Scholar] [CrossRef]
- Li, G.; Qin, Y.; Wu, M.; Zhang, B.; Wu, X.; Tong, G.; Liu, J. The pore structure of the transitional shale in the Taiyuan formation, Linxing area, Ordos Basin. J. Pet. Sci. Eng. 2019, 189, 106183. [Google Scholar] [CrossRef]
- Lu, W.; Zhuang, Z.; Zhang, W.; Zhang, C.; Song, S.; Wang, R.; Kong, B. Study on the Pore and Crack Change Characteristics of Bituminous Coal and Anthracite after Different Temperature Gradient Baking. Energy Fuels 2021, 35, 19448–19463. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, C.; Liu, H. Comprehensive characteristics of pore structure and factors influencing micropore development in the Laochang mining area, eastern Yunnan, China. J. Pet. Sci. Eng. 2020, 190, 107090. [Google Scholar] [CrossRef]
- Wei, Y.; Li, J.; Du, Y.; Lu, S.; Li, W.; Yang, J.; Feng, W.; Song, Z.; Zhang, Y. Classification Evaluation of Gas Shales Based on High-Pressure Mercury Injection: A Case Study on Wufeng and Longmaxi Formations in Southeast Sichuan, China. Energy Fuels 2021, 35, 9382–9395. [Google Scholar] [CrossRef]
- Chalmers, G.R.; Bustin, R.M.; Power, I.M. Characterization of gas shale pore systems by porosimetry, pycnometry, surface area, and field emission scanning electron microscopy/transmission electron microscopy image analyses: Examples from the Barnett, Woodford, Haynesville, Marcellus, and Doig units. AAPG Bull. 2012, 96, 1099–1119. [Google Scholar]
- Zhou, S.; Liu, D.; Cai, Y.; Karpyn, Z.; Yao, Y. Comparative analysis of nanopore structure and its effect on methane adsorption capacity of Southern Junggar coalfield coals by gas adsorption and FIB-SEM tomography. Microporous Mesoporous Mater. 2018, 272, 117–128. [Google Scholar] [CrossRef]
- Li, Z.; Liu, D.; Cai, Y.; Wang, Y.; Teng, J. Adsorption pore structure and its fractal characteristics of coals by N2 adsorption/desorption and FESEM image analyses. Fuel 2019, 257, 116031. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, Z.; Shu, S.; Chang, J.; Zhu, L.; Li, X.; Li, J. Full-Scale Pore Structure and Fractal Dimension of the Longmaxi Shale from the Southern Sichuan Basin: Investigations Using FE-SEM, Gas Adsorption and Mercury Intrusion Porosimetry. Minerals 2019, 9, 3–26. [Google Scholar] [CrossRef]
- Mastalerz, M.; Drobniak, A.; Rupp, J. Meso-and micropore characteristics of coal lithotypes: Implications for CO2 adsorption. Energy Fuels 2008, 22, 4049–4061. [Google Scholar] [CrossRef]
- Chen, S.; Tao, S.; Tang, D.; Xu, H.; Li, S.; Zhao, J.; Jiang, Q.; Yang, H. Pore structure characterization of different rank coals using N2 and CO2 adsorption and its effect on CH4 adsorption capacity: A case in Panguan Syncline, Western Guizhou, China. Energy Fuels 2017, 31, 6034–6044. [Google Scholar] [CrossRef]
- Li, Y.; Song, D.; Liu, S.; Pan, J. Characterization of Ultra-Micropores and Analysis of Their Evolution in Tectonically Deformed Coals by Low-Pressure CO2 Adsorption, XRD and HRTEM Techniques. Energy Fuels 2020, 34, 9436–9449. [Google Scholar] [CrossRef]
- Han, W.; Zhou, G.; Gao, D.; Zhang, Z.; Wei, Z.; Wang, H.; Yang, H. Experimental analysis of the pore structure and fractal characteristics of different metamorphic coal based on mercury intrusionnitrogen adsorption porosimetry. Powder Technol. 2020, 362, 386–398. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, M.; Zhao, X.; Dai, X.; He, Y. Study of the Microstructural Characteristics of Low-Rank Coal under Different Degassing Pressures. Energies 2022, 15, 3691. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D. Comparison of low-field NMR and mercury intrusion porosimetry in characterizing pore size distributions of coals. Fuel 2012, 95, 152–158. [Google Scholar] [CrossRef]
- Okolo, G.N.; Everson, R.C.; Neomagus, H.W.J.P.; Roberts, M.J.; Sakurovs, R. Comparing the porosity and surface areas of coal as measured by gas adsorption, mercury intrusion and SAXS techniques. Fuel 2015, 141, 293–304. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, Y.; Liu, S.; Chen, Z.; Yuan, L. Pore structure characterization of coal by synchrotron radiation nano-CT. Fuel 2018, 215, 102–110. [Google Scholar] [CrossRef]
- Yu, S.; Bo, J.; Meijun, Q. Molecular dynamic simulation of self-and transport diffusion for CO2/CH4/N2 in low-rank coal vitrinite. Energy Fuel 2018, 32, 3085–3096. [Google Scholar] [CrossRef]
- Amarasekera, G.; Scarlett, M.J.; Mainwaring, D.E. Micropore size distributions and specific interactions in coals. Fuel 1995, 74, 115–118. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Bustin, R.M. Variation in micropore capacity and size distribution with composition in bituminous coal of the Western Canadian Sedimentary Basin: Implications for coalbed methane potential. Fuel 1996, 75, 1483–1498. [Google Scholar] [CrossRef]
- Centeno, T.A.; Stoeckli, F. The assessment of surface areas in porous carbons by two model-independent techniques, the DR equation and DFT. Carbon 2010, 48, 2478–2486. [Google Scholar] [CrossRef]
- Landers, J.; Gor, G.Y.; Neimark, A.V. Density functional theory methods for characterization of porous materials. Colloids Surf. A Physicochem. Eng. Asp. 2013, 437, 3–32. [Google Scholar] [CrossRef]
- Zhu, H.; Ju, Y.; Lu, W.; Han, K.; Qi, Y.; Neupane, B. The characteristics and evolution of micro-nano scale pores in shales and coals. J. Nanosci. Nanotechnol. 2017, 17, 6124–6138. [Google Scholar] [CrossRef]
- Guo, S.B.; Mao, W.J. Division of diagenesis and pore evolution of a Permian Shanxi shale in the Ordos Basin, China. J. Pet. Sci. Eng. 2019, 182, 920–4105. [Google Scholar] [CrossRef]
- Kuang, L.; Dong, D.; He, W.; Wen, S.; Sun, S.; Li, S.; Qiu, Z.; Liao, X.; Li, Y.; Wu, J.; et al. Geological characteristics and development potential of transitional shale gas in the east margin of the Ordos Basin, NW China. Pet. Explor. Dev. 2020, 47, 471–482. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Y.; Liu, S.; Chen, S.; Li, W.; Wang, Y. Molecular structure controls on micropore evolution in coal vitrinite during coalification. Int. J. Coal Geol. 2018, 199, 19–30. [Google Scholar] [CrossRef]
- Liu, C.; Zhong, J.; Wang, X.; Cao, M.; Wu, J.; Zhang, S.; Wu, X.; Sun, N.; Du, Y.; Liu, Y. Petrological characteristics and the impact of mineral content on reservoir quality in coal-bearing strata of Linxing area, eastern margin of Ordos Basin, China. Energy Explor. Exploit. 2018, 36, 872–894. [Google Scholar] [CrossRef]
- Zhao, L.P.; Lu, J.; Li, X.; Li, Y.; He, Q.; Ma, Z. Logging calculation method and application of geochemical parameters of source rocks with different lithologies in marine-continental transitional facies in Ordos Basin, China. Arab. J. Geosci. 2022, 15, 1111. [Google Scholar] [CrossRef]
- Zhang, M.; Fu, X. Characterization of pore structure and its impact on methane adsorption capacity for semi-anthracite in Shizhuangnan Block, Qinshui Basin. J. Nat. Gas Sci. Eng. 2018, 53, 370–384. [Google Scholar] [CrossRef]
- Loucks, R.G.; Reed, R.M.; Ruppel, S.C.; Jarvie, D.M. Morphology, Genesis, and Distribution of Nanometer-scale Pores in Siliceous Mudstones of the Mississippian Barnett Shale. J. Sediment. Res. 2009, 79, 848–861. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, D.; Cai, Y.; Li, X. Variation of petrophysical properties and adsorption capacity in different rank coals: An experimental study of coals from the Junggar, Ordos and Qinshui Basins in China. Energies 2019, 12, 986. [Google Scholar] [CrossRef]
- Ravikovitch, P.I.; Haller, G.L.; Neimark, A.V. Density functional theory model for calculating pore size distributions: Pore structure of nanoporous catalysts. Adv. Colloid Interface Sci. 1998, 76, 203–226. [Google Scholar] [CrossRef]
- Mahamud, M.; Lopez, O.; Pis, J.J.; Pajares, J.A. Textural characterization of coals using fractal analysis. Fuel Process. Technol. 2003, 81, 127–142. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Pan, Z.; Niu, X.; Meng, S. Pore structure and its fractal dimensions of transitional shale: A cross-section from east margin of the Ordos Basin, China. Fuel 2019, 241, 417–431. [Google Scholar] [CrossRef]
- Dubinin, M.M. Adsorption in micropores. J. Colloid Interface Sci. 1967, 23, 487–499. [Google Scholar] [CrossRef]
- Marsh, H.; Rand, B. The characterization of microporous carbons by means of the Dubinin-Radushkevich equation. J. Colloid Interface Sci. 1970, 33, 101–116. [Google Scholar] [CrossRef]
- Evans, R.; Marconi, U.M.B.; Tarazona, P. Capillary condensation and adsorption in cylindrical and slit-like pores. J. Chem. Soc. 1986, 82, 1763–1787. [Google Scholar] [CrossRef]
- Gelb, L.D.; Gubbins, K.E.; Radhakrishnan, R.; Sliwinska-Bartkowiak, M. Phase separation in confined systems. Rep. Prog. Phys. 1999, 62, 1573–1659. [Google Scholar] [CrossRef]
- El-Merraoui, M.; Aoshima, M.; Kaneko, K. Micropore size distribution of activated carbon fiber using the density functional theory and other methods. Langmuir 2000, 16, 4300–4304. [Google Scholar] [CrossRef]
- Ji, X.; Song, D.; Ni, X.; Li, Y.; Zhao, H. Coal Matrix Deformation and Pore Structure Change in High-Pressure Nitrogen Replacement of Methane. Energies 2018, 11, 2–18. [Google Scholar] [CrossRef]
- Wei, Z.; Fu, X.; Hao, M.; Li, G.; Pan, J.; Niu, Q.; Zhou, H. Experimental insights into the adsorption-desorption of CH4/N2 and induced strain for medium-rank coals. J. Petrol. Sci. Eng. 2021, 204, 108705. [Google Scholar]
- Jagiello, J.; Thommes, M. Comparison of DFT characterization methods based on N2, Ar, CO2, and H2 adsorption applied to carbons with various pore size distributions. Carbon 2004, 42, 1227–1232. [Google Scholar] [CrossRef]
- Pan, J.; Wang, K.; Hou, Q.; Niu, Q.; Wang, H.; Ji, Z. Micro-pores and fractures of coals analysed by field emission scanning electron microscopy and fractal theory. Fuel 2016, 164, 277–285. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Wei, Q.; Sun, K.; Zhang, G.; Wang, F. Characterization of Full-Sized Pore Structure and Fractal Characteristics of Marine–Continental Transitional Longtan Formation Shale of Sichuan Basin, South China. Energy Fuels 2017, 31, 10490–10504. [Google Scholar] [CrossRef]
- Jaroniec, M.; Lu, X.; Madey, R.; Choma, J. Evaluation of structural heterogeneities and surface irregularities of microporous solids. Mater. Chem. Phys. 1990, 26, 87–97. [Google Scholar] [CrossRef]
- Machin, W.D. Temperature dependence of hysteresis and the pore size distributions of two mesoporous adsorbents. Langmuir 1994, 10, 1235–1240. [Google Scholar] [CrossRef]
- Jaroniec, M.; Gilpin, R.K.; Choma, J. Correlation between microporosity and fractal dimension of active carbons. Carbon 1993, 31, 325–331. [Google Scholar] [CrossRef]
- Stoeckli, H.F.; Ballerini, L.; Bernardini, S.D. On the evolution of micropore widths and areas in the course of activation. Carbon 2009, 27, 501–502. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhou, S.; Jiao, P.; Yang, M.; Zhou, J.; Wei, W.; Cai, J. Fractal analysis of micropore structures in coal and shale based on lowtemperature CO2 adsorption. Nat. Gas Geosci. 2020, 31, 1028–1040. [Google Scholar]
- Reucroft, P.J.; Sethuraman, A.R. Effect of pressure on carbon dioxide induced coal swelling. Energy Fuels 1987, 1, 72–75. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Bustin, R.M. The effect of pore structure and gas pressure upon the transport properties of coal: A laboratory and modeling study. 1. Isotherms and pore volume distributions. Fuel 1999, 78, 1345–1362. [Google Scholar] [CrossRef]
- Li, J.; Li, B.; Ren, C.; Yang, K.; Zhang, Y. Characterization of Methane Adsorption Behavior on Wet Shale under Different Temperature Conditions. Energy Fuels 2020, 34, 2832–2848. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, S.; Zhao, W.; Wang, L. Intrinsic relationship between Langmuir sorption volume and pressure for coal: Experimental and thermodynamic modeling study. Fuel 2019, 241, 105–117. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Mosher, K.; He, J.; Liu, Y.; Rupp, E.; Wilcox, J. Molecular simulation of methane adsorption in micro-and mesoporous carbons with applications to coal and gas shale systems. Int. J. Coal Geol. 2013, 109, 36–44. [Google Scholar] [CrossRef]
- Jia, A.; Hu, D.; He, S. Variations of Pore Structure in Organic-Rich Shales with Different Lithofacies from the Jiangdong Block, Fuling Shale Gas Field, SW China: Insights into Gas Storage and Pore Evolution. Energy Fuels 2020, 34, 12457–12475. [Google Scholar] [CrossRef]
- Zhou, L.; Qian, Y.; Zhang, L.; Lan, X.; Wu, Y.; Wang, Q.; Zhang, G. Seismic prediction of oolitic beach thin-bed reservoir based on favorable facies belt constraints: Taking the second member of Feixianguan Formation in Jiulongshan area, Northwest Sichuan, China. J. Nat. Gas Geosci. 2021, 6, 329–344. [Google Scholar] [CrossRef]
- Bustin, R.M.; Bustin, A.M.M.; Cui, X.; Ross, D.J.K.; Murthy, P.V.S. Impact of shale properties on pore structureand storage characteristics. In Proceedings of the Shale Gas Production Conference, Fort Worth, TX, USA, 16–18 November 2008. [Google Scholar]
- Fu, H.J.; Tang, D.Z.; Xu, T.; Tan, S.; Yin, Z.Y.; Chen, B.L.; Zhang, C.; Wang, L.L. Characteristics of pore structure and fractural dimension of low-rank coal: A case study of Lower Jurassic Xishayao coal in the southern Junggar Basin, NW China. Fuel 2017, 193, 254–264. [Google Scholar] [CrossRef]
- Shang, Z.; Dong, L.; Niu, L.; Shi, H. Adsorption of Methane, Nitrogen, and Carbon Dioxide in Atomic-Scale Fractal Nanopores by Monte Carlo Simulation I: Single-Component Adsorption. Energy Fuels 2019, 33, 10457–10475. [Google Scholar] [CrossRef]
- Zhang, C.; Yao, Y.; Dong, Y. Heterogeneous development of micro- and meso-pores in shale kerogen: New insights from chemical structure analysis. J. Nat. Gas Sci. Eng. 2022, 102, 104552. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, S. Characterization of whole-aperture pore structure and its effect on methane adsorption capacity for transitional shales. Energy Fuels 2018, 32, 3176–3188. [Google Scholar] [CrossRef]
- Zhong, L.W.; Zhang, H.; Yuan, Z.R.; Lei, C.L. Influence of specific pore area and pore volume of coal on adsorption capacity. Coal Geol. Explor. 2002, 30, 26–28. [Google Scholar]
- Sang, S.X.; Qin, Y.; Guo, X.B.; Chen, Y.H. Storing characteristics of Jurassic coalbed gas in Junggar and Tuha Basins. Geol. J. China Univ. 2003, 9, 365–372. [Google Scholar]
- Thommes, M.; Cychosz, K.A. Physical adsorption characterization of nanoporous materials: Progress and challenges. Adsorption 2014, 20, 233–250. [Google Scholar] [CrossRef]




| Samples | Strata | Coal Seam | Depth (m) | Ro,max% | Proximate Analysis (%) | Macerals (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mad | Ad | Vdaf | FCad | Vitrinite | Inertinite | Minerals | |||||
| PM-1 | Shanxi | 5 # | 2195.3 | 2.93 | 1.1 | 12.6 | 7.2 | 79.1 | 62.7 | 27.8 | 9.5 |
| PM-2 | Shanxi | 5 # | 2195.7 | 3.13 | 0.8 | 10.3 | 6.8 | 82.2 | 52.9 | 39.5 | 7.6 |
| PM-3 | Shanxi | 5 # | 2196.5 | 3.14 | 0.8 | 5.8 | 6.8 | 86.7 | 41.8 | 52.5 | 5.7 |
| PM-4 | Shanxi | 5 # | 2197 | 3.30 | 1.0 | 6.8 | 6.5 | 85.7 | 62.7 | 35.1 | 2.2 |
| PM-5 | Benxi | 8 # | 2274.1 | 3.15 | 1.2 | 12.7 | 7.0 | 79.2 | 52 | 43.9 | 4.1 |
| PM-6 | Benxi | 8 # | 2274.4 | 3.15 | 0.8 | 12.6 | 10.1 | 76.5 | 64.3 | 26.6 | 9.1 |
| PM-7 | Benxi | 8 # | 2275.7 | 3.17 | 0.7 | 7.3 | 6.3 | 85.7 | 34.1 | 61.3 | 4.6 |
| PM-8 | Benxi | 8 # | 2276.4 | 3.21 | 1.3 | 6.4 | 6.6 | 85.8 | 58 | 38.5 | 3.5 |
| PM-9 | Benxi | 8 # | 2277.1 | 3.15 | 1.1 | 8.3 | 7.3 | 83.3 | 57.83 | 35.37 | 6.8 |
| Model | Parameters | PM-1 | PM-2 | PM-3 | PM-4 | PM-5 | PM-6 | PM-7 | PM-8 | PM-9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CO2 adsorption | DR | PV (cm3/g) | 0.065 | 0.071 | 0.076 | 0.075 | 0.075 | 0.073 | 0.084 | 0.079 | 0.077 |
| SSA (m2/g) | 182.437 | 199.568 | 214.939 | 212.133 | 211.343 | 204.318 | 236.571 | 222.042 | 216.809 | ||
| DA | PV (cm3/g) | 0.078 | 0.086 | 0.083 | 0.090 | 0.082 | 0.079 | 0.113 | 0.094 | 0.092 | |
| GCMC | PV (cm3/g) | 0.056 | 0.063 | 0.070 | 0.068 | 0.073 | 0.071 | 0.092 | 0.076 | 0.075 | |
| SSA (m2/g) | 187.447 | 205.006 | 236.368 | 227.242 | 238.084 | 230.864 | 277.147 | 250.915 | 244.416 | ||
| NLDFT | PV (cm3/g) | 0.062 | 0.066 | 0.079 | 0.078 | 0.077 | 0.075 | 0.092 | 0.081 | 0.079 | |
| SSA (m2/g) | 209.408 | 224.502 | 266.137 | 257.523 | 260.323 | 252.787 | 291.810 | 275.762 | 267.185 | ||
| N2 adsorption | BET | SSA (m2/g) | 0.269 | 0.302 | 0.305 | 0.449 | 0.515 | 0.376 | 0.173 | 0.291 | 0.454 |
| BJH | PV (cm3/g) | 0.002 | 0.001 | 0.001 | 0.002 | 0.003 | 0.002 | 0.001 | 0.002 | 0.001 | |
| SSA (m2/g) | 0.638 | 0.557 | 0.451 | 0.873 | 0.835 | 0.688 | 0.458 | 0.558 | 0.613 | ||
| NLDFT | PV (cm3/g) | 0.001 | 0.001 | 0.001 | 0.002 | 0.002 | 0.001 | 0.001 | 0.001 | 0.001 | |
| SSA (m2/g) | 0.388 | 0.349 | 0.337 | 0.522 | 0.592 | 0.449 | 0.281 | 0.390 | 0.414 | ||
| Total micropore | PV (cm3/g) | 0.059 | 0.063 | 0.074 | 0.073 | 0.072 | 0.070 | 0.086 | 0.076 | 0.074 | |
| SSA (m2/g) | 204.380 | 219.385 | 258.675 | 250.065 | 253.102 | 245.765 | 282.415 | 268.210 | 259.860 | ||
| Samples | Model | |||||
|---|---|---|---|---|---|---|
| BJH | NLDFT | |||||
| PV (cm3/g) | SSA (m2/g) | Fitting Error (%) | PV (cm3/g) | SSA (m2/g) | Fitting Error (%) | |
| PM-1 | 0.002 | 0.638 | 1.37 | 0.001 | 0.388 | 0.44 |
| PM-2 | 0.001 | 0.557 | 0.84 | 0.001 | 0.349 | 0.16 |
| PM-3 | 0.001 | 0.451 | 0.48 | 0.001 | 0.337 | 0.11 |
| PM-4 | 0.002 | 0.873 | 0.94 | 0.002 | 0.522 | 0.16 |
| PM-5 | 0.003 | 0.835 | 0.62 | 0.002 | 0.592 | 0.15 |
| PM-6 | 0.002 | 0.688 | 0.83 | 0.001 | 0.449 | 0.19 |
| PM-7 | 0.001 | 0.458 | 1.65 | 0.001 | 0.281 | 0.62 |
| PM-8 | 0.002 | 0.558 | 0.92 | 0.001 | 0.390 | 0.34 |
| PM-9 | 0.001 | 0.613 | 0.35 | 0.001 | 0.414 | 0.09 |
| Samples | Fitting Equation | Slope | Fractal Dimension | Degree of Fitting |
|---|---|---|---|---|
| PM-1 | lnJ(x) = −0.6417lnx − 1.113 | −0.6417 | 2.6417 | 0.9659 |
| PM-2 | lnJ(x) = −0.6203lnx − 1.1126 | −0.6203 | 2.6203 | 0.9643 |
| PM-3 | lnJ(x) = −5115lnx − 0.9715 | −0.5115 | 2.5115 | 0.984 |
| PM-4 | lnJ(x) = −0.6485lnx − 1.0866 | −0.6485 | 2.6485 | 0.9676 |
| PM-5 | lnJ(x) = −0.6646lnx − 1.0911 | −0.6646 | 2.6646 | 0.9858 |
| PM-6 | lnJ(x) = −0.6530lnx − 1.0800 | −0.653 | 2.653 | 0.9858 |
| PM-7 | lnJ(x) = −0.4441lnx − 0.6732 | −0.4441 | 2.4441 | 0.9946 |
| PM-8 | lnJ(x) = −0.6231lnx − 1.0348 | −0.6231 | 2.6231 | 0.9862 |
| PM-9 | lnJ(x) = −0.6195lnx − 1.0486 | −0.6195 | 2.6195 | 0.9856 |
| Samples | PV (cm3/g) | SSA (m2/g) | ||||
|---|---|---|---|---|---|---|
| <0.4 nm | 0.4–0.7 nm | 0.7–2.0 nm | <0.4 nm | 0.4–0.7 nm | 0.7–2.0 nm | |
| PM-1 | 0.0047 | 0.039 | 0.0153 | 26.66 | 145.66 | 32.06 |
| PM-2 | 0.0053 | 0.0416 | 0.0161 | 30.93 | 154.63 | 33.83 |
| PM-3 | 0.0083 | 0.0449 | 0.021 | 48.15 | 167.48 | 43.05 |
| PM-4 | 0.0073 | 0.044 | 0.0213 | 42.48 | 163.59 | 44 |
| PM-5 | 0.0085 | 0.0435 | 0.0204 | 48.86 | 162.25 | 41.99 |
| PM-6 | 0.0082 | 0.0414 | 0.0207 | 47.48 | 155.15 | 43.14 |
| PM-7 | 0.0068 | 0.0482 | 0.0308 | 38.6 | 178.78 | 65.05 |
| PM-8 | 0.0088 | 0.0465 | 0.0211 | 51.19 | 173.51 | 43.51 |
| PM-9 | 0.0084 | 0.0443 | 0.0216 | 48.94 | 165.89 | 45.03 |
| Samples | PV (cm3/g) | SSA (m2/g) | PV Proportion (%) | SSA Proportion (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Micro | Meso | Macro | Micro | Meso | Macro | Micro | Meso | Macro | Micro | Meso | Macro | |
| PM-1 | 0.0591 | 0.0011 | 0.0002 | 204.38 | 0.38 | 0.01 | 97.89 | 1.81 | 0.31 | 99.81 | 0.18 | 0.01 |
| PM-2 | 0.063 | 0.0009 | 0.0001 | 219.39 | 0.34 | 0.01 | 98.35 | 1.48 | 0.17 | 99.83 | 0.16 | 0.01 |
| PM-3 | 0.0742 | 0.001 | 0.0002 | 258.68 | 0.33 | 0.01 | 98.47 | 1.3 | 0.23 | 99.86 | 0.13 | 0.01 |
| PM-4 | 0.0726 | 0.0014 | 0.0001 | 250.07 | 0.52 | 0.01 | 97.95 | 1.92 | 0.12 | 99.78 | 0.21 | 0.01 |
| PM-5 | 0.0724 | 0.0017 | 0.0003 | 253.1 | 0.46 | 0.02 | 97.25 | 2.31 | 0.44 | 99.81 | 0.18 | 0.01 |
| PM-6 | 0.0703 | 0.0013 | 0.0001 | 245.77 | 0.44 | 0.01 | 98.06 | 1.78 | 0.16 | 99.81 | 0.18 | 0.01 |
| PM-7 | 0.0858 | 0.0008 | 0.0001 | 282.42 | 0.28 | 0.01 | 99.03 | 0.92 | 0.05 | 99.89 | 0.1 | 0.01 |
| PM-8 | 0.0765 | 0.0011 | 0.0002 | 268.21 | 0.38 | 0.01 | 98.28 | 1.43 | 0.29 | 99.85 | 0.14 | 0.01 |
| PM-9 | 0.0743 | 0.0011 | 0.0001 | 259.86 | 0.41 | 0.01 | 98.36 | 1.48 | 0.16 | 99.83 | 0.16 | 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Tian, F.; Deng, Z.; Hu, H. The Characteristic Development of Micropores in Deep Coal and Its Relationship with Adsorption Capacity on the Eastern Margin of the Ordos Basin, China. Minerals 2023, 13, 302. https://doi.org/10.3390/min13030302
Wang T, Tian F, Deng Z, Hu H. The Characteristic Development of Micropores in Deep Coal and Its Relationship with Adsorption Capacity on the Eastern Margin of the Ordos Basin, China. Minerals. 2023; 13(3):302. https://doi.org/10.3390/min13030302
Chicago/Turabian StyleWang, Tao, Fenghua Tian, Ze Deng, and Haiyan Hu. 2023. "The Characteristic Development of Micropores in Deep Coal and Its Relationship with Adsorption Capacity on the Eastern Margin of the Ordos Basin, China" Minerals 13, no. 3: 302. https://doi.org/10.3390/min13030302
APA StyleWang, T., Tian, F., Deng, Z., & Hu, H. (2023). The Characteristic Development of Micropores in Deep Coal and Its Relationship with Adsorption Capacity on the Eastern Margin of the Ordos Basin, China. Minerals, 13(3), 302. https://doi.org/10.3390/min13030302









