Mineral Prospecting Prediction via Transfer Learning Based on Geological Big Data: A Case Study of Huayuan, Hunan, China

Abstract

In the big data era, mineral explorations need to accommodate for the growth in spatial dimensions and data dimensions, as well as the data volume and the correlation between data. Aiming to overcome the problems of limited and scattered data sources, chaotic data types, questionable data quality, asymmetric data information, and small sample sizes in current mineral prospecting data, this paper improved traditional 3D prediction methods based on the characteristics and actual needs of relevant mineral prospecting data. First, for the regions with incomplete data, a new 3D prediction method based on transfer learning was proposed. Meanwhile, random noise was adopted to compensate for the limited sample size in mineral prediction. By taking the Huayuan Mn deposit in Hunan Province as the study area, 22 proposed ore-controlling variables were divided into six groups for comparative tests under different combinations, and each group was further divided into the 3D CNN prediction method and the transfer learning prediction method. After the similarities between the regional metallogenic backgrounds were proven, the convolution kernel of the Minle area was transferred to that of the Huayuan area with poor data. Then, both were used to train a 3D prediction model to realize the training and transfer of the spatial correlation between the spatial distribution of ore-controlling factors and the manganese ore. The results indicated that the accuracy of the transfer learning model in test 6 could reach 100%, with good stability of the transfer learning prediction model and a high convergence speed. By comparing the 3D-predicted targets before and after the transfer learning of tests 5 and 6, it was found that the 3D CNN model of test 5 still performed well, but the transfer learning model of test 6 was superior. In verifications based on superposition with the basin model and the growth fault model, the prediction results were consistent with the geological characteristics of the research area. To sum up, the 3D CNN prediction method has advantages in mineral prediction when big data are available, and transfer learning based on the 3D CNN algorithm helps to realize 3D deep mineral prospect prediction in the case of incomplete data.

1. Introduction

With global informatization entering the advanced stage, human beings are gradually stepping into the big data era [1,2]. As the basic information of the professional field, geological data conform to the characteristics of big data. Big data knowledge discovery technology and deep mining methods have been combined to conduct intelligent predictions and evaluations of mineral resources, where strengthening the effectiveness and accuracy of mineral prospecting prediction is the main goal in this field [3]. Recently, with the continuous development of metallogenic theories, the application of intelligent big data mining technology in geological information processing, metallogenic anomaly information extraction, and comprehensive information metallogenic prediction has significantly promoted the intelligent development of mineral prediction [4]. Existing metallogenic prediction methods can be divided into knowledge-driven methods and data-driven methods [5]. Specifically, the knowledge-driven method involves parameter assignment based on the experience of experts and the integration of multivariate information, while the data-driven method conducts a quantitative analysis based on correlation by establishing mathematical models between predictive variables and known mines. Due to the multi-source and multi-mode features of metallogenic information, especially for 3D deep metallogenic prediction, a complicated data model poses a great challenge to mineral prediction. With a relatively simple model structure, traditional machine learning algorithms are unable to achieve excellent prediction performance [6,7]. Therefore, introducing deep learning into 3D deep metallogenic prediction is significant for intelligent mineral prediction, which is also a very meaningful exploration of applying the big data intelligent algorithm in geological research [8,9,10].

The most widely used deep learning algorithms in the field of mineral prediction mainly include convolutional neural networks (CNNs) [11,12,13,14], recurrent neural networks (RNNs) [15], stack automatic coding (stack denoising automatic coding and stacked sparse autoencoder) [16,17], deep networks with a restricted Boltzmann machine as the core (deep belief network and deep Boltzmann machine) (DBN)) [18], and the fully convolutional neural network (FCN) [19]. Moreover, deep learning has also achieved breakthroughs in various applications such as logging lithology identification, seismic fracture identification [20], and earthquake time prediction [21], generating a profound impact in the field of geology. In the practical applications of mineral prediction, the combination of metallogenic theories and deep learning methods is the key to solving the problems of metallogenic prediction [22]. When conducting 3D mineral prediction, different monitoring methods are employed to collect geological, geochemical, and other spatial information from the same collection point of geological features, including mineralization information, underground mineral information, and geological evolution information. Thus, it is of great significance to apply 3D CNNs to underground space feature recognition, underground anomaly information extraction, and comprehensive prediction.

In addition, traditional linear prediction methods and nonlinear prediction methods can only be conducted with rich information on the research object, and therefore cannot effectively make predictions in the study area with incomplete databases and information. Through the transfer learning method, Zhang Ye et al. realized automatic identification and classification of rock lithology, and its robustness and generalization ability were fully proven, which accelerated the convergence rapidity, enhanced the learning efficiency of the model, and provided inspiration for solving the 3D quantitative mineral resource prediction under the conditions of asymmetric information [23]. Machine learning enables machines to autonomously mine knowledge from data to solve practical problems, while transfer learning is an important branch of machine learning, which transfers models learned in the old domain to the new domain based on the similarity of tasks, models, or data. Currently, the method has not been applied to mineral prediction, so the effectiveness of the method in the actual mineral prediction process is worth consideration, and also has great application prospects.

This paper bridges the knowledge gap in applying transfer learning to mineral prospection by using the Huayuan manganese deposits in Hunan Province, China, as an example. First, for the area with the most mineralized potential and detailed data, the 3DCNN algorithm is adopted to implement deep 3D mineral prediction on a small scale. Second, for underground 3D data with limited information in the study area, a transfer prediction method based on a similar metallogenic background is proposed. While guaranteeing the similarity of the metallogenic background in the study area, the area with the most abundant data is taken as a pre-training area, and the convolution kernel is transferred to the target study area to ensure the accuracy of deep 3D mineral prediction in the target area with incomplete data. Third, aiming to solve the universal problem of limited sample size in intelligent mineral prediction, an automatic noise generation technology based on machine learning is developed, which greatly improves the sample size of the training set without affecting the prediction accuracy and guarantees the stability of the model.

2. Study Area

2.1. Geological Background

The study area is located on the border area of Hunan and Guizhou provinces (as shown in Figure 1), and is one of the most significant accumulation areas of manganese ore resources in China. Recently, breakthrough progress has been made in manganese ore prospection [24]. As one of the most important metallogenic belts in China, there are many large- and medium-sized ore deposits in the northwest of Hunan. A comparison of the geological data between the study area and other favorable areas of sedimentary manganese ore indicates that the adjacent areas of Hunan and Guizhou provinces have a favorable environment for sedimentary manganese ore mineralization. Therefore, the geological structure pattern and the paleo-sedimentary environment of the adjacent areas of Hunan and Guizhou provinces have gradually become a research focus, and the study area becomes a vital potential area for further exploring the “Datangpo-type” sedimentary manganese ore of the Nanhua Period (728 ± 27 Ma) in China [25,26,27].

2.1.1. Stratigraphy

Numerous sedimentary rocks, containing clastic rocks and carbonate rocks, are distributed in the study area. The outlying strata include Qingbaikou, Nanhua, Sinian, Early Paleozoic Cambrian, Ordovician, Silurian, late Paleozoic Devonian, Permian strata, and a small amount of Cenozoic Quaternary alluvium (Figure 1). The strata related to mineralization in this area are mainly Nanhua strata, including the Fulu Formation, Datangpo Formation, and Nantuo Formation (Figure 2b). In particular, the Datangpo Formation mainly occurs in the central and western parts of the map area, i.e., in the Datu–Motianling–Tianjia area of Huayuan County and in the Jiulongpo–Silongshan–Buzhen area of Songtao County, Hunan Province. In addition, it is characterized by the conformable contact relationship to the underlying Fulu Formation and a thickness of 221.05 m, and it is divided into the Upper Member and Lower Member according to the lithological combination features, among which the Lower Member contains the important Mn deposits in the area. The metallogenic period of Mn deposits in this study area is dominated by the Middle Nanhua Period; consequently, the main study object is the sequence strata of the Nanhua Period. Meanwhile, the Nanhua System can be divided into five three-level sedimentary sequences mainly bounded by type I interfaces (SB1) and type II interfaces (SB2) (Figure 2b). According to an analysis of the sequence strata, the “Datangpo-type” Mn deposits mainly appear in the third sequence of the sequence strata, and the lithology below and above the interface is slate and carbonaceous shale, respectively, indicating a continuous rise in sea level. The sequence belongs to a sequence of “condensed section (CS) + highstand systems tract (HST)”, and it consists of the lower part of the Datangpo Formation.

2.1.2. Structure

The study area is located in the northwest of Hunan Province on the southeastern edge of the Upper Yangtze block. It spans two secondary tectonic units, i.e., the Upper Yangtze Block and the Jiangnan Block (the northwestern margin). With the development of folds and faults, the direction of the tectonic line is gradually deflected from NE to NE- NE to near E-W (Figure 2a). According to the structural characteristics of this area, the Upper Yangtze weak deformation belt, the Wulingshan weak deformation belt, and the Luxi Mayang transition belt can be divided into three tectonic belts from north to south.

Fold Structure

According to the crustal deformation of the main tectonic movement period, this area can be divided into four fold tectonic layers (regions): the Wuling fold layer, the Xuefeng-Caledonian fold layer, the early Yanshanian fold, and the late Yanshanian fault basin. The Xuefeng-Caledonian fold layer is the most important. The fold tectonic belt formed by this layer had its beginning in the Wuling stage. The Xuefeng stage involved an underwater uplift and depression, which was shaped in the Caledonian Stage. The Caledonian fold and its early stage are mainly distributed in the northwest margin of the Uplift block and the Jiangnan Block, forming the Guzhangfu anticline, the Motianling anticline, the Tuzha-Hekou syncline, and other large complex folds. The secondary folds in the Caledonian fold and the early Yanshanian fold are closed, synclinal, or recumbent. The Yanshanian fold is mainly distributed in the Jura fold deformation area in the northern part of the Upper Yangtze block, forming a huge mulberry syncline and later a fault basin.

(1) The Guzhangfu anticline consists of a series of secondary anticlines, and its minerals are mainly lead–zinc ore and manganese ore. (2) The Motianling anticline is located between two deep fault belts, namely the Zhangjiajie Huayuan fault belt and the Malichang fault belt, and it controls the distribution of Minle manganese deposits in the northeast direction. (3) The west of the Sangzhi polysyncline mainly produces lead–zinc ore, and it is the distribution area of Luota lead–zinc ore field, and the east Guandiping syncline is the distribution area of copper ore. (4) The Tuzha-Heku syncline is located in the southeast of the Guzhangfu anticline and the northwest margin of the Mayang Basin, and it is a depression belt with a strike of about 40°. The main structural features are folds.

Fault Structure

A long active deep fault zone has been developed in this area, which is composed of the Huayuan Zhangjiajie fault, the Jishou-Guzhang fault, the northeast Marichang fault, and a series of secondary faults. It is a broom-shaped arc fault zone spreading in the southwest direction, traversing the whole area.

(1) The Huayuan Zhangjiajie fault extends in the direction of NE and NE, with an extension length of about 230 km. The fault has an obvious controlling effect on the lithofacies and minerals on both sides. It has been proven that the fault is the main ore-guiding structure of the lead–zinc deposit in the area. (2) The Jishou-Guzhang fault, with a length of 150 km and a strike of 35°–40°, runs through the core of the Guzhangfu anticline. The fault controls the distribution of lithofacies in several sedimentary zones, and the ore-controlling action mainly shows that the manganese deposits in the Guzhang-Fenghuang area are distributed roughly parallel to the extension direction of the fault along the paraxial wing of the Guzhangfu anticline. (3) The Maclichang fault is located on the Hunan–Guizhou border at the southern end of this area, with a total length of 150 km and a general northeastward trend. This fault is the main ore transport channel of zinc mercury deposits and one of the ore-guiding structures of lead–zinc deposits.

2.1.3. Lithologic Paleogeography

Lithofacies paleogeography is an important factor controlling manganese ore in this area. In the semi-restricted manganese-bearing shale subphase in the inner part of the Bay facies, closed and semi-closed basins with poor connectively to the shallow water are formed. These basins are generally large in scale, have weak hydrodynamics, and algae organisms dominated by cyanobacteria grow and reproduce abundantly. Near the ancient land, the sources of manganese are abundant, and the lithology of shale and manganese-bearing shale is stable and thick. In addition, large to medium manganese deposits are mostly formed (such as Songtao Datang Po, Huayuan Minle, Guzhang Yezhu, etc.) (Figure 2a).

2.2. Mineralization

As Zhou Qi et al. [25] pointed out, due to the continuous effect of the cracking activity, the shallow crust fault system gradually connects the lower crust and mantle in the secondary graben basin; meanwhile, gas leaks occur along the fracture in the basin due to abiogenic gas upwelling, causing deep rich manganese rocks to form a gas–liquid rich in manganese and sulfur which arises along the fracture. Consequently, ancient natural gas seepage deposits appear in the center of the graben basin, forming rhodochroganite bodies of ancient natural gas seepage deposits. The areas extending outward from the center of the ancient natural gas leakage (generally a narrow strip) can be divided into three facies zones, central facies, transitional facies, and marginal facies, with the grade and thickness of manganese ore gradually decreasing (the reaction equation is CH₄ + SO₄²⁻ → HCO³⁻ + HS⁻ + H₂O; 2HCO³⁻ + Mn²⁺ → MnCO₃ + CO₂ + H₂O).

As the glaciers during the Ancient City Ice Age of the Nanhua Period sealed the sea water, there was no obvious stratification of the sea water. Meanwhile, the sea was a reducing environment, and manganese ions entering the sea water from the deep fault continuously accumulated to form a huge manganese pool [26] and numerous natural gas water compounds at the bottom of the deep sea. After the glacial period, with the melting of surface glaciers, the unstratified sea water gradually exhibited oxygen-rich, oxygen-poor, and anoxic stratified characteristics, and manganese ore began to deposit under the weak oxidation–weak reduction redox conditions in the bay (Songtao-Huayuan Basin). In the tidal flat lagoon basin (Guzhang, Fenghuang, and Qianyang) along the coast, the freshwater was injected with continuous land glacier melt, gradually forming a flow to the sea. Due to the impact of the density gap between the sea water and the lagoon water, the sea water circulated in the tidal flat lagoon direction. In this way, the upper water body in the tidal flat lagoon basin presented the water stratified characteristics of a light water body in the upper water layer and a thick and heavy water body in the lower layer. From top to bottom, it can be divided into a fresh water layer, a normal seawater layer, and a reduced seawater layer. Long-term hypoxia in the bottom reducing sea water layer leads to the propagation of anaerobic bacteria, and decomposed sulfate causes the accumulation of H₂S gas. Meanwhile, H₂S reacts with CO₂ in the water body to form HCO³⁻, which reacts with manganese ions brought by seawater reflux to form rhombmanganese ore (Figure 3b).

Based on the analysis results of big data models combined with field investigations, the mineral prediction models in the study area can be summarized regarding ore-induced anomalies (geology, geophysical, geochemical, and remote sensing) and ore-guided anomalies (metallogenic geological background, metallogenic period, genetic type, and mineralization type) in

Table 1. The conceptual prediction model of Songtao-Huayuan manganese deposits.

Ore Deposit Type	Factor Type	Ore-Controlling Factors
“Datangpo type” sedimentary manganese ore	Rock	Rock strata: interglacial period, thick moraine conglomerate
	Morphology of ore body	Lenticular and interlaminar
	Stratigraphic marks	Metallogenic age: Datangpo formation of the Nanhua period
		Manganese-bearing rock series outcropped
		Speculated distribution of manganese-bearing rock series
	Structural marks	Manganese-forming sedimentary basin
		Syndepositional fault
		Lithofacies paleogeography
	Geophysics	Gravity anomalies
		Gravity anomaly transition zone
	Geochemistry	Mn geochemical anomaly
		P geochemical anomaly
		Y geochemical anomaly

.

3. Research Methods

The deep learning-based quantitative delineation of metallogenic systems is conducive to the in-depth understanding of mineralization at different scales. With the new technical method of delineating the metallogenic prospect area, comprehensive information utilization, effective information mining, and quantitative description of the prospect area can be achieved. Taking the manganese ore in the Songtao-Huayuan area as an example, this paper makes 2D regional metallogenic predictions based on an intelligent algorithm and roughly delineates five metallogenic prospect areas. To further explore the mineral distribution in the study area, this study implements 3D deep metallogenic predictions based on an intelligent mining algorithm for the area with detailed data. Considering the actual situation, the 3D intelligent prediction of the study area does not traverse all possible combinations of ore-controlling factors, so comparison tests were conducted by setting different ore-controlling factor groups. According to different combinations, the twenty-two proposed ore-controlling variables were divided into six groups for comparison, and each group is further divided into the 3DCNN method and the weight-of-evidence method (WofE). Through the coupling correlation between the spatial distribution of variables and the underground emplacement space of the manganese ore body and the correlation between different ore-controlling factors, the best intelligent prediction model could be trained while eliminating the “interference” factor.

The overall framework of 3D metallogenic prediction based on the migration model proposed in this study is illustrated in Figure 4, which mainly includes four parts.

Part one: Dataset construction of the pre-training area. The pre-training area generally refers to the area with detailed data. The data collected in this study mainly include 46 prospecting line profile maps of the Minle manganese mine and the Huomachong mining area, 90 map sections of the Minle manganese mine, 212 pieces of borehole data, the 1:100,000 lithofacies paleogeographic map of the Songtao-Huayuan area, the 1:10,000 topographic geological map of the Minle Manganese mine area, the 1:50,000 Heku geological map and Malichang geological map in western Hunan, Aster remote sensing data with a resolution of 30 m, and the detailed geological survey report of the Minle manganese mine. These data provide a strong basis for constructing a 3D digital model in the mining area. The data preprocessing procedure has been described in the previous section and will not be repeated here. To ensure the spatial similarity between the pre-training area and the target mining area, the overall shape and block proportion of the pre-training area should be consistent with the target area. Additionally, the attribute information of each block model should be consistent. Moreover, to ensure the effectiveness of the research, it is better to compare the conceptual model of the pre-training area with that of the target area and determine whether the key ore-controlling factors are consistent before training.

Part two: Convolution kernel training in the pre-training area. The transfer learning method adopted in this study outputs and transfers the parameters of the two convolution layers of the model by training with data of the pre-training area. As there are no relevant parameters in the pooling layer and dropout layer of the model, only the parameters of the convolution layer need to be transferred. Among the preprocessed positive and negative samples, 80% are taken as the training set and 20% as the validation set. To enhance the validity of the model, this study enlarges the sample size by adding random noise. The block model is stored in a central point way. Each centroid point is expanded in all directions by 5 points, respectively, which is composed of 11 × 11 × 11 particles. Different attributes of each sample block are input into the model, and the spatial distribution characteristics of the factors in the detailed data area are exploited to train the convolution kernel of the model by utilizing the excellent spatial feature extraction ability of the network structure.

Part three: Convolution kernel migration and prediction for the target study area. The dataset construction method for the target study area has been described in the previous section and will not be repeated here. The framework of the migration model is consistent with that of the pre-training model. The parameters of the pre-trained two-layer convolution kernel are output and visualized and then transferred to the model of the target study area for model verification. The potential correlation of spatial distribution of all input ore-controlling factors and the mineralization is implied. Finally, two classes of scores, namely the ore-containing score and the ore-free score, are obtained for each test sample on the target test set by the migration model, respectively.

Part four: Output result prediction and model evaluation. The output score of the fully connected layer is normalized by the Softmax layer, and finally, a score between 0 and 1 is obtained, which is the ore-containing and ore-free probability. Two indexes, i.e., accuracy and loss, are used to test the classification accuracy of 3D CNN models under different factor combinations. Meanwhile, the ROC curve and the confusion matrix are applied to evaluate the accuracy of the prediction model. By comparing the model evaluation results under different factor combinations, the best combination of predictive factors is obtained, and the corresponding prediction results are output. The position of each block is determined by coordinates for 3D model visualization.

Through the above technological method, the mineral prediction data in the study area with incomplete information, and the space distribution characteristics of the area with rich data, the potential relevance of the training classification model can be intelligently processed, thus allowing for deep mining predictions in the target study area and obtaining the localization and probability from the 3D prediction process.

3.1. Construction of Large Spatial Database

In the study of metallogenic prediction, the accurate, systematic, and comprehensive sorting of basic data in the study area is the basis and premise of model construction. The basic data of the study area during the preparation stage of the metallogenic prediction study should be collected and sorted and a detailed basic database of the study area needs to be constructed, thus laying the foundation for establishing an accurate model in the follow-up work. The basic data in the study area mainly consist of text data, two-dimensional data, and three-dimensional data.

To address the issue of incomplete basic geological data in the study area, the study area was divided into the “2D prediction area”, the “3D deep learning area”, and the “3D migration learning area” according to the actual degree of detail of the basic data in the study area, corresponding to the Songtao-Huanyuan area, the Huayuan area, and the Minle area, whose relative 2D and 3D positions are shown in Figure 1. Specifically, Area A is a two-dimensional prediction area (Songhua-Huayuan), Area B is a three-dimensional deep learning area (Huayuan), and Area C is a three-dimensional transfer learning pre-training area (Minle). The degree of detail of the basic data in the three areas increases successively. All the data collected in each area were sorted to construct the spatial datasets of the three areas. Then, the spatial datasets of the three areas were integrated into the basic database of the study area. The spatial data after collation are listed in

Table 2. The collected data in the Songtao-Huayuan 2D prediction area.

Data Name	Scale	Number	Investigation Depth (m)
Statistical table of geochemical element content	1:200,000	39	Earth’s surface
Geochemistry mapping	1:200,000	20	Earth’s surface
Geological and mineral map of the Songtao-Huayuan area	1:200,000	1	Earth’s surface
Lithofacies paleogeography map of the Datangpo period in the Songtao-Huayuan area	1:100,000	1	Earth’s surface
Distribution map of the Datangpo Formation in the Songtao-Huayuan area	1:100,000	1	Earth’s surface
Sedimentary tectonic map of the Songtao-Huayuan area	1:100,000	1	Earth surface
Residual gravity anomaly map in the Songtao-Huayuan area	1:100,000	1	-
MT profile inversion map	1:100,000	2	4000

Illustrate: ”-” in Table 2 means there is no depth data of residual gravity anomaly map in the Songtao-Huayuan area.

,

Table 3. The collected data in the Huayuan 3D deep learning area.

Data Name	Scale	Number	Investigation Depth (m)
Prospecting line profile map of Minle	1:2000	46	700
Geological map of Heku and Malichang in the Huayuan area	1:50,000	1	Earth’s surface
Borehole data of the Minle Mn mine	-	212	660
Lithofacies paleogeography of the Datangpo period in the Songtao-Huayuan area	1:100,000	1	Earth’s surface
Schematic diagram of the cut section design	1:50,000	1	Earth’s surface
Map cut profiles of the Minle Mn mine	1:50,000	23	1500
DEM data	Aster30m	1	Earth’s surface

Illustrate: ”-” in Table 3 and Table 4 means there is no scale of borehole data.

and

Table 4. The collected data in the 3D transfer learning area of Minle.

Data Name	Scale	Number	Investigation Depth (m)
Borehole data of the Minle Mn mine	-	212	660
Prospecting line profile map of Minle	1:2000	46	700
Lithofacies paleogeography of the Datangpo period in the Songtao-Huayuan area	1:100,000	1	Earth’s surface
DEM data	Aster30m	1	Earth’s surface
Topographic geological map of the Minle Mn mining area	1:10,000	1	Earth’s surface
Schematic diagram of the cut section design	1:10,000	1	Earth’s surface
Map cut profiles of the Minle Mn mine	1:10,000	90	700

Illustrate: ”-” in Table 3 and Table 4 means there is no scale of borehole data.

.

3.2. 3D Modeling and Prediction Layer Construction

Guided by the intelligent prospecting theory of cognitive maps and combined with various data mining methods, this study aims to conduct multi-scale metallogenic prediction for the Songtao-Huayuan manganese deposit area. A 2D regional metallogenic prediction based on the Alexnet network is carried out in Area A (Songtao-Huayuan), and a 3D deep metallogenic prediction is implemented by the 3DCNN algorithm combined with borehole data and the section data in Area B (Huayuan). With further progress in mineral prediction, it was observed that there are incomplete data in the 3D modeling area of Area B. This study employed Surpac software to explicitly model the variables related to mineralization. Most of the exploration lines and borehole data are concentrated in Area D (Figure 1). Therefore, to obtain a better quantitative prediction of mineral resources and improve the prediction efficiency, the unknown hidden information of geological mineralization needs to be explored deeply. This study optimizes the basic principle of the classical convolutional neural network and takes Area C (the Minle mining area), which has a similar metallogenic background and metallogenic mechanism as the pre-training area, and applies a transductive transfer learning method to transfer the convolution kernel of the deep neural network for the pre-training area to the target study area, i.e., area B (the Huayuan mining area). Thus, the improved CNN contains the potential spatial correlation between the ore-controlling factors and the ore body in the training area, and this spatial distribution correlation can be transferred to the target study area. From another point of view, due to the diverse and complex geological characteristics, and their spatio-temporal variation, it is difficult to embed the quantitative study of the algorithm into the convolution kernel to improve the metallogenic characteristics of the training. The CNN algorithm is superior in efficiency and simplicity as a result of the shared weight. If the convolution kernel is changed directly, a simple model will involve hundreds of thousands of weight factors. In this case, the model cannot be operated manually due to the significant calculation amount. However, the model-based migration method overcomes this difficulty. When there is incomplete information between deep and shallow data in the study area, this method can still be used to transfer the convolution kernel from the rich data area to the poor data area.

Additionally, to solve the problems of limited training samples in metallogenic prediction, the loss of geological meaning, and the increase in CNN training difficulty caused by the traditional data extension method, this paper proposes a data expansion method suitable for the prediction of metallogenic prospect areas, which not only retains most spatial features of the data but also solves the problem of limited sample data. Hence, the convergence speed of the model is improved and the metallogenic prediction accuracy of the Songtao-Huayuan 3D modeling area is enhanced.

3.2.1. Modeling of the Pre-Training Area

The data collected in area D (the Minle mining area) include 46 pieces of prospecting line profile maps, 90 pieces of map cut profiles, 212 pieces of borehole data, a 1:100,000 lithofacies paleogeographic map of the Songtao-Huayuan area, a 1:10,000 topographic geological map of the Minle manganese deposit area, a 1:50,000 Heku-Mali geological map of the western Hunan area, Aster remote sensing data with a resolution of 30 m, and a detailed geological survey report of Minle manganese deposits, which provide a powerful tool for constructing a 3D digital model of the mining area.

According to the existing data of the Minle mining area and the prospective geological model constructed above, this study establishes 3D models for the surface, fractures, ore body, Nantuo moraine layer, and Datangpo area in the study area based on different ore-controlling factors (such as structure, ore body, and stratum) and constructs an prospective ore digital model for the Minle mining area (

Table 5. The prospective ore model for the Minle mining area.

Ore-Controlling Factors	Metallogenic Geological Anomaly	Ore Prospecting Digital Model
Stratum	The stratum of the Datangpo Formation	Stratum digital model of the Datangpo Formation
Rock stratum indicator	The thick moraine conglomerate, as the top plate of the ore bed, can indicate the mineralization	Digital model of the Nantuo moraine layer
Structure	Deep fracture and tectonic convergence (submarine volcanic eruption, sedimentary manganese deposit, and ancient natural gas leakage)	Fracture digital model
Lithofacies paleogeography	The secondary rift basin	Digital model of the basin control fracture and basin margin fracture
Ore body	The manganese ore body	3D digital model of the manganese ore body

). Since the borehole in Minle mining area has not hit any fractures, all the fracture entity models in this area are constructed according to 46 exploration line profiles and the topographic geological map of the Minle mining area.

Some ore-controlling factors, such as finer sub-members, sequence stratigraphy, and geomorphology under the Datangpo Formation in the Minle mining area, cannot be expressed by 3D digital models, so this study adopts 3D reconstruction mainly for the subparts of the ancient landform, the manganese-bearing rock series, the sequence stratigraphy, and the Datangpo Formation (

Table 6. 3D spatial reconstruction of the Minle manganese mine.

Ore-Controlling Factors	Metallogenic Geological Anomaly	3D Spatial Reconstruction of Metallogenic Anomaly
Stratum	Sub-members under the Datangpo Formation	3D spatial reconstruction of the lower sub-members under the Datangpo Formation
		3D spatial reconstruction of the medium sub-members under the Datangpo Formation
		3D spatial reconstruction of the upper sub-members under the Datangpo Formation
Sequence stratigraphy	Favorable third-sequence stratigraphy	3D spatial reconstruction of the condensation layer
		3D spatial reconstruction of the high-stand domain
Rock stratum indicator	Favorable rock stratum indicator	3D spatial reconstruction of manganese-bearing rock series
Lithofacies paleogeography	Favorable sedimentary facies	Secondary rift basin
Ancient landform	Ancient landform of the geological evolution period related to mineralization	3D spatial reconstruction of the ancient landform

).

3.2.2. Construction of 3D Pre-Training Layer

The Minle manganese ore block model was constructed according to the statistics of the data in the study area combined with the digital model of the surface range (Figure 5). To guarantee the smooth progress of transfer learning, the total number of model blocks in the small block model should be consistent with the large block model, and thus the unit block size was set to 25 m × 25 m × 25 m. The model includes 2,606,100 blocks, of which the total number of positive samples is 1560 blocks and the total number of negative samples is 1450 blocks, and each unit block is endowed with the attributes in the prospective geological model (modeling area X_max = 635,975, X_min = 630,025; Y_max = 3,147,062, Y_min = 3,137,937; Z_max = 450, Z_min = −350).

According to the 3D weight of the evidence method, the evidence weight of each factor in the study area is shown in

Table 7. The evidence weight of Minle manganese mine variables.

Predictor Numbers	Evidence Item	W+	W-	C
Predictor 1	The third sequence	4.337955	1.802756	2.5352
Predictor 2	Datangpo Formation	3.620267	1.877229	1.743037
Predictor 3	Favorable metallogenic buffer zone of the Nantuo moraine layer	4.367813	−0.36435	4.732164
Predictor 4	Interlaminar anomalous body of ancient landform of Datangpo Formation	3.546471	−7.98981	11.53628
Predictor 5	Interlaminar anomalous body of ancient landform of Nantuo Formation	2.821807	2.024608	0.797199
Predictor 6	Interlaminar anomalous body of ancient landform of Nanhua Period	2.866911	1.833689	1.033222
Predictor 7	Fault	2.861902	1.564909	1.296994
Predictor 8	50 m Fault buffer	2.776001	1.329269	1.446732
Predictor 9	100 m Fault buffer	2.673975	1.17519	1.498785
Predictor 10	150 m Fault buffer	2.535793	0.878388	1.657405
Predictor 11	200 m Fault buffer	0.687016	2.197602	−1.51059
Predictor 12	250 m Fault buffer	2.535793	0.878388	1.657405
Predictor 13	Interlaminar anomalous body of ancient landform of Fulu Formation	2.535793	0.878388	1.657405
Predictor 14	300 m Fault buffer	2.264051	2.09229	0.171761
Predictor 15	350 m Fault buffer	0	0	0
Predictor 16	Equidensity	2.540403	2.085783	0.45462
Predictor 17	Azimuth anomalous degree	2.624474	2.092335	0.532139
Predictor 18	Anomalous azimuth	2.2477	2.091067	0.156634
Predictor 19	Centrosymmetry degree	0	0	0
Predictor 20	Normalization frequency	0	0	0
Predictor 21	Number of normalization intersections	4.337955	1.802756	2.5352
Predictor 22	Nantuo moraine layer	3.620267	1.877229	1.743037

, which intuitively reflects the relationship between various factors and mineralization.

The process of 3D modeling and construction of the prediction layer of the target study Area B (Huayuan mining area) has been described in the previous research [29].

3.3. 3D CNN Modeling

3.3.1. 3D CNN Algorithm

Generally, 3D CNN adopts 3D convolutional layers, 3D pooling layers, and dense layers to extract images, and then it obtains a score by connecting a Softmax layer [30,31]. In addition, each layer has several channels, and each channel represents a type of feature. In a 3D CNN, convolution and pooling is actually a cubic 3D characteristic block. Unlike 2D features, 3D features are presented as a set of neurons in a 3D form. In this study, the 3D spatial distribution of the 22 ore-controlling factors is taken as the input of the 3D CNN prediction model, then the ore-bearing probability of each voxel can be obtained after the processing of two convolutional layers and two pooling layers, as well as the flatten layer, dropout layer, dense layer, and Softmax layer (Figure 6). The specific principle of the 3D CNN model has been shown in previous research [29].

The super-parameter settings for each layer of the 3D CNN model adopted in this study is shown in Figure 7. (1) The first layer (convolutional layer): the size of the convolutional kernel = [5,5,5], stride = [1,1,1], output channel = 32, and padding = same (expanded edge, the input equals to the output). (2) The second layer (pooling layer): pool_size = [2,2,2], stride = [2,2,2], output channel = 32 (default), and padding = same. (3) The third layer (convolutional layer): the size of the convolutional kernel = [5,5,5], stride = [1,1,1], output channel = 32, and padding = same. (4) The fourth layer (pooling layer): pool_size = [2,2,2], stride = [1,1,1], output channel = 32, and padding = same. Each convolutional layer contains the ReLU activation function, and subsequently the downsampling operation (i.e., pooling processing). As the activation function of the CNN, ReLU outperforms Sigmoid in terms of the verification effect in the deeper network, and it can solve the gradient diffusion problem faced by Sigmoid in the deeper network. Subsequently, the output results of the 3D CNN are fed into the dense layer after the flatten operation, and the process of preventing overfitting of the dropout layer is imposed on the subsequent dense layers. Finally, the ore-bearing probability and non-ore-bearing probability of each block can be obtained through the Softmax operation.

3.3.2. Localization and Probability Determination

By acquiring the coordinates of the prediction results, the predicted ore-bearing areas and the areas developing known deposits (occurrences) are given different colors for outputting, and the output results are saved in the CSV format. Meanwhile, the ore-bearing probability can be determined by the Softmax activation function, where the details are described in Section 3.2.1. However, the Softmax activation function can only be applied to a neuron with more than one output, and it guarantees that the sum of all the output neurons is 1.0, so the output is a probability value less than or equal to 1, which makes it easy to compare various output values. Regarding $P_k$ as the ore-bearing or non-ore-bearing “probability”, for example, if the output of type A “ore-bearing” is 0.8, it can be considered that the ore-bearing probability of the area delineated by the prediction model is 80%.

3.4. Transfer Learning Model

Compared with machine learning’s automatically exploration of knowledge from data to address instant issues, transfer learning, as a significant branch of machine learning, is the process of transferring a model from the previous domain to a new one in accordance with the similarity of the task, model, or data. Since data or tasks are correlated in applications, the already trained model parameter (knowledge) is transferred to a new model to increase its convergence speed and learning efficiency, and the new model does not start from scratch. Zhang Ye et al. realized the automatic identification and classification of rock lithology with transfer learning, which provided a new approach for the automatic classification of rock lithology, and its robustness and generalization abilities were verified [23]. The most important issue of transfer learning lies in the detection of the similarity of two domains, and the task can be completed after similarity confirmation.

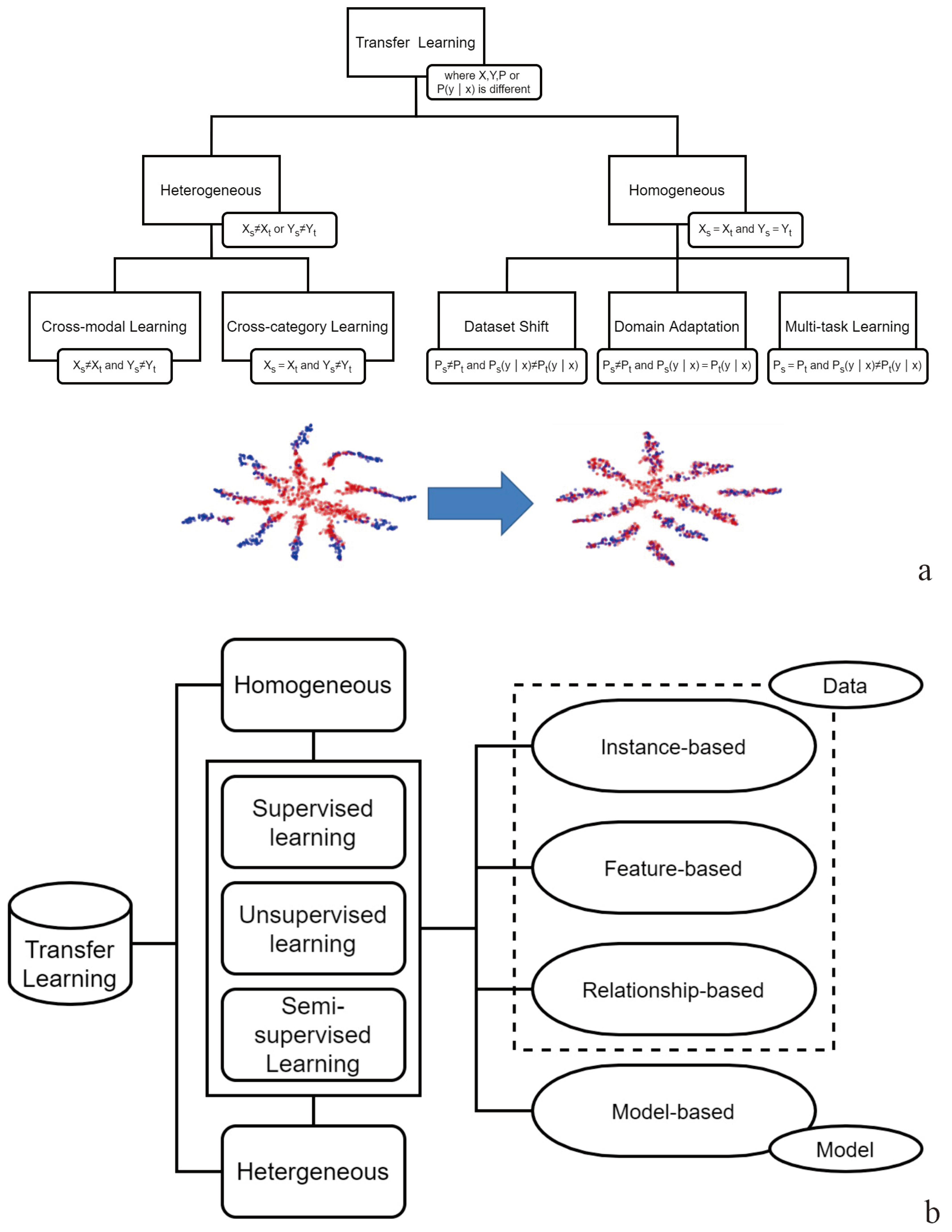
The domain and task are two important concepts of transfer learning; the former is identified as a special field and data features differ in different fields, and thus the task can be considered the target of business scenarios. For instance, emotion recognition and automatic question answering are two different tasks. Thus, data for different tasks may originate from different domains. Transfer learning is a type of solution philosophy rather than a specific algorithm. The detailed transfer learning process comprises two steps: (1) pre-training is conducted on the model based on super-sized data and (2) fine adjustment (on weight or terminal structure) is performed according to a specific task. There exists heterogeneous transfer learning and isomorphic transfer learning, named for whether the feature space and label space are identical (Figure 8a). According to the method used, there is instance (sample)-based transfer learning, feature-based transfer learning, parameter (model)-based transfer learning, and relationship-based transfer learning (Figure 8b). In this study, model-based transfer learning is adopted for mineral prediction.

3.4.1. Sample Data Expansion

Data expansion refers to the application of a series of deformations on a group of marked training data to obtain diversified training data for sample expansion. Many sample expansion methods have been proposed, including flipping and rotation [32], shearing and scaling [33], and changing the intensity of the RGB channel [34]. The most important principle of sample expansion is that the adopted deformation will not change the label meaning of the sample [35], the frequently used data expansion methods such as flipping and rotation of geological data may change the data direction. These methods are likely to generate a new direction of faults and intrusive rocks, which are either irrelevant to mineral deposits or beyond the study area. Consequently, such expansion seems to be invalid and may increase the training difficulty of the CNN prediction model.

A sample expansion method for metallogenic prediction is proposed in this study which ensures the diversification of expanded data and maintains the geological meaning. The basic principle of such a method is to add random noise to the sample data while reserving the geological meaning of the data. In contrast to most previous metallogenic prediction research, CNN focuses on spatial distribution and data correlation instead of the value of a specific point. Thus, most spatial data features contain noise, and there are insufficient training samples for metallogenic prediction driven by data. Unlike picture processing, the data in mineral prediction are hindered by geological meanings. For instance, a ridiculous scenario of significant spatial difference between two neighboring points and a specific fault may appear. Therefore, this study proposes an approach to expand sample data based on random noise, and its validity in the CNN model has been previously proven [36]. This study has made some modifications, and the principle of the proposed approach is presented in Figure 9:

Step 1: The dropout value of the noise scale is set to 20.0% in this study. Step 2: Sample data are captured as shown in Figure 9; the step is set to 100, batch_size is 32, and the sample number is 0–65. There are 66 recognized samples in total, 32 of which are randomly iteratively selected. Step 3: Random noise samples are developed, and Gaussian distribution is applied to acquire noise distribution. A total of 20% of all samples are in the study area, and 32 samples iteratively selected each time are imposed with random noise distribution to develop 32 new random samples, 80% of which are adopted as training data and the rest are verification data. Steps 2 and 3 are repeated, and the maximum step*batch-size samples will be obtained until there are sufficient positive and negative samples to train the CNN model.

3.4.2. Operating Characteristic Curve

As one of the visible methods to evaluate the performance of classifiers, the receiver operating characteristic curve (ROC) is widely used in geochemical anomaly and mineral resource qualitative prediction [37,38,39,40]. The abnormal distribution of model prediction is compared with known mineral deposits (points), and their spatial relationship is measured generally by statistical indicators such as AUC (area under the curve), ZAUC (Z-area under the curve), etc. Figure 10a shows the spatial relationship between the predicted classification result and mineral distribution in four categories: (1) mineral exists in reality and in the prediction (TP); (2) mineral exists in reality but not in the prediction (FN); (3) mineral exists in the prediction but not in reality (FP); (4) mineral neither exists in reality nor in the prediction (TN). Finally, a confusion matrix is established, as shown in Figure 10b.

In the ROC, different threshold values are defined and one threshold is selected each time to obtain an FPR (False Positive Ratio) and TPR (true positive ratio), with the former on the horizontal line and the latter on the vertical line, connecting numerous points to develop the blue curve in Figure 10a. The calculation formulae of FPR and TPR are shown below [42]:

$$FPR=\frac{FN}{N},TPR=\frac{TP}{P}$$

(1)

In the ROC shown in Figure 11a, the red dummy line linking (0, 0) and (1, 1) is random, the point (A) equates to a random process when TPR = FPR, and the point (B) above the line indicates that TPR > FPR, where the probability that the mineral exists in both reality and in the prediction is higher than that of the mineral existing in the prediction but not in reality. The closer the ROC approaches the point (0, 1) in the upper-left corner, the better the prediction efficiency of the prediction model towards predicting known mineral deposits (points).

To conduct a qualitative evaluation of classification performance, the AUC formed by ROC and the coordinate, e.g., the gray part in Figure 11b, can be calculated. Then, the predicted results of the model can be qualitatively compared based on the AUC [43]; an AUC of >0.5 indicates better prediction results than the random process and an AUC of <0.5 indicates a better random process than the predicted results. The higher the value, the better the prediction results [44]. The calculation formula of the AUC is as follows:

$$AUC=\frac{1}{p\times n}{\sum }_{i=1}^p{\sum }_{j=1}^n\phi \left(x_i,y_j\right)$$

(2)

where, $\phi \left(x_i,y_j\right)=\left\{\begin{array}{c}1,x_i>y_j\\ 0.5,x_i=y_j\\ 0,x_i<y_j\end{array}\right.$.

The calculation formula of the AUC standard deviation, $S_{AUC}$, is as follows:

$$S_{AUC}=\sqrt{\frac{AUC\left(1-AUC\right)+\left(p-1\right)\left(Q_1-{AUC}^2\right)+\left(n-1\right)\left(Q_2-{AUC}^2\right)}{p\times n}}$$

(3)

where, $Q_1=\frac{AUC}{2-AUC},Q_2=\frac{2{AUC}^2}{1+AUC}$This study performs a comparative analysis of the performance of the transfer learning model and the 3DCNN model under different factor combinations via the ROC and the confusion matrix to determine the optimal factor combination and prediction method.

4. Results and Discussion

This study employs a transfer learning method to transfer the pre-training area to the output and transfer the two convolution parameters of the model. As the parameters of the pooling and dropout layers in the model are irrelevant, only the parameters of convolution need to be transferred. A total of 80% of pre-processed positive and negative samples are taken as the training set and the remaining 20% are used as the validation set. Meanwhile, random noise is added to increase the sample size for higher model validity. The block-model-centered storage extends the center of mass forwards, backward, left, and right by 5 points, leading to 11 × 11 × 11 mass points. Different attributes of each sample block are input into the model, and the convolution kernel of the model is trained by the distribution feature of space elements with the assistance of the outstanding spatial characteristic extraction capability of such a network structure.

The pre-trained parameters of two convolution kernels are output and visualized to perform model verification after they are transferred to the target study area. In this process, the potential links between the spatial distribution of all inserted ore-controlling factors and metallogeny are included. For each test sample, two values (containing minerals and not) are obtained by the transfer model for the target test set. The pre-trained convolution kernel is rendered according to weight, and the size of each convolution kernel is 5 × 5 × 5, with the input channel shown in Figure 6 (the structure of the 3DCNN prediction model), where there are 22 prediction stratums and 32 output channels in total. Therefore, 176,000 weight factors of convolution kernels are output, and they are arranged as a 5 × 5 × 5 cubic, as shown in Figure 12.

4.1. Comparison of Different Factor Combinations

A contrast test was carried out on six groups of twenty-two ore-controlling factors, with comprehensive prospecting prediction applied by transfer learning and the 3D CNN to obtain the optimum ore-controlling factor combinations by comparing the training accuracy, training loss, validation accuracy, and validation loss of the prediction models trained on different factor layers, with the results shown in

Table 8. Comparison of model indicators in the group test.

No	Prediction Factors/pcs	3D Prediction Layers Combination	Network Size/m	Iteration Frequency/Times	Training Accuracy	Training Loss	Validation Accuracy /%	Validation Loss
1	22	1–22	100 × 100 × 100	215	100%	0.000021	100%	0.000116
2	21	1–21 (remove 22)	100 × 100 × 100	215	100%	0.000203	100%	0.000299
3	15	1–15 (remove 16–22)	100 × 100 × 100	215	100%	0.000576	100%	0.000741
4	13	1–13 (remove 14–22)	100 × 100 × 100	215	100%	0.000004	100%	0.000099
5	12	1–12 (remove 13–22)	100 × 100 × 100	215	100%	0.000105	100%	0.000079
6	6	1–6 (remove 7–22)	100 × 100 × 100	215	100%	0.000022	100%	0.000022

. Meanwhile, a comparative analysis was conducted on transfer learning, and the prediction results of the 3D CNN were exploited to evaluate the feasibility and superiority of transfer learning methods in 3D metallogenic prediction.

Based on the evaluation of six groups of prediction models under transfer learning and the development of the confusion matrix and ROC curve of these models, it is indicated that the ROC curves of all models approach the upper-left corner point (0, 1), demonstrating the excellent prediction performance of these models towards known mineral deposits (points). Then, a qualitative evaluation of classification performance was realized by the AUC formed by the ROC and the coordinate (Figure 13). The AUC values of all six groups of prediction models are above 0.5 and close to 1, indicating that the prediction models are appropriate because of their advantages over random models in terms of prediction capacity. Specifically, the best and worst prediction performances were obtained in test 6 and test 4, respectively, with the latter’s AUC equaling 0.978 with the factor combination 1–13. Compared with test 4, test 5 deletes factor 13 of the Fulu Fm ancient landform interlayer anomalies, and it exhibits a stronger prediction ability.

According to a comparison analysis (Figure 14) of the training loss, training accuracy, validation accuracy, and validation loss of the six groups of transfer learning models, it can be observed that the curve of the final model reaches convergence, and the loss value approaches 0. The highest training accuracy and validation accuracy reach 100%, and they are obtained in test 6, which shows the optimum prediction performance and stability, with the factor combination ranging from 1–6 (the third sequence, the stratum of the Datangpo Formation, the favorable metallogenic buffer zone of the Nantuo moraine layer, the interlaminar anomalous body of the ancient landform of the Datangpo Formation, the interlaminar anomalous body of the ancient landform of the Nantuo Formation, and the interlaminar anomalous body of the ancient landform of the Nanhua Period). Among these six tests, the worse prediction performance appears in test 1, and in this test, the training accuracy was 93.75%, the validation accuracy was 87.5%, the training loss was 0.1965, and the validation loss was 0.1240 when the factor combination ranged from 1–22, indicating that interference factors affect the test results in 22 ore-controlling factors.

4.2. Comparative Test on 3DCMM and TL

By plotting the success rate curves and ore-controlling rate curves, this study further quantitatively evaluated the performance of the 3D CNN model and the 3D CNN-TL model (Figure 15). It is worth mentioning that there are differences between the predicted results and the results obtained by the calculation method of the 3D CNN, since both models have generated random noise via a Gaussian distribution to increase the sample quantity. The calculation process of the success rate is described as follows: firstly, the predicted ore-bearing probability of all the blocks in descending sequence is obtained and the blocks with the predicted ore-bearing probability greater than or equal to 0.5 are extracted. Then, the extracted probability is reclassified by setting various thresholds. Finally, the success rate is calculated by conducting statistics on the number of known blocks in various segments [45]. The calculation process of the ore-controlling rate involves conducting statistical analyses and calculations of all blocks in the study area.

In Figure 15a,d, the success rate curves and ore-controlling rate curves of 12 tests are presented, indicating that the success rate of the CNN model (3D CNN-TL) in tests 1–5 exceeds 70% at a threshold value of 10% after transfer learning, while only the last three tests for the 3D CNN model reach a similar level. In other words, the first 10% of minerals predicted by the 3D CNN-TL model cover more than 70 known minerals. It is obvious that the 3D CNN-TL outperforms the 3D CNN in the predicted results, and there is a big discrepancy in the convergence of different tests and a significant difference in the growth of convergence. In contrast, the convergence of the 3D CNN-TL model is much smoother, and the overall tendency of factors in different groups is similar. Under the influence of Gaussian noise, the 3D CNN-TL model maintains stable predictions with strong robustness (Figure 15b–c). A comparative analysis on different test groups indicates that test 4 and test 5 achieve the best performance regardless of the model. The ore-controlling factor combinations for test 4 are 1–13 while for test 5, they are 1–12.

In Figure 15d, the ore-controlling rate curves reveal that the ore-controlling rate exceeds 95% at a threshold value of 10%. To further investigate the differences in all 12 tests, this study analyzed the variation tendency (Figure 15e–f) of ore-controlling rates in different tests by selecting the ore-controlling rate between 95% and 100%. In Figure 11f, all known ore body blocks are contained in the blocks of the top 20% with ore-bearing potential in the 3D CNN-TL, while only 98% of blocks are included in the blocks of the top 20% with ore-bearing potential in the 3D CNN. The prediction result of the 3D CNN model includes all known ore body blocks only when the threshold value reaches 30%. However, the convergence rapidity of TL-6 is slower than other groups regarding the success rate curves and ore-controlling rate curves in transfer learning models. Therefore, ore-controlling factors containing 1–6 in test 6 may be unsuitable for applications in transfer learning models.

To sum up, the transfer learning prediction model demonstrates high stability and convergence rapidity, since five tests achieve a good performance. The exception is test 6, which has lower convergence speed but the highest prediction accuracy of 100%.

Based on a comparative analysis of the prediction probability distribution and prediction results of the 3D CNN model and the WofE model with different ore-controlling factors in six groups, it can be concluded that the 3D proof layers 1–12 and 1–6 included in test 5 and test 6 contribute to a superior performance. Three-dimensional metallogenic prospects (Figure 16 and Figure 17) were developed by 3D CNN and 3D CNN-TL prediction models using the same dataset, block size, and variable. On the Earth’s surface, the blocks of a high probability rate are mainly distributed in places where Datangpo formation appears (Figure 16a,b and Figure 17a,b). In profile, the known ore bodies of test 5 and test 6 are firmly embraced in blocks with a 3D CNN prediction probability ranging from 0.8–1.0 (Figure 16c,e and Figure 17c,e). The predicted ore is widely distributed, while the probability of other non-predicted areas is much lower. However, there are many seriously faulted predicted ore blocks under the probability range of 0.5–0.7 in the transfer learning results of test 5. This is because prediction factors 7–12 are faults and different areas of fault buffer zones, which affect the predicted results of the model. Thus, the predicted results of test 6 are better, where the combination of ore-controlling factors is 1–6 (the third sequence, the stratum of the Datangpo formation, the favorable metallogenic buffer zone of the Nantuo moraine layer, the interlaminar anomalous body of the ancient landform of the Datangpo formation, the interlaminar anomalous body of the ancient landform of the Nantuo formation, and the interlaminar anomalous body of the ancient landform of the Nanhua Period). However, the 3D CNN performs better under the same factor conditions, as shown in Figure 16b–f. After integrating the predicted results of ore bodies based on an intelligent algorithm with 12 ore-controlling factor layers, it can be seen that predicted ore bodies exist in the third sequence (the stratum of the Datangpo formation, the favorable metallogenic buffer zone of the Nantuo moraine layer, the interlaminar anomalous body of the ancient landform of the Datangpo formation, the interlaminar anomalous body of the ancient landform of the Nantuo formation, and the interlaminar anomalous body of the ancient landform of the Nanhua Period) and beside faults. Thus, these blocks are areas of high prospective potential (Figure 16g,h and Figure 17g,h).

Further study on test 6 with a better prediction effect (Figure 17) indicates that the prediction results of the non-transfer learning model are relatively disperse (Figure 17b–f) due to a large number of predicting blocks and the absence of known ore blocks in some of the high-valued areas. In comparison, the prediction of the transfer learning model is concentrated, and the predicted area includes ore blocks, while known ore areas extend peripherally. Therefore, the transfer model is advantageous in prediction under the factor combinations of test 6.

To sum up, ore-controlling factors of 1–6 are superior, while those of 1–12 in the fault layers significantly affect the learning results. The 3D CNN model performs well with no disturbances and realizes accurate prediction. With the ore-controlling factor combinations of 1–6, the transfer learning model is better because of the scarcity and concentration of high probability blocks predicted. Thus, the 3D prediction method based on transfer learning in this study is feasible and accurate.

4.3. Comprehensive Analysis of Prediction Results

According to a study on the genetic types of Datangpo-type manganese ore in the Huayuan area, the metallogenic model of ancient manganese ore gas leaks in the rift basin is one of the most important genetic types in this area [25]. The location of ancient natural gas vents has a significant effect on the formation and production location of this type of manganese ore. The deep and large faults can serve not only as a favorable location for the ancient natural gas vents but also as the most favorable channel for hydrothermal migration and storage. Based on speculation, the growth fault model of the Nanhua Period is established in this study. In addition, the deep rift basin is responsible for the abundance of manganese sedimentary ore in Hunan and Guizhou. Therefore, the fault basins analyzed based on lithofacies were compared with the geophysical exploration data, the five basins were finally determined, shown in the following figure, and 3D models were constructed (Figure 18a,b). However, the basin model and the growth fault model were established on the speculation of geological and geophysical materials, and thus cannot be applied as a variable (3D pre-training layers) in intelligent prediction, so overlaying the geological model with the predicted results has a certain validation significance.

After integrating the prediction results of test 5, which achieves the optimal model performance with the 3D CNN algorithm, with those of test 6, which achieves the best performance in transfer learning with the predicted growth faults and manganese basins (both are indispensable metallogenic factors for sedimentary manganese), it can be observed that the prediction results correspond to basin 1 and 2 to the highest degree. Since basin 1 is the already mined Minle manganese, its surrounding favorable districts are not identified as metallogenic prospects (the yellow circle). Meanwhile, there is a high coincidence between the delineated metallogenic prospect and the predicted manganese basin, with the former being located on the hanging side of the growth fault, providing the best metallogenic conditions. When the threshold value of the delineated prospect is 0.65, the prediction results based on transfer learning are dispersed in the east and south, which are not affected by the distribution of other basins. However, it converges between two basins as the threshold value increases, and there is some directivity in the prediction results which corresponds to the geological features of this study area, thus verifying the feasibility and validity of this intelligent prediction method.

5. Conclusions

This study conducted 3D metallogenic prediction based on the transfer learning of a 3D CNN model of Huayuan manganese mine, Hunan province. Through analysis of the prediction results of the rift basin and syn-sedimentary fault, the method was proven to be effective. The following conclusions are obtained:

(1)

Twenty-two proposed ore-controlling variables were divided into six groups for comparative experiments with different combinations, and each group was further divided into the 3D CNN prediction method and the transfer learning prediction method. After proving the similarity of the regional metallogenic background, the convolution kernel of the Minle area was transferred to that of the Huayuan area with poor data. Then, both were used to train a 3D prediction model to realize the training and transfer of the spatial correlation between the spatial distribution of ore-controlling factors and the manganese ore. The results indicated that the accuracy of the transfer learning model in test 6 could reach 100%, showing the strong stability of the transfer learning prediction model and a fast convergence speed.

(2)

By comparing the 3D predicted targets before and after the transfer learning of tests 5 and 6, the 3D CNN model and the prediction models after transfer learning were compared and analyzed in terms of the ROC curve and ore-controlling ratio. It was found that if the 7–12 fracture and each fracture buffer layer are added, the 3D CNN model will perform well, and if they are not added, the transfer learning model will be superior, with an accuracy of 100%. The blocks with high probability values in the prediction results are few and concentrated.

(3)

The final prediction results were superimposed and verified with the solid model of the rift basin and the growth fault model in the unpredicted area. The analysis results demonstrated that the delineated metallogenic prospect area had a high degree of overlap with the rift basin, and it is located in the hanging wall of the growth fault, with excellent metallogenic conditions. To sum up, the 3D CNN prediction method has great potential and is advantageous in mineral prediction when big data are available, and transfer learning based on the 3D CNN algorithm greatly improves 3D deep mineral prediction in the case of incomplete data.