Mechanism for the Combined Li–Na Ionic Conductivity in Sugilite (Fe2Na2K[Li3Si12O30])-Type Compounds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Electron Probe Micro Analysis (EPMA)
2.3. High-Resolution Neutron Powder Diffraction (HRNPD)
2.4. Impedance Spectroscopy (IS)
2.5. Synchrotron X-ray Single-Crystal Diffraction (XSD)
2.6. Structure Analysis
3. Results and Discussion
3.1. Results from EPMA
3.2. Phase Identification of Sugilite#2 Using HRNPD
3.3. Thermally Activated Relaxation Modes and Activation Energies from IS
3.4. Results from XSD
3.4.1. Thermal Stability
3.4.2. Site Symmetry of Na and Thermal Motions
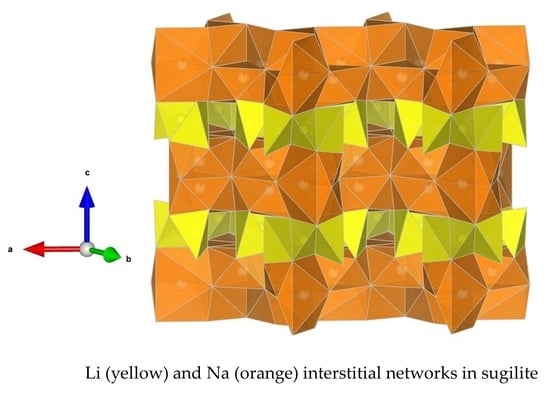
3.4.3. Locations of Interstitials
3.4.4. BVS Landscape Maps
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tarascon, J.-M.; Armand, M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar] [CrossRef]
- Hull, S. Superionics: Crystal structures and conduction processes. Rep. Prog. Phys. 2004, 67, 1233–1314. [Google Scholar] [CrossRef]
- Tarascon, J.M.; Recham, N.; Armand, M.; Chotard, J.N.; Barpanda, P.; Walker, W.; Dupont, L. Hunting for Better Li-Based Electrode Materials via Low Temperature Inorganic Synthesis. Chem. Mater. 2010, 22, 724–739. [Google Scholar] [CrossRef]
- Kamaya, N.; Homma, K.; Yamakawa, Y.; Hirayama, M.; Kanno, R.; Yonemura, M.; Kamiyama, T.; Kato, Y.; Hama, S.; Kawamoto, K.; et al. A lithium superionic conductor. Nat. Mater. 2011, 10, 682–686. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Richards, W.D.; Ong, S.P.; Miara, L.J.; Kim, J.C.; Mo, Y.; Ceder, G. Design principles for solid-state lithium superionic conductors. Nat. Mater. 2015, 14, 1026–1031. [Google Scholar] [CrossRef] [PubMed]
- Kato, Y.; Hori, S.; Saito, T.; Suzuki, K.; Hirayama, M.; Mitsui, A.; Yonemura, M.; Iba, H.; Kanno, R. High-power all-solid-state batteries using sulfide superionic conductors. Nat. Energy 2016, 1, 16030. [Google Scholar] [CrossRef]
- He, X.; Zhu, Y.; Mo, Y. Origin of fast ion diffusion in super-ionic conductors. Nat. Commun. 2017, 8, 15893. [Google Scholar] [CrossRef]
- Janek, J.; Zeier, W.G. A solid future for battery development. Nat. Energy 2016, 1, 16141. [Google Scholar] [CrossRef]
- Bhardwaj, R.K.; Zitoun, D. Recent Progress in Solid Electrolytes for All-Solid-State Metal(Li/Na)–Sulfur Batteries. Batteries 2023, 9, 110. [Google Scholar] [CrossRef]
- Park, S.-H.; Hoelzel, M.; Boysen, H.; Schmidbauer, E. Lithium conductivity in an Li-bearing double-ring silicate mineral, sogdianite. J. Solid State Chem. 2007, 180, 1306–1317. [Google Scholar] [CrossRef]
- Röska, B.; Akter, I.; Hoelzel, M.; Park, S.-H. Na+/Li+-ionic conductivity in Fe2Na2K[Li3Si12O30]. J. Solid State Chem. 2018, 264, 98–107. [Google Scholar] [CrossRef]
- Forbes, W.C.; Baur, W.H.; Khan, A.A. Crystal Chemistry of milarite-type minerals. Am. Mineral. 1972, 57, 463–472. [Google Scholar]
- Armbruster, T.; Oberhänsli, R. Crystal chemistry of double-ring silicates: Structures of Sugilite and Brannockite. Am. Mineral. 1988, 73, 595–600. [Google Scholar]
- Hawthorne, F.C.; Kimata, M.; Cerny, P.; Ball, N.A.; Rossman, G.R.; Grice, J.D. Crystal chemistry of the milarite-group minerals. Am. Mineral. 1991, 76, 1836–1856. [Google Scholar]
- Sokolova, E.V.; Hawthorne, F.C.; Pautov, L.A. The crystal chemistry of Li- bearing minerals with the milarite-type structure: The crystal structure of end- member sogdianite. Can. Mineral. 2000, 38, 835–859. [Google Scholar] [CrossRef]
- Gagné, O.C.; Hawthorne, F.C. Chemographic Exploration of the Milarite-Type Structure. Can. Mineral. 2016, 54, 1229–1247. [Google Scholar] [CrossRef]
- Murakami, N.; Kato, T.; Miura, Y. Sugilite, a new silicate mineral from Iwagi Islet, Southwest Japan. Mineral. J. 1976, 8, 110–121. [Google Scholar] [CrossRef]
- Kato, T.M.; Miura, Y.; Murakami, N. Crystal structure of sugilite. Mineral. J. 1976, 8, 184–192. [Google Scholar] [CrossRef]
- Dunn, P.J.; Brummer, J.J.; Belsky, H. Sugilite, a second occurrence: Wessels mine, Kalahari manganese field, Republic of South Africa. Can. Mineral. 1980, 18, 37–39. [Google Scholar]
- Clark, A.M.; Fejer, E.E.; Couper, A.G.; Bearne, G.S.; Din, V.K. Additional data on Sugilite. Mineral. Mag. 1980, 43, 947–949. [Google Scholar] [CrossRef]
- Cooper, M.H.; Hawthorne, F.C.; Grew, E.S. The crystal chemistry of sogdianite, a milarite-group mineral. Am. Mineral. 1999, 84, 764–768. [Google Scholar] [CrossRef]
- Ferraris, G.; Prencipe, M.; Pautov, L.A.; Sokolova, E.V. The crystal structure of darapiosite and a comparison with Li- and Zn-bearing minerals of the milarite group. Can. Mineral. 1999, 37, 769–774. [Google Scholar]
- Park, S.-H. Development of a new type of Li-battery materials based on the milarite-family. Acta Cryst. 2008, A64, C532. [Google Scholar] [CrossRef]
- Pouchou, J.L.; Pichoir, F. Un nouveau modèle de calcul pour la microanalyse quantitative par spectrométrie de rayons X. Partie I: Application à l’analyse des échantillons homogènes. La Rech. Aérospatiale 1984, 3, 167–192. [Google Scholar]
- Hunt, J.B.; Clift, P.D.; Lacasse, C.; Vallier, T.L.; Werner, R. Interlaboratory comparison of electron microprobe microanalysis of glass geochemistry. In Proceedings, Ocean Drilling Program, Scientific Results; Saunders, A.D., Larsen, H.C., Wise, S.W., Eds.; 1998; Volume 152, pp. 85–91. [Google Scholar] [CrossRef]
- Hoelzel, M.; Senyshyn, A.; Juenke, N.; Boysen, H.; Schmahl, W.; Fuess, H. High- resolution neutron powder diffractometer SPODI at research reactor FRM I-I. Nucl. Instrum. Methods Phys. Res. Sect. A Acceler Ators Spectrometers Detect. Assoc. Equip. 2012, 667, 32–37. [Google Scholar] [CrossRef]
- Kabsch, W.J.J. Automatic processing of rotation diffraction data from crystals of initially unknown symmetry and cell constants. Appl. Crystallogr. 1993, 26, 795–800. [Google Scholar] [CrossRef]
- Paulmann, C.; Phoscor. Department of Earth System Sciences, Institute of Mineralogy and Petrography, University of Hamburg, Grindelallee 48, 20146 Hamburg, Germany. Personal Communications, 2007.
- Blessing, R.H. SORTAV. Acta Cryst. 1995, A51, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Petříček, V.; Dušek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General features. Z. Krist. Cryst. Mater. 2014, 229, 345–352. [Google Scholar] [CrossRef]
- Brown, I.D. The Chemical Bond in Inorganic Chemistry—The Bond Valence Model; IUCr monographs on Crystallography 12; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Adams, S. From bond valence maps to energy landscapes for mobile ions in ion-conducting solids. Solid State Ion. 2006, 177, 1625–1630. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Fullprof Program. Phys. B 2011, 55, 192. [Google Scholar]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Cryst. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Kumar, M.; Shankar, S.; Brijmohan; Kumar, S.; Thakur, O.P.; Ghosh, A.K. Impedance spectroscopy and conductivity analysis of multiferroic BFO–BT solid solutions. Phys. Lett. 2017, A381, 379–386. [Google Scholar] [CrossRef]
- Hueso, K.B.; Armand, M.; Rojo, T. High temperature sodium batteries: Status, challenges and future trends. Energy Environ. Sci. 2013, 6, 734–749. [Google Scholar] [CrossRef]
- Duba, A.G.; Ghose, S. Electrical conductivity and ionic conduction mechanism in NaLiZrSi6O15 single crystals. Solid State Ion. 1983, 9–10, 813–816. [Google Scholar] [CrossRef]
- Shaikh, A.M.; Ghose, S. A first-order phase transition in zektzerite, NaLiZrSi6O15: High-temperature single-crystal X-ray diffraction study. Phys. Chem. Miner. 2015, 42, 747–759. [Google Scholar] [CrossRef]
- Park, S.-H.; Chucholowski, C.J.; Lara, L.G.B.; Hoelzel, M.; Paulmann, C. Investigation of a new willemite-type compound, (Li, Na, H)0.16Zn1.92SiO4. J. Solid State Chem. 2013, 200, 328–340. [Google Scholar] [CrossRef]
- Park, S.-H.; Pedersen, B.; Meven, M.; Krüger, H. Cation dynamics in six-membered ring and -chain lithosilicates. In Proceedings of the DGK (Germany Crystallographic Meeting), Hannover, Germany, 24–27 February 2010. [Google Scholar]
- Zucker, U.H.; Schulz, H. Statistical Approaches for the Treatment of Anharmonic Motion in Crystals. I. A Comparison of the Most Frequently Used Formalisms of Anharmonic Thermal Vibrations. Acta Cryst. 1982, A38, 563–568. [Google Scholar] [CrossRef]
- Zucker, U.H.; Schulz, H. Statistical Approaches for the Treatment of Anharmonic Motion in Crystals. II. Anharmonic Thermal Vibrations and Effective Atomic Potentials in the Fast Ionic Conductor Lithium Nitride (Li3N). Acta Cryst. 1982, A38, 568–576. [Google Scholar] [CrossRef]
- Kuhs, W.F. The Anharmonic Temperature Factor in Crystallographic Analysis. Aust. J. Phys. 1988, 41, 369–382. [Google Scholar] [CrossRef]
- Kuhs, W.F. Generalized Atomic Displacements in Crystallographic Structure Analysis. Acta Cryst. 1992, A48, 80–98. [Google Scholar] [CrossRef]
- Trueblood, K.N.; Bürgi, H.-B.; Burzlaff, H.; Dunitz, J.D.; Gramaccioli, C.M.; Schulz, H.H.; Shmueli, U.; Abrahams, S.C. Atomic displacement parameter nomenclature. Report of a subcommittee on atomic displacement parameter nomenclature. Acta Cryst. 1996, A52, 770–781. [Google Scholar] [CrossRef]
- Boysen, H. The determination of anharmonic probability densities from static and dynamic disorder by neutron powder diffraction. Z. Krist. 2003, 218, 123–131. [Google Scholar] [CrossRef]















| Temperature (K) | 298 | 423 | 573 | 723 | 873 | 1023 | |
|---|---|---|---|---|---|---|---|
| Lattice metric | a (Å) | 10.039 (3) | 10.039 (2) | 10.046 (3) | 10.055 (1) | 10.062 (1) | 10.073 (2) |
| c (Å) | 14.050 (5) | 14.053 (3) | 14.063 (9) | 14.080 (1) | 14.0940 (1) | 14.106 (1) | |
| Density | V (Å3) | 1226.3 (7) | 1226.5 (4) | 1229.1 (9) | 1232.8 (2) | 1235.8 (2) | 1239.5 (4) |
| (g/cm3) | 2.781 | 2.780 | 2.774 | 2.766 | 2.759 | 2.751 | |
| Data range | h | −25~12 | −23~12 | −25~25 | −25~25 | −25~24 | −17~24 |
| k | −24~24 | −20~13 | −25~25 | −25~24 | −22~25 | −25~25 | |
| l | −24~23 | −16~21 | −19~23 | −23~21 | −21~23 | −23~21 | |
| Total reflections | 48,020 | 24,125 | 46,778 | 48,630 | 48,951 | 49,317 | |
| Unique reflections | 2887 | 2446 | 2828 | 2844 | 2857 | 2865 | |
| Absorption correction Tmin/Tmax | 0.6983 0.7093 | 0.7437 0.7530 | 0.7437 0.7531 | 0.7437 0.7532 | 0.7437 0.7532 | 0.6983 0.7094 | |
| Rmerge | 0.024 | 0.048 | 0.040 | 0.030 | 0.026 | 0.025 | |
| Goodness of fit | 2.867 | 2.995 | 2.609 | 3.750 | 3.710 | 2.254 | |
| wR (against I) | 0.073 | 0.057 | 0.068 | 0.045 | 0.045 | 0.034 | |
| Weighting w | 1/σ2(I) | 1/σ2(I) | 1/σ2(I) | 1/σ2(I) | 1/σ2(I) | 1/σ2(I) | |
| sinθ/λ (Å−1) | 1.2496 | 1.2496 | 1.2499 | 1.2496 | 1.2498 | 1.2493 | |
| Δρmax; Δρmin (e/Å3) | 0.11; −0.17 | 0.34; −0.58 | 1.15; −1.02 | 0.21; −0.31 | 0.17; −0.20 | 0.12; −0.07 | |
| T (K) | Site | Type | Coordinates | Occupancy | Multiplicity | ||
|---|---|---|---|---|---|---|---|
| x | y | z | |||||
| 298 | A | Fe | 0.333333 | 0.666667 | 0.25 | 0.925 § | 4 |
| B | Na | 0.333333 | 0.666667 | 0 | 1 | 4 | |
| C | K | 0 | 0 | 0.25 | 1 | 2 | |
| TII | Li | 0.5 | 0 | 0.25 | 1 | 6 | |
| TI | Si | 0.35553 (1) | 0.11899 (1) | 0.38711 (1) | 1 | 24 | |
| O1 | O | 0.39699 (6) | 0.13771 (6) | 0.5 | 1 | 12 | |
| O2 | O | 0.22207 (3) | 0.94497 (3) | 0.36246 (3) | 1 | 24 | |
| O3 | O | 0.50823 (3) | 0.16506 (3) | 0.33023 (3) | 1 | 24 | |
| 423 | TI | Si | 0.35535 (1) | 0.11910 (1) | 0.38727 (1) | ||
| O1 | O | 0.39686 (9) | 0.13753 (9) | 0.5 | |||
| O2 | O | 0.22217 (4) | 0.94518 (3) | 0.36274 (4) | |||
| O3 | O | 0.50785 (3) | 0.16526 (4) | 0.33030 (3) | |||
| 573 | TI | Si | 0.35519 (2) | 0.11916 (1) | 0.38734 (1) | ||
| O1 | O | 0.3968 (1) | 0.1380 (1) | 0.5 | |||
| O2 | O | 0.22223 (5) | 0.94532 (4) | 0.36282 (5) | |||
| O3 | O | 0.50773 (4) | 0.16543 (4) | 0.33036 (4) | |||
| 723 | TI | Si | 0.35492 (1) | 0.11939 (1) | 0.38756 (1) | ||
| O1 | O | 0.3966 (1) | 0.1374 (1) | 0.5 | |||
| O2 | O | 0.22220 (4) | 0.94560 (3) | 0.36276 (4) | |||
| O3 | O | 0.50725 (3) | 0.16570 (3) | 0.33061 (3) | |||
| 873 | TI | Si | 0.35471 (1) | 0.11963 (1) | 0.38772 (1) | ||
| O1 | O | 0.3969 (1) | 0.1381 (1) | 0.5 | |||
| O2 | O | 0.22234 (5) | 0.94590 (3) | 0.36273 (5) | |||
| O3 | O | 0.50689 (3) | 0.16604 (4) | 0.33064 (4) | |||
| 1023 | TI | Si | 0.35435 (1) | 0.11991 (1) | 0.38778 (1) | ||
| O1 | O | 0.3974 (1) | 0.1387 (1) | 0.5 | |||
| O2 | O | 0.22248 (5) | 0.94620 (3) | 0.36241 (4) | |||
| O3 | O | 0.50637 (3) | 0.16624 (4) | 0.33073 (3) | |||
| Li at T(II) | C113 = 0.0008(3); C123 = C113 = 0.0008 |
| Na at A | C111 = 0.0034(2); C112 = 0.0033(2); C122 = C112 − C111 = −0.00007; C222 = −C111 = −0.0034 |
| D1133 = −0.00047(8); D1233 = 0.5; D1133 = −0.00023; D2233 = D1133 = −0.00047; D3333 = −0.0005(2) |
| Site (Type) | Ligands | Bonding Distance (Å) | BV (v.u.) | BVS (v.u.) |
|---|---|---|---|---|
| A (Fe) | O3 (×6) | 2.0048 (4) | 0.515 (1) ×6 | 3.088 (1) |
| B(Na) | O1 (×3) | 2.4257 (10) | 0.186 (1) ×3 | |
| O3 (×9) | 2.9023 (4) | 0.051 (0) ×9 | 0.865 (1) | |
| C (K) | O2 (×12) | 3.0074 (5) | 0.094 (0) ×12 | 1.126 (0) |
| TI (Si) | O1 | 1.6271 (3) | 0.992 (1) | |
| O2 | ×1.6217 (3) | 1.006 (1) | ||
| O2 * | 1.6207 (5) | 1.009 (1) | ||
| O3 | 1.5797 (4) | 1.127 (1) | 4.134 (2) | |
| TII (Li) | O3 (×4) | 1.9994 (4) | 0.237 (1) ×4 | 0.946 (0) |
| Site (Type) | Ligands | Bonding Distance (Å) | BV (v.u.) | BVS (v.u.) |
|---|---|---|---|---|
| LiX1 (Li) | O2 (×2) | 1.8874 (5) | 0.320 (0) ×2 | |
| O3 (×2) | 2.0269 (3) | 0.220 (0) ×2 | 1.080 (1) | |
| LiX2 (Li) | O2 | 2.3354 (4) | 0.095 (0) | |
| O2 * | 1.8061 (5) | 0.399 (1) | ||
| O2 * | 2.3568 (5) | 0.090 (0) | ||
| O2 * | 1.7918 (5) | 0.415 (1) | ||
| O3 | 2.4579 (4) | 0.069 (0) | ||
| O3 * | 2.4686 (3) | 0.067 (0) | 1.134 (1) | |
| NaX1(Na) | O1 (×3) | 2.4818 (12) | 0.160 (1) ×3 | |
| O3 (×3) | 2.4886 (4) | 0.157 (0) ×3 | 0.949 (1) | |
| NaX2 (Li) | O1 | 2.5528 (13) | 0.132 (0) | |
| O1 * | 2.2990 (9) | 0.262 (1) | ||
| O1 * | 2.5592 (11) | 0.130 (0) | ||
| O2 | 2.2098 (5) | 0.391 (0) | ||
| O3 | 2.1504 (4) | 0.333 (0) | ||
| O3 | 2.7205 (3) | 0.084 (0) | ||
| O3 | 2.8429 (4) | 0.060 (0) | 1.391 (1) | |
| NaX3(Na) | O1 (×2) | 2.1133 (9) | 0.432 (1) ×2 | |
| O3 (×4) | 2.8986 (4) | 0.052 (0) ×4 | 1.072 (2) |
| Compound | Ionic Conductivity (S·cm−1) | Na:Li Ratio (pfu) | SiO4 Configuration |
|---|---|---|---|
| Sugilite mass (Fe,Al,Mn)2Na2K[Li3Si12O30] ([23], this study) | 1.7·10−3 at 943 K | 2:3 | double 6MR |
| Sogdianite (Zr,Al,Fe)2Na0.36K[Li3Si12O30] ⊥ [001] [10] | 4.1·10−5 at 923 K | 0.36:3 | double 6MRs |
| Synthetic powder sample Fe2Na2K[Li3Si12O30] [11] | 1.2·10−5 at 923 K | 2:3 | double 6MRs |
| Zektzerite Zr2Na2Li2Si12O30 highest || [001] [37,38] | 3·10−5 at 1173 K | 2:2 | double 6MCs |
| Pezzottaite Cs[(Be2Li)Al2Si6O18] [40] ⊥ [001] || [001] | 8.3·10−6 at 1093 K 1.1·10−5 at 1093 K | 0:1 | single 6MRs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-H.; Paulmann, C.; Hoelzel, M.; Hochleitner, R. Mechanism for the Combined Li–Na Ionic Conductivity in Sugilite (Fe2Na2K[Li3Si12O30])-Type Compounds. Minerals 2023, 13, 620. https://doi.org/10.3390/min13050620
Park S-H, Paulmann C, Hoelzel M, Hochleitner R. Mechanism for the Combined Li–Na Ionic Conductivity in Sugilite (Fe2Na2K[Li3Si12O30])-Type Compounds. Minerals. 2023; 13(5):620. https://doi.org/10.3390/min13050620
Chicago/Turabian StylePark, So-Hyun, Carsten Paulmann, Markus Hoelzel, and Rupert Hochleitner. 2023. "Mechanism for the Combined Li–Na Ionic Conductivity in Sugilite (Fe2Na2K[Li3Si12O30])-Type Compounds" Minerals 13, no. 5: 620. https://doi.org/10.3390/min13050620
APA StylePark, S.-H., Paulmann, C., Hoelzel, M., & Hochleitner, R. (2023). Mechanism for the Combined Li–Na Ionic Conductivity in Sugilite (Fe2Na2K[Li3Si12O30])-Type Compounds. Minerals, 13(5), 620. https://doi.org/10.3390/min13050620