Investigating Effects of Structural Deformation Regimes on Mineralization Distributions in Fluid-Saturated Rocks: Computational Simulation Approach through Generic Models
Abstract
1. Introduction
2. Mathematical Governing Equations for the Coupled Rock Deformation, Porosity-Permeability Evolution and Pore-Fluid Flow Problem
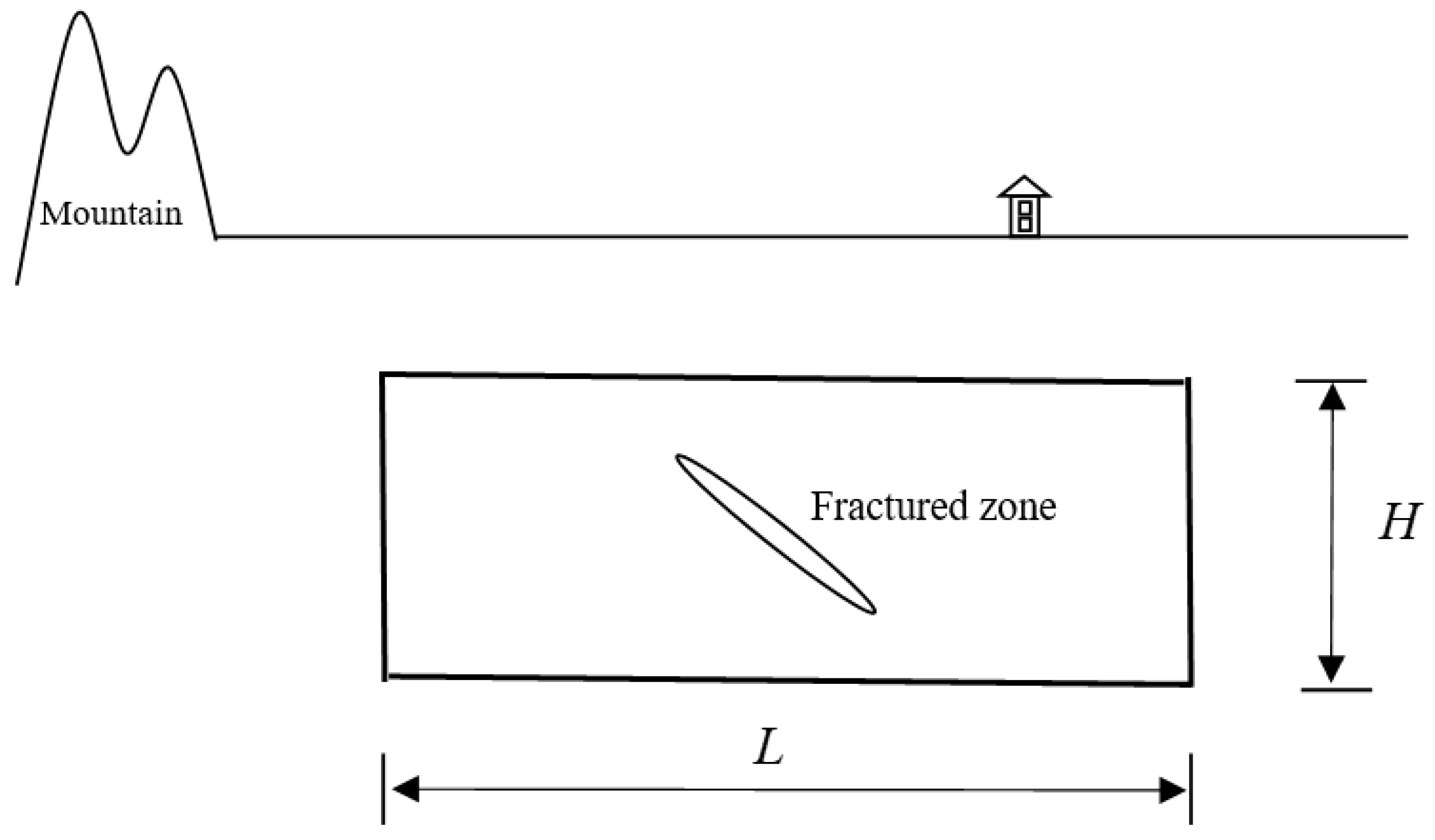
2.1. Generic Model
2.2. Mathematical Model
2.3. Computational Simulation Algorithm
3. Verification of the Proposed Computational Simulation Algorithm
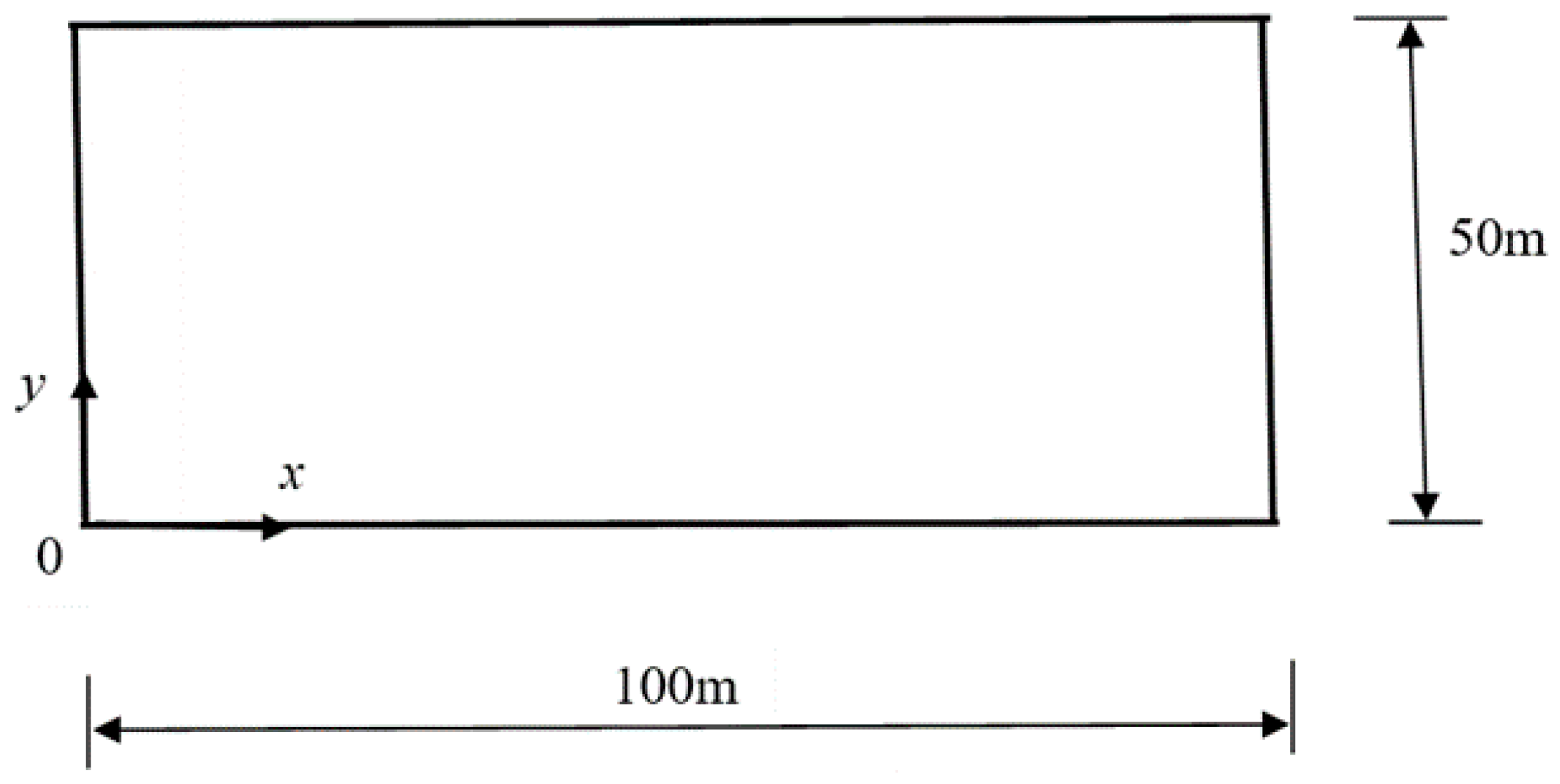
3.1. Brief Description of Deriving the Analytical Solutions for a Benchmark Problem
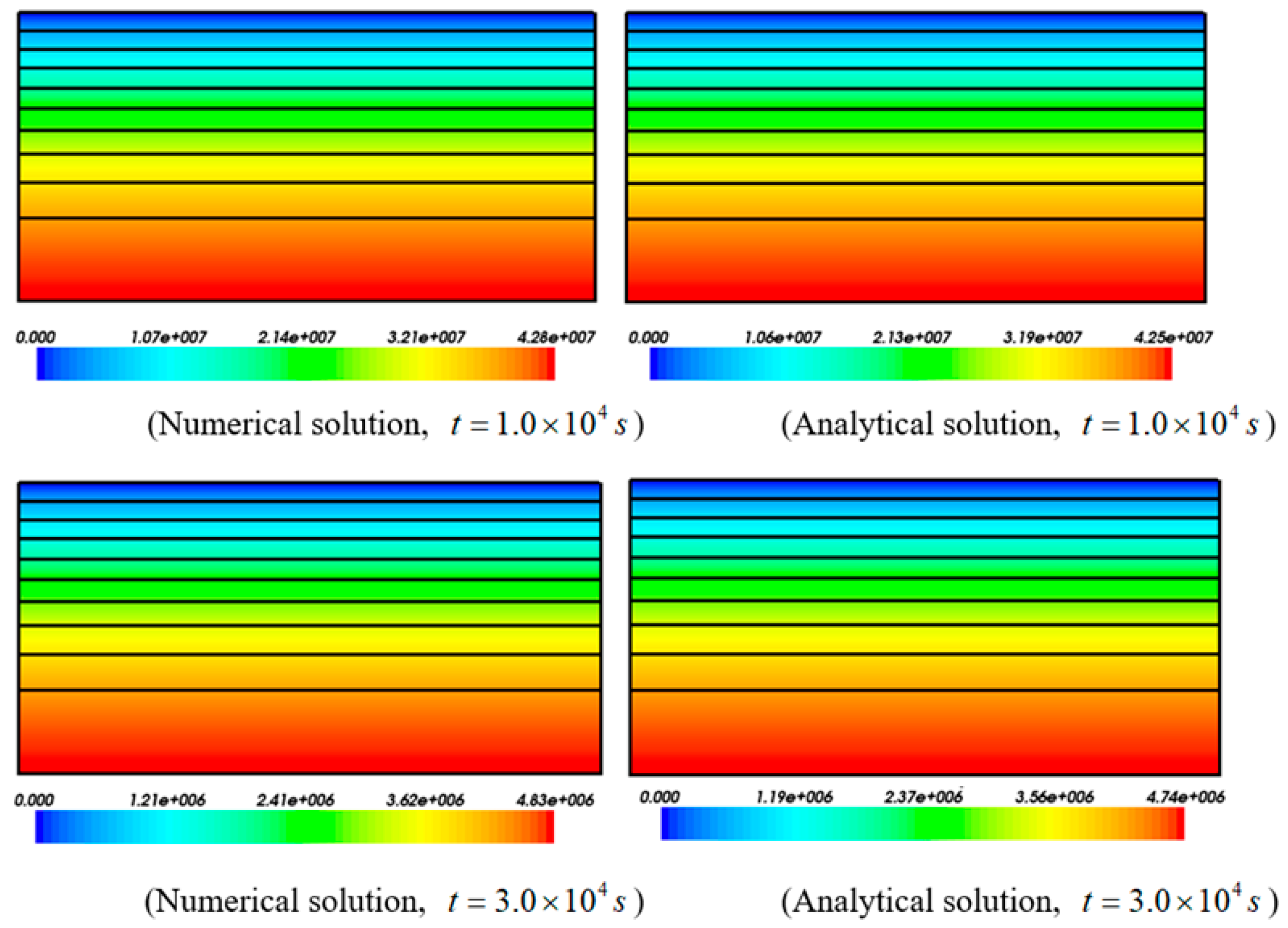
3.2. Verification of the Proposed Computational Simulation Algorithm Using the Benchmark Problem
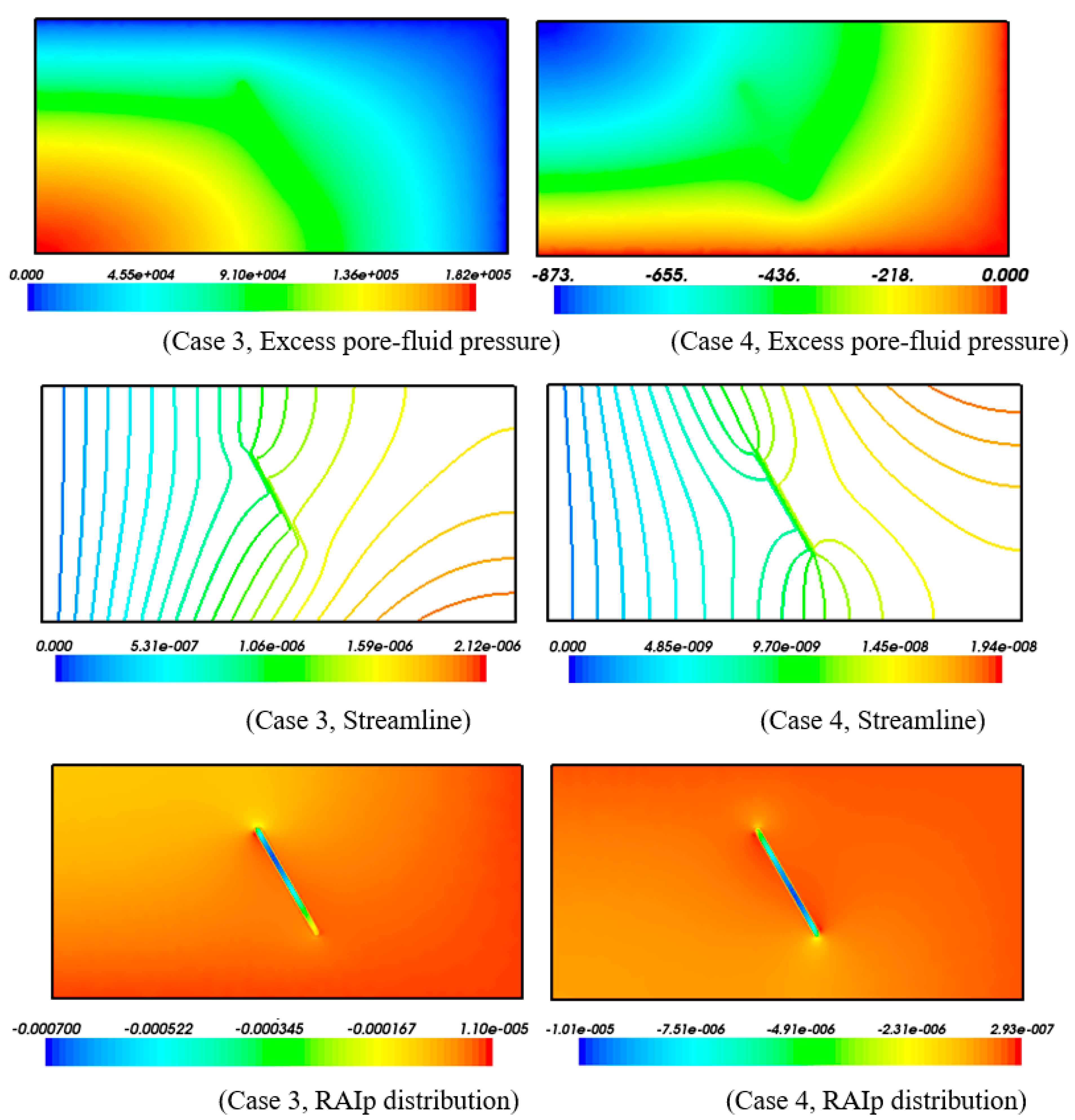
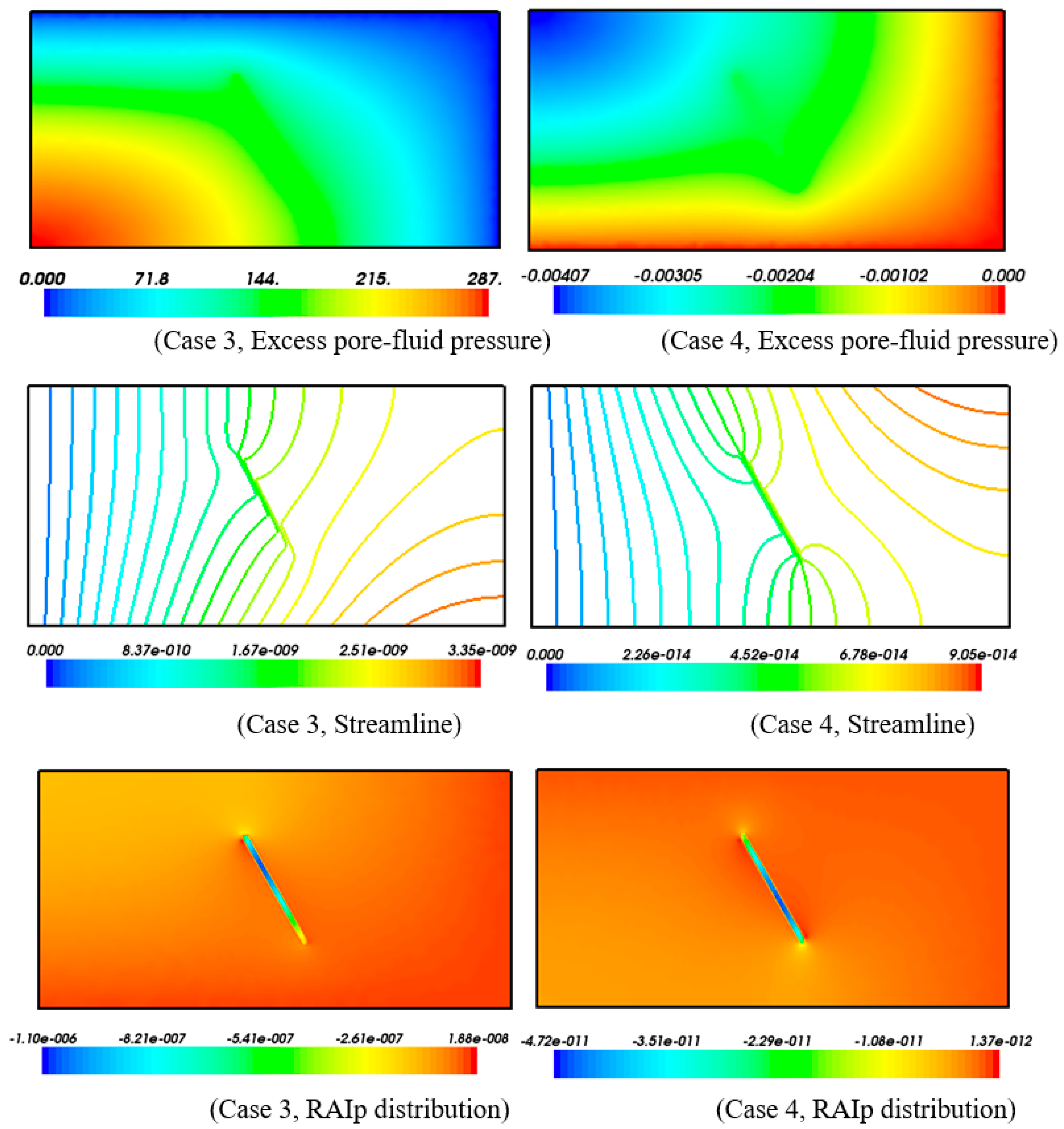
4. Effects of Structural Deformation Regimes on Mineralization Distributions in Permeable Fractured Zones within Fluid-Saturated Rocks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, C.; Hobbs, B.; Ord, A. Chemical dissolution-front instability associated with water-rock reactions in groundwater hydrology: Analyses of porosity-permeability relationship effects. J. Hydrol. 2016, 540, 1078–1087. [Google Scholar] [CrossRef]
- Zhao, C.; Schaubs, P.; Hobbs, B. Computational simulation of seepage instability problems in fluid-saturated porous rocks: Potential dynamic mechanisms for controlling mineralisation patterns. Ore Geol. Rev. 2016, 79, 180–188. [Google Scholar] [CrossRef]
- Zhao, C.-B.; Hobbs, B.; Ord, A. Effects of different numerical algorithms on simulation of chemical dissolution-front instability in fluid-saturated porous rocks. J. Cent. South Univ. 2018, 25, 1966–1975. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, T.; Xia, S.; Tian, H. Computational simulation of iron ore-forming processes in the Caiyuanzi siderite ore district, Guizhou, China. J. Geochem. Explor. 2015, 158, 155–167. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, Y.; Dai, T.; Mao, X.; Lei, Y.; Lai, J.; Tian, H. Finite difference modeling of metallogenic processes in the Hutouya Pb-Zn deposit, Qinghai, China: Implications for hydrothermal mineralization. Ore Geol. Rev. 2017, 91, 463–476. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Elsevier: Amsterdam, The Netherlands, 1972. [Google Scholar]
- Phillips, O.M. Flow and Reactions in Permeable Rocks; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 1992. [Google Scholar]
- Zhao, C.; Hobbs, B.; Ord, A. A new alternative approach for investigating acidization dissolution front propagation in fluid-saturated carbonate rocks. Sci. China Technol. Sci. 2017, 60, 1197–1210. [Google Scholar] [CrossRef]
- Zhao, C.; Hobbs, B.; Ord, A. Transient-state instability analysis of dissolution-timescale reactive infiltration in fluid-saturated porous rocks: Purely mathematical approach. Sci. China Technol. Sci. 2019, 63, 319–328. [Google Scholar] [CrossRef]
- Zhao, C.; Hobbs, B.E.; Ord, A. Fundamentals of Computational Geoscience: Numerical Methods and Algorithms; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Zhao, C.; Reid, L.B.; Regenauer-Lieb, K. Some fundamental issues in computational hydrodynamics of mineralization: A review. J. Geochem. Explor. 2012, 112, 21–34. [Google Scholar] [CrossRef]
- Hobbs, B.E.; Zhang, Y.H.; Ord, A.; Zhao, C. Application of coupled deformation, fluid flow, thermal and chemical modelling to predictive mineral exploration. J. Geochem. Explor. 2000, 69, 505–509. [Google Scholar] [CrossRef]
- Gow, P.; Upton, P.; Hill, K.; Zhao, C. Copper-Gold mineralization in the New Guinea: Numerical modeling of collision, fluid flow and intrusion-related hydrothermal system. Aust. J. Earth Sci. 2002, 49, 753–771. [Google Scholar] [CrossRef]
- Ord, A.; Hobbs, B.E.; Zhang, Y.; Broadbent, G.C.; Brown, M.; Willetts, G.; Sorjonen-Ward, P.; Walshe, J.L.; Zhao, C. Geodynamic modeling of the Century deposit, Mt Isa Province, Queensland. Aust. J. Earth Sci. 2002, 49, 1011–1039. [Google Scholar] [CrossRef]
- Schaubs, P.; Zhao, C. Numerical modelling of gold-deposit formation in the Bendigo-Ballarat zone, Victoria. Aust. J. Earth Sci. 2002, 49, 1077–1096. [Google Scholar] [CrossRef]
- Sorjonen-Ward, P.; Zhang, Y.; Zhao, C. Numerical modelling of orogenic processes and mineralization in the south eastern part of the Yilgarn Craton, Western Australia. Aust. J. Earth Sci. 2002, 49, 935–964. [Google Scholar] [CrossRef]
- Cox, S.F. Coupling between deformation, fluid pressures, and fluid flow in ore-producing hydrothermal systems at depth in the crust. Econ. Geol. 2005, 100, 39–75. [Google Scholar]
- Potma, W.; Roberts, P.A.; Schaubs, P.M.; Sheldon, H.A.; Zhang, Y.; Hobbs, B.E.; Ord, A. Predictive targeting in Australian orogenic-gold systems at the deposit to district scale using numerical modelling. Aust. J. Earth Sci. 2008, 55, 101–122. [Google Scholar] [CrossRef]
- Hu, F.F.; Fan, H.R.; Jiang, X.H.; Li, X.C.; Yang, K.F.; Mernagh, T. Fluid inclusions at different depths in the Sanshandao gold deposit, Jiaodong Peninsula, China. Geofluids 2013, 13, 528–541. [Google Scholar] [CrossRef]
- Gao, X.; Zhang, D.; Absai, V.; Feng, H.; Yi, J. Computational simulation of coupled geodynamics for forming the Makeng deposit in Fujian Province, China: Constraints of mechanics, thermotics and hydrology. J. Geochem. Explor. 2015, 160, 31–43. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, T. Numerical modeling of pore-fluid flow and heat transfer in the Fushan iron ore district, Hebei, China: Implications for hydrothermal mineralization. J. Geochem. Explor. 2014, 144, 115–127. [Google Scholar] [CrossRef]
- Liu, X.; Xing, H.; Zhang, D. Influences of fluid properties on the hydrothermal fluid flow and alteration halos at the Dajishan tungsten deposit, China. J. Geochem. Explor. 2016, 163, 53–69. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, T.; Qiu, L.; Xia, S. Three-dimensional numerical simulation of ore-forming processes of the Fushan skarn iron deposit in Handan-Xingtai ore cluster, North China: Implication for tectonic effects on skarn-iron mineralization. J. Geochem. Explor. 2016, 169, 144–156. [Google Scholar] [CrossRef]
- Liu, X.; Ma, Y.; Xing, H.; Zhang, D. Chemical responses to hydraulic fracturing and wolframite precipitation in the vein-type tungsten deposits of southern China. Ore Geol. Rev. 2018, 102, 44–58. [Google Scholar] [CrossRef]
- Yang, J.H.; Zhang, Z.; Peng, J.T.; Liu, L.; Leng, C.B. Metal source and wolframite precipitation process at the Xihuashan tungsten deposit, South China: Insights from mineralogy, fluid inclusion and stable isotope. Ore Geol. Rev. 2019, 111, 102965. [Google Scholar] [CrossRef]
- Zou, Y.-H.; Liu, Y.; Pan, Y.; Yang, K.-D.; Dai, T.-G.; Mao, X.-C.; Lai, J.-Q.; Tian, H.-L. Numerical simulation of hydrothermal mineralization associated with simplified chemical reactions in Kaerqueka polymetallic deposit, Qinghai, China. Trans. Nonferrous Met. Soc. China 2019, 29, 165–177. [Google Scholar] [CrossRef]
- Ju, M.; Zhao, C.; Dai, T.; Yang, J. Finite element modeling of pore-fluid flow in the Dachang ore district, Guangxi, China: Implications for hydrothermal mineralization. Geosci. Front. 2011, 2, 463–474. [Google Scholar] [CrossRef]
- Zhao, C.; Lin, G.; Hobbs, B.; Wang, Y.; Mühlhaus, H.; Ord, A. Finite element modelling of reactive fluids mixing and mineralization in pore-fluid saturated hydrothermal/sedimentary basins. Eng. Comput. 2002, 19, 364–387. [Google Scholar] [CrossRef]
- Zhao, C.; Hobbs, B.E.; Ord, A. Convective and Advective Heat Transfer in Geological Systems; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Chadam, J.; Hoff, D.; Merino, E.; Ortoleva, P.; Sen, A. Reactive Infiltration Instabilities. IMA J. Appl. Math. 1986, 36, 207–221. [Google Scholar] [CrossRef]
- Chen, J.-S.; Liu, C.-W. Numerical simulation of the evolution of aquifer porosity and species concentrations during reactive transport. Comput. Geosci. 2002, 28, 485–499. [Google Scholar] [CrossRef]
- Chen, J.-S.; Liu, C.-W. Interaction of reactive fronts during transport in a homogeneous porous medium with initial small non-uniformity. J. Contam. Hydrol. 2004, 72, 47–66. [Google Scholar] [CrossRef]
- Chen, J.-S.; Liu, C.-W.; Lai, G.-X.; Ni, C.-F. Effects of mechanical dispersion on the morphological evolution of a chemical dissolution front in a fluid-saturated porous medium. J. Hydrol. 2009, 373, 96–102. [Google Scholar] [CrossRef]
- Zhao, C.; Hobbs, B.E.; Hornby, P.; Ord, A.; Peng, S.; Liu, L. Theoretical and numerical analyses of chemical-dissolution front instability in fluid-saturated porous rocks. Int. J. Numer. Anal. Method. Géoméch. 2007, 32, 1107–1130. [Google Scholar] [CrossRef]
- Zhao, C.; Hobbs, B.E.; Ord, A.; Peng, S. Effects of Mineral Dissolution Ratios on Chemical-Dissolution Front Instability in Fluid-Saturated Porous Media. Transp. Porous Media 2009, 82, 317–335. [Google Scholar] [CrossRef]
- Lai, K.-H.; Chen, J.-S.; Liu, C.-W.; Hsu, S.-Y.; Steefel, C. Effect of medium permeability anisotropy on the morphological evolution of two non-uniformities in a geochemical dissolution system. J. Hydrol. 2015, 533, 224–233. [Google Scholar] [CrossRef]
- Itasca Consulting Group. Fast Lagrangian Analysis of Continua (FLAC); Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 1995. [Google Scholar]
- Carman, P.C. Flow of Gases through Porous Media; Academic Press: New York, NY, USA, 1956. [Google Scholar]
- Zienkiewicz, O.C. The Finite Element Method; McGraw-Hill: London, UK, 1977. [Google Scholar]
- Lewis, R.W.; Schrefler, B.A. The Finite Element Method in the Static and Dynamic Deformation and Consolidation of Porous Media; John Wiley and Sons: New York, NY, USA, 1998. [Google Scholar]
- Zhao, C.; Hobbs, B.; Ord, A. Near-field performance of chemical dissolution-front instability around a circular acid-injection-well in fluid-saturated porous media. Sci. China Technol. Sci. 2023, 66, 1–11. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley and Sons: New York, NY, USA, 1943. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Liu, Q. Investigating Effects of Structural Deformation Regimes on Mineralization Distributions in Fluid-Saturated Rocks: Computational Simulation Approach through Generic Models. Minerals 2023, 13, 664. https://doi.org/10.3390/min13050664
Zhao C, Liu Q. Investigating Effects of Structural Deformation Regimes on Mineralization Distributions in Fluid-Saturated Rocks: Computational Simulation Approach through Generic Models. Minerals. 2023; 13(5):664. https://doi.org/10.3390/min13050664
Chicago/Turabian StyleZhao, Chongbin, and Qibo Liu. 2023. "Investigating Effects of Structural Deformation Regimes on Mineralization Distributions in Fluid-Saturated Rocks: Computational Simulation Approach through Generic Models" Minerals 13, no. 5: 664. https://doi.org/10.3390/min13050664
APA StyleZhao, C., & Liu, Q. (2023). Investigating Effects of Structural Deformation Regimes on Mineralization Distributions in Fluid-Saturated Rocks: Computational Simulation Approach through Generic Models. Minerals, 13(5), 664. https://doi.org/10.3390/min13050664




