Effect of Cation Chloride Concentration on the Dissolution Rates of Basaltic Glass and Labradorite: Application to Subsurface Carbon Storage
Abstract
:1. Introduction
2. Theoretical Background
3. Materials and Methods
3.1. Solids
3.2. Reactive Fluids
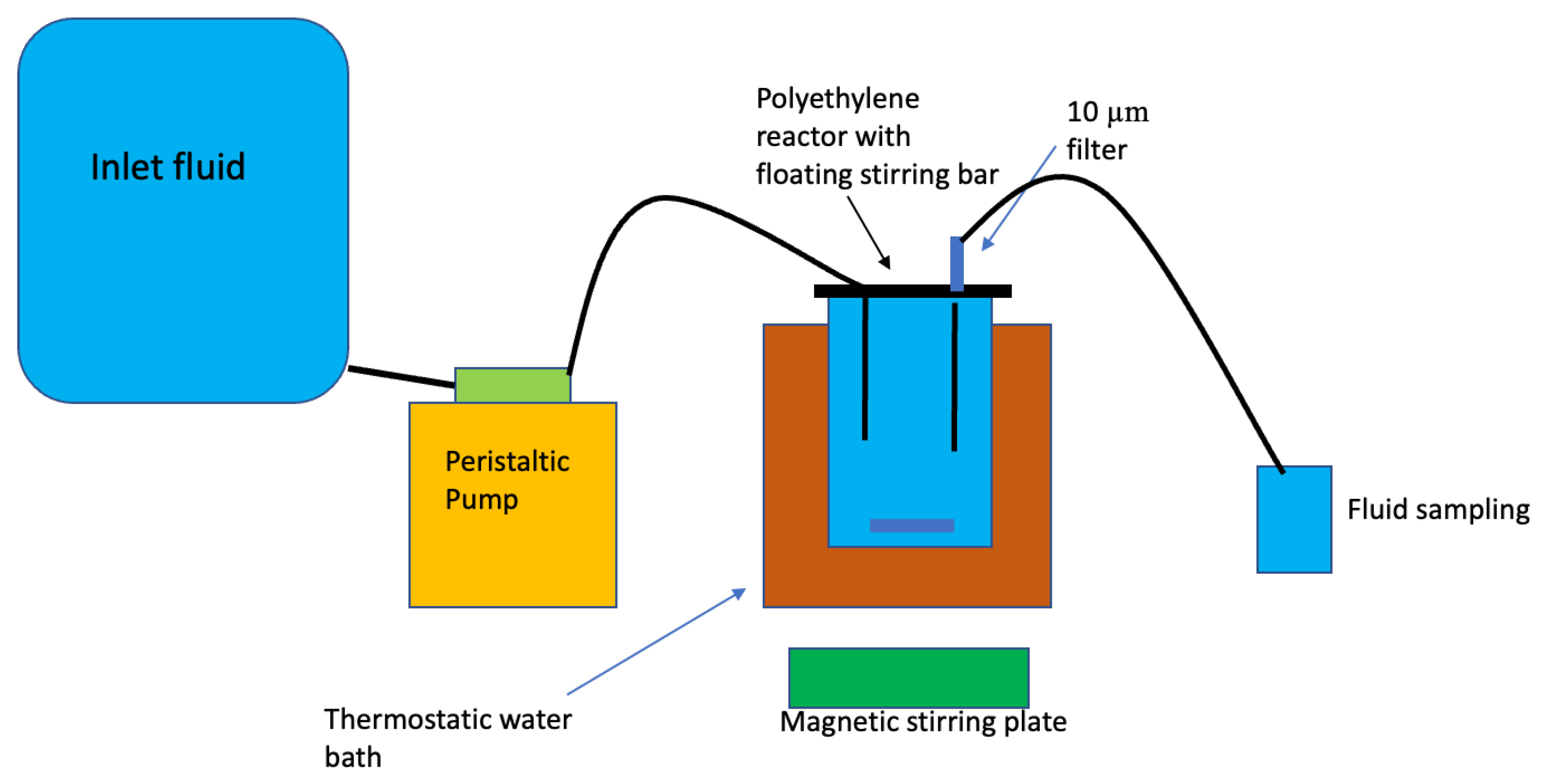
3.3. Experimental Design
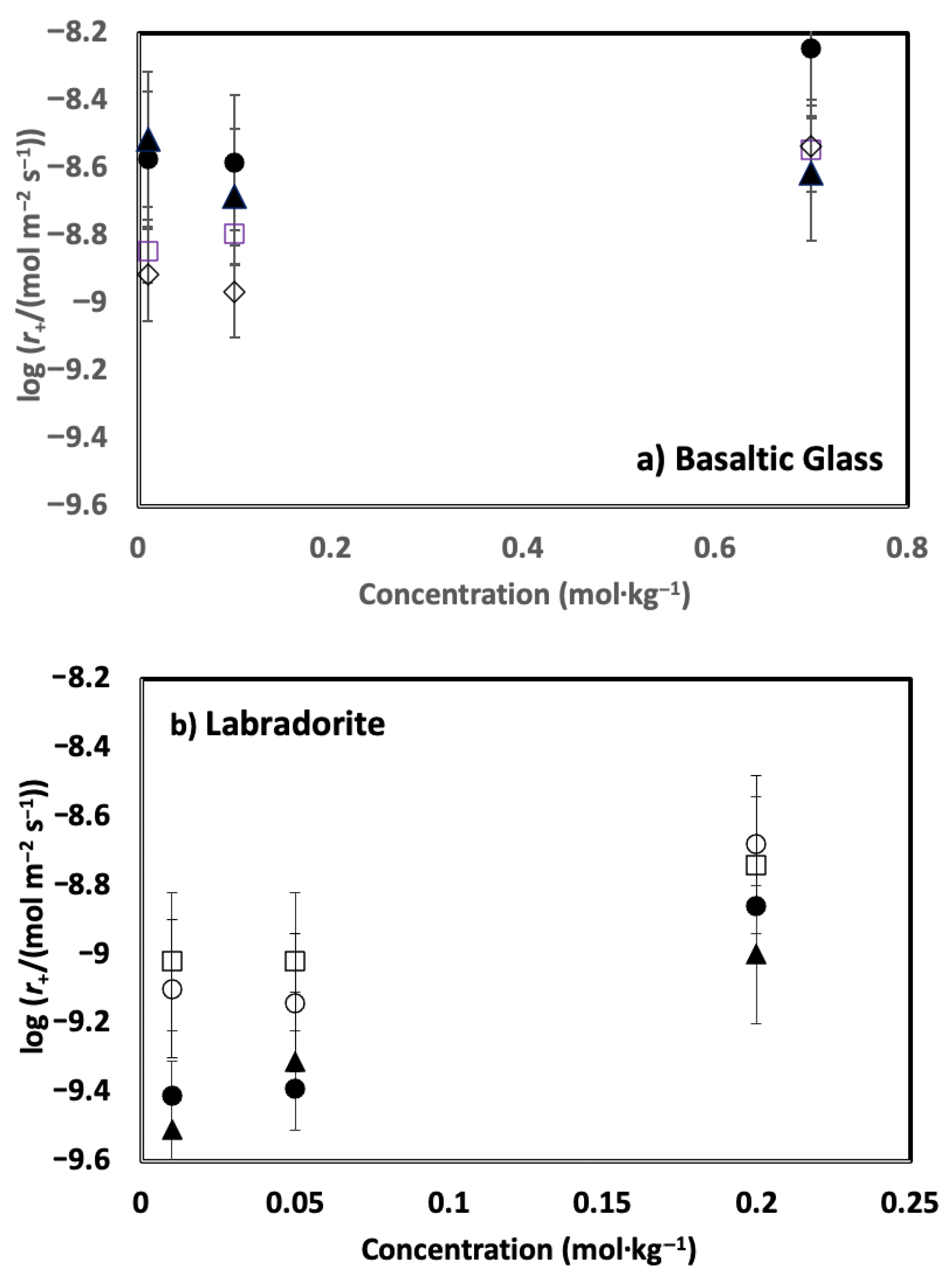
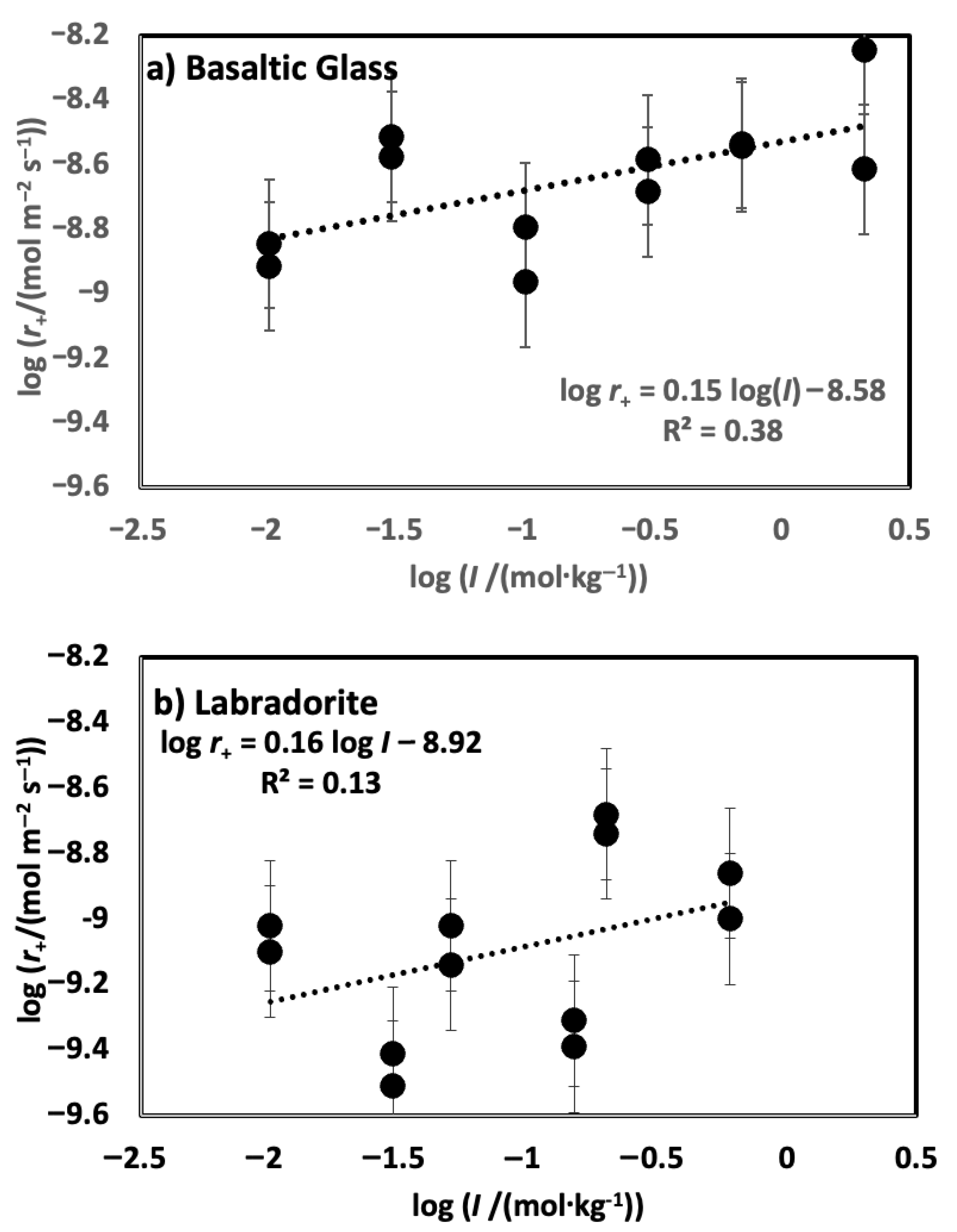
4. Results
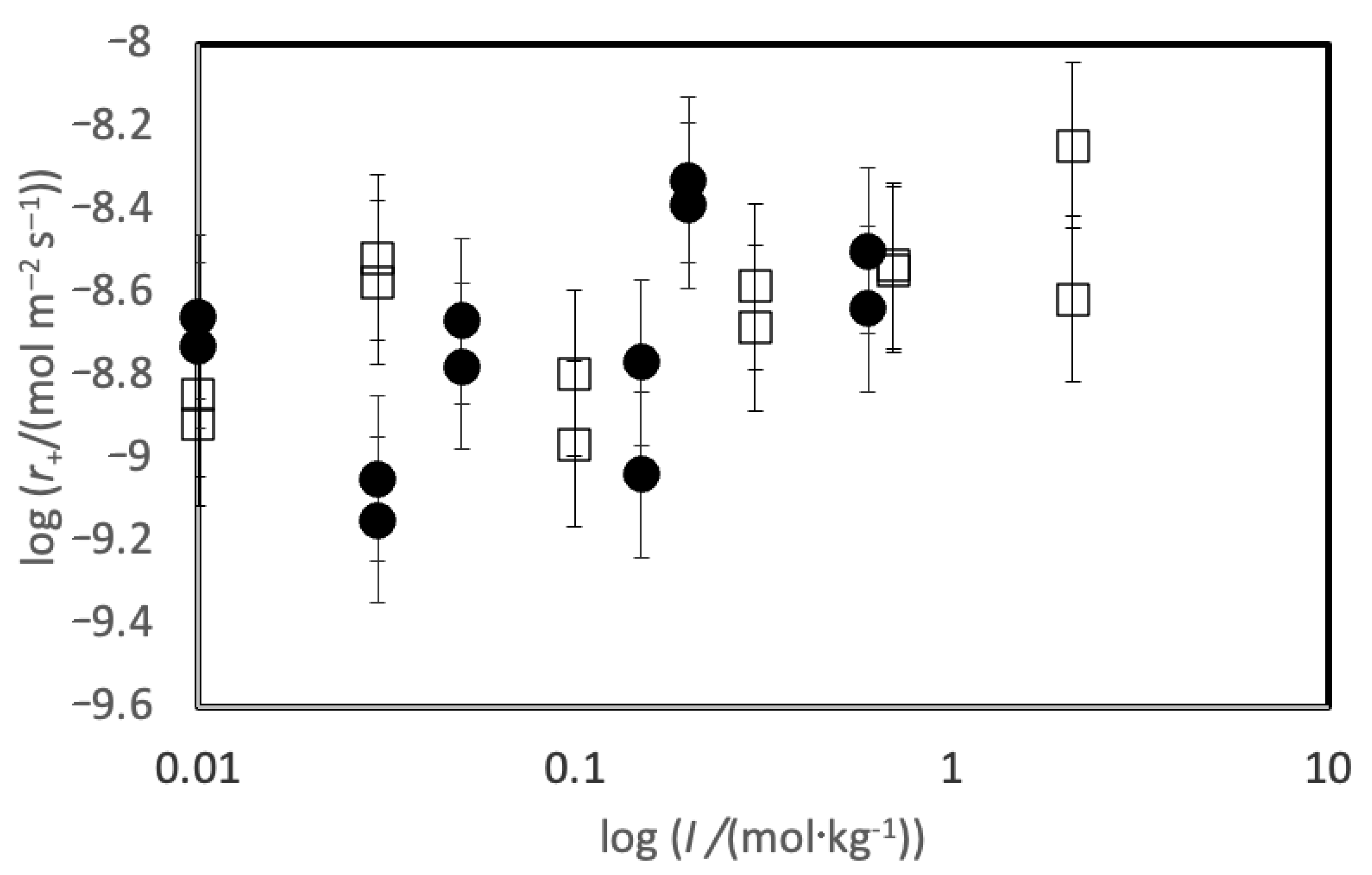
5. Discussion
5.1. Comparison of Basaltic Glass and Labradorite Si Release Rates
5.2. Comparison to Previously Measured Rates
5.3. Implications for the Dissolution Mechanism of Basaltic Glass and Feldspars
5.4. Consequences for Carbon Mineral Storage in Saline Aquifers
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McGrail, B.P.; Schaef, H.T.; Ho, A.M.; Chien, Y.-J.; Dooley, J.J.; Davidson, C.L. Potential for carbon dioxide sequestration in flood basalts. J. Geophys. Res. 2006, 111, B12201. [Google Scholar] [CrossRef]
- McGrail, B.P.; Spane, F.A.; Amonette, J.E.; Thompson, C.R.; Brown, C.F. Injection and Monitoring at the Wallula Basalt Pilot Project. Energy Procedia 2014, 63, 2939–2948. [Google Scholar] [CrossRef]
- Matter, J.M.; Takahashi, T.; Goldberg, D. Experimental evaluation of in-situ CO2–water–rock reactions during CO2 injection in basaltic rocks: Implications for geological CO2 sequestration. Geochem. Geophys. Geosyst. 2007, 8, Q02001. [Google Scholar] [CrossRef]
- Matter, J.M.; Broecker, W.S.; Gislason, S.R.; Gunnlaugsson, E.; Oelkers, E.H.; Stute, M.; Sigurdardottir, H.; Stefansson, A.; Alfreðsson, H.A.; Aradóttir, E.S.; et al. The CarbFix Pilot Project-Storing carbon dioxide in basalt. Energy Procedia 2011, 4, 5579–5585. [Google Scholar] [CrossRef]
- Matter, J.M.; Stute, M.; Snæbjörnsdottir, S.Ó.; Oelkers, E.H.; Gislason, S.R.; Aradottir, E.S.; Sigfusson, B.; Gunnarsson, I.; Sigurdardottir, H.; Gunnlaugsson, E.; et al. Rapid carbon mineralization for permanent disposal of anthropogenic carbon dioxide emissions. Science 2016, 352, 1312–1314. [Google Scholar] [CrossRef]
- Alfredsson, H.A.; Hardarson, B.S.; Franzson, H.; Gislason, S.R. CO2 sequestration in basaltic rock at the Hellisheidi site in SW Iceland: Stratigraphy and chemical composition of the rocks at the injection site. Min. Mag. 2008, 72, 1. [Google Scholar] [CrossRef]
- Goldberg, D.S.; Takahashi, T.; Slagel, A. Carbon dioxide sequestration in deep-sea basalt. Proc. Nat. Acad. Sci. USA 2008, 105, 9920–9925. [Google Scholar] [CrossRef]
- Goldberg, D.S.; Slagle, A.L. A global assessment of deep-sea basalt sites for carbon storage. Energy Proced. 2009, 1, 3675–3682. [Google Scholar] [CrossRef]
- Matter, J.M.; Kelemen, P.B. Enhanced in situ carbonation of peridotite for permanent CO2 storage. Geochim. Cosmochim. Acta 2009, 73, A848. [Google Scholar]
- Schaef, H.T.; McGrail, B.P.; Owen, A.T. Basalt–CO2–H2O interactions and variability in carbonate mineralization rates. Energy Procedia 2009, 1, 4899–4906. [Google Scholar] [CrossRef]
- Shikazono, N.; Harada, H.; Ikeda, N.; Kashiwagi, H. Dissolution of basaltic rocks and its application to underground sequestration of CO2—Estimate of mineral trapping by dissolution–precipitation simulation. Jpn. Mag. Mineral. Petrol. Sci. 2009, 38, 149–160. [Google Scholar]
- Gislason, S.R.; Wolff-Boenisch, D.; Stefansson, A.; Oelkers, E.H.; Gunnlaugsson, E.; Sigurdardottir, H.; Sigfusson, B.; Broecker, W.S.; Matter, J.M.; Stute, M.; et al. Mineral sequestration of carbon dioxide in basalt: A preinjection overview of the CarbFix project. Int. J. Greenh. Gas Control 2010, 4, 537–545. [Google Scholar] [CrossRef]
- Kampman, N.; Bickle, K.; Becker, J.; Assayag, N.; Chapman, H. Feldspar dissolution kinetics and Gibbs free energy dependence in a CO2-enriched groundwater system, Green River Utah. Earth Planet. Sci. Lett. 2009, 284, 473–488. [Google Scholar] [CrossRef]
- Schaef, H.T.; McGrail, B.P. Dissolution of Columbia River Basalt under mildly acidic conditions as a function of temperature: Experimental results relevant to the geological sequestration of carbon dioxide. Appl. Geochem. 2009, 24, 980–987. [Google Scholar] [CrossRef]
- Gysi, A.P.; Stefansson, A. CO2–water–basalt interaction. Numerical simulation of low temperature CO2 sequestration into basalts. Geochim. Cosmochim. Acta 2011, 75, 4728–4751. [Google Scholar] [CrossRef]
- Pham, V.T.H.; Lu, P.; Aagaard, P.; Zhu, C.; Hellevang, H. On the potential of CO2–water–rock interactions for CO2 storage using a modified kinetic model. Int. J. Greenh. Gas Contr. 2011, 5, 1002–1015. [Google Scholar] [CrossRef]
- Wolff-Boenisch, D.; Wenau, S.; Gislason, S.R.; Oelkers, E.H. Dissolution of basalts and peridotite in seawater, in the presence of ligands, and CO2: Implications for mineral sequestration of carbon dioxide. Geochim. Cosmochim. Acta 2011, 75, 5510–5525. [Google Scholar] [CrossRef]
- Munz, I.A.; Brandvoll, Ø.; Haug, T.A.; Iden, K.; Smeets, R.; Kihle, J.; Johansen, H. Mechanisms and rates of plagioclase carbonation reactions. Geochim. Cosmochim. Acta 2012, 77, 27–51. [Google Scholar] [CrossRef]
- Hellevang, H.; Pham, V.T.H.; Aagaard, P. Kinetic modelling of CO2–water–rock interactions. Int. J. Greenh. Gas Control. 2013, 15, 3–15. [Google Scholar] [CrossRef]
- Wolff-Boenisch, D.; Galeczka, I.M. Flow-through reactor experiments on basalt-(sea)water-CO2 reactions at 90 °C and neutral pH. What happens to the basalt pore space under post-injection conditions? Int. J. Greenh. Gas Control 2018, 68, 176–190. [Google Scholar] [CrossRef]
- Tutolo, B.M.; Aaolayo, A.; Brown, C. Alkalinity generation constraints on basalt carbonation for carbon dioxide removal at the gigaton-per-year scale. Environ. Sci. Technol. 2021, 55, 11906–11915. [Google Scholar] [CrossRef]
- Snæbjörnsdóttir, S.Ó.; Gislason, S.R.; Galeczka, I.M.; Oelkers, E.H. Reaction path modelling of in-situ mineralisation of CO2 at the CarbFix site at Hellisheidi, SW-Iceland. Geochim. Cosmochim. Acta 2018, 220, 348–366. [Google Scholar] [CrossRef]
- Snæbjörnsdóttir, S.Ó.; Sigfússon, B.; Marieni, C.; Goldberg, D.; Gislason, S.R.; Oelkers, E.H. Carbon dioxide storage through mineral carbonation. Nat. Rev. Earth Environ. 2020, 1, 90–102. [Google Scholar] [CrossRef]
- Kelemen, P.B.; Benson, S.M.; Pilorge, H.; Psarras, P.; Wilcox, J. An overview of the status and challenges of CO2 storage in minerals and geological formations. Front. Clim. 2019, 1, 9. [Google Scholar] [CrossRef]
- Kelemen, P.B.; McQueen, N.; Wilcox, J.; Renforth, P.; Dipple, G.; Vankeuren, A.P. Engineered carbon mineralization in ultramafic rocks for CO2 removal from air: Review and new insights. Chem. Geol. 2020, 550, 119628. [Google Scholar] [CrossRef]
- Galeczka, I.M.; Stefánsson, A.; Kleine, B.I.; Gunnarsson-Robin, J.; Snæbjörnsdóttir, S.Ó.; Sigfússon, B.; Gunnarsdóttir, S.H.; Weisenberger, T.B.; Oelkers, E.H. A pre-injection assessment of CO2 and H2S mineralization reactions at the Nesjavellir (Iceland) geothermal storage site. Int. J. Greenh. Gas Control 2022, 115, 103610. [Google Scholar] [CrossRef]
- Oelkers, E.H.; Gislason, S.R.; Kelemen, P.B. Moving Subsurface Carbon Mineral Storage Forward. Carbon Capture Sci. Tech. 2023, 7, 100098. [Google Scholar] [CrossRef]
- Crovisier, J.L.; Fritz, B.; Grambow, B.; Eberhart, J.P. Dissolution of basaltic glass in seawater: Experiments and thermodynamic modelling. MRS Online Proc. Libr. 1985, 50, 273–282. [Google Scholar] [CrossRef]
- Crovisier, J.L.; Honnorez, J.; Eberhart, J.P. Dissolution of basaltic glass in seawater: Mechanism and rate. Geochim. Cosmochim. Acta 1987, 51, 2977–2990. [Google Scholar] [CrossRef]
- Gislason, S.R.; Eugster, H.P. Meteoric water-basalt interactions: I. A laboratory study. Geochim. Cosmochim. Acta 1987, 51, 2827–2840. [Google Scholar] [CrossRef]
- Guy, C. Mécanismes de Dissolution des Solides Dans les Solutions Hydrothermales Deduits du Comportement des Verres Basaltiques et de Calcites Deformees; Universite Paul Sabatier: Toulouse, France, 1989. [Google Scholar]
- Oelkers, E.H.; Gislason, S.R. The mechanism, rates and consequences of basaltic glass dissolution: I. An experimental study of the dissolution rates of basaltic glass as a function of aqueous Al, Si and oxalic acid concentration at 25 °C and pH = 3 and 11. Geochim. Cosmochim. Acta 2001, 65, 3671–3681. [Google Scholar] [CrossRef]
- Wolff-Boenisch, D.; Gislason, S.R.; Oelkers, E.H. The effect of fluoride on the dissolution rates of natural glasses at pH 4 and 25 °C. Geochim. Cosmochim. Acta 2004, 68, 4571–4582. [Google Scholar] [CrossRef]
- Wolff-Boenisch, D.; Gislason, S.R.; Oelkers, E.H.; Putnis, C.V. The dissolution rates of natural glasses as a function of their composition at pH 4 and 10.6, and temperatures from 25 to 74 °C. Geochim. Cosmochim. Acta 2004, 68, 4843–4858. [Google Scholar] [CrossRef]
- Wolff-Boenisch, D.; Gislason, S.R.; Oelkers, E.H. The effect of crystallinity on dissolution rates and CO2 consumption capacity of silicates. Geochim. Cosmochim. Acta 2006, 70, 858–870. [Google Scholar] [CrossRef]
- Stockmann, G.J.; Wolff-Boenisch, D.; Gislason, S.R.; Oelkers, E.H. Do carbonate precipitates affect dissolution kinetics? 1: Basaltic glass. Chem. Geol. 2011, 284, 306–316. [Google Scholar] [CrossRef]
- Parruzot, B.; Jollivet, P.; Rebiscoul, D.; Gin, S. Long-term alteration of basaltic glass: Mechanisms and rates. Geochim. Cosmochim. Acta 2015, 154, 28–48. [Google Scholar] [CrossRef]
- Sjoberg, L. The effect of pH and phthalic acid on labradorite dissolution kinetics. Geol. Föreningen I Stockh. Förhandlingar 1985, 107, 311–313. [Google Scholar] [CrossRef]
- Casey, W.H.; Westrich, H.R.; Arnold, G.W. Surface chemistry of labradorite feldspar reacted with aqueous solutions at pH 2, 3, and 12. Geochim. Cosmochim. Acta 1988, 52, 2795–2807. [Google Scholar] [CrossRef]
- Casey, W.H.; Westrich, H.R.; Arnold, G.W.; Banfield, J.F. The surface chemistry of dissolving labradorite feldspar. Geochim. Cosmochim. Acta 1989, 53, 821–832. [Google Scholar] [CrossRef]
- Cygan, R.T.; Casey, W.H.; Boslough, M.B.; Westrich, H.R.; Carr, M.J.; Holdren, G.R., Jr. Dissolution kinetics of experimentally shocked silicate minerals. Chem. Geol. 1989, 78, 229–244. [Google Scholar] [CrossRef]
- Nesbitt, H.; Macrae, N.; Shotyk, W. Congruent and incongruent dissolution of labradorite in dilute, acidic, salt solutions. J. Geol. 1991, 99, 429–442. [Google Scholar] [CrossRef]
- Welch, S.A.; Ullman, W.J. Feldspar dissolution in acidic and organic solutions. Compositional and pH dependence of dissolution rate. Geochim. Cosmochim. Acta 1996, 60, 2939–2948. [Google Scholar] [CrossRef]
- Taylor, A.S.; Blum, J.D.; Lasaga, A.C. The dependence of labradorite dissolution and Sr isotope release rates on solution saturation state. Geochim. Cosmochim. Acta 2000, 64, 2389–2400. [Google Scholar] [CrossRef]
- Carroll, S.A.; Knauss, K.G. Dependence of labradorite dissolution kinetics on CO2(aq), Al(aq), and temperature. Chem. Geol. 2005, 217, 213–225. [Google Scholar] [CrossRef]
- Gudbrandsson, S.; Wolff-Boenisch, D.; Gislason, S.R.; Oelkers, E.H. Experimental determination of plagioclase dissolution rates as a function of its composition and pH at 22 °C. Geochim. Cosmochim. Acta 2014, 139, 154–172. [Google Scholar] [CrossRef]
- Wild, B.; Daval, D.; Guyot, F.; Knauss, K.G.; Pollet-Villard, M.; Imfeld, G. pH-dependent control of feldspar dissolution rate by altered surface layers. Chem. Geol. 2016, 442, 148–159. [Google Scholar] [CrossRef]
- Gadikota, G.; Matter, J.; Kelemen, P.; Brady, P.V.; Park, A.-H. Elucidating the differences in the carbon mineralization behaviours of calcium and magnesium bearing alumino-silicates and magnesium silicates for CO2 storage. Fuel 2020, 277, 117900. [Google Scholar] [CrossRef]
- de Obeso, J.C.; Awolayo, A.N.; Nightingale, M.J.; Tan, C.; Tutolo, B.M. Experimental study on plagioclase dissolution rates at conditions relevant to mineral carbonation of seafloor basalts. Chem. Geol. 2023, 620, 121348. [Google Scholar] [CrossRef]
- Celia, M.A.; Bachu, S.; Nordbotten, J.M.; Bandilla, K.W. Status of CO2 storage in deep saline aquifers with emphasis on modeling approaches and practical simulations. Water Resour. Res. 2015, 51, 6846–6892. [Google Scholar] [CrossRef]
- Kumar, S.; Foroozesh, J.; Edlmann, K.; Rezk, M.G.; Lim, C.Y. A comprehensive review of value-added CO2 sequestration in subsurface saline aquifers. J. Nat. Gas Sci. Eng. 2020, 81, 103437. [Google Scholar] [CrossRef]
- Ringrose, P.S.; Furre, A.-K.; Gilfillan, S.M.V.; Krevor, S.; Landrø, M.; Leslie, R.; Meckel, T.; Nazarian, B.; Zahid, A. Storage of carbon dioxide in saline aquifers: Physicochemical processes, key constraints, and scale-up potential. Ann. Rev. Chem. Biomol. 2021, 12, 471–494. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Xu, R.; Jiang, P. Effect of reactive surface area of minerals on mineralization trapping of CO2 in saline aquifers. Pet. Sci. 2012, 9, 400–407. [Google Scholar] [CrossRef]
- Marieni, C.; Voigt, M.; Clark, D.E.; Gíslason, S.R.; Oelkers, E.H. Mineralization potential of water-dissolved CO2 and H2S injected into basalts as function of temperature: Freshwater versus Seawater. Int. J. Greenh. Gas Control 2021, 109, 103357. [Google Scholar] [CrossRef]
- Voigt, M.; Marieni, C.; Baldermann, A.; Galeczka, I.M.; Wolff-Boenisch, D.; Oelkers, E.H.; Gislason, S.R. An experimental study of basalt–seawater–CO2 interaction at 130 °C. Geochim. Cosmochim Acta 2021, 308, 21–41. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations. US Geol. Surv. Tech. Methods 2013, 6, 497. [Google Scholar]
- Voigt, M.; Marieni, C.; Clark, D.E.; Gíslason, S.R.; Oelkers, E.H. Evaluation and refinement of thermodynamic databases for mineral carbonation. Energy Procedia 2018, 146, 81–91. [Google Scholar] [CrossRef]
- Brantley, S.L.; Kubicki, J.; White, A. (Eds.) Kinetics of Water-Rock Interaction; Springer: New York, NY, USA, 2008; 833p. [Google Scholar]
- Aagaard, P.; Helgeson, H.C. Thermodynamic and kinetic constraints on the dissolution of feldspars. Geol. Soc. Am. Abstr. Progr. 1977, 9, 873. [Google Scholar]
- Aagaard, P.; Helgeson, H.C. Thermodynamic and kinetic constraints on reaction-rates among minerals and aqueous-Solutions. 1. Theoretical Considerations. Am. J. Sci. 1982, 282, 237–285. [Google Scholar] [CrossRef]
- Lasaga, A.C. Transition state theory. Rev. Min. 1981, 8, 135–169. [Google Scholar]
- Schott, J.; Oelkers, E.H. Dissolution and crystallization rates of silicate minerals as a function of chemical affinity. Pure Appl. Chem. 1995, 67, 903–910. [Google Scholar] [CrossRef]
- Oelkers, E.H. General kinetic description of multioxide silicate mineral and glass dissolution. Geochim. Cosmochim. Acta 2001, 65, 3703–3719. [Google Scholar] [CrossRef]
- Oelkers, E.H.; Schott, J.; Devidal, J.-L. The effect of aluminium, pH, and chemical affinity on the rates of aluminosilicate dissolution reactions. Geochim. Cosmochim. Acta 1994, 58, 2011–2024. [Google Scholar] [CrossRef]
- Eyring, H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107. [Google Scholar] [CrossRef]
- Schott, J.; Pokrovsky, O.S.; Oelkers, E.H. The link between mineral dissolution/precipitation kinetics and solution chemistry. Rev. Mineral. Geochem. 2009, 70, 207–258. [Google Scholar] [CrossRef]
- Oelkers, E.H.; Schott, J. Experimental study of anorthite dissolution and the relative mechanism of feldspar hydrolysis. Geochim. Cosmochim. Acta 1995, 59, 5039–5053. [Google Scholar] [CrossRef]
- Tester, J.W.; Worley, W.G.; Robinson, B.A.; Grigsby, C.O.; Feerer, J.L. Correlating quartz dissolution kinetics in pure water from 25 to 625 °C. Geochim. Cosmochim. Acta 1994, 58, 2407–2420. [Google Scholar] [CrossRef]
- Gislason, S.R.; Oelkers, E.H. Mechanism, rates, and consequences of basaltic glass dissolution: II. An experimental study of the dissolution rates of basaltic glass as a function of pH and temperature. Geochim. Cosmochim. Acta 2003, 67, 3817–3832. [Google Scholar] [CrossRef]
- Flaathen, T.K.; Gislason, S.R.; Oelkers, E.H. The effect of aqueous sulphate on basaltic glass dissolution rates. Chem. Geol. 2010, 277, 345–354. [Google Scholar] [CrossRef]
- Stockmann, G.J.; Shirokova, L.S.; Pokrovsky, O.S.; Bénézeth, P.; Bovet, N.; Gislason, S.R.; Oelkers, E.H. Does the presence of heterotrophic bacterium Pseudomonas reactans affect basaltic glass dissolution rates? Chem. Geo. 2012, 296–297, 1–18. [Google Scholar] [CrossRef]
- Prikryl, J.; Jha, D.; Stefansson, A.; Stipp, S.L.S. Mineral dissolution in porous media: An experimental and modelling study on kinetics, porosity and surface area evolution. Appl. Geochem. 2017, 87, 57–70. [Google Scholar] [CrossRef]
- Saetre, C.; Hellevang, H.; Riu, L.; Dypvik, H.; Pilorget, C.; Poulet, F.; Werner, S.C. Experimental hydrothermal alteration of basaltic glass with relevance to Mars. Meteorit. Planet. Sci. 2018, 54, 357–378. [Google Scholar] [CrossRef]
- Clark, D.E.; Galeczka, I.M.; Dideriksen, K.; Voigt, M.J.; Wolff-Boenisch, D.; Gislason, S.R. Experimental observations of CO2-water-basaltic glass interaction in a large column reactor experimental 50 °C. Int. J. Greenh. Gas Control 2019, 89, 9–19. [Google Scholar] [CrossRef]
- Ralston, S.J.; Peretyazhko, T.S.; Sutter, B.; Ming, D.W.; Morris, R.V.; Garcia, A.; Ostwald, A. Phyllosilicate formation on early Mars via open-system acid alteration of basaltic glass. Earth Planet. Sci. Let. 2023, 603, 117987. [Google Scholar] [CrossRef]
- Kristmannsdottir, H. Anorthosite inclusions in tertiary dolerite from the island groups Hrappsey and Purkey, West Iceland. J. Geol. 1971, 79, 741–748. [Google Scholar] [CrossRef]
- Saldi, G.D.; Schott, J.; Pokrovsky, O.S.; Oelkers, E.H. An experimental study of magnesite dissolution rates at neutral to alkaline conditions and 150 and 200 °C as a function of pH, total dissolved carbonate concentration, and chemical affinity. Geochim. Cosmochim. Acta 2010, 74, 6344–6356. [Google Scholar] [CrossRef]
- Oelkers, E.H.; Golubev, S.V.; Pokrovsky, O.S.; Bénézeth, P. Do organic ligands affect calcite dissolution rates? Geochim. Cosmochim. Acta 2011, 75, 1799–1813. [Google Scholar] [CrossRef]
- Brantley, S.L. Reaction Kinetics of Primary Rock-forming Minerals under Ambient Conditions. Treatise Geochem. 2003, 5, 605. [Google Scholar]
- Heřmanská, M.; Voigt, M.J.; Marieni, C.; Declercq, J.; Oelkers, E.H. A comprehensive and internally consistent mineral dissolution rate database: Part I: Primary silicate minerals and glasses. Chem. Geol. 2022, 597, 120807. [Google Scholar] [CrossRef]
- Oxburgh, R.; Drever, J.I.; Sun, Y.-T. Mechanism of plagioclase dissolution in acid solution at 25 °C. Geochim. Cosmochim. Acta 1994, 58, 661–669. [Google Scholar]
- Icenhower, J.P.; Dove, P.M. Solution kinetic effects of amorphous silica into sodium chloride solutions: Effects of temperature and ionic strength. Geochim. Cosmochim. Acta 2000, 64, 4193–4203. [Google Scholar] [CrossRef]
- Brady, P.V.; Walther, J.V. Kinetics of quartz dissolution at low temperatures. Chem. Geol. 1990, 82, 253–264. [Google Scholar] [CrossRef]


| Solid | Chemical Composition | Ageo (m2/g) |
|---|---|---|
| Normalized to 1 silicon atom | ||
| Basaltic glass | Si1.000Al0.365Fe0.191Mn0.003Mg0.294Ca0.263Na0.081K0.008Ti0.025P0.004O3.405 | 0.0251 |
| Labradorite | Si1.000Al0.684Ca0.286Na0.139K0.002Fe0.008O3.107 | 0.0284 |
| Normalized to 8 oxygen atoms | ||
| Basaltic glass | Si2.281Al0.833Fe0.436Mn0.007Mg0.669Ca0.6 Na0.184K0.019Ti0.058 P0.008O8 | 0.0251 |
| Labradorite | Si2.359Al1.612Ca0.674Na0.327K0.006Fe0.018O8 | 0.0284 |
| Experiment ID | Inlet Fluid Composition 1 | Ionic Strength (mol·kg−1) | Exp. Duration (h) | pH In | pH Out | (Si) Out (mol × 105) | Log r+si Geo 1 |
|---|---|---|---|---|---|---|---|
| G-NaCl-10 | 10 × 10−3 mol·kg−1 NaCl | 0.01 | 210 | 3.59 | 3.67 | 0.95 | −8.85 |
| G-KCl-10 | 10 × 10−3 mol·kg−1 KCl | 0.01 | 176 | 3.57 | 3.60 | 0.81 | −8.92 |
| G-CaCl2-10 | 10 × 10−3 mol·kg−1 CaCl2·2H2O | 0.03 | 193 | 3.55 | 3.61 | 1.77 | −8.58 |
| G-MgCl2-10 | 10 × 10−3 mol·kg−1 MgCl2·6H2O | 0.03 | 209 | 3.64 | 3.67 | 2.00 | −8.52 |
| G-NaCl-100 | 100 × 10−3 mol·kg−1 NaCl | 0.1 | 210 | 3.86 | 3.80 | 1.06 | −8.80 |
| G-KCl-100 | 100 × 10−3 mol·kg−1 KCl | 0.1 | 176 | 3.65 | 3.66 | 0.71 | −8.97 |
| G-CaCl2-100 | 100 × 10−3 mol·kg−1 CaCl2·2H2O | 0.3 | 193 | 3.53 | 3.66 | 1.75 | −8.59 |
| G-MgCl2-100 | 100 × 10−3 mol·kg−1 MgCl2·6H2O | 0.3 | 209 | 3.59 | 3.64 | 1.37 | −8.69 |
| G-NaCl-700 | 700 × 10−3 mol·kg−1 NaCl | 0.7 | 210 | 3.57 | 3.71 | 1.92 | −8.55 |
| G-KCl-700 | 700 × 10−3 mol·kg−1 KCl | 0.7 | 176 | 3.64 | 3.58 | 1.94 | −8.54 |
| G-CaCl2-700 | 700 × 10−3 mol·kg−1 CaCl2·2H2O | 2.1 | 193 | 3.56 | 3.74 | 3.77 | −8.25 |
| G-MgCl2-700 | 700 × 10−3 mol·kg−1 MgCl2·6H2O | 2.1 | 209 | 3.63 | 3.67 | 1.62 | −8.62 |
| L-NaCl-10 | 10 × 10−3 mol·kg−1 NaCl | 0.01 | 208 | 3.68 | 3.76 | 1.80 | −9.02 |
| L-KCl-10 | 10 × 10−3 mol·kg−1 KCl | 0.01 | 223 | 3.62 | 3.73 | 1.38 | −9.09 |
| L-CaCl2–10 | 10 × 10−3 mol·kg−1 CaCl2·2H2O | 0.03 | 236 | 3.64 | 3.72 | 0.67 | −9.41 |
| L-MgCl2–10 | 10 × 10−3 mol·kg−1 MgCl2·6H2O | 0.03 | 237 | 3.64 | 3.70 | 0.53 | −9.51 |
| L-NaCl-50 | 50 × 10−3 mol·kg−1 NaCl | 0.05 | 208 | 3.64 | 3.74 | 1.64 | −9.03 |
| L-KCl-50 | 50 × 10−3 mol·kg−1 KCl | 0.05 | 223 | 3.66 | 3.73 | 1.26 | −9.14 |
| L-CaCl2-50 | 50 × 10−3 mol·kg−1 CaCl2·2H2O | 0.15 | 236 | 3.61 | 3.65 | 0.70 | −9.40 |
| L-MgCl2-50 | 50 × 10−3 mol·kg−1 MgCl2·6H2O | 0.15 | 237 | 3.65 | 3.65 | 0.84 | −9.13 |
| L-NaCl-200 | 200 × 10−3 mol·kg−1 NaCl | 0.2 | 208 | 3.63 | 3.71 | 3.12 | −8.75 |
| L-KCl-200 | 200 × 10−3 mol·kg−1 KCl | 0.2 | 223 | 3.66 | 3.65 | 3.57 | −8.69 |
| L-CaCl2–200 | 200 × 10−3 mol·kg−1 CaCl2·2H2O | 0.6 | 236 | 3.66 | 3.69 | 2.37 | −8.86 |
| L-MgCl2–200 | 200 × 10−3 mol·kg−1 MgCl2·6H2O | 0.6 | 237 | 3.68 | 3.70 | 1.73 | −9.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mesfin, K.G.; Wolff-Boenisch, D.; Gislason, S.R.; Oelkers, E.H. Effect of Cation Chloride Concentration on the Dissolution Rates of Basaltic Glass and Labradorite: Application to Subsurface Carbon Storage. Minerals 2023, 13, 682. https://doi.org/10.3390/min13050682
Mesfin KG, Wolff-Boenisch D, Gislason SR, Oelkers EH. Effect of Cation Chloride Concentration on the Dissolution Rates of Basaltic Glass and Labradorite: Application to Subsurface Carbon Storage. Minerals. 2023; 13(5):682. https://doi.org/10.3390/min13050682
Chicago/Turabian StyleMesfin, Kiflom G., Domenik Wolff-Boenisch, Sigurdur R. Gislason, and Eric H. Oelkers. 2023. "Effect of Cation Chloride Concentration on the Dissolution Rates of Basaltic Glass and Labradorite: Application to Subsurface Carbon Storage" Minerals 13, no. 5: 682. https://doi.org/10.3390/min13050682
APA StyleMesfin, K. G., Wolff-Boenisch, D., Gislason, S. R., & Oelkers, E. H. (2023). Effect of Cation Chloride Concentration on the Dissolution Rates of Basaltic Glass and Labradorite: Application to Subsurface Carbon Storage. Minerals, 13(5), 682. https://doi.org/10.3390/min13050682






