Optimizing Semi-Airborne Electromagnetic Survey Design for Mineral Exploration
Abstract
1. Introduction
2. Methodology
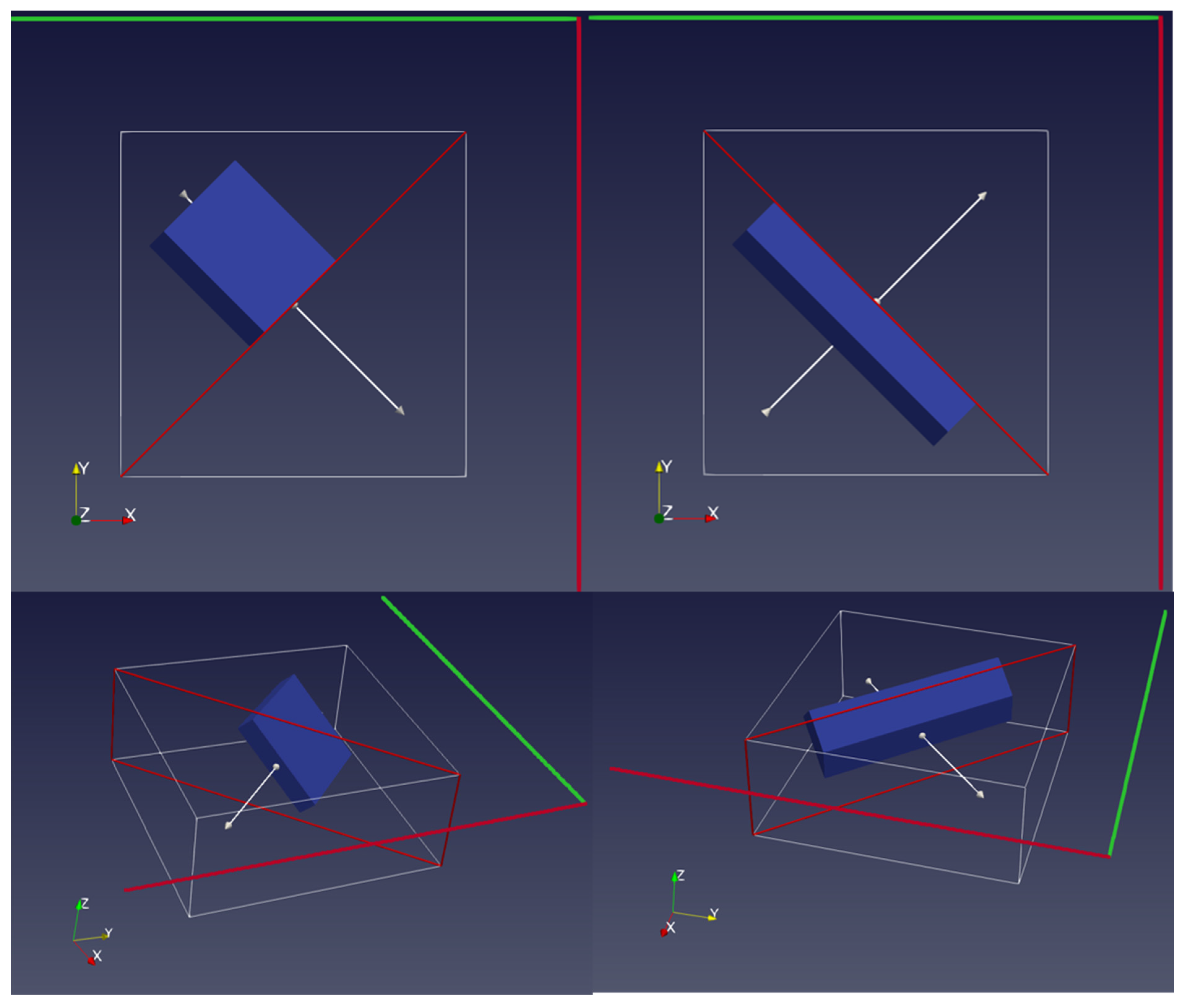
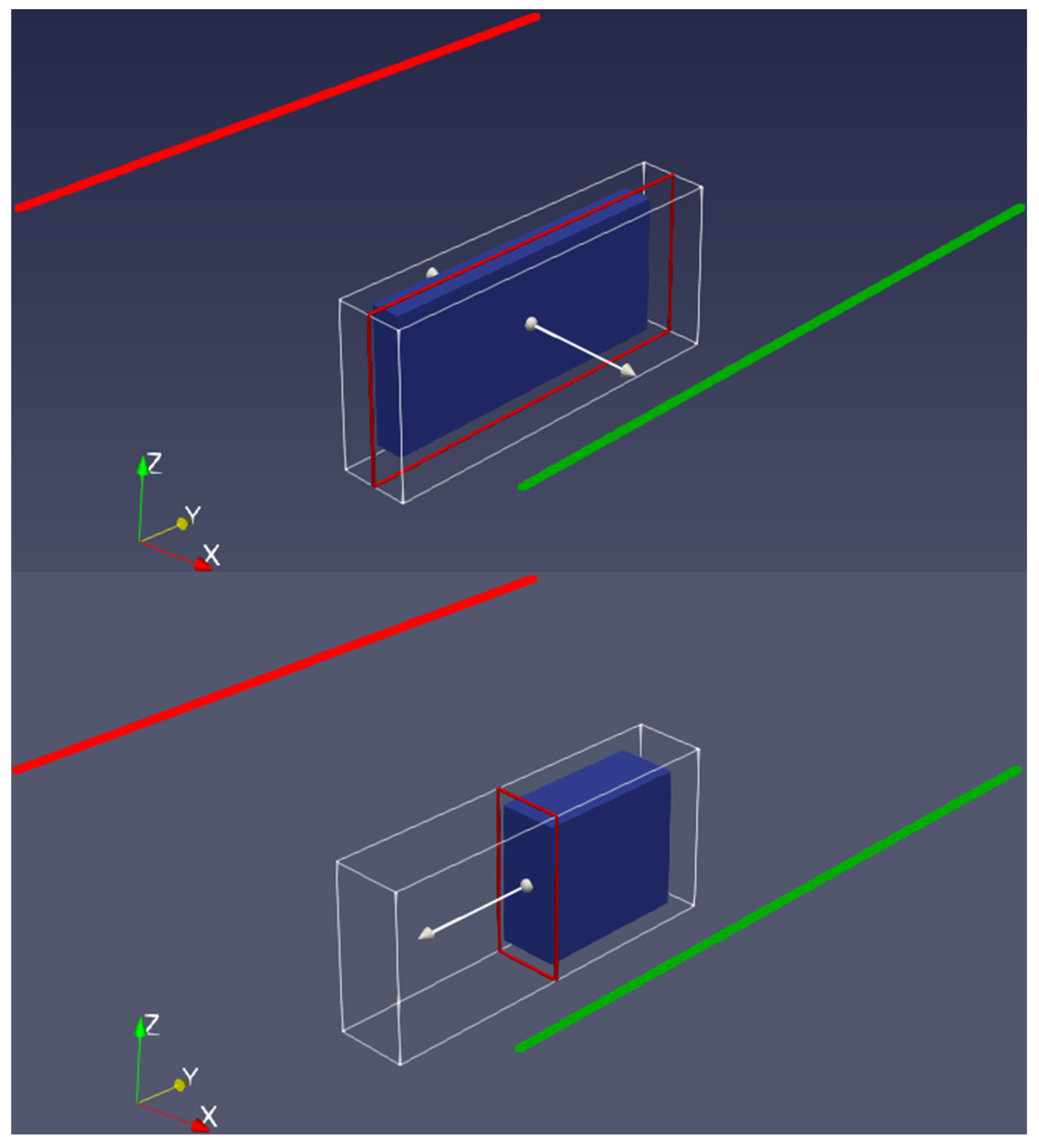
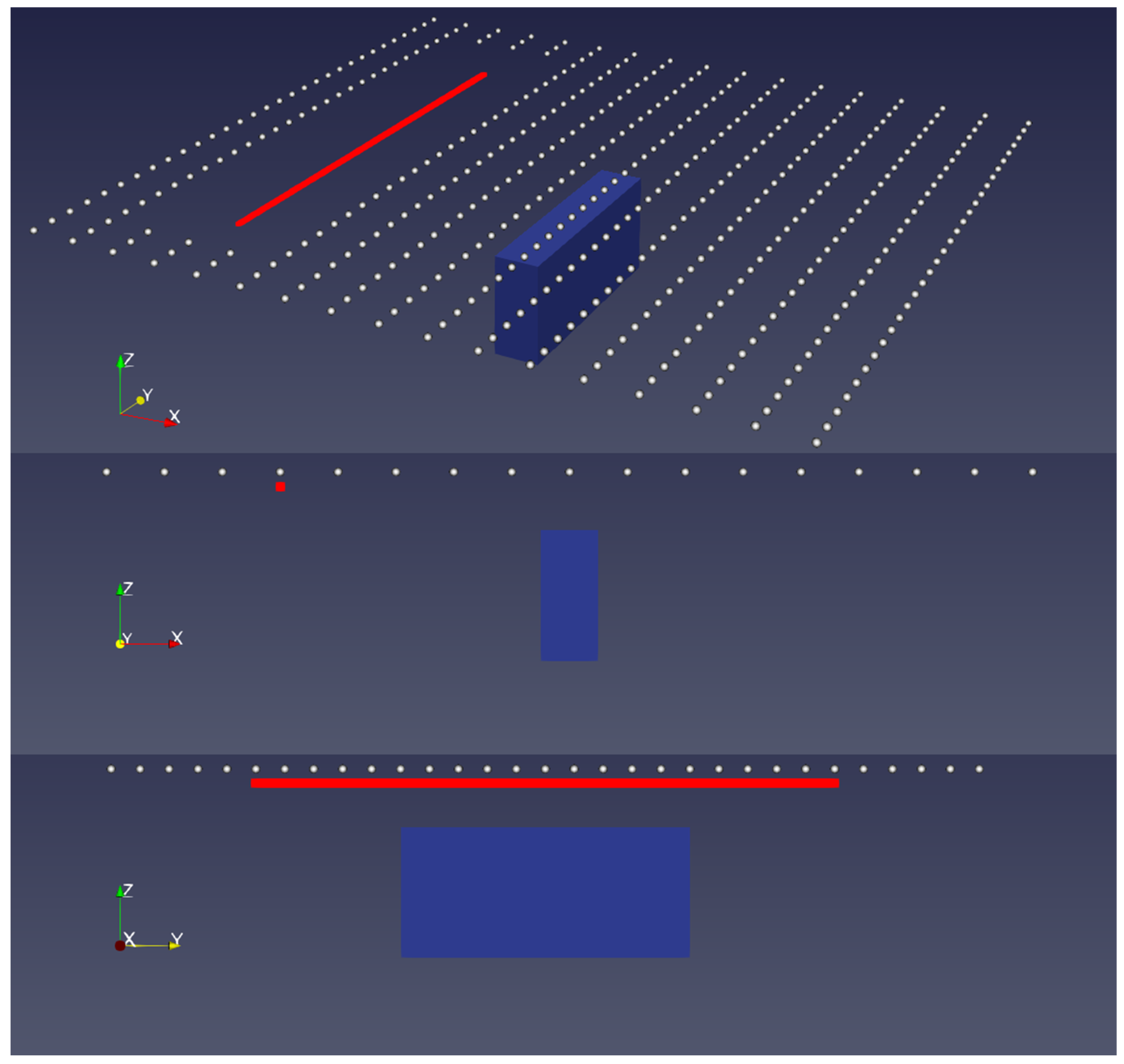
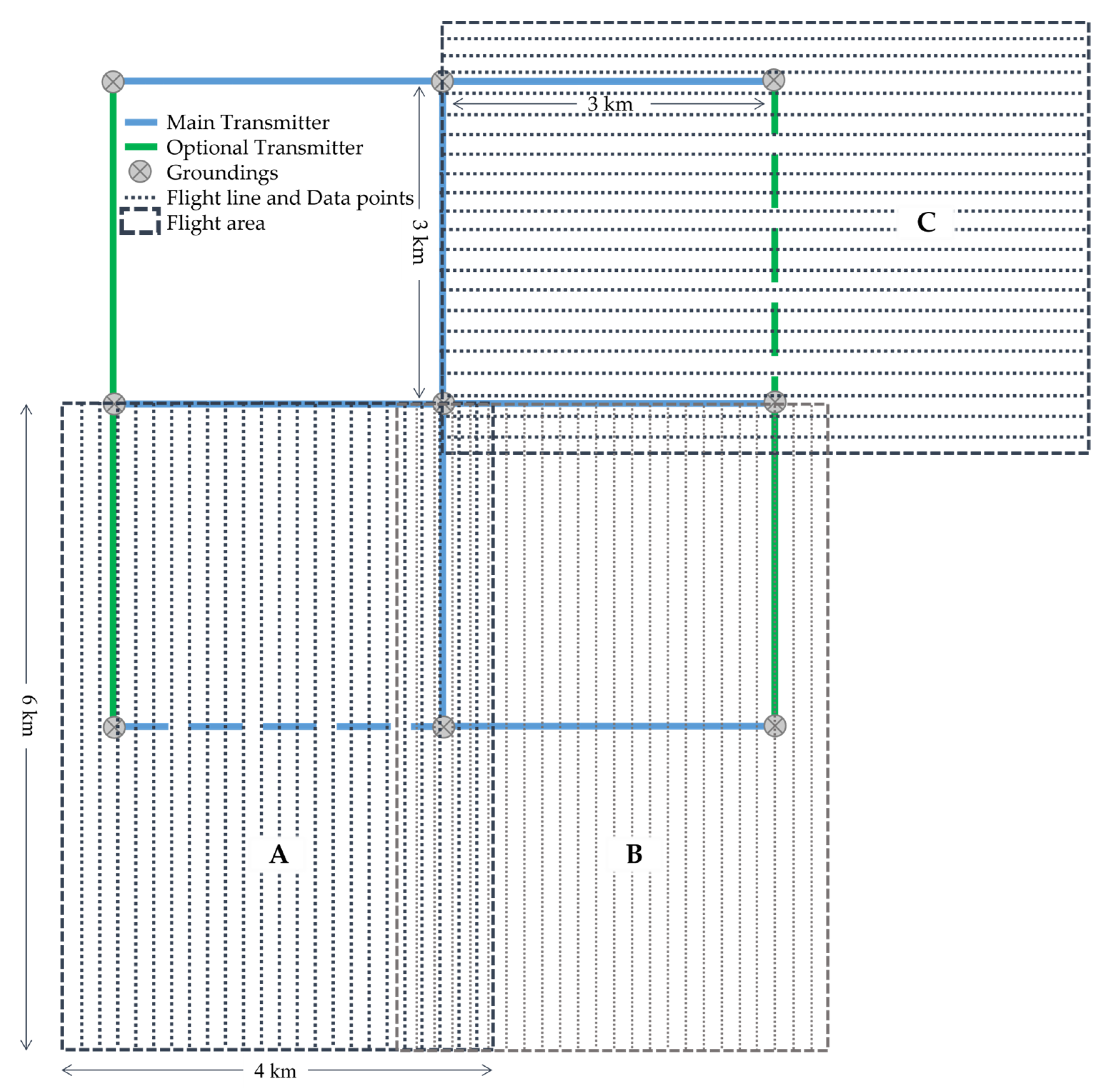
2.1. Scheme
2.2. Forward Problem and Inversion
2.3. Synthetic Experiments
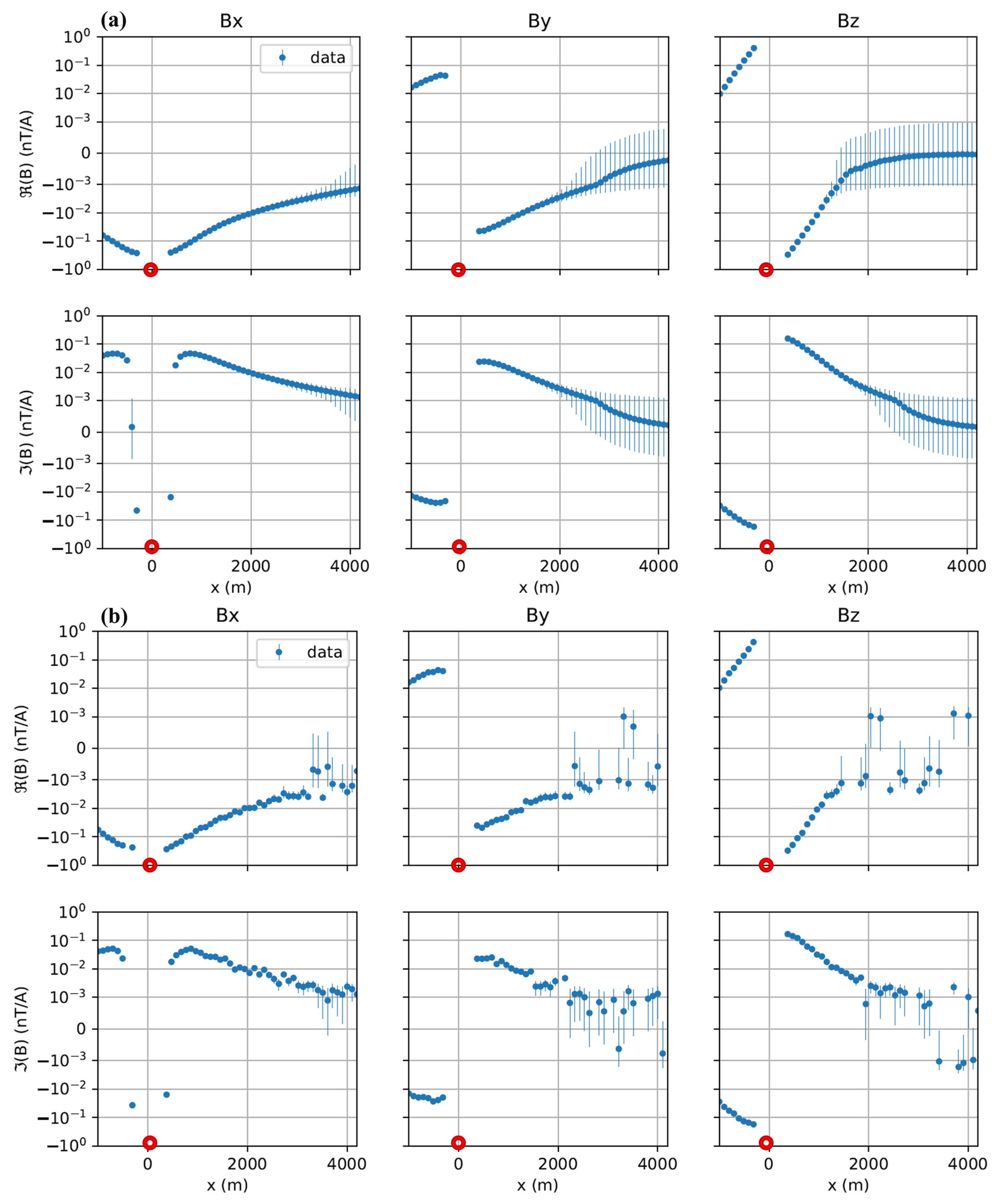
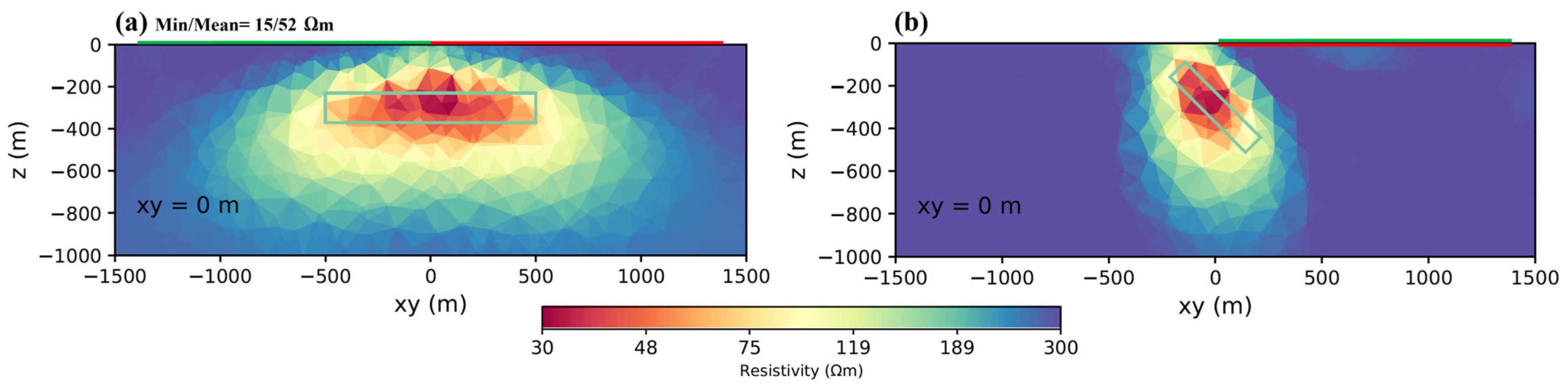
3. Single- and Multi-Component Inversion
4. Survey Parameters
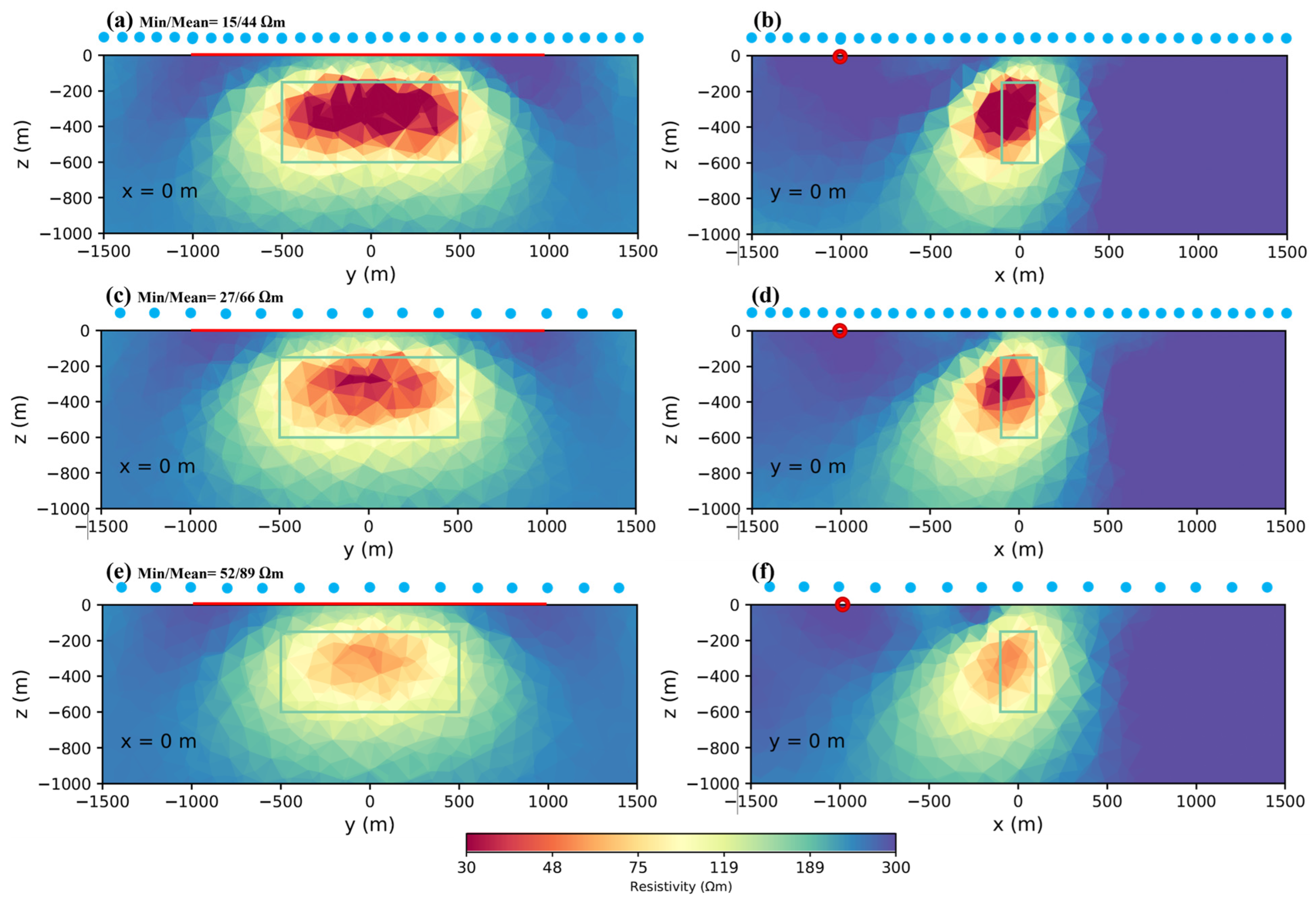
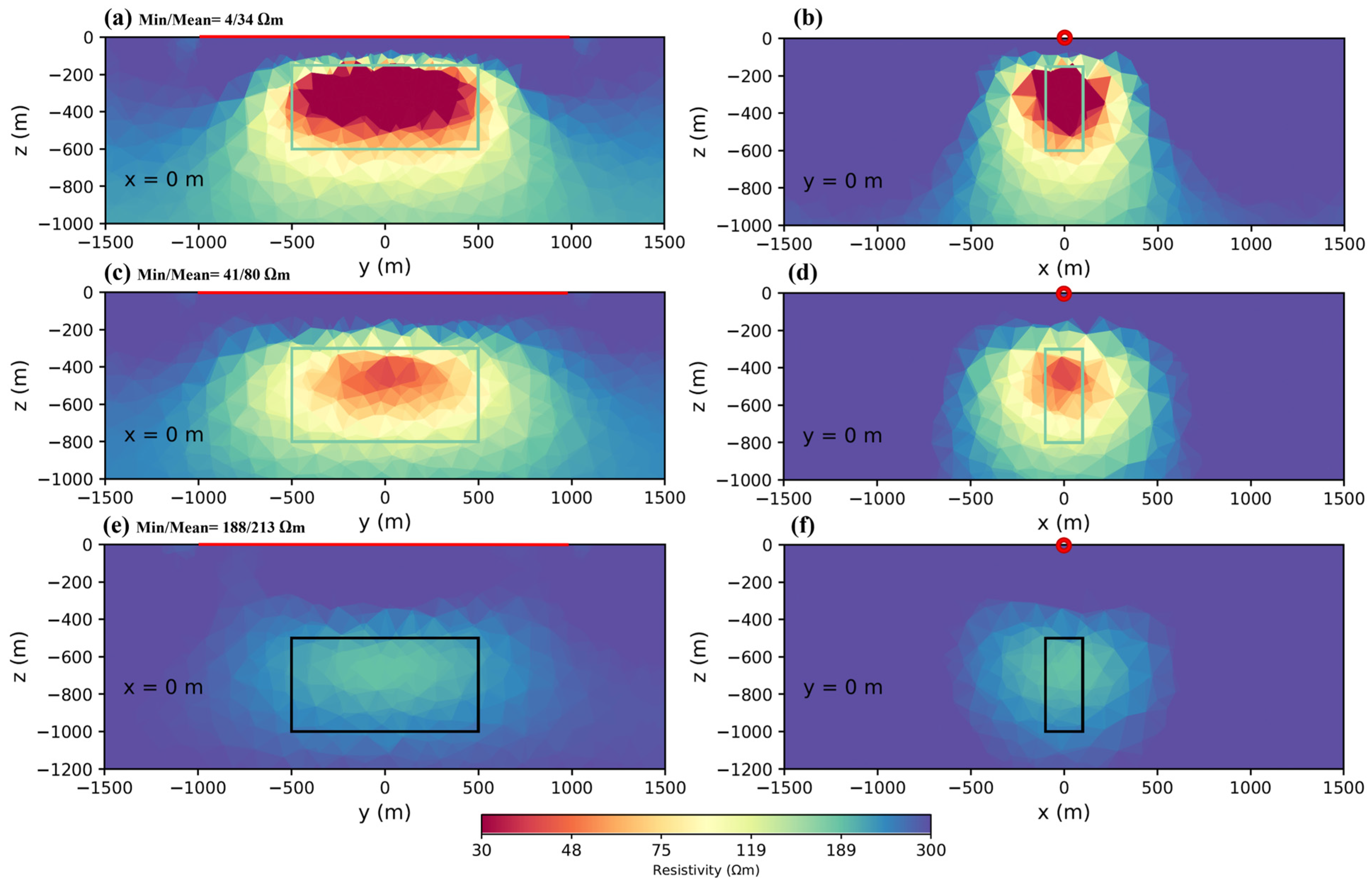
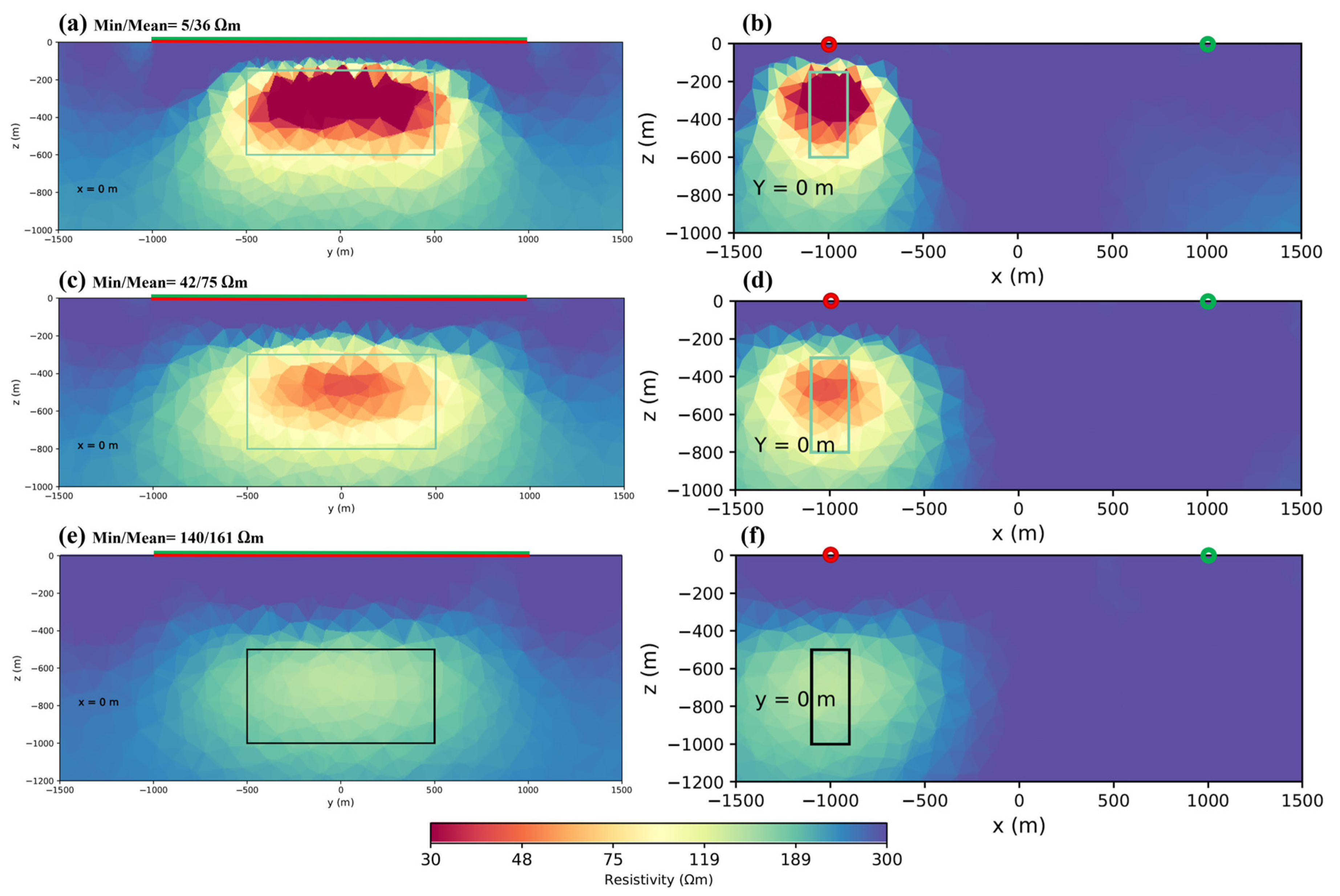
4.1. Surveying Data Density
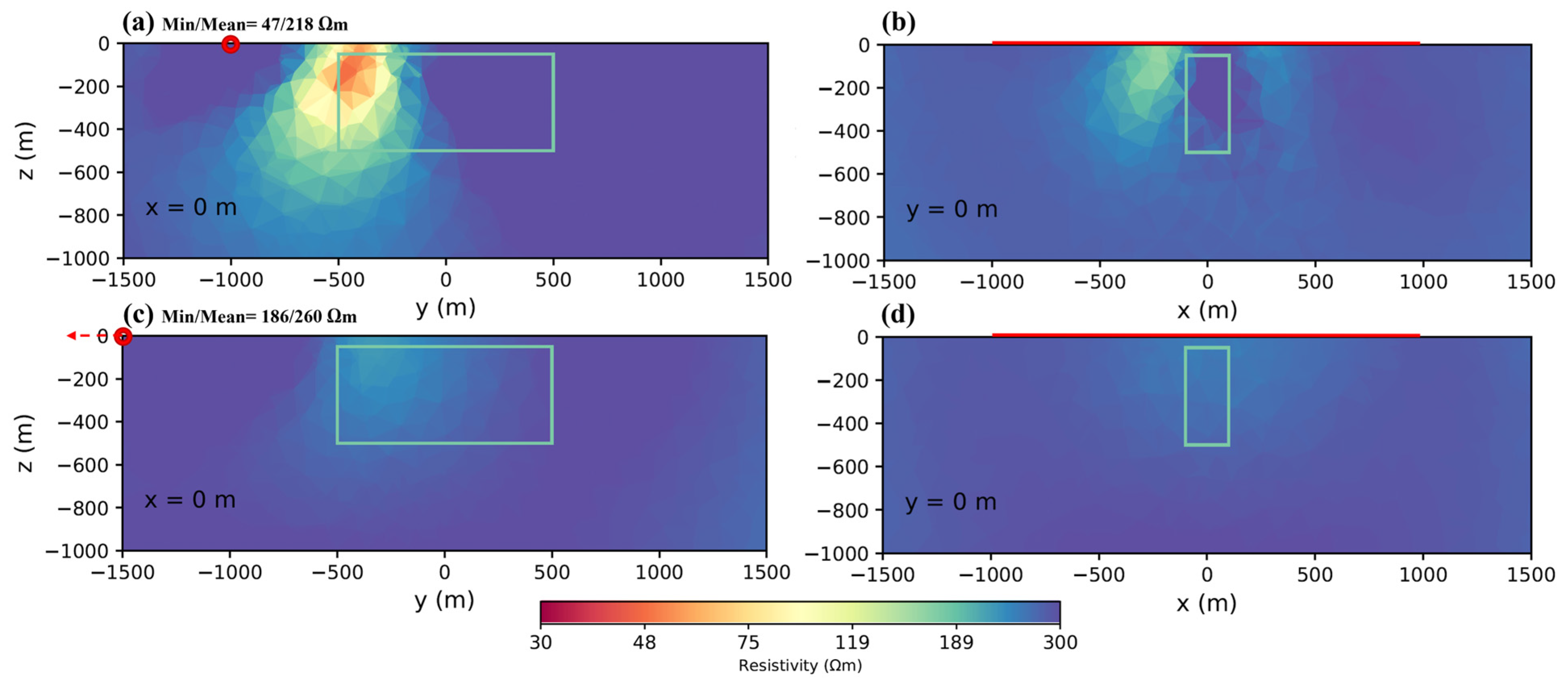
4.2. Transmitter Length
4.3. Transmitter Orientation with Respect to the Block
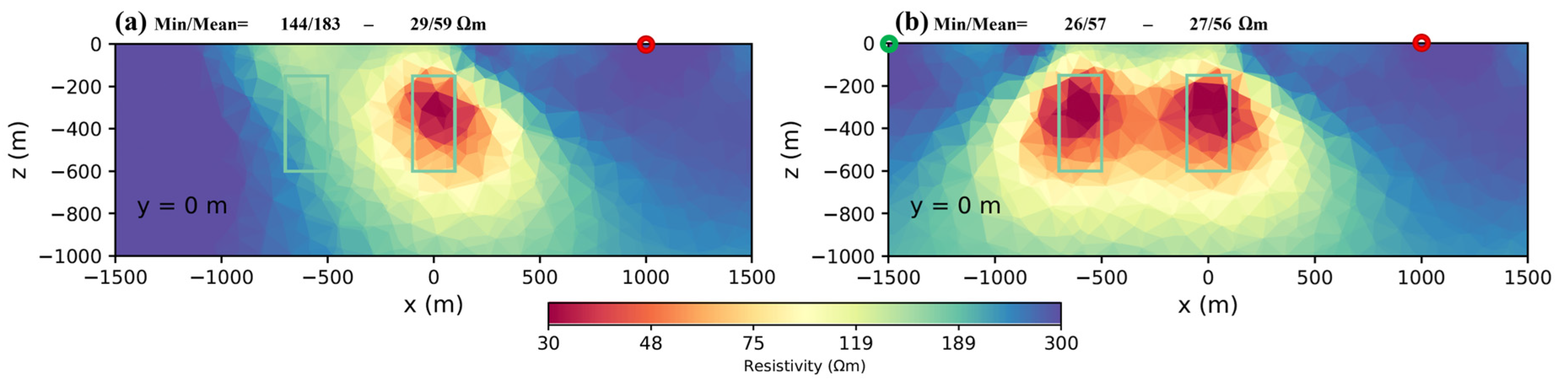
4.4. Using More Than One Transmitter
4.5. Transmitter Orientation with Respect to Each Other
4.6. The Distance of the Transmitters from Each Other
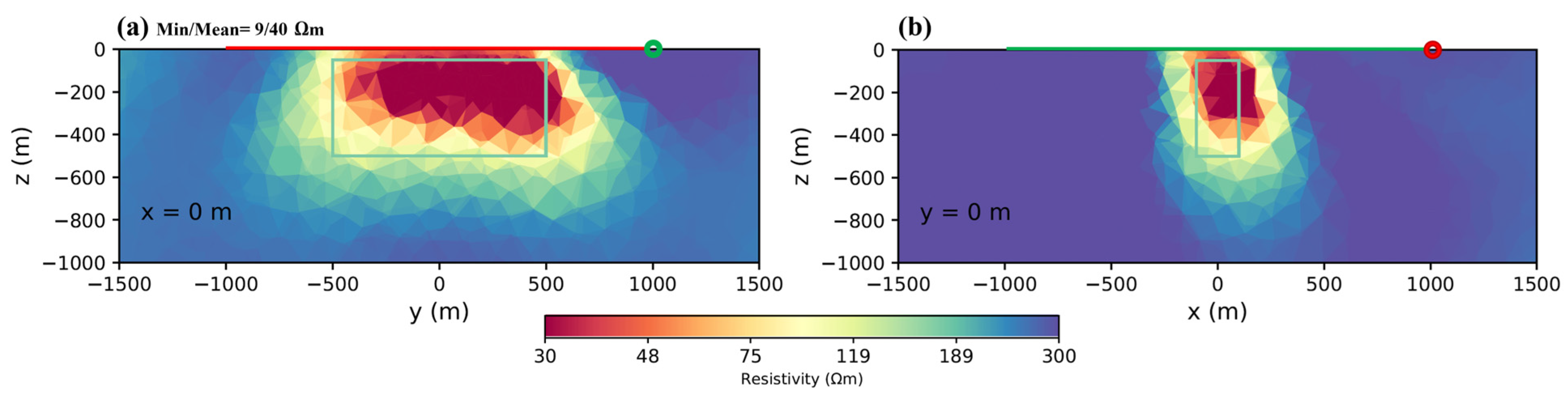
4.7. Anomalies under the Transmitter
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Becken, M.; Nittinger, C.G.; Smirnova, M.; Steuer, A.; Martin, T.; Petersen, H. DESMEX Working Group. DESMEX: A novel system development for semi-airborne electromagnetic exploration. Geophysics 2008, 85, E253–E267. [Google Scholar] [CrossRef]
- Kearey, P.; Brooks, M.; Hill, I. An Introduction to Geophysical Exploration; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Dentith, M.; Mudge, S.T. Geophysics for the Mineral Exploration Geoscientist; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- King, R.B.; Constable, S. How low can you go: An investigation of depth sensitivity and resolution using towed marine CSEM systems. Geophys. Prospect. 2023, 71, 722–733. [Google Scholar] [CrossRef]
- Maurer, H.; Boerner, D.E.; Curtis, A. Design strategies for electromagnetic geophysical surveys. Inverse Probl. 2000, 16, 1097. [Google Scholar] [CrossRef]
- Hennig, T.; Weller, A.; Möller, M. Object orientated focussing of geoelectrical multielectrode measurements. J. Appl. Geophys. 2008, 65, 57–64. [Google Scholar] [CrossRef]
- Coscia, I.; Marescot, L.; Maurer, H.; Greenhalgh, S.; Linde, N. Experimental design for crosshole electrical resistivity tomography data sets. In Near Surface 2008—14th EAGE European Meeting of Environmental and Engineering Geophysics; cp-64-00054; EAGE Publications B.V.: Houten, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Loke, M.H.; Wilkinson, P. Rapid parallel computation of optimized arrays for electrical imaging surveys. In Near Surface 2009—15th EAGE European Meeting of Environmental and Engineering Geophysics; cp-134-00049; EAGE Publications B.V.: Houten, The Netherlands, 2009. [Google Scholar] [CrossRef]
- Nowruzi, G.H. Optimum Design of Survey Grid in Magnetic Studies; University College of Engineering: Tehran, Iran, 1997; Volume 30. [Google Scholar]
- Ahmadi, R. Application of geometric probability to design exploration grid of mineral deposits, case study: Porphyry copper index located in the south-west of Kerman. J. Anal. Numer. Methods Min. Eng. 2018, 8, 39–54. [Google Scholar] [CrossRef]
- Agocs, W.B. Line spacing effect and determination of optimum spacing illustrated by Marmora, Ontario magnetic anomaly. Geophysics 1955, 20, 871–885. [Google Scholar] [CrossRef]
- McCammon, R.B. Target intersection probabilities for parallel line and continuous grid types of search. J. Math. Geol. 1977, 9, 369–382. [Google Scholar] [CrossRef]
- Chung, C.F. Application of the Buffon needle problem and its extensions to parallel-line search sampling scheme. J. Int. Assoc. Math. Geol. 1981, 13, 371–390. [Google Scholar] [CrossRef]
- Ajo-Franklin, J.B. Optimal experiment design for time-lapse traveltime tomography. Geophysics 2009, 74, Q27–Q40. [Google Scholar] [CrossRef]
- Brenders, A.J.; Pratt, R.G. Waveform tomography of marine seismic data: What can limited offset offer. In 2007 SEG Annual Meeting; OnePetro: Richardson, TX, USA, 2007. [Google Scholar]
- Curtis, A.; Snieder, R. Reconditioning inverse problems using the genetic algorithm and revised parameterization. Geophysics 1997, 62, 1524–1532. [Google Scholar] [CrossRef]
- Liner, C.L.; Underwood, W.D.; Gobeli, R. 3-D seismic survey design as an optimization problem. Lead. Edge 1999, 18, 1054–1060. [Google Scholar] [CrossRef]
- Sirgue, L.; Pratt, R.G. Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies. Geophysics 2004, 69, 231–248. [Google Scholar] [CrossRef]
- Smirnova, M.V.; Becken, M.; Nittinger, C.; Yogeshwar, P.; Mörbe, W.; Rochlitz, R.; Steuer, A.; Costabel, S.; Smirnov, M. DESMEX Working Group. A novel semiairborne frequency-domain controlled-source electromagnetic system: Three-dimensional inversion of semiairborne data from the flight experiment over an ancient mining area near Schleiz, Germany. Geophysics 2019, 84, E281–E292. [Google Scholar] [CrossRef]
- Chen, C.; Sun, H. Characteristic analysis and optimal survey area definition for semi-airborne transient electromagnetics. J. Appl. Geophys. 2020, 180, 104134. [Google Scholar] [CrossRef]
- Ke, Z.; Liu, Y.; Su, Y.; Wang, L.; Zhang, B.; Ren, X.; Ma, X. Three-Dimensional Inversion of Multi-Component Semi-Airborne Electromagnetic Data in an Undulating Terrain for Mineral Exploration. Minerals 2023, 13, 230. [Google Scholar] [CrossRef]
- Siemon, B.; Christiansen, A.V.; Auken, E. A review of helicopter-borne electromagnetic methods for groundwater exploration. Near Surf. Geophys. 2009, 7, 629–646. [Google Scholar] [CrossRef]
- Smith, R. Electromagnetic induction methods in mining geophysics from 2008 to 2012. Surv. Geophys. 2014, 35, 123–156. [Google Scholar] [CrossRef]
- Stolz, R.; Zakosarenko, V.; Schulz, M.; Chwala, A.; Fritzsch, L.; Meyer, H.G.; Köstlin, E.O. Magnetic full-tensor SQUID gradiometer system for geophysical applications. Lead. Edge 2006, 25, 178–180. [Google Scholar] [CrossRef]
- Rudd, J.; Chubak, G.; Larnier, H.; Stolz, R.; Schiffler, M.; Zakosarenko, V.; Meyer, M. Commercial operation of a SQUID-based airborne magnetic gradiometer. Lead. Edge 2022, 41, 486–492. [Google Scholar] [CrossRef]
- Rochlitz, R.; Skibbe, N.; Günther, T. custEM: Customizable finite-element simulation of complex controlled-source electromagnetic data. Geophysics 2019, 84, F17–F33. [Google Scholar] [CrossRef]
- Rochlitz, R. Analysis and Open-Source Implementation of Finite Element Modeling Techniques for Controlled-Source Electromagnetics. Ph.D. Thesis, Westfälische Wilhelms-Universität Münster, Münster, Germany, 2020. [Google Scholar]
- Rochlitz, R.; Becken, M.; Günther, T. Three-dimensional inversion of semi-airborne electromagnetic data with a second-order finite-element forward solver. Geophys. J. Int. 2023, 234, 528–545. [Google Scholar] [CrossRef]
- Rücker, C.; Günther, T.; Wagner, F.M. pyGIMLi: An open-source library for modelling and inversion in geophysics. Comput. Geosci. 2017, 109, 106–123. [Google Scholar] [CrossRef]
- Günther, T.; Rücker, C.; Spitzer, K. Three-dimensional modelling and inversion of DC resistivity data incorporating topography—II. Inversion. Geophys. J. Int. 2006, 166, 506–517. [Google Scholar] [CrossRef]
- Kim, H.J.; Kim, Y. A unified transformation function for lower and upper bounding constraints on model parameter in electrical and electromagnetic inversion. J. Geophys. Eng. 2011, 8, 21–26. [Google Scholar] [CrossRef]
- Steuer, A.; Smirnova, M.; Becken, M.; Schiffler, M.; Günther, T.; Rochlitz, R.; Müller, F. Comparison of novel semi-airborne electromagnetic data with multi-scale geophysical, petrophysical and geological data from Schleiz, Germany. J. Appl. Geophys. 2020, 182, 104172. [Google Scholar] [CrossRef]




| Grid Size (m) | Number of Data Points | Runtime (h) |
|---|---|---|
| 100 × 100 | 1023 | 19 |
| 200 × 100 | 528 | 6 |
| 200 × 200 | 272 | 3 |
| Figures | Parameter | Mean Cells (Ωm) | Min Cells (Ωm) | Anomaly Gain (%) |
|---|---|---|---|---|
| 3. Single and multi-component inversion | ||||
| Figure 2a,b | X | 108 | 76 | 24 |
| Y | 167 | 125 | 15 | |
| Figure 2c,d | Z | 112 | 72 | 25 |
| Figure 2e,f | XYZ | 66 | 27 | 42 |
| 4.1. Surveying data density | ||||
| Figure 3a,b | 100 × 100 m | 44 | 15 | 53 |
| Figure 3c,d | 200 × 100 m | 66 | 27 | 42 |
| Figure 3e,f | 200 × 200 m | 89 | 52 | 31 |
| 4.2. Transmitter length | ||||
| Figure 4a | 1KmTx1kmfromblock | 40 | 11 | 58 |
| Figure 4c | 2KmTx1kmfromblock | 35 | 10 | 60 |
| Figure 4e | 3KmTx1kmfromblock | 34 | 7 | 66 |
| Figure 4b | 1KmTx2kmfromblock | 112 | 71 | 25 |
| Figure 4d | 2KmTx2kmfromblock | 68 | 22 | 46 |
| Figure 4f | 3KmTx2kmfromblock | 60 | 19 | 48 |
| Figure 5a | 1KmTx3kmfromblock | 245 | 192 | 8 |
| Figure 5b | 2KmTx3kmfromblock | 191 | 157 | 11 |
| Figure 5c | 3KmTx3kmfromblock | 111 | 68 | 26 |
| Figure 5d | 4KmTx3kmfromblock | 99 | 50 | 31 |
| 4.6. The distance of the transmitters from each other | ||||
| Figure 10a | 150mDepth2kmTx | 40 | 11 | 58 |
| Figure 10b | 150mDepth3kmTx | 80 | 36 | 37 |
| Figure 10c | 150mDepth4kmTx | 134 | 72 | 25 |
| Figure 10d | 300mDepth2kmTx | 71 | 36 | 37 |
| Figure 10e | 300mDepth3kmTx | 126 | 91 | 21 |
| Figure 10f | 300mDepth4kmTx | 192 | 142 | 13 |
| Figure 10g | 500mDepth2kmTx | 149 | 121 | 16 |
| Figure 10h | 500mDepth3kmTx | 204 | 151 | 12 |
| Figure 10i | 500mDepth4kmTx | 255 | 152 | 12 |
| 4.7. Anomalies under the transmitter | ||||
| Figure 11a,b | Under1Tx150mDepth | 34 | 4 | 76 |
| Figure 11c,d | Under1Tx300mDepth | 80 | 41 | 35 |
| Figure 11e,f | Under1Tx500mDepth | 213 | 188 | 8 |
| Figure 12a,b | Under2Tx150mDepth | 36 | 5 | 72 |
| Figure 12c,d | Under2Tx300mDepth | 75 | 42 | 34 |
| Figure 12e,f | Under2Tx500mDepth | 161 | 140 | 13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazari, S.; Rochlitz, R.; Günther, T. Optimizing Semi-Airborne Electromagnetic Survey Design for Mineral Exploration. Minerals 2023, 13, 796. https://doi.org/10.3390/min13060796
Nazari S, Rochlitz R, Günther T. Optimizing Semi-Airborne Electromagnetic Survey Design for Mineral Exploration. Minerals. 2023; 13(6):796. https://doi.org/10.3390/min13060796
Chicago/Turabian StyleNazari, Saeed, Raphael Rochlitz, and Thomas Günther. 2023. "Optimizing Semi-Airborne Electromagnetic Survey Design for Mineral Exploration" Minerals 13, no. 6: 796. https://doi.org/10.3390/min13060796
APA StyleNazari, S., Rochlitz, R., & Günther, T. (2023). Optimizing Semi-Airborne Electromagnetic Survey Design for Mineral Exploration. Minerals, 13(6), 796. https://doi.org/10.3390/min13060796








