Abstract
Kaolinite is one of the principal rare earth element (REE) ion-adsorption clays that hosts a wide range of elements, including Dy(III) as a representative example. Ammonium sulfate is a typical salt used to leach REEs. Due to the carbon dioxide emissions which occur during ammonia production, it is urgently necessary to develop low environmental pollution leaching agents that can replace (NH4)2SO4. MgSO4 is regarded as the most promising eco-friendly leaching agent. Herein, the first-principles plane-wave pseudopotential method based on the density functional theory (DFT) was used to investigate the stable adsorption structures of Dy(III) and its hydrated ions, MgSO4 leaching agent ions and the corresponding hydrated ions on the surface of kaolinite, which revealed the adsorption mechanism of Dy(III), Mg(II), and SO42− on the silico–oxygen plane and the aluminum–hydroxyl plane of kaolinite. Based on the research results of the steric hindrance effect of Dy(III) on the silico–oxygen plane and the aluminum–hydroxyl plane of kaolinite, the adsorption of Dy(H2O)103+ was more stable on the silico–oxygen plane. It was easier to leach out Dy(III) with MgSO4, while SO42− tended to interact with the rare earth ions in an aqueous solution. The results provide theoretical guidance for efficient rare earth extraction and obtaining novel efficient leaching agents.
1. Introduction
Rare earth elements collectively refer to the 17 elements that are extensively applied in the fields of metal products, magnetic materials, chemical catalysis, and optical instruments [1,2,3]. The main forms of rare earth in nature are categorized into mineral-type rare earth ore, such as fluocerite and monazite, and ionic rare earth ore. Rare earth ore consisting of rare earth ions adsorbed by clay minerals is defined as ionic rare earth ore and serves as the major supply source of rare earth needed by high-tech fields due to the richness of heavy rare earth elements in this type of ore and its characteristics which ensure a simple extraction and high value [4,5].
To recycle ionic rare earth resources effectively, studies have been conducted on the corresponding mineralized regularity and extraction methods [6]. In ionic rare earth ore, rare earth elements are adsorbed by clay minerals such as kaolinite and halloysite in ionic states. Currently, the most adopted extraction method is ion exchange adsorption with an ammonium salt solution [7,8,9]. Wu et al. [10] applied X-ray diffraction to semi-quantitatively calculate the contents of each mineral via the K-value method, proposing that kaolinite and halloysite are the predominant components in the surface soil layer and the upper-middle complete weathering layer, while the contents of feldspar and illite build up significantly with the increase in depth. Zhang et al. [11] investigated the mineral deposit characteristics of ionic rare earth ore in some places of southern China and discovered the two types of rare earth grade distribution in the weathering layer, ‘up low-down high’ and ‘up high-down low’. The ore-forming mechanism was explained by the migration of rare earth ions mixed with an acidic solution to the lower part of the ore body and the subsequent adsorption and enrichment in the weathering layer. Liu et al. [12] conducted research on the enrichment and differentiation constraints of rare earth elements from the perspective of ore evolution which elucidated that ionic state rare earth elements are mainly adsorbed by kaolinite and halloysite and exhibit an increasing content trend from the bedrock to the rare earth enriched layer. Montmorillonite and illite are distributed in the partially weathering layer, whereas kaolinite and halloysite can be found in each layer. These studies have led to the agreement that ionic rare earth ore in nature is formed by the adsorption of rare earth ions on clay minerals. According to this characteristic of the ore, ammonium salt leaching has been adopted for the extraction of ionic rare earth ore. However, the extraction rate of rare earth ions is still unsatisfactory on both research and production scales. Meanwhile, the ammonium salt leaching agents used in industry pose a severe threat to the environment. Therefore, it is necessary to understand the adsorption mechanism of rare earth ions onto clay minerals in depth, for the purpose of providing a basis for highly efficient rare earth extraction and tackling the environmental pollution issue of leaching agents. Some scientists have applied quantum chemistry calculation methods to investigate the mechanisms for rare earth ion adsorption on clay minerals. Zhai et al. [13] studied the electronic configuration of kaolinite, which showed an indirect band gap of 4.89 eV. In kaolinite, metal cations form ionic bonds with oxygen-containing anions, accompanied by covalent bonds as well. Ning et al. [14] analyzed the categories and structures of montmorillonite and adsorbed rare earth ions. Yao et al. [15] investigated the adsorption energy for the interaction between the Na-(001) (surface containing sodium ions) and None-(001) surfaces (surface without sodium ions) of montmorillonite and La(H2O)103+ via a density functional calculation. Du et al. [16] studied the adsorption characteristics of hydrated hydrogen ions on the (001) plane and the (010) plane of illite. Zou et al. [17,18,19] probed into the adsorption characteristics of Pr ions on the montmorillonite surface. Evidently, the calculation and simulation of rare earth adsorption with the quantum chemistry method are of great significance in the research on the cause of rare earth adsorption on clay minerals and the development of novel leaching agents.
Herein, the first-principles method based on density functional theory (DFT) was adopted to investigate the parameters of adsorption of hydrated Dy(III), Mg2+, and SO42− on the (001) planes of kaolinite, including the adsorption configuration, adsorption energy, adsorption force, electron transfer, and density of states. Further, we studied the stable configurations of the hydrates of these ions and the corresponding adsorption characteristics on the silico–oxygen plane and the aluminum–hydroxyl plane, and explained the adsorption mechanism, thereby providing theoretical guidance for the highly efficient rare earth extraction of ionic rare earth ore and the development of novel leaching agents.
2. Kaolinite Structure
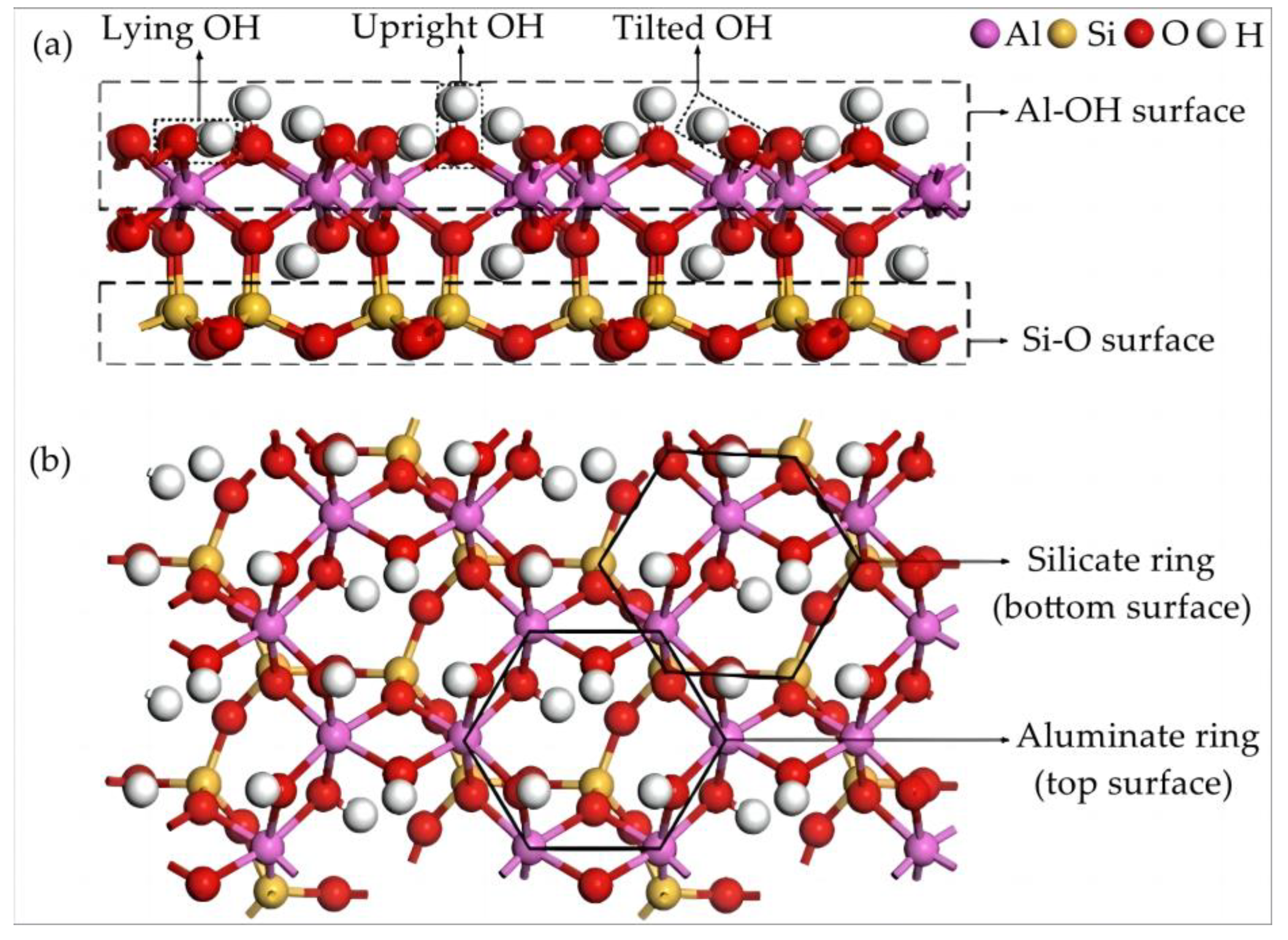
In nature, the cleavage surfaces of kaolinite are divided into three types, the (001) surface, the (010) surface, and the (110) surface [20]. Quantum chemical analysis and broken bond analysis have shown that the (001) surface is completely cleaved, and the (010) surface and the (110) surface are more difficult to cleave. After the surface of kaolinite (001) is completely cleaved, there are two kinds of surfaces: the Al–OH surface and the Si–O surface [21].
The CASTEP module was used to optimize the structure of kaolinite. After the optimized kaolinite unit cell was obtained, the Cleave Surface function of the MS 2016 was used to cut the Al–OH surface and the Si–O surface of kaolinite. The model of the water molecule layer on the surface of kaolinite was built by the AC module in the MS 2016. The interaction between Y ions and the water molecule layer is due mainly to the participation of water molecules in the lower half. The use of 20 water molecules is suitable for the kaolinite surface system constructed in this paper. The water molecule layer on the kaolinite surface was added to establish the (Al–OH)-H2O and the (Si–O)-H2O adsorption interface models for the structure calculation and the property analysis of rare earth yttrium ion adsorption, as shown in Figure 1.
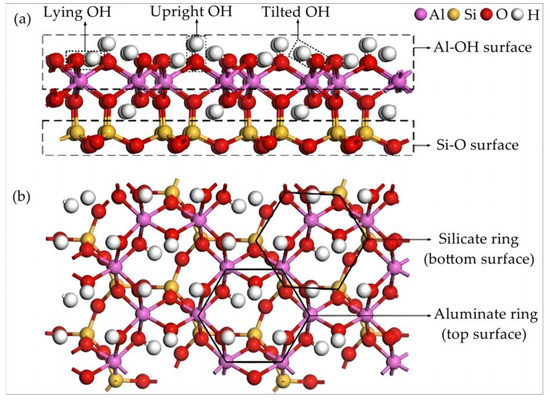
Figure 1.
Schematic illustration of kaolinite crystalline structure. (a) Front view and (b) top view.
As a typical rare earth containing mineral ore, kaolinite is a layered silicate clay mineral formed by silicate minerals such as feldspar after long-term weathering [22]. The theoretical composition is Al4Si4O10(OH)8, with 41.2% A12O3, 48.0% SiO2, and 10.8% H2O. The crystalline structure of kaolinite is shown in Figure 1, where a 1:1 type layered silicate structure constructed by one silicon–oxygen tetrahedron and one aluminum–oxide polyhedron through the connection of a shared vertex O. Each layer consists of a six-atom sub-layer of H-O-Al-O-Si-O, while each structural unit is mainly connected by hydrogen bonds [23,24]. The common cleavage plane in kaolinite is the (001) plane, which can be divided into aluminum–hydroxyl planes and silico–oxygen planes [25]. In this study, the initial cell parameters were determined by the neutron powder diffraction method at a low temperature (1.5 K), which are a = 5.1535 Å, b = 8.9419 Å, c = 7.3906 Å, α = 91.926°, β = 105.046°, and γ = 89.797°.
3. Calculation Method and Model
The CASTEP module in Materials Studio (MS) software was adopted to implement the first-principles plane-wave pseudopotential method based on the density functional theory [26,27,28]. The calculation used ultrasoft pseudopotential and GGA-PBE as the exchange–correlation functional. The cut-off energy was 360 eV. A K-point mesh of (1 × 1 × 1) was sampled. Rare earth ions and water molecules were placed into a 15 × 15 × 15 Å3 periodic cell where optimization was repeated until the optimal structure was obtained. The valence electron configurations of atoms in the pseudopotential calculation were H 1s1, O 2s22p4, Dy 4f106s2, and Y4d15s2. The convergence criteria were as follows. The convergence threshold of energy was 5 × 10−5 eV·atom−1. The convergence threshold of inter-atomic force was 0.07 ev·Å−1. The convergence threshold of internal crystal stress was 0.2 GPa. The convergence threshold of atomic displacement was 0.005 Å, and the self-consistent iterative convergence accuracy was 5.0 × 10−5 eV·atom−1.
To investigate the binding situation of different elements such as Dy(III) with H2O, the binding energy was adopted to reveal the binding strength, of which the calculation equation is shown as Equation (1).
In the equation, Ebinding is the binding energy of the element hydrates, ETol stands for the total energy of the element hydrate system, EH2O represents the energy of H2O molecules, ERE is the energy of rare earth elements, and n stands for the number of H2O molecules. The lower binding energy of the hydrates of each of the elements indicates the higher stability of the structure.
Equation (2) was adopted to study the adsorption strength of each hydrated ion on clay minerals.
Thereinto Eads stands for the adsorption energy of hydrated ions and ERE/S and ERE represent the energy of the hydrated ions and the surface before adsorption, respectively. EM/S is the total energy of the hydrated ions complex system after adsorption and EM and ES denote the total energies of the hydrated ions complex and Mt (001) surface, respectively. A smaller adsorption energy means a more robust adsorption of the hydrated ions on the clay minerals.
Through a series of tests on adsorption sites, the initial adsorption configuration was set by placing the hydrated rare earth ions right above the center Al during adsorption on the aluminum–hydroxyl plane. For adsorption on the silico–oxygen plane, the initial adsorption configuration was the hydrated rare earth ions placed right above the central silico–oxygen ring.
4. Results and Discussion
4.1. Stable Configuration of Hydrated Dy(III)
4.1.1. Equilibrium Configuration Parameter and Binding Energy of Dy(H2O)n3+
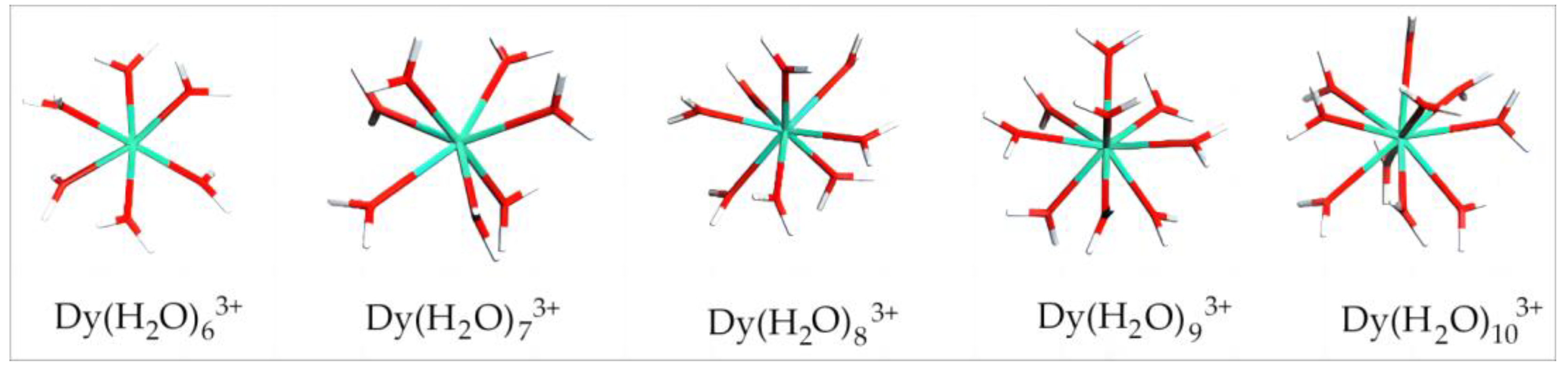
Studies have shown that the number of coordinated water molecules to rare earth ions in aqueous media is generally no less than six [29]. Thus, herein, the calculation started from six coordinated water molecules. Figure 2 shows the equilibrium geometry configuration of Dy(H2O)6–103+ from the DFT calculation. It can be seen that chemical bonds were formed between Dy and O in the surrounding water molecules. The coordinated water molecules are distributed uniformly around Dy. As the number of coordinated water molecules increases, the coordination bonds between some water molecules and Dy are elongated but not cleaved. With 10 coordinated water molecules, the surroundings of Dy are already quite crowded, although the hydrated structure can still exist stably. The configuration of Dy(H2O)103+ is formed with a binding energy of −2403.8 kJ/mol. As a result, the potential maximum hydration number in the first hydration layer of Dy(III) in an aqueous environment is 10.
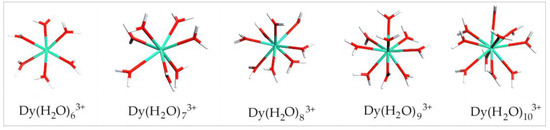
Figure 2.
Equilibrium geometry configuration of Dy(H2O)6–103+. Note: Red stands for O, white stands for H, and light green stands for Dy.
Table 1 lists the equilibrium geometry configuration parameters and binding energy of Dy(H2O)n3+. According to the table, the number of coordinated water molecules exerts great influence on the average bond length and binding energy. With a small coordination number, the average bond length of Dy–O is short. As the coordinated water molecule number increases, the average bond strength also increases. When the water molecule number increases to 10, Rmean reaches 2.5184 Å. Additionally, with the increase in hydration number, the binding energy gradually decreases, suggesting a higher stability of the structure. The binding energy reaches a minimum value of −2403.8 kJ/mol when the coordinated water molecule number is 10.

Table 1.
Equilibrium geometry configuration parameters and binding energy of Dy(H2O)n3+ (n = 6~10).
There is a large energy jump between n = 9 and n = 10 because the hydrated ions are in an increasingly unstable state when n = 10. From this, it can be assumed that the critical water molecule number is 10, at which time the calculation software can no longer place more water molecules.
Therefore, Dy(H2O)103+ was selected as the initial configuration of hydrated Dy(III) in surface adsorption on clay minerals.
4.1.2. Electronic Structure and Properties of Dy(H2O)103+
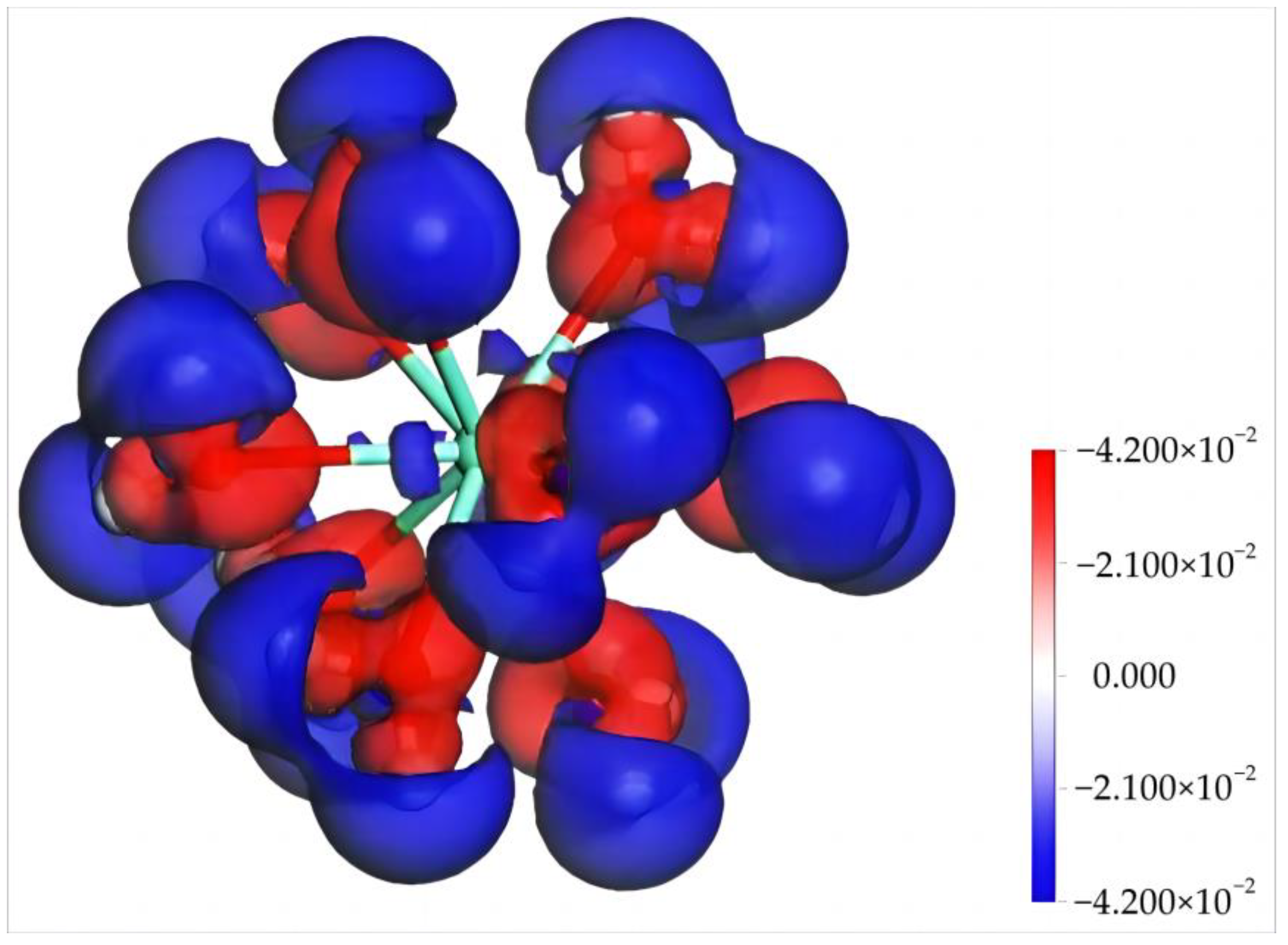
The Mulliken charge population and charge differential density of Dy(H2O)103+ were calculated to further understand its electronic structure and properties [30,31,32]. Table 2 shows the electron gain and loss of each orbital of Dy and O in Dy(H2O)103+. It can be seen that, upon the formation of Dy(III) hydrates, the valence state of Dy is 2.22. According to orbital electron gain and loss, the 2s orbital of Dy gains 0.19 e, whereas the 2p, 5d, and 4f orbitals lose 0.28, 0.3, and 1.83 e, respectively. The O atoms exhibit an electron gain state on the whole, obtaining electrons from Dy and H atoms with an overall charge between −0.92 and −0.96 e. Figure 3 shows the charge differential density of Dy(H2O)103+, where the red area and the blue area represent the electron gain region and the electron loss region, respectively. According to the diagram, after obtaining the electron of H, O closely binds with Dy, facilitating the formation of an electron-deficient region (blue) surrounding Dy(H2O)103+. This leads to the positive charge state of Dy(H2O)103+ due to the overall electron deficiency, which agrees well with the computational results in Table 2.

Table 2.
Mulliken charge population of Dy(H2O)103+.
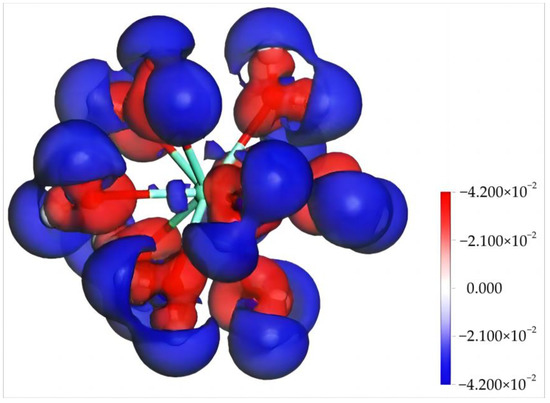
Figure 3.
The difference charge density of [Dy(H2O)10]3+ (the isodensity surface difference is ±0.042 electrons/Å3).
Table 3 lists the bonding population of Dy and O and the bond length in Dy(H2O)103+. The population of Dy–O coordination bonds is relatively small, between 0.11 and 0.14, indicating weak covalence bonding. The length of Dy–O bonds ranges between 2.43 and 2.64 Å, which also suggests a weak covalency in agreement with the population. The maximum population value of Dy–O is 0.14.

Table 3.
Overlap population of the Dy–O bond.
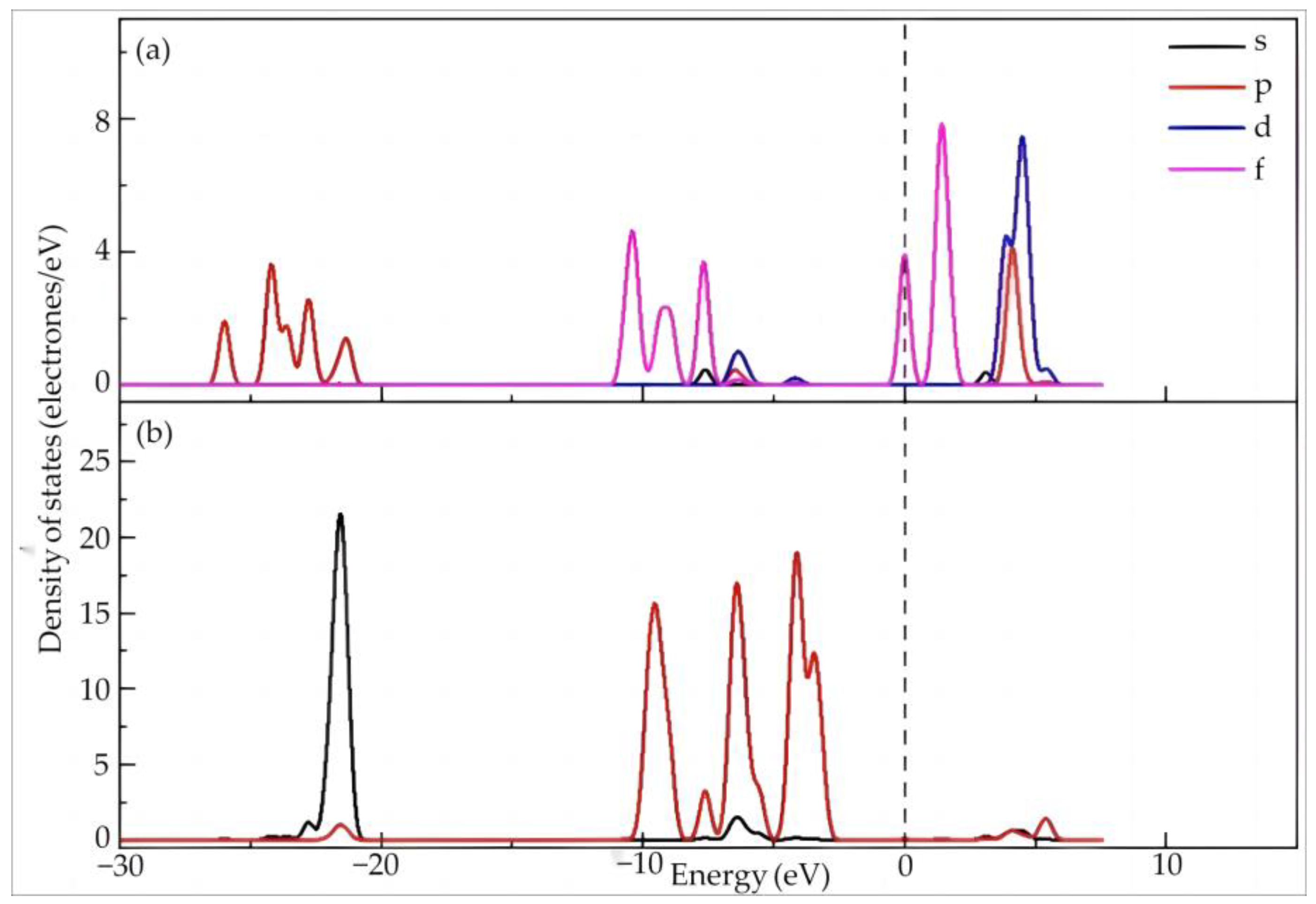
As shown in Figure 4, the 4f orbitals of Dy are mainly distributed between −11 and −7.5 eV and between −0.2 and 2.5 eV across the Fermi level, which endows them with high reactivity. The Dy 5p orbitals are mainly distributed between −26 and −21 eV with four consecutive peaks, while also exhibiting distribution at 3~5 eV. Meanwhile, Dy 5d orbitals are mainly distributed in the high energy region of 3~6 eV. The 2s orbital of O is mainly distributed at a low energy of −23~−21 eV, showing a high sharp peak, while the distribution in the other regions is minimal. The distribution of the O 2p orbitals is mainly around −10~−2.5 eV, exhibiting four consecutive high sharp peaks with one low sharp peak, but can also be found in the high energy region of 5 eV~15 eV. The O 2p orbital peak overlaps with that of the Dy 5d orbitals. The latter is contained in the former, indicating hybridization in this high energy region. In combination with the charge population, the bonding orbital filling of Dy–O is larger than the anti-bonding orbital filling.
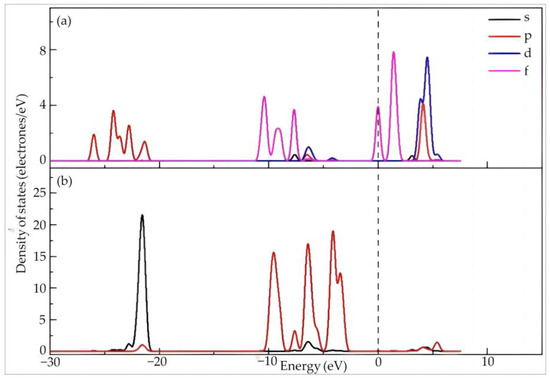
Figure 4.
The partial density of states of Dy (a) and O (b) in Dy(H2O)103+.
4.2. Adsorption of Dy(H2O)103+ Ions on the Silico–Oxygen Plane of Kaolinite
4.2.1. Adsorption Configuration and Adsorption Energy of Dy(H2O)103+
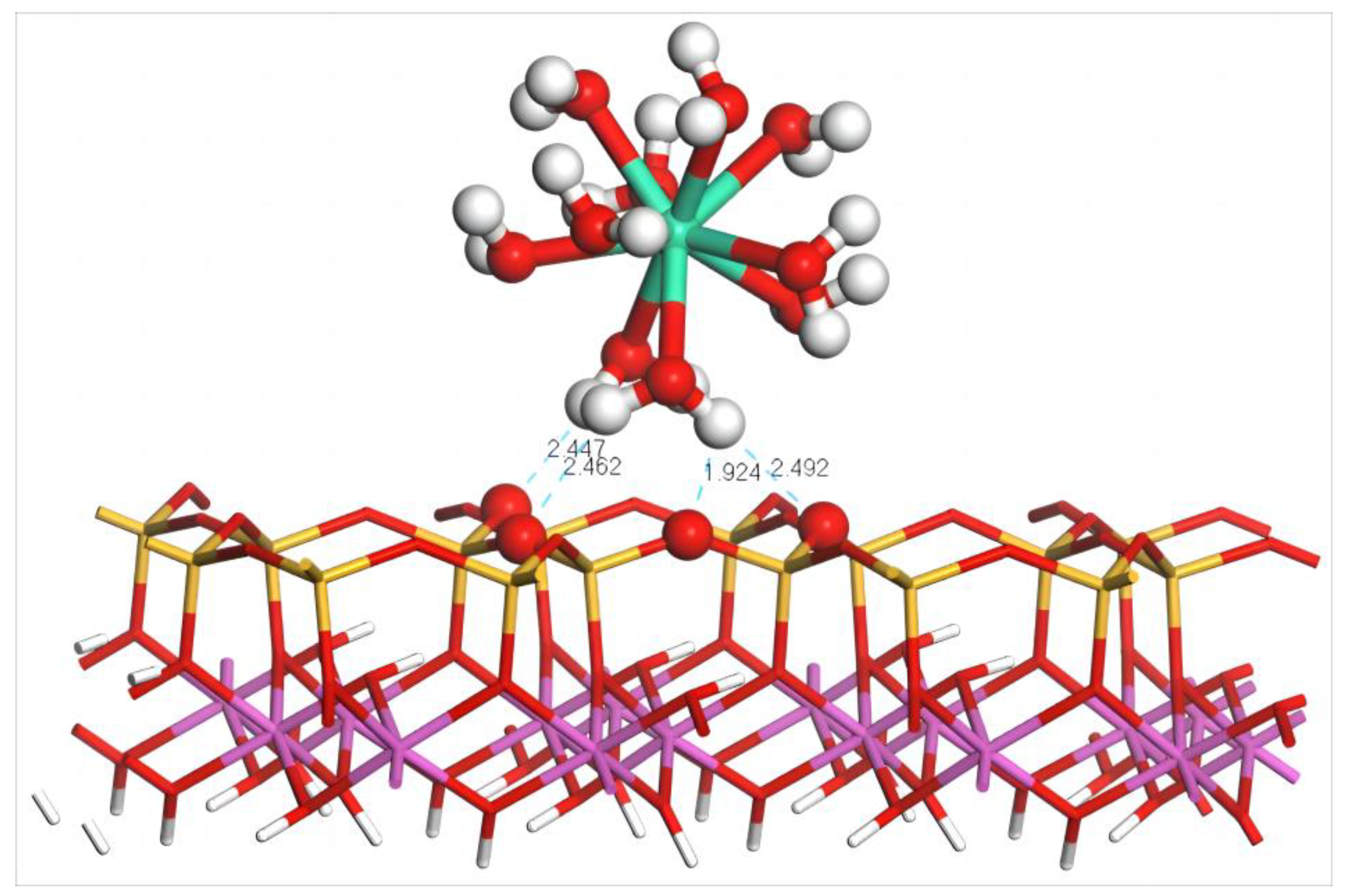
The equilibrium geometry configuration of Dy(H2O)103+ after adsorption on the (001) silico–oxygen plane of kaolinite is shown in Figure 5. According to the diagram, hydrated Dy(III) is closer to the silico–oxygen plane of kaolinite after adsorption. The H atoms in Dy(H2O)103+ form four hydrogen bonds with O atoms on the silico–oxygen plane, of which the bond lengths are 2.447, 2.462, 1.924, and 2.492 Å. These four hydrogen bonds are the principal reason why Dy(H2O)103+ can be adsorbed on the silico–oxygen plane of kaolinite. During adsorption, due to the steric hindrance effect of the kaolinite surface, the coordinated water molecules of hydrated Dy(III) undergo extrusion to different extents, leading to the displacement of most of the coordinated water molecules away from the kaolinite surface. Only two water molecules that form hydrogen bonds with the surface are kept in the lower part, resulting in the compromised symmetry of the whole hydrated Dy(III).
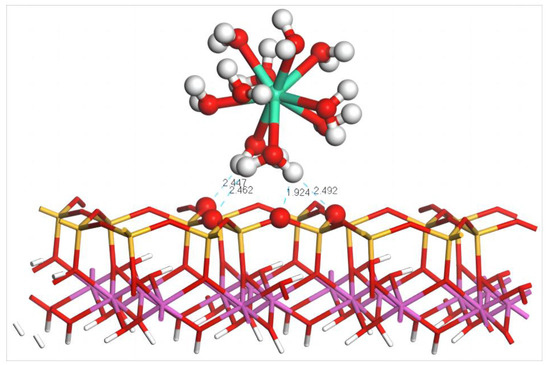
Figure 5.
Adsorption structure of Dy(H2O)103+ on the (001) silico–oxygen plane of kaolinite. Note: Red stands for O, white stands for H, light green stands for Dy, orange–yellow stands for Si, purple stands for Al, and the dotted line stands for bond length.
According to the equilibrium geometry configuration parameters and binding energy of Dy(H2O)103+ before and after adsorption listed in Table 4, the distances between the water molecules and Dy are no longer uniform after adsorption due to the extrusion among the coordinated water molecules. The average distance between Dy(III) and the O atoms in the coordinated water molecules decreases from 2.58 to 2.51 Å and the system adsorption energy is −544.3 kJ/mol.

Table 4.
Configuration parameters and adsorption energy of Dy(H2O)103+ before and after adsorption on the (001) silico–oxygen plane of kaolinite.
4.2.2. Dy(H2O)103+ Electron Transfer and State Density Study
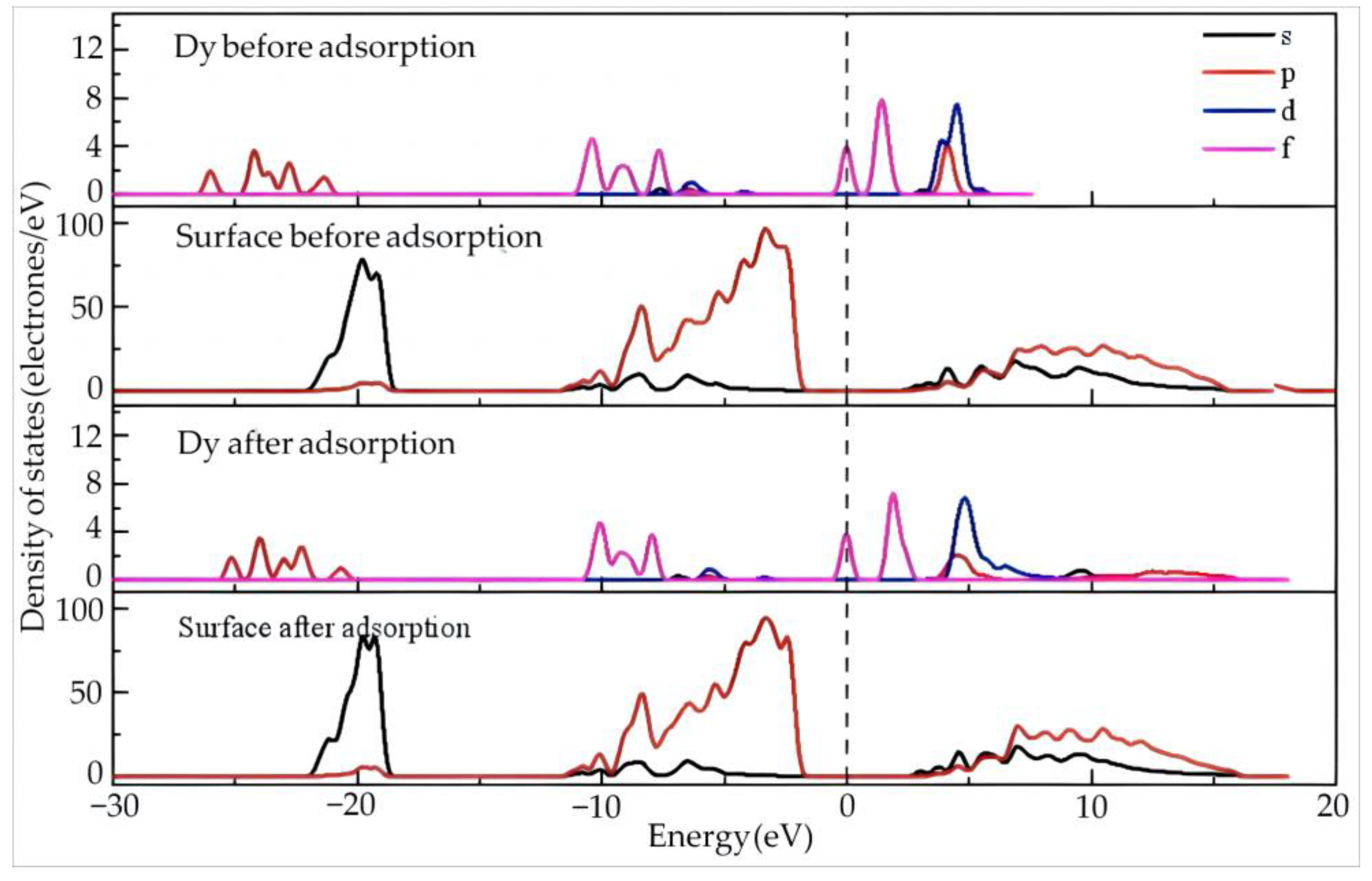
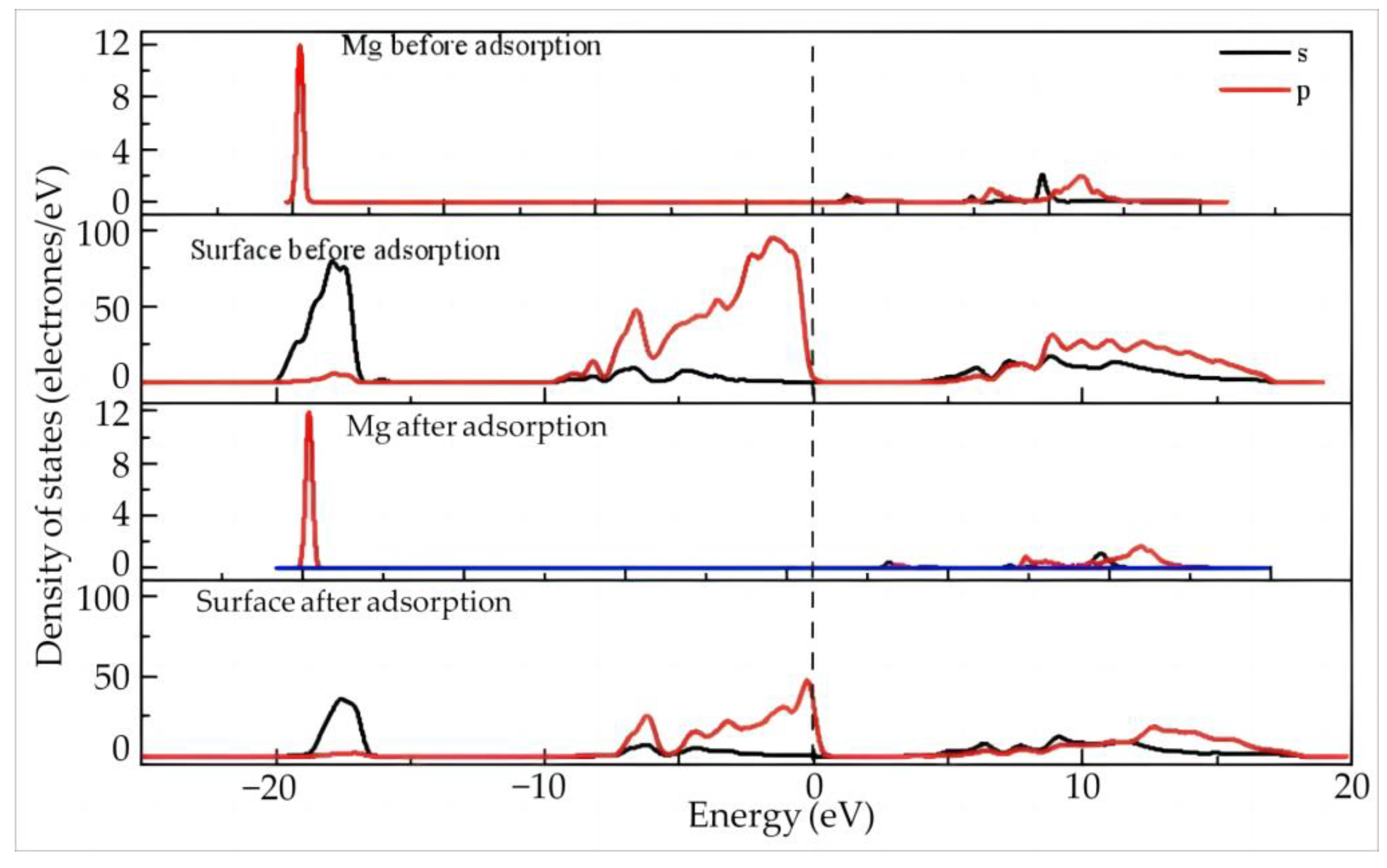
Figure 6 shows the density of states of Dy and the surface before and after adsorption of Dy(H2O)103+ on the silico–oxygen plane of kaolinite.
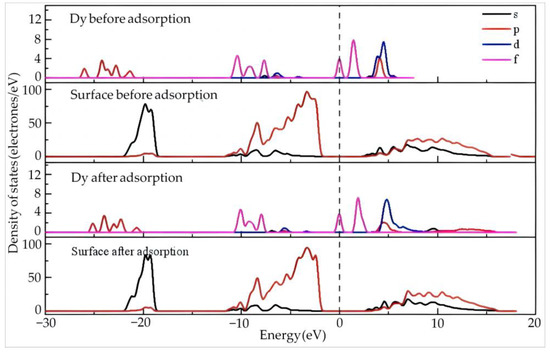
Figure 6.
The density of states of Dy and the surface before and after the adsorption of Dy(H2O)103+ on the silico–oxygen plane of kaolinite.
Before adsorption, the Dy 4f orbitals contribute the most at the Fermi level, suggesting high reactivity of the orbitals since 4f orbitals belong to the valence electron orbitals with a high tendency of electron gain and loss on the outer layer of Dy. By comparison, a certain gap exists between the density of states of the kaolinite surface and the Fermi level, indicating a relatively low reactivity.
After adsorption, the Dy 4f orbitals move slightly in the high energy direction but still stay close to the Fermi level. This means that Dy keeps its high reactivity even though it is adsorbed on the silico–oxygen plane. Combining this with the results in Table 5, it can be deduced that the Dy 4f orbitals lose 0.34 electrons after adsorption, which is obviously higher than other orbitals. In addition, the reactivity of the Dy 5d orbitals is weakened by adsorption, accompanied by enhanced localization. The Dy 6p and 5d orbitals gain 0.06 and 0.1 electrons, respectively. On the whole, Dy exhibits an electron-deficient state. Compared with that before adsorption, the valence state of Dy increases from 1.81 to 1.99. After adsorption, the density of states on the surface of kaolinite does not exhibit noticeable changes.

Table 5.
The Mulliken charge population of the atomic charges of Dy before and after adsorption of Dy(H2O)103+ on the (001) silico–oxygen plane of kaolinite.
4.3. Adsorption of Dy(H2O)103+ Ions on the Aluminum–Hydroxyl Plane of Kaolinite
4.3.1. Adsorption Configuration and Adsorption Energy of Dy(H2O)103+
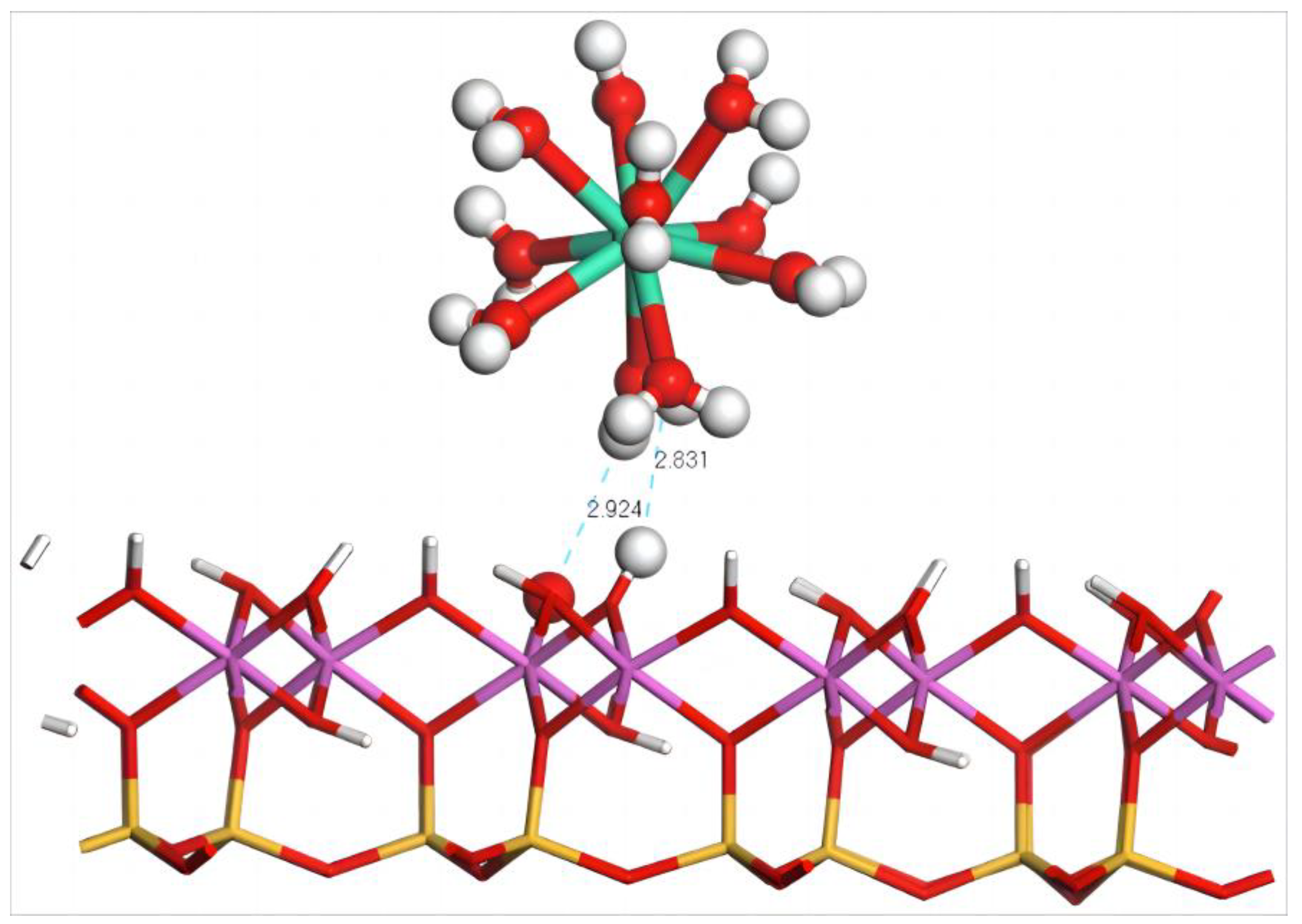
The geometric equilibrium configuration of Dy(H2O)103+ after adsorption on the (001) aluminum–hydroxyl plane of kaolinite is shown in Figure 7. After adsorption, the coordinated water molecules of Dy(III) form two hydrogen bonds with the surface whose lengths are 2.831 and 2.924 Å, significantly larger than those on the silico–oxygen plane which also has a lower quantity of hydrogen bonds. This accounts for the large amount of erected hydroxy groups on the aluminum–hydroxyl plane of kaolinite that induce a severe steric hindrance effect, thereby hindering the approach of Dy(H2O)103+. Table 6 lists the geometric equilibrium configuration parameters and binding energy of Dy(H2O)103+ before and after adsorption. It can be seen that, after adsorption, the coordinated water molecules of Dy(H2O)103+ remain in good symmetry. The distance of 2.583 Å between Dy(III) and the coordinated water molecules are almost unaffected which can be explained by the large distance between Dy(H2O)103+ and the surface, making for little extrusion on the water molecules. The system adsorption energy is −194.4 kJ/mol, significantly higher than the adsorption energy of Dy(H2O)103+ on the silico–oxygen plane of kaolinite.
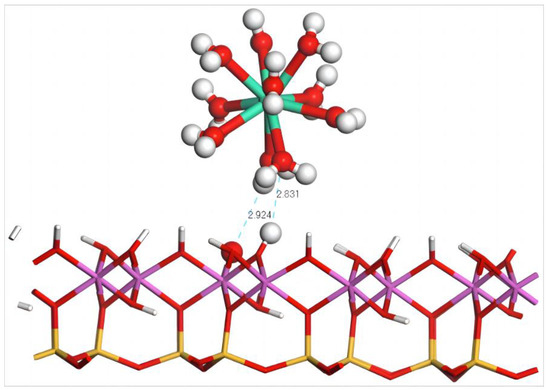
Figure 7.
Adsorption structure of Dy(H2O)103+ on the (001) aluminum–hydroxyl plane of kaolinite. Note: Red stands for O, white stands for H, light green stands for Dy, orange–yellow stands for Si, purple stands for Al, and the dotted line stands for bond length.

Table 6.
Configuration parameters and adsorption energy of Dy(H2O)103+ before and after adsorption on the (001) aluminum–hydroxyl plane of kaolinite.
4.3.2. State Density and Electron Transfer of Dy(H2O)103+
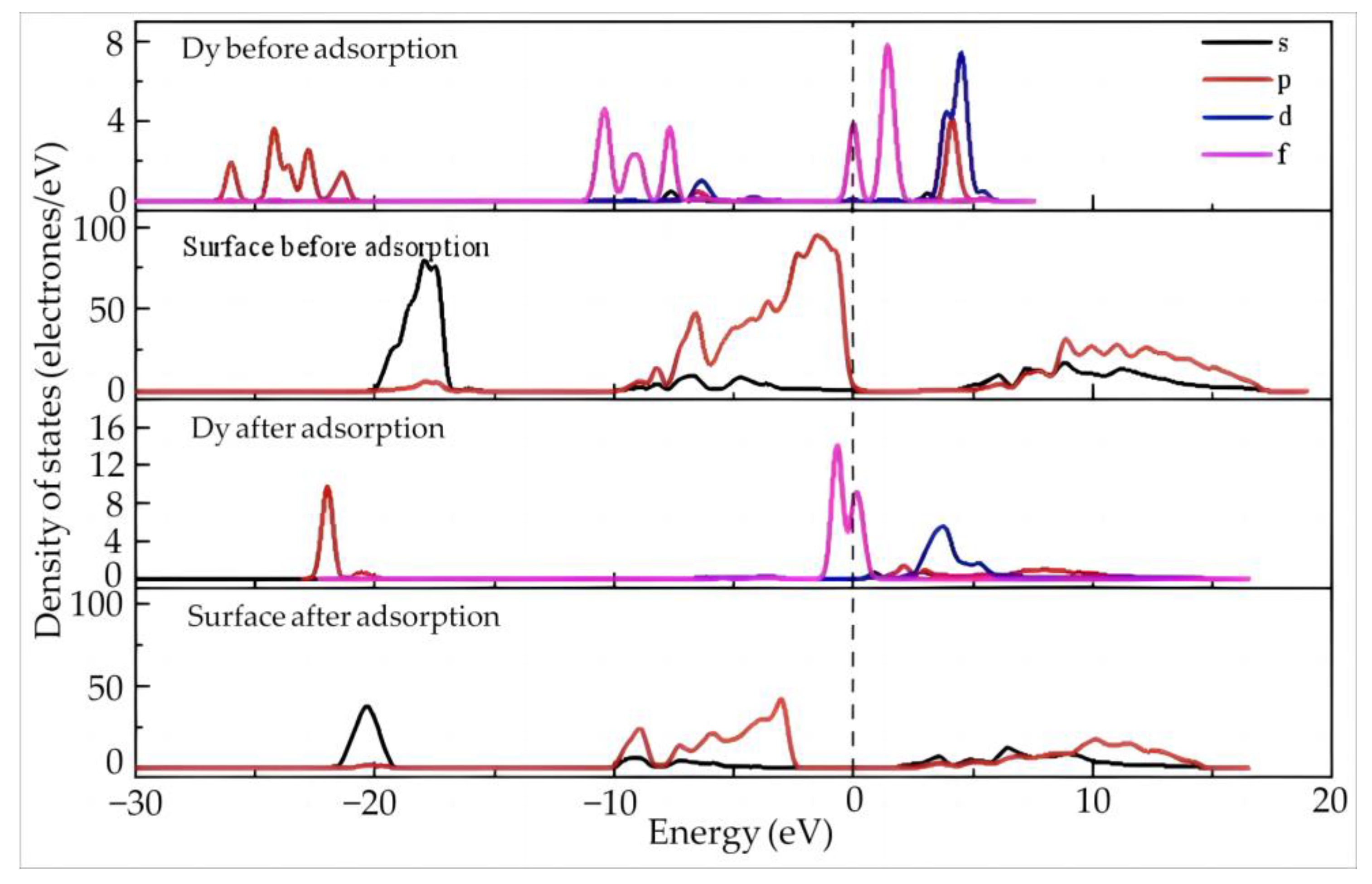
Figure 8 shows the density of the states of Dy and the surface before and after the adsorption of Dy(H2O)103+ on the aluminum–hydroxyl plane of kaolinite. Before adsorption, the Dy 4f orbitals exhibit a wide distribution located at −11~−7.5 eV and −0.2~2.5 eV across the Fermi level, suggesting the high activity and high tendency of electron gain and loss of the orbitals. Different from the situation on the silico–oxygen plane of kaolinite, the density of the states of the aluminum–hydroxyl plane is located around the Fermi level before adsorption, which means that the reactivity of the aluminum–hydroxyl plane is higher than that of the silico–oxygen plane. Once the adsorption occurs, despite the Dy 4f orbitals at −0.2~2.5 and the 5d orbitals moving toward the low energy direction, they still stay near the Fermi level, indicating the high activity of Dy is maintained after adsorption. Meanwhile, the density of the states of the 2p orbitals of the kaolinite aluminum–hydroxyl plane moves significantly toward the low energy direction away from the Fermi level after adsorption. This suggests that the aluminum–hydroxyl plane becomes more stable after adsorption. According to the Mulliken charge population of Dy before and after adsorption (Table 7), the 5d and 4f orbitals of Dy lose 0.25 and 0.73 electrons after adsorption, respectively, while the valence state increases from 1.81 to 2.55, suggesting a higher tendency of electron loss.
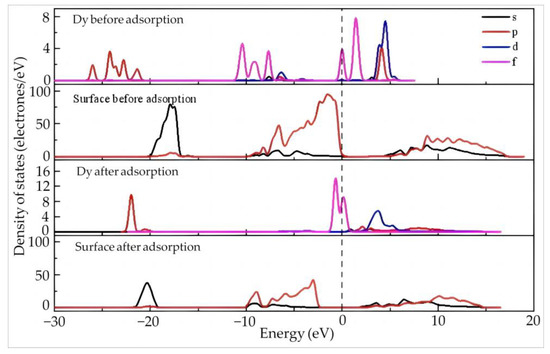
Figure 8.
Density of states of Dy and the surface before and after the adsorption of Dy(H2O)103+ on the aluminum–hydroxyl plane of kaolinite.

Table 7.
The Mulliken charge population of the atomic charges of Dy before and after the adsorption of Dy(H2O)103+ on the aluminum–hydroxyl plane of kaolinite.
4.4. Adsorption of Cations and Anions of MgSO4 Leaching Agent on Kaolinite Surface
(NH4)2SO4 is the extensively used leaching agent at present. Due to the environmental pollution issue induced by ammonia production, it is urgent to develop novel leaching agents that can replace (NH4)2SO4. MgSO4 is regarded as the most promising leaching agent for the replacement of (NH4)2SO4. Accordingly, the adsorption of the ions and the corresponding hydrates of MgSO4 were investigated in this work.
Some research indicates that in aqueous media, the hydrated magnesium ion is bonded with six water molecules via coordination bonds and forms a stable hydrated structure of Mg(H2O)62+ [33]. Herein, we investigate the adsorption of Mg(H2O)62+ on the silico–oxygen plane and the aluminum–hydroxyl plane of kaolinite in the CASTEP module.
4.4.1. Adsorption of Mg(H2O)62+ on the Silico–Oxygen Plane of Kaolinite
- (1)
- Adsorption Configuration and Adsorption Energy
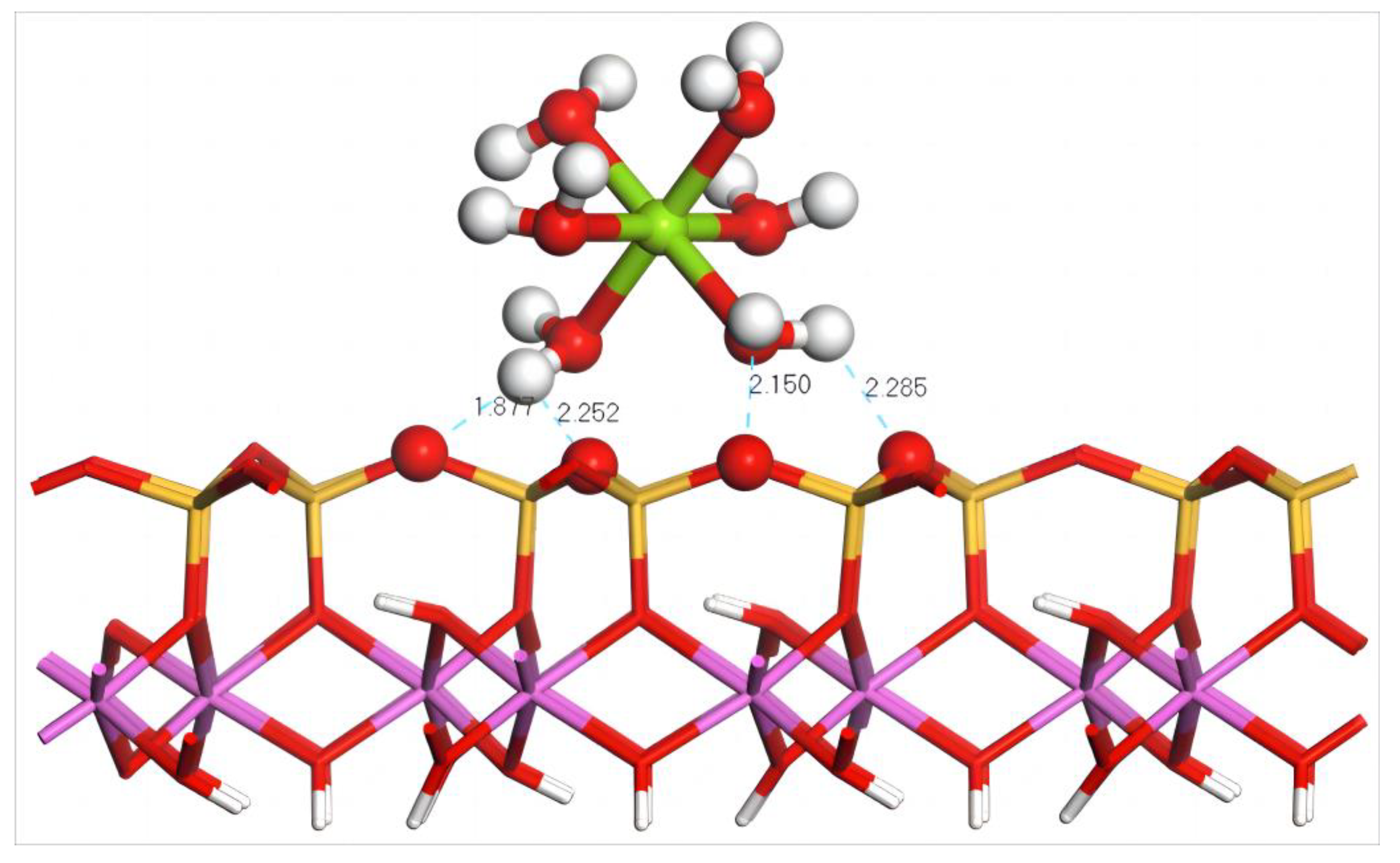
Figure 9 shows the equilibrium geometry configuration of Mg(H2O)62+ absorbed on the (001) silico–oxygen plane of kaolinite. It can be seen that three H atoms in the coordinated water molecules of Mg(H2O)62+ form four hydrogen bonds with four O atoms on the surface after adsorption, of which the lengths are 1.877, 2.252, 2.150, and 2.285 Å, endowing the stable adsorption of hydrated Mg2+ on the surface of kaolinite. Combining with the configuration parameters and adsorption energy of Mg(H2O)62+ before and after adsorption on the silico–oxygen plane of kaolinite, it can be deduced that during the approach of Mg(H2O)62+ to kaolinite, coordinated water molecules are subjected to extrusion, which leads to the change in the distance between Mg and its coordinated water molecules from equidistant to irregularly distributed after adsorption. The average bond length increases to 2.52 Å from 2.26 Å before adsorption, as shown in Table 8. The calculation indicates that the adsorption energy of Mg(H2O)62+ on the silico–oxygen plane of kaolinite is −230.4 kJ/mol, lower than −544.32 kJ/mol of Dy(H2O)103+, suggesting that a higher external energy is required to leach Dy out of kaolinite, namely that a higher concentration of leaching agents is needed.
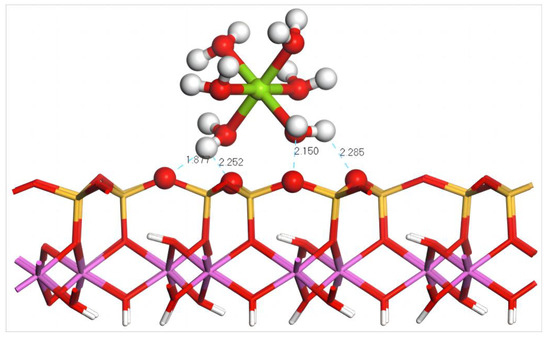
Figure 9.
Adsorption structure of Mg(H2O)62+ on the (001) silico–oxygen plane of kaolinite. Note: Red stands for O, white stands for H, dark green stands for Mg, orange–yellow stands for Si, purple stands for Al, and the dotted line stands for bond length.

Table 8.
Configuration parameters and adsorption energy of Mg(H2O)62+ before and after adsorption on the (001) silico–oxygen plane of kaolinite.
- (2)
- Electron Transfer and State Density Study
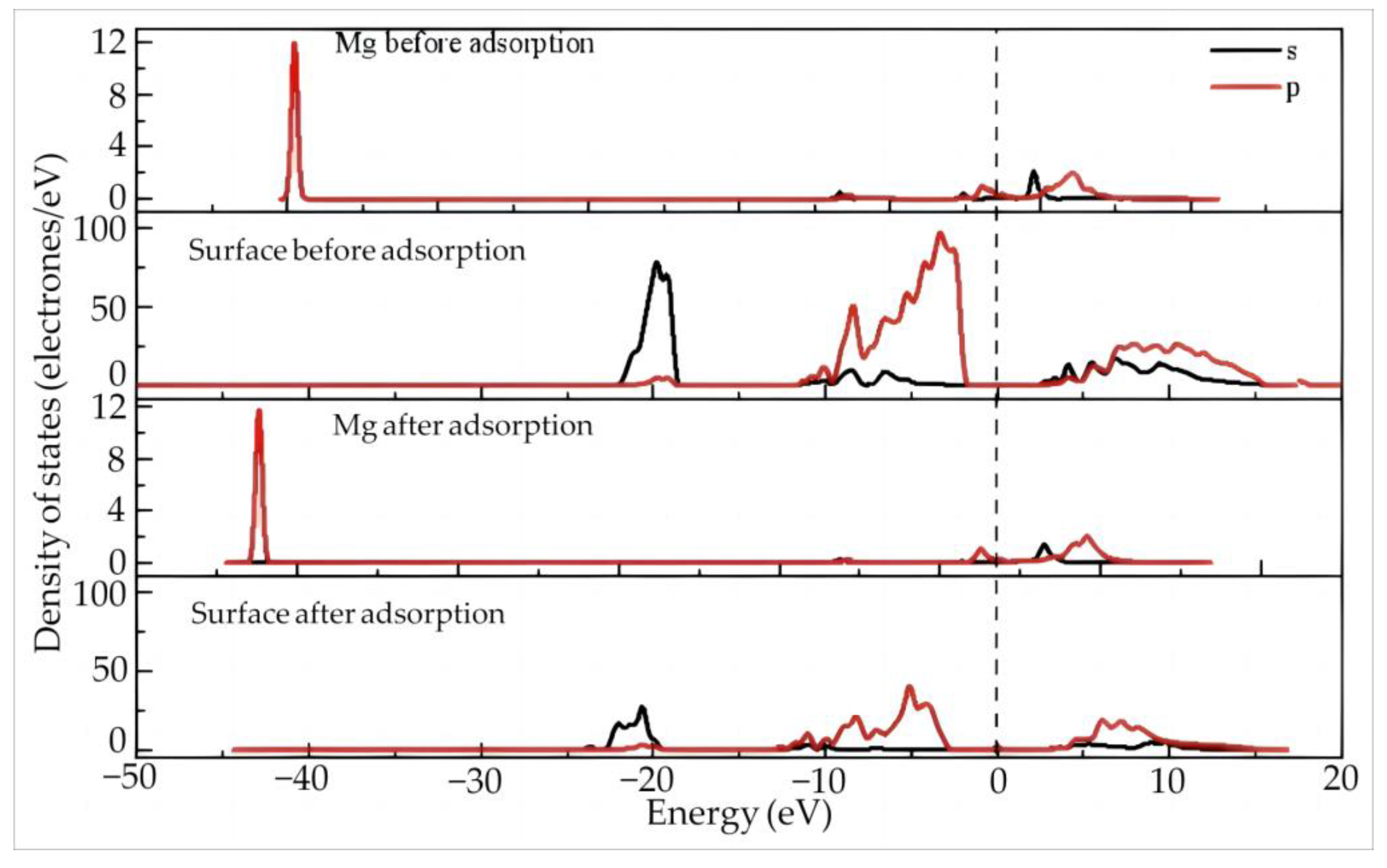
Figure 10 shows the density of states of Mg and the surface before and after the adsorption of Mg(H2O)63+ on the silico–oxygen plane of kaolinite. Before adsorption, the Mg 2s and 2p orbitals are far away from the Fermi level, indicating that the overall reactivity of Mg ions is lower than that of rare earth ions. This can be explained by the strong attraction effect of the atomic nucleus on the surrounding electron cloud due to the small radius of Mg which makes it difficult to lose electrons. The 2p orbitals of the (001) silico–oxygen plane of kaolinite before adsorption are located around the Fermi level, exhibiting a certain reactivity. After adsorption, all orbitals of Mg2+ move toward the low energy direction, away from the Fermi level. The 2s and 2p orbitals of the kaolinite surface also move away from the Fermi level to the low energy direction, accompanied by a decrease in intensity, suggesting that the system energy is lowered after adsorption and stability are enhanced. According to Table 9, the Mg 2p orbitals and 2s orbital lose 0.1 and 0.04 electrons after adsorption, respectively, while the valence state increases from 1.68 to 1.82.
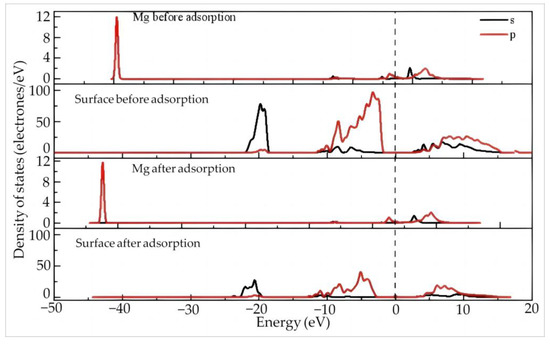
Figure 10.
The density of states of Mg and the surface before and after adsorption of Mg(H2O)63+ on the silico–oxygen plane of kaolinite.

Table 9.
The Mulliken charge population of the atomic charges of Mg before and after the adsorption of Mg(H2O)63+ on the silico–oxygen plane of kaolinite.
4.4.2. Adsorption of SO42− on the Silico–Oxygen Plane of Kaolinite
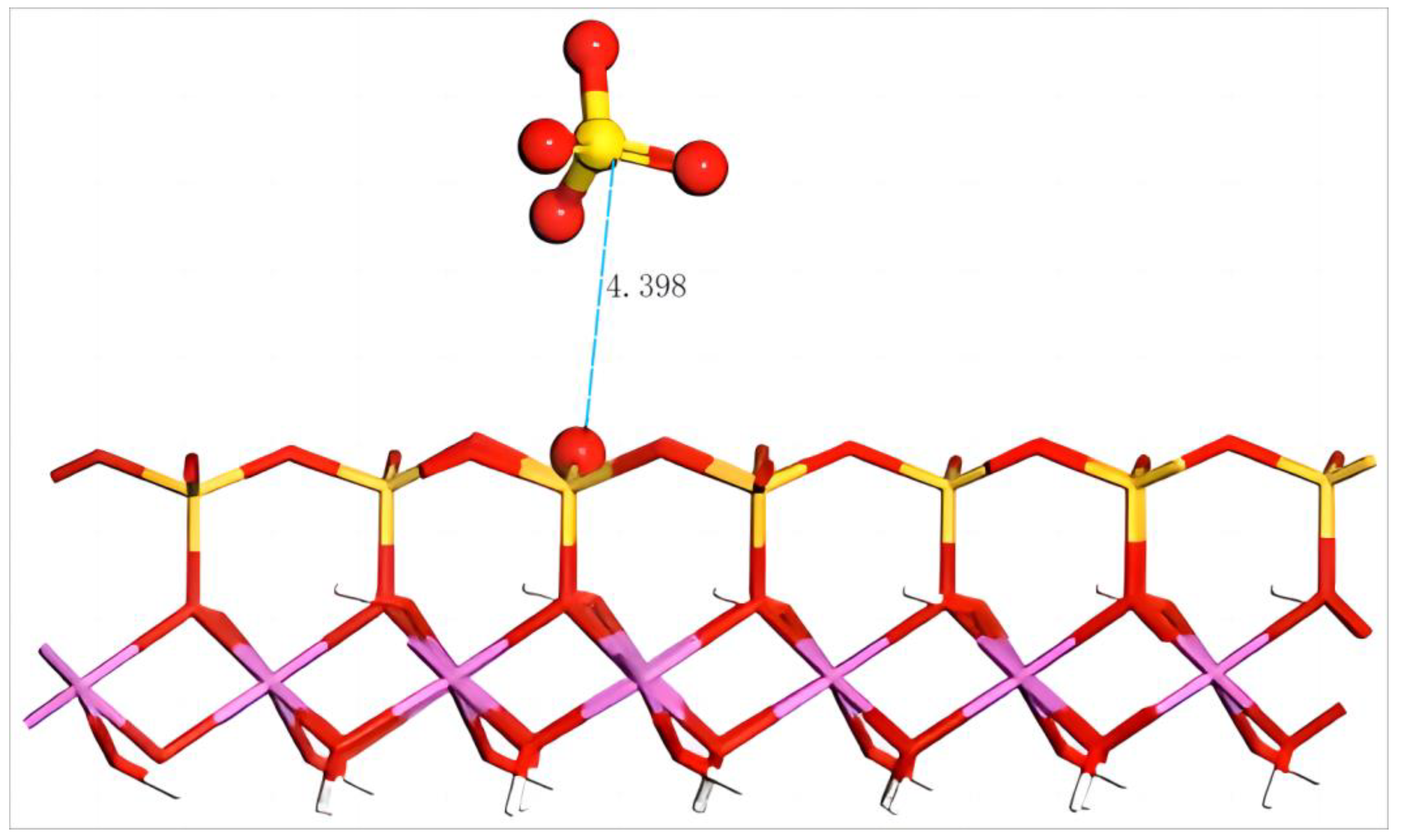
The equilibrium geometry configuration of SO42− after adsorption on the silico–oxygen plane of kaolinite is shown in Figure 11. It can be seen that SO42− keeps a certain distance from the silico–oxygen plane of kaolinite. The distance between SO42− and the nearest O on the surface is 4.398 Å. The approaching of anions is hindered as the negative charges on the kaolinite surface induce the mutual repulsion of the two. After optimization, the adsorption energy of SO42− on the surface is a positive 467.7 kJ/mol, suggesting that such anions can not be adsorbed on the silico–oxygen plane of kaolinite spontaneously. Due to the large negative charges carried by SO42−, it tends to bind with the rare earth ions in an aqueous solution, thus facilitating the transfer of rare earth ions from the surface of kaolinite to the aqueous solution. This result agrees well with the results in industrial production.
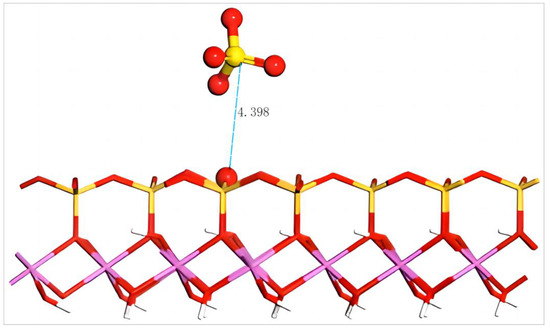
Figure 11.
Adsorption structure of SO42− on the (001) silico–oxygen plane of kaolinite. Note: Red stands for O, white stands for H, yellow stands for S, orange–yellow stands for Si, purple stands for Al, and the dotted line stands for bond length.
4.5. Adsorption of MgSO4 on the Aluminum–Hydroxyl Plane of Kaolinite
4.5.1. Adsorption of Mg(H2O)62+ on the Aluminum–Hydroxyl Plane of Kaolinite
- (1)
- Adsorption Configuration and Adsorption Energy
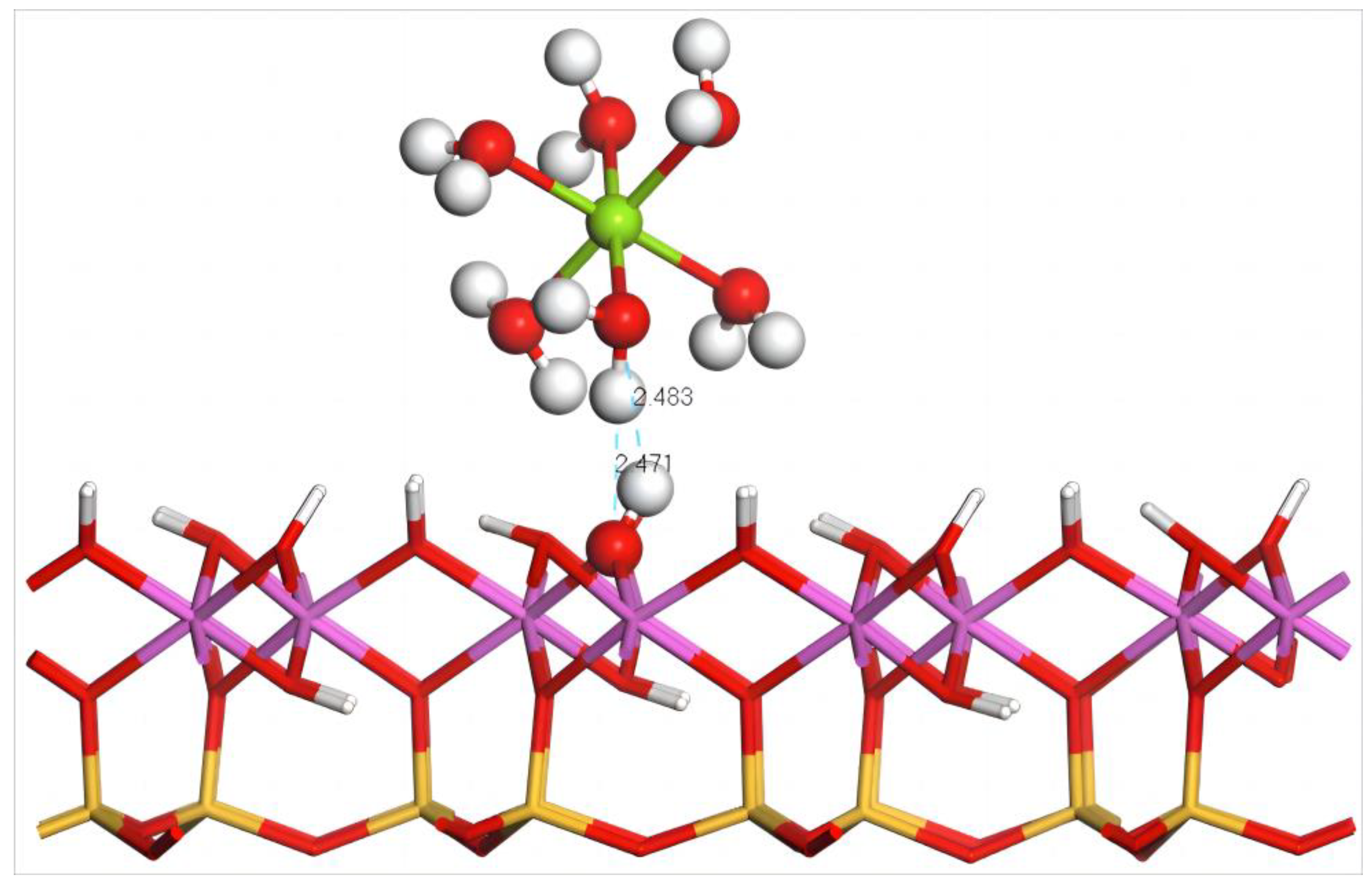
Figure 12 illustrates the equilibrium geometry configuration of Mg(H2O)62+ absorbed on the (001) aluminum–hydroxyl plane of kaolinite. After adsorption, one H atom and one O atom in the coordinated water molecules of Mg(H2O)62+ form two hydrogen bonds with one O atom and one H atom of the surface hydroxy groups, respectively, and the bond lengths are 2.483 and 2.471 Å, which promotes the stable adsorption of hydrated Mg2+ on the aluminum–hydroxyl plane. Combined with the configuration parameters and adsorption energy of Mg(H2O)62+ before and after adsorption on the (001) aluminum–hydroxyl plane of kaolinite, during the approaching process of Mg(H2O)62+, the coordinated water molecules experience extrusion to varied extents so that the average bond length between Mg and the coordinated water molecules increases to 2.43 Å from 2.26 Å before adsorption, smaller than that after adsorption on the silico–oxygen plane.
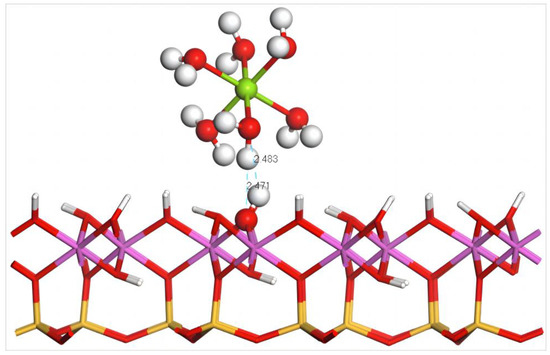
Figure 12.
Adsorption structure of Mg(H2O)62+ on the (001) aluminum–hydroxyl plane of kaolinite. Note: Red stands for O, white stands for H, dark green stands for Mg, orange–yellow stands for Si, purple stands for Al, and the dotted line stands for bond length.
The calculation results as shown in Table 10 indicate that the adsorption energy of Mg(H2O)62+ on the aluminum–hydroxyl plane of kaolinite is −180.5 kJ/mol, which is at a similar level to that of Dy(H2O)103+ on the aluminum–hydroxyl plane of kaolinite (−194.4 kJ/mol). This means that hydrated Mg2+ exhibits strong exchange capability to hydrated rare earth ions. Compared with the rare earth ions adsorbed on the silico–oxygen plane of kaolinite, hydrated Mg ions show a higher tendency to leach rare earth ions from the aluminum–hydroxyl plane.

Table 10.
Configuration parameters and adsorption energy of Mg(H2O)62+ before and after adsorption on the (001) aluminum–hydroxyl plane of kaolinite.
- (2)
- Electron Transfer and State Density Study
Figure 13 gives the density of states of Mg and the surface before and after adsorption of Mg(H2O)63+ on the (001) aluminum–hydroxyl plane of kaolinite. It can be seen that the Mg 2s and 2p orbitals are far away from the Fermi level before adsorption, meaning that the overall activity of Mg2+ is lower than that of rare earth ions. After adsorption, the Mg2+ 2p and 2s orbitals are still away from the Fermi level without obvious variation in the orbital peaks, while the 2p orbitals of the kaolinite surface are still located at the Fermi level. As seen in Table 11, Mg loses 0.17 electrons in total after adsorption and the valence state increases from 1.68 to 1.85.
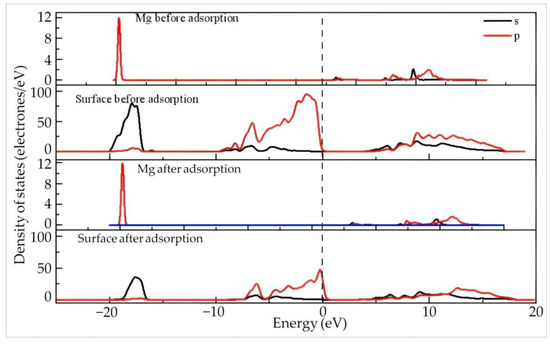
Figure 13.
The density of states of Mg and the surface before and after adsorption of Mg(H2O)63+ on the aluminum–hydroxyl plane of kaolinite.

Table 11.
The Mulliken charge population of the atomic charges of Mg before and after the adsorption of Mg(H2O)63+ on the aluminum–hydroxyl plane of kaolinite.
4.5.2. Adsorption of SO42− on the Aluminum–Hydroxyl Plane of Kaolinite
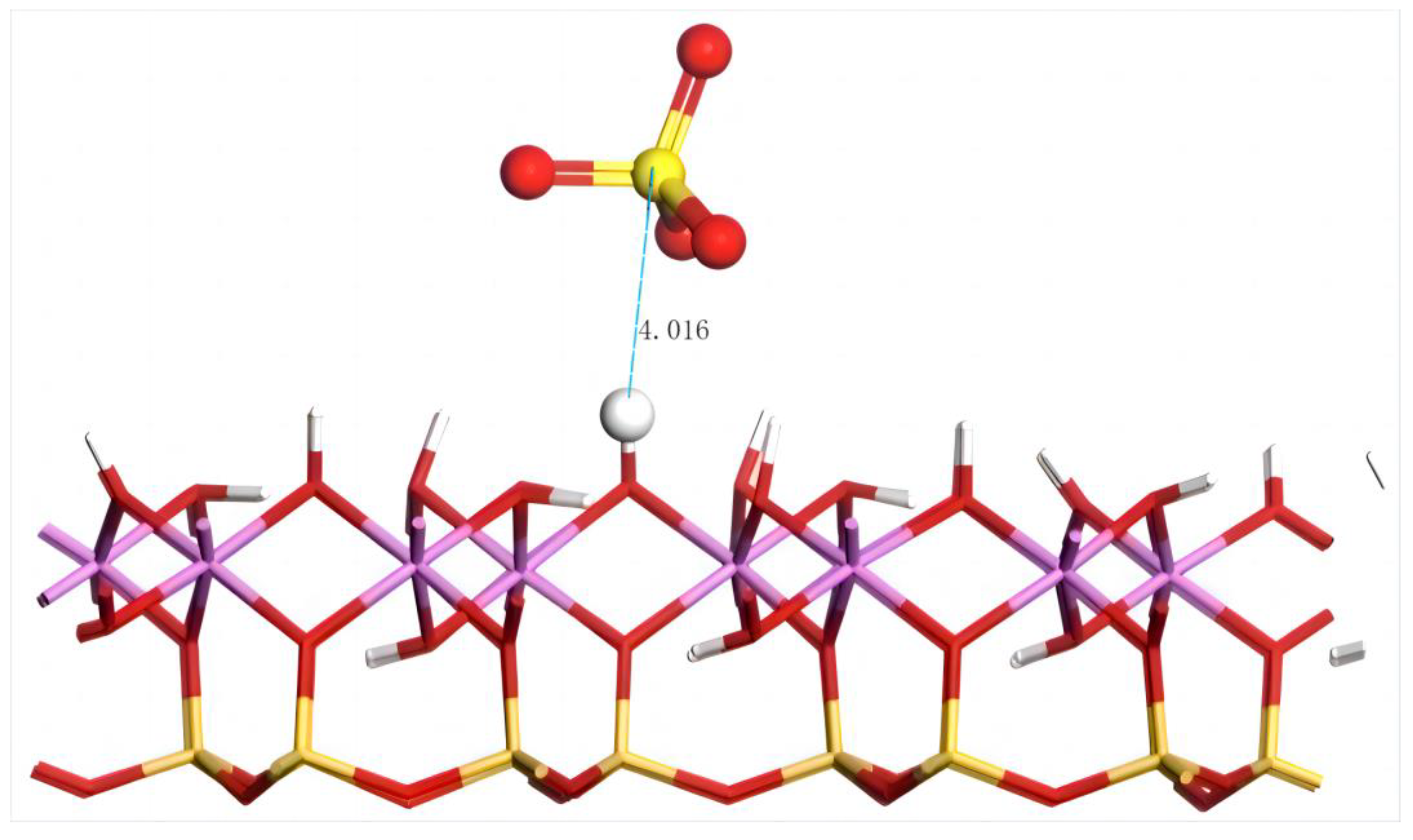
The geometric equilibrium configuration of SO42− after adsorption on the aluminum–hydroxyl plane of kaolinite is shown in Figure 14.
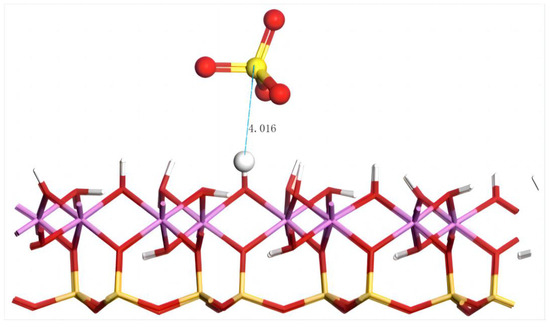
Figure 14.
The adsorption structure of SO42− on the (001) aluminum–hydroxyl plane of kaolinite. Note: Red stands for O, white stands for H, yellow stands for S, orange–yellow stands for Si, purple stands for Al, and the dotted line stands for bond length.
The distance between SO42− and the nearest H on the aluminum–hydroxyl plane of kaolinite is 4.016 Å, which exceeds the range of chemical bonds. The adsorption energy is 154.4 kJ/mol. Compared with that on the silico–oxygen plane of kaolinite, the adsorption energy of SO42− on the aluminum–hydroxyl plane is lower, which might have resulted from the larger repulsive force on the negatively charged anions induced by the more negative charges on the silico–oxygen plane. Similarly, it indicates that SO42− tends to combine with the rare earth ions in an aqueous solution which facilitates the transport of rare earth ions from kaolinite surfaces to the aqueous solution.
5. Conclusions
The first-principles plane-wave pseudopotential method based on the density functional theory was used to investigate the stable configuration and properties of the hydrates of Dy(III) ions. On that basis, the adsorption characteristics of the stable configuration of Dy(III) hydrates on the (001) silico–oxygen plane and aluminum–hydroxyl plane of kaolinite were studied. In aqueous media, Dy(III) is bonded with 10 water molecules via coordination bonds and forms a stable hydrated structure of Dy(H2O)103+, whose binding energy is −2403.8 kJ/mol. Dy(H2O)103+ is adsorbed on the (001) silico–oxygen plane of kaolinite through four hydrogen bonds with lengths of 2.447, 2.462, 1.924, and 2.492 Å and an adsorption energy of −544.3 kJ/mol. The valence state changes to 1.99 from 1.81 before adsorption.
After adsorption of Dy(H2O)103+ on the (001) aluminum–hydroxyl plane of kaolinite, the coordinated water molecules of the Dy atoms form two hydrogen bonds with the surface, with bond lengths of 2.831 and 2.924 Å and a system adsorption energy of −194.4 kJ/mol. The valence state of Dy then increases from 1.81 to 2.55.
Studies on leaching agents indicate that in kaolinite, hydrated Mg2+ shows a higher tendency to leach out rare earth Dy while SO42− cannot be adsorbed spontaneously on the (001) plane of kaolinite but tends to stay in the aqueous solution. This facilitates the transfer of rare earth ions on the kaolinite surface to the solution, thus promoting the leaching of rare earth ions which has great guiding significance to the selection of leaching agents for ionic rare earth ore.
Author Contributions
L.H.: Writing–original draft and visualization. Z.Z.: Conceptualization ideas. S.L.: Investigation. L.L.: Methodology, writing–review and editing. W.X.: Investigation. Y.Q.: Investigation. S.A.: Investigation. W.H.: funding acquisition and methodology. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The National Natural Science Foundation of China (grant No. 41662004 and 41362003). The Personnel Training Program of Suqu Zhi Guang in Ganzhou City Jiangxi Province.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the editors and reviewers for their excellent support. The authors are also grateful to the School of Resource and Environmental Engineering, Jiangxi University of Science and Technology in China, and the WA School of Mines: Minerals, Energy and Chemical Engineering, Curtin University in Australia, and the Department of Chemical and Biological Engineering, University of Saskatchewan in Canada.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationship that could have appeared to influence the work reported in this paper.
References
- Brown, B.; Ma, B.M.; Chen, Z.M. Developments in the processing and properties of NdFeb-type permanent magnets. J. Magn. Magn. Mater. 2002, 248, 432–440. [Google Scholar] [CrossRef]
- Zeng, S.H.; Du, D.P.; Bai, F.H.; Su, H.Q. Bridging complexes of rare earth and cobalt cluster as catalyst precursors for Fischer-Tropsch synthesis. J. Rare Earths 2011, 29, 349–353. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Y.H. Photoluminescence and cathodoluminescence properties of novel rare-earth free narrow-band bright green-emitting ZnB2O4:Mn2+ phosphor for LEDs and FEDs. Chem. Eng. J. 2019, 361, 314–321. [Google Scholar] [CrossRef]
- Huang, L.J.H.; Xiao, B.; Liu, L.H.; Li, W.H.; Duan, X.G.; Huang, W.F.; Fan, C.Y.; Dong, Y.; Liu, S.M. Selective recovery of Gd(III) by benzimidazole- and benzoxazole-linked 3D porous polymers. J. Water Process Eng. 2023, 51, 103378. [Google Scholar] [CrossRef]
- Huang, W.F.; Zou, Z.Q.; Zhong, X.X.; Huang, X.L. Occurrence characteristics and leaching rules of different weathering rare earth ores. J. Chin. Soc. Rare Earths 2017, 35, 253–261. [Google Scholar]
- Huang, L.J.H.; Liu, H.L.; Huang, W.F.; Zhao, B.X.; Shen, Z.F.; Bao, Y.Q. Recovery of lanthanum cations by functionalized magnetic multi-walled carbon nanotube bundles. RSC Adv. 2021, 11, 4751–4759. [Google Scholar] [CrossRef]
- Xiao, Y.F.; Chen, Y.Y.; Feng, Z.Y.; Huang, X.W.; Huang, L.J.H.; Long, Z.Q.; Cui, D.L. Leaching characteristics of ion-adsorption type rare earths ore with magnesium sulfate. Nonferr. Metal. Soc. 2015, 25, 3784–3790. [Google Scholar] [CrossRef]
- Xiao, Y.F.; Feng, Z.Y.; Huang, X.W.; Huang, L.J.H.; Chen, Y.Y.; Wang, L.S.; Long, Z.Q. Recovery of rare earths from weathered crust elution-deposited rare earth ore without ammonia-nitrogen pollution: I. leaching with magnesium sulfate. Hydrometallurgy 2015, 153, 58–65. [Google Scholar]
- He, Z.Y.; Zhang, Z.Y.; Yu, J.X.; Xu, Z.G.; Xu, Y.L.; Zhou, F.; Chi, R.A. Column leaching process of rare earth and aluminum from weathered crust elution-deposited rare earth ore with ammonium salts. Trans. Nonferrous Met. Soc. China 2016, 26, 3024–3033. [Google Scholar] [CrossRef]
- Wu, P.Q.; Zhou, J.W.; Huang, J.; Lin, X.J.; Liang, X.L. Enrichment and fractionation of rare earth elements in ion-adsorption rare earth elements deposits: Constraints of iron oxide-clay mineral composites. Geochimica 2022, 51, 271–282. [Google Scholar]
- Zhang, M.; He, X.C.; Tan, W.; Ma, L.Y.; Zhao, F.F. Geochemical characteristics and genesis of ion-adsorption type REE deposit in the Lincang granite, Yunnan Province. Geol. China 2022, 49, 201–214. [Google Scholar]
- Liu, E.H.; Huang, J.; Tan, W.; Liang, X.L.; Ma, L.Y. Constraints on the Ree enrichment-fractionation in weathering crust by the mineral evolution in the weathering and leaching processes: A case study of the Renju Ree deposit in the Meizhou Area, Guangdong, China. Bull. Mineral. Petrol. Geochem. 2022, 41, 517–526. [Google Scholar]
- Zai, X.S.; Li, J.P.; Xin, J.Z.; Fang, Z.J.; Mo, J.C. Detection and finite element analysis for a stone arch bridge. J. Guangxi Univ. Sci. Technol. 2016, 27, 66–70. [Google Scholar]
- Ning, L.; Gou, K.Y.; Liu, M.L.; Zeng, J.S.; Lu, Y.; Zhou, X.; Fang, Z.J. Clay mineral montmorillonite crystals and their structural analysis. J. Guangxi Univ. Sci. Technol. 2020, 31, 75–81. [Google Scholar]
- Yao, X.H.; Huang, L.J.H.; Huang, W.F.; Zeng, X.R.; Huang, B.L.; Bao, Y.Q. Density functional calculation of La(H2O)3+10 adsorption on surface of montmorillonite (001). Bull. Chin. Ceram. Soc. 2021, 40, 3769–3776. [Google Scholar]
- Du, J.; Min, F.F.; Zhang, M.X.; Peng, C.L.; Fang, F. Adsorption of H3O+ on (001) basal and (010) edge surface of illite: A DFT study. J. China Coal Soc. 2018, 43, 2625–2632. [Google Scholar]
- Zou, Z.Q.; Huang, L.J.H.; Li, X.D.; Xu, J.; Zeng, X.R.; Shu, R.H.; Xiao, B.; Ou, J.C.; Huang, W.F. Adsorption of Hydrated Pr3+ and NH4+/Mg2+ Ions onto the (001) Surface of Montmorillonite: A DFT Analysis with Experimental Verification. Minerals 2022, 12, 1454. [Google Scholar] [CrossRef]
- Weshahy, A.R.; Gouda, A.A.; Atia, B.M.; Sakr, A.K.; Al-Otaibi, J.S.; Almuqrin, A.; Hanfi, M.Y.; Sayyed, M.I.; El Sheikh, R.; Radwan, H.A.; et al. Efficient recovery of rare earth elements and zinc from spent Ni-metal hydride batteries: Statistical studies. Nanomaterials 2022, 12, 2305. [Google Scholar] [CrossRef]
- Allam, E.M.; Lashen, T.A.; Abou El-Enein, S.A.; Hassanin, M.A.; Sakr, A.K.; Cheira, M.F.; Almuqrin, A.; Hanfi, M.Y.; Sayyed, M.I. Rare earth group separation after extraction using sodium diethyldithiocarbamate/polyvinyl chloride from lamprophyre dykes leachate. Materials 2022, 15, 1211. [Google Scholar] [CrossRef]
- Lee, S.G.; Choi, J.I.; Koh, W.; Jang, S.S. Adsorption of β-d-glucose and cellobiose on kaolinite surfaces: Density functional theory (DFT) approach. Appl. Clay Sci. 2013, 71, 73–81. [Google Scholar] [CrossRef]
- Qiu, S.; Yan, H.; Qiu, X.; Wu, H.; Zhou, X.; Wu, H.; Li, X.; Qiu, T. Adsorption of La on kaolinite (001) surface in aqueous system: A combined simulation with an experimental verification. J. Mol. Liq. 2021, 347, 117956. [Google Scholar] [CrossRef]
- Chen, J.; Min, F.F.; Liu, L.Y.; Jia, F.F. Adsorption of methylamine cations on kaolinite basal surfaces: A DFT study. Physicochem. Probl. Miner. Process. 2020, 56, 338–349. [Google Scholar] [CrossRef]
- Chen, J.; Min, F.F.; Liu, L.Y.; Liu, C.F. Mechanism research on surface hydration of kaolinite, insights from DFT and MD simulations. Appl. Surf. Sci. 2019, 476, 6–15. [Google Scholar] [CrossRef]
- Chen, J.; Min, F.F.; Liu, L.Y. The interactions between fine particles of coal and kaolinite in aqueous, insights from experiments and molecular simulations. Appl. Surf. Sci. 2019, 467, 12–21. [Google Scholar] [CrossRef]
- Patrick, V.B.; Randall, T.C.; Kathryn, L.N. Molecular controls on kaolinite surface charge. J. Colloid Interface Sci. 1996, 183, 356–364. [Google Scholar]
- Heimann, J.E.; Grimes, R.T.; Rosenzweig, Z.; Bennett, J.W. A density functional theory (DFT) investigation of how small molecules and atmospheric pollutants relevant to art conservation adsorb on kaolinite. Appl. Clay Sci. 2021, 206, 106075. [Google Scholar] [CrossRef]
- Li, M.L.; Wang, X.P.; Zhang, J.; Gao, Y.H.; Zhang, W. Cu-loaded MOF-303 for iodine adsorption: The roles of Cu species and pyrazole ligands. Appl. Surf. Sci. 2023, 619, 156819. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, J.; Dong, X.T.; Li, M.L.; He, Q.; Zhao, S.; Xie, L.X. Fluorinated metal–organic frameworks for enhanced stability and iodine adsorption selectivity under humid conditions. Chem. Eng. J. 2023, 461, 142058. [Google Scholar] [CrossRef]
- Zeng, X.R.; Zeng, B.; Huang, L.J.H.; Zhong, L.; Li, X.D.; Huang, W.F. Adsorption of Y(III) on the Interface of Kaolinite-H2O: A DFT Study. Minerals 2022, 12, 1128. [Google Scholar] [CrossRef]
- Xu, H.Y.; Guan, D.Q.; Ma, L. The bio-inspired heterogeneous single-cluster catalyst Ni100-Fe4S4 for enhanced electrochemical CO2 reduction to CH4. Nanoscale 2023, 15, 2756–2766. [Google Scholar] [CrossRef]
- Xiao, W.; Kiran, G.K.; Yoo, K.; Kim, J.-H.; Xu, H.Y. The dual-site adsorption and high redox activity enabled by hybrid organic-inorganic vanadyl ethylene glycolate for high-rate and long-durability lithium-sulfur batteries. Small 2023, 19, 2206750. [Google Scholar] [CrossRef]
- Xu, H.Y.; Guan, D.Q. Exceptional anisotropic noncovalent interactions in ultrathin nanorods: The terminal sigma-hole. ACS Appl. Mater. Interfaces 2022, 14, 51190–51199. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Zhou, Q.; Yuan, Z.T.; Zhao, L.; Dong, J.D. Adsorption of Mg2+ and K+ on the kaolinite (001) surface in aqueous system: A combined DFT and AIMD study with an experimental verification. Appl. Surf. Sci. 2021, 538, 148158. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).