Three-Dimensional Inversion of Long-Offset Transient Electromagnetic Method over Topography
Abstract
:1. Introduction
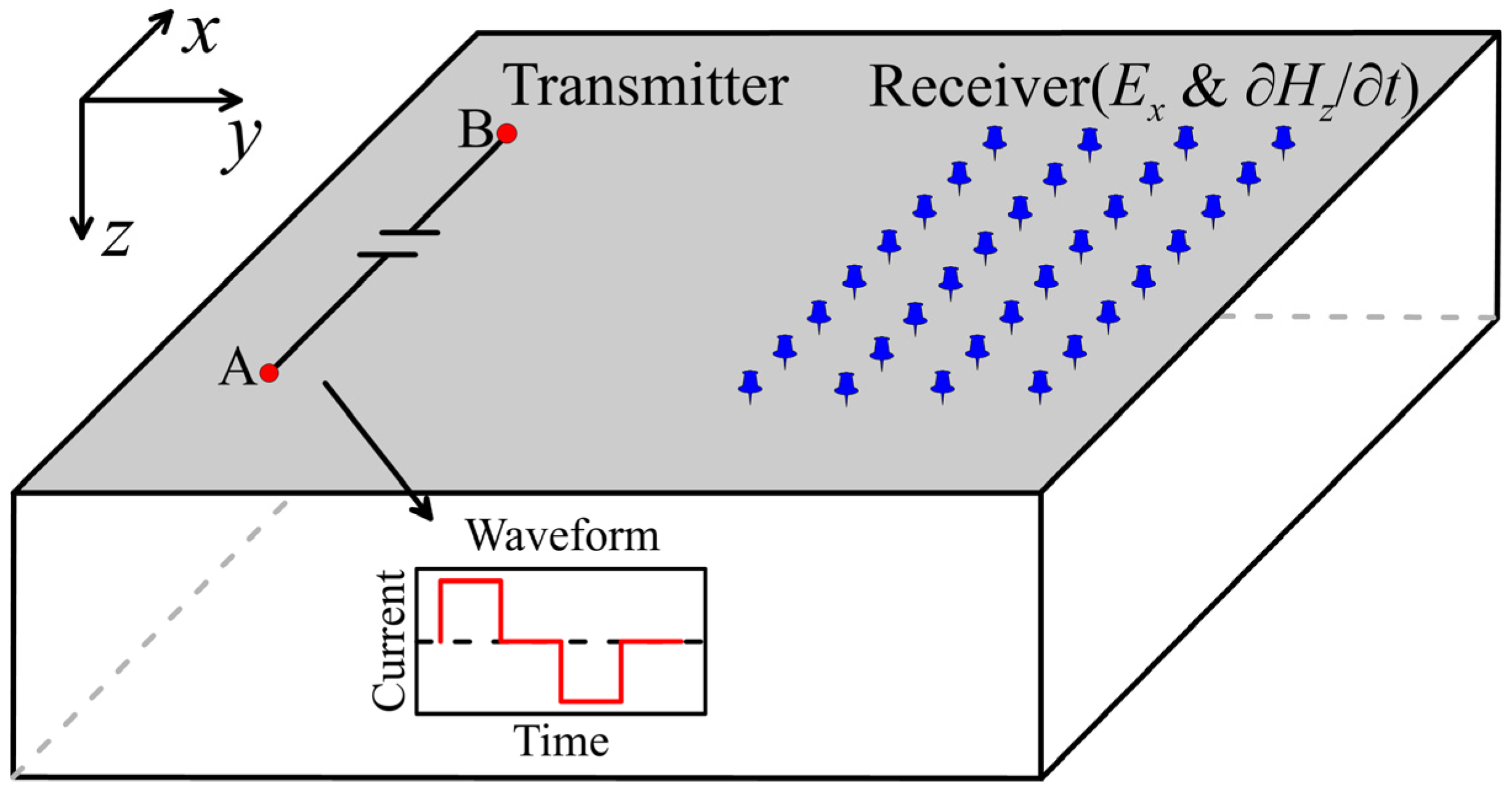
2. Methods
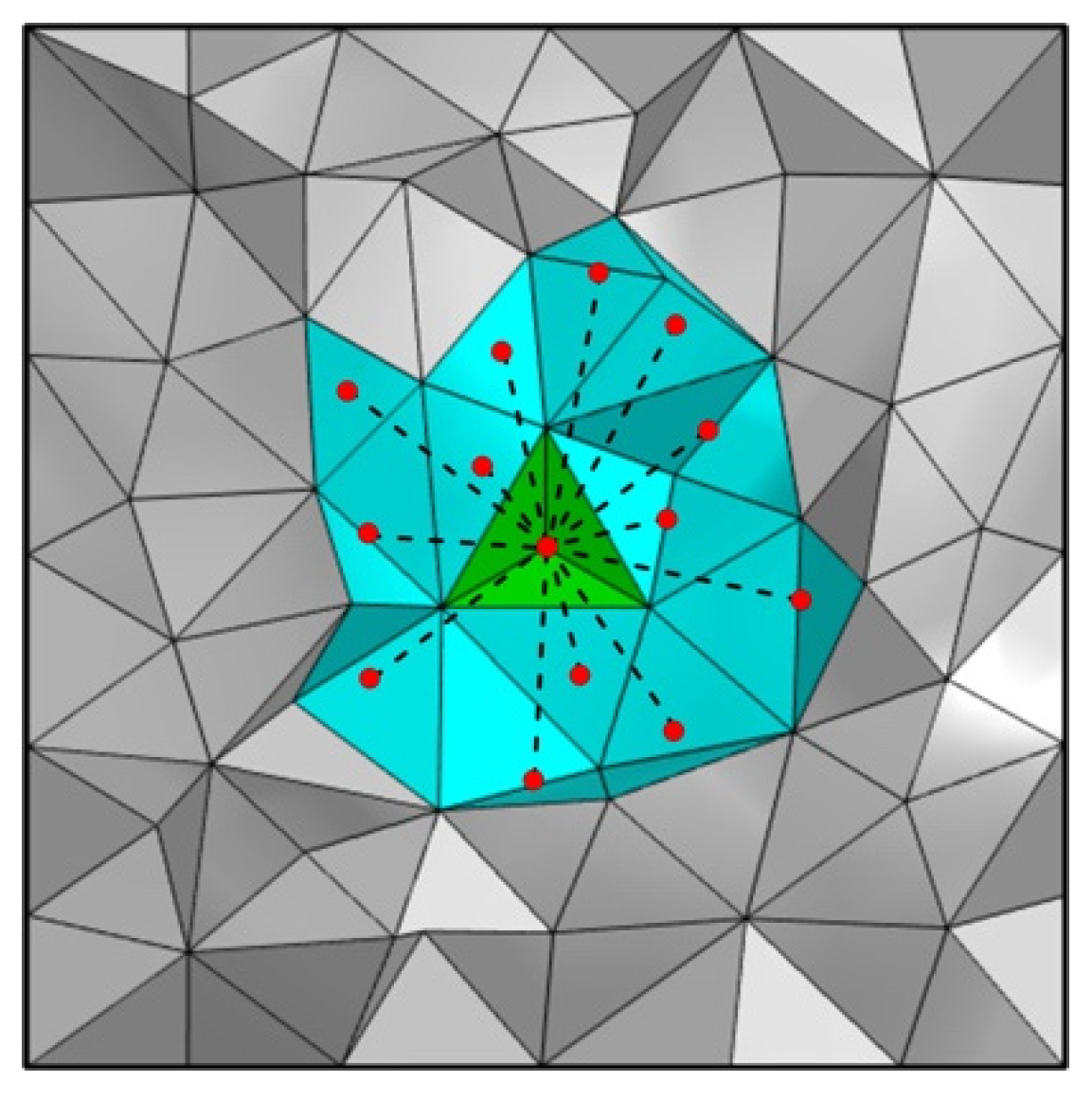
2.1. Forward Modeling
2.2. Inverse Problem
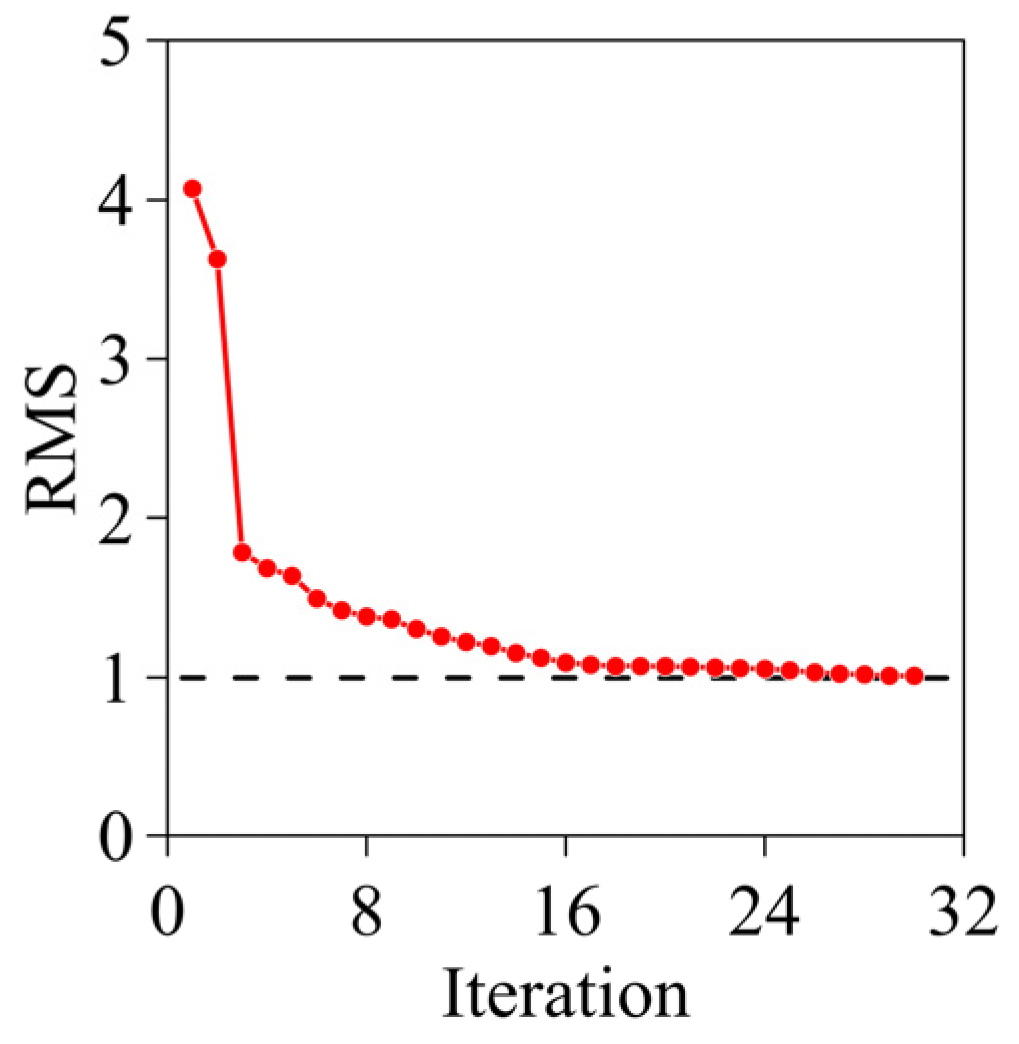
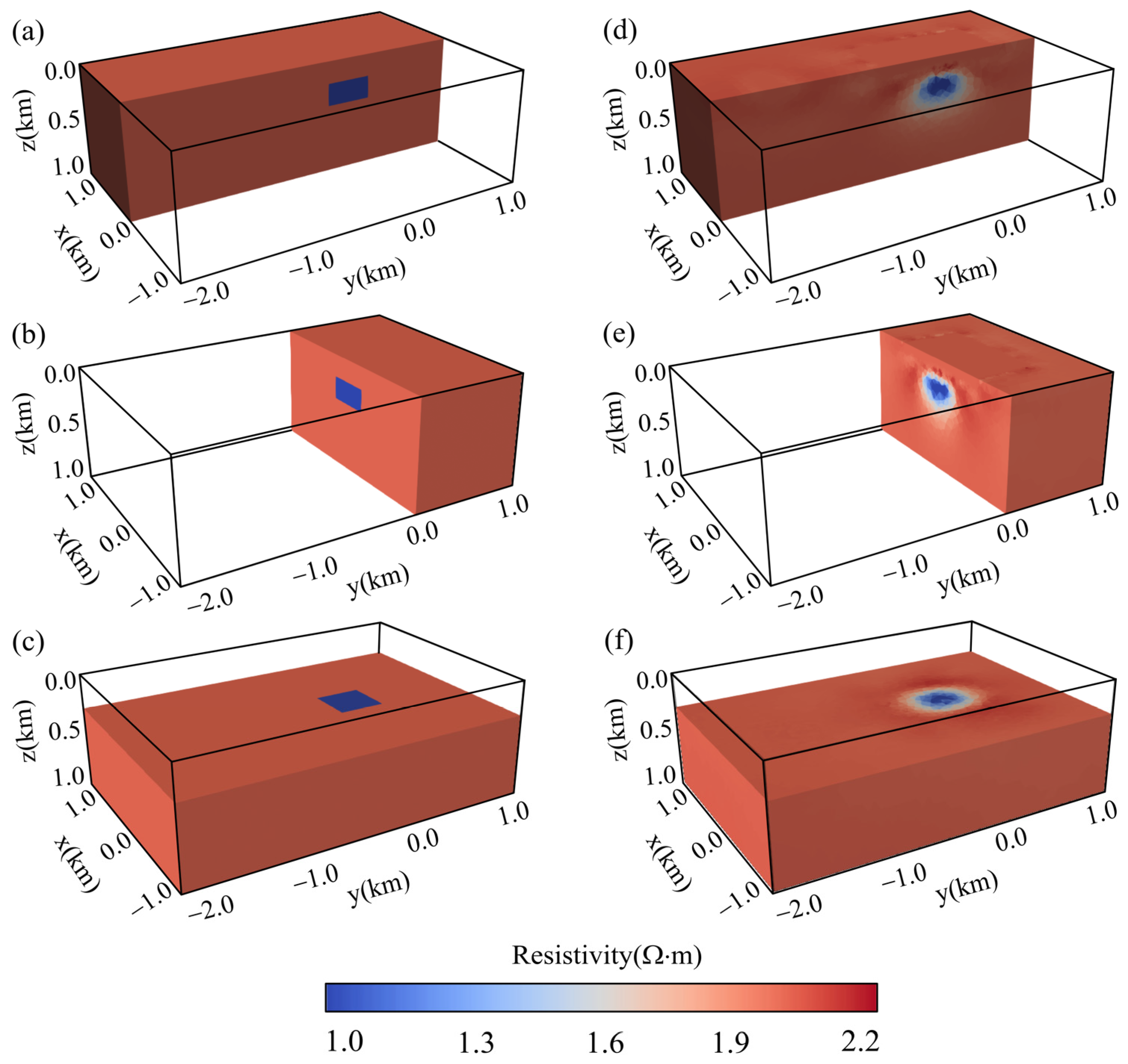
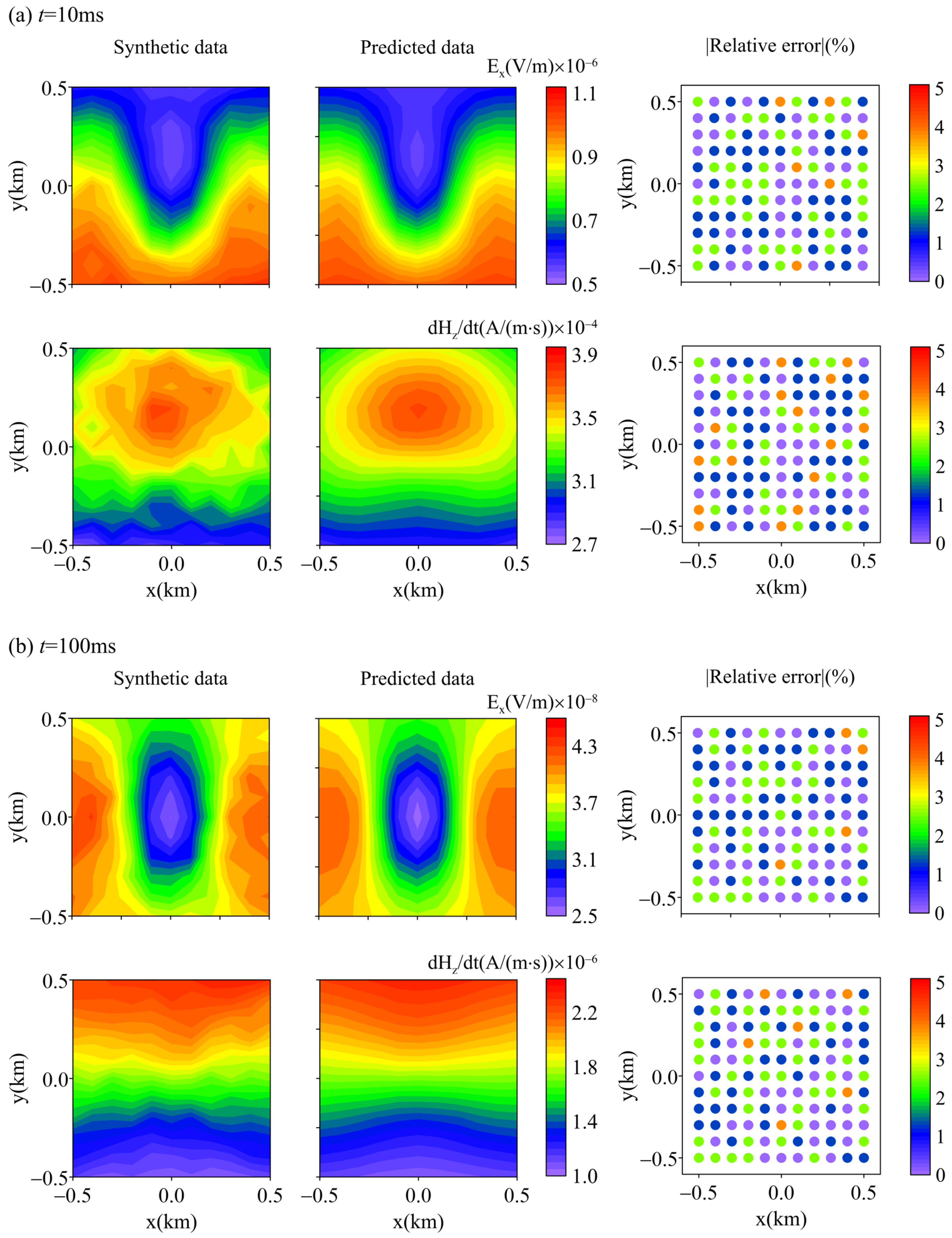
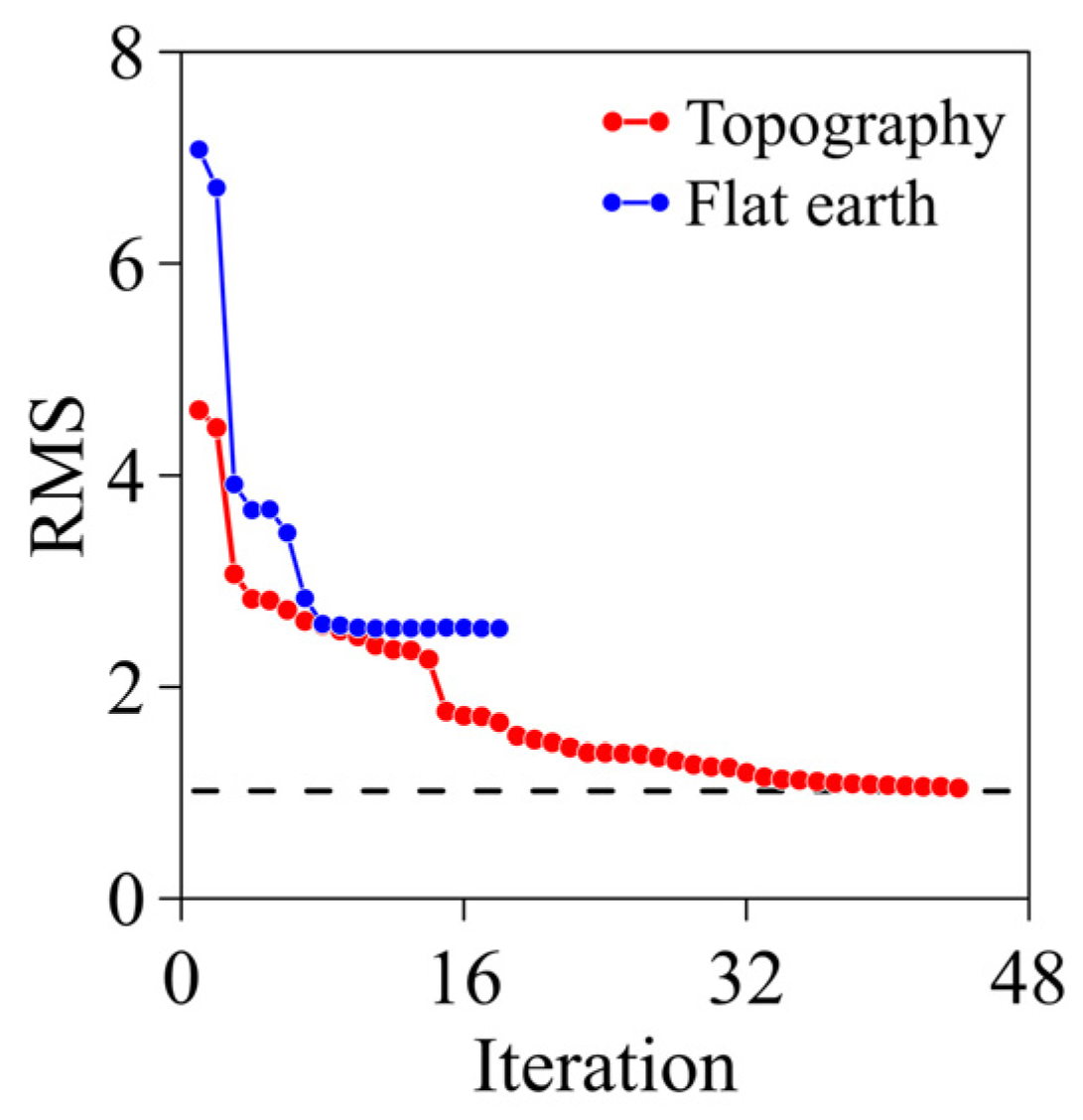
3. Synthetic Examples
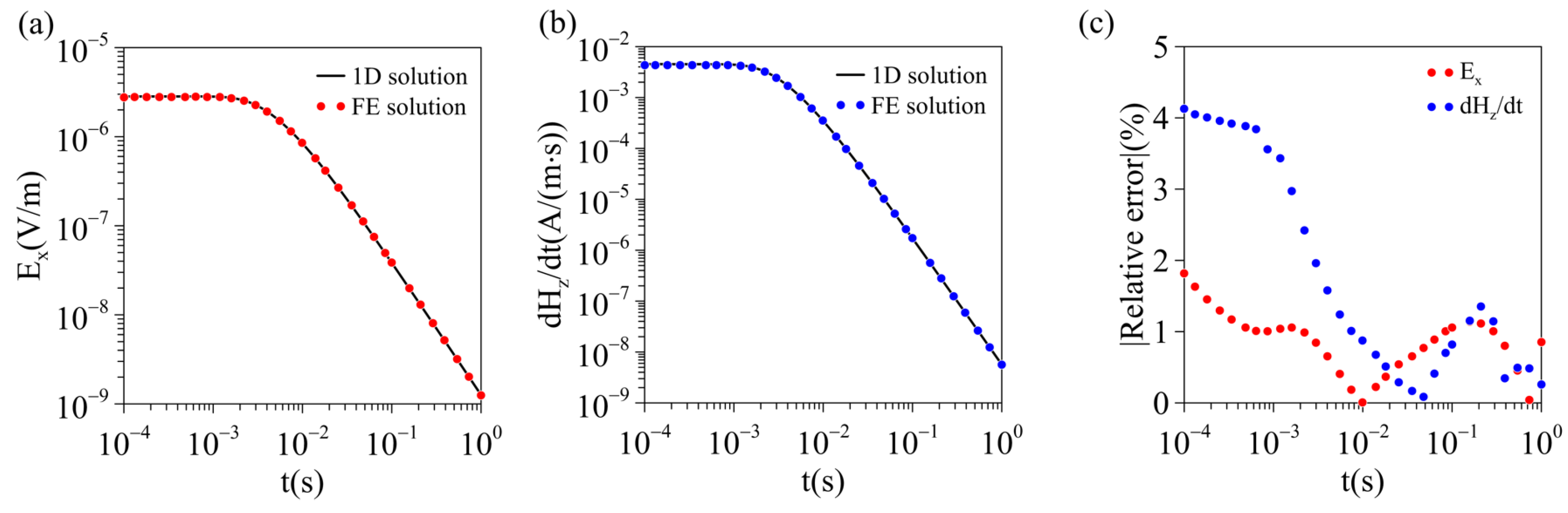
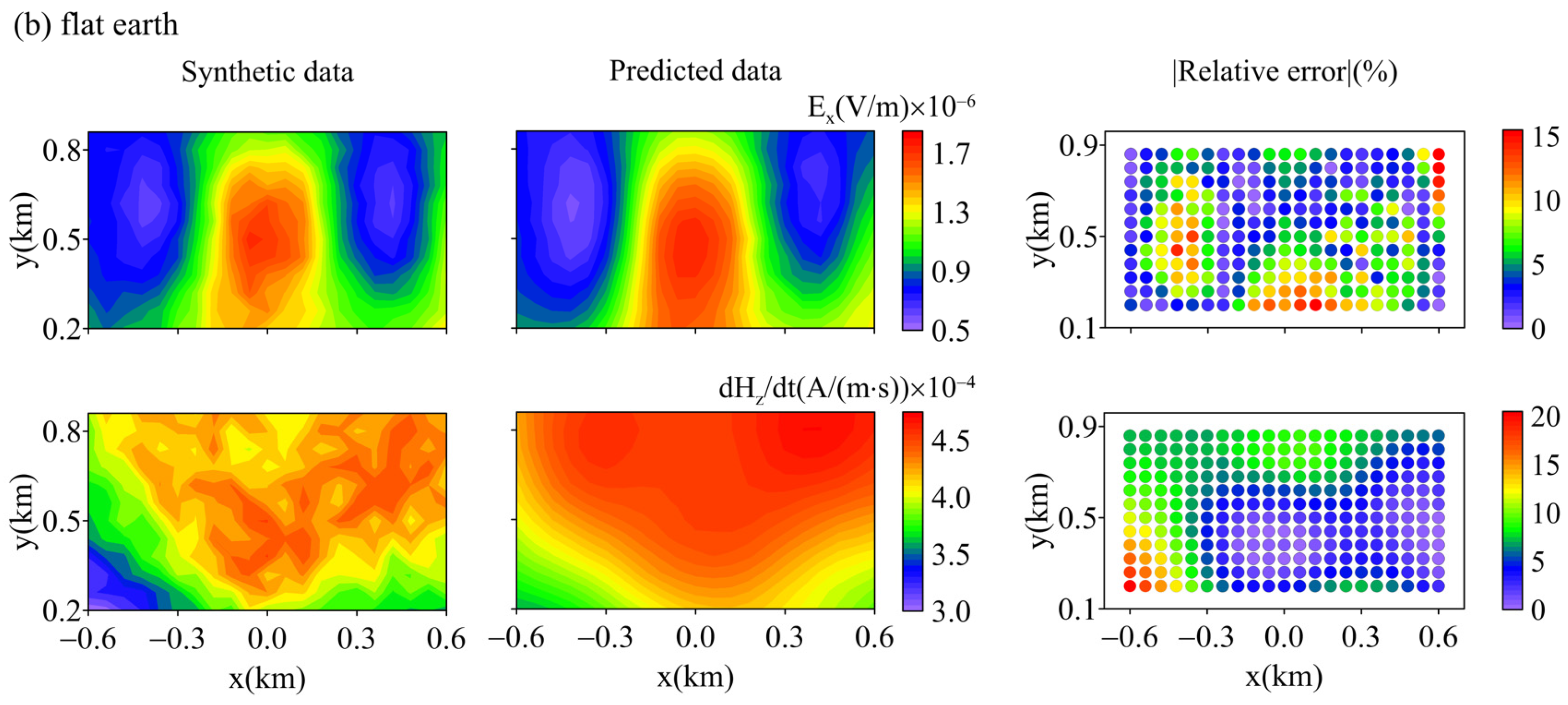
3.1. Flat Earth Model
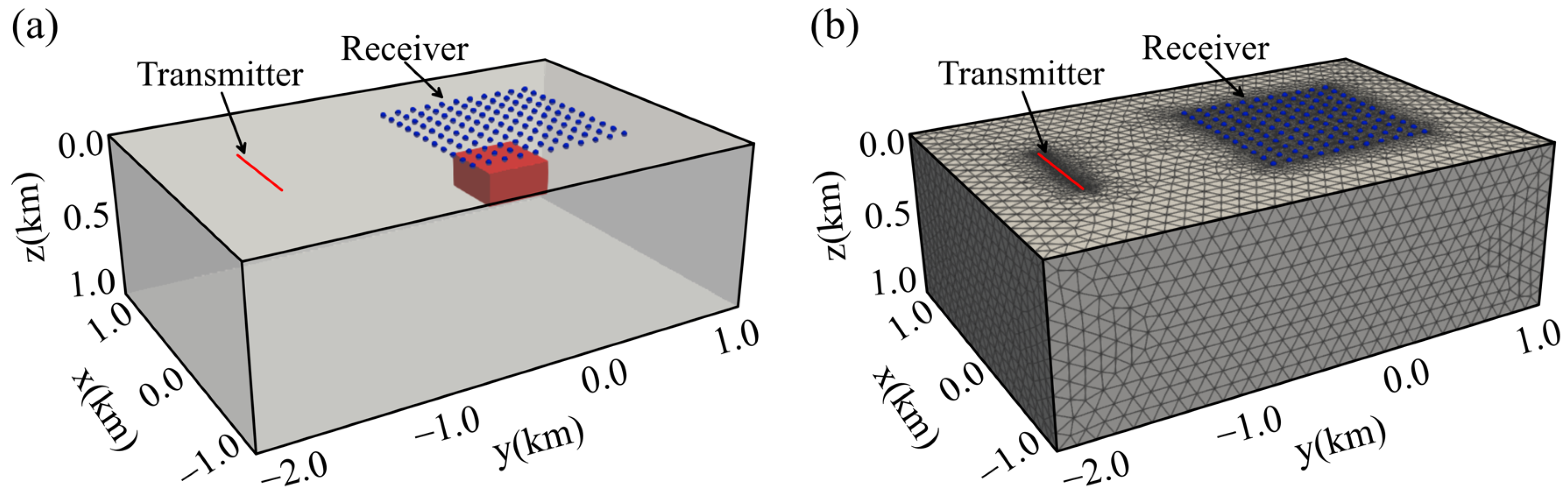
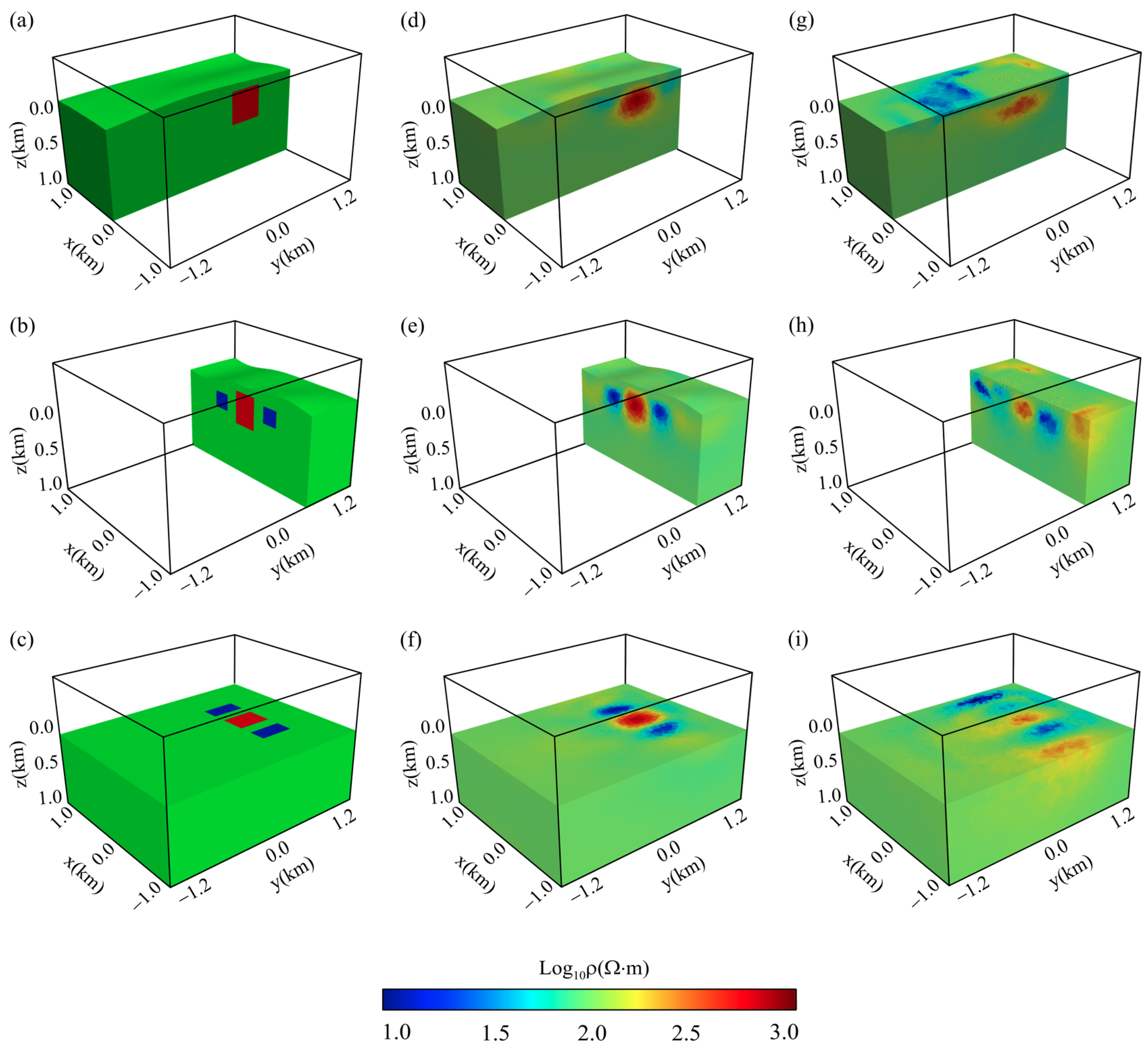
3.2. Synthetic Model with Topography
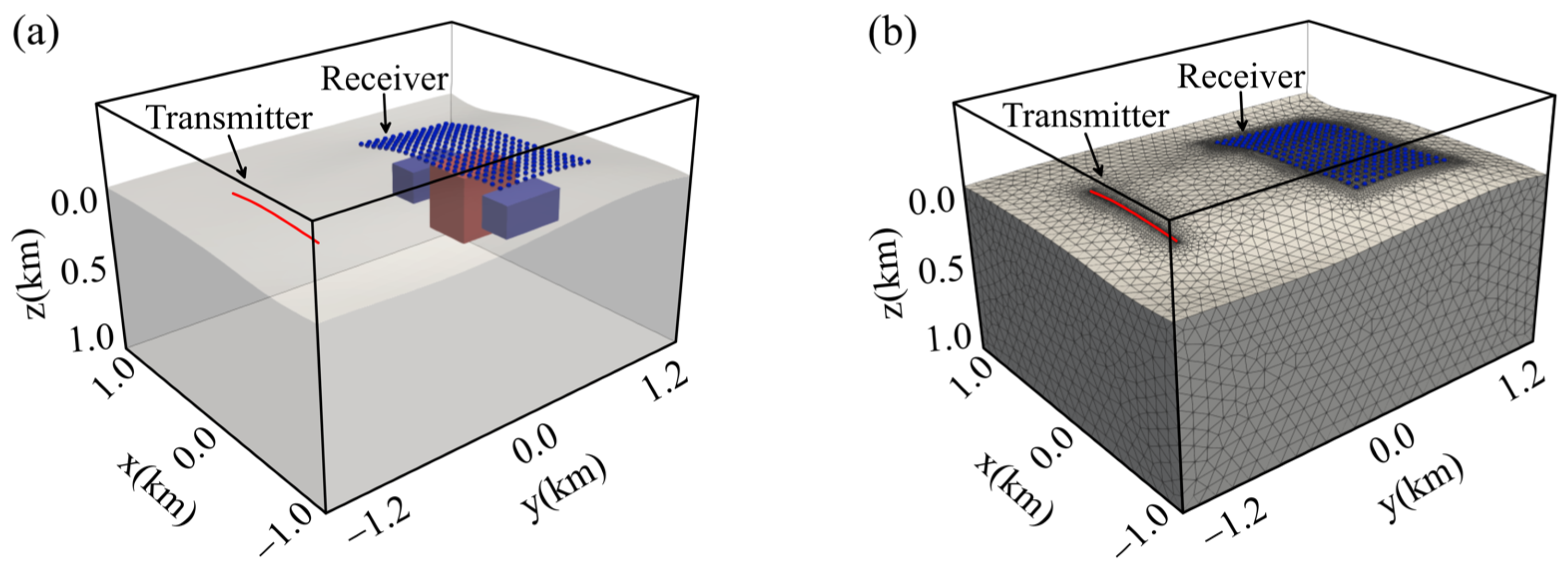
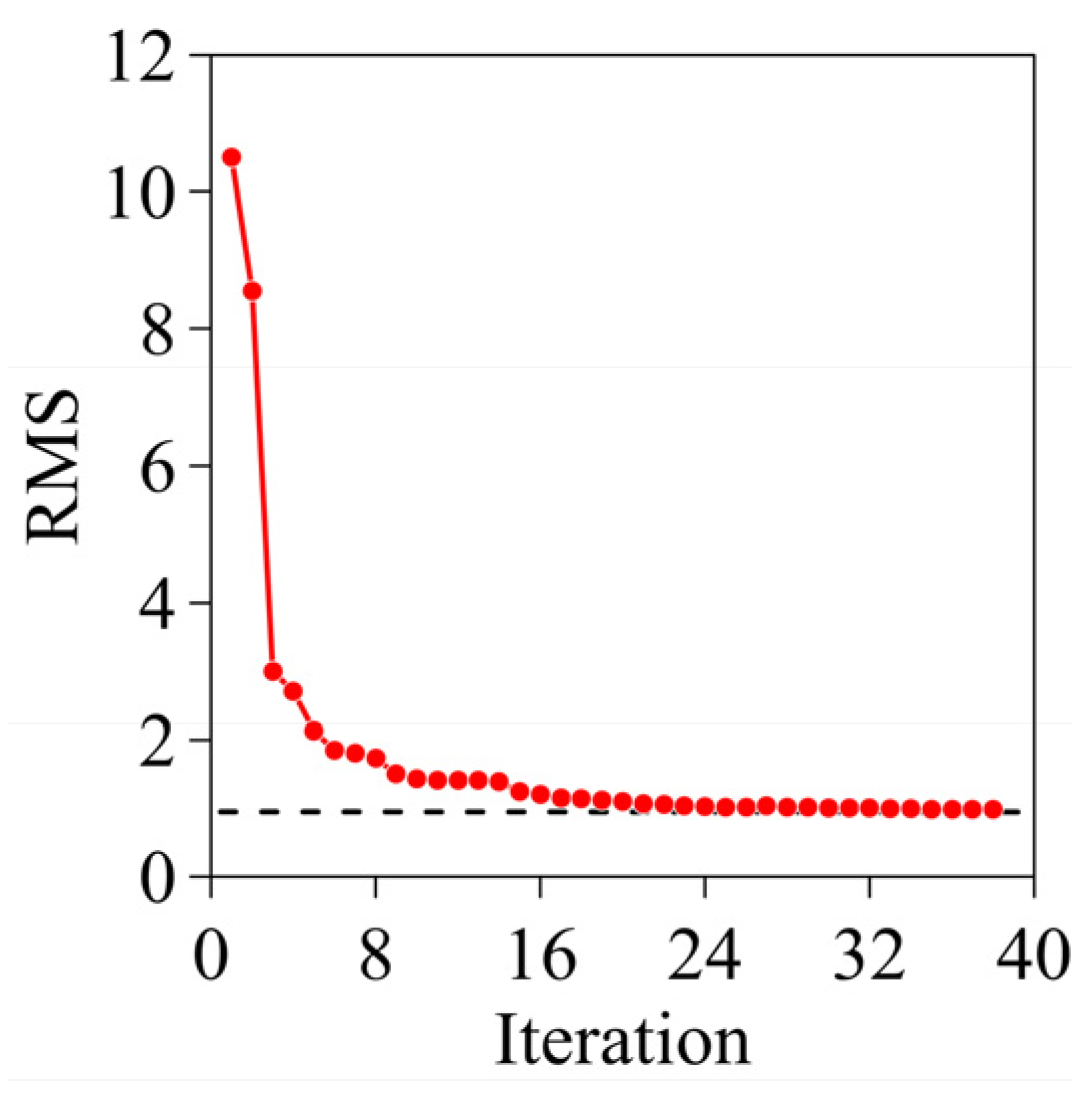
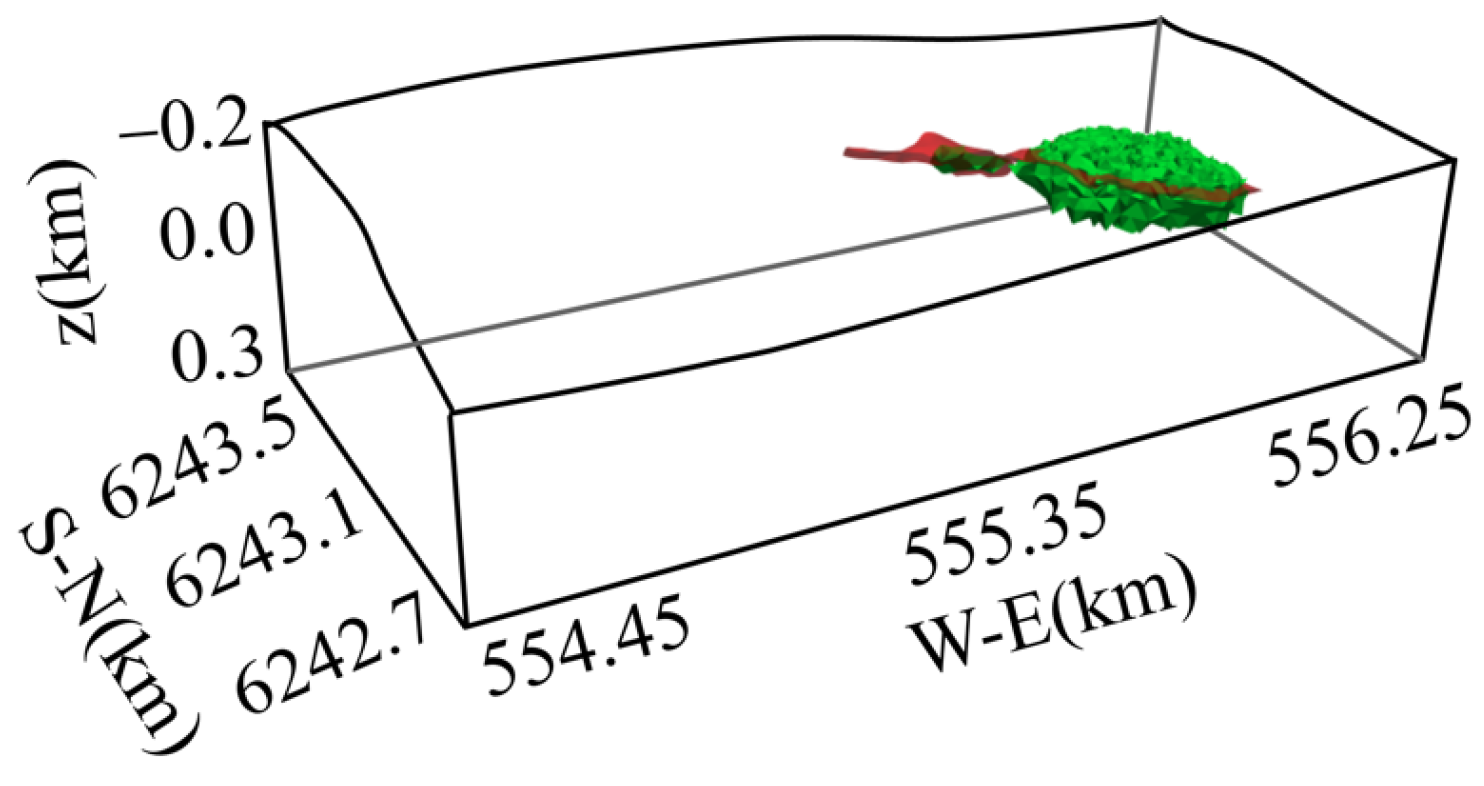
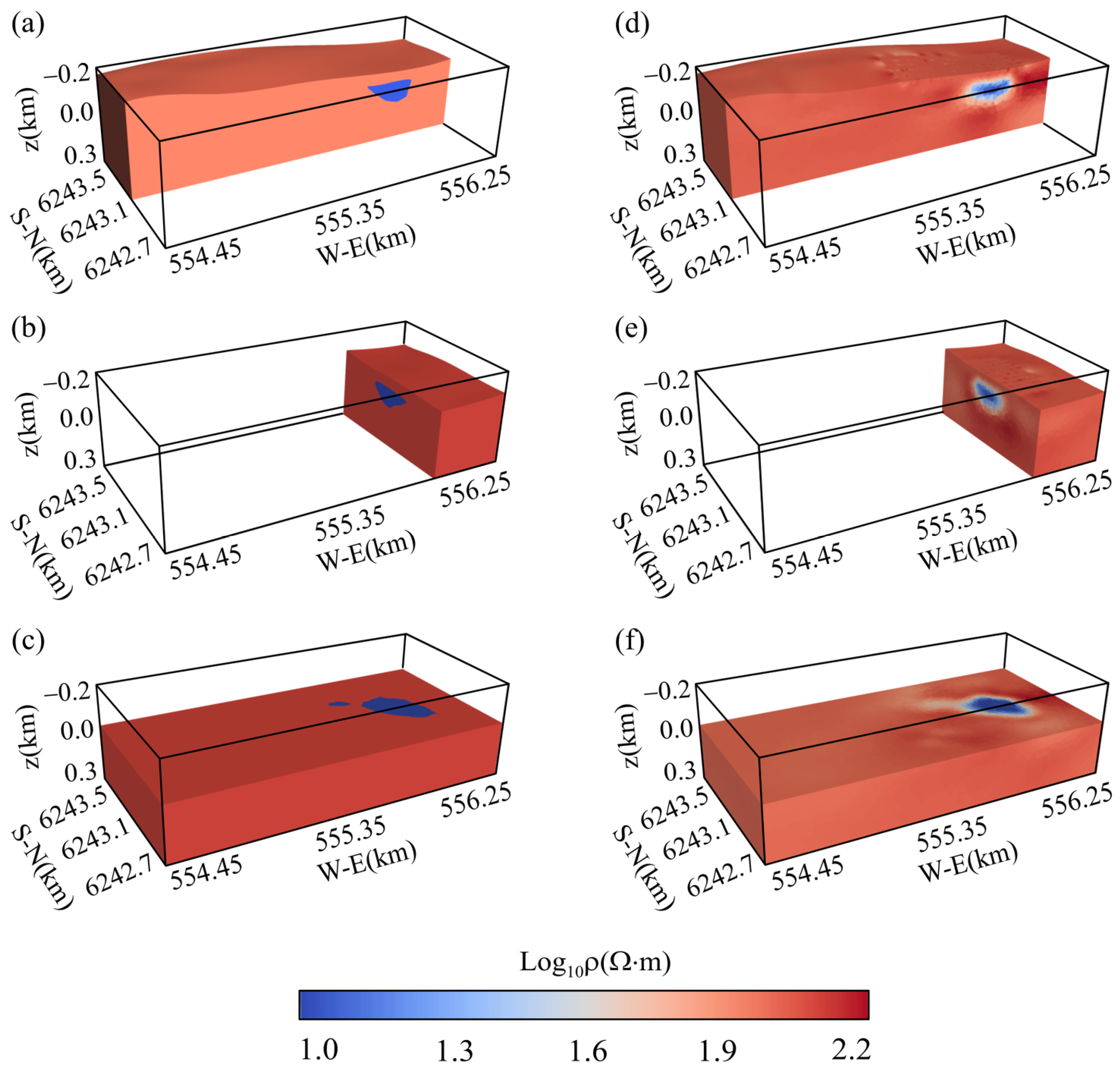
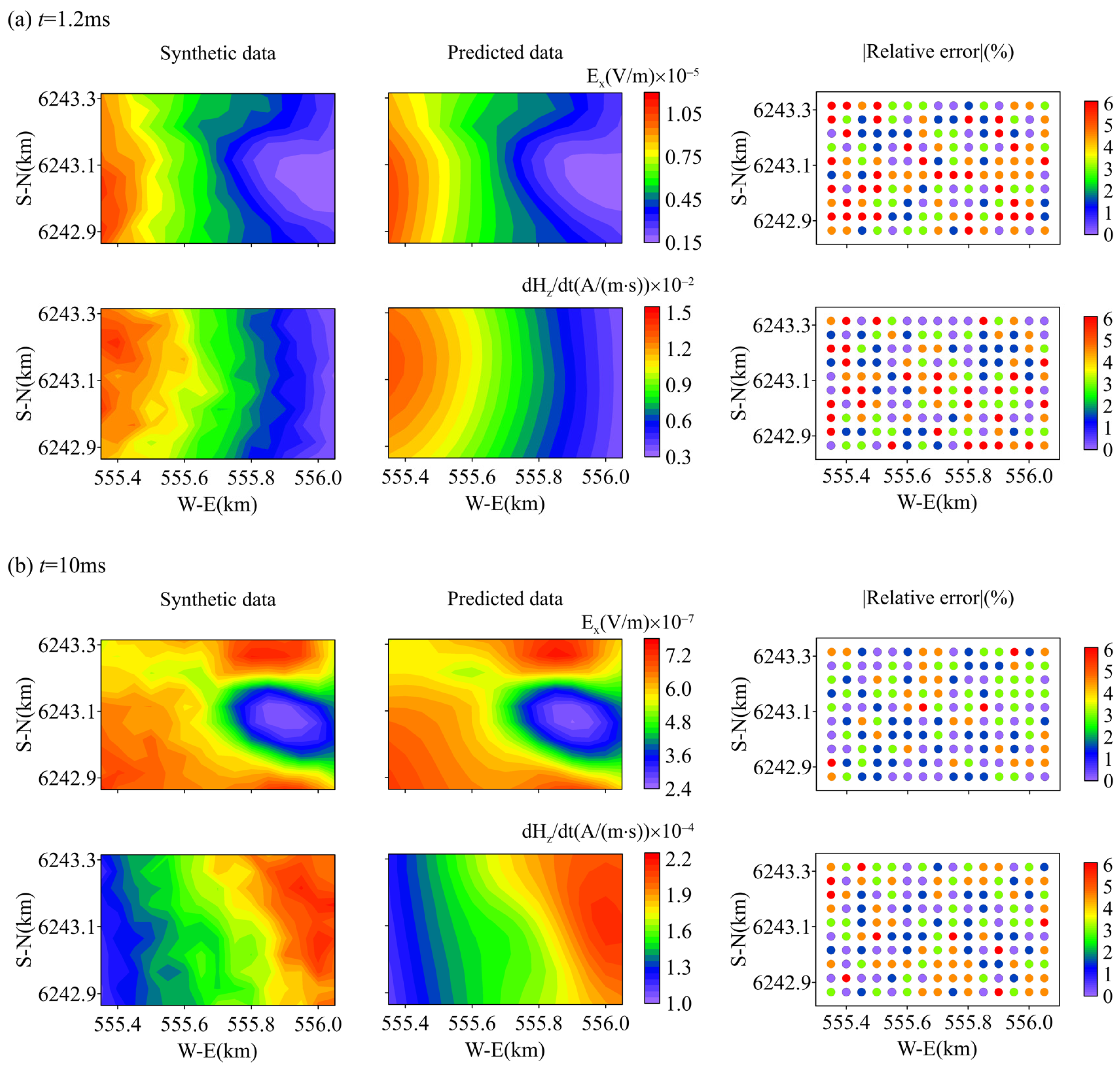
4. Application to a Realistic Mineral Deposit Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Strack, K.M. Exploration with Deep Transient Electromagnetics; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Commer, M.; Helwig, S.L.; Hördt, A.; Scholl, C.; Tezkan, B. New results on the resistivity structure of Merapi Volcano (Indonesia), derived from three-dimensional restricted inversion of long-offset transient electromagnetic data. Geophys. J. Int. 2006, 167, 1172–1187. [Google Scholar] [CrossRef] [Green Version]
- Vozoff, K.; Moss, D.; LeBrocq, K.; McAllister, K. LOTEM electric field measurements for mapping resistive horizons in petroleum exploration. Explor. Geophys. 1985, 16, 309–312. [Google Scholar] [CrossRef]
- Xie, X.; Lei, Z.; Yan, L.; Hu, W. Remaining oil detection with time-lapse long offset & window transient electromagnetic sounding. Oil Geophys. Prospect. 2016, 51, 605–612. [Google Scholar]
- Yan, L.J.; Chen, X.X.; Tang, H.; Xie, X.B.; Zhou, L.; Hu, W.B.; Wang, Z.X. Continuous TDEM for monitoring shale hydraulic fracturing. Appl. Geophys. 2018, 15, 26–34. [Google Scholar] [CrossRef]
- Keller, G.V.; Pritchard, J.I.; Jacobson, J.J.; Harthill, N. Megasource time-domain electromagnetic sounding methods. Geophysics 1984, 49, 993–1009. [Google Scholar] [CrossRef]
- Stephan, A.; Schniggenfittig, H.; Strack, K.M. Long-offset transient em sounding north of the rhine-ruhr coal district, germany1. Geophys. Prospect. 1991, 39, 505–525. [Google Scholar] [CrossRef]
- Müller, M.; Hördt, A.; Neubauer, F. Internal structure of Mount Merapi, Indonesia, derived from long-offset transient electromagnetic data. J. Geophys. Res. Solid Earth 2002, 107, ECV 2-1–ECV 2-14. [Google Scholar] [CrossRef]
- Haroon, A.; Adrian, J.; Bergers, R.; Gurk, M.; Tezkan, B.; Mammadov, A.; Novruzov, A. Joint inversion of long-offset and central-loop transient electromagnetic data: Application to a mud volcano exploration in Perekishkul, Azerbaijan. Geophys. Prospect. 2015, 63, 478–494. [Google Scholar] [CrossRef]
- Zhou, N.N.; Xue, G.Q.; Li, H.; Lei, K.X.; Chen, W.Y. Comparison of transient electromagnetic fields excited by single-and double-line grounded-wire sources on land. Geophys. J. Int. 2022, 229, 1856–1869. [Google Scholar] [CrossRef]
- Zhou, N.N.; Xue, G.Q.; Li, H.; Chen, W.Y.; Lei, K.X. Electromagnetic characteristics of the magmatic Ni-Cu sulfide deposits in the orogenic belt: A case study from Kalatongke deposits in the Central Asian orogenic belt. Econ. Geol. 2022, 117, 1779–1789. [Google Scholar] [CrossRef]
- Strack, K.; Lüschen, E.; Kötz, A. Long-offset transient electromagnetic (LOTEM) depth soundings applied to crustal studies in the Black Forest and Swabian Alb, Federal Republic of Germany. Geophysics 1990, 55, 834–842. [Google Scholar] [CrossRef]
- Hördt, A.; Druskin, V.L.; Knizhnerman, L.A.; Strack, K.M. Interpretation of 3-D effects in long-offset transient electromagnetic (LOTEM) soundings in the Münsterland area/Germany. Geophysics 1992, 57, 1127–1137. [Google Scholar] [CrossRef]
- Hördt, A.; Jödicke, H.; Strack, K.M.; Vozoff, K.; Wolfgram, P. Inversion of long-offset TEM soundings near the borehole Münsterland 1, Germany, and comparison with MT measurements. Geophys. J. Int. 1992, 108, 930–940. [Google Scholar] [CrossRef] [Green Version]
- Di, Q.Y.; Fang, G.Y.; Zhang, Y.M. Research of the surface electromagnetic prospecting (SEP) system. Chin. J. Geophys. 2013, 56, 3629–3639. [Google Scholar]
- Lü, Q.; Zhang, X.; Tang, J.; Jin, S.; Liang, L.; Niu, J.; Wang, X.; Lin, P.; Yao, C.; Gao, W. Review on advancement in technology and equipment of geophysical exploration for metallic deposits in China. Chin. J. Geophys. 2019, 62, 3629–3664. [Google Scholar]
- Stolz, R.; Schiffler, M.; Becken, M.; Thiede, A.; Schneider, M.; Chubak, G.; Marsden, P.; Bergshjorth, A.B.; Schaefer, M.; Terblanche, O. SQUIDs for magnetic and electromagnetic methods in mineral exploration. Miner. Econ. 2022, 35, 467–494. [Google Scholar] [CrossRef]
- Hördt, A.; Müller, M. Understanding LOTEM data from mountainous terrain. Geophysics 2000, 65, 1113–1123. [Google Scholar] [CrossRef]
- Wang, T.; Hohmann, G.W. A finite-difference, time-domain solution for three-dimensional electromagnetic modeling. Geophysics 1993, 58, 797–809. [Google Scholar] [CrossRef] [Green Version]
- Haber, E.; Oldenburg, D.W.; Shekhtman, R. Inversion of time domain three-dimensional electromagnetic data. Geophys. J. Int. 2007, 171, 550–564. [Google Scholar] [CrossRef] [Green Version]
- Oldenburg, D.W.; Haber, E.; Shekhtman, R. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics 2013, 78, E47–E57. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Oldenburg, D.W.; Haber, E. 3-D inversion of airborne electromagnetic data parallelized and accelerated by local mesh and adaptive soundings. Geophys. J. Int. 2014, 196, 1492–1507. [Google Scholar] [CrossRef] [Green Version]
- Cai, H.; Liu, M.; Zhou, J.; Li, J.; Hu, X. Effective 3D-transient electromagnetic inversion using finite-element method with a parallel direct solver. Geophysics 2022, 87, E377–E392. [Google Scholar] [CrossRef]
- Commer, M.; Newman, G. A parallel finite-difference approach for 3D transient electromagnetic modeling with galvanic sources. Geophysics 2004, 69, 1192–1202. [Google Scholar] [CrossRef] [Green Version]
- Tang, X.G.; Hu, W.B.; Yan, L.J. Topographic effects on long offset transient electromagnetic response. Appl. Geophys. 2011, 8, 277–284. [Google Scholar] [CrossRef]
- Liu, Y.; Yogeshwar, P.; Hu, X.; Peng, R.; Tezkan, B.; Mörbe, W.; Li, J. Effects of electrical anisotropy on long-offset transient electromagnetic data. Geophys. J. Int. 2020, 222, 1074–1089. [Google Scholar] [CrossRef]
- Li, J.; Hu, X.; Cai, H.; Liu, Y. A finite-element time-domain forward-modelling algorithm for transient electromagnetics excited by grounded-wire sources. Geophys. Prospect. 2020, 68, 1379–1398. [Google Scholar] [CrossRef]
- Khan, M.Y.; Xue, G.Q.; Chen, W.Y.; Zhong, H.S. Analysis of long-offset transient electromagnetic (LOTEM) data in time, frequency, and pseudo-seismic domain. J. Environ. Eng. Geophys. 2018, 23, 15–32. [Google Scholar] [CrossRef]
- Carter, S.; Xie, X.; Zhou, L.; Yan, L. Hybrid Monte Carlo 1-D joint inversion of LOTEM and MT. J. Appl. Geophys. 2021, 194, 104424. [Google Scholar] [CrossRef]
- Scholl, C. The Influence of Multidimensional Structures on the Interpretation of Lotem Data with One-Dimensional Models and the Application to Data from Israel. Ph.D. Thesis, Universität Zu Köln, Cologne, Germany, 2005. [Google Scholar]
- Sudha, K.; Tezkan, B.; Israil, M.; Rai, J. Combined electrical and electromagnetic imaging of hot fluids within fractured rock in rugged Himalayan terrain. J. Appl. Geophys. 2011, 74, 205–214. [Google Scholar] [CrossRef]
- Cai, J.; Yogeshwar, P.; Mörbe, W.; Smirnova, M.; Haroon, A.; Becken, M.; Tezkan, B. 2-D joint inversion of semi-airborne CSEM and LOTEM data in eastern Thuringia, Germany. Geophys. J. Int. 2022, 229, 1475–1489. [Google Scholar] [CrossRef]
- Mitsuhata, Y.; Uchida, T.; Amano, H. 2.5-D inversion of frequency-domain electromagnetic data generated by a grounded-wire source. Geophysics 2002, 67, 1753–1768. [Google Scholar] [CrossRef]
- Sasaki, Y.; Yi, M.J.; Choi, J.; Son, J.S. Frequency and time domain three-dimensional inversion of electromagnetic data for a grounded-wire source. J. Appl. Geophys. 2015, 112, 106–114. [Google Scholar] [CrossRef]
- Revil, A.; Woodruff, W.; Torres-Verdín, C.; Prasad, M. Complex conductivity tensor of anisotropic hydrocarbon-bearing shales and mudrocks. Geophysics 2013, 78, D403–D418. [Google Scholar] [CrossRef] [Green Version]
- Woodruff, W.F.; Revil, A.; Torres-Verdín, C. Laboratory determination of the complex conductivity tensor of unconventional anisotropic shales. Geophysics 2014, 79, E183–E200. [Google Scholar] [CrossRef]
- Cai, H.; Hu, X.; Xiong, B.; Zhdanov, M.S. Finite-element time-domain modeling of electromagnetic data in general dispersive medium using adaptive Padé series. Comput. Geosci. 2017, 109, 194–205. [Google Scholar] [CrossRef]
- Jahandari, H.; Farquharson, C.G. A finite-volume solution to the geophysical electromagnetic forward problem using unstructured grids. Geophysics 2014, 79, E287–E302. [Google Scholar] [CrossRef]
- Um, E.S.; Harris, J.M.; Alumbaugh, D.L. 3D time-domain simulation of electromagnetic diffusion phenomena: A finite-element electric-field approach. Geophysics 2010, 75, F115–F126. [Google Scholar] [CrossRef]
- Jin, J.M. The Finite Element Method in Electromagnetics; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Liu, Y.; Yin, C.; Qiu, C.; Hui, Z.; Zhang, B.; Ren, X.; Weng, A. 3-D inversion of transient EM data with topography using unstructured tetrahedral grids. Geophys. J. Int. 2019, 217, 301–318. [Google Scholar] [CrossRef]
- Bollhöfer, M.; Eftekhari, A.; Scheidegger, S.; Schenk, O. Large-scale sparse inverse covariance matrix estimation. SIAM J. Sci. Comput. 2019, 41, A380–A401. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Arsenin, V.Y. Soulutions of Ill-Posed Problems. SIAM Rev. 1977, 21, 266. [Google Scholar]
- Cao, X.Y.; Yin, C.C.; Zhang, B.; Huang, X.; Liu, Y.H.; Cai, J. 3D magnetotelluric inversions with unstructured finite-element and limited-memory quasi-Newton methods. Appl. Geophys. 2018, 15, 556–565. [Google Scholar] [CrossRef]
- Key, K. MARE2DEM: A 2-D inversion code for controlled-source electromagnetic and magnetotelluric data. Geophys. J. Int. 2016, 207, 571–588. [Google Scholar] [CrossRef] [Green Version]
- Commer, M.; Newman, G.A. New advances in three-dimensional controlled-source electromagnetic inversion. Geophys. J. Int. 2008, 172, 513–535. [Google Scholar] [CrossRef]
- Balch, S.; Crebs, T.; King, A.; Verbiski, M. Geophysics of the Voisey’s Bay Ni-Cu-Co deposits. In SEG Technical Program Expanded Abstracts 1998; Society of Exploration Geophysicists: Houston, TX, USA, 1998; pp. 784–787. [Google Scholar]
- Li, J.; Lu, X.; Farquharson, C.G.; Hu, X. A finite-element time-domain forward solver for electromagnetic methods with complex-shaped loop sources. Geophysics 2018, 83, E117–E132. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Cai, H.; Liu, L.; Revil, A.; Hu, X. Three-Dimensional Inversion of Long-Offset Transient Electromagnetic Method over Topography. Minerals 2023, 13, 908. https://doi.org/10.3390/min13070908
Wang X, Cai H, Liu L, Revil A, Hu X. Three-Dimensional Inversion of Long-Offset Transient Electromagnetic Method over Topography. Minerals. 2023; 13(7):908. https://doi.org/10.3390/min13070908
Chicago/Turabian StyleWang, Xinyu, Hongzhu Cai, Lichao Liu, André Revil, and Xiangyun Hu. 2023. "Three-Dimensional Inversion of Long-Offset Transient Electromagnetic Method over Topography" Minerals 13, no. 7: 908. https://doi.org/10.3390/min13070908
APA StyleWang, X., Cai, H., Liu, L., Revil, A., & Hu, X. (2023). Three-Dimensional Inversion of Long-Offset Transient Electromagnetic Method over Topography. Minerals, 13(7), 908. https://doi.org/10.3390/min13070908






