CO2 Leakage Scenarios in Shale Overburden
Abstract
:1. Introduction
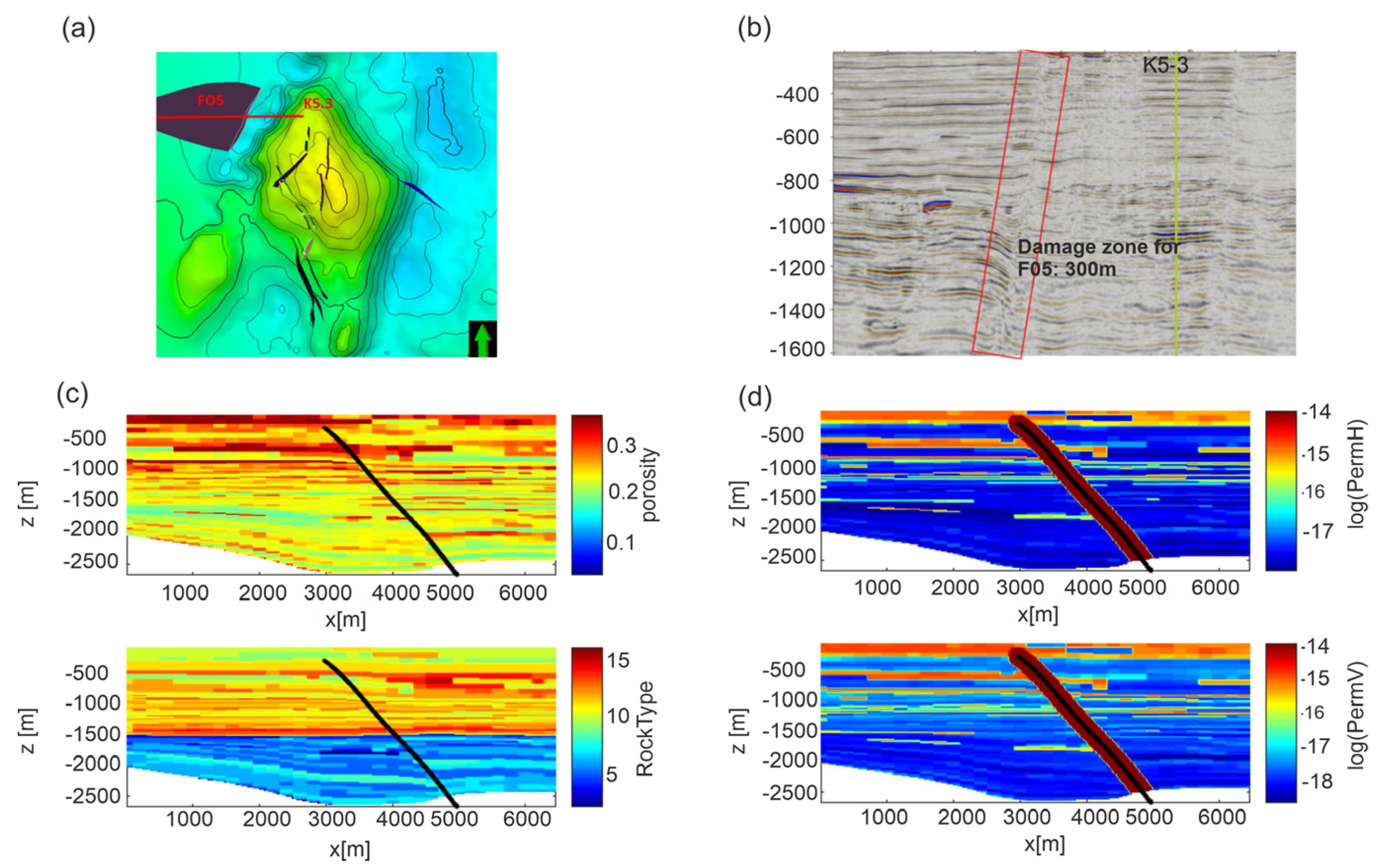
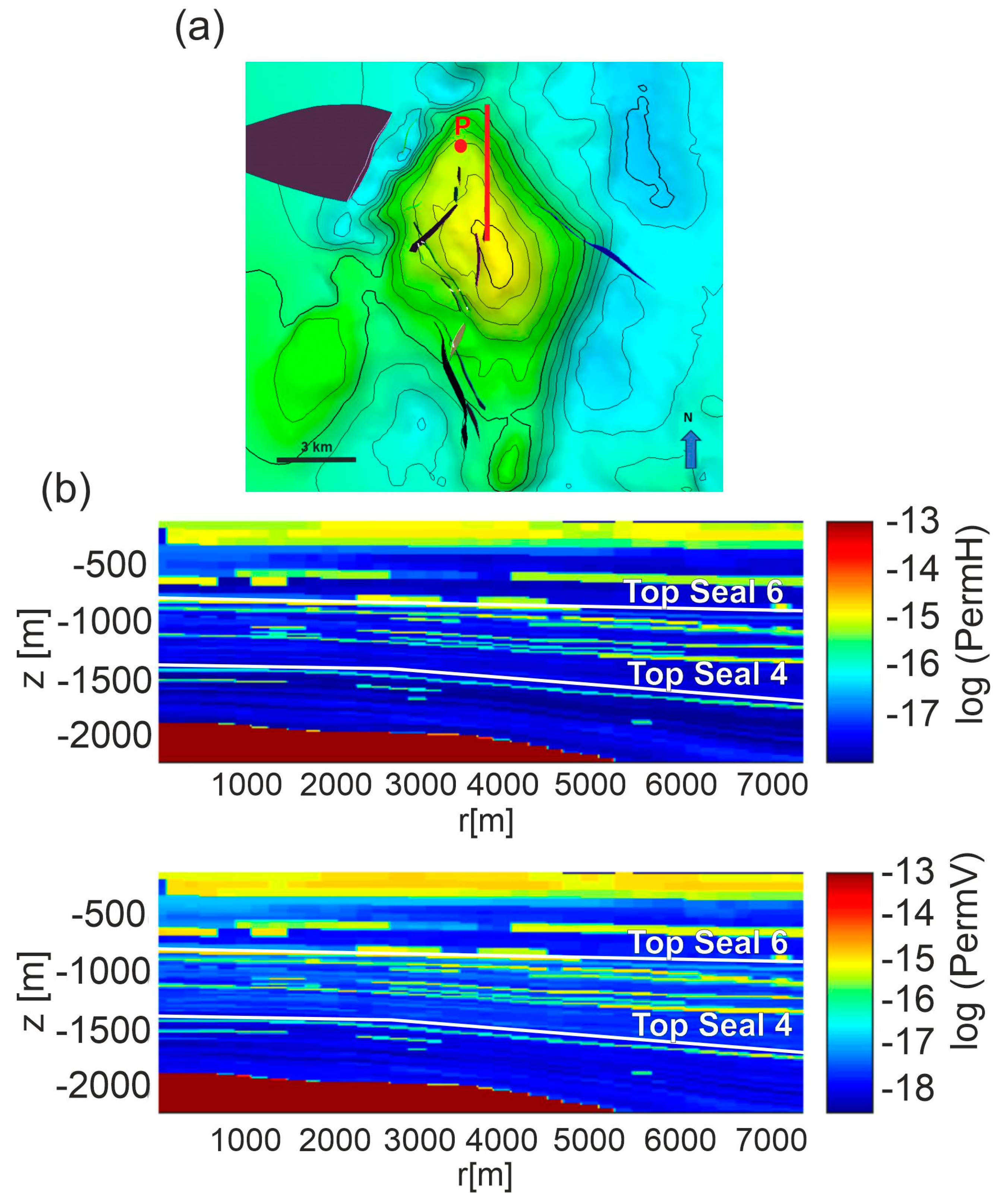
2. Site Description and Characterization
3. Numerical Modeling
3.1. Code Modification
3.2. Geochemical Modeling
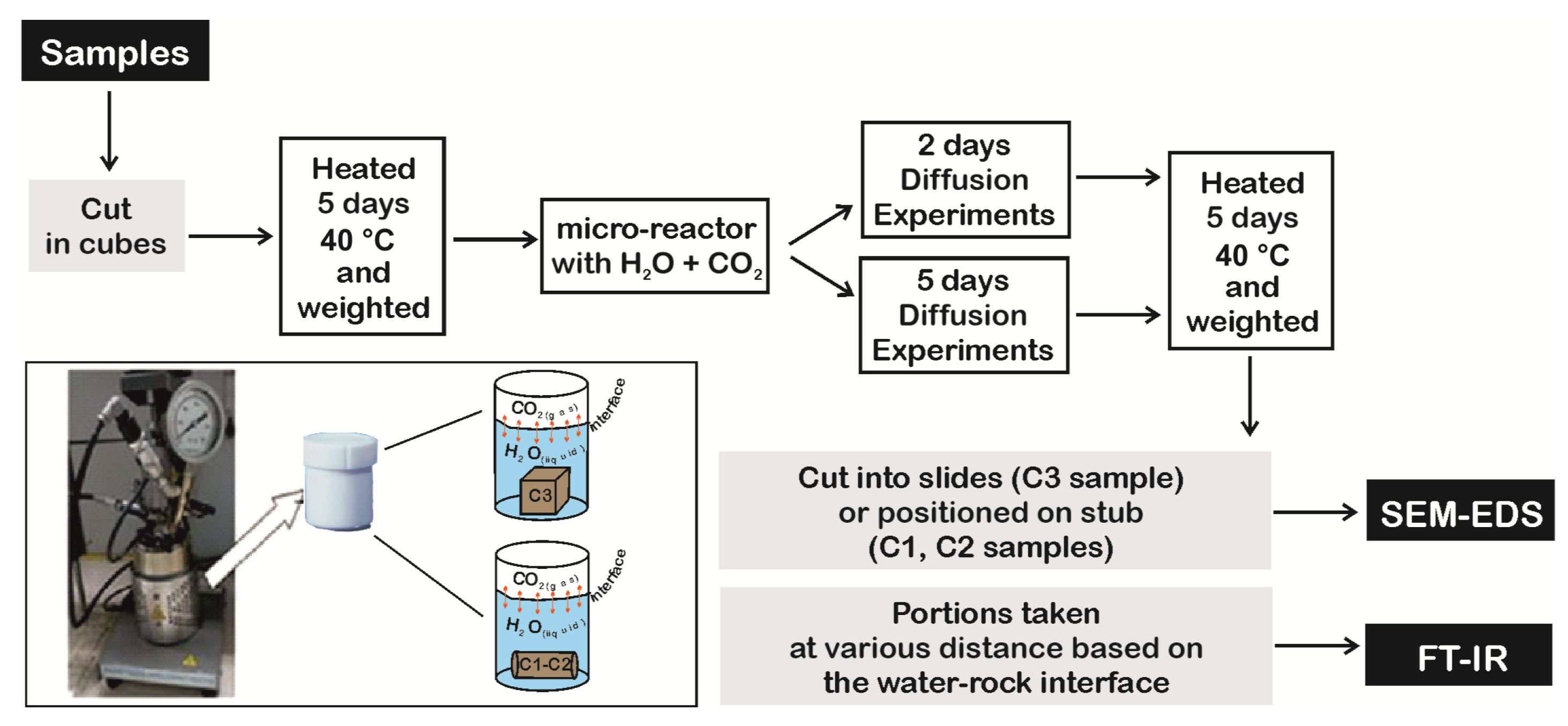
3.3. Reaction-Diffusion Experiments Model
4. Models Parameters
5. Leakage Scenarios
6. Results and Discussion
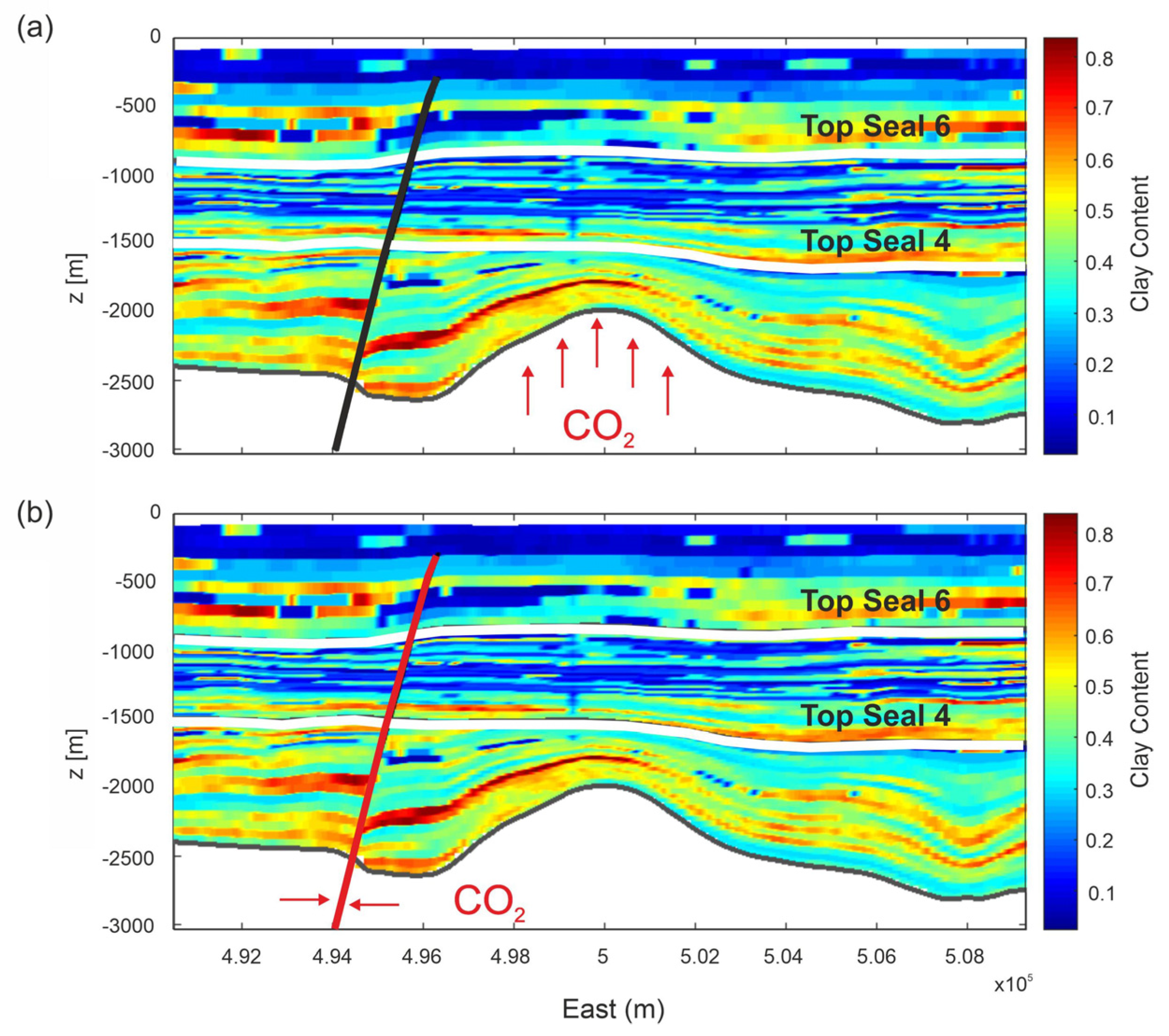
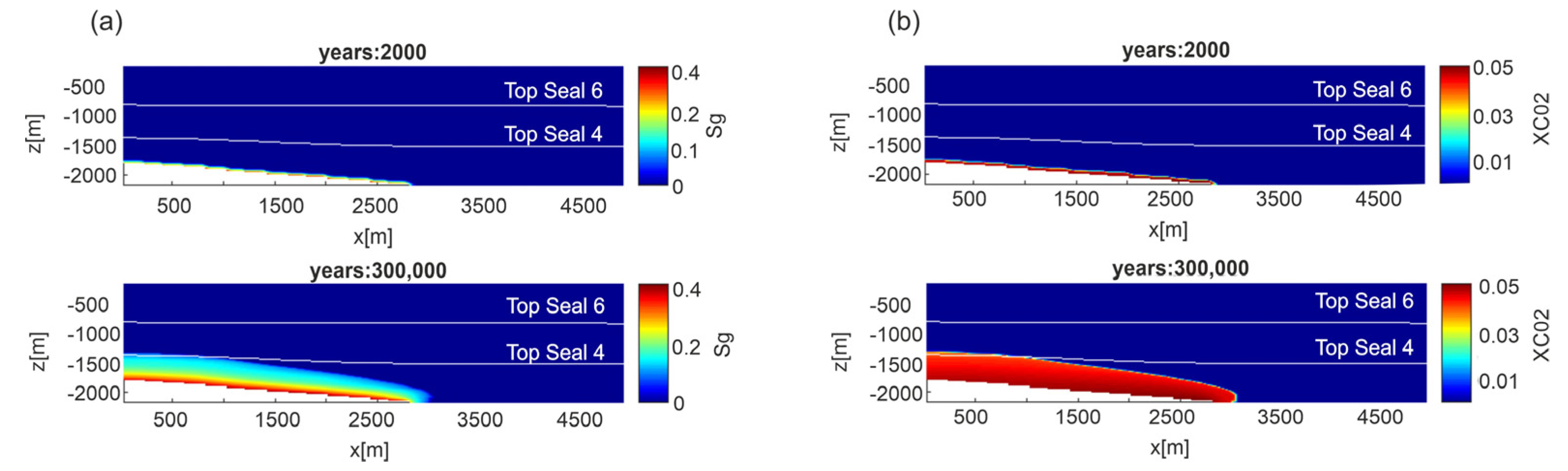
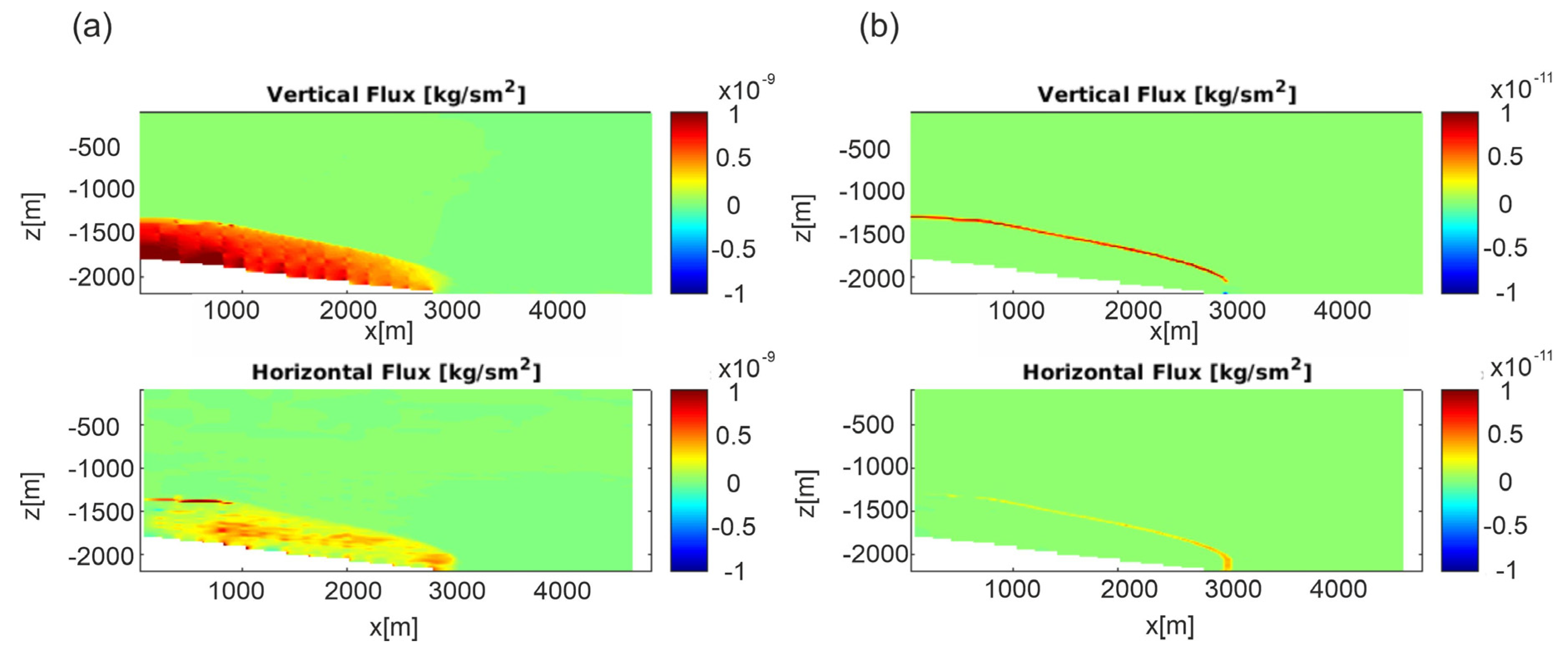
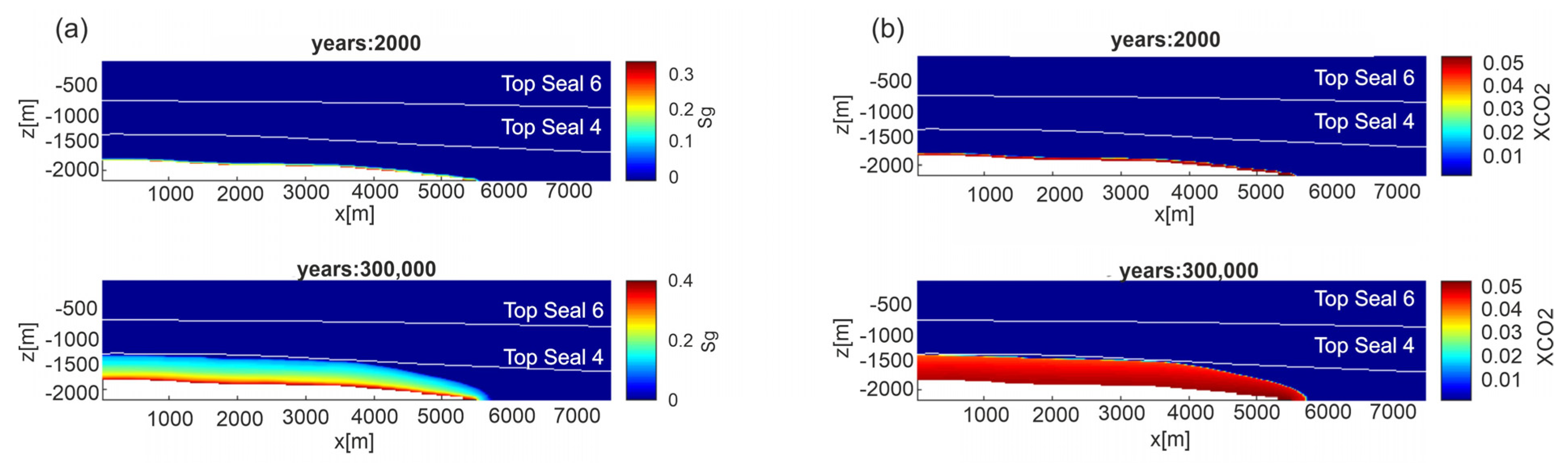
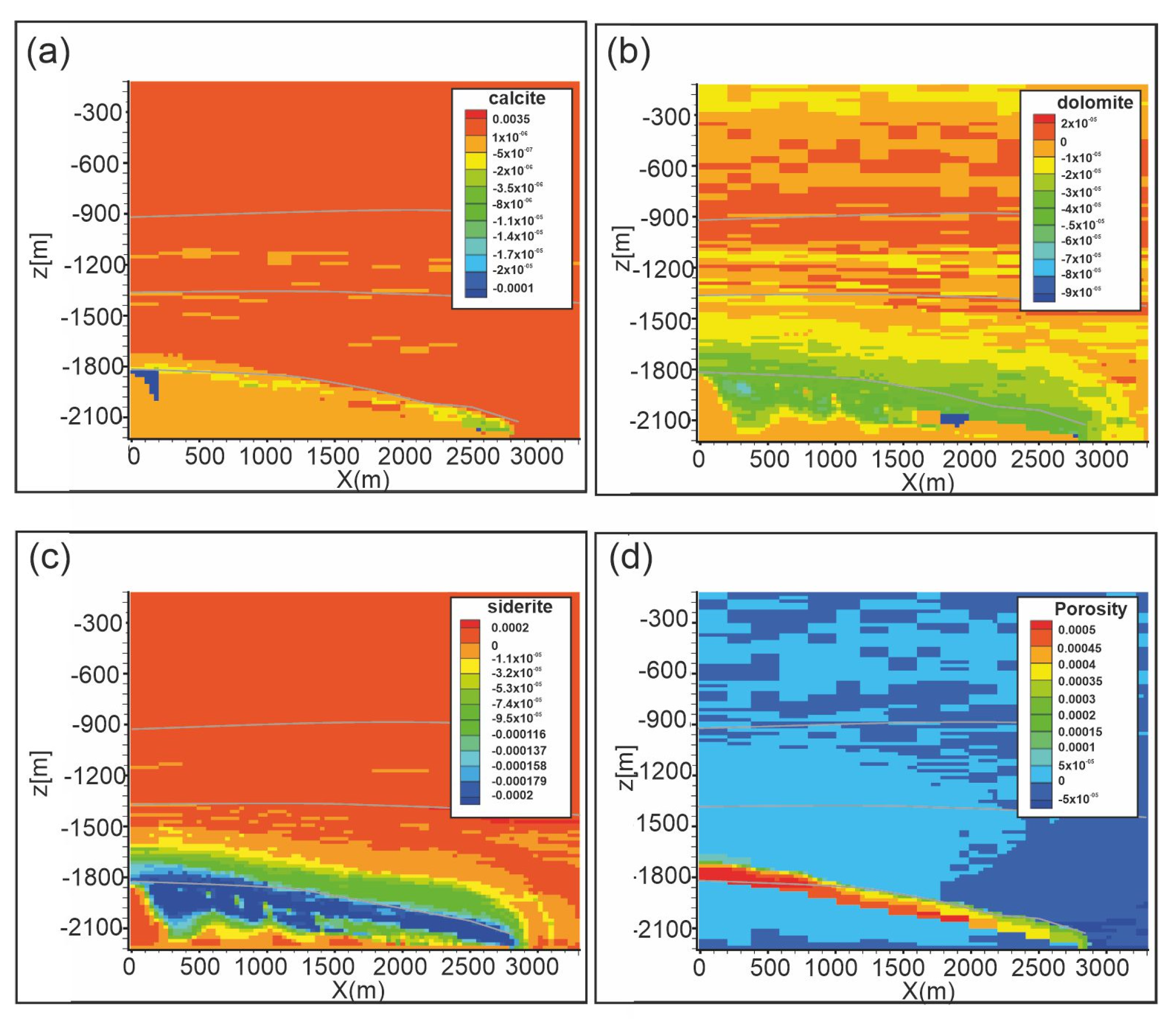
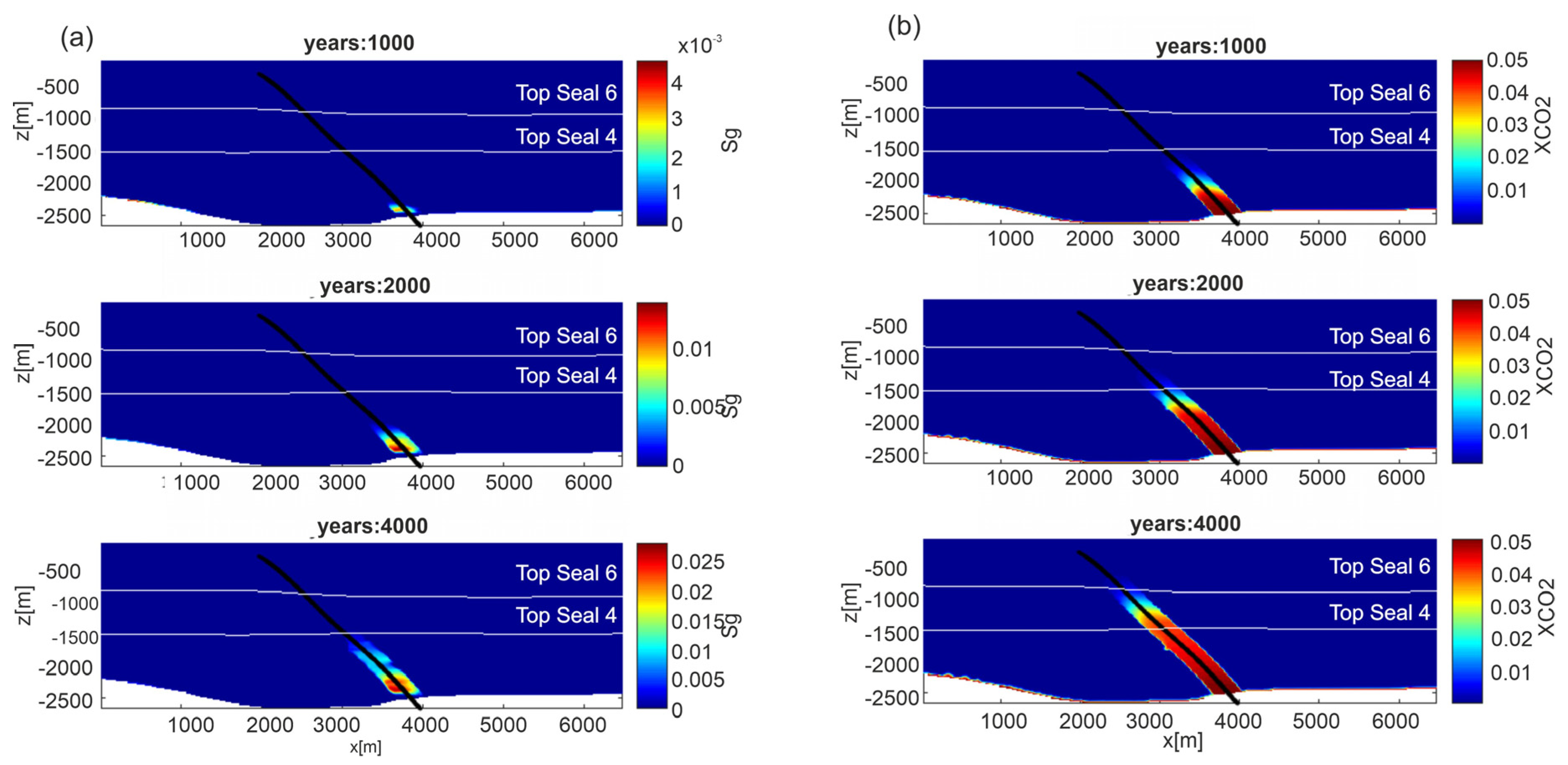
6.1. Scenario 1—Leakage from Reservoir
6.2. Scenario 2—Leakage from Faults
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Metz, B. Carbon Dioxide Capture and Storage: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Metz, B.; Davidson, O.R.; Bosh, P.R.; Dave, R.; Meyer, L.A. Contribution of Working Group III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, 2007; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- IPCC. 2013 Revised Supplementary Methods and Good Practice Guidance Arising from the Kyoto Protocol; IPCC: Geneva, Switzerland, 2014; ISBN 978-92-9169-140-1. [Google Scholar]
- IEA. Greenhouse Gas R&D Programme Natural and Industrial Analugues for Geological Storage of Carbon Dioxide; IEA Greenhouse Gas R&D Programme: Cheltenham, UK, 2009. [Google Scholar]
- Celia, M.A.; Nordbotten, J.M.; Bachu, S.; Dobossy, M.; Court, B. Risk of Leakage versus Depth of Injection in Geological Storage. Energy Procedia 2009, 1, 2573–2580. [Google Scholar] [CrossRef]
- Imbus, S.W.; Dodds, K.; Otto, C.J.; Trautz, R.C.; Christopher, C.A.; Agarwal, A.; Benson, S.M. CO2 Storage Contingencies Initiative: Detection, Intervention and Remediation of Unexpected CO2 Migration. Energy Procedia 2013, 37, 7802–7814. [Google Scholar] [CrossRef]
- Gholami, R.; Raza, A.; Iglauer, S. Leakage Risk Assessment of a CO2 Storage Site: A Review. Earth-Sci. Rev. 2021, 223, 103849. [Google Scholar] [CrossRef]
- Gaus, I. Role and Impact of CO2–Rock Interactions during CO2 Storage in Sedimentary Rocks. Int. J. Greenh. Gas Control 2010, 4, 73–89. [Google Scholar] [CrossRef]
- Esposito, A.; Benson, S.M. Evaluation and Development of Options for Remediation of CO2 Leakage into Groundwater Aquifers from Geologic Carbon Storage. Int. J. Greenh. Gas Control 2012, 7, 62–73. [Google Scholar] [CrossRef]
- Vialle, S.; Druhan, J.L.; Maher, K. Multi-Phase Flow Simulation of CO2 Leakage through a Fractured Caprock in Response to Mitigation Strategies. Int. J. Greenh. Gas Control 2016, 44, 11–25. [Google Scholar] [CrossRef]
- Brunet, J.-P.L.; Li, L.; Karpyn, Z.T.; Huerta, N.J. Fracture Opening or Self-Sealing: Critical Residence Time as a Unifying Parameter for Cement–CO2–Brine Interactions. Int. J. Greenh. Gas Control 2016, 47, 25–37. [Google Scholar] [CrossRef]
- Zhang, M.; Bachu, S. Review of Integrity of Existing Wells in Relation to CO2 Geological Storage: What Do We Know? Int. J. Greenh. Gas Control 2011, 5, 826–840. [Google Scholar] [CrossRef]
- Ingram, G.M.; Urai, J.L.; Naylor, M.A. Sealing Processes and Top Seal Assessment. In Norwegian Petroleum Society Special Publications; Elsevier: Amsterdam, The Netherlands, 1997; Volume 7, pp. 165–174. ISBN 978-0-444-82825-5. [Google Scholar]
- Watts, N.L. Theoretical Aspects of Cap-Rock and Fault Seals for Single- and Two-Phase Hydrocarbon Columns. Mar. Pet. Geol. 1987, 4, 274–307. [Google Scholar] [CrossRef]
- Almutairi, A.; Al-Bazali, T. Capillary Pressure Behavior of CO2—Shale System at Elevated Temperatures. Int. Res. J. Pure Appl. Chem. 2022, 23, 1–16. [Google Scholar] [CrossRef]
- Hemme, C.; Van Berk, W. Change in Cap Rock Porosity Triggered by Pressure and Temperature Dependent CO2–Water–Rock Interactions in CO2 Storage Systems. Petroleum 2017, 3, 96–108. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Miao, X.; Gan, M.; Li, X. Geochemistry in Geologic CO2 Utilization and Storage: A Brief Review. Adv. Geo-Energ. Res. 2019, 3, 304–313. [Google Scholar] [CrossRef]
- Xu, T.; Pruess, K. Modeling multiphase non-isothermal fluid flow and reactive geochemical transport in variably saturated fractured rocks: 1. Methodology 2001, 301, 16–33. [Google Scholar] [CrossRef]
- Xu, T.; Sonnenthal, E.; Spycher, N.; Pruess, K. TOUGHREACT—A Simulation Program for Non-Isothermal Multiphase Reactive Geochemical Transport in Variably Saturated Geologic Media: Applications to Geothermal Injectivity and CO2 Geological Sequestration. Comput. Geosci. 2006, 32, 145–165. [Google Scholar] [CrossRef]
- Soltanian, M.R.; Hajirezaie, S.; Hosseini, S.A.; Dashtian, H.; Amooie, M.A.; Meyal, A.; Ershadnia, R.; Ampomah, W.; Islam, A.; Zhang, X. Multicomponent Reactive Transport of Carbon Dioxide in Fluvial Heterogeneous Aquifers. J. Nat. Gas Sci. Eng. 2019, 65, 212–223. [Google Scholar] [CrossRef]
- Ershadnia, R.; Wallace, C.D.; Soltanian, M.R. CO2 Geological Sequestration in Heterogeneous Binary Media: Effects of Geological and Operational Conditions. Adv. Geo-Energy Res. 2020, 4, 392–405. [Google Scholar] [CrossRef]
- Yin, Y.; Qu, Z.; Prodanović, M.; Landry, C.J. Identifying the Dominant Transport Mechanism in Single Nanoscale Pores and 3D Nanoporous Media. Fundam. Res. 2023, 3, 409–421. [Google Scholar] [CrossRef]
- Freeman, C.M.; Moridis, G.J.; Blasingame, T.A. A Numerical Study of Microscale Flow Behavior in Tight Gas and Shale Gas Reservoir Systems. Transp. Porous Media 2011, 90, 253–268. [Google Scholar] [CrossRef]
- Civan, F. Modeling transport in porous media by control volume analysis. J. Por. Media 2010, 13, 855–873. [Google Scholar] [CrossRef]
- Khosrokhavar, R.; Griffiths, S.; Wolf, K.H. Shale Gas Formations and Their Potential for Carbon Storage: Opportunities and Outlook. Environ. Process. 2014, 1, 595–611. [Google Scholar] [CrossRef]
- Busch, A.; Alles, S.; Gensterblum, Y.; Prinz, D.; Dewhurst, D.N.; Raven, M.D.; Stanjek, H.; Krooss, B.M. Carbon Dioxide Storage Potential of Shales. Int. J. Greenh. Gas Control 2008, 2, 297–308. [Google Scholar] [CrossRef]
- Trevisan, L.; Krishnamurthy, P.G.; Meckel, T.A. Impact of 3D Capillary Heterogeneity and Bedform Architecture at the Sub-Meter Scale on CO2 Saturation for Buoyant Flow in Clastic Aquifers. Int. J. Greenh. Gas Control 2017, 56, 237–249. [Google Scholar] [CrossRef]
- Li, B.; Benson, S.M. Influence of Small-Scale Heterogeneity on Upward CO2 Plume Migration in Storage Aquifers. Adv. Water Resour. 2015, 83, 389–404. [Google Scholar] [CrossRef]
- Saadatpoor, E.; Bryant, S.L.; Sepehrnoori, K. New Trapping Mechanism in Carbon Sequestration. Transp. Porous Med. 2010, 82, 3–17. [Google Scholar] [CrossRef]
- Nghiem, L.; Yang, C.; Shrivastava, V.; Kohse, B.; Hassam, M.; Card, C. Risk Mitigation through the Optimization of Residual Gas and Solubility Trapping for CO2 Storage in Saline Aquifers. Energy Procedia 2009, 1, 3015–3022. [Google Scholar] [CrossRef]
- Gaus, I.; Audigane, P.; André, L.; Lions, J.; Jacquemet, N.; Durst, P.; Czernichowski-Lauriol, I.; Azaroual, M. Geochemical and Solute Transport Modelling for CO2 Storage, What to Expect from It? Int. J. Greenh. Gas Control 2008, 2, 605–625. [Google Scholar] [CrossRef]
- Wang, J.; Luo, H.; Liu, H.; Cao, F.; Li, Z.; Sepehrnoori, K. An Integrative Model to Simulate Gas Transport and Production Coupled with Gas Adsorption, Non-Darcy Flow, Surface Diffusion, and Stress Dependence in Organic-Shale Reservoirs. SPE J. 2017, 22, 244–264. [Google Scholar] [CrossRef]
- Vahrenkamp, V.C. Miocene Carbonates of the Luconia Province, Offshore Sarawak: Implications for Regional Geology and Reservoir Properties from Strontium-Isotope Stratigraphy. BGSM 1998, 42, 1–13. [Google Scholar] [CrossRef]
- Ting, K.K.; Chung, E.; Al Jaaidi, O. Evolution and Controlling Factors of Miocene Carbonate Build-up in Central Luconia, SE Asia: Insights from Integration of Geological and Seismic Characterization; ICIPEG: Kuala Lumpur, Malaysia, 2010. [Google Scholar]
- Madon, M.; Kim, C.L.; Wong, R. The Structure and Stratigraphy of Deepwater Sarawak, Malaysia: Implications for Tectonic Evolution. J. Asian Earth Sci. 2013, 76, 312–333. [Google Scholar] [CrossRef]
- Janjuhah, H.T.; Salim, A.M.A.; Shah, M.M.; Ghosh, D.; Alansari, A. Quantitative Interpretation of Carbonate Reservoir Rock Using Wireline Logs: A Case Study from Central Luconia, Offshore Sarawak, Malaysia. Carbonates Evaporites 2017, 32, 591–607. [Google Scholar] [CrossRef]
- Rankey, E.C.; Schlaich, M.; Mokhtar, S.; Ghon, G.; Ali, S.H.; Poppelreiter, M. Seismic Architecture of a Miocene Isolated Carbonate Platform and Associated Off-Platform Strata (Central Luconia Province, Offshore Malaysia). Mar. Pet. Geol. 2019, 102, 477–495. [Google Scholar] [CrossRef]
- Ho, K.F. Stratigraphic Framework for Oil Exploration in Sarawak. Bull. Geol. Soc. Malays. 1978, 10, 1–13. [Google Scholar] [CrossRef]
- Montegrossi, G.; Cantucci, B.; Piochi, M.; Fusi, L.; Misnan, M.S.; Rashidi, M.R.A.; Abu Bakar, Z.A.; Tuan Harith, Z.Z.; Bahri, N.H.S.; Hashim, N. CO2 Reaction-Diffusion Experiments in Shales and Carbonates. Minerals 2022, 13, 56. [Google Scholar] [CrossRef]
- Mualem, Y. A New Model for Predicting the Hydraulic Conductivity of Unsaturated Porous Media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Comisky, J.T.; Newsham, K.E.; Rushing, J.A.; Blasingame, T.A. A Comparative Study of Capillary-Pressure-Based Empirical Models for Estimating Absolute Permeability in Tight Gas Sands. Proc. SPE Annu. Tech. Conf. Exhib. 2007, 3, 1821–1838. [Google Scholar] [CrossRef]
- Kampman, N.; Busch, A.; Bertier, P.; Snippe, J.; Hangx, S.; Pipich, V.; Di, Z.; Rother, G.; Harrington, J.F.; Evans, J.P.; et al. Observational Evidence Confirms Modelling of the Long-Term Integrity of CO2-Reservoir Caprocks. Nat. Commun. 2016, 7, 12268. [Google Scholar] [CrossRef]
- Klinkenberg, L.J. The Permeability of Porous Media to Liquids and Gases. Drill. Prod. Pract. Am. Pet. Inst. 1941, 200–213. [Google Scholar] [CrossRef]
- Spycher, N.; Pruess, K.; Ennis-King, J. CO2-H2O Mixtures in the Geological Sequestration of CO2. I. Assessment and Calculation of Mutual Solubilities from 12 to 100 °C and up to 600 Bar. Geochim. Cosmochim. Acta 2003, 67, 3015–3031. [Google Scholar] [CrossRef]
- Spycher, N.; Pruess, K. CO2-H2O Mixtures in the Geological Sequestration of CO2. II. Partitioning in Chloride Brines at 12–100 °C and up to 600 Bar. Geochim. Cosmochim. Acta 2005, 69, 3309–3320. [Google Scholar] [CrossRef]
- Spycher, N.; Pruess, K. A Phase-Partitioning Model for CO2-Brine Mixtures at Elevated Temperatures and Pressures: Application to CO2-Enhanced Geothermal Systems. Transp. Porous Media 2010, 82, 173–196. [Google Scholar] [CrossRef]
- Pan, L.; Spycher, N.; Doughty, C.; Pruess, K. ECO2N V. 2.0: A New TOUGH2 Fluid Property Module for Mixtures of Water, NaCl, and CO2; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2014; p. 112. [Google Scholar]
- Lasaga, A.C. Chemical Kinetics of Water-Rock Interactions. J. Geophys. Res. 1984, 89, 4009–4025. [Google Scholar] [CrossRef]
- Lasaga, A.C.; Soler, J.M.; Ganor, J.; Burch, T.E.; Nagy, K.L. Chemical Weathering Rate Laws and Global Geochemical Cycles. Geochim. Cosmochim. Acta 1994, 58, 2361–2386. [Google Scholar] [CrossRef]
- Steefel, C.I.; Lasaga, A.C. A Coupled Model for Transport of Multiple Chemical Species and Kinetic Precipitation/Dissolution Reactions with Application to Reactive Flow in Single Phase Hydrothermal Systems. Am. J. Sci. 1994, 294, 529. [Google Scholar] [CrossRef]
- Palandri, J.L.; Kharaka, Y.K. A Compilation of Rate Parameters of Water-Mineral Interaction Kinetics for Application to Geochemical Modeling; U.S. Geological survey: Reston, VA, USA, 2004.
- Marini, L. Geological Sequestration of Carbon Dioxide, Volume 11: Thermodynamics, Kinetics, and Reaction Path Modeling; Elsevier: Burlington, ON, Canada, 2006; ISBN 978-0-08-046688-0. [Google Scholar]
- Pokrovsky, O.S.; Golubev, S.V.; Schott, J.; Castillo, A. Calcite, Dolomite and Magnesite Dissolution Kinetics in Aqueous Solutions at Acid to Circumneutral PH, 25 to 150 °C and 1 to 55 Atm PCO2: New Constraints on CO2 Sequestration in Sedimentary Basins. Chem. Geol. 2009, 265, 20–32. [Google Scholar] [CrossRef]
- Blanc, P.; Lassin, A.; Piantone, P.; Azaroual, M.; Jacquemet, N.; Fabbri, A.; Gaucher, E.C. Thermoddem: A Geochemical Database Focused on Low Temperature Water/Rock Interactions and Waste Materials. Appl. Geochem. 2012, 27, 2107–2116. [Google Scholar] [CrossRef]
- Johnson, J.W.; Oelkers, E.H.; Helgeson, H.C. SUPCRT92: A Software Package for Calculating the Standard Molal Thermodynamic Properties of Minerals, Gases, Aqueous Species, and Reactions from 1 to 5000 Bar and 0 to 1000 °C. Comput. Geosci. 1992, 18, 899–947. [Google Scholar] [CrossRef]
- Gil, A.; Trujillano, R.; Vicente, M.A.; Korili, S.A. Analysis of the Structure of Alumina-Pillard Clays by Nitrogen and Carbon Dioxide Adsorption. Adsorpt. Sci. Technol. 2007, 25, 217–226. [Google Scholar] [CrossRef]
- Do, D.D. Adsorption Analysis: Equilibria and Kinetics: (With CD Containing Computer Matlab Programs); Series on Chemical Engineering; Imperial College Press: London, UK; World Scientific: Singapore, 1998; Volume 2, ISBN 978-1-86094-130-6. [Google Scholar]
- Carcione, J.M.; Gei, D.; Picotti, S.; Misnan, M.S.; Rashidi, M.R.A.; Bakar, Z.A.A.; Harith, Z.Z.T.; Bahri, N.H.S.; Hashim, N. Porosity and Permeability of the Overburden from Wireline Logs: A Case Study from Offshore Malaysia. Geomech. Geophys. Geo-Energy Geo-Resoure 2020, 6, 48. [Google Scholar] [CrossRef]
- Clauser, C.; Huenges, E. Thermal Conductivity of Rocks and Minerals. Rock Phys. Phase Relat. A Handb. Phys. Constants 1995, 3, 105–126. [Google Scholar]
- Clauser, C. The Thermal Regime of the Earth and Heat Transport Processes in the Earth’s Crust. Surv. Geophys. 2006, 30, 163–191. [Google Scholar] [CrossRef]
- Cantucci, B.; Montegrossi, G.; Lucci, F.; Quattrocchi, F. Reconstruction of Rocks Petrophysical Properties as Input Data for Reservoir Modeling: Rocks Petrophysical Properties. Geochem. Geophys. Geosyst. 2016, 17, 4534–4552. [Google Scholar] [CrossRef]
- Wu, W.; Reece, J.S.; Gensterblum, Y.; Zoback, M.D. Permeability Evolution of Slowly Slipping Faults in Shale Reservoirs. Geophys. Res. Lett. 2017, 44, 11368–11375. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R. An Improved Model Calculating CO2 Solubility in Pure Water and Aqueous NaCl Solutions from 273 to 533 K and from 0 to 2000 Bar. Chem. Geol. 2003, 193, 257–271. [Google Scholar] [CrossRef]
- Duan, Z.; Sun, R.; Zhu, C.; Chou, I.-M. An Improved Model for the Calculation of CO2 Solubility in Aqueous Solutions Containing Na+, K+, Ca2+, Mg2+, Cl−, and SO42−. Mar. Chem. 2006, 98, 131–139. [Google Scholar] [CrossRef]
- Heinemann, N.; Haszeldine, R.S.; Shu, Y.; Stewart, R.J.; Scott, V.; Wilkinson, M. CO2 Sequestration with Limited Sealing Capability: A New Injection and Storage Strategy in the Pearl River Mouth Basin (China). Int. J. Greenh. Gas Control 2018, 68, 230–235. [Google Scholar] [CrossRef]
- Ukaegbu, C.; Gundogan, O.; Mackay, E.; Pickup, G.; Todd, A.; Gozalpour, F. Simulation of CO2 Storage in a Heterogeneous Aquifer. Proc. Inst. Mech. Eng. Part A J. Power Energy 2009, 223, 249–267. [Google Scholar] [CrossRef]
- Weniger, P.; Kalkreuth, W.; Busch, A.; Krooss, B.M. High-Pressure Methane and Carbon Dioxide Sorption on Coal and Shale Samples from the Paraná Basin, Brazil. Int. J. Coal Geol. 2010, 84, 190–205. [Google Scholar] [CrossRef]
- Siemons, N.; Busch, A. Measurement and Interpretation of Supercritical CO2 Sorption on Various Coals. Int. J. Coal Geol. 2007, 69, 229–242. [Google Scholar] [CrossRef]
- Chi, Y.; Zhao, C.; Lv, J.; Zhao, J.; Zhang, Y. Thermodynamics and Kinetics of CO2/CH4 Adsorption on Shale from China: Measurements and Modeling. Energies 2019, 12, 978. [Google Scholar] [CrossRef]
- Rex, R.W. Clay Mineral Formation in Sea Water by Submarine Weathering of K-Feldspar. Clays Clay Miner. 1966, 14, 235–240. [Google Scholar] [CrossRef]


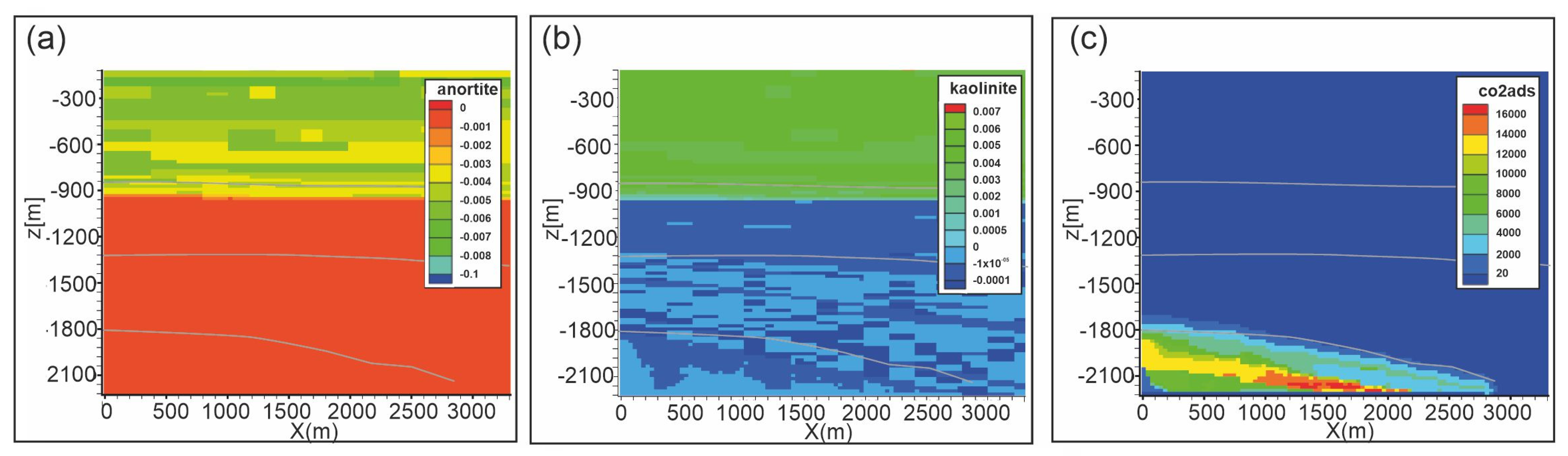

| Sample | λ | Slr | 1/P0 | P | Sgr |
|---|---|---|---|---|---|
| Seal 6—soft sediments | 0.243 | 0.274 | 3.211 × 10−8 | 1.200 × 108 | 0.041 |
| Seal 4 | 0.223 | 0.209 | 2.872 × 10−7 | 1.200 × 108 | 0.051 |
| Reservoir | 0.327 | 0.539 | 8.412 × 10−8 | 1.200 × 108 | 0.008 |
| Clay Class | 0–0.063 | 0.063–0.142 | 0.142–0.282 | 0.282–0.422 | 0.422–0.562 | 0.562–0.702 | >0.702 | Res. | S 106 (m2/m3) |
|---|---|---|---|---|---|---|---|---|---|
| Seal 4 | |||||||||
| Kaolinite | 1.16 | 3.76 | 7.78 | 12.92 | 18.06 | 23.20 | 28.27 | 6.38 | |
| Fe-Illite | 1.91 | 6.20 | 12.83 | 21.30 | 29.77 | 38.24 | 46.59 | 4.50 | |
| Chlorite | 0.09 | 0.29 | 0.59 | 0.98 | 1.37 | 1.76 | 2.15 | 5.11 | |
| Quartz | 52.90 | 48.95 | 42.85 | 35.06 | 27.27 | 19.48 | 11.79 | 1.78 | |
| Fe-celadonite (Fe-muscovite) | 17.46 | 16.18 | 14.21 | 11.68 | 9.16 | 6.63 | 4.14 | 3.58 | |
| Anorthite | 7.23 | 6.70 | 5.88 | 4.84 | 3.79 | 2.75 | 1.72 | 2.34 | |
| Siderite | 11.38 | 10.54 | 9.26 | 7.61 | 5.97 | 4.32 | 2.70 | 2.15 | |
| Dolomite | 5.08 | 4.71 | 4.14 | 3.40 | 2.67 | 1.93 | 1.21 | 1.19 | |
| Calcite | 1.80 | 1.67 | 1.47 | 1.21 | 0.95 | 0.69 | 0.43 | 1.32 | |
| Pyrite | - | - | - | - | - | - | - | 0.09 | |
| Seal 6 | |||||||||
| Kaolinite | 0.83 | 2.69 | 5.56 | 9.23 | 12.90 | 16.57 | 20.19 | 17.73 | |
| Fe-Illite | 2.01 | 6.53 | 13.50 | 22.41 | 31.33 | 40.24 | 49.03 | 12.50 | |
| Chlorite | 0.32 | 1.04 | 2.14 | 3.56 | 4.97 | 6.39 | 7.78 | 14.20 | |
| Quartz | 55.07 | 50.96 | 44.62 | 36.51 | 28.41 | 20.30 | 12.31 | 4.83 | |
| Fe-celadonite (Fe-muscovite) | 13.77 | 12.76 | 11.20 | 9.21 | 7.22 | 5.23 | 3.27 | 9.95 | |
| Anorthite | 17.03 | 15.78 | 13.86 | 11.39 | 8.93 | 6.47 | 4.04 | 6.50 | |
| Siderite | 3.93 | 3.64 | 3.20 | 2.63 | 2.06 | 1.49 | 0.93 | 5.98 | |
| Dolomite | 3.43 | 3.18 | 2.79 | 2.30 | 1.80 | 1.30 | 0.81 | 3.30 | |
| Calcite | 2.62 | 2.43 | 2.13 | 1.75 | 1.37 | 1.00 | 0.62 | 1.32 | |
| Pyrite | - | - | - | - | - | - | - | 0.02 | |
| Reservoir | |||||||||
| Kaolinite | 4.70 | 17.73 | |||||||
| Fe-Illite | 3.85 | 12.50 | |||||||
| Chlorite | 1.59 | 14.20 | |||||||
| Quartz | 10.04 | 4.83 | |||||||
| Fe-celadonite (Fe-muscovite) | 1.57 | 9.95 | |||||||
| Anorthite | 2.05 | 6.50 | |||||||
| Siderite | 0.64 | 5.98 | |||||||
| Dolomite | 11.63 | 3.30 | |||||||
| Calcite | 63.94 | 0.99 | |||||||
| Pyrite | 1.00 | 0.05 |
| Mineral | Dissolution Reaction | LogCads 0 °C | LogCads 25 °C | LogCads 60 °C | LogCads 100 °C | LogCads 150 °C | LogCads 200 °C | LogCads 250 °C | LogCads 300 °C |
|---|---|---|---|---|---|---|---|---|---|
| CO2ads | −7.3403 | −7.0983 | −7.0033 | −7.0973 | −7.4013 | −7.8483 | −8.4203 | −9.1573 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Currenti, G.; Cantucci, B.; Montegrossi, G.; Napoli, R.; Misnan, M.S.; Rashidi, M.R.A.; Abu Bakar, Z.A.; Harith, Z.Z.T.; Bahri, N.H.S.; Hashim, N. CO2 Leakage Scenarios in Shale Overburden. Minerals 2023, 13, 1016. https://doi.org/10.3390/min13081016
Currenti G, Cantucci B, Montegrossi G, Napoli R, Misnan MS, Rashidi MRA, Abu Bakar ZA, Harith ZZT, Bahri NHS, Hashim N. CO2 Leakage Scenarios in Shale Overburden. Minerals. 2023; 13(8):1016. https://doi.org/10.3390/min13081016
Chicago/Turabian StyleCurrenti, Gilda, Barbara Cantucci, Giordano Montegrossi, Rosalba Napoli, M. Shahir Misnan, M. Rashad Amir Rashidi, Zainol Affendi Abu Bakar, Zuhar Zahir Tuan Harith, Nabila Hannah Samsol Bahri, and Noorbaizura Hashim. 2023. "CO2 Leakage Scenarios in Shale Overburden" Minerals 13, no. 8: 1016. https://doi.org/10.3390/min13081016
APA StyleCurrenti, G., Cantucci, B., Montegrossi, G., Napoli, R., Misnan, M. S., Rashidi, M. R. A., Abu Bakar, Z. A., Harith, Z. Z. T., Bahri, N. H. S., & Hashim, N. (2023). CO2 Leakage Scenarios in Shale Overburden. Minerals, 13(8), 1016. https://doi.org/10.3390/min13081016






