Exploring the High-Pressure Phases of Carbon through X-ray Diffraction of Dynamic Compression Experiments on Sandia’s Z Pulsed Power Facility
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dynamic Compression Concepts
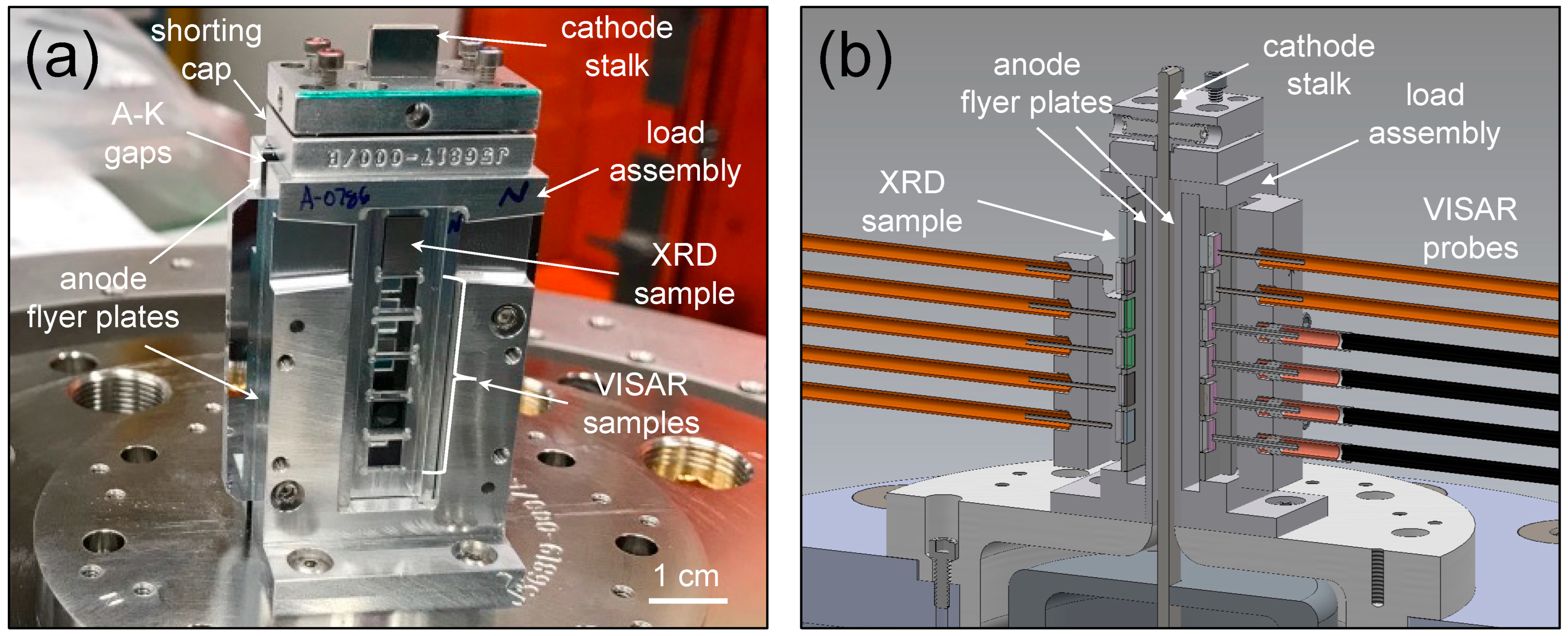
2.2. Pulsed Power Dynamic Compression
2.3. Z-XRD Diagnostics
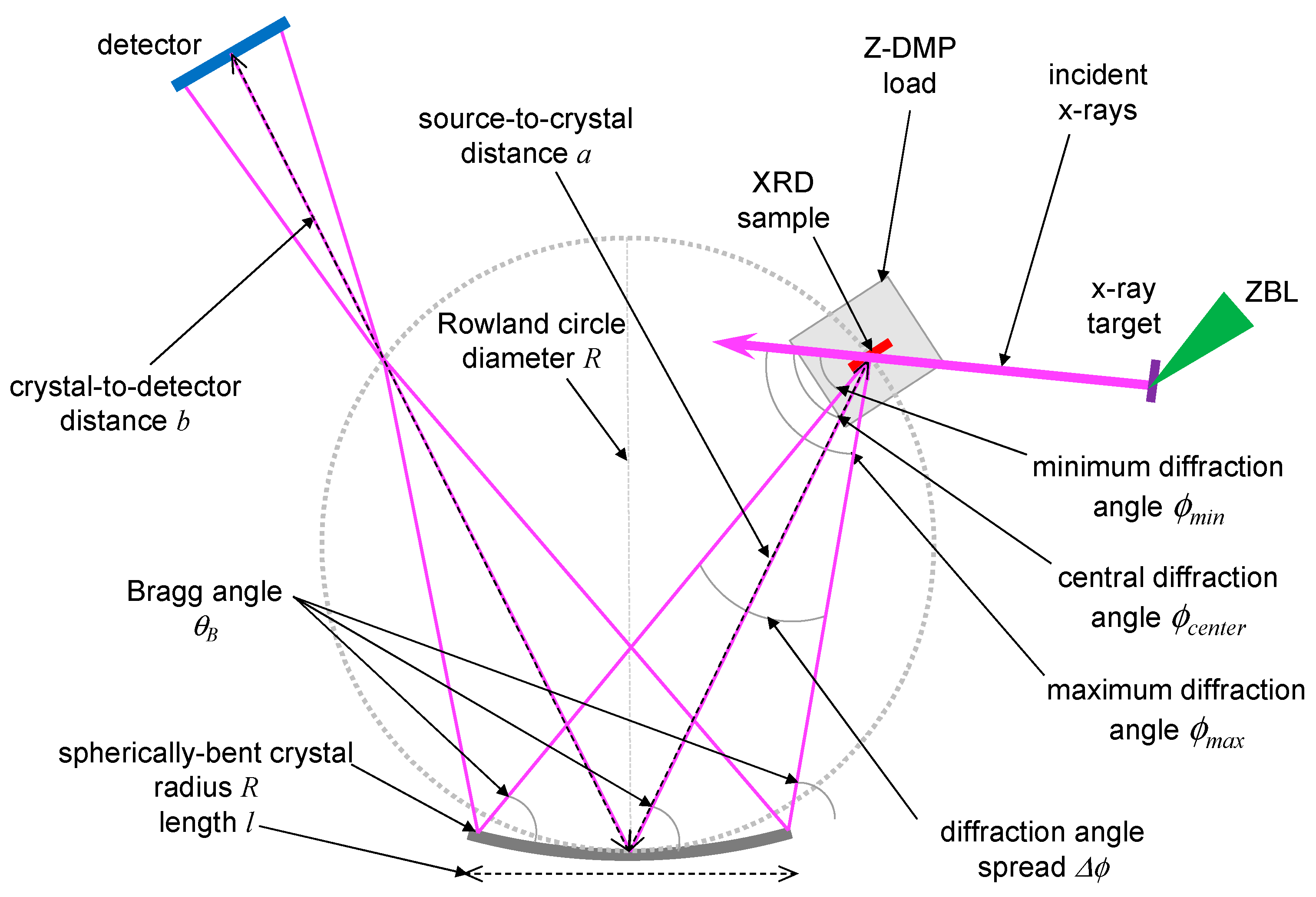
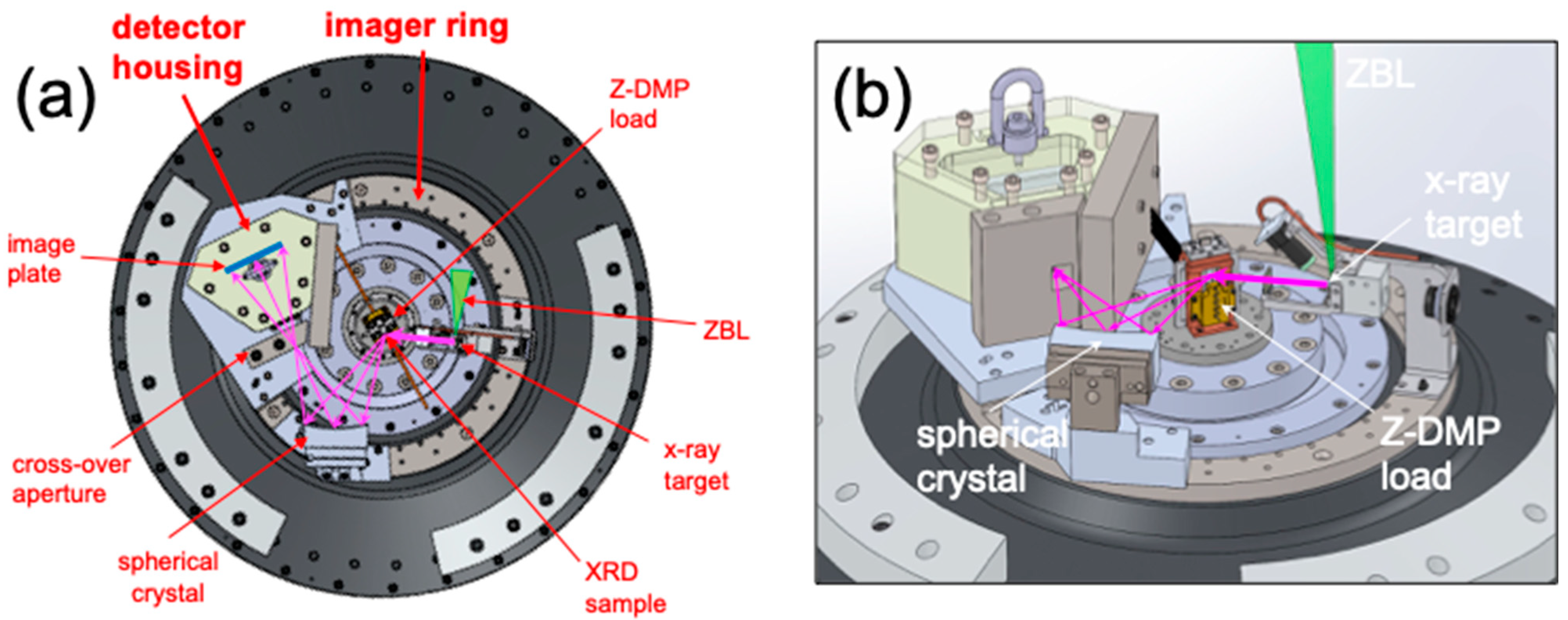
2.3.1. Spherical Crystal Diffraction Imager (SCDI)
2.3.2. DIffraction SCintillator Optic (DISCO)
- “front-end”, passive X-ray-to-optical light converter (scintillator) and optical light collection optics (lenses);
- “imaging-fiber-cable”, passive imaging fiber bundle to transport the data out of the harsh environment;
- “back-end”, camera coupling optics (lenses) that can be attached to a commercial-off-the-shelf time-gated camera.
3. Results
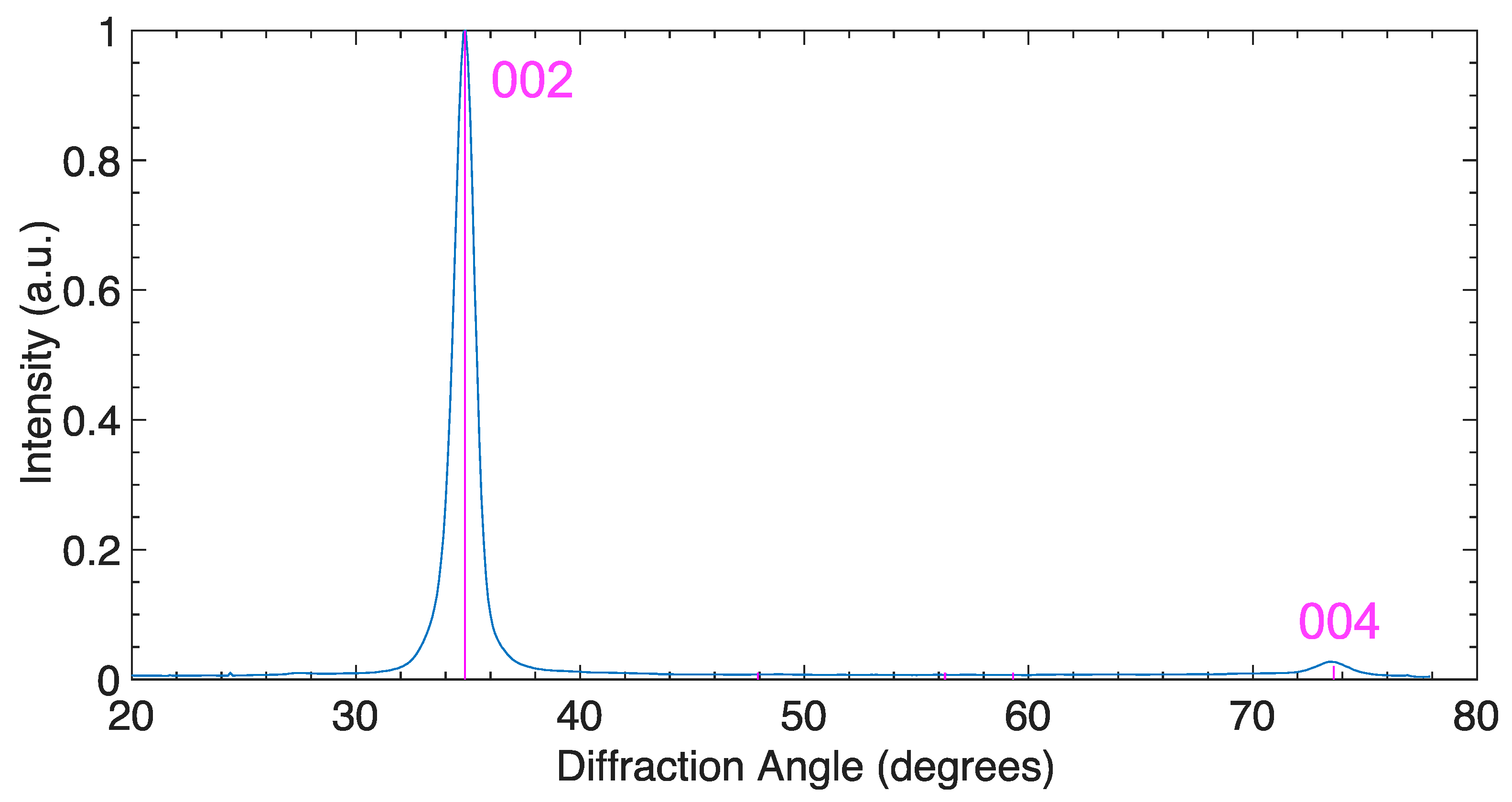
3.1. Ambient Calibrations
3.2. Z-XRD Experiments
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, X.; Scandolo, S.; Car, R. Carbon phase diagram from ab initio molecular dynamics. Phys. Rev. Lett. 2005, 95, 185701. [Google Scholar] [CrossRef]
- Correa, A.A.; Bonev, S.A.; Galli, G. Carbon under extreme conditions: Phase boundaries and electronic properties from first-principles theory. Proc. Nat. Acad. Sci. USA 2006, 103, 1204–1208. [Google Scholar] [CrossRef]
- Benedict, L.X.; Driver, K.P.; Hamel, S.; Militzer, B.; Qi, T.; Correa, A.A.; Saul, A.; Schwegler, E. Multiphase equation of state for carbon addressing high pressures and temperatures. Phys. Rev. B 2014, 89, 224109. [Google Scholar] [CrossRef]
- Remington, B.A.; Drake, R.P.; Ryutov, D.D. Experimental astrophysics with high power lasers and Z pinches. Rev. Mod. Phys. 2006, 78, 755–807. [Google Scholar] [CrossRef]
- Lindl, J.D.; Amendt, P.; Berger, R.L.; Glendinning, S.G.; Glenzer, S.H.; Haan, S.W.; Kauffman, R.L.; Landen, O.L.; Suter, L.J. The physics basis for ignition using indirect-drive targets on the National Ignition Facility. Phys. Plasmas 2003, 11, 339–491. [Google Scholar] [CrossRef]
- Madhusudhan, N.; Lee, K.K.M.; Mousis, O. A possible carbon-rich interior in super-Earth 55 Cancri e. Astrophys. J. 2012, 759, L40. [Google Scholar] [CrossRef]
- Segretain, L.; Chabrier, G.; Hernanz, M.; Garica-Berro, E.; Isern, J.; Mochkovitch, R. Cooling theory of crystallized white dwarfs. Astrophys. J. 1994, 434, 641–651. [Google Scholar] [CrossRef]
- Metcalf, T.S.; Montgomery, M.H.; Kannan, A. Testing white dwarf crystallization theory with asteroseismology of the massive pulsating DA star BPM 37093. Astrophys. J. 2004, 605, L133–L136. [Google Scholar] [CrossRef]
- Ross, M. The ice layer in Uranus and Neptune—Diamonds in the sky? Nature 1981, 292, 435–436. [Google Scholar] [CrossRef]
- Hubbard, W.B. Interiors of gas giants. Science 1981, 214, 145–149. [Google Scholar] [CrossRef]
- Benedetti, L.R.; Nguyen, J.H.; Caldwell, W.A.; Liu, H.; Kruger, M.; Jeanloz, R. Dissociation of CH4 at high pressures and temperatures: Diamond formation in giant planet interiors? Science 1999, 286, 100–102. [Google Scholar] [CrossRef] [PubMed]
- Abu-Shawareb, H.; Acree, R.; Adams, P.; Adams, J.; Addis, B.; Aden, R.; Adrian, P.; Afeyan, B.B.; Aggleton, M.; Aghaian, L.; et al. Lawson criterion for ignition exceeded in an inertial fusion experiment. Phys. Rev. Lett. 2022, 129, 075001. [Google Scholar] [CrossRef] [PubMed]
- Zylstra, A.B.; Kritcher, A.L.; Hurricane, O.A.; Callahan, D.A.; Ralph, J.E.; Casey, D.T.; Pak, A.; Landen, O.L.; Bachmann, B.; Baker, K.L.; et al. Experimental achievement and signatures of ignition at the National Ignition Facility. Phys. Rev. E 2022, 106, 025202. [Google Scholar] [CrossRef] [PubMed]
- Kritcher, A.L.; Zylstra, A.B.; Callahan, D.A.; Hurricane, O.A.; Weber, C.R.; Clark, D.S.; Young, C.V.; Ralph, J.E.; Casey, D.T.; Pak, A.; et al. Design of an inertial fusion experiment exceeding the Lawson criterion for ignition. Phys. Rev. E 2022, 106, 025201. [Google Scholar] [CrossRef]
- Bernal, J.D. The structure of graphite. Proc. R. Soc. A 1924, 106, 749–773. [Google Scholar] [CrossRef]
- Smith, W.H.; Leeds, D.H. Pyrolytic graphite. In Modern Materials; Gonser, B.W., Ed.; Academic Press, Inc.: New York, NY, USA, 1970; pp. 139–221. [Google Scholar] [CrossRef]
- Guentert, O.J. X-ray study of pyrolytic graphites. J. Chem. Phys. 1962, 19, 884–891. [Google Scholar] [CrossRef]
- Moore, A.W. Highly oriented pyrolytic graphite. In Chemistry and Physics of Carbon; Walker, P.L., Jr., Thrower, P.A., Eds.; Dekker: New York, NY, USA, 1973; Volume 11, pp. 69–187. [Google Scholar]
- Fahy, S.; Louie, S.G. High-pressure structural and electronic properties of carbon. Phys. Rev. B 1987, 36, 3373–3385. [Google Scholar] [CrossRef]
- Stachel, T.; Harris, J.W. Formation of diamond in the Earth’s mantle. J. Phys. Condens. Matter 2009, 21, 364206. [Google Scholar] [CrossRef]
- Field, J.E. The mechanical and strength properties of diamond. Rep. Prog. Phys. 2012, 75, 126505. [Google Scholar] [CrossRef]
- Bundy, F.; Hall, T.; Strong, H.M.; Wentorf, R.H. Man-made diamonds. Nature 1955, 176, 51–55. [Google Scholar] [CrossRef]
- Hazen, R.M. The Diamond Makers; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Hanneman, R.E.; Strong, H.M.; Bundy, F.F. Hexagonal diamonds in meteorites: Implications. Science 1967, 155, 995–997. [Google Scholar] [CrossRef]
- Frondel, C.; Marvin, U.B. Lonsdaleite, a hexagonal polymorph of diamond. Nature 1967, 214, 587–589. [Google Scholar] [CrossRef]
- Bundy, F.P.; Kasper, J.S. Hexagonal diamond—A new form of carbon. J. Chem. Phys. 1967, 46, 3437–3446. [Google Scholar] [CrossRef]
- Nemeth, P.; Garvie, L.A.J.; Aoki, T.; Dubrovinskaia, N.; Dubrovinsky, L.; Buseck, P.R. Lonsdaleite is faulted and twinned cubic diamond and does not exist as a discrete material. Nat. Commun. 2014, 5, 5447. [Google Scholar] [CrossRef]
- Salzmann, C.G.; Murray, B.J.; Shephard, J.J. Extent of stacking disorder in diamond. Diam. Relat. Mater. 2015, 59, 69–72. [Google Scholar] [CrossRef]
- Bundy, F.P. Direct conversion of graphite to diamond in static pressure apparatus. J. Chem. Phys. 1963, 38, 631–643. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Spain, I.L. X-ray diffraction data for graphite to 20 GPa. Phys. Rev. B 1989, 40, 993–997. [Google Scholar] [CrossRef]
- Yagi, T.; Utsumi, W.; Yamakata, M.A.; Kikegawa, T.; Shimomura, O. High-pressure in situ X-ray-diffraction study of the phase transformation from graphite to hexagonal diamond at room temperature. Phys. Rev. B 1992, 46, 6031–6039. [Google Scholar] [CrossRef]
- DeCarli, P.S.; Jamieson, J.C. Formation of diamond by explosive shock. Science 1961, 133, 1821–1822. [Google Scholar] [CrossRef]
- Erskine, D.J.; Nellis, W.J. Shock-induced martensitic phase transformation of oriented graphite to diamond. Nature 1991, 349, 317–319. [Google Scholar] [CrossRef]
- Erskine, D.J.; Nellis, W.J. Shock-induced martensitic transformation of highly oriented graphite to diamond. J. Appl. Phys. 1992, 71, 4882–4886. [Google Scholar] [CrossRef]
- Rygg, J.R.; Eggert, J.H.; Lazicki, A.E.; Coppari, F.; Hawreliak, J.A.; Hicks, D.G.; Smith, R.F.; Sorce, C.M.; Uphaus, T.M.; Yaakobi, B.; et al. Powder diffraction from solids in the terapascal regime. Rev. Sci. Instrum. 2012, 83, 113904. [Google Scholar] [CrossRef] [PubMed]
- Rygg, J.R.; Smith, R.F.; Lazicki, A.E.; Braun, D.G.; Fratanduono, D.E.; Kraus, R.G.; McNaney, J.M.; Swift, D.C.; Wehrenberg, C.E.; Coppari, F.; et al. X-ray diffraction at the National Ignition Facility. Rev. Sci. Instrum. 2020, 91, 043902. [Google Scholar] [CrossRef]
- Gleason, A.E.; Bolme, C.A.; Galtier, E.; Lee, H.J.; Granados, E.; Dolan, D.H.; Seagle, C.T.; Ao, T.; Ali, S.; Lazicki, A.; et al. Compression freezing kinetics of water to ice VII. Phys. Rev. Lett. 2017, 119, 025701. [Google Scholar] [CrossRef]
- Turneaure, S.J.; Sinclair, N.; Gupta, Y.M. Real-time examination of atomistic mechanisms during shock-induced structural transformation in silicon. Phys. Rev. Lett. 2016, 117, 045502. [Google Scholar] [CrossRef]
- Turneaure, S.J.; Sharma, S.M.; Volz, T.J.; Winey, J.M.; Gupta, Y.M. Transformation of shock-compressed graphite to hexagonal diamond in nanoseconds. Sci. Adv. 2017, 3, eaao3561. [Google Scholar] [CrossRef] [PubMed]
- Volz, T.J.; Gupta, Y.M. Graphite to diamond transformation under shock compression: Role of orientational order. J. Appl. Phys. 2019, 125, 245902. [Google Scholar] [CrossRef]
- Volz, T.J.; Turneaure, S.J.; Sharma, S.M.; Gupta, Y.M. Role of graphite crystal structure on the shock-induced formation of cubic and hexagonal diamond. Phys. Rev. B 2020, 101, 224109. [Google Scholar] [CrossRef]
- Bradley, D.K.; Eggert, J.H.; Hicks, D.G.; Celliers, P.M.; Moon, S.J.; Cauble, R.C.; Collins, G.W. Shock compressing diamond to a conducting fluid. Phys. Rev. Lett. 2004, 93, 195506. [Google Scholar] [CrossRef]
- Nagao, H.; Nakamura, K.G.; Kondo, K.; Ozaki, N.; Takamatsu, K.; Ono, T.; Shiota, T.; Ichinose, D.; Tanaka, K.A.; Wakabayashi, K.; et al. Hugoniot measurements of diamond under laser shock compression up to 2 TPa. Phys. Plasmas 2006, 12, 052705. [Google Scholar] [CrossRef]
- Brygoo, S.; Henry, E.; Loubeyre, P.; Eggert, J.; Koenig, M.; Loupias, B.; Benuzzi-Mounaiz, A.; Rabec le Gloachec, M. Laser-shock compression of diamond and evidence of a negative-slope melting curve. Nat. Mater. 2007, 6, 274–277. [Google Scholar] [CrossRef]
- Kraus, D.; Ravasio, A.; Gauthier, M.; Gericke, D.O.; Vorberger, J.; Frydrych, S.; Helfrich, J.; Fletcher, L.B.; Schaumann, G.; Nagler, B.; et al. Nanosecond formation of diamond and lonsdaleite by shock compression of graphite. Nat. Commun. 2016, 7, 10970. [Google Scholar] [CrossRef]
- Knudson, M.D.; Desjarlais, M.P.; Dolan, D.H. Shock-wave exploration the high-pressure phases of carbon. Sci. Rep. 2008, 322, 1822–1825. [Google Scholar] [CrossRef]
- Murri, M.; Smith, R.L.; McColl, K.; Hart, M.; Alvaro, M.; Jones, A.P.; Németh, P.; Salzmann, C.G.; Corà, F.; Domeneghetti, M.C.; et al. Quantifying hexagonal stacking in diamond. Sci. Rep. 2019, 9, 10334. [Google Scholar] [CrossRef]
- Scandolo, S.; Bernasconi, M.; Chiarotti, G.L.; Focher, P.; Tosatti, E. Pressure-induced transformation path of graphite to diamond. Phys. Rev. Lett. 1995, 74, 4015–4018. [Google Scholar] [CrossRef]
- Mundy, C.J.; Curioni, A.; Goldman, N.; Kuo, I.-F.W.; Reed, E.J.; Fried, L.E.; Ianuzzi, M. Ultrafast transformation of graphite to diamond: An ab initio study of graphite under shock compression. J. Chem. Phys. 2008, 128, 184701. [Google Scholar] [CrossRef] [PubMed]
- Pineau, N. Molecular simulations of shock compressed graphite. J. Phys. Chem. C 2013, 117, 12778. [Google Scholar] [CrossRef]
- Kroonblawd, M.P.; Goldman, N. Mechanochemcial formation of heterogenous diamond structures during rapid uniaxial compression in graphite. Phys. Rev. B 2018, 97, 184106. [Google Scholar] [CrossRef]
- McQueen, R.G.; Marsh, S.P.; Taylor, J.W.; Fritz, J.N.; Carter, W.J. The equation of state of solids from shock wave studies. In High-Velocity Impact Phenomena; Kinslow, R., Ed.; Academic: New York, NY, USA, 1970; pp. 293–417. [Google Scholar] [CrossRef]
- Duvall, G.E.; Graham, R.A. Phase transitions under shock-wave loading. Rev. Mod. Phys. 1977, 49, 523–579. [Google Scholar] [CrossRef]
- Asay, J.R.; Mohsen, S. High Pressure Shock Compression of Solids; Springer: New York, NY, USA, 1993. [Google Scholar] [CrossRef]
- Forbes, J.W. The history of the APS topical group on shock compression of condensed matter. In Shock Compression of Condensed Matter—2001; Furnish, M.D., Thadhani, N.N., Horie, Y., Eds.; American Institute of Physics: Melville, NY, USA, 2002; pp. 11–19. [Google Scholar] [CrossRef]
- Forbes, J.W. Shock Wave Compression of Condensed Matter: A Primer; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Band, W.; Duvall, G.E. Physical nature of shock propagation. Am. J. Phys. 1961, 29, 780–785. [Google Scholar] [CrossRef]
- Mitchell, A.C.; Nellis, W.J. Shock compression of aluminum, copper and tantalum. J. Appl. Phys. 1981, 52, 3363–3374. [Google Scholar] [CrossRef]
- Knudson, M.D.; Asay, J.R.; Deeney, C. Adiabatic release measurements in aluminum form 240- to 500-GPa states on the principal Hugoniot. J. Appl. Phys. 2005, 97, 073514. [Google Scholar] [CrossRef]
- Celliers, P.M.; Collins, G.W.; Hicks, D.G.; Eggert, J.H. Systematic uncertainties in shock-wave impedance-match analysis and the high-pressure equation of state of Al. J. Appl. Phys. 2005, 98, 113529. [Google Scholar] [CrossRef]
- Matzen, M.K.; Sweeney, M.A.; Adams, R.G.; Asay, J.R.; Bailey, J.E.; Bennett, G.R.; Bliss, D.E.; Bloomquist, D.D.; Brunner, T.A.; Campbell, R.B.; et al. Pulsed-power-driven high energy density physics and inertial confinement fusion research. Phys. Plasmas 2005, 12, 055503. [Google Scholar] [CrossRef]
- Sinars, D.B.; Sweeney, M.A.; Alexander, C.S.; Ampleford, D.J.; Ao, T.; Apruzese, J.P.; Aragon, C.; Armstrong, D.J.; Austin, K.N.; Awe, T.J.; et al. Review of pulsed power-driven high energy density physics research on Z at Sandia. Phys. Plasmas 2020, 27, 070501. [Google Scholar] [CrossRef]
- Barker, L.M.; Hollenbach, R.E. Laser interferometer for measuring high velocities of any reflecting surface. J. Appl. Phys. 1972, 43, 4669–4675. [Google Scholar] [CrossRef]
- Sinars, D.B.; Bennett, G.R.; Wenger, D.F.; Cuneo, M.E.; Hanson, D.L.; Porter, J.L.; Adams, R.G.; Rambo, P.K.; Rovang, D.C.; Smith, I.C. Monochromatic X-ray imaging experiments on the Sandia National Laboratories Z facility (invited). Rev. Sci. Instrum. 2004, 75, 3672–3677. [Google Scholar] [CrossRef]
- Bennett, G.R.; Sinars, D.B.; Wenger, D.F.; Cuneo, M.E.; Adams, R.G.; Barnard, W.J.; Beutler, D.E.; Burr, R.A.; Campbell, D.V.; Claus, L.D.; et al. High-brightness, high-spatial-resolution, 6.151 keV X-ray imaging of inertial confinement fusion capsule implosion and complex hydrodynamics experiments on Sandia’s Z accelerator (invited). Rev. Sci. Instrum. 2006, 77, 10E322. [Google Scholar] [CrossRef]
- Schollmeier, M.S.; Geissel, M.; Shores, J.E.; Smith, I.C.; Porter, J.L. Performance of bent-crystal X-ray microscopes for high energy density physics research. Appl. Opt. 2015, 54, 5147–5161. [Google Scholar] [CrossRef]
- Ao, T.; Schollmeier, M.; Kalita, P.; Gard, P.D.; Smith, I.C.; Shores, J.E.; Speas, C.S.; Seagle, C.T. A spherical crystal diffraction imager for Sandia’s Z Pulsed Power Facility. Rev. Sci. Instrum. 2020, 91, 043106. [Google Scholar] [CrossRef]
- Rambo, P.; Schwarz, J.; Schollmeier, M.; Geissel, M.; Smith, I.; Kimmel, M.; Speas, C.; Shores, J.; Armstrong, D.; Bellum, J.; et al. Sandia’s Z-Backlighter Laser Facility. Proc. SPIE 2016, 10014, 100140Z. [Google Scholar] [CrossRef]
- Schollmeier, M.S.; Loisel, G.P. Systematic search for spherical crystal X-ray microscopes matching 1–25 keV spectral line sources. Rev. Sci. Instrum. 2015, 87, 123511. [Google Scholar] [CrossRef] [PubMed]
- Ao, T.; Harding, E.C.; Bailey, J.E.; Loisel, G.; Patel, S.; Sinars, D.B.; Mix, L.P.; Wenger, D.F. Relative X-ray collection efficiency, spatial resolution, and spectral resolution of spherically-bent quartz, mica, germanium, and pyrolytic graphite crystals. J. Quant. Spectrosc. Radiat. Transf. 2014, 144, 92–107. [Google Scholar] [CrossRef]
- Henke, B.L.; Gullikson, E.M.; Davis, J.C. X-Ray Interactions: Photoabsorption, Scattering, Transmission, and Reflection at E = 50–30,000 eV, Z = 1–92. At. Data Nucl. Data Tables 1993, 54, 181–342. [Google Scholar] [CrossRef]
- Amemiya, T.; Miyahara, J. Imaging plate illuminates many fields. Nature 1998, 336, 89. [Google Scholar] [CrossRef] [PubMed]
- Gales, S.G.; Bentley, C.D. Image plates as X-ray detectors in plasma physics experiments. Rev. Sci. Instrum. 2004, 75, 4001–4003. [Google Scholar] [CrossRef]
- Madden, T.J.; McGuigan, W.; Molitsky, M.; Naday, I.; McArthur, A.; Westbrook, E.M. Lens-coupled CCD detector for X-ray crystallography. IEEE Trans Nucl. Sci. 2006, 2, 729–734. [Google Scholar] [CrossRef]
- Naday, I.; Ross, S.; Westbrook, E.M.; Zental, G. Charge-coupled device/fiber optic taper array X-ray detector for protein crystallography. Opt. Eng. 1998, 37, 1235–1244. [Google Scholar] [CrossRef]
- Gruner, S.M.; Tate, M.W.; Eikenberry, E.F. Charge-coupled device area X-ray detector. Rev. Sci. Instrum. 2002, 73, 2815–2842. [Google Scholar] [CrossRef]
- Kerley, G.I. Theoretical equation of state for aluminum. Int. J. Impact Eng. 1987, 5, 441–449. [Google Scholar] [CrossRef]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Cryst. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Gleason, A.E.; Bolme, C.A.; Lee, H.J.; Nagler, B.; Galtier, E.; Milathianaki, D.; Hawreliak, J.; Kraus, R.G.; Eggert, J.H.; Fratanduono, D.E.; et al. Ultrafast visualization of crystallization and grain growth in shock-compressed SiO2. Nat. Commun. 2015, 6, 8191. [Google Scholar] [CrossRef] [PubMed]
- Briggs, R.; Gorman, M.G.; Coleman, A.L.; McWilliams, R.S.; McBride, E.E.; McGonegle, D.; Wark, J.S.; Peacock, L.; Rothman, S.; Macleod, S.G.; et al. Ultrafast X-ray diffraction studies of the phase transitions and equation of state of scandium shock compressed to 82 GPa. Phys. Rev. Lett. 2017, 118, 025501. [Google Scholar] [CrossRef] [PubMed]
- Kalita, P.; Specht, P.; Root, S.; Sinclair, N.; Schuman, A.; White, M.; Cornelius, A.L.; Smith, J.; Sinogeikin, S. Direct observations of a dynamically driven phase transition with in situ X-ray diffraction in a simple ionic crystal. Phys. Rev. Lett. 2017, 119, 255701. [Google Scholar] [CrossRef] [PubMed]
- Eggert, J.H.; Hicks, D.G.; Celliers, P.M.; Bradley, D.K.; McWilliams, R.S.; Jeanloz, R.; Miller, J.E.; Boehly, T.R.; Collins, G.W. Melting temperature of diamond at ultrahigh pressure. Nat. Phys. 2009, 6, 40–43. [Google Scholar] [CrossRef]
- Hartsfield, T.M.; Dolan, D.H. Establishing temperature from radiance of dynamically compresses metals. J. Appl. Phys. 2022, 131, 185901. [Google Scholar] [CrossRef]



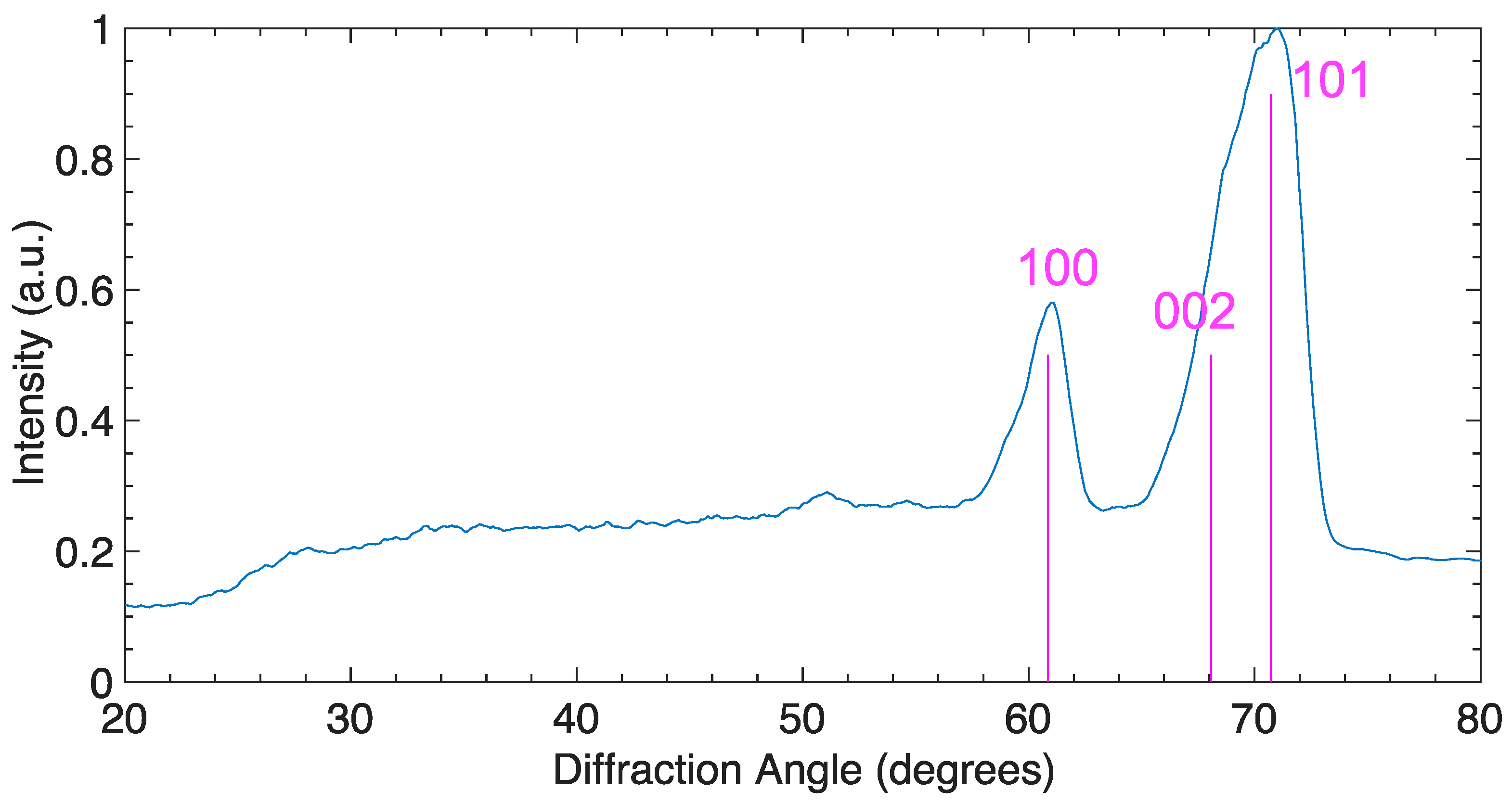
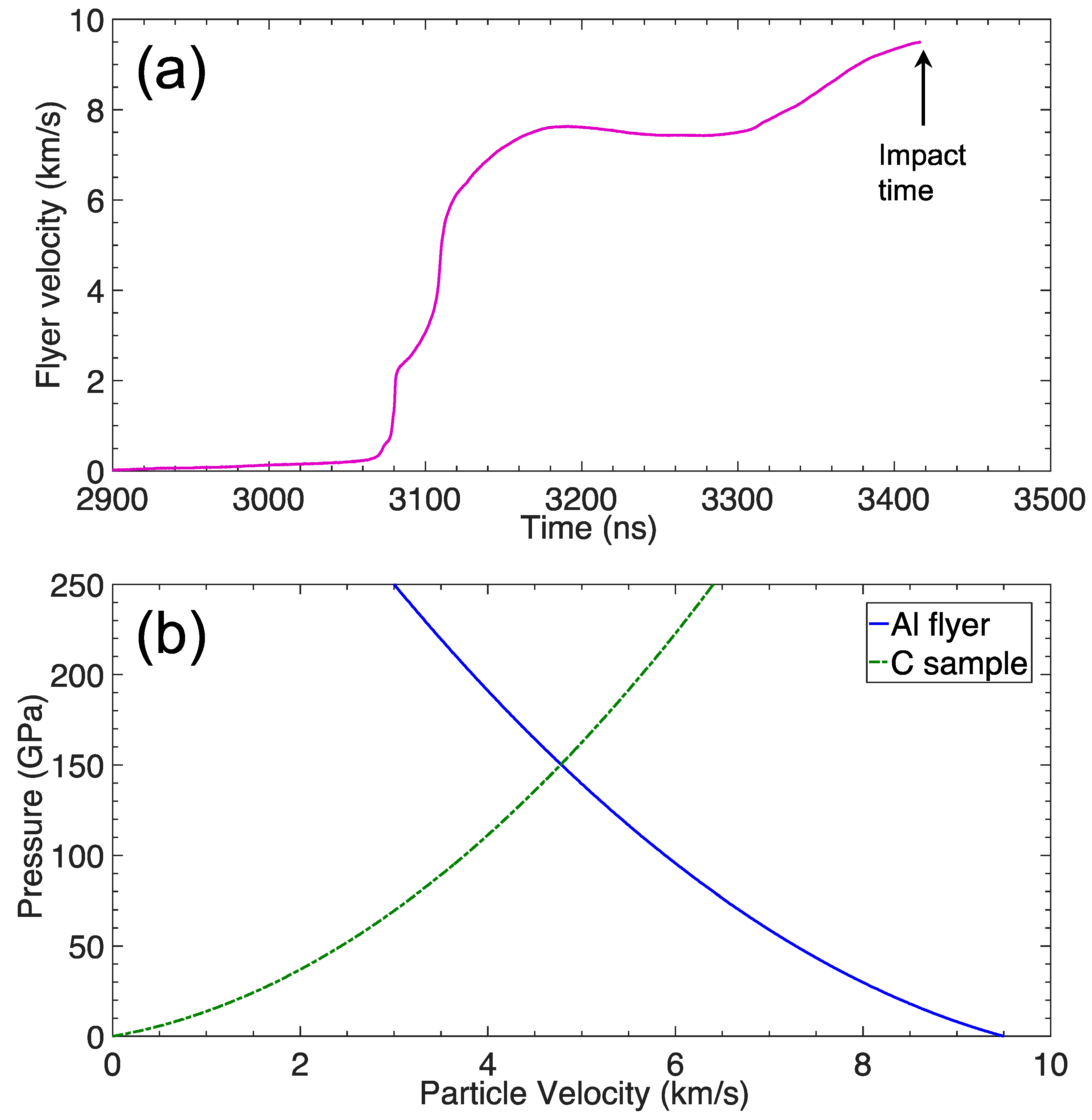
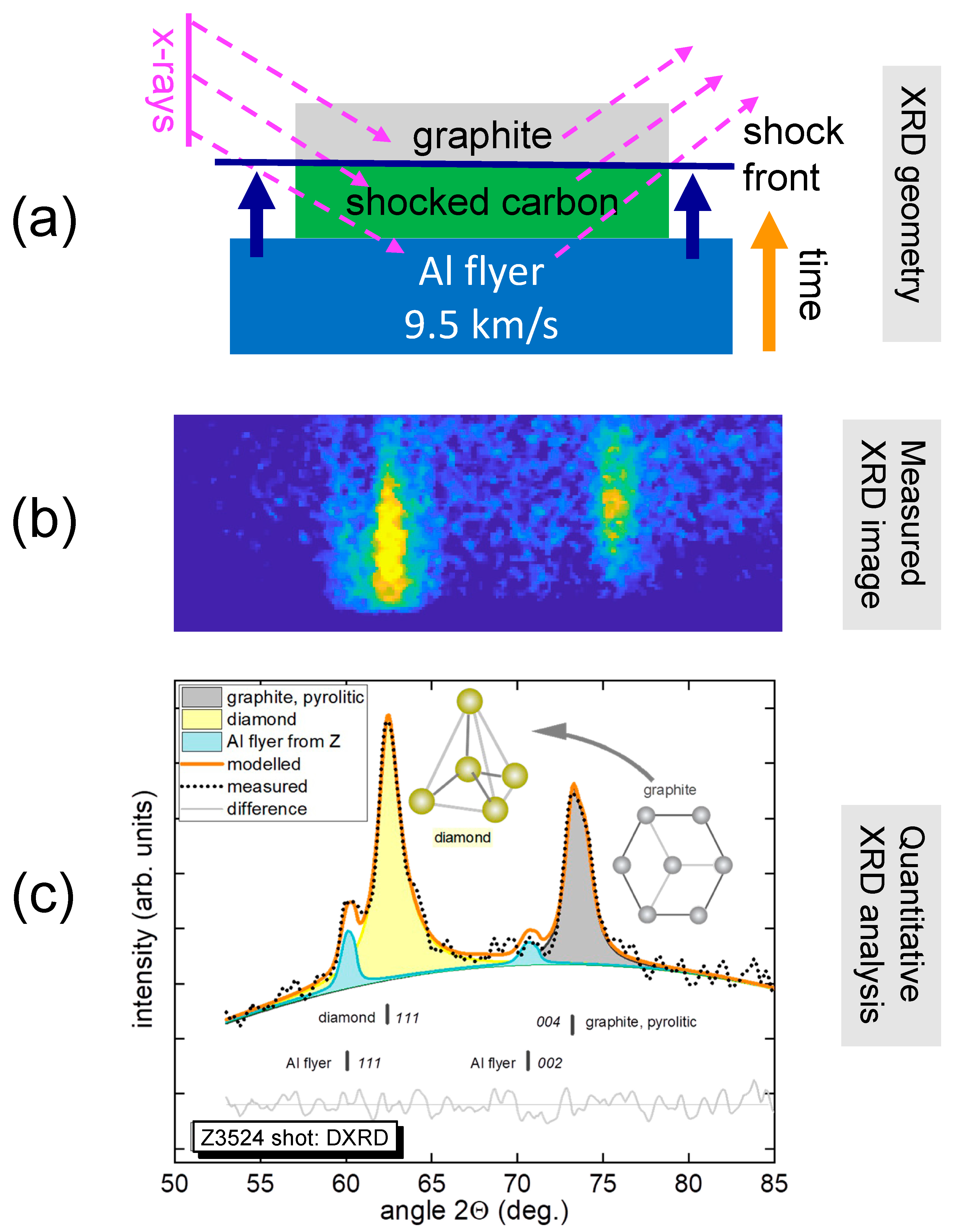
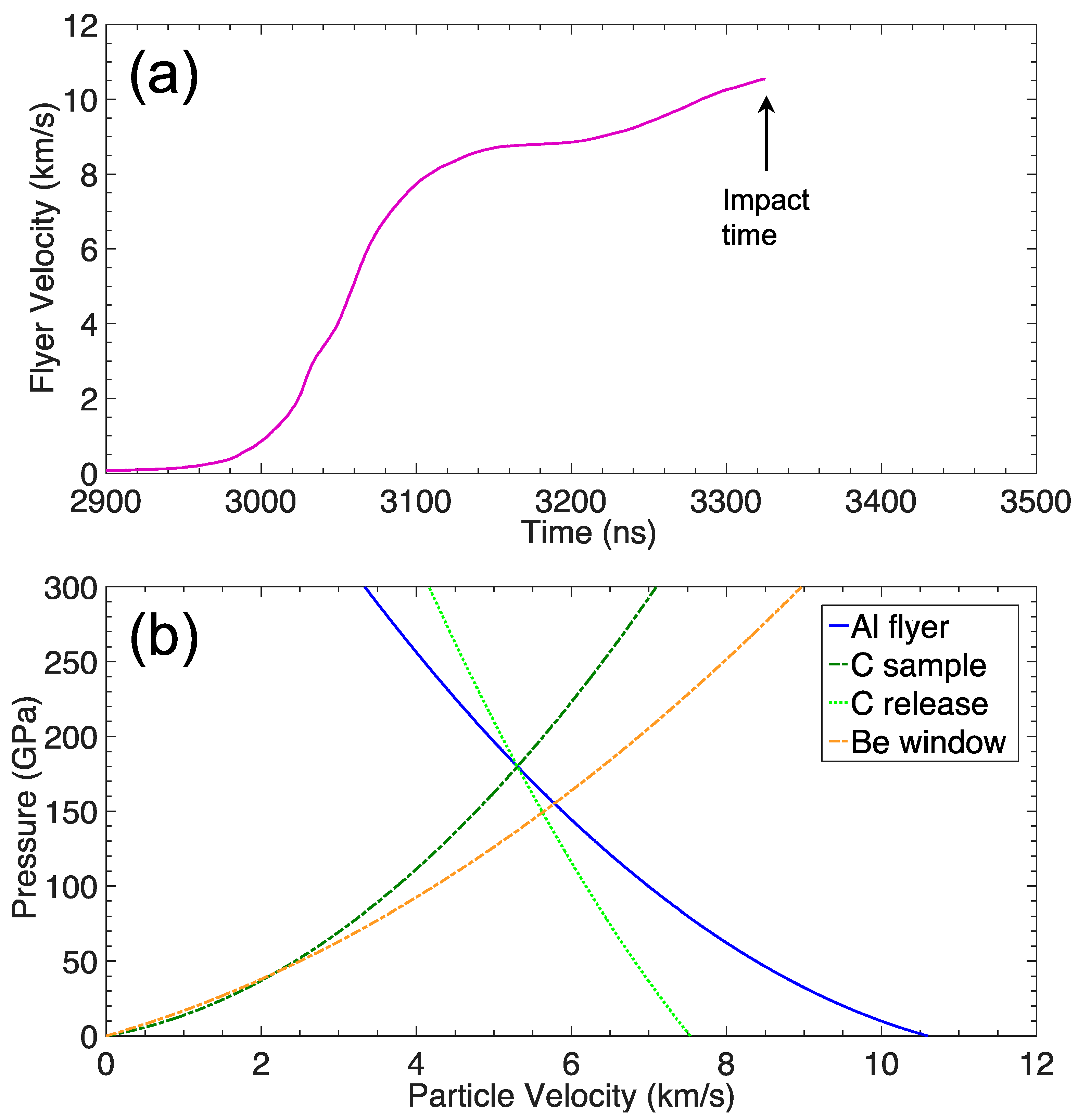
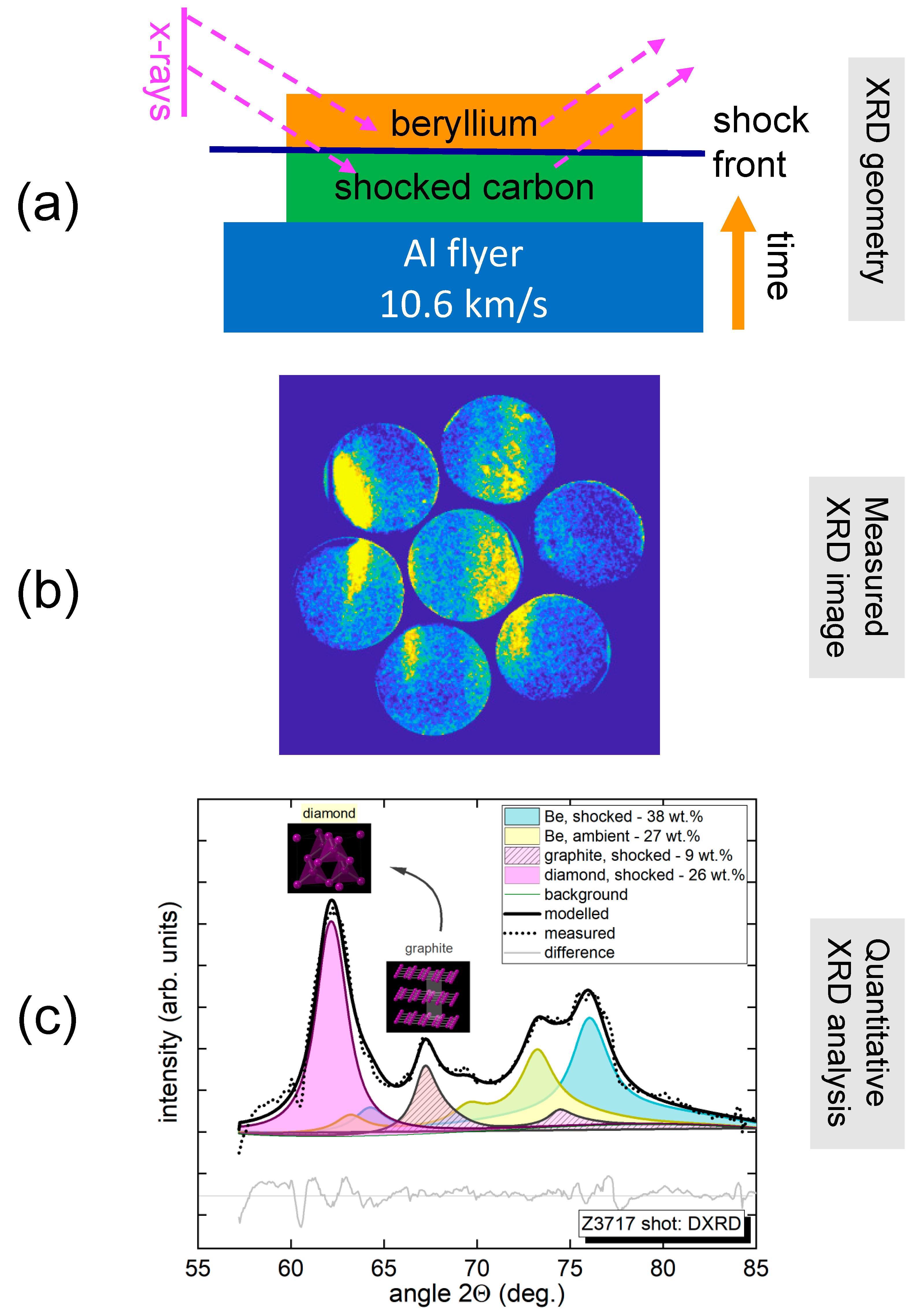
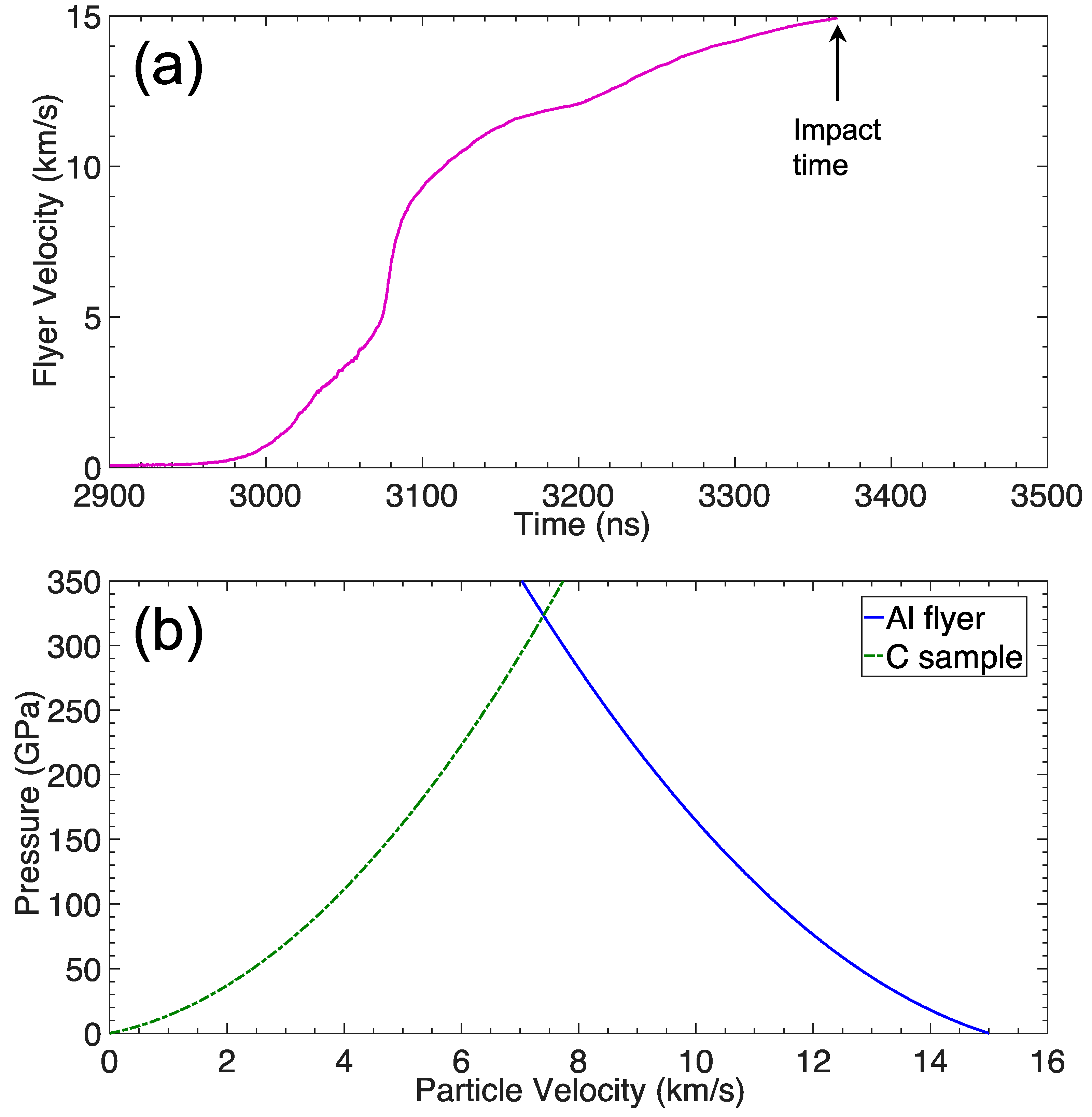
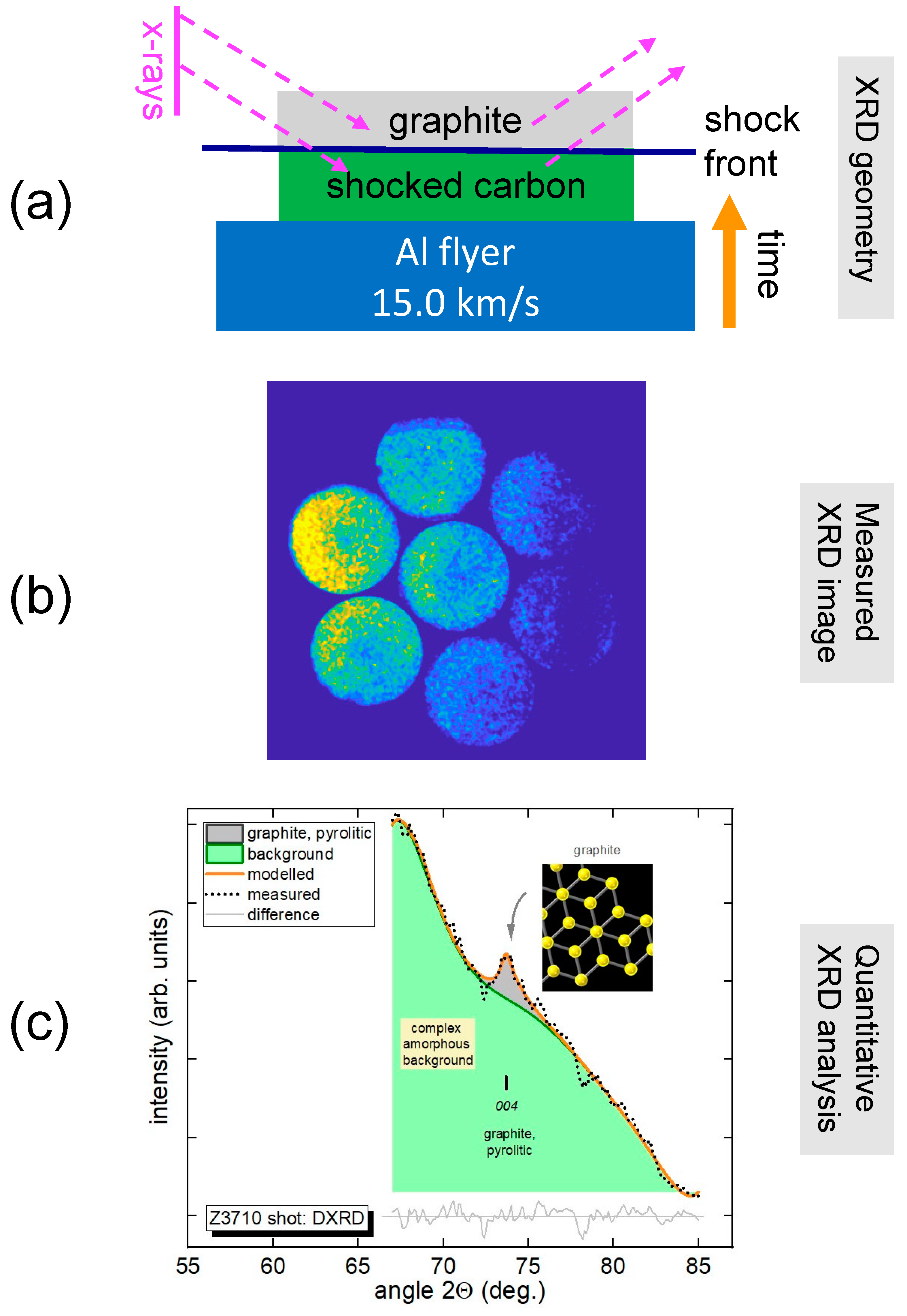
| Z Shot Number | Al Flyer Impact Velocity (km/s) | Impact Shock Pressure (GPa) | X-ray Window | Sample/X-ray Window Shock Pressure (GPa) | X-ray Diagnostic |
|---|---|---|---|---|---|
| Z3524 | 9.5 | 150 | carbon | 150 | SCDI |
| Z3717 | 10.6 | 180 | beryllium | 150 | DISCO |
| Z3710 | 15.0 | 320 | carbon | 320 | DISCO |
| Material | C (km/s) | S |
|---|---|---|
| Aluminum | 5.288 | 1.376 |
| Carbon graphite | 4.260 | 2.170 |
| Carbon diamond | 18.33 | 2.070 |
| Beryllium | 7.998 | 1.124 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ao, T.; Kalita, P.; Blada, C.; Brown, N.P.; Fulford, K.; Gard, P.; Geissel, M.; Hanshaw, H.; Montoya, M.; Payne, S.; et al. Exploring the High-Pressure Phases of Carbon through X-ray Diffraction of Dynamic Compression Experiments on Sandia’s Z Pulsed Power Facility. Minerals 2023, 13, 1203. https://doi.org/10.3390/min13091203
Ao T, Kalita P, Blada C, Brown NP, Fulford K, Gard P, Geissel M, Hanshaw H, Montoya M, Payne S, et al. Exploring the High-Pressure Phases of Carbon through X-ray Diffraction of Dynamic Compression Experiments on Sandia’s Z Pulsed Power Facility. Minerals. 2023; 13(9):1203. https://doi.org/10.3390/min13091203
Chicago/Turabian StyleAo, Tommy, Pat Kalita, Caroline Blada, Nathan P. Brown, Karin Fulford, Paul Gard, Matthias Geissel, Heath Hanshaw, Michael Montoya, Sheri Payne, and et al. 2023. "Exploring the High-Pressure Phases of Carbon through X-ray Diffraction of Dynamic Compression Experiments on Sandia’s Z Pulsed Power Facility" Minerals 13, no. 9: 1203. https://doi.org/10.3390/min13091203
APA StyleAo, T., Kalita, P., Blada, C., Brown, N. P., Fulford, K., Gard, P., Geissel, M., Hanshaw, H., Montoya, M., Payne, S., Scoglietti, E., Smith, A., Speas, C. S., Porter, J. L., & Seagle, C. T. (2023). Exploring the High-Pressure Phases of Carbon through X-ray Diffraction of Dynamic Compression Experiments on Sandia’s Z Pulsed Power Facility. Minerals, 13(9), 1203. https://doi.org/10.3390/min13091203






