Modelling of the Corrosion-Induced Gas Impact on Hydraulic and Radionuclide Transport Properties of Geological Repository Barriers
Abstract
:1. Introduction
2. Methodology
- Isothermal conditions (H model);
- Non-isothermal conditions (impact of temperature) (TH model);
- Non-isothermal conditions under mechanical load (impact of mechanical deformations) (THM).
2.1. Mathematical Model
2.1.1. Radionuclide Transport
2.1.2. Water, Gas, Energy Transport
2.1.3. Mechanical Deformations
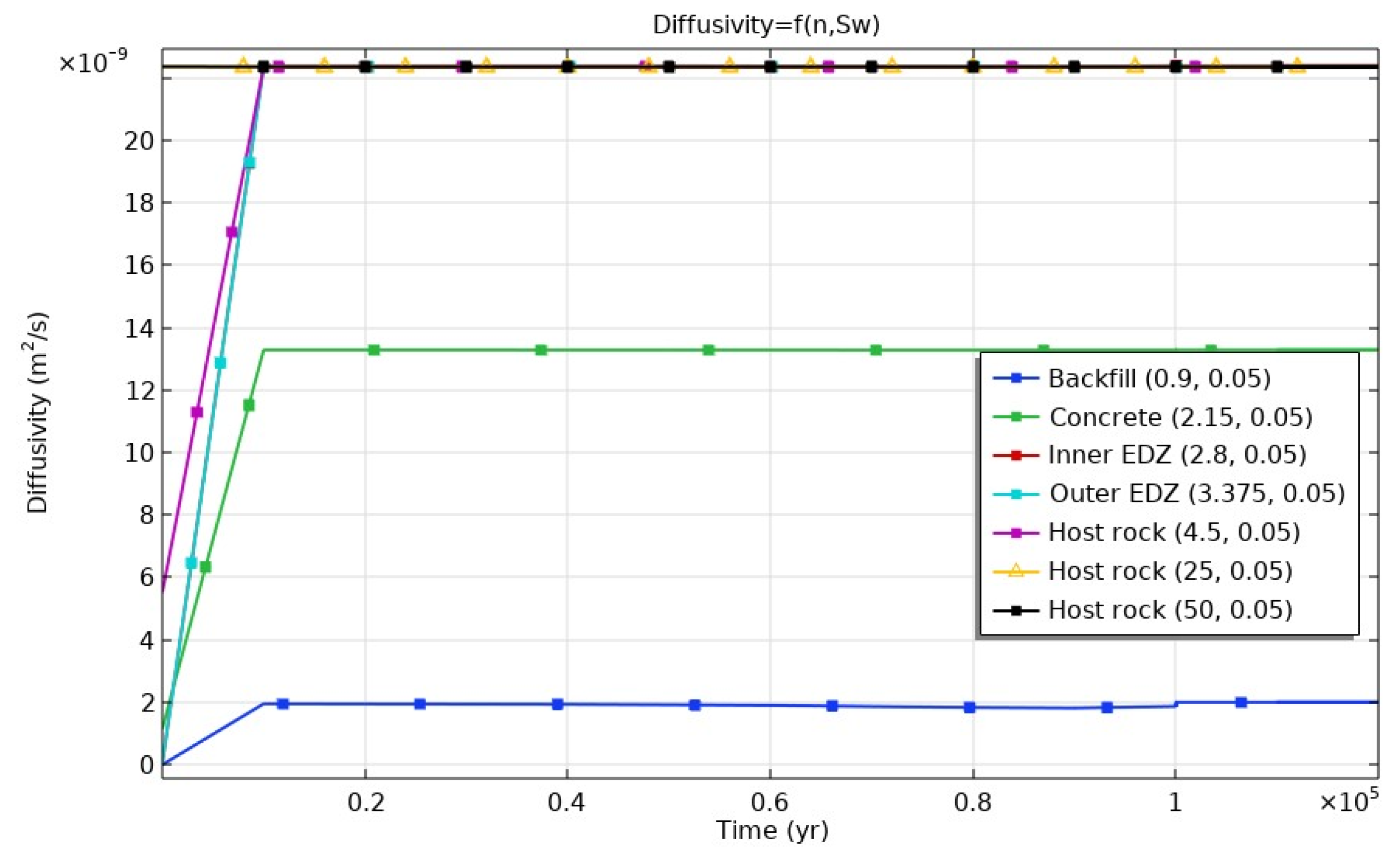
2.1.4. Effective Diffusivity
2.1.5. Water Retention
2.2. Numerical Model
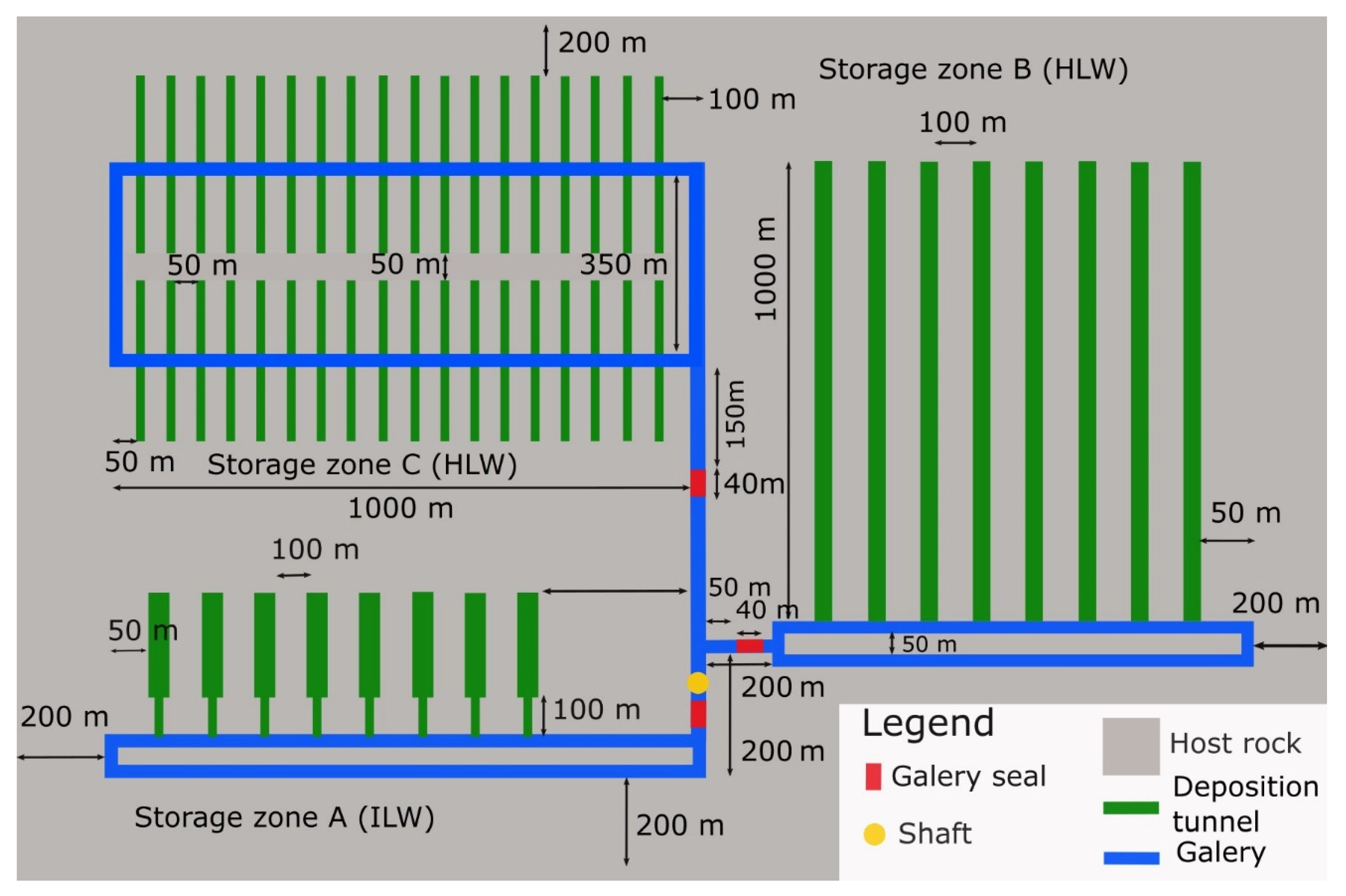
Geometry and Discretization
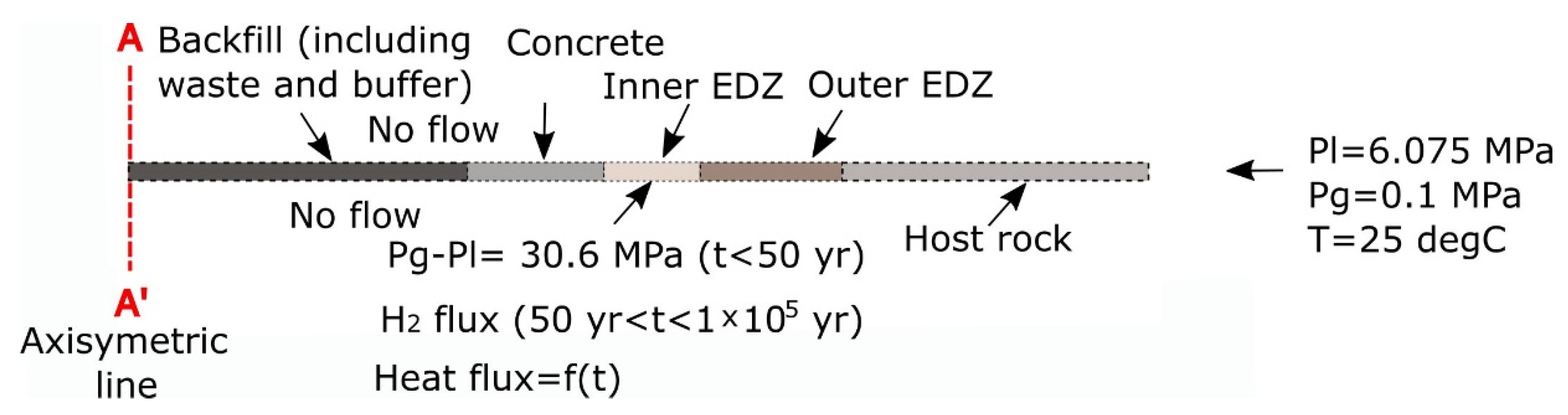
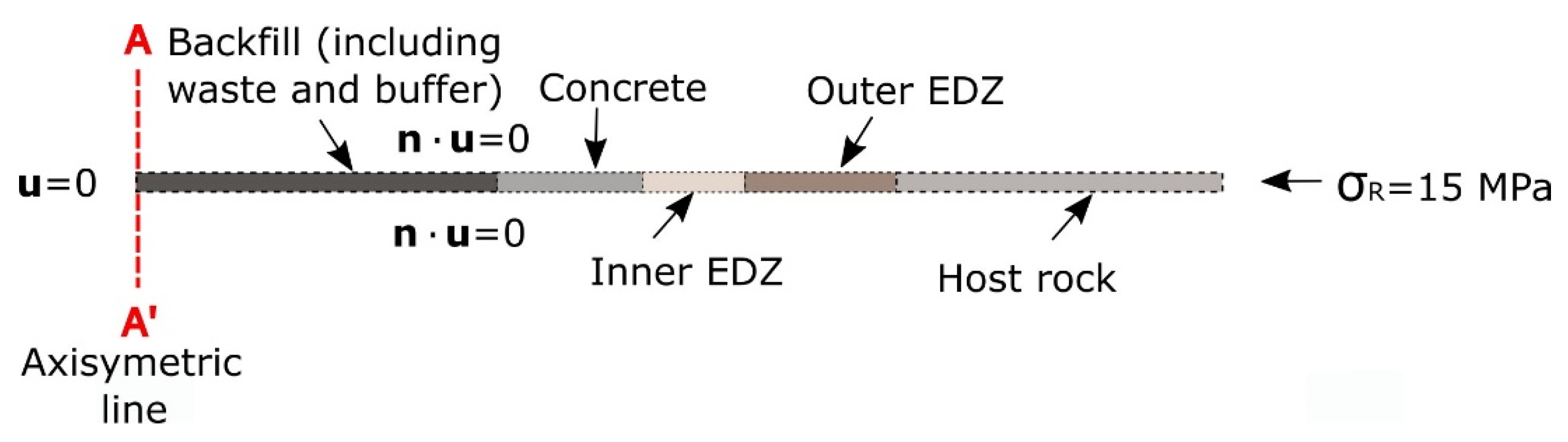
2.3. Initial and Boundary Conditions
2.4. Input Parameters
3. Results and Discussion
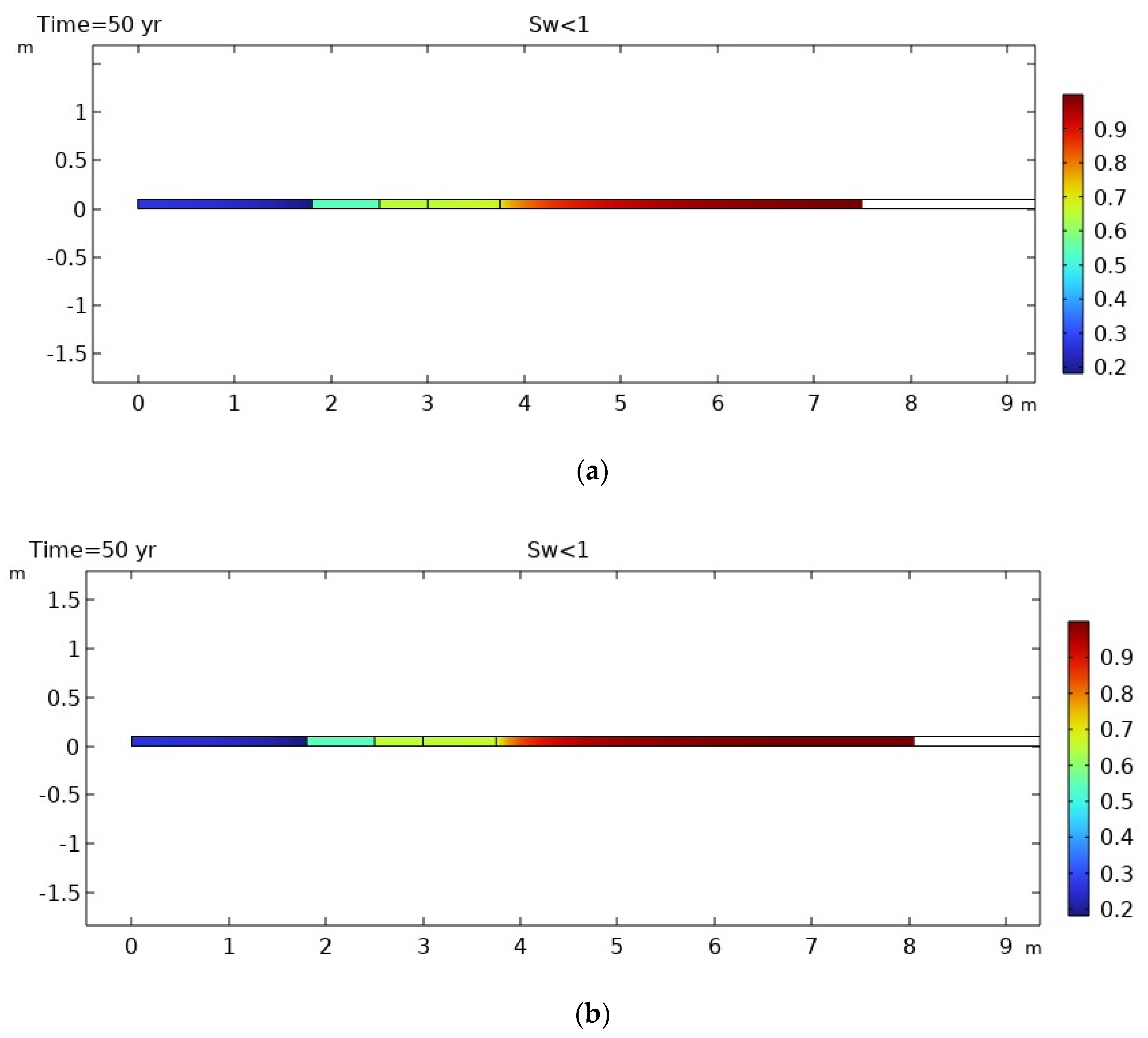
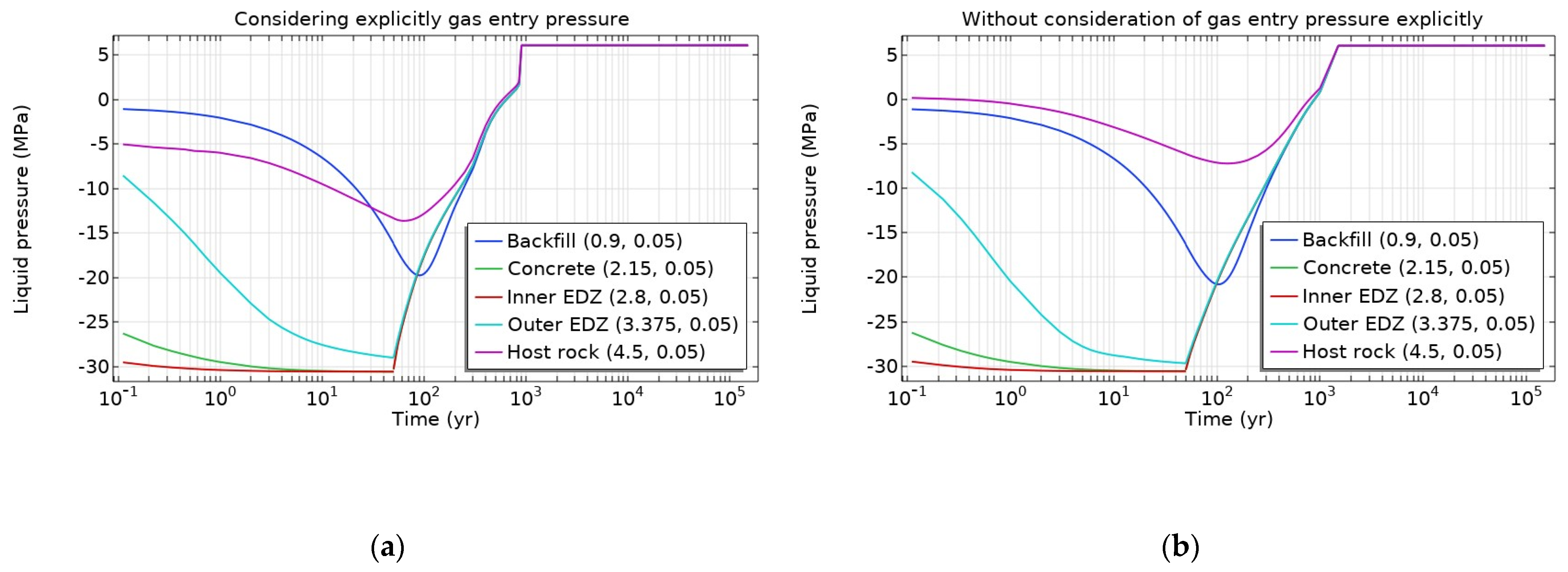
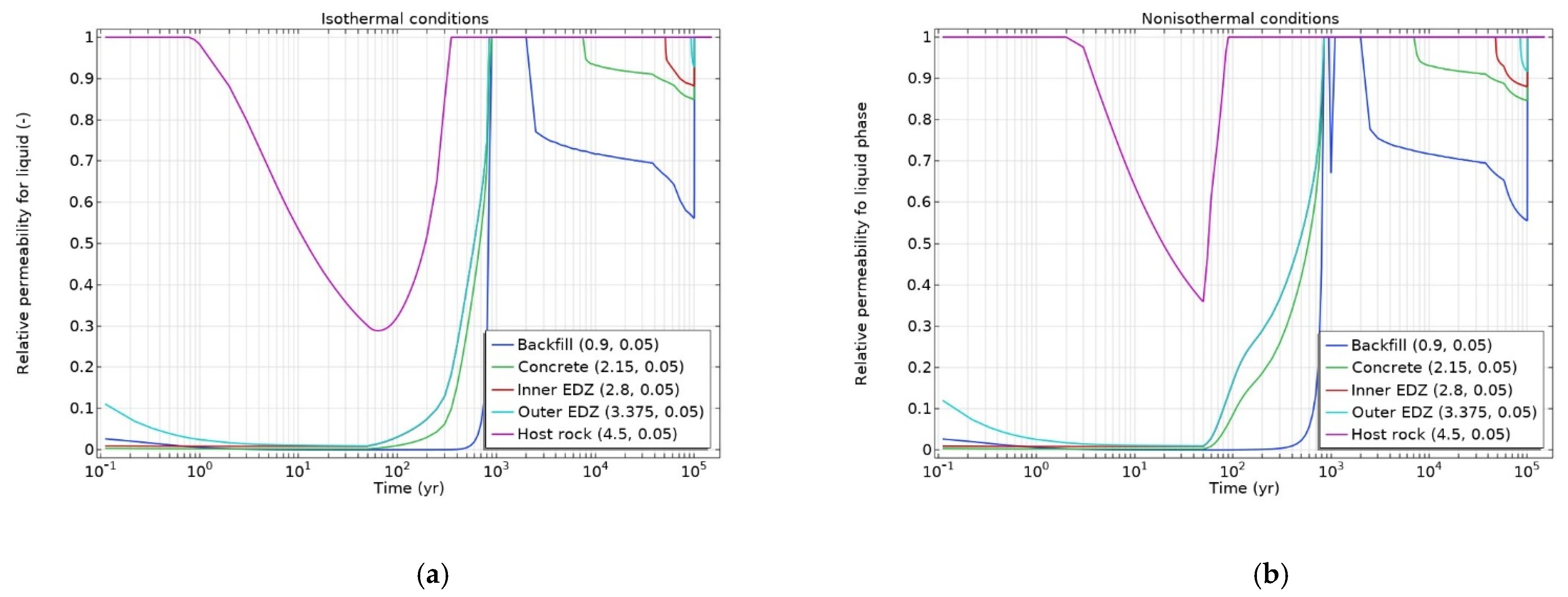
3.1. Isothermal Conditions
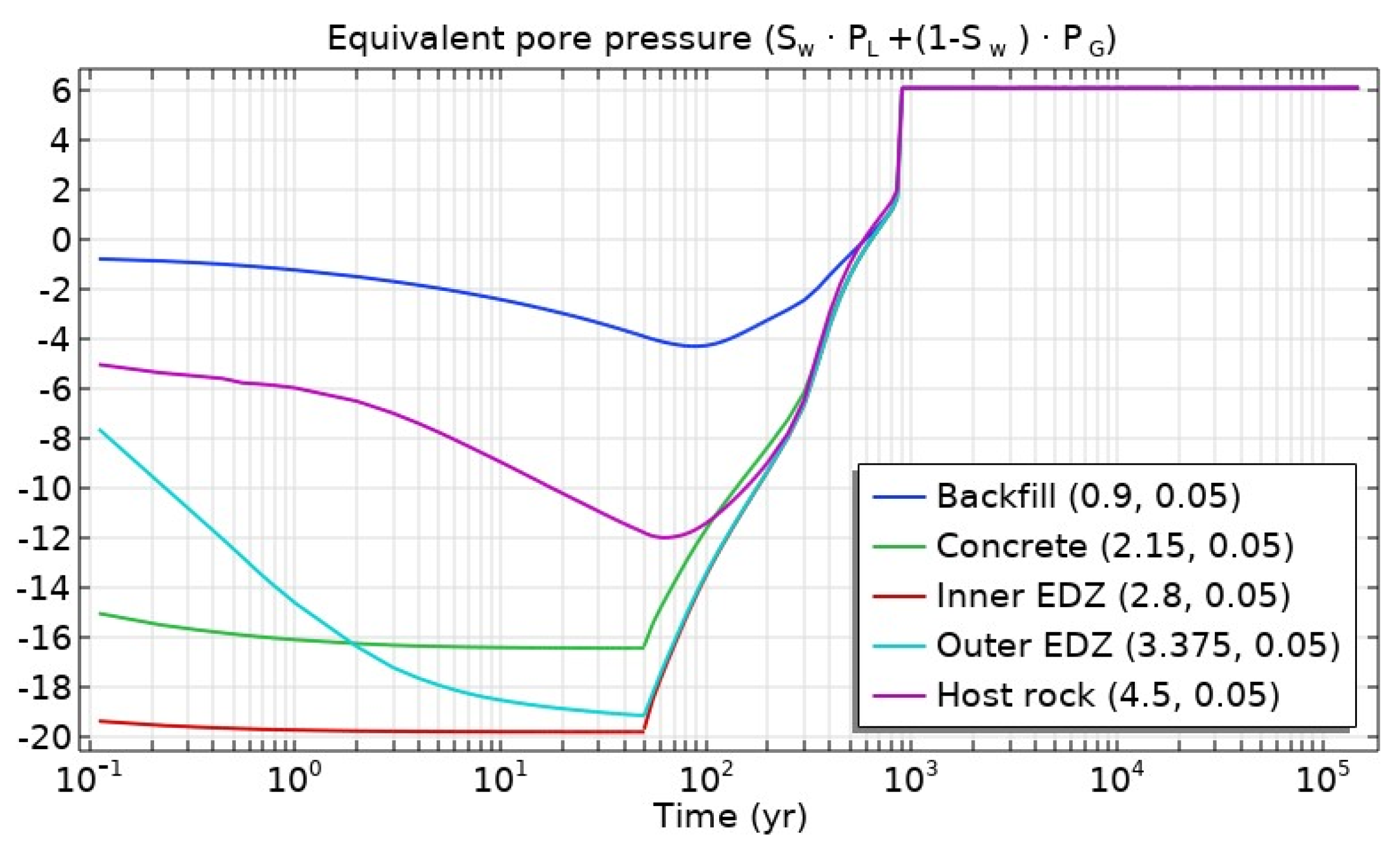
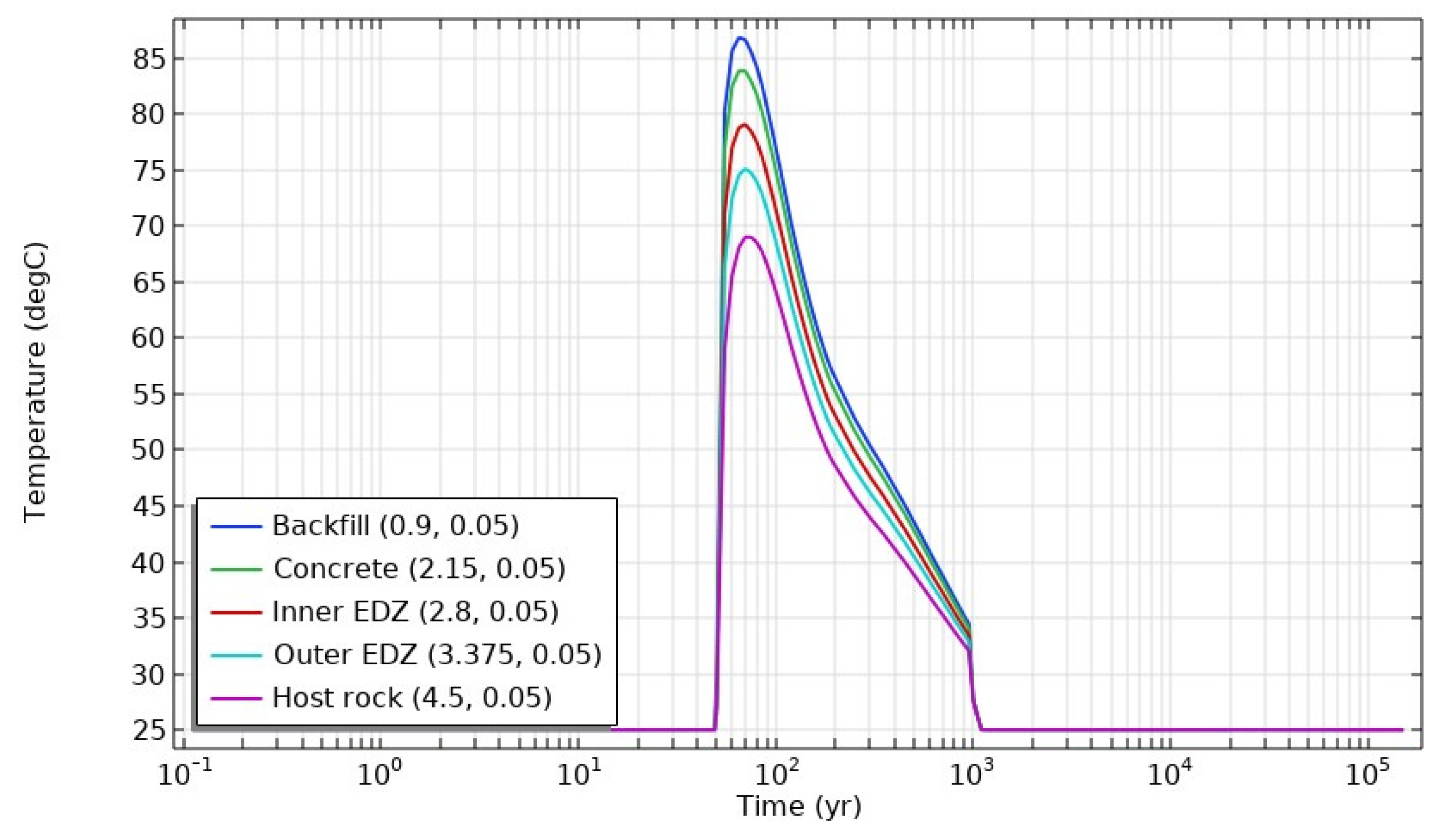
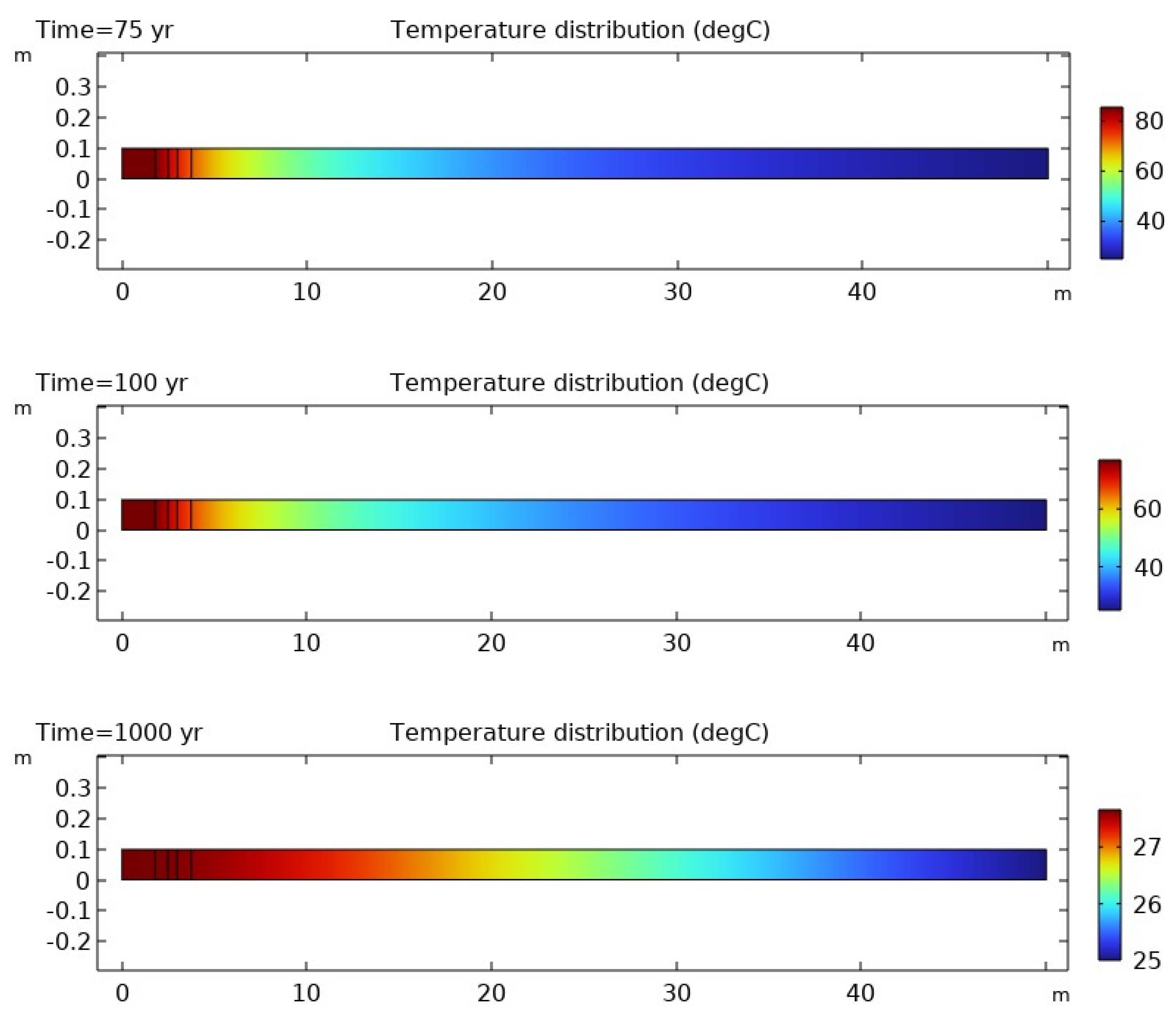
3.2. Non-Isothermal Conditions
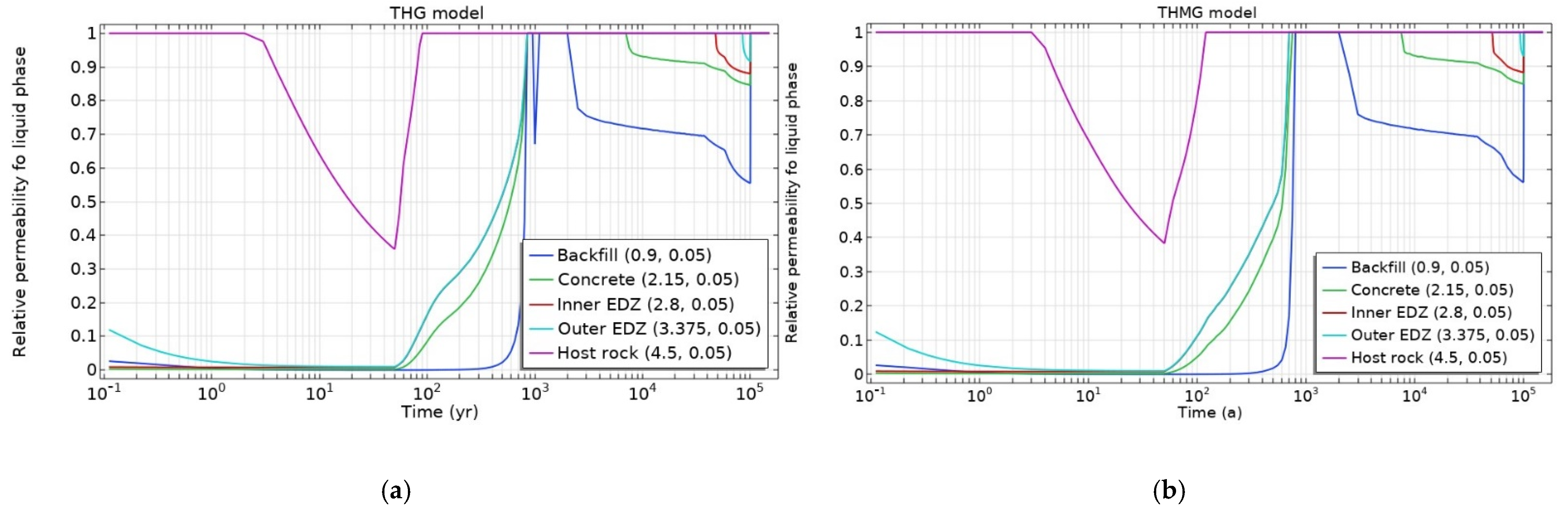
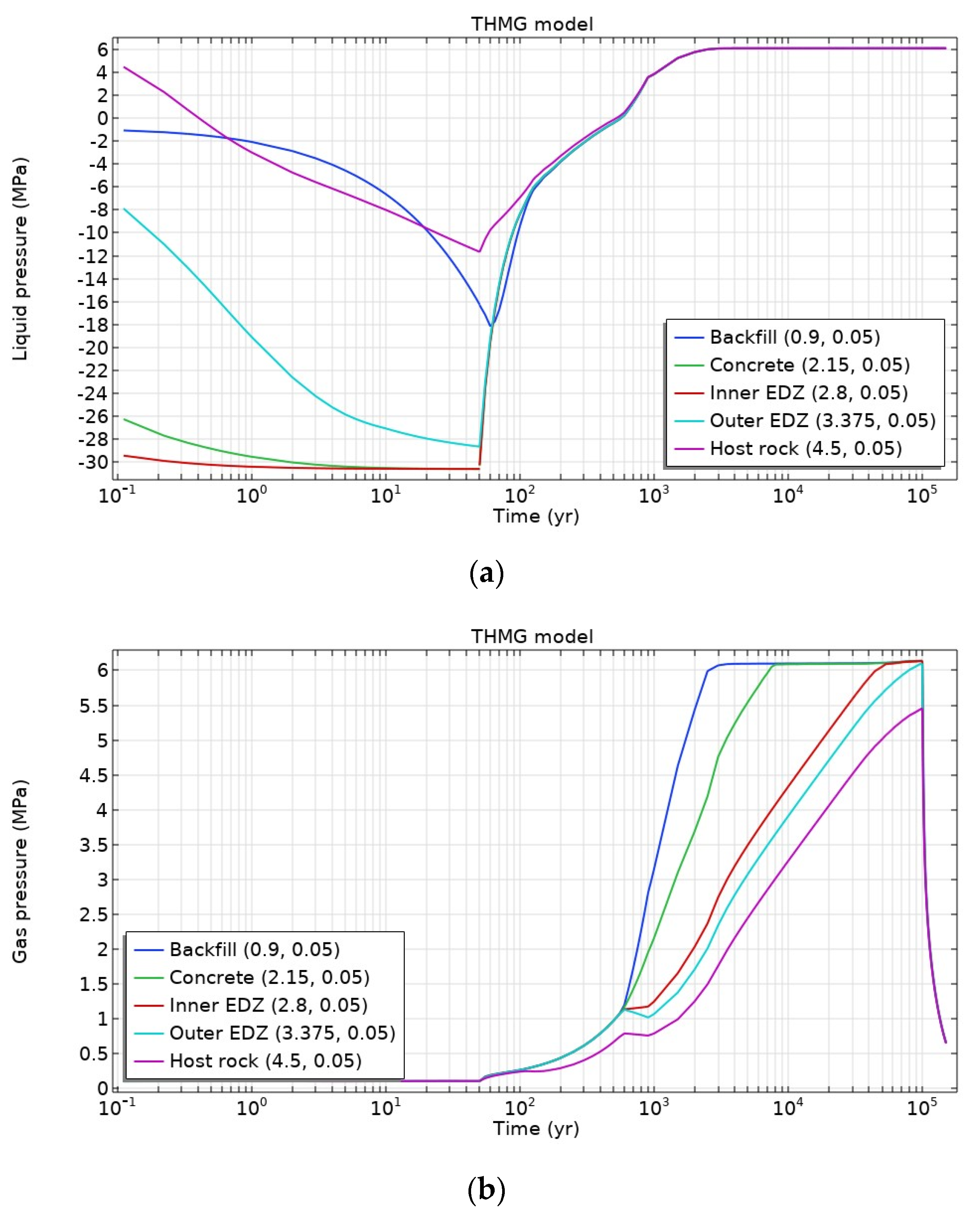
3.3. Impact of Mechanical Deformations
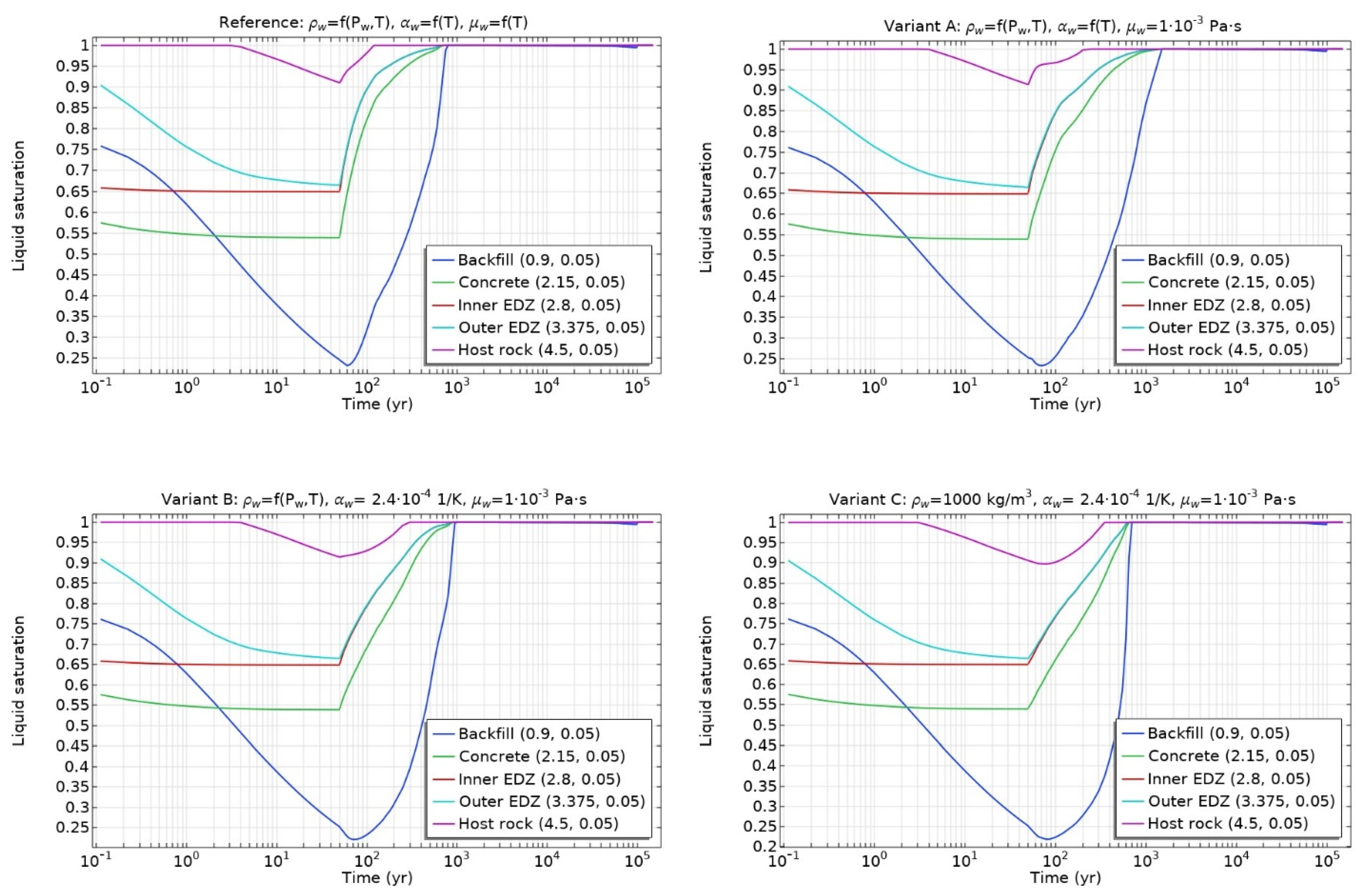
3.4. Impact of Water Thermal Properties
- Reference (THMG model): ρw = f(Pw,T), αw = f(T) μw = f(T)
- Variant A: ρw = f(Pw,T), αw = f(T), μw = 1 × 10−3 Pa∙s
- Variant B: ρw = f(Pw,T), αw = 2.4 × 10−4 1/K, μw = 1 × 10−3 Pa∙s
- Variant C: ρw = 1000 kg/m3, αw = 2.4 × 10−4 1/K, μw = 1 × 10−3 Pa∙s
3.5. Impact on Radionuclide Transport
4. Conclusions
- Desaturation of the excavation disturbed zone (EDZ) and the host rock to some extent was observed due to potential ventilation of 50 years.
- Despite the hydrogen gas generation, all materials became water-resaturated with groundwater coming from the host rock before ~1500 years in all cases.
- Continuing hydrogen gas generation in the deposition tunnel led to the second desaturation of the engineered barriers and the EDZ close to the gas generation place vanishing soon after the end of gas generation, while the host rock remained saturated during the gas generation phase (50–100,000 years).
- Under the analyzed conditions, the gas transport in the engineered barriers and parts of the host rock (EDZ) would be governed by a capillary-controlled two-phase flow, while in the major part of the host rock, the gas transport would be governed by diffusion in the dissolved form.
- Simulated gas and liquid pressure would lead to equivalent pore pressure of ~6 MPa magnitude, and materials under isotropic total compressive stress of 15 MPa would remain in compressive effective stress state, and thus gas-induced fractures would not be expected and the barrier integrity would not be affected. Therefore, a preferential flow pathway for gas and radionuclide transport would not be developed and barrier transport properties would not be affected.
- Hydrogen gas generation does not lead to liquid saturation less than 0.994, and thus the impact on radionuclide diffusivity would not be significant.
- For the soluble nuclide I-129 transport from the generic repository under the analyzed conditions (start of release after hydrogen gas generation), there would be no impact of corrosion-induced gas on radionuclide migration.
- For any other geometric dimensions, gas generation rates and its time evolution, other boundary conditions and/or material properties, THMG analysis needs to be re-run for the conclusion on the impact on repository barrier integrity and radionuclide transport properties.
- The modelling results will serve for further investigation of gas transport and its impact on repository barrier integrity under elevated temperature conditions considering additional gas sources in other repository structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Nuclear Association. How Can Nuclear Combat Climate Change? Available online: https://world-nuclear.org/nuclear-essentials/how-can-nuclear-combat-climate-change.aspx (accessed on 20 October 2023).
- World Nuclear Association. Storage and Disposal of Radioactive Waste. Available online: https://world-nuclear.org/information-library/nuclear-fuel-cycle/nuclear-waste/storage-and-disposal-of-radioactive-waste.aspx (accessed on 20 October 2023).
- Council Directive 2011/70/Euratom of 19 July 2011 Establishing a Community Framework for the Responsible and Safe Management of Spent Fuel and Radioactive Waste. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex%3A32011L0070 (accessed on 20 October 2023).
- Jacops, E.; Yu, L.; Chen, G.; Levasseur, S. Gas Transport in Boom Clay: The Role of the HADES URL in Process Understanding; Geological Society, London, Special Publications: London, UK, 2023; Volume 536, pp. 75–92. [Google Scholar] [CrossRef]
- Yang, J.; Fall, M.; Guo, G. A Three-Dimensional Hydro-mechanical Model for Simulation of Dilatancy Controlled Gas Flow in Anisotropic Claystone. Rock Mech. Rock Eng. 2020, 53, 4091–4116. [Google Scholar] [CrossRef]
- Levasseur, S.; Collin, F.; Daniels, K.; Dymitrowska, M.; Harrington, J.; Jacops, E.; Kolditz, O.; Marschall, P.; Norris, S.; Sillen, X.; et al. Initial State of the Art on Gas Transport in Clayey Materials. Deliverable D6.1 of the HORIZON 2020 project EURAD, Work Package Gas. 2021. EC Grant agreement no: 847593. Available online: https://www.ejp-eurad.eu/publications/eurad-d61-initial-state-art-gas-transport-clayey-materials (accessed on 20 October 2023).
- Marschall, P.; Horseman, S.; Gimmi, T. Characterisation of gas transport properties of the Opalinus clay, a potential host rock formation for radioactive waste disposal. Oil Gas Sci. Technol. 2005, 60, 121–139. [Google Scholar] [CrossRef]
- Liaudat, J.; Dieudonne, A.-C.; Vardon, P.J. Modelling gas fracturing in saturated clay samples using triple-node zero-thickness interface elements. Comput. Geotech. 2023, 154, 105128. [Google Scholar] [CrossRef]
- Vu, M.N.; Armand, G.; Plua, C. Thermal Pressurization Coefficient of Anisotropic Elastic Porous Media. Rock Mech. Rock Eng. 2020, 53, 2027–2031. [Google Scholar] [CrossRef]
- Guo, R.; Thatcher, K.; Seyedi, D.; Plúa, C. Calibration of the thermo-hydro-mechanical parameters of the Callovo-Oxfordian claystone and the modelling of the ALC experiment. Int. J. Rock Mech. Min. Sci. 2020, 132, 104351. [Google Scholar] [CrossRef]
- ANDRA. Task 4 Technical Note Defining a Generic Repository Configuration, Sets of Parameters, Conditions and Relevant Indicators. EURAD WP GAS Milestone 61, 2021. (to be released, will be available online: https://www.ejp-eurad.eu/publications).
- Subsurface Flow Module. User’s Guide. Comsol Multiphysics. 2021. Available online: https://doc.comsol.com/6.0/doc/com.comsol.help.ssf/SubsurfaceFlowModuleUsersGuide.pdf (accessed on 20 October 2023).
- Navarro, V.; Asensio, L.; Gharbieh, H.; De la Morena, G.; Pulkkanen, V. Development of a multiphysics numerical solver for modeling the behavior of clay-based engineered barriers. Nucl. Eng. Technol. 2019, 51, 1047–1059. [Google Scholar] [CrossRef]
- Pollock, D.W. Simulation of fluid flow and energy transport processes associated with high-level radioactive waste disposal in unsaturated alluvium. Water Resour. Res. 1986, 22, 765–775. [Google Scholar] [CrossRef]
- Rutqvist, J.; Borgesson, L.; Chijimatsu, M.; Kobayashi, A.; Jing, L.; Nguyen, T.S.; Noorishad, J.; Tsang, C.-F. Thermohydromechanics of partially saturated geological media: Governing equations and formulation of four finite element models. Int. J. Rock Mech. Min. Sci. 2001, 38, 105–127. [Google Scholar] [CrossRef]
- Amri, A.; Saâdi, Z.; Ababou, R. Parametric Sensitivity to Capillary Entry Pressure in Two-Phase Water–Gas Flow Models: Deep Geologic Disposal of Radioactive Waste. Transp. Porous Media 2022, 145, 13–43. [Google Scholar] [CrossRef]








| Time from Waste Emplacement (Years) | Heat Flux (W/m2) | Time from Emplacement (Years) | Heat Flux (W/m2) |
|---|---|---|---|
| 0 | 2.65 × 101 | 140 | 9.11 |
| 5 | 2.46 × 101 | 150 | 8.93 |
| 10 | 2.29 × 101 | 160 | 8.66 |
| 15 | 2.13 × 101 | 170 | 8.48 |
| 20 | 2.00 × 101 | 180 | 8.29 |
| 25 | 1.87 × 101 | 190 | 8.12 |
| 30 | 1.78 × 101 | 200 | 7.93 |
| 40 | 1.59 × 101 | 210 | 7.82 |
| 50 | 1.45 × 101 | 220 | 7.69 |
| 60 | 1.34 × 101 | 230 | 7.51 |
| 70 | 1.24 × 101 | 330 | 6.42 |
| 80 | 1.17 × 101 | 430 | 5.50 |
| 90 | 1.11 × 101 | 530 | 4.72 |
| 100 | 1.05 × 101 | 630 | 4.06 |
| 110 | 1.01 × 101 | 730 | 3.50 |
| 120 | 9.73 | 830 | 3.02 |
| 130 | 9.37 | 930 | 2.61 |
| Material | Coordinates (R, Z) | Notes |
|---|---|---|
| Backfill | (0.9 m, 0.05m) | Middle point |
| Concrete | (2.15 m, 0.05 m) | Middle point |
| Inner EDZ | (2.8 m, 0.05 m) | Middle point |
| Outer EDZ | (3.375 m, 0.05 m) | Middle point |
| Host rock | (4.5 m, 0.05 m) | 2 m from tunnel wall |
| Properties | Backfill | Concrete | Inner EDZ | Outer EDZ | Rock |
|---|---|---|---|---|---|
| Porosity | 0.4 | 0.15 | 0.2 | 0.2 | 0.2 |
| Thermal properties | |||||
| Thermal conductivity λs (W/m/K) | 1.3 | 2.3 | 1.7 | 1.7 | 1.7 |
| Solid specific heat Cp,s (J/kg/K) | 500 | 900 | 720 | 720 | 720 |
| Thermal expansions of solids βTg (1/°C) | 2 × 10−5 | 2 × 10−5 | 4 × 10−5 | 4 × 10−5 | 4 × 10−5 |
| Hydraulic properties | |||||
| Intrinsic permeability kL (m2) | 1 × 10−16 | 1 × 10−16 | 1 × 10−16 | 1 × 10−18 | 1 × 10−20 |
| Intrinsic permeability kG (m2) | 1 × 10−16 | 1 × 10−16 | 1 × 10-16 | 1 × 10−17 | 1 × 10−18 |
| van Genuchten parameter n | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
| van Genuchten Pr (MPa) | 1 | 10 | 16 | 16 | 16 |
| Gas entry pressure Pe (MPa) | 0 | 0 | 0 | 2 | 6 |
| Residual water saturation Slr (-) | 0 | 0 | 0 | 0 | 0 |
| Dissolved H2 parameters a and b for Millington–Quirk (-) | a = 1 b = 15 | a = 2 b = 4 | a = 1.5 b = 10 | a = 1.5 b = 10 | a = 1.5 b = 10 |
| Gaseous H2 parameters a and b for Millington–Quirk (-) | a = 3 b = 3 | a = 0 b = 5 | a = 2.5 b = 2.5 | a = 2.5 b = 2.5 | a = 2.5 b = 2.5 |
| Dissolved I-129 parameters a and b for Millington–Quirk (-) | a = 1 b = 20 | a = 2 b = 4 | a = 2.5 b = 15 | a = 2.5 b = 15 | a = 2.5 b = 15 |
| Gaseous I-129 parameters a and b for Millington–Quirk (-) | No gas phase for I-129 | ||||
| Dissolved H2 D0 (m2/s) | 5 × 10−9 | ||||
| Gaseous H2 D0 (m2/s) | 9 × 10−5 | ||||
| Dissolved 129I D0 (m2/s) | 2 × 10−9 | ||||
| Henry’s coefficient for H2 (1/Pa) | 1.4 × 10−10 | ||||
| Mechanical properties | |||||
| Isotropic Young’s modulus E (MPa) | 40,000 * | 40,000 | 500 | 5000 | 5000 |
| Poisson’s ratio ν | 0.25 | 0.25 | 0.3 | 0.3 | 0.3 |
| Properties | Expression | Units | |
|---|---|---|---|
| Density of water ρw | 998.2 × exp(5 × 10−7 (PL − 100) − αw∙(T − 12)) | PL in kPa, T in °C | |
| Volumetric thermal expansion coefficient αw∙10−4 (1/°C) | 4 × 10−6 × T3 − 0.001 × T2 + 0.1404 × T − 0.3795 | T in °C | |
| Kinematic viscosity η (m2/s) (dynamic viscosity μw = ρw∙η) | 1.384 × 10−3 × (T + 50)(−C1) C1(T) = 1.7 − 0.0156 × (0.01 × T)1.8 | T in °C | |
| Specific heat of water Cp,w (J/kg/K) | 4190 × (1 + 0.0025 × (0.01 × T))4.6) | T in °C | |
| Density of saturated vapor ρv0 (kg/m3) | exp(0.06374 × T − 0.1634 × 10−3 × T2)/194.4 | T in °C | |
| Diffusivity of vapor Dv (m2/s) | 5.9 × 10−6 × T2.3/PG | T in K | |
| Dynamic viscosity of vapor μv (Pa∙s) | 273.15–373.15 K | 3 × 10−8 × T + 9 × 10−6 | T in °C |
| 373.15–473.15 K | 4 × 10−8 × T + 8 × 10−6 | T in °C | |
| Specific enthalpy of vapor at T0 hv0 (J/kg) | 2.45 × 10−6 | ||
| Specific heat of vapor Cp,v (J/kg/K) | 0–50 °C | C1 + C2 × T + C3 × T2 + (p − ptr)/(C4 + C5 × T + C6 × T2) | C1 = 1877.2, C2 = −0.49545, C3 = 8.1818 × 10−3, C4 = 22.537, C5 = 0.49321, C6 = 0.048927, ptr = 611.657 Pa, T in °C |
| Above 50 °C | C7 + C8 × T + C9 × T2 + (p − ptr)/(C4 + C5 × T + C6 × T2) | C7 = 1856.1, C8 = 0.28056, C9 = 6.9444 × 10−4, C4 = 22.537, C5 = 0.49321, C6 = 0.048927, T in °C | |
| Specific heat of H2 (J/(g∙K)) | 14.304 | ||
| Dynamic viscosity of H2 gas μH2 (Pa·s) | 1 × 10−5 | ||
| Dynamic viscosity of gas mixture (H2 and vapor) μG (Pa·s) | , —mass fraction of vapor and H2 gas | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narkuniene, A.; Poskas, G.; Bartkus, G. Modelling of the Corrosion-Induced Gas Impact on Hydraulic and Radionuclide Transport Properties of Geological Repository Barriers. Minerals 2024, 14, 4. https://doi.org/10.3390/min14010004
Narkuniene A, Poskas G, Bartkus G. Modelling of the Corrosion-Induced Gas Impact on Hydraulic and Radionuclide Transport Properties of Geological Repository Barriers. Minerals. 2024; 14(1):4. https://doi.org/10.3390/min14010004
Chicago/Turabian StyleNarkuniene, Asta, Gintautas Poskas, and Gytis Bartkus. 2024. "Modelling of the Corrosion-Induced Gas Impact on Hydraulic and Radionuclide Transport Properties of Geological Repository Barriers" Minerals 14, no. 1: 4. https://doi.org/10.3390/min14010004
APA StyleNarkuniene, A., Poskas, G., & Bartkus, G. (2024). Modelling of the Corrosion-Induced Gas Impact on Hydraulic and Radionuclide Transport Properties of Geological Repository Barriers. Minerals, 14(1), 4. https://doi.org/10.3390/min14010004








