A Review of Mineral Prospectivity Mapping Using Deep Learning
Abstract
:1. Introduction
2. Data Foundation
2.1. Data Types
- (1)
- Accuracy of data. The accuracy of data directly affects the credibility of data analysis and decision-making. If there are errors or biases in the data, it may lead to incorrect decision-making and analysis results.
- (2)
- Integrity of data. Collecting more complete data can lead to more accurate mineral deposit prediction, such as specific information about known mineral deposits.
- (3)
- Accuracy of data. In geological work, geological mapping, geophysical prospecting, geochemical prospecting, and remote sensing are all carried out at a certain scale. In practical work, the higher the precision and resolution, the more beneficial it is for predicting results.
- (4)
- The timeliness of data. As the times change and people’s perceptions evolve, some data may become outdated, so we need to regularly filter the data we collect.
2.2. Geological Database
2.2.1. Strata and Magmatic Rocks
2.2.2. Geological Structure
- Metallogenic magma and fluid often migrate along geological weak surfaces (fault plane, fold plane, shear zone, etc.);
- The structural plane (fault plane, fold plane, shear zone, etc.) is the main channel of heat source and the main place where heat exchange occurs;
- The repeated sliding of faults drives rapid changes in fluid pressure, velocity, and stress. When the induced fluid channel growth destroys the dynamic balance of the fluid system, the resulting rapid fluid depressor becomes the key driving factor for metal precipitation and mineralization [47];
- Metallogenic material precipitation often occurs in the weak structural plane and near the contact zone between the weak plane and the surrounding rock.
2.3. Geophysical Data
2.4. Geochemical Data
2.5. Remote Sensing Image Data
3. Deep Learning Technology
3.1. Deep Autoencoder
3.2. Generative Adversarial Network
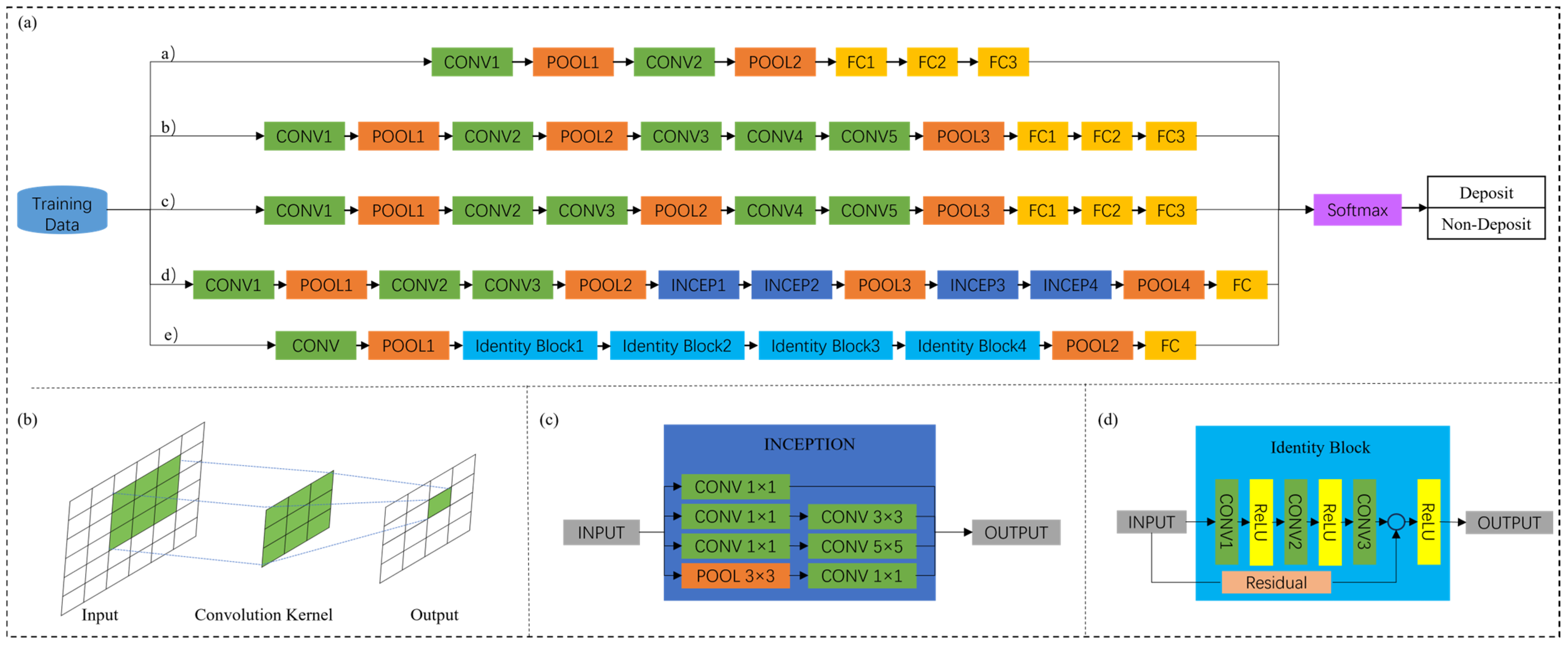
3.3. Convolutional Neural Network
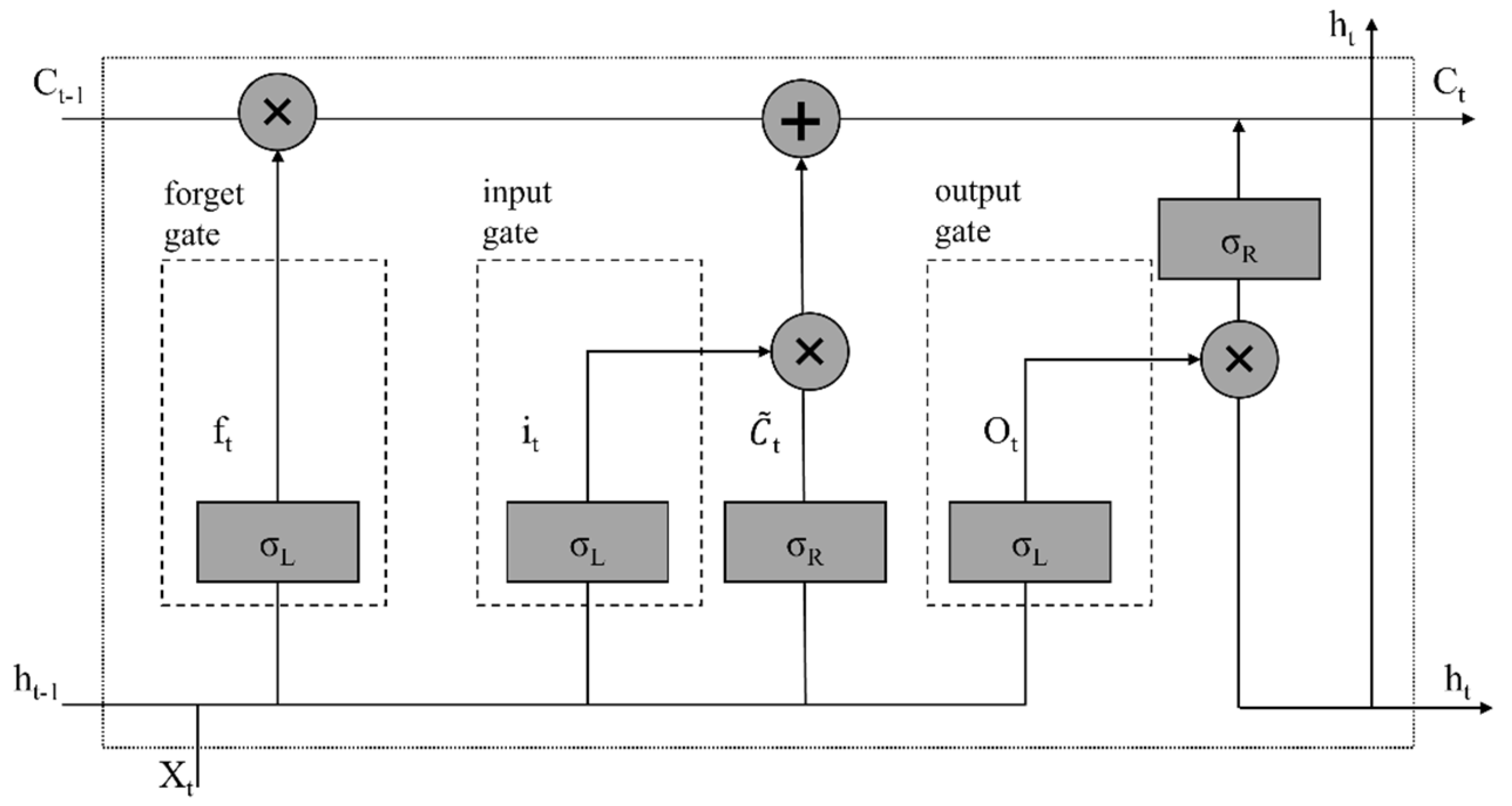
3.4. Recurrent Neural Network
4. Application of Deep Learning in Mineral Prospectivity Mapping
4.1. Application of DAE
4.2. Application of CNN
4.3. Application of RNN
4.4. Application of GAN
4.5. Application of Mixed Algorithm
5. Discussion
5.1. Preprocessing of Geological Data
5.2. Improvement of Data Enhancement Method in Mineral Prospectivity Mapping
5.3. Deep Learning in Mineral Prospectivity Mapping
- (1)
- The support for the algorithm by textual geological data. Deep learning algorithms need to convert some text information into numerical information for computation. In the application of geological information, the data can only be displayed, but a lot of geological information will be discarded. For example, when applying fault data, the distance between different positions and faults will be reflected, but different types of faults will not be reflected, which is unreasonable in geological understanding. Natural language processing (NLP) is a branch of computer science and artificial intelligence that studies how computers understand, generate, and translate human language. RNNs can process sequence data and are particularly effective for natural language processing tasks, so the application of RNNs in geological data can be increased in future research.
- (2)
- The research on geological data enhancement methods. Data enhancement can enrich data, but the large-scale use of data enhancement methods will increase the complexity of training, sometimes resulting in some categories being “over-enhanced”, and others being ignored, resulting in an imbalance between categories. Nowadays, many scholars try to use the combination of transfer learning and deep learning for rock and ore analysis and mineral prospecting prediction [108,129,130,131]. The robustness and generalization ability of transfer learning are proved, the convergence speed of deep learning is accelerated, and the learning efficiency of the prospecting prediction model is enhanced. So, we believe that the use of transfer learning and the adversarial generation network in the future will greatly improve the reliability and logic of enhanced data, which will greatly improve the accuracy of prospecting prediction.
- (3)
- Avoidance and treatment of model overfitting. Overfitting often occurs when testing with a small number of training sets, and will greatly affect the test results and the performance of the model. The most direct way to improve the performance of neural networks is to increase the number of parameters such as depth and network, but this will make it easier for the updated network to reach the overfitting state, especially when the number of positive samples, such as in prospecting prediction, is limited. At present, in other fields, the methods to solve the overfitting of deep learning models mainly include data preprocessing, simplifying the model structure, adding regularization terms, adding Dropout layers, and adjusting model parameters. In mineral prospectivity mapping, the application of Dropout layers has achieved good results. Krizhevsky et al. [101] solve the overfitting problem by increasing the number and size of layers while using the method of Dropout. Li et al. [117] believe that increasing the number of layers and parameters will increase the computational amount of learning, and adding Dropout can reduce the training time during the training process with a large amount of data. Moreover, from the application point of view [90], after using Dropout, the hidden neurons no longer depend on the existence of other hidden neurons, and the co-adaptability with other neurons decreases, which has a good effect on solving the overfitting problem. In the next research process, the diversity of data can be increased in the data preprocessing process, and the learning rate, batch size, and other parameters in the model can be adjusted in time.
- (4)
- Adjustment of parameters of the model. In some research examples, we can see that researchers often need to constantly try to modify various parameters, such as the learning rate, the epoch, the batch size, and so on, according to the size of data or the quality of data to obtain better prediction results. This is because the deep learning model needs to optimize the performance of the model by adjusting parameters during the training process, so that it can better fit the training data and generalize to the unseen data. Therefore, we may need to continue to strengthen the self-adaptive research of the model, so that the model can automatically adjust parameters according to the original data and the target.
- (5)
- The choice of backbone architecture and the effectiveness of different deep learning algorithms. Convolutional neural network is the most widely used deep learning algorithm in mineral prospectivity mapping at present, including LeNet, AlexNet, VggNet, GoogleNet, ResNet, U-Net and other structural types. The most common methods of recurrent neural networks include Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU). We need to choose the backbone architecture and deep learning algorithms according to the actual situation.
- (6)
- The explanation of the model “black box” mechanism. The “black box” mechanism of deep learning cannot know about the drivers of underlying phenomena and processes [125], so the interpretability of model outputs, the relationship between data input and output, and the internal operation mechanism need further study. At present, the Google DeepMind team is exploring the “black box” mechanism in deep learning from the perspective of cognitive psychology [132], but there is still a long way to go. To enhance the explainability of deep learning, Fu et al. [27] used the SHAP library in Python to explain the individual output results of deep learning. The results showed that the different types of data selected for distinguishing between the presence and absence of minerals in the study area are of significantly different importance. Many scholars have found that the predictive results of deep learning are not as good as those of SVM or random forest algorithms in some cases, and a major reason for this is the type of data used [4,22].
5.4. Accuracy Evaluation Method in Mineral Prospectivity Mapping
- (1)
- Type and accuracy of data. The correlation between the data and the ore deposit and the number of data types affects the prediction accuracy. Yang et al. [9] selected three kinds of geological data and eight kinds of geochemical prospecting factors, for a total of 11 predictive variables, to predict gold deposits in Fengxian County in China by the CNN, and the training accuracy was 1.00. Liu et al. [33] only selected Pb in the geochemical element to predict lead–zinc ore deposits in Anhui, China, and a training accuracy of 0.93 was obtained. The accuracy of the data affects the prediction accuracy all the same. Li et al. [117] selected 1:200,000 geochemical data to use for mineral prospectivity mapping in the southwestern Fujian Province, China, and the accuracy was 0.95. Using 1:50,000 stream sediment geochemical survey data, Fu et al. [27] predicted the deposit with an accuracy of 0.993. The study of Zuo [58] shows that the size of different scales has a slight influence on metallogenic prediction.
- (2)
- The number and distribution of known deposits. It is clear that the number of known mineral sites in the study area determines the prediction results. More importantly, due to the spatial heterogeneity of the deposit itself, the spatial distribution characteristics of known deposits also affect the prediction results. Therefore, collecting more comprehensive ore deposits in the study area will be helpful for prospecting prediction.
- (3)
- Types of algorithms. The metallogenic systems and processes under different regional frameworks are discrepant, so we should select the data type according to the characteristics of the study area to be used for metallogenic prediction, then select targeted deep learning algorithms according to different data characteristics. Luo et al. [120] efficiently extracted anomalies from geochemical data using the GAN, and the corresponding AUC was 0.893. Wang et al. [96] used a Long Short-Term Memory network to extract and integrate the deep-level geological prospecting information among the weighted evidence layers, and almost all known iron ore deposits developed in delineated high prospective areas. We believe that the selection of deep learning algorithms should rely on the comprehensive consideration of data types and regional characteristics.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, S. Multi-Geoinformation Integration for Mineral Prospectivity Mapping in the Hezuo-Meiwu District, Gansu Province. Ph.D. Thesis, China University of Geoscience, Beijing, China, 2022. [Google Scholar]
- Zhao, P. Quantitative mineral prediction and deep mineral. Earth Sci. Front. 2007, 14, 001–010. [Google Scholar]
- Xiao, K.; Ding, J.; Liu, R. The Discussion of Three-part Form of Non-fuel Mineral Resource Assessment. Geol. Rev. 2006, 52, 793–798. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, Z.; Yang, J.; Hong, Z. Mineral Prospectivity Prediction by Integration of Convolutional Autoencoder Network and Random Forest. Nat. Resour. Res. 2022, 31, 1103–1119. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Data-driven predictive mapping of gold prospectivity, Baguio district, Philippines: Application of Random Forests algorithm. Ore Geol. Rev. 2015, 71, 777–787. [Google Scholar] [CrossRef]
- Carranza, E.J.M. Geocomputation of mineral exploration targets. Comput. Geosci. 2011, 37, 1907–1916. [Google Scholar] [CrossRef]
- Porwal, A.; Carranza, E.J.M. Introduction to the Special Issue: GIS-based mineral potential modelling and geological data analyses for mineral exploration. Ore Geol. Rev. 2015, 71, 477–483. [Google Scholar] [CrossRef]
- Zhang, D. Spatially Weighted Technology for Logistic Regression and Its Application in Mineral Prospective Mapping. Ph.D. Thesis, China University of Geoscience, Wuhan, China, 2015. [Google Scholar]
- Yang, N.; Zhang, Z.; Yang, J.; Hong, Z. Applications of data augmentation in mineral prospectivity prediction based on convolutional neural networks. Comput. Geosci. 2022, 161, 105075. [Google Scholar] [CrossRef]
- Singer, D.A. Basic concepts in three-part quantitative assessments of undiscovered mineral resources. Nonrenew. Resour. 1993, 2, 69–81. [Google Scholar] [CrossRef]
- Zhao, P.; Hu, J.; Li, Z. The theory and practices of statistical prediction for mineral deposits. Earth Sci.- J. Wuhan Coll. Geol. 1983, 4, 107–121. [Google Scholar]
- Cheng, Q. Ideas and methods for mineral resources integrated prediction in covered areas. Earth Sci.- J. Wuhan Coll. Geol. 2012, 37, 1109–1125. [Google Scholar]
- Agterberg, F.P.; Cheng, Q. Conditional Independence Test for Weights-of-Evidence Modeling. Nat. Resour. Res. 2002, 11, 249–255. [Google Scholar] [CrossRef]
- Cheng, Q. BoostWofE: A New Sequential Weights of Evidence Model Reducing the Effect of Conditional Dependency. Math. Geosci. 2015, 47, 591–621. [Google Scholar] [CrossRef]
- Chen, S. Research of Multiple Geoscience Information Prospecting Prediction in Xikuangshan Antimony Ore Field. Ph.D. Thesis, China University of Geoscience, Beijing, China, 2012. [Google Scholar]
- Li, X.; Yuan, F.; Zhang, M.; Jia, C.; Jowitt, S.; Ord, A.; Zheng, T.; Hu, X.; Li, Y. Three-dimensional mineral prospectivity modeling for targeting of concealed mineralization within the Zhonggu iron orefield, Ningwu Basin, China. Ore Geol. Rev. 2015, 71, 633–654. [Google Scholar] [CrossRef]
- Porwal, A.; González-Álvarez, I.; Markwitz, V.; McCuaig, T.C.; Mamuse, A. Weights-of-evidence and logistic regression modeling of magmatic nickel sulfide prospectivity in the Yilgarn Craton, Western Australia. Ore Geol. Rev. 2010, 38, 184–196. [Google Scholar] [CrossRef]
- Zuo, R.; Carranza, E.J.M. Support vector machine: A tool for mapping mineral prospectivity. Comput. Geosci. 2011, 37, 1967–1975. [Google Scholar] [CrossRef]
- Shabankareh, M.; Hezarkhani, A. Application of support vector machines for copper potential mapping in Kerman region, Iran. J. Afr. Earth Sci. 2017, 128, 116–126. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, W. Application of one-class support vector machine to quickly identify multivariate anomalies from geochemical exploration data. Geochem. Explor. Environ. Anal. 2017, 17, 231–238. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, W. Mapping mineral prospectivity by using one-class support vector machine to identify multivariate geological anomalies from digital geological survey data. Aust. J. Earth Sci. 2017, 64, 639–651. [Google Scholar] [CrossRef]
- Sun, T.; Chen, F.; Zhong, L.; Liu, W.; Wang, Y. GIS-based mineral prospectivity mapping using machine learning methods: A case study from Tongling ore district, eastern China. Ore Geol. Rev. 2019, 109, 26–49. [Google Scholar] [CrossRef]
- Carranza, E.J.M.; Laborte, A.G. Random forest predictive modeling of mineral prospectivity with small number of prospects and data with missing values in Abra (Philippines). Comput. Geosci. 2015, 74, 60–70. [Google Scholar] [CrossRef]
- Wang, Z.; Zuo, R.; Dong, Y. Mapping geochemical anomalies through integrating random forest and metric learning methods. Nat. Resour. Res. 2019, 28, 1285–1298. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, Z.; Xiong, Y.; Zuo, R. Mapping mineral prospectivity for Cu polymetallic mineralization in southwest Fujian Province, China. Ore Geol. Rev. 2016, 75, 16–28. [Google Scholar] [CrossRef]
- Zhang, F.M.A. Research on Deep Learning Extraction Method in Open Mining Area Based on Multi-Source Remote Sensing Images; Anhui University: Hefei, China, 2020. [Google Scholar]
- Fu, Y.; Cheng, Q.; Jing, L.; Ye, B.; Fu, H. Mineral Prospectivity Mapping of Porphyry Copper Deposits Based on Remote Sensing Imagery and Geochemical Data in the Duolong Ore District, Tibet. Remote Sens. 2023, 15, 439. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, Q.; Luo, J. Deeply mining the intrinsic value of geodata to improve the accuracy of predicting by quantitatively optimizing method for prospecting target areas. Earth Sci. Front. 2022, 29, 403–411. [Google Scholar] [CrossRef]
- Zhang, C.; Zuo, R. Recognition of multivariate geochemical anomalies associated with mineralization using an improved generative adversarial network. Ore Geol. Rev. 2021, 136, 104264. [Google Scholar] [CrossRef]
- Xiong, Y.; Zuo, R. Recognition of geochemical anomalies using a deep autoencoder network. Comput. Geosci. 2016, 86, 75–82. [Google Scholar] [CrossRef]
- Zuo, R.; Xiong, Y. Big Data Analytics of Identifying Geochemical Anomalies Supported by Machine Learning Methods. Nat. Resour. Res. 2018, 27, 5–13. [Google Scholar] [CrossRef]
- Shi, L.; Jianping, C.; Jie, X. Prospecting Information Extraction by Text Mining Based on Convolutional Neural Networks–A Case Study of the Lala Copper Deposit, China. IEEE Access 2018, 6, 52286–52297. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, L.; Zhou, Y. Application of Convolutional Neural Network in prospecting prediction of ore deposits: Taking the Zhaojikou Pb-Zn ore deposit in Anhui Province as a case. Acta Petrol. Sin. 2018, 34, 3217–3224. [Google Scholar]
- Liu, Y. Experimental research on big data mining and intelligent prediction of prospecting target area—Application of convolutional neural network model. Geotecton. Metallog. 2020, 44, 192–202. [Google Scholar]
- Zheng, X.; Zhang, M.; Ren, W. Application of convolution neural networks in gold exploration and prediction in Shandong Province. Geophys. Geochem. Explor. 2023, 47, 1433–1440. [Google Scholar]
- Li, Q.; Chen, G.; Luo, L. Mineral prospectivity mapping using attention-based convolutional neural network. Ore Geol. Rev. 2023, 156, 105381. [Google Scholar] [CrossRef]
- Li, Y.-S.; Chai, S.-L. Soil geochemical prospecting prediction method based on deep convolutional neural networks-Taking Daqiao Gold Deposit in Gansu Province, China as an example. China Geol. 2022, 5, 71–83. [Google Scholar]
- Du, Y.; Cao, Y.; Huo, D.; Li, D.; Gao, Z. Petrology and geochemistry of Silurian-Triassic sedimentary rocks in the Tongling area; Constraints on the genesis of stratabound skarn deposits. Earth Sci. Front. 2014, 21, 228–239. [Google Scholar]
- Ling, Q.; LIU, C. REE behavior during formation of st ra ta-bound skarn and related deposit: A case study of Dongguashan ska rn deposit in Anh ui province, China. Acta Petrol. Sin. 2003, 19, 192–200. [Google Scholar]
- Deng, Y.; Song, X.; Jie, W.; Yuan, F.; Zhao, Z.; Wei, S.; Zhu, J.; Kang, J.; Wang, K.; Liang, Q.; et al. Determination of sedimentary ages of strata in the Huangshan-Jingerquan mineralization belt and its geological significance. Acta Geol. Sin. 2021, 95, 362–376. [Google Scholar] [CrossRef]
- Xue, S.; Wang, Q.; Tang, D.; Mao, Y.; Yao, Z. Contamination mechanism of magmatic Ni-Cu sulfide deposits in orogenic belts: Examples from Permian Ni-Cu deposits in Tianshan-Beishan. Miner. Depos. 2022, 41, 1–20. [Google Scholar]
- Grobler, D.F.; Brits, J.A.N.; Maier, W.D.; Crossingham, A. Litho- and chemostratigraphy of the Flatreef PGE deposit, northern Bushveld Complex. Miner. Depos. 2019, 54, 3–28. [Google Scholar] [CrossRef]
- Li, L.-J.; Li, D.-X.; Mao, X.-C.; Liu, Z.-K.; Lai, J.-Q.; Su, Z.; Ai, Q.-X.; Wang, Y.-Q. Evolution of magmatic sulfide of the giant Jinchuan Ni-Cu deposit, NW China: Insights from chalcophile elements in base metal sulfide minerals. Ore Geol. Rev. 2023, 158, 105497. [Google Scholar] [CrossRef]
- Mukasa, S.B.; Vidal, C.C.E.; Injoque-Espinoza, J. Lead isotope-bearing on the metallogenesis of sulfide ore deposits in central and southern Peru. Econ. Geol. 1990, 85, 1438–1446. [Google Scholar] [CrossRef]
- Elongo, V.; Lecumberri-Sanchez, P.; Legros, H.; Falck, H.; Adlakha, E.E.; Roy-Garand, A. Paragenetic constraints on the Cantung, Mactung and Lened tungsten skarn deposits, Canada: Implications for grade distribution. Ore Geol. Rev. 2020, 125, 103677. [Google Scholar] [CrossRef]
- Ord, A.; Hobbs, B.E.; Lester, D.R. The mechanics of hydrothermal systems: I. Ore systems as chemical reactors. Ore Geol. Rev. 2012, 49, 1–44. [Google Scholar] [CrossRef]
- Yang, L.; Yang, W.; Zhang, L.; Gao, X.; Shen, S.; Wang, S.; Xu, H.; Jia, X.; Deng, J. Developing structural control models for hydrothermal metallogenic systems: Theoretical and methodological principles and applications. Earth Sci. Front. 2024, 31, 239–266. [Google Scholar]
- Liu, Z. Ore-controlling structure of Withnell gold deposit, Pilbara Craton, Australia. J. Geol. 2021, 45, 154–160. [Google Scholar] [CrossRef]
- Song, M.; Wang, B.; Song, Y.; Li, J.; Zheng, J.; Li, S.; Fan, J.; Yang, Z.; He, C.; Gao, M.; et al. Spatial coupling relationship between faults and gold deposits in the Jiaodong ore concentration area and the effect of thermal doming-extension on mineralisation. Ore Geol. Rev. 2023, 153, 105277. [Google Scholar] [CrossRef]
- Lv, Q.; Dong, S.; Tang, J.; Shi, D.; Chang, Y. Multi-scale and integrated geophysical data revealing mineral systems and exploring for mineral deposits at depth: A synthesis from SinoProbe-03. Chin. J. Geophys. 2015, 58, 4319–4343. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Q.; Luo, Y. An overview on the development of the electrical prospecting method in China. Acta Geophys. Sin. 1994, 37, 408–424. [Google Scholar]
- Wu, Y.; Liu, B.; Gao, Y.; Li, C.; Tang, R.; Kong, Y.; Xie, M.; Li, K.; Dan, S.; Qi, K.; et al. Mineral prospecting mapping with conditional generative adversarial network augmented data. Ore Geol. Rev. 2023, 163, 105787. [Google Scholar] [CrossRef]
- Shebl, A.; Abdellatif, M.; Elkhateeb, S.O.; Csámer, Á. Multisource Data Analysis for Gold Potentiality Mapping of Atalla Area and Its Environs, Central Eastern Desert, Egypt. Minerals 2021, 11, 641. [Google Scholar] [CrossRef]
- Shebl, A.; Abdellatif, M.; Hissen, M.; Ibrahim Abdelaziz, M.; Csámer, Á. Lithological mapping enhancement by integrating Sentinel 2 and gamma-ray data utilizing support vector machine: A case study from Egypt. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102619. [Google Scholar] [CrossRef]
- Spicer, B. Geophysical signature of the Victoria property, vectoring toward deep mineralization in the Sudbury Basin. Interpret. A J. Subsurf. Charact. 2016, 4, T281–T290. [Google Scholar] [CrossRef]
- Wang, R.; Hao, X.; Hu, L.; Chen, H.; Liu, H.; Chen, F.; Yu, L.; Liu, W.; Fang, L.; Kang, Y. Discovery of skarn iron-rich deposit based on gravity and magnetic data in the Qihe-Yucheng, Shandong Province: Enlightenment to prospecting of the superdeep coverage area. Geol. China 2023, 50, 331–346. [Google Scholar]
- Wang, S. The new development of theory and method of synthetic information mineral resources prognosis. Geol. Bull. China 2010, 29, 1399–1403. [Google Scholar]
- Zuo, R. Exploring the effects of cell size in geochemical mapping. J. Geochem. Explor. 2012, 112, 357–367. [Google Scholar] [CrossRef]
- Luo, X.; Yang, X. Study and prospecting prediction of hidden deposits by geoelectrochemical survey. Geol. Explor. 1989, 54, 43–51. [Google Scholar]
- Liu, Y.; Luo, X.; Liu, P.; Zheng, C.; Liu, G.; Song, B.; Song, G. Application of geo-electrochemical integration technology to search for concealed Pb-Zn ore in the Geluqiduishan mining area and its periphery, Inner Mongolia. Geol. Explor. 2018, 54, 1001–1012. [Google Scholar] [CrossRef]
- Yue, D.; Liu, P.; Liao, X.; Chen, J.; Li, J.; Yang, Q.; Yang, X. Research and application of AMT and geo-electrochemical measurements in deep prospecting of the Murong lithium deposit in Yajiang, western Sichuan Province. Geol. Explor. 2023, 59, 760–773. [Google Scholar]
- Yang, Q.; Luo, X.; Yue, D.; Liu, P.; Gao, W.; Wen, M.; Liao, X.; Li, J.; Liang, M.; Liu, Y. Intelligent prospecting method based on probabilistic neural network: Taking the Murong lithium deposit in Yajiang County of Sichuan Province as an example. Geol. Explor. 2023, 59, 985–999. [Google Scholar]
- Henry, C.D.; John, D.A.; Leonardson, R.W.; McIntosh, W.C.; Heizler, M.T.; Colgan, J.P.; Watts, K.E. Timing of Rhyolite Intrusion and Carlin-Type Gold Mineralization at the Cortez Hills Carlin-Type Deposit, Nevada, USA. Econ. Geol. 2023, 118, 57–91. [Google Scholar] [CrossRef]
- Yang, B.; Li, C.; Bo, H.; Hou, X.; Su, P.; Fan, S. Geochemical characteristics and genesis of Changhangou crystalline graphite deposit in Hadamengou area, Inner Mongolia. Miner. Depos. 2023, 42, 444–462. [Google Scholar] [CrossRef]
- Min, X.; Pengbo, Q.; Fengwei, Z. Research and application of logging lithology identification for igneous reservoirs based on deep learning. J. Appl. Geophys. 2020, 173, 103929. [Google Scholar] [CrossRef]
- Liu, J.-J.; Liu, J.-C. Integrating deep learning and logging data analytics for lithofacies classification and 3D modeling of tight sandstone reservoirs. Geosci. Front. 2022, 13, 101311. [Google Scholar] [CrossRef]
- Shirmard, H.; Farahbakhsh, E.; Beiranvand Pour, A.; Muslim, A.M.; Müller, R.D.; Chandra, R. Integration of Selective Dimensionality Reduction Techniques for Mineral Exploration Using ASTER Satellite Data. Remote Sens. 2020, 12, 1261. [Google Scholar] [CrossRef]
- Zidan, U.; Desouky, H.A.E.; Gaber, M.M.; Abdelsamea, M.M. From Pixels to Deposits: Porphyry Mineralization With Multispectral Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 9474–9486. [Google Scholar] [CrossRef]
- Hunt, G.R.; Ashley, R.P. Spectra of altered rocks in the visible and near infrared. Econ. Geol. 1979, 74, 1613–1629. [Google Scholar] [CrossRef]
- Shirmard, H.; Farahbakhsh, E.; Müller, R.D.; Chandra, R. A review of machine learning in processing remote sensing data for mineral exploration. Remote Sens. Environ. 2022, 268, 112750. [Google Scholar] [CrossRef]
- Shebl, A.; Abdellatif, M.; Badawi, M.; Dawoud, M.; Fahil, A.S.; Csámer, Á. Towards better delineation of hydrothermal alterations via multi-sensor remote sensing and airborne geophysical data. Sci. Rep. 2023, 13, 7406. [Google Scholar] [CrossRef]
- Haynes, D. The Olympic Dam ore deposit discovery—A personal view. SEG Newsl. 2006, 66, 1–15. [Google Scholar] [CrossRef]
- Guo, J.; Zhu, G.; Zou, L.; Wang, R.; Han, Y.; Wang, W.; Xiang, A. Remote sensing geological survey of bauxite deposits in Dazhuyuan-Longxing area of north Guizhou. Miner. Resour. Geol. 2016, 30, 117–121. [Google Scholar]
- Xiao, L. Lithologic and mineral information extraction for bauxite deposits exploration using ASTER data in the Wuchuan-Zheng’an-Daozhen area, northern Guizhou province, China. J. Mines Met. Fuels 2018, 66, 280–286. [Google Scholar]
- van Gerven, M.; Bohte, S. Editorial: Artificial Neural Networks as Models of Neural Information Processing. Front. Comput. Neurosci. 2017, 11, 114. [Google Scholar] [CrossRef] [PubMed]
- Jiao, L.; Yang, S.; Liu, F.; Wang, S.; Feng, Z. Seventy years beyond neural networks: Retrospect and prospect. Chin. J. Comput. 2016, 39, 1697–1716. [Google Scholar]
- Majumdar, A. Graph structured autoencoder. Neural Netw. 2018, 106, 271–280. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Dep. Comput. Sci. Univ. Tor. 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Xie, M.; Liu, B.; Wang, L.; Li, C.; Kong, Y.; Tang, R. Auto encoder generative adversarial networks—Based mineral prospectivity mapping in Lhasa area, Tibet. J. Geochem. Explor. 2023, 255, 107326. [Google Scholar] [CrossRef]
- Zhang, S.; Xiao, K.; Carranza, E.J.M.; Yang, F.; Zhao, Z. Integration of auto-encoder network with density-based spatial clustering for geochemical anomaly detection for mineral exploration. Comput. Geosci. 2019, 130, 43–56. [Google Scholar] [CrossRef]
- Vincent Dumoulin, I.B.; Poole, B.; Lamb, A.; Arjovsky, M.; Mastropietro, O.; Courville, A. Adversarially Learned Inference. arXiv 2016, arXiv:1606.00704. [Google Scholar]
- Chen, Y.; Wang, Y.; Kirschen, D.; Zhang, B. Model-Free Renewable Scenario Generation Using Generative Adversarial Networks. IEEE Trans. Power Syst. 2018, 33, 3265–3275. [Google Scholar] [CrossRef]
- Farahbakhsh, E.; Maughan, J.; Müller, R.D. Prospectivity modelling of critical mineral deposits using a generative adversarial network with oversampling and positive-unlabelled bagging. Ore Geol. Rev. 2023, 162, 105665. [Google Scholar] [CrossRef]
- Anders Boesen Lindbo, L.; Søren Kaae, S.; Larochelle, H.; Winther, O. Autoencoding beyond pixels using a learned similarity metric. In Proceedings of the International Conference on Machine Learning, New York City, New York, USA, 19–24 June 2016; pp. 1558–1566. [Google Scholar]
- Liu, W.; Liang, X.; Qu, H. Learning performance of convolutional neural networks with different pooling models. J. Image Graph. 2016, 21, 1178–1190. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, Z.; Yang, J.; Hong, Z.; Shi, J. A Convolutional Neural Network of GoogLeNet Applied in Mineral Prospectivity Prediction Based on Multi-source Geoinformation. Nat. Resour. Res. 2021, 30, 3905–3923. [Google Scholar] [CrossRef]
- Li, Z.; Xue, L.; Ran, X.; Li, Y.; Dong, G.; Li, Y.; Dai, J. Intelligent prospect prediction method based on convolutional neural network: A case study of copper deposits in Longshoushan Area, Gansu Province. J. Jilin Univ. (Earth Sci. Ed.) 2022, 52, 418–433. [Google Scholar]
- Sankar, M.; Batri, K.; Parvathi, R. Earliest diabetic retinopathy classification using deep convolution neural networks. Int. J. Adv. Eng. Technol. 2016, 10, M9. [Google Scholar]
- Li, J.; Yuan, Z.; Li, Z.; Ren, A.; Ding, C.; Draper, J.; Nazarian, S.; Qiu, Q.; Yuan, B.; Wang, Y. Normalization and dropout for stochastic computing-based deep convolutional neural networks. Integration 2019, 65, 395–403. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, J. Deep convolutional neural network model based chemical process fault diagnosis. Comput. Chem. Eng. 2018, 115, 185–197. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Wang, Z.; Zuo, R. Mineral prospectivity mapping using a joint singularity-based weighting method and long short-term memory network. Comput. Geosci. 2022, 158, 104974. [Google Scholar] [CrossRef]
- Yin, B.; Zuo, R.; Xiong, Y. Mineral Prospectivity Mapping via Gated Recurrent Unit Model. Nat. Resour. Res. 2022, 31, 2065–2079. [Google Scholar] [CrossRef]
- Huijie Zhao, K.D.; Li, N.; Wang, Z.; Wei, W. Hierarchical Spatial-Spectral Feature Extraction with Long Short Term Memory (LSTM) for Mineral Identification Using Hyperspectral Imagery. Sensors 2020, 20, 6854. [Google Scholar] [CrossRef]
- Wang, Z.; Li, T.; Zuo, R. Leucogranite mapping via convolutional recurrent neural networks and geochemical survey data in the Himalayan orogen. Geosci. Front. 2024, 15, 181–192. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z.; Xie, Z.; Cai, H.; Niu, P.; Liu, H. Mineral prospectivity mapping by deep learning method in Yawan-Daqiao area, Gansu. Ore Geol. Rev. 2021, 138, 104316. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Li, S.; Chen, J.; Xiang, J. Applications of deep convolutional neural networks in prospecting prediction based on two-dimensional geological big data. Neural Comput. Appl. 2020, 32, 2037–2053. [Google Scholar] [CrossRef]
- Li, S.; Chen, J.; Xiang, J.; Zhang, Z.; Zhang, Y. Two-dimensional prospecting prediction based on AlexNet network: A case study of sedimentary Mn deposits in Songtao-Huayuan area. Geol. Bull. China 2019, 38, 2022–2032. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; Volume 7, pp. 1–9. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Gao, L.; Huang, Y.; Zhang, X.; Liu, Q.; Chen, Z. Prediction of Prospecting Target Based on ResNet Convolutional Neural Network. Appl. Sci. 2022, 12, 11433. [Google Scholar] [CrossRef]
- Boiger, R.; Churakov, S.V.; Ballester Llagaria, I.; Kosakowski, G.; Wüst, R.; Prasianakis, N.I. Direct mineral content prediction from drill core images via transfer learning. Swiss J. Geosci. 2024, 117, 8. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. pp. 234–241. [Google Scholar]
- Liu, C.; Wang, W.; Tang, J.; Wang, Q.; Zheng, K.; Sun, Y.; Zhang, J.; Gan, F.; Cao, B. A deep-learning-based mineral prospectivity modeling framework and workflow in prediction of porphyry–epithermal mineralization in the Duolong ore District, Tibet. Ore Geol. Rev. 2023, 157, 105419. [Google Scholar] [CrossRef]
- Mou, N.; Carranza, E.J.; Wang, G.; Sun, X. A Framework for Data-Driven Mineral Prospectivity Mapping with Interpretable Machine Learning and Modulated Predictive Modeling. Nat. Resour. Res. 2023, 32, 2439–2462. [Google Scholar] [CrossRef]
- Wang, D.; Huang, F.; Wang, Y.; He, H.; Li, X.; Liu, X.; Sheng, J.; Liang, T. Regional metallogeny of Tungsten-tin-polymetallic deposits in Nanling region, South China. Ore Geol. Rev. 2020, 120, 103305. [Google Scholar] [CrossRef]
- Jordão, H.; Azevedo, L.; Sousa, A.J.; Soares, A. Generative adversarial network applied to ore type modeling in complex geological environments. Math. Geosci. 2022, 54, 1165–1182. [Google Scholar] [CrossRef]
- Li, T.; Zuo, R.; Zhao, X.; Zhao, K. Mapping prospectivity for regolith-hosted REE deposits via convolutional neural network with generative adversarial network augmented data. Ore Geol. Rev. 2022, 142, 104693. [Google Scholar] [CrossRef]
- Guo, M.; Chen, Y. A SMOTified-GAN-augmented bagging ensemble model of extreme learning machines for detecting geochemical anomalies associated with mineralization. Geochemistry 2024, 126156. [Google Scholar] [CrossRef]
- Zhang, S.; Carranza, E.J.M.; Wei, H.; Xiao, K.; Yang, F.; Xiang, J.; Zhang, S.; Xu, Y. Data-driven mineral prospectivity mapping by joint application of unsupervised convolutional auto-encoder network and supervised convolutional neural network. Nat. Resour. Res. 2021, 30, 1011–1031. [Google Scholar] [CrossRef]
- Li, T.; Zuo, R.; Xiong, Y.; Peng, Y. Random-Drop Data Augmentation of Deep Convolutional Neural Network for Mineral Prospectivity Mapping. Nat. Resour. Res. 2020, 30, 27–38. [Google Scholar] [CrossRef]
- Li, S.; Chen, J.; Liu, C.; Wang, Y. Mineral Prospectivity Prediction via Convolutional Neural Networks Based on Geological Big Data. J. Earth Sci. 2021, 32, 327–347. [Google Scholar] [CrossRef]
- Chen, L.; Guan, Q.; Feng, B.; Yue, H.; Wang, J.; Zhang, F. A multi-convolutional autoencoder approach to multivariate geochemical anomaly recognition. Minerals 2019, 9, 270. [Google Scholar] [CrossRef]
- Luo, Z.; Zuo, R.; Xiong, Y.; Wang, X. Detection of geochemical anomalies related to mineralization using the GANomaly network. Appl. Geochem. 2021, 131, 105043. [Google Scholar] [CrossRef]
- Xiong, Y.; Zuo, R.; Carranza, E.J.M. Mapping mineral prospectivity through big data analytics and a deep learning algorithm. Ore Geol. Rev. 2018, 102, 811–817. [Google Scholar] [CrossRef]
- Xiong, Y.; Zuo, R. GIS-based rare events logistic regression for mineral prospectivity mapping. Comput. Geosci. 2018, 111, 18–25. [Google Scholar] [CrossRef]
- Atalay, F. Estimation of Fe Grade at an Ore Deposit Using Extreme Gradient Boosting Trees (XGBoost). Min. Metall. Explor. 2024, 41, 2119–2128. [Google Scholar] [CrossRef]
- Filzmoser, P.; Garrett, R.G.; Reimann, C. Multivariate outlier detection in exploration geochemistry. Comput. Geosci. 2005, 31, 579–587. [Google Scholar] [CrossRef]
- Hronsky, J.M.A.; Kreuzer, O.P. Applying spatial prospectivity mapping to exploration targeting: Fundamental practical issues and suggested solutions for the future. Ore Geol. Rev. 2019, 107, 647–653. [Google Scholar] [CrossRef]
- Zhang, C.; Zuo, R.; Xiong, Y. Detection of the multivariate geochemical anomalies associated with mineralization using a deep convolutional neural network and a pixel-pair feature method. Appl. Geochem. 2021, 130, 104994. [Google Scholar] [CrossRef]
- Brandmeier, M.; Cabrera Zamora, I.G.; Nykänen, V.; Middleton, M. Boosting for Mineral Prospectivity Modeling: A New GIS Toolbox. Nat. Resour. Res. 2019, 29, 71–88. [Google Scholar] [CrossRef]
- Chen, L.; Guan, Q.; Xiong, Y.; Liang, J.; Wang, Y.; Xu, Y. A Spatially Constrained Multi-Autoencoder approach for multivariate geochemical anomaly recognition. Comput. Geosci. 2019, 125, 43–54. [Google Scholar] [CrossRef]
- Li, S.; Liu, C.; Chen, J. Mineral Prospecting Prediction via Transfer Learning Based on Geological Big Data: A Case Study of Huayuan, Hunan, China. Minerals 2023, 13, 504. [Google Scholar] [CrossRef]
- Mantilla-Dulcey, A.; Goyes-Peñafiel, P.; Baez-Rodríguez, R.; Khurama, S. Porphyry-type mineral prospectivity mapping with imbalanced data via prior geological transfer learning. Gondwana Res. 2024, 136, 236–250. [Google Scholar] [CrossRef]
- Wu, B.; Li, X.; Yuan, F.; Li, H.; Zhang, M. Transfer learning and siamese neural network based identification of geochemical anomalies for mineral exploration: A case study from the CuAu deposit in the NW Junggar area of northern Xinjiang Province, China. J. Geochem. Explor. 2022, 232, 106904. [Google Scholar] [CrossRef]
- Ritter, S.; Barrett, D.G.T.; Santoro, A.; Botvinick, M.M. Cognitive psychology for deep neural networks: A shape bias case study. Int. Conf. Mach. Learn. 2017, 2940–2949. [Google Scholar]
- Yousefi, M.; Carranza, E. Prediction–area (P–A) plot and C–A fractal analysis to classify and evaluate evidential maps for mineral prospectivity modeling. Comput. Geosci. 2015, 79, 69–81. [Google Scholar] [CrossRef]
- Roshanravan, B.; Aghajani, H.; Yousefi, M.; Kreuzer, O. An Improved Prediction-Area Plot for Prospectivity Analysis of Mineral Deposits. Nat. Resour. Res. 2019, 28, 1089–1105. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Sanchez-Castillo, M.; Chica-Olmo, M.; Chica-Rivas, M. Machine learning predictive models for mineral prospectivity: An evaluation of neural networks, random forest, regression trees and support vector machines. Ore Geol. Rev. 2015, 71, 804–818. [Google Scholar] [CrossRef]
- Nathwani, C.L.; Wilkinson, J.J.; Brownscombe, W.; John, C.M. Mineral Texture Classification Using Deep Convolutional Neural Networks: An Application to Zircons From Porphyry Copper Deposits. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025933. [Google Scholar] [CrossRef]
- Zuo, R.; Cheng, Q.; Agterberg, F.P. Application of a hybrid method combining multilevel fuzzy comprehensive evaluation with asymmetric fuzzy relation analysis to mapping prospectivity. Ore Geol. Rev. 2009, 35, 101–108. [Google Scholar] [CrossRef]
- Zuo, R.; Zhang, Z.; Zhang, D.; Carranza, E.J.M.; Wang, H. Evaluation of uncertainty in mineral prospectivity mapping due to missing evidence: A case study with skarn-type Fe deposits in Southwestern Fujian Province, China. Ore Geol. Rev. 2015, 71, 502–515. [Google Scholar] [CrossRef]
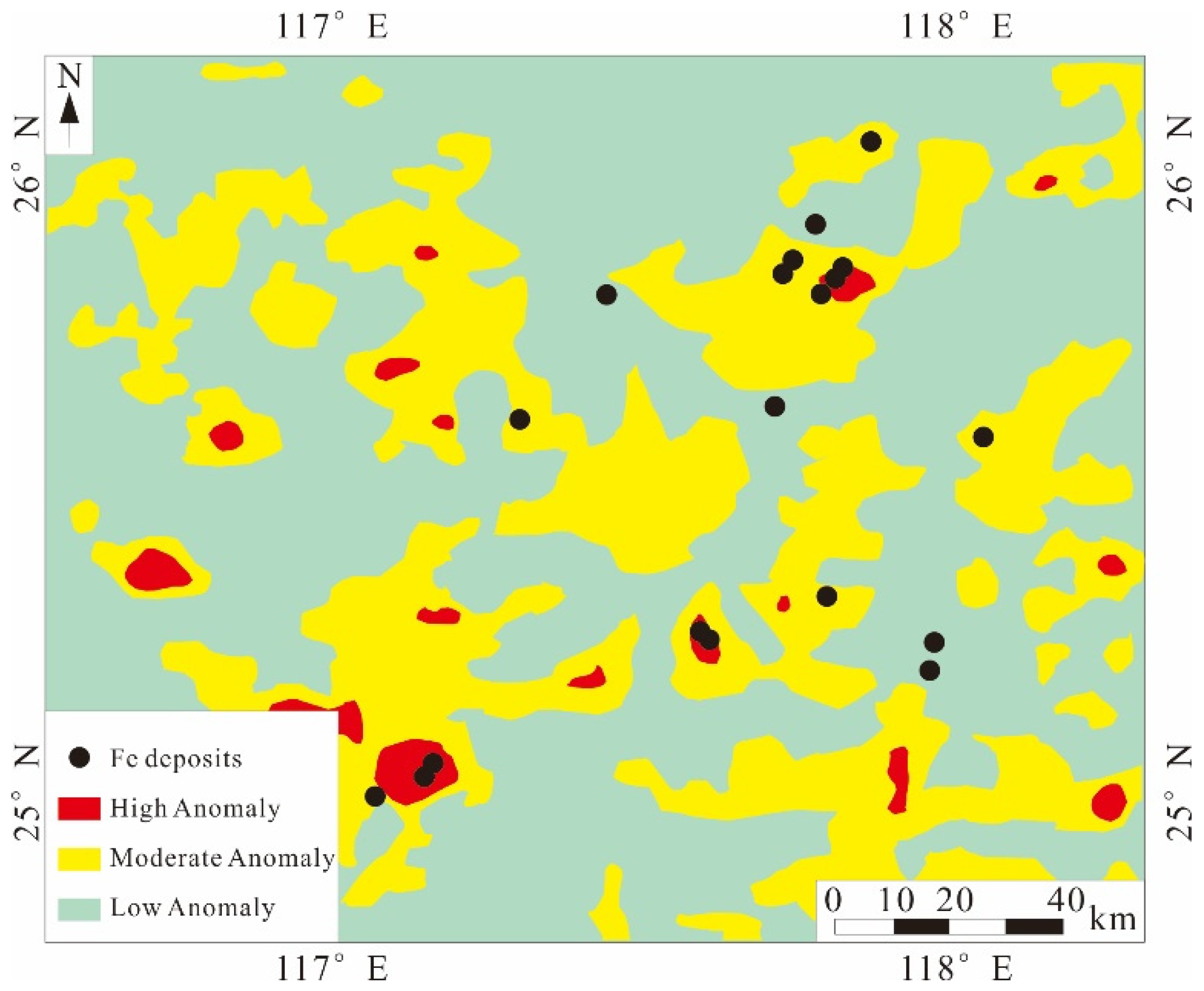
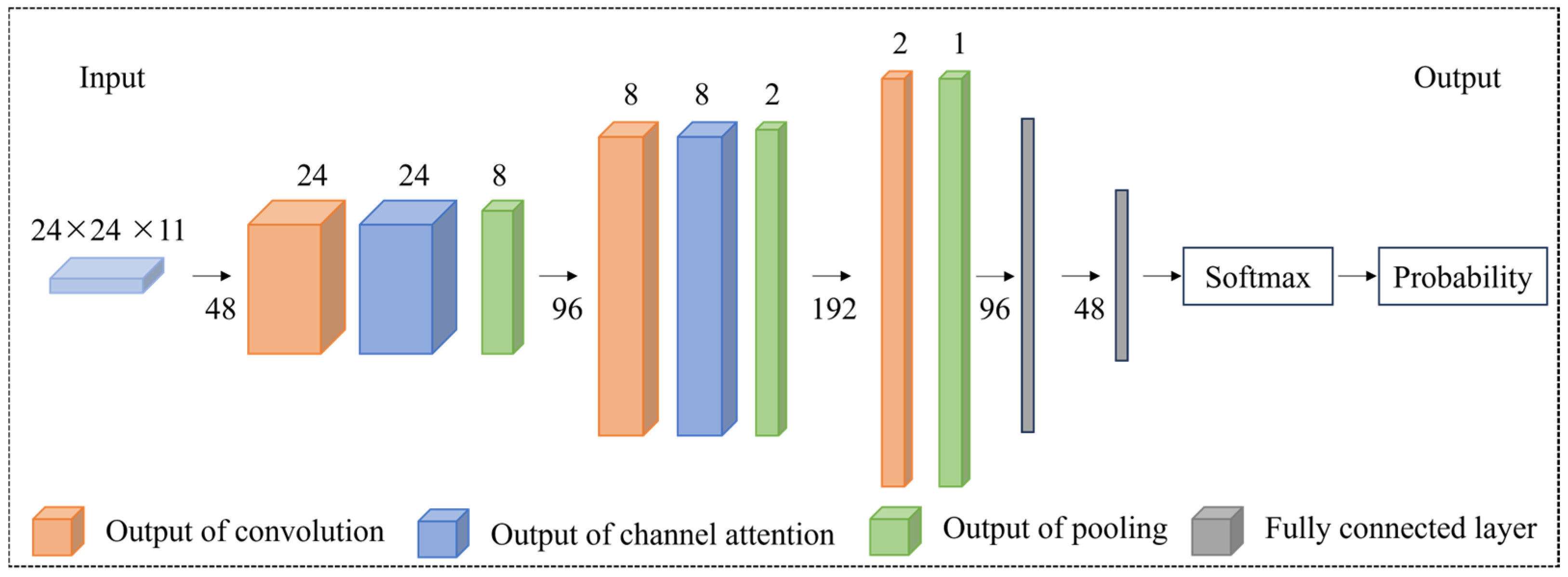

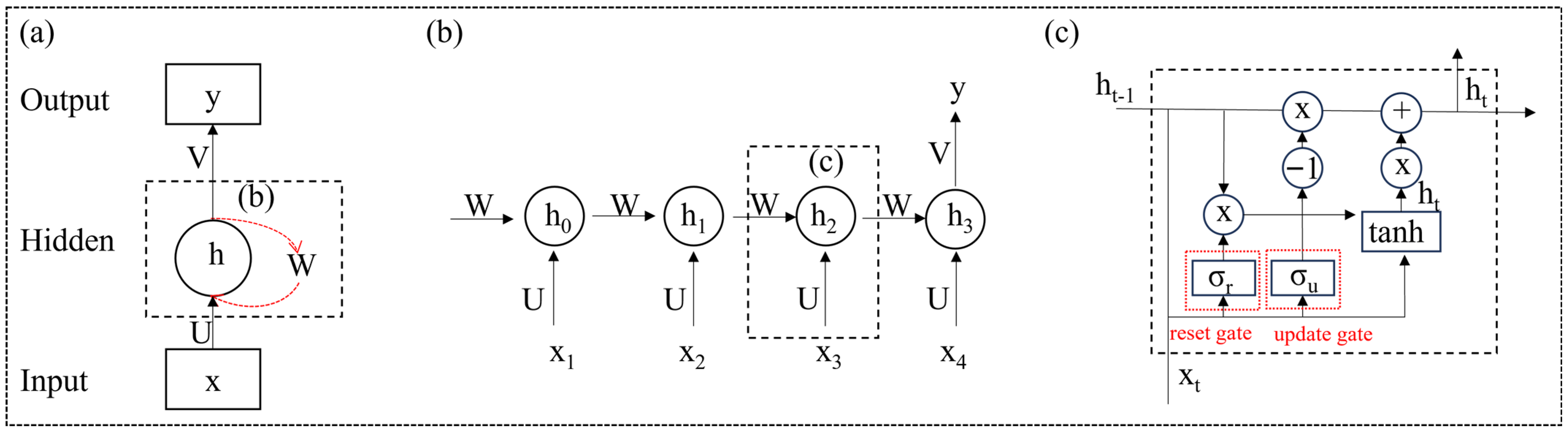
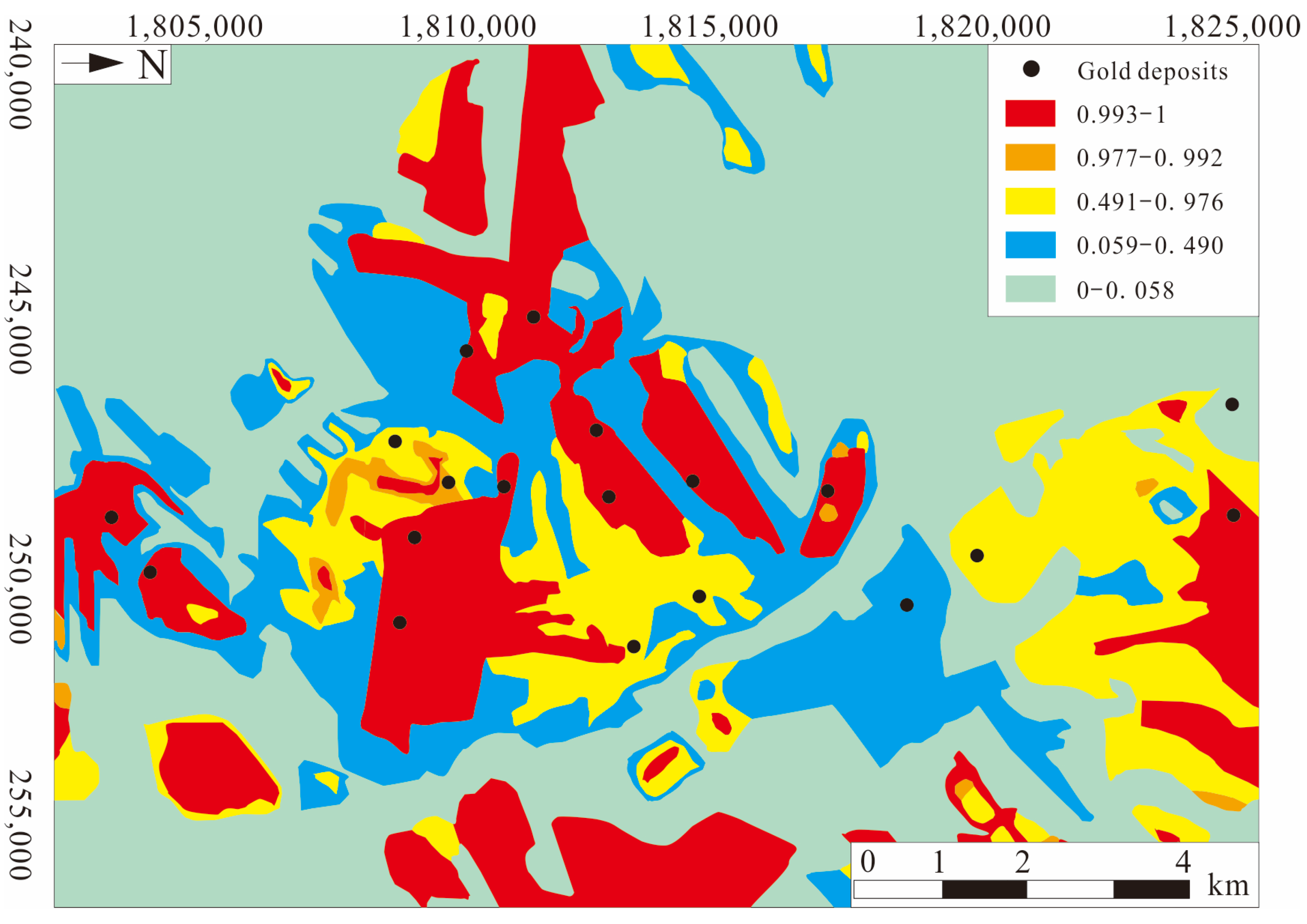

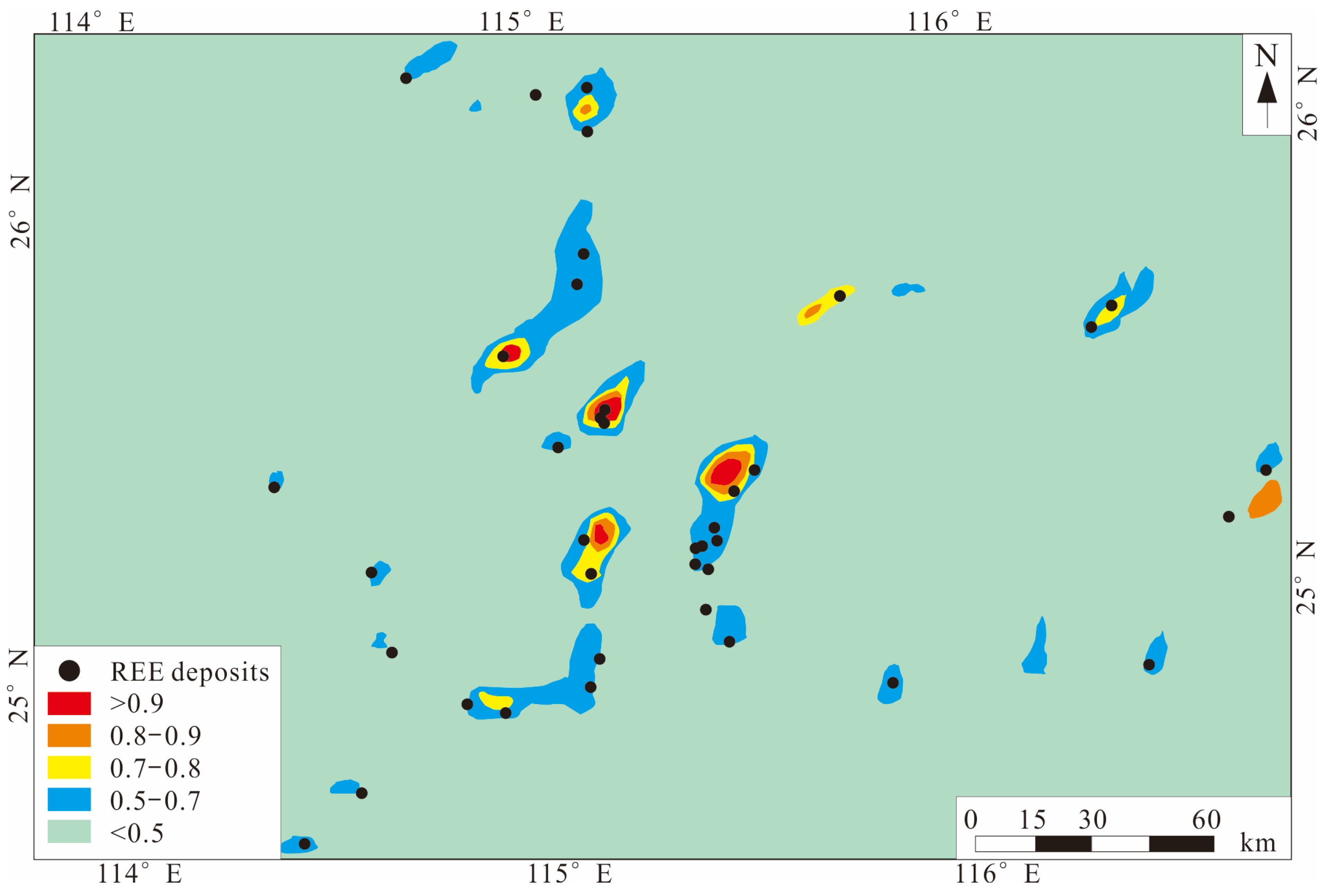
| Model Types | Different Category | Key Features |
|---|---|---|
| knowledge-driven model | “three-part” metallogenic prediction | delineate geologically feasible areas for prospecting; standard grade tonnage model; metallogenic prospect area |
| similarity analogy, difference seeking, and quantitative combined ore control | similar geological environments have similar mineralization series and deposits; geological anomalies leading to mineral deposits; geological condition combination controls mineral deposits | |
| data-driven model | evidence weight | combined with geological mineralization; graded weight of evidence; the metallogenic prediction factors correspond to the metallogenic conditions by evidence weight method |
| regression analysis | quantitative extraction of ore-controlling factors; a posteriori probability is calculated to evaluate the metallogenic potential | |
| support vector machine | the important factors which can correctly predict the ore deposit are automatically selected from many metallogenic factors | |
| random forest | construct multiple decision trees and synthesize their outputs; dealing with the complexity and uncertainty of mineral geological information | |
| deep learning algorithms | ability to process large amounts of geological data; automatic feature extraction; excavate abnormal and potential deposits |
| Data Type | Application Examples |
|---|---|
| Strata and magmatic rocks | Gao et al. [25], Li et al. [117], Li et al. [118], Li et al. [114], Xie et al. [80], Farahbakhsh et al. [84] |
| Geological structure | Li et al. [117], Li et al. [118], Yang et al. [87], Zhang et al. [116], Yang et al. [9], Yang et al. [4], Wu et al. [52], Xie et al. [80], Farahbakhsh et al. [84] |
| Geophysical data | Li et al. [117], Li et al. [36], Xie et al. [80], Farahbakhsh et al. [84] |
| Geochemical data | Xiong et al. [30], Zuo et al. [31], Chen et al. [119], Zhang et al. [81], Li et al. [102], Li et al. [117], Luo et al. [120], Yang et al. [87], Zhang et al. [29], Gao et al. [107], Yang et al. [9], Yang et al. [4], Li et al. [37], Li et al. [114], Fu et al. [27], Wu et al. [52], Li et al. [36], Xie et al. [80], Farahbakhsh et al. [84] |
| Remote sensing image data | Zhao et al. [98], Zidan et al. [68], Fu et al. [27], Farahbakhsh et al. [84] |
| Data Enhancement | Application Examples |
|---|---|
| Sliding window | Li et al. [37], Li et al. [36] |
| Adding random zero noise | Li et al. [117], Yang et al. [4], Li et al. [36], Wu et al. [52] |
| Clipping and repairing | Yang et al. [9] |
| Pixel-to-feature | Zhang et al. [126] |
| Autoencoder | Zhang et al. [116] |
| Algorithm | Data Volume | Epoch | AUC | Learning Rate | Batch Size |
|---|---|---|---|---|---|
| DAE | 6682 data [30] | 100 [80] | 0.9 [31] | 0.001 [80] | 16 [80] |
| 9041 data [81] | 200 [30,31,81] | 0.85 [81] | |||
| 36 data layers [119] 39 data layers [31,128] | 0.89 [116,119,128] 0.8 | ||||
| CNN | 5488 data [32] | 40 [52] | 0.95 [116] | 0.01 [107,126] | 12 [27] |
| 7234 data [107] | 50 [27] | 0.97 [87] | 0.0005 [36] | 32 [107] | |
| 9041 data [116] | 30 [36] | 0.958 [9] | 0.00001 [114] | 64 [36] | |
| 9 data layers [116] | 100 [116,120] | 0.944 [126] | 0.00005 [52] | 128 [99,126] | |
| 11 data layers [9,36,87] | 120 [107] | 0.982 [27] | |||
| 14 data layers [52] | 500 [32] | 0.987 [36] | |||
| 17 data layers [27] | 1000 [9,87] | ||||
| 21 data layers [102] | 1200 [114] | ||||
| 39 data layers | 2000 [114] | data | |||
| GAN | 5 data layers [120] | 10 [117] | 0.863 [29] | 0.001 [80] | 16 [80] |
| 14 data layers [52] | 40 [52] | 0.0001 [29] | 64 [117] | ||
| 100 [29,80] | 0.00001 [117] | 128 [29] | |||
| 2000 [114] | 0.00005 [52] | ||||
| RNN | 13,740 data [99] | 200 [96] | 0.0001 [99] | 1 [97] | |
| 50 bands [98] | 600 [99] | 0.0005 [98] | 3 [96] | ||
| 44 data layers [96] | 1000 [97,98] | 128 [99] |
| Accuracy Evaluation Method | Application Examples |
|---|---|
| Accuracy | Brandmeier et al. [127], Yang et al. [9], Yang et al. [4], Li et al. [37], Yin et al. [97], Li et al. [114], Fu et al. [27] |
| Recall rate, Precision, and F1 | Sun et al. [22], Chen et al. [128], Li et al. [102], Yin et al. [97], Wang et al. [96], Yang et al. [9], Yang et al. [4], Gao et al. [107], Li et al. [36], Zidan et al. [68], Wu et al. [52] |
| ROC and AUC | Gao et al. [25], Zuo et al. [31], Xiong et al. [122], Chen et al. [119], Chen et al. [128], Zhang et al. [81], Chen et al. [119], Chen et al. [128], Sun et al. [22], Zhang et al. [29], Luo et al. [120], Luo et al. [120], Zhang et al. [116], Gao et al. [107], Yin et al. [97], Yang et al. [9], Yang et al. [4], Yang et al. [4], Nathwani et al. [136], Li et al. [36], Xie et al. [80], Fu et al. [27], Wang et al. [99] |
| Kappa | Rodriguez-Galiano et al. [135], Gao et al. [25], Sun et al. [22], Shirmard et al. [67], Yang et al. [4], Yin et al. [97], Yang et al. [9], Li et al. [36], Wu et al. [52] |
| Predicted area curve | Xiong et al. [122], Sun et al. [22], Shirmard et al. [67], Zhang et al. [29], Yang et al. [9], Yang et al. [4], Li et al. [36] |
| Success rate curve | Zuo et al. [137], Zuo et al. [138], Rodriguez-Galiano et al. [135], Gao et al. [25], Xu et al. [100], Li et al. [118], Wang et al. [96], Yin et al. [97], Yang et al. [4], Yang et al. [9], Wang et al. [99] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, K.; Chen, Y.; Geng, G.; Lu, Z.; Zhang, W.; Song, Z.; Guan, J.; Zhao, Y.; Zhang, Z. A Review of Mineral Prospectivity Mapping Using Deep Learning. Minerals 2024, 14, 1021. https://doi.org/10.3390/min14101021
Sun K, Chen Y, Geng G, Lu Z, Zhang W, Song Z, Guan J, Zhao Y, Zhang Z. A Review of Mineral Prospectivity Mapping Using Deep Learning. Minerals. 2024; 14(10):1021. https://doi.org/10.3390/min14101021
Chicago/Turabian StyleSun, Kang, Yansi Chen, Guoshuai Geng, Zongyue Lu, Wei Zhang, Zhihong Song, Jiyun Guan, Yang Zhao, and Zhaonian Zhang. 2024. "A Review of Mineral Prospectivity Mapping Using Deep Learning" Minerals 14, no. 10: 1021. https://doi.org/10.3390/min14101021
APA StyleSun, K., Chen, Y., Geng, G., Lu, Z., Zhang, W., Song, Z., Guan, J., Zhao, Y., & Zhang, Z. (2024). A Review of Mineral Prospectivity Mapping Using Deep Learning. Minerals, 14(10), 1021. https://doi.org/10.3390/min14101021








