Effect of Rate-Dependent Breakage on Strength and Deformation of Granular Sample—A DEM Study
Abstract
:1. Introduction
2. Numerical Modelling
2.1. DEM Working Methodology
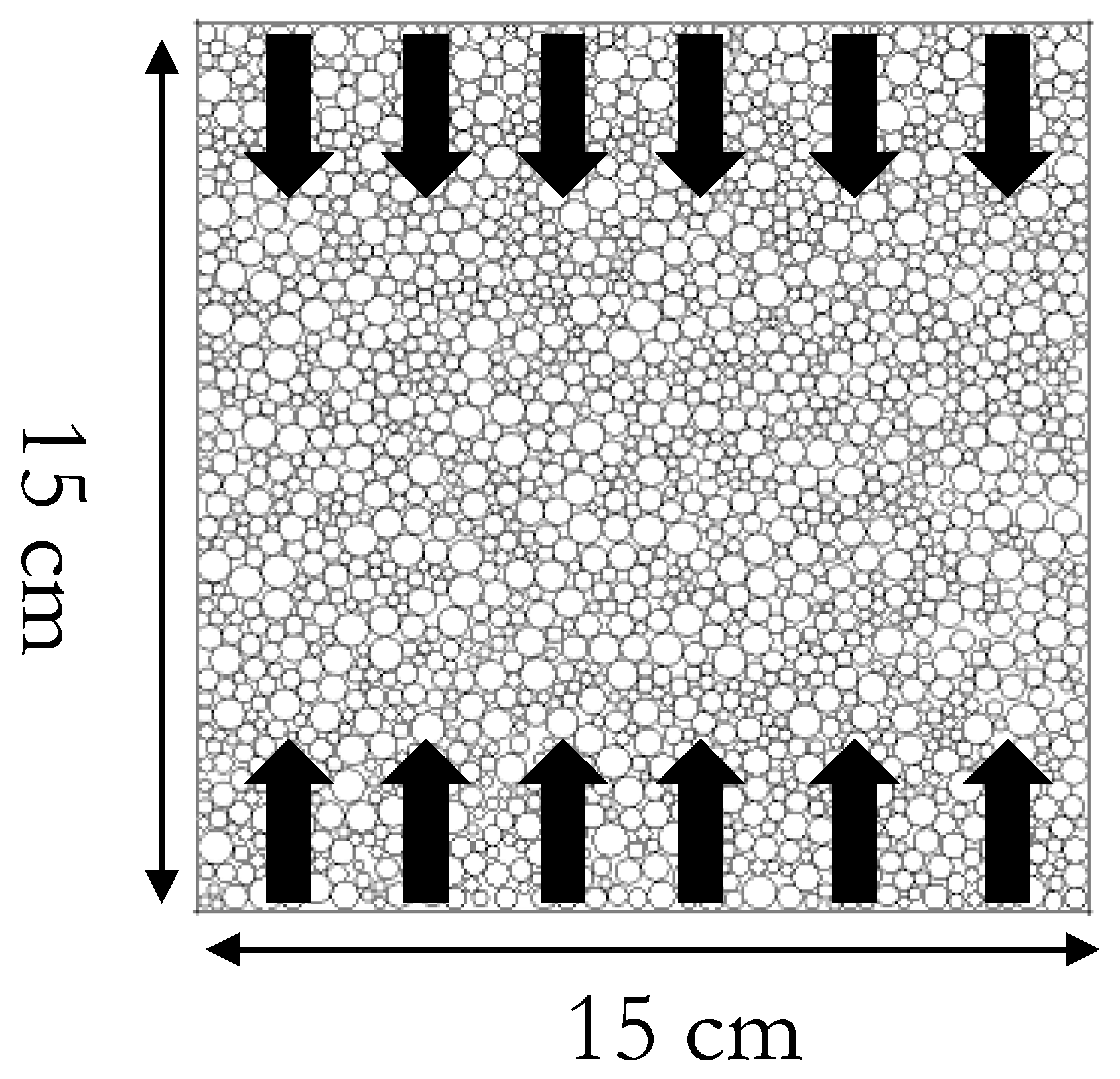
2.2. Modelling Scheme
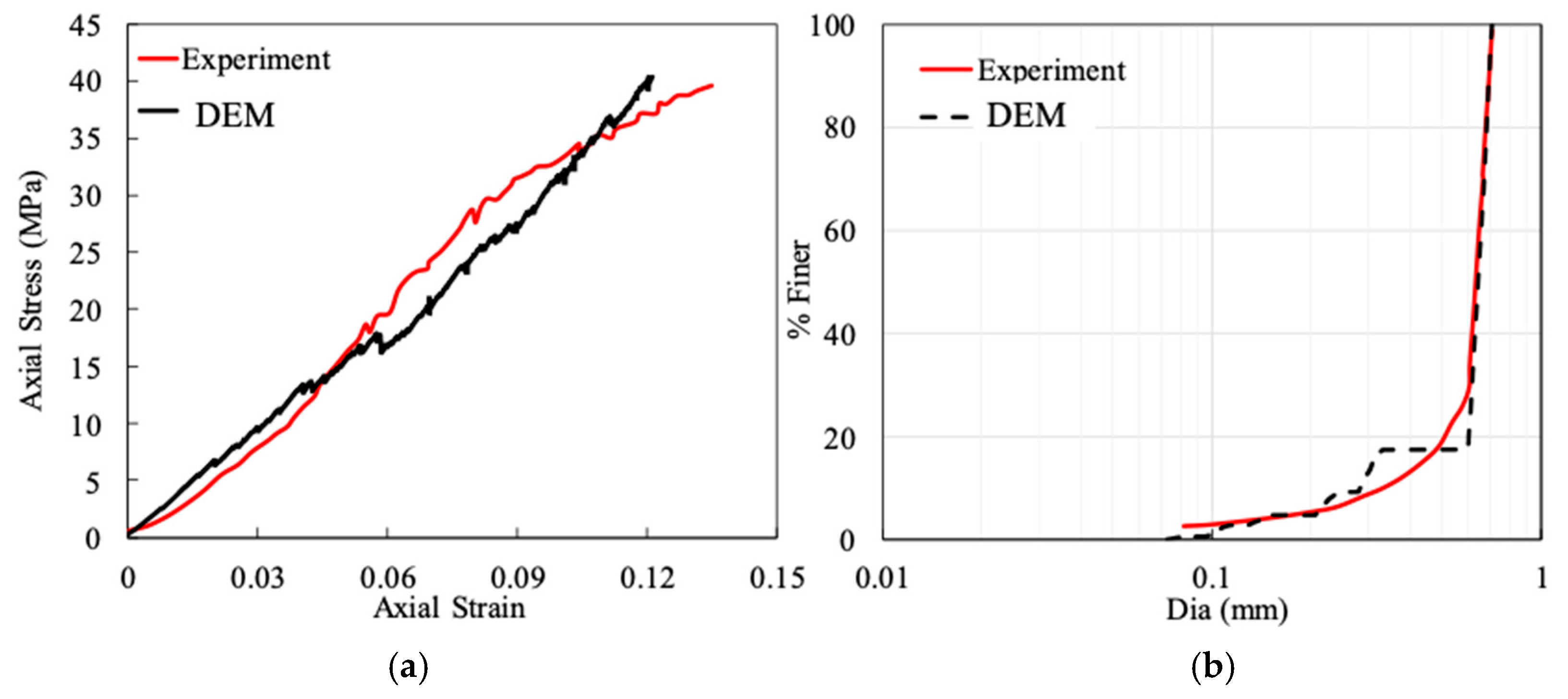
2.3. Model Properties
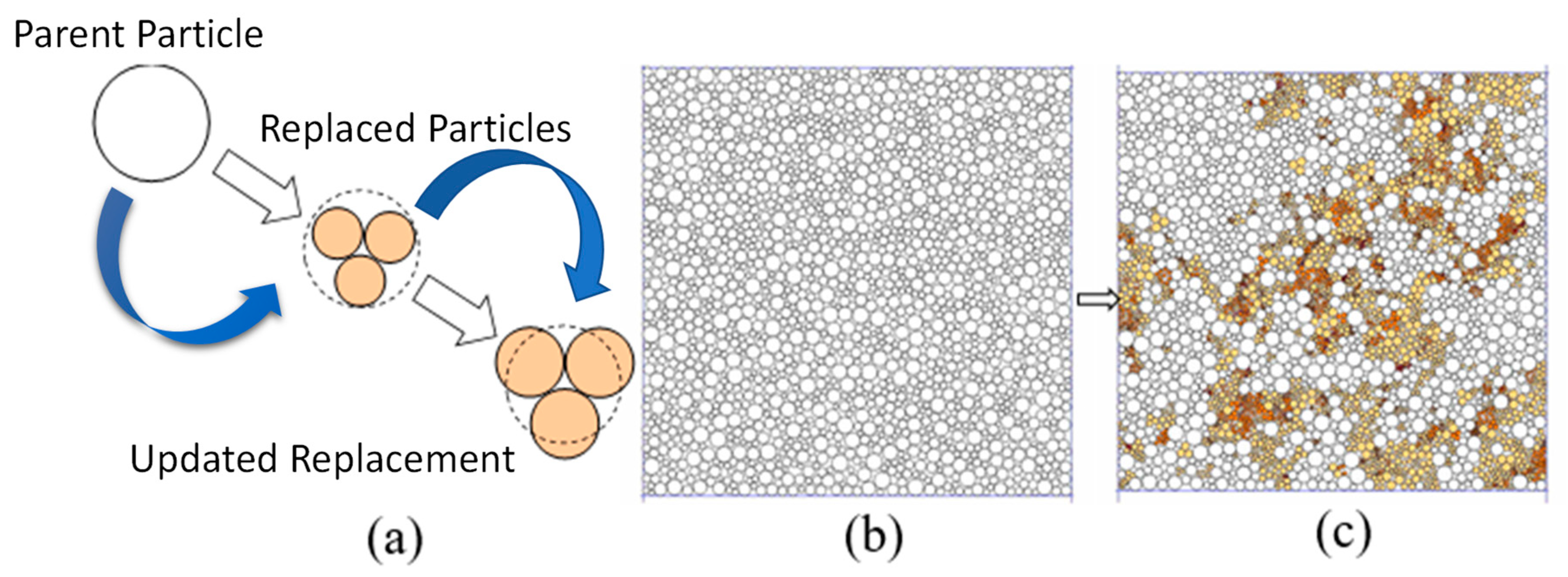
2.4. Breakage Methodology
3. Results and Discussions
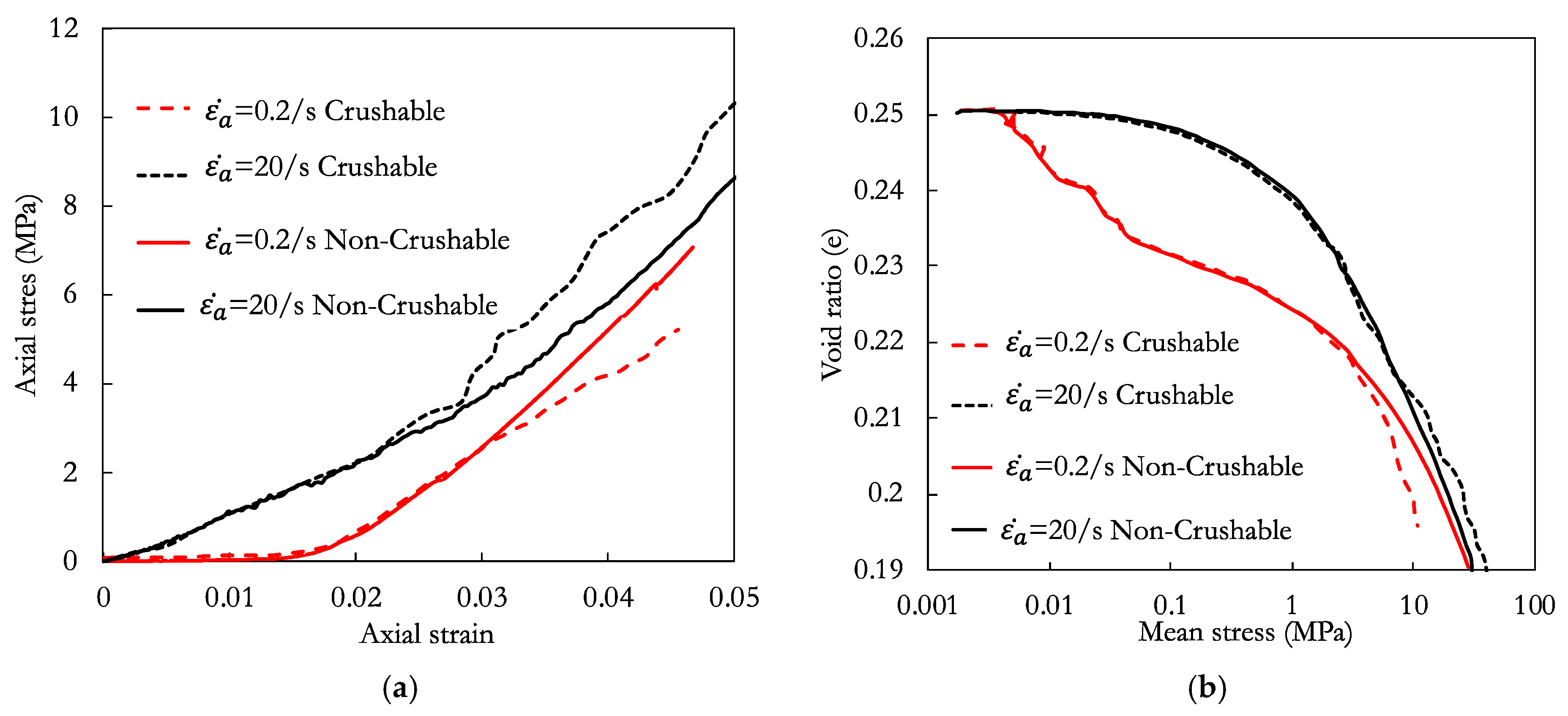
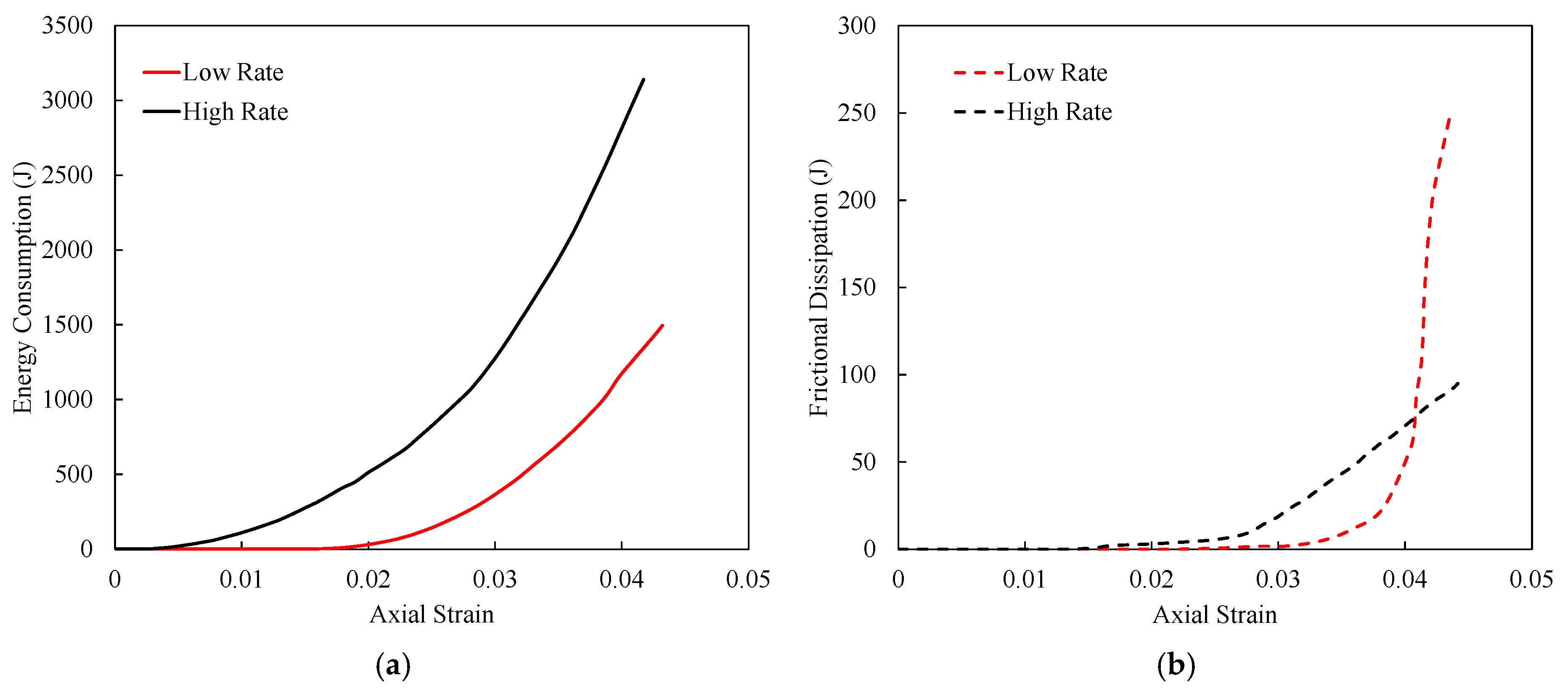
3.1. Stress–Strain Response
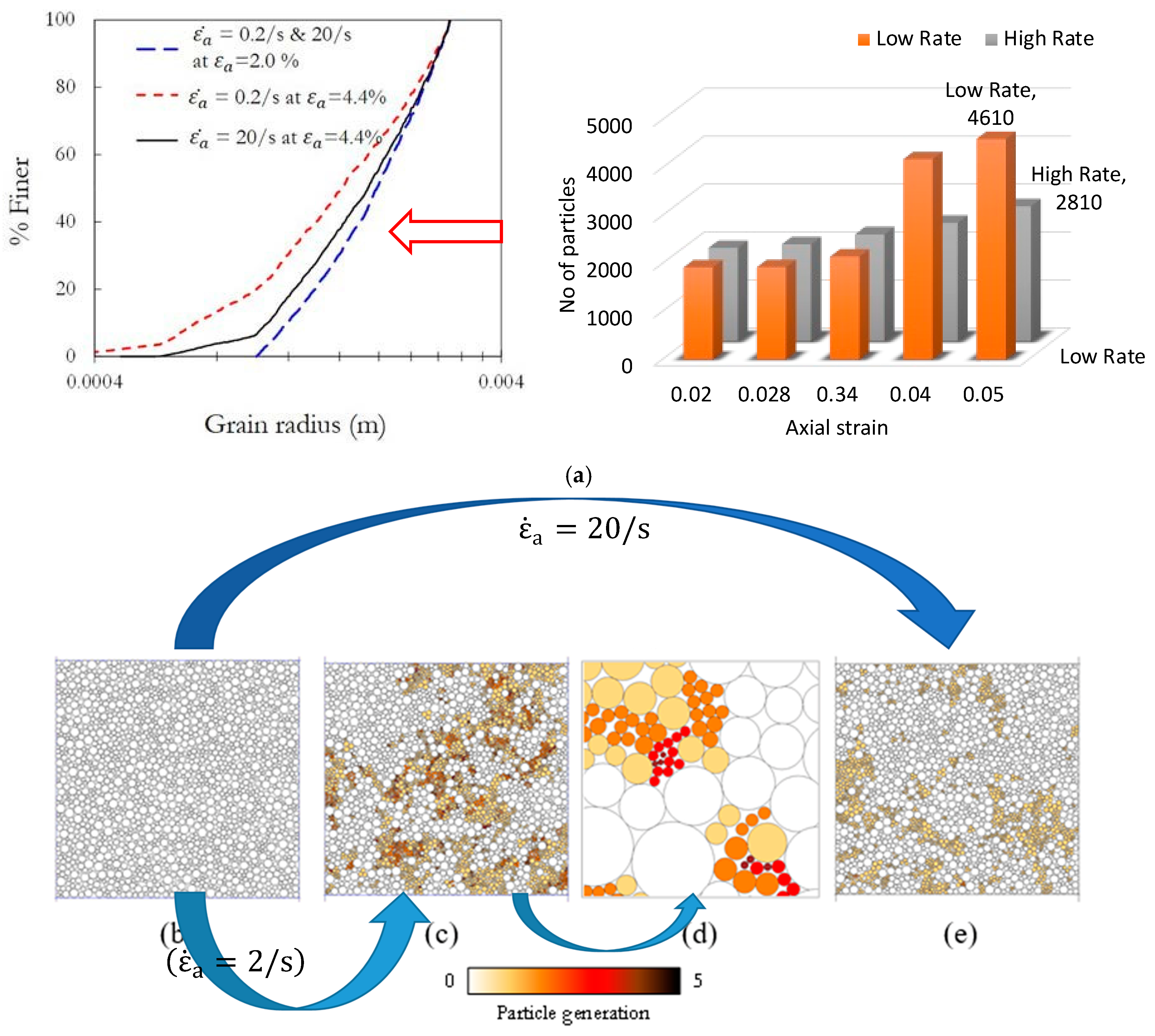
3.2. Breakage Response
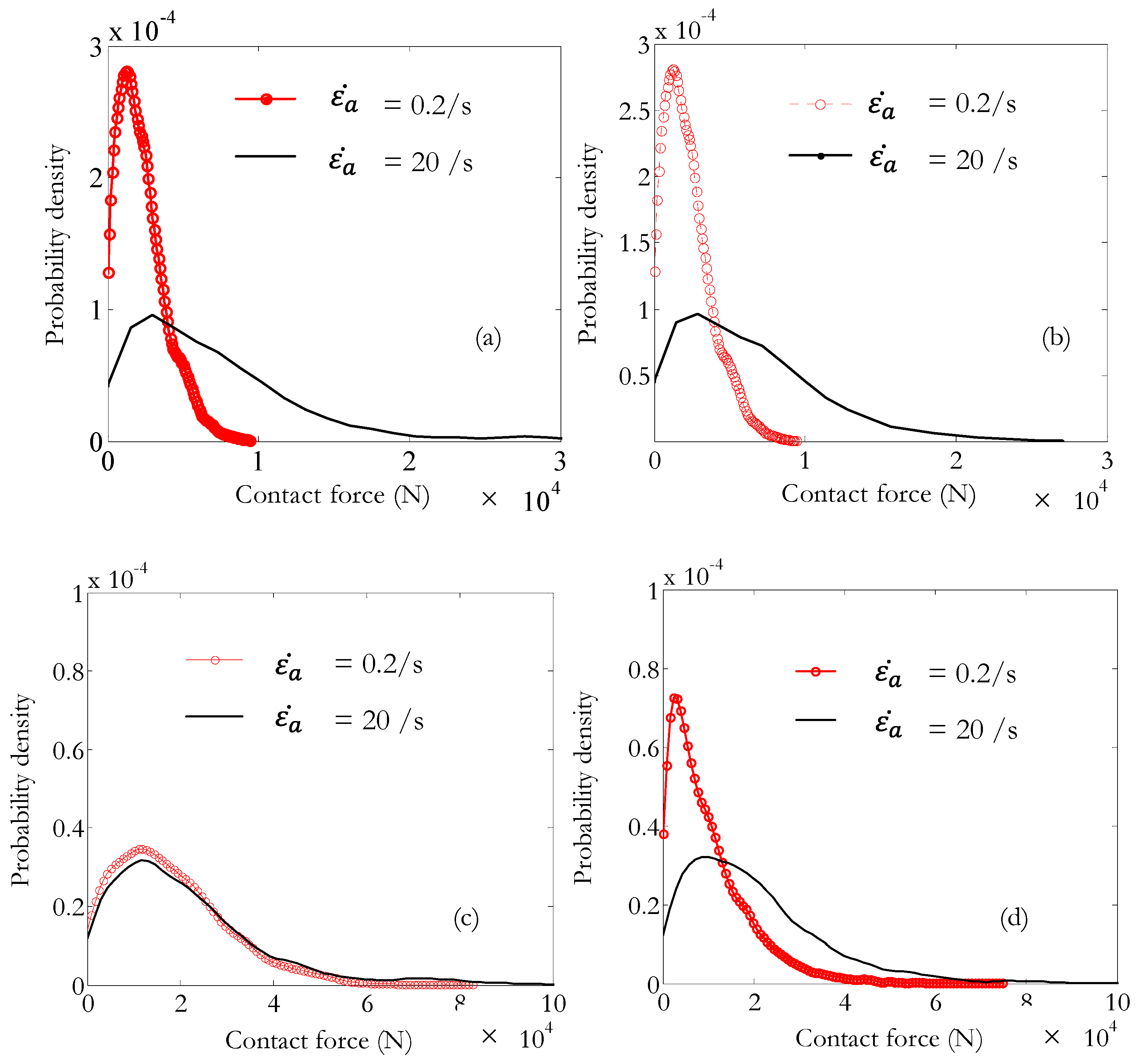
3.3. Spatial Contact Force Network
3.4. Variation of Particle Contacts
3.5. Particle Velocity Profile
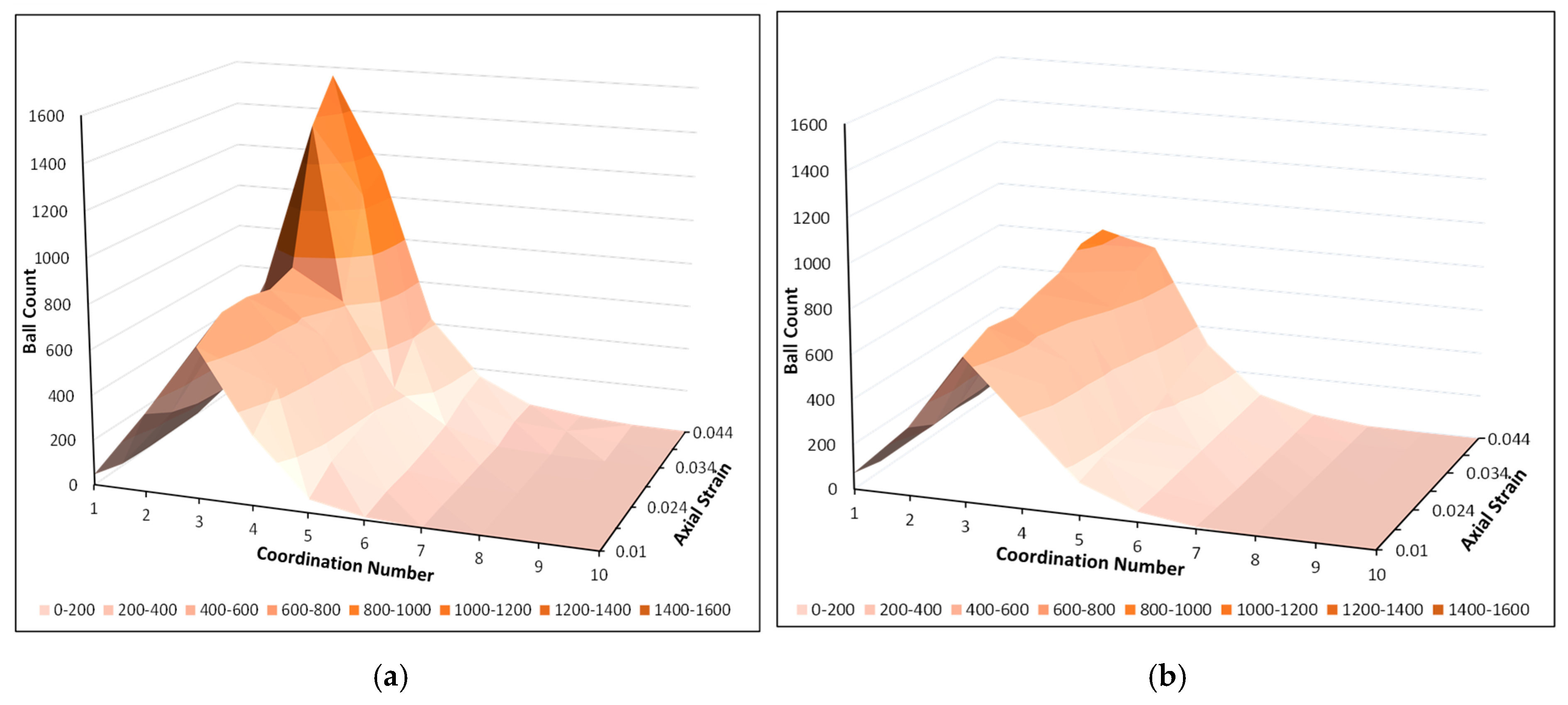
3.6. Coordination Number Profile
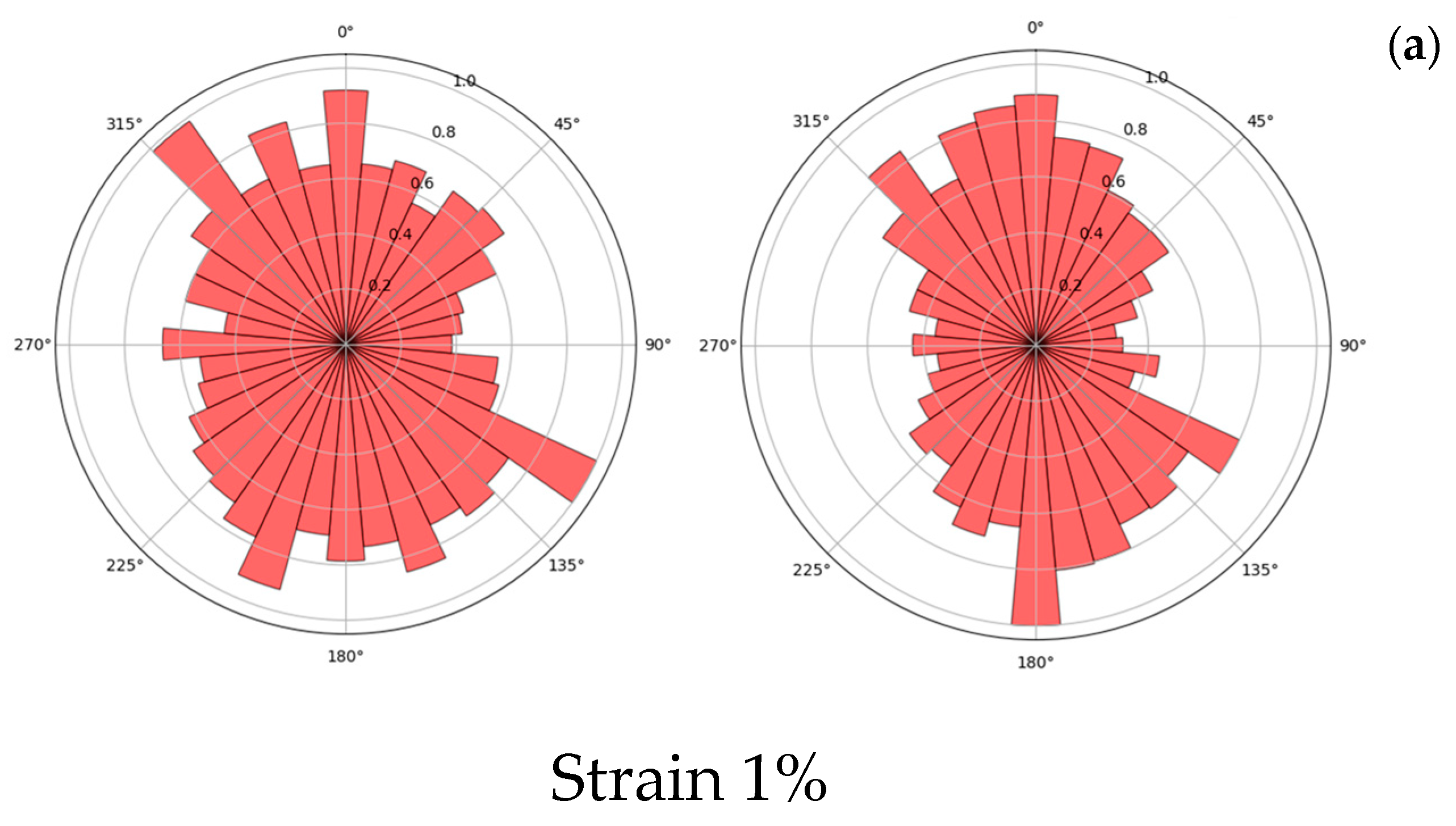
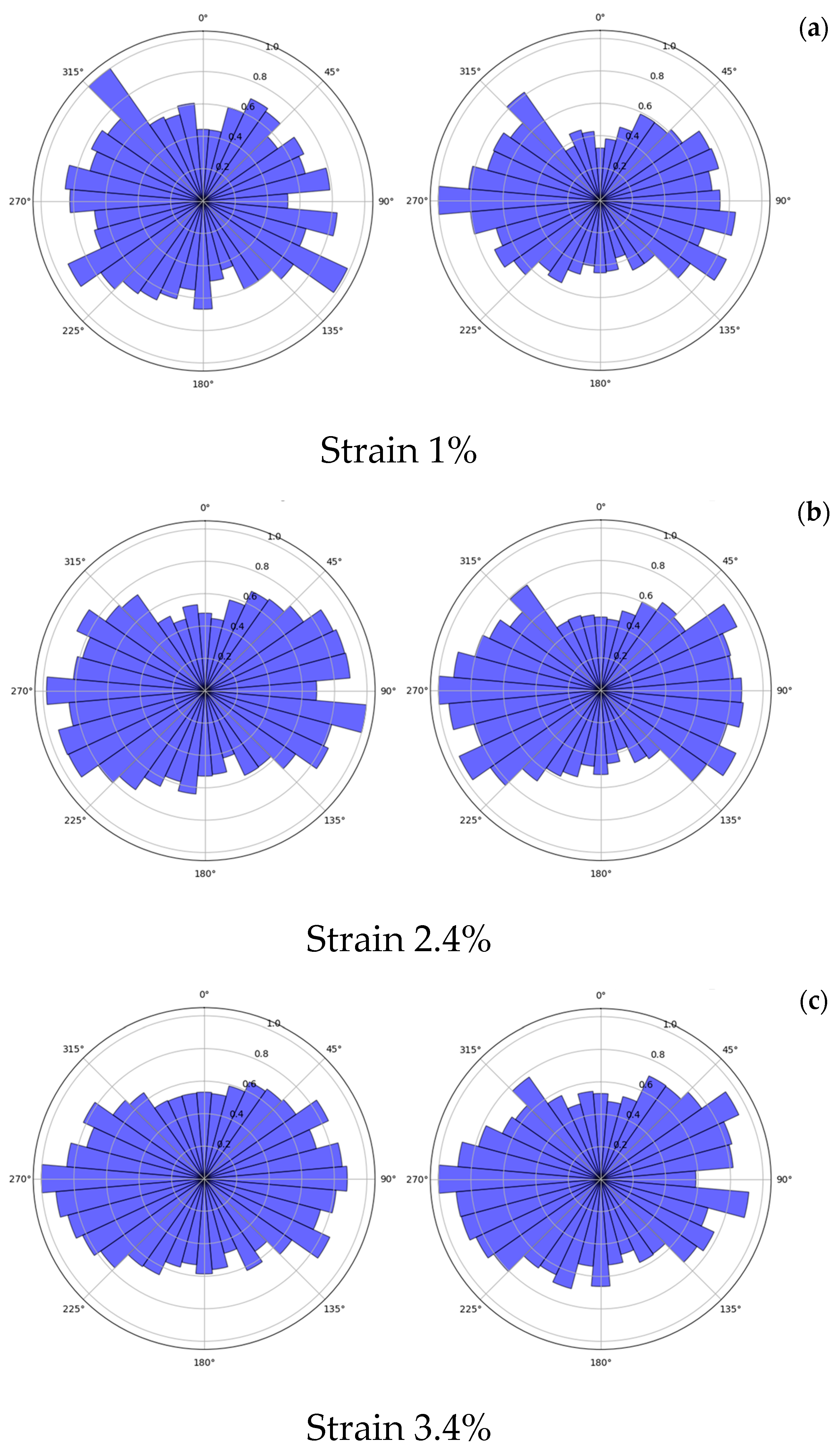
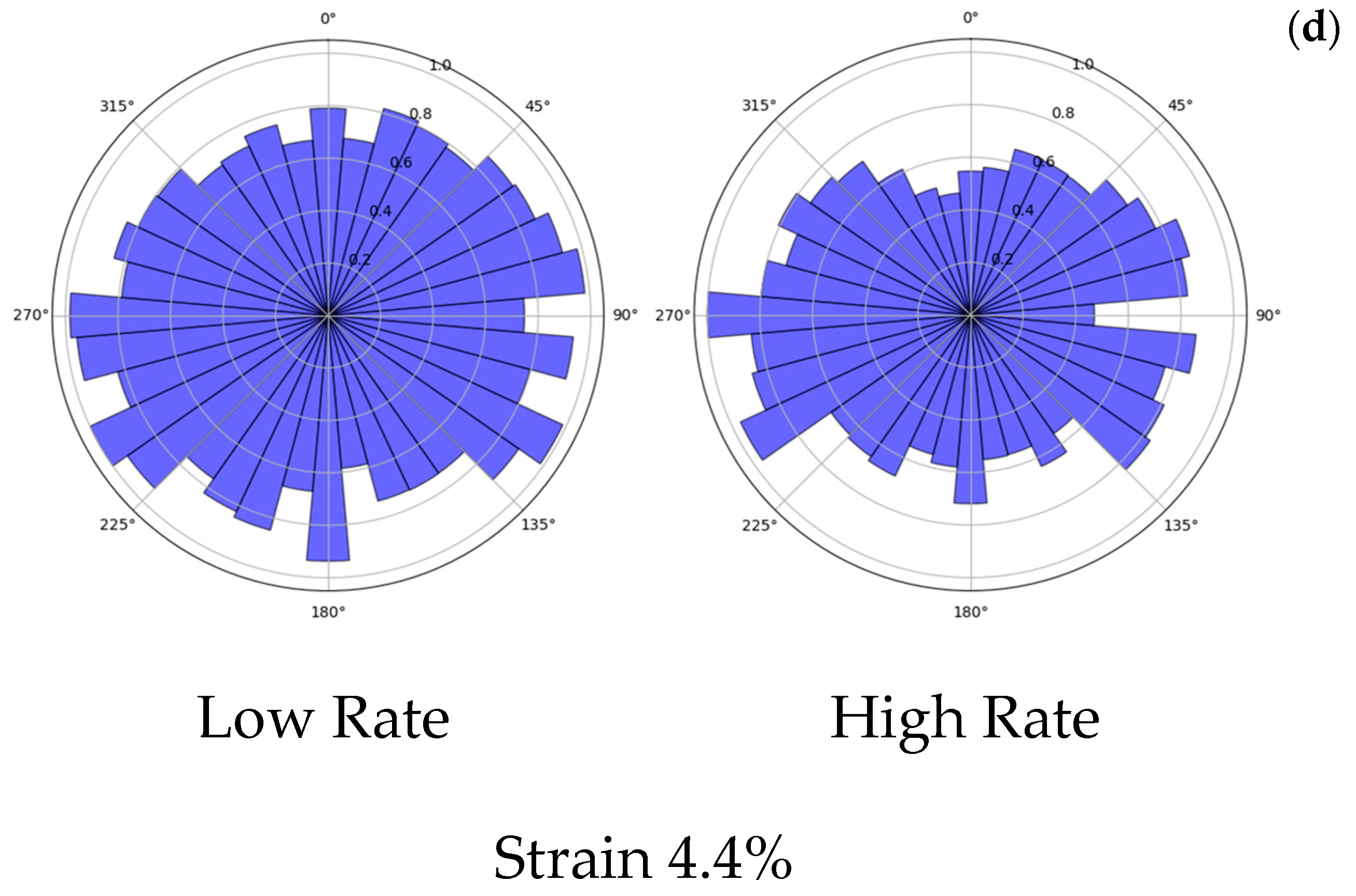
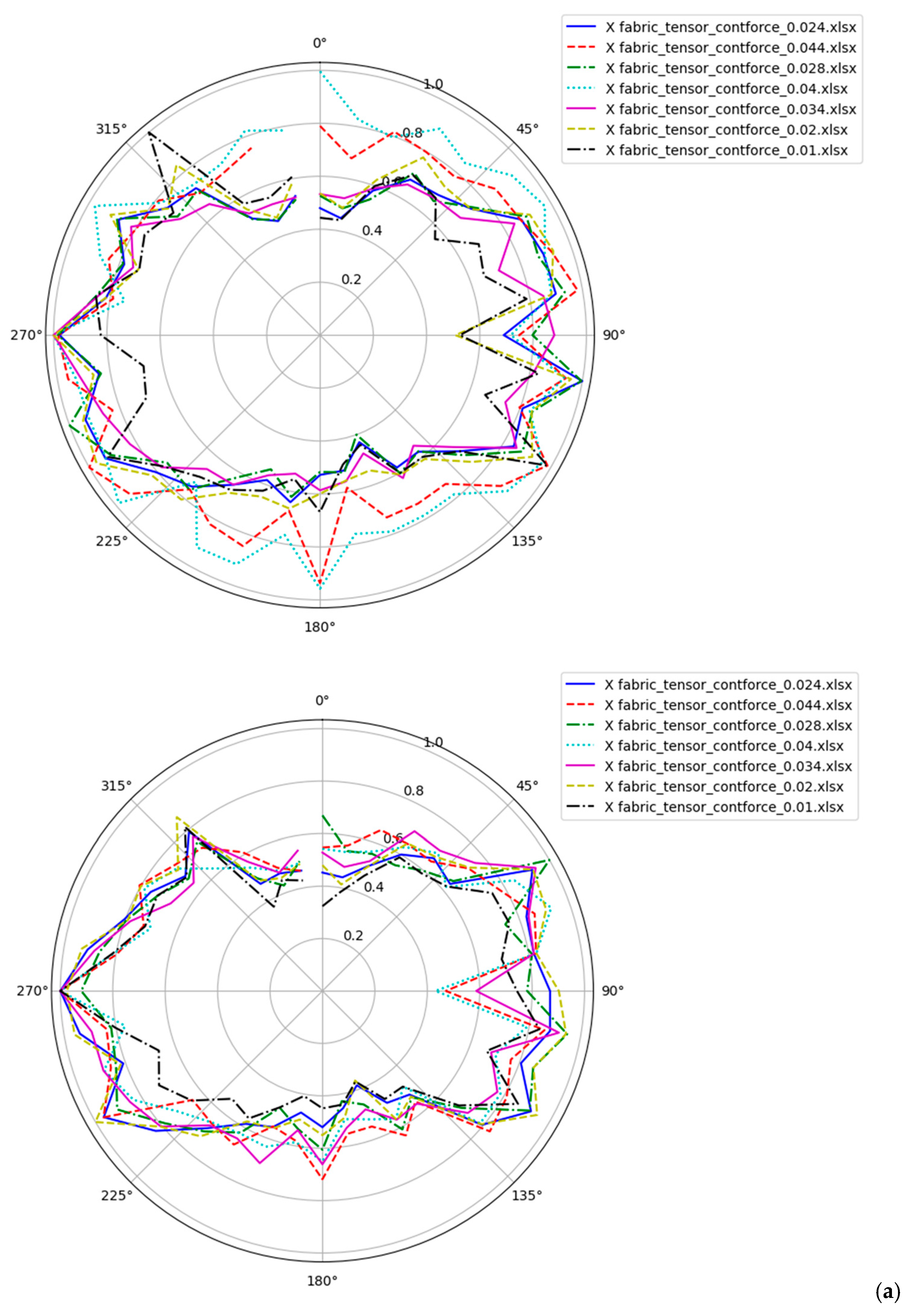
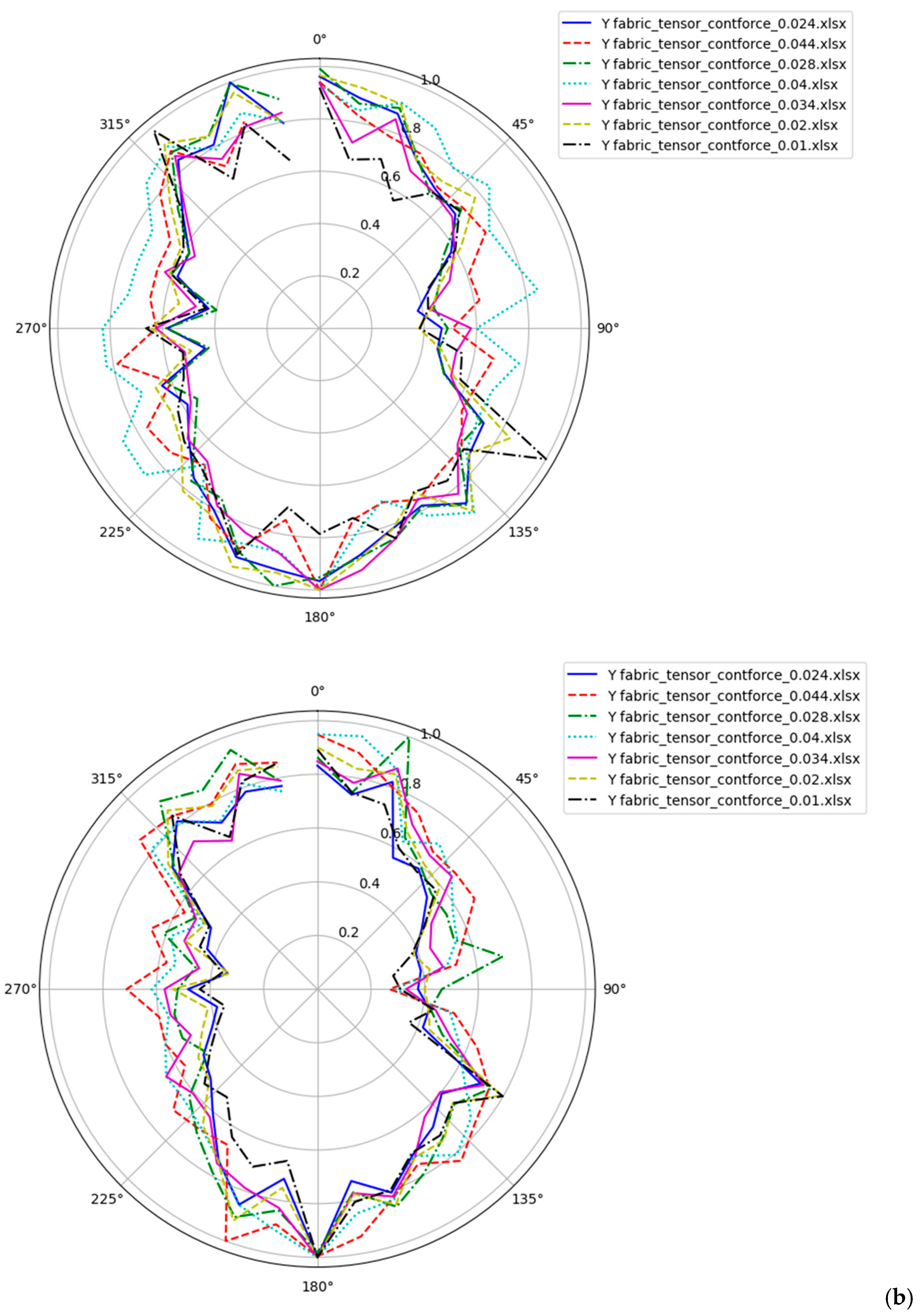
3.7. Fabric Tensor Evolution
3.8. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cola, F.D.; Pellegrino, A.; Glößner, C.; Penumadu, D.; Petrinic, N. Effect of Particle Morphology, Compaction, and Confinement on the High Strain Rate Behavior of Sand. Exp. Mech. 2018, 58, 223–242. [Google Scholar] [CrossRef]
- Gong, D.; Nadolski, S.; Sun, C.; Klein, B.; Kou, J. The Effect of Strain Rate on Particle Breakage Characteristics. Powder Technol. 2018, 339, 595–605. [Google Scholar] [CrossRef]
- Suescun-Florez, E.; Iskander, M. Effect of Fast Constant Loading Rates on the Global Behavior of Sand in Triaxial Compression. Geotech. Test. J. 2017, 40, 52–71. [Google Scholar] [CrossRef]
- Lade, P.V.; Karimpour, H. Static Fatigue Controls Particle Crushing and Time Effects in Granular Materials. Soils Found. 2010, 50, 573–583. [Google Scholar] [CrossRef]
- Yamamuro, J.A.; Abrantes, A.E.; Lade, P.V. Effect of Strain Rate on the Stress-Strain Behavior of Sand. J. Geotech. Geoenviron. Eng. 2011, 137, 1169–1178. [Google Scholar] [CrossRef]
- Gong, G.; Thornton, C.; Chan, A.H.C. DEM Simulations of Undrained Triaxial Behavior of Granular Material. J. Eng. Mech. 2012, 138, 560–566. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Z.; Ye, Q.; Zha, J. Particle Breakage Evolution of Coral Sand Using Triaxial Compression Tests. J. Rock Mech. Geotech. Eng. 2021, 13, 321–334. [Google Scholar] [CrossRef]
- Kodicherla, S.P.K.; Gong, G.; Fan, L.; Wilkinson, S.; Moy, C.K.S. Discrete Element Modelling of Strength and Critical State Characteristics of Granular Materials under Axial Compression and Axial Extension Stress Path Tests. Particuology 2021, 56, 152–162. [Google Scholar] [CrossRef]
- Das, S.K.; Verma, S.K.; Das, A. Numerical Assessment of Effects of Strain Rate on the Critical State of Crushable Sand. Geotech. Lett. 2022, 12, 8–13. [Google Scholar] [CrossRef]
- Tian, J.; Lai, Y.; Liu, E.; Yang, Y. A Micromechanics-Based Elasto-Plastic Model for Granular Media Combined with Cosserat Continuum Theory. Acta Geotech. 2022, 17, 2259–2285. [Google Scholar] [CrossRef]
- Kim, E.; Stine, M.A.; de Oliveira, D.B.M. Effects of Water Content and Loading Rate on the Mechanical Properties of Berea Sandstone. J. S. Afr. Inst. Min. Metall. 2020, 119, 1077–1082. [Google Scholar] [CrossRef]
- Christie, D.; Lackenby, J.; Indraratna, B.; McDowell, G. Effect of Confining Pressure on Ballast Degradation and Deformation under Cyclic Triaxial Loading. Géotechnique 2007, 57, 527–536. [Google Scholar] [CrossRef]
- Lyu, H.; Gu, J.; Zhou, J.; Li, B. Mechanical Behavior and Particle Breakage of Calcareous Sand in Triaxial Test. Mar. Geophys. Res. 2023, 44, 18. [Google Scholar] [CrossRef]
- Gerolymos, N.; Gazetas, G. A Model for Grain-Crushing-Induced Landslides-Application to Nikawa, Kobe 1995. Soil Dyn. Earthq. Eng. 2007, 27, 803–817. [Google Scholar] [CrossRef]
- Cardoso, F.W.; Silva, M.C.; de C. Meira, N.F.; Rabelo Oliveira, R.A.; Bianchi, A.G.C. Advancing Particle Size Detection in Mineral Processing: Exploring Edge AI Solutions; Springer: Cham, Switzerland, 2024; pp. 97–118. [Google Scholar]
- Nyembwe, A.M.; Cromarty, R.D.; Garbers-Craig, A.M. Relationship Between Iron Ore Granulation Mechanisms, Granule Shapes, and Sinter Bed Permeability. Miner. Process. Extr. Metall. Rev. 2017, 38, 388–402. [Google Scholar] [CrossRef]
- Guimaraes, M.S.; Valdes, J.R.; Palomino, A.M.; Santamarina, J.C. Aggregate Production: Fines Generation during Rock Crushing. Int. J. Miner. Process. 2007, 81, 237–247. [Google Scholar] [CrossRef]
- Alhani, I.J.; Albadri, W.M.; Noor, M.J.M.; Lim, S.M.; Alwash, A. Effect of Particle Breakage on Strength Characteristics of Limestone Aggregate. Geotech. Geol. Eng. 2022, 40, 5295–5306. [Google Scholar] [CrossRef]
- Harireche, O.; McDowell, G.R. Discrete Element Modelling of Cyclic Loading of Crushable Aggreates. Granul. Matter 2003, 5, 147–151. [Google Scholar] [CrossRef]
- Gawenda, T.; Saramak, D. Optimization of Aggregate Production Circuit through Modeling of Crusher Operation. Minerals 2022, 12, 78. [Google Scholar] [CrossRef]
- Pacana, A.; Siwiec, D.; Bednarova, L.; Sofranko, M.; Vegsoova, O.; Cvoliga, M. Influence of Natural Aggregate Crushing Process on Crushing Strength Index. Sustainability 2021, 13, 8353. [Google Scholar] [CrossRef]
- Beemer, R.D.; Sadekov, A.; Lebrec, U.; Shaw, J.; Bandini-Maeder, A.; Cassidy, M.J. Impact of Biology on Particle Crushing in Offshore Calcareous Sediments. In Proceedings of the Geo-Congress 2019, Philadelphia, 21 March 2019; American Society of Civil Engineers: Reston, VA, USA; pp. 640–650. [Google Scholar]
- Wei, X. Mechanical Behavior and Particle Crushing of Marine Carbonate Gravel in Xisha Islands, South China Sea. Eur. J. Environ. Civ. Eng. 2024, 28, 973–992. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Nan, J. Prediction of Dynamic Pore Water Pressure for Calcareous Sand Mixed with Fine-Grained Soil under Cyclic Loading. Soil Dyn. Earthq. Eng. 2022, 157, 107276. [Google Scholar] [CrossRef]
- Liu, L.; Orense, R.P.; Pender, M.J. Crushing-Induced Liquefaction Characteristics of Pumice Sand. In Proceedings of the 2015 Annual Technical Conference on New Zealand Society for Earthquake Engineering (NZSEE), Wellington, New Zealand, 10–12 April 2015; New Zealand Society for Earthquake Engineering: Wellington, New Zealand, 2015; pp. 521–528. [Google Scholar]
- Ovalle, C.; Frossard, E.; Dano, C.; Hu, W.; Maiolino, S.; Hicher, P.Y. The Effect of Size on the Strength of Coarse Rock Aggregates and Large Rockfill Samples through Experimental Data. Acta Mech. 2014, 225, 2199–2216. [Google Scholar] [CrossRef]
- Xiao, Y.; Meng, M.; Wang, C.; Wu, H.; Fang, Q.; Liu, S. Breakage Critical State of Gravels with Different Gradings. Part I: Experimental Results. Transp. Geotech. 2023, 42, 101087. [Google Scholar] [CrossRef]
- Lin, T.-K.; Hsieh, B.-Z. Prevention of Seabed Subsidence of Class-1 Gas Hydrate Deposits via CO2-EGR: A Numerical Study with Coupled Geomechanics-Hydrate Reaction-Multiphase Fluid Flow Model. Energies 2020, 13, 1579. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, Q.; Luo, L.; Cui, S. Pore-Water Pressure Model for Carbonate Fault Materials Based on Cyclic Triaxial Tests. Front. Earth Sci. 2022, 10, 842765. [Google Scholar] [CrossRef]
- Ahmed, M.M. Effect of Comminution on Particle Shape and Surface Roughness and Their Relation to Flotation Process. Int. J. Miner. Process. 2010, 94, 180–191. [Google Scholar] [CrossRef]
- Wang, C.; Sun, C.; Liu, Q. Entrainment of Gangue Minerals in Froth Flotation: Mechanisms, Models, Controlling Factors, and Abatement Techniques—A Review. Min. Metall. Explor. 2021, 38, 673–692. [Google Scholar] [CrossRef]
- Wei, H.; Yin, M.; Zhao, T.; Yan, K.; Shen, J.; Meng, Q.; Wang, X.; He, J. Effect of Particle Breakage on the Shear Strength of Calcareous Sands. Mar. Geophys. Res. 2021, 42, 23. [Google Scholar] [CrossRef]
- Einav, I. Breakage Mechanics-Part I: Theory. J. Mech. Phys. Solids 2007, 55, 1274–1297. [Google Scholar] [CrossRef]
- Tengattini, A.; Das, A.; Einav, I. A Constitutive Modelling Framework Predicting Critical State in Sand Undergoing Crushing and Dilation. Géotechnique 2016, 66, 695–710. [Google Scholar] [CrossRef]
- Liu, M.; Wang, F. Numerical Simulation of Influence of Coarse Aggregate Crushing on Mechanical Properties of Concrete under Uniaxial Compression. Constr. Build. Mater. 2022, 342, 128081. [Google Scholar] [CrossRef]
- Bubakova, P.; Pivokonsky, M.; Filip, P. Effect of Shear Rate on Aggregate Size and Structure in the Process of Aggregation and at Steady State. Powder Technol. 2013, 235, 540–549. [Google Scholar] [CrossRef]
- Karimpour, H.; Lade, P. V Time Effects Relate to Crushing in Sand. J. Geotech. Geoenviron. Eng. 2010, 136, 1209–1219. [Google Scholar] [CrossRef]
- Karimpour, H.; Lade, P.V. Creep Behavior in Virginia Beach Sand. Can. Geotech. J. 2013, 1178, 1159–1178. [Google Scholar] [CrossRef]
- Augustesen, A.; Liingaard, M.; Lade, P.V.P.V.; Asce, M. Evaluation of Time-Dependent Behavior of Soils. Int. J. Geomech. 2004, 4, 137–156. [Google Scholar] [CrossRef]
- Wang, P.; Arson, C. Energy Distribution during the Quasi-Static Confined Comminution of Granular Materials. Acta Geotech. 2018, 13, 1075–1083. [Google Scholar] [CrossRef]
- Weerasekara, N.S.; Powell, M.S.; Cleary, P.W.; Tavares, L.M.; Evertsson, M.; Morrison, R.D.; Quist, J.; Carvalho, R.M. The Contribution of DEM to the Science of Comminution. Powder Technol. 2013, 248, 3–24. [Google Scholar] [CrossRef]
- Weerasekara, N.S.; Liu, L.X.; Powell, M.S. Estimating Energy in Grinding Using DEM Modelling. Miner. Eng. 2016, 85, 23–33. [Google Scholar] [CrossRef]
- He, S.; Shan, H.-F.; Xia, T.-D.; Liu, Z.-J.; Ding, Z.; Xia, F. The Effect of Temperature on the Drained Shear Behavior of Calcareous Sand. Acta Geotech. 2020, 7, 613–633. [Google Scholar] [CrossRef]
- Das, S.K.; Das, A. A Critical State Based Viscoplastic Model for Crushable Granular Materials. Soils Found. 2022, 62. [Google Scholar] [CrossRef]
- Wang, F.; Sassa, K. Relationship Between Grain Crushing and Excess Pore Pressure Generation by Sandy Soils in Ring-Shear Tests. J. Nat. Disaster Sci. 2000, 22, 87–96. [Google Scholar] [CrossRef]
- Li, Y.; Lin, Z.; Li, B.; He, L.; Gong, J. Effects of Gradation and Grain Crushing on the Liquefaction Resistance of Calcareous Sand. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 1–16. [Google Scholar] [CrossRef]
- Sönmezer, Y.B.; Akyüz, A.; Kayabalı, K. Investigation of the Effect of Grain Size on Liquefaction Potential of Sands. Geomech. Eng. 2020, 20, 243–254. [Google Scholar] [CrossRef]
- Andò, E.; Viggiani, G.; Hall, S.A.; Desrues, J. Experimental Micro-Mechanics of Granular Media Studied by x-Ray Tomography: Recent Results and Challenges. Géotechnique Lett. 2013, 3, 142–146. [Google Scholar] [CrossRef]
- Parab, N.D.; Claus, B.; Hudspeth, M.C.; Black, J.T.; Mondal, A.; Sun, J.; Fezzaa, K.; Xiao, X.; Luo, S.N.; Chen, W. Experimental Assessment of Fracture of Individual Sand Particles at Different Loading Rates. Int. J. Impact Eng. 2014, 68, 8–14. [Google Scholar] [CrossRef]
- Kruszelnicka, W.; Macko, M.; Łączny, D.; Bałdowska-Witos, P.; Lewandowski, J. The Use of Simulation Software Using the Discrete Element Method (DEM) for the Process of Materials Comminution. MATEC Web Conf. 2022, 357, 07005. [Google Scholar] [CrossRef]
- Cleary, P.W.; Sinnott, M.D.; Morrison, R.D. DEM Prediction of Particle Flows in Grinding Processes. Int. J. Numer. Methods Fluids 2008, 58, 319–353. [Google Scholar] [CrossRef]
- Syed, Z.; Tekeste, M.; White, D. A Coupled Sliding and Rolling Friction Model for DEM Calibration. J. Terramech. 2017, 72, 9–20. [Google Scholar] [CrossRef]
- Shi, D.; Cao, D.; Xue, J.; Deng, Y.; Liang, Y. DEM Studies on the Effect of Particle Breakage on the Critical State Behaviours of Granular Soils under Undrained Shear Conditions. Acta Geotech. 2022, 17, 4865–4885. [Google Scholar] [CrossRef]
- Hanley, K.J.; O’Sullivan, C.; Huang, X. Particle-Scale Mechanics of Sand Crushing in Compression and Shearing Using DEM. Soils Found. 2015, 55, 1100–1112. [Google Scholar] [CrossRef]
- Itasca Consulting Group Inc. PFC3D-Particle Flow Code 3 Dimension; Ver. 6.0; User’s Manual; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2010. [Google Scholar]
- Tsoungui, O.; Vallet, D.; Charmet, J.C. Numerical Model of Crushing of Grains inside Two-Dimensional Granular Materials. Powder Technol. 1999, 105, 190–198. [Google Scholar] [CrossRef]
- Chen, L.; He, Y.; Yang, Y.; Niu, S.; Ren, H. The Research Status and Development Trend of Additive Manufacturing Technology. Int. J. Adv. Manuf. Technol. 2017, 89, 3651–3660. [Google Scholar] [CrossRef]
- Da Cruz, F.; Emam, S.; Prochnow, M.; Roux, J.N.; Chevoir, F. Rheophysics of Dense Granular Materials: Discrete Simulation of Plane Shear Flows. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 72, 021309. [Google Scholar] [CrossRef]
- Andrade, J.E.; Chen, Q.; Le, P.H.; Avila, C.F.; Matthew Evans, T. On the Rheology of Dilative Granular Media: Bridging Solid- and Fluid-like Behavior. J. Mech. Phys. Solids 2012, 60, 1122–1136. [Google Scholar] [CrossRef]
- Das, S.K.; Das, A. Influence of Quasi-Static Loading Rates on Crushable Granular Materials: A DEM Analysis. Powder Technol. 2019, 344, 393–403. [Google Scholar] [CrossRef]
- Zheng, W.; Tannant, D.D. Grain Breakage Criteria for Discrete Element Models of Sand Crushing under One-Dimensional Compression. Comput. Geotech. 2018, 95, 231–239. [Google Scholar] [CrossRef]
- Lobo-Guerrero, S.; Vallejo, L.E. Application of Weibull Statistics to the Tensile Strength of Rock Aggregates. J. Geotech. Geoenviron. Eng. 2006, 132, 786–790. [Google Scholar] [CrossRef]
- Cil, M.B.; Buscarnera, G. DEM Assessment of Scaling Laws Capturing the Grain Size Dependence of Yielding in Granular Soils. Granul. Matter 2016, 18, 1–15. [Google Scholar] [CrossRef]
- Laufer, I. Grain Crushing and High-Pressure Oedometer Tests Simulated with the Discrete Element Method. Granul. Matter 2015, 17, 389–412. [Google Scholar] [CrossRef]
- McDowell, G.R.; Harireche, O. Discrete Element Modelling of Soil Particle Fracture. Géotechnique 2002, 52, 131–135. [Google Scholar] [CrossRef]
- Wang, J.F.; Huang, R.Q. DEM Study on Energy Allocation Behavior in Crushable Soils. Adv. Mater. Res. 2014, 871, 119–123. [Google Scholar] [CrossRef]
- Liu, H.Y.; Kou, S.Q.; Lindqvist, P.-A. Numerical Studies on the Inter-Particle Breakage of a Confined Particle Assembly in Rock Crushing. Mech. Mater. 2005, 37, 935–954. [Google Scholar] [CrossRef]
- Bagherzadeh, K.A.; Mirghasemi, A.A.; Mohammadi, S.; Bagherzadeh, K.A.; Mirghasemi, A.A.; Mohammadi, S. Numerical Simulation of Particle Breakage of Angular Particles Using Combined DEM and FEM. Powder Technol. 2011, 205, 15–29. [Google Scholar] [CrossRef]
- Zhu, F.; Zhao, J. Modeling Continuous Grain Crushing in Granular Media: A Hybrid Peridynamics and Physics Engine Approach. Comput. Methods Appl. Mech. Eng. 2019, 348, 334–355. [Google Scholar] [CrossRef]
- Ma, G.; Chen, Y.; Yao, F.; Zhou, W.; Wang, Q. Evolution of Particle Size and Shape towards a Steady State: Insights from FDEM Simulations of Crushable Granular Materials. Comput. Geotech. 2019, 112, 147–158. [Google Scholar] [CrossRef]
- Zhang, J.-Z.; Zhou, X.-P.; Zhu, J.-Y.; Xian, C.; Wang, Y.-T. Quasi-Static Fracturing in Double-Flawed Specimens under Uniaxial Loading: The Role of Strain Rate. Int. J. Fract. 2018, 211, 75–102. [Google Scholar] [CrossRef]
- Ben-Nun, O.; Einav, I.; Tordesillas, A. Force Attractor in Confined Comminution of Granular Materials. Phys. Rev. Lett. 2010, 104, 108001. [Google Scholar] [CrossRef]
- Ben-Nun, O.; Einav, I. The Role of Self-Organization during Confined Comminution of Granular Materials. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 231–247. [Google Scholar] [CrossRef]
- Suescun-Florez, E.; Kashuk, S.; Iskander, M.; Bless, S. Predicting the Uniaxial Compressive Response of Granular Media over a Wide Range of Strain Rates Using the Strain Energy Density Concept. J. Dyn. Behav. Mater. 2015, 1, 330–346. [Google Scholar] [CrossRef]
- Einav, I. Breakage Mechanics-Part II: Modelling Granular Materials. J. Mech. Phys. Solids 2007, 55, 1298–1320. [Google Scholar] [CrossRef]
- Lade, P.V.; Yamamuro, J.A.; Bopp, P.A. Significance of Particle Crushing in Granular Materials. J. Geotech. Geoenviron. Eng. 1997, 123, 889–890. [Google Scholar] [CrossRef]
- Kruyt, N.P.; Rothenburg, L. Shear Strength, Dilatancy, Energy and Dissipation in Quasi-Static Deformation of Granular Materials. J. Stat. Mech. Theory Exp. 2006, 2006, P07021. [Google Scholar] [CrossRef]
- Das, S.K.; Das, A. Strain-Rate Dependent Energy Redistribution during Isotropic Confined Comminution. Géotechnique Lett. 2020, 10, 542–549. [Google Scholar] [CrossRef]
- Hanley, K.J.; Huang, X.; O’Sullivan, C.; Kwok, F. Challenges of Simulating Undrained Tests Using the Constant Volume Method in DEM. AIP Conf. Proc. 2013, 1542, 277–280. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| ) | 2650 |
| Initial grain diameter (d) (m) | 0.001–0.003 |
| 0.2 | |
| Number of grains | 1932 |
| (N/m) | |
| 0.5 | |
| Weibull modulus (m) | 4.0 |
| Material strength * ) (MPa) | 14.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, S.K.; Abuel-Naga, H. Effect of Rate-Dependent Breakage on Strength and Deformation of Granular Sample—A DEM Study. Minerals 2024, 14, 1102. https://doi.org/10.3390/min14111102
Das SK, Abuel-Naga H. Effect of Rate-Dependent Breakage on Strength and Deformation of Granular Sample—A DEM Study. Minerals. 2024; 14(11):1102. https://doi.org/10.3390/min14111102
Chicago/Turabian StyleDas, Soukat Kumar, and Hossam Abuel-Naga. 2024. "Effect of Rate-Dependent Breakage on Strength and Deformation of Granular Sample—A DEM Study" Minerals 14, no. 11: 1102. https://doi.org/10.3390/min14111102
APA StyleDas, S. K., & Abuel-Naga, H. (2024). Effect of Rate-Dependent Breakage on Strength and Deformation of Granular Sample—A DEM Study. Minerals, 14(11), 1102. https://doi.org/10.3390/min14111102






