Methods for Estimating the Bond Work Index for Ball Mills

Abstract

Mining is a crucial sector in the global economy, providing essential materials for various industries, including construction, electronics, and energy. However, traditional mining practices often have significant negative impacts on the environment. Therefore, integrating sustainable practices into mining has become vital. Grinding is a crucial stage in the mineral processing industry, essential in liberating valuable minerals from ore. However, it is also one of the most energy-intensive processes in mining operations, consuming a substantial amount of electricity. Understanding and optimising electricity consumption in the grinding process is essential for enhancing energy efficiency and reducing operational costs. The relationship between electricity consumption in the grinding process and the Bond Work Index (BWI) is a crucial aspect of mineral processing and energy management in the mining industry. Understanding this relationship helps optimise grinding operations and improve energy efficiency. This review paper continues a previous work, where possible alternative modified methods for estimating the BWI in a Bond ball mill are presented. An analysis of selected methods is also provided to assess and obtain an accurate value of the BWI, which is essential in the grinding process. The methods for estimating the BWI using the wet method are presented. It is shown how the BWI can be estimated using dynamic elastic parameters and how changes in the Bond ball mill affect the BWI value. New equations for calculating the BWI and alternative procedures for evaluating the BWI in samples of non-standard size are proposed. The paper presents a comparative analysis of all presented methods.

1. Introduction

As one of the most energy-intensive industries, mining has a significant environmental impact, consuming large amounts of electricity and fuel. As the demand for minerals crucial to renewable energy technologies increases (lithium, cobalt, boron, nickel), improving energy efficiency in these processes becomes even more essential [1]. Not only does this mitigate emissions, but it also helps manage the overall environmental impact of resource extraction, which can be energy-intensive and polluting if not managed effectively. Improving energy efficiency in mining operations is crucial for advancing the global energy transition. Mining companies can reduce greenhouse gas emissions, lower operational costs, and conserve natural resources by enhancing energy efficiency. Thus, they can align with global goals for a low-carbon future, positioning the mining industry as a responsible partner in sustainable development. With a growing demand for minerals essential to renewable technologies, such as lithium, copper, and rare earth elements, improving energy practices in mining can directly support a cleaner, greener economy [1].

The International Energy Agency (IEA) [1] emphasises that transitioning mining processes to greener, more efficient systems will be vital for a low-carbon future, particularly as the demand projection for these minerals will grow rapidly with the expansion of green technologies. For instance, energy-efficient milling processes, such as implementing advanced comminution methods and more efficient equipment, can help reduce both energy use and operational costs, contributing to sustainable mining practices that align with global emissions goals. Furthermore, organisations like the World Economic Forum [2] stress the importance of responsible mining practices, including innovations in energy efficiency, to reduce the carbon footprint associated with mineral extraction and processing. The shift toward efficient energy use in mining is viewed as a necessary step to address the challenges of mineral supply for clean energy transitions while meeting net-zero targets.

Comminution operations account for a substantial portion of a mining site’s energy consumption. Mining companies can significantly reduce energy use and carbon emissions by adopting more efficient technologies and practices in milling, such as advanced grinding methods or better process controls. Enhancing energy efficiency in milling not only cuts costs and environmental impact but also contributes to the sustainability of mineral supply chains, making it a critical factor in supporting the shift toward a low-carbon future.

The Bond Work Index (BWI) of ores is a fundamental metric in mining and mineral processing that measures an ore’s resistance to crushing and grinding [3]. Mining companies have used this index for several objectives, as listed below. The comminution process typically accounts for a significant share of energy consumption in mining and mineral processing operations, ranging from 30% to 50% of the total energy used in the plant, depending on the material and process. In some cases, such as in hard rock mining, this figure can reach up to 70% [4,5,6].

• Energy efficiency: The BWI directly correlates with the energy required to reduce an ore to a specific particle size. Its value usually changes among different faces within the same mine. Hence, good knowledge of the BWI allows us to estimate the energy needed for grinding, making it a critical factor in assessing the energy efficiency of milling operations. Lower BWI values indicate ores have better grindability, potentially reducing energy costs.
• Equipment sizing and selection: The BWI value [7] is used in calculations to select the appropriate grinding equipment size and type. The BWI helps calculate the ideal energy input and load requirements, ensuring that equipment is not oversized or undersized for the task, improving operational efficiency and avoiding unnecessary equipment wear.
• Cost estimating: The BWI of an ore allows a more accurate estimate of milling costs (and potential deviations), helping in budgeting and cost control, especially in large-scale operations where grinding can account for a significant portion of operational expenses.
• Process optimisation: The BWI also aids process optimisation when designing grinding circuits to maximise throughput and minimise energy consumption. When possible, ores with high BWI values can be milled when the energy costs are lower, while processing ores with lower BWI when the electricity market is less favourable. In some cases, ores with high BWIs may benefit from pre-treatment processes to reduce hardness before milling, thereby saving energy [8].
• Comparison across ore types: The BWI provides a standardised way to compare the grindability of different ores. This comparison is valuable for feasibility studies, resource assessments, and benchmarking across operations, especially when sourcing ores from multiple deposits.
• In this paper, the revision of alternative procedures for estimating the BWI performed by Nikolić et al. [9] is updated and completed.

2. Alternative Methods for Estimating the Bond Work Index—Review

As previously stated, the Bond grindability test is often used to determine the energy requirements for grinding materials in rod and ball mills and for selecting equipment in comminution plants. Due to the difficulties in obtaining the BWI using the standard method, many researchers have developed alternative approaches [10]. Bond’s methodology can be considered a state-of-the-art procedure in milling plants based on Bond’s equation (Equation (1)) [3]. Despite its many advantages, this method has disadvantages, including its long duration and the need for a particular mill for experimental grinding. Nikolić et al. [9] described alternative shortened and simplified methods for estimating the BWI. This paper presents alternative modified methods based on which the BWI can be estimated.

$$BWI=1.1·{\displaystyle \frac{44.5}{{P_c}^{0.23}·G^{0.82}·\left(\frac{10}{\sqrt{P_{80}}}-\frac{10}{\sqrt{F_{80}}}\right)}} \left[{\displaystyle \frac{\mathrm{k}\mathrm{W}\mathrm{h}}{\mathrm{t}}}\right]$$

(1)

where: P_c is the closing screen size (μm), G is the net mass (grams) of undersize product per unit revolution of the mill, in g/rev, P₈₀ is the 80% passing product particle size (μm) and F₈₀ is the 80% passing feed particle size (μm).

Tüzün [11] stated that the range of activities involved in the Bond test can introduce errors that may easily affect the results due to a lack of understanding of the scope and limits of the test itself. It was found that when a 53 µm sieve is used as the comparative sieve, the values obtained for the BWI are higher than expected. The BWI values obtained in such cases are generally elevated due to errors that may arise during dry sieving. Dry sieving can cause sample agglomeration, which may lead to poor results when sieving finer fractions. The research was conducted on a quartz sample, using comparative sieves of (53, 75, 106) µm. This paper presents alternative modified methods based on which the BWI can be estimated. The procedure for the BWI via the wet method follows the standard Bond test, but with 1 kg of water added at each grinding stage and wet sieving conducted for 10 min. The oversize is then filtered and dried, and its mass is measured to calculate the mass of the undersize required to the mass of the newly created undersize per mill revolution, G [g/rev]. The test is complete when the mass of the undersize on the comparative sieve remains constant over three trials and is approximately equal to the mass of the ideal milling product. At that point, the Bond Work Index is calculated using Bond’s equation (Equation (1)), and the resulting value is multiplied by a correction factor of 1.3, as determined by Bond. The errors for this procedure ranged from 0.56% to −5.70%.

Deniz and Ozdag [12] investigated the influence of elastic parameters on grinding and their relationship. They studied the correlation between the parameters of Bond’s equation (BWI [kWh/t] and G [g/rev]) and the dynamic elastic parameters of the raw material (shear modulus G_d, elasticity modulus E_d and bulk modulus K_d). Once the relationship between these parameters had been determined, the next step was to find a practical method for estimating the grindability and BWI. Their investigations showed that the best correlation could be achieved between the BWI, [kWh/t], and the bulk modulus K_d. The bulk modulus K_d can also be called the modulus of rigidity. This parameter considers the state of porosity and discontinuities, such as joints in a material. The mean error determined for this method was 14.54%.

Deniz et al. [13] investigated the relationship between BWI, the circulating load (CL) and the size of the closing screen size P₁₀₀ (μm). Tests were performed on four samples of natural amorphous silica using the standard Bond grindability test with three different sizes of the closing screen size P₁₀₀ (150, 106 and 63 μm) and for four different circulating loads CL (100%, 250%, 400% and 550%). The BWI values were calculated using Equation (1). The results of the tests are shown in

Table 1. The values of the parameters G [g/rev] and the Bond Work Index for different closing screen sizes and circulating loads, according to [13].

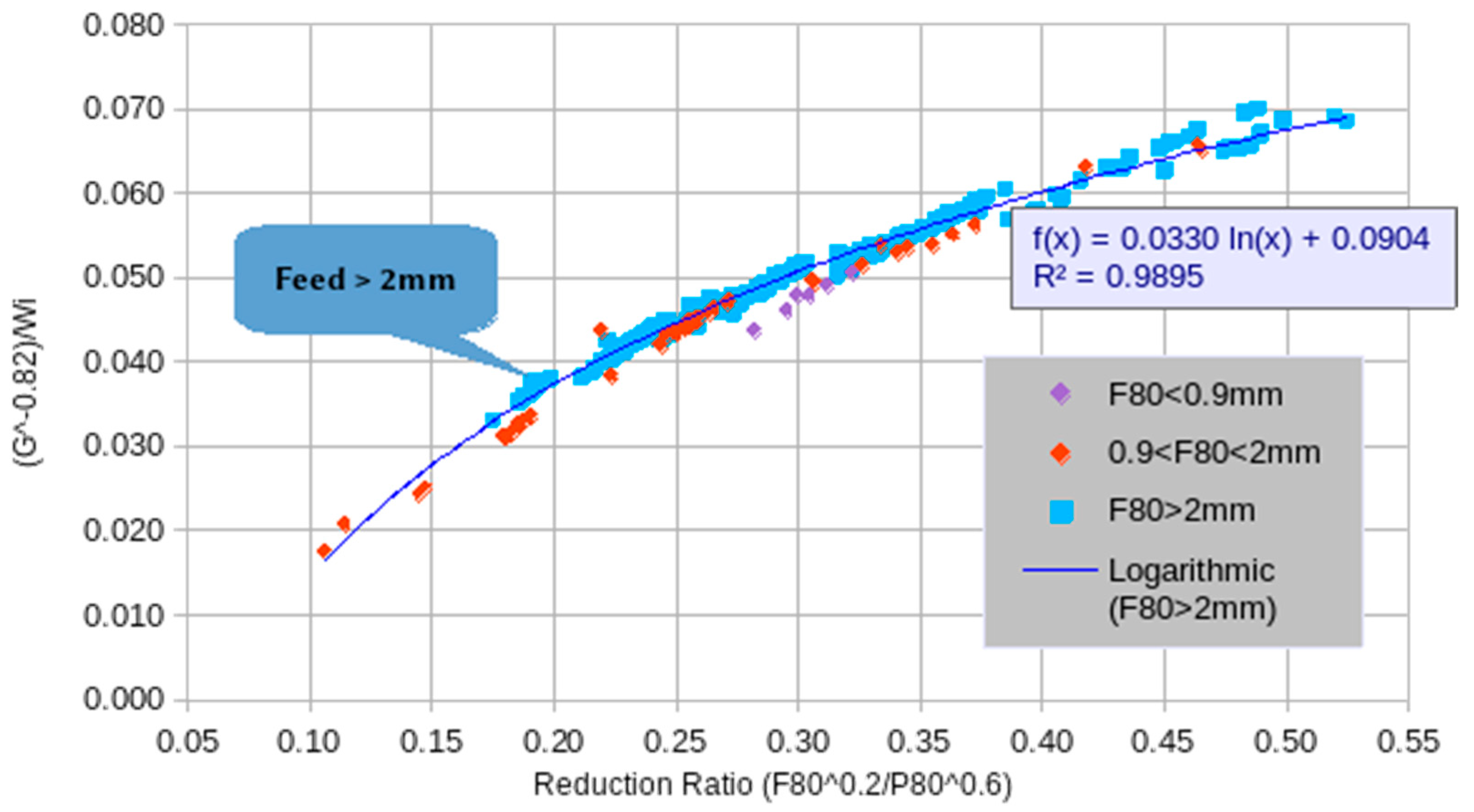
		Sample 1		Sample 2		Sample 3		Sample 4
P100	CL	G	BWI	G	BWI	G	BWI	G	BWI
150	100	2.091	11.11	2.066	11.41	1.627	12.99	1.895	11.89
150	250	2.911	8.94	3.297	8.05	2.272	10.78	2.055	10.83
150	400	3.047	8.52	3.720	7.05	2.386	10.28	2.450	10.07
150	550	3.247	8.12	4.036	6.51	2.639	9.61	2.737	9.19
106	100	1.454	13.77	1.307	14.62	1.239	14.95	1.349	14.30
106	250	1.958	11.44	1.858	11.94	1.739	12.67	1.584	13.16
106	400	2.095	11.18	2.709	9.25	1.823	12.16	1.759	12.42
106	550	2.195	10.75	3.143	8.24	1.951	11.53	1.927	11.77
63	100	0.755	18.11	0.679	19.16	0.652	19.45	0.688	19.07
63	250	1.216	14.62	1.095	15.88	1.051	15.88	1.110	15.48
63	400	1.360	13.40	1.567	11.93	1.405	13.11	1.282	14.66
63	550	1.516	12.25	1.807	10.50	1.505	12.37	1.476	12.38

. It was found that the BWI value increases with a lower circulating load for each sieve size and that the BWI value increases with the decreasing size of the sieve.

Kaya et al. [14] presented a study on the repeatability of the Bond grindability test with three commercially available Bond ball mills. Three ball mills were used, two were already used, and one was brand new. The inner surface of the new mill was quite rough and resembled the texture of an orange peel, while the other two mills had very smooth surfaces due to the long period of use. The irregularities or roughness of the surface of the new mill were removed using an electric sander and sandpaper. The BWI for this mill was obtained before and after removing the surface irregularities (roughness). The size, mass and number of balls used in these tests are presented in

Table 2. Distribution of milling balls in the Bond mill [14].

Nominal Ball Size [cm]	Bond’s Original Balls		Charge 1		Charge 2		Charge 3		Charge 4
	Nº of Balls	Mass [g]	Nº of Balls	Mass [g]	Nº of balls	Mass [g]	Nº of balls	Mass [g]	Nº of Balls	Mass [g]
3.68	43	8800	43	9106	43	8901	25	5885	18	4508
2.97	67	7209	67	7402	67	7206	39	4801	36	5378
2.54	10	672	10	660	10	605	60	3945	58	4208
1.91	71	2012	71	2125	78	2168	68	3331	71	3426
1.55	94	1432	94	832	66	1063	93	2163	102	2605
1.27					21	182
Total	285	20,125	285	20,125	285	20,125	285	20,125	285	20,125

.

The dimensions of some balls were removed and replaced by balls with new dimensions, and the number of balls was adjusted. After every tenth test, the weights of the balls were checked, and any ball whose initial weight was reduced by 10 g was replaced by a new one. Replacing worn balls with new ones results in higher operating costs, but these costs are minimal compared to the investment required for the test. The BWI was determined using the standard procedure for copper porphyry ore and calculated using Equation (1). The results of these tests (see

Table 3. Bond work index results in different mills with different ball charges [14].

Mill	Ball Charge	BWI (kWh/t)
Mill 1	Charge 1	12.50
	Charge 2	12.33
	Charge 3	11.77
	Charge 4	11.82
Mill 2	Charge 1	13.04
	Charge 2	12.75
	Charge 3	12.78
	Charge 4	12.31
Mill 3 without irregularities	Charge 1	12.11
	Charge 2	12.03
	Charge 3	11.77
	Charge 4	-
Mill 3 with irregularities	Charge 1	10.66
	Charge 2	10.85

) show that the BWI values can vary considerably for different standard Bond ball mills.

Ozkahraman [15] showed that the BWI [kWh/t] and the grindability index G [g/rev] can be estimated based on the brittleness value S of the material. He found a linear relationship between G and the brittleness value S of the material, which is expressed by Equation (2). The correlation coefficient is very high at 0.99.

G = 0.171 + 0.021∙S

(2)

The relationship between the brittleness value S of the material and the BWI also shows a high correlation of 0.97, and this relationship is expressed by Equation (3).

BWI = 61.839 ∙ 10.158 ∙ ln(S)

(3)

Chandar et al. [16] attempted to obtain the BWI using ore properties such as density (ρ), Protodyakonov strength coefficient (PSI) and ore hardness (RHN). The BWI was determined on samples of class −3.35 mm using the standard Bond method until a circulating load of 250% was reached. Two mathematical models were used to analyse the laboratory results: Artificial Neural Networks (ANNs) and regression analysis. Artificial Neural Networks (ANNs) were used to check the accuracy of the data based on the experimental results, while regression analysis was used to find correlative mathematical factors. The ANN was used to validate the reliability of the experiment data. It was found that the percentage deviation between the actual BWI values from the laboratory test and the predicted results derived from the ANN ranged from a maximum deviation of 5.44% to a minimum deviation of 0.05%. The correlation coefficient was determined individually for the relationships between the density, the Protodyakonov strength coefficient, the ore hardness and the BWI. A combined relationship was also established between the BWI and all other parameters. The models obtained from the regression analysis are given in Equations (4)–(6).

BWI = 8.85∙ρ − 12.58

(4)

BWI = 4.32∙(PSI) − 2.2

(5)

BWI = 0.34∙(RHN) − 6.61

(6)

The predicted values of the BWI are pretty close to the standard values determined by the Bond test. When estimating BWI with Equation (4), the error was between 0.27% and 7.46%, with Equation (5) between 0.09% and 9.91% and with Equation (6) between 0.02% and 5.34%.

Menéndez et al. [17] determined the BWI for six different samples (calcite, magnesite, feldspar, quartz, andalusite and glass). The particle size distribution results showed significant differences in the granulometric composition of all six samples. These differences in particle size distribution indicate that different values for the P₈₀ are obtained, and these data will show whether the P₈₀ parameter affects the grinding product. After ten grinding tests, all balls in the mill were checked. The BWI was calculated using Equation (1).

They used closing screen sizes with 500, 250, 125, 90, and 63 µm openings. At least four grindings were performed until the mass of the closing screen size became constant. Wet sieving was performed when the grinding product was sieved with the 90 and 63 µm sieves. The results are shown in

Table 4. P₈₀ values for all samples used in the Bond test [17].

Pk (μm)	P80 (μm)
	Andalusite	Quartz	Glass	Feldspar	Magnesite	Calcite
500	393	406	399	409	409	410
250	195	200	203	207	193	193
125	94	95	94	94	94	89
90	73	72	71	72	70	71
63	52	52	52	51	50	51

.

Table 4 shows that the P₈₀ values for all six samples are very similar. Based on these results, mathematical models were proposed to calculate the P₈₀ values:

P₈₀ = 0.8133∙P_c − 3.4562

(7)

P₈₀ =0.7704 ∙ P_c^1.0051

(8)

P₈₀ = 0.0001 ∙P_c² + 0.7539 ∙ P_c + 1.681

(9)

Based on the resulting data set, it was shown that Equation (7) provides the best results, with the error in the calculation of P₈₀ using Equation (7) being between 0.08% and 3.42%.

Again, Menéndez et al. [18] proposed a corrected formula for estimating the BWI. The study was conducted on five samples (quartz, glass, feldspar, magnesite and calcite) of class −3.35 mm. Closing screen sizes of 500, 250, 125, 90 and 63 µm were used. Wet sieving was performed with the 90 and 63 µm closing screen sizes to accurately obtain the mass of the oversize of the closing screen size and the particle size distribution. The BWI was determined using the standard Bond method. Alternative formulas were proposed for the mass of the newly formed undersize per revolution of the mill G [g/rev] and for calculating the BWI. They concluded that G depends on the percentage of fine fractions of the fresh sample fed to the mill for the new grinding test. On this basis, the alternative equation (Equation (10)) for the mass of new undersized grain produced per mill revolution G_f [g/rev] was derived.

$$G_f={\displaystyle \frac{G}{\left(1-\left(0.01·\frac{U}{3.5}\right)\right)}}$$

(10)

where $G_f$ is the corrected mass of the newly produced undersize grain per mill revolution [g/rev], $G$ is the mass of the newly produced undersize grain per mill revolution and $U$ is the mass of the sample.

Since the BWI is based on a constant sample volume of 700 cm³, but the results are expressed in grams, two samples with the same grindability but different densities must have different values for the parameter G. A new equation (Equation (11)) was proposed to calculate G_γ [g/rev], as shown below:

$$G_{\gamma }={\displaystyle \frac{G_f}{\gamma }}={\displaystyle \frac{G}{\gamma ·\left[1-\left(0.01·\frac{U}{3.5}\right)\right]}}$$

(11)

where $\gamma$ is the density of the sample.

The alternative formula for calculating the corrected BWI can be found in Equation (12).

$$BW{i}_c={\displaystyle \frac{49.1}{\left[{P_c}^{0.23}·{\left\{\frac{G}{\gamma ·\left[1-\left(0.01·\frac{U}{3.5}\right)\right]}\right\}}^{0.82}·\left(\left(\frac{10}{\sqrt{P_{80}}}\right)-\left(\frac{10}{\sqrt{F_{80}}}\right)\right)\right]}}$$

(12)

When comparing the values of the BWI determined using the standard Bond Equations (1) and (12), the error ranged from 10.21% to 30.16%, the worst adjustment among the revised alternatives.

Josefin and Doll [19] presented a method for correcting the work index measured on a sample from one closing screen size $P_{80}$ to another closing screen size $P_{80}$ using a calibration sample. They developed a framework suitable for metallurgical data sets that allows practitioners to calibrate and correct any work index for any variable closing screen size based on a given corresponding calibration. A standard Bond test was performed in a ball mill on a −3.35 mm grade sample using different closing screen sizes (300, 212, 150, 106 and 75 μm). Two different samples are needed to create a model that adapts to the process: a reference sample to calibrate the exponent (−a) and another to adjust and determine the coefficient (K_test). The corrected BWI is calculated using Equation (13), as shown below:

$$BW{I}_{corrected}={\displaystyle \frac{K_{test}·{\left(P_{80}\right)}^{-a}}{10·\left({\left(P_{80}\right)}^{-0.5}-{\left(F_{80}\right)}^{-0.5}\right)}}$$

(13)

where $-a$ is the exponent derived from the reference sample and $K_{test}$, a sample-specific coefficient, which varies between unknown samples, is calculated using Equation (14).

$$K_{test}={\displaystyle \frac{10·BWI·\left({\left(P_{80}\right)}^{-0.5}-{\left(F_{80}\right)}^{-0.5}\right)}{{\left(P_{80}\right)}^{-a}}}$$

(14)

The procedure is carried out as follows:

• Calculate the specific energy for each calibration sample to determine the relationship between energy and particle size of the sample.
• Plot the energy versus particle size graph and adjust the power level. Read the exponent value (−a).
• Determine the BWI in the ball mill for the desired sample at each closing screen size.
• Calculate the coefficient (K_test) using Equation (14). Determine the values $P_{80}$ and $F_{80}$ from the particle size distribution analysis.
• Calculate the corrected BWI using Equation (13) for the desired $P_{80}$ parameter and the obtained K_test value.

Based on their studies of porphyry copper ore, Josefin and Doll [19] found that the value of the exponent $-a$ is (−0.56). Using a fixed exponent of (−0.56) for different types of ores, where the actual exponent differs significantly from this value, can lead to a high error percentage in the measured values. This exponent only applies to porphyry copper and other ores with exponents in this range. The values obtained for the corrected work index and those obtained with the Bond test are shown in

Table 5. Comparison of the results of the corrected BWI and the results obtained with the standard Bond method [19].

${\mathit{P}}_{\mathit{c}}$ (μm)	$\mathbf{BWI} \left(\mathbf{k}\mathbf{W}\mathbf{h}/\mathbf{t}\right)$		$\mathbf{Specific} \mathbf{Energy} \left(\mathbf{k}\mathbf{W}\mathbf{h}/\mathbf{t}\right)$		Error Δ (%)
	Measured Work Index	Calibrated Work Index	Measured Energy	Calibrated Energy
300	20.92	21.09	10.09	10.17	0.8
212	19.89	20.08	12.45	12.57	1.0
150	19.50	19.50	15.10	15.10	0.0
106	19.39	19.09	18.45	18.17	1.5
75	19.37	18.80	23.32	22.64	2.9

.

Ciribeni et al. [20] continued their research on the relationship between the kinetic parameters obtained with the cumulative kinetic model (CKM) and the parameters of the standard Bond test (G and BWI were used to propose an alternative method for evaluating the Bond Work Index with practical advantages). The aim was to establish a correlation between the kinetic CKM parameter k and the energy consumption parameters in the standard Bond test. The procedure follows the methodology described by Ciribeni et al. [21], where the kinetic parameter $k$ is determined by Equation (15) and the kinetic parameters C and n by Equation (16). Their investigations revealed a relationship between the parameter G (determined by the standard Bond method) and the kinetic parameter $k$ (determined by simulation), represented by Equation (17).

$$\ln \left(W_{\left(x,t\right)}\right)-\ln \left(W_{\left(x,0\right)}\right)=k·t$$

(15)

$$\ln \left(k\right)=\ln \left(C\right)+n·\ln \left(x\right)$$

(16)

$$G=14.97·k$$

(17)

In addition, they found a relationship between the BWI (calculated by the standard Bond Equation (1) and the kinetic parameter $k$ (determined by simulation), represented by Equation (18).

$$W_{i_{\left(SIM\right)}}=-10.07·\ln \left(k\right)-7.28$$

(18)

The comparative values of the BWI, which were determined using the standard Bond Equation (1) and the values derived from Equation (18), showed an error ranging from 1.10% to −8.99%.

García et al. [22] analysed grinding results over various particle sizes and critical metal ores. They investigated the variability of the BWI in the Bond ball mill and Bond rod mill to propose a methodology to model this variability. A series of tests were defined to analyse the variations in grindability characteristics for selected ores. Each test was performed using different comparative sieves for each ore. For each obtained value of BWI and $G$ for each sample, they tried to model the variation with the comparative sieve size. Based on the results, they concluded that the BWI values varied significantly depending on the particle size of the milled product in both the Bond ball mill grindability tests and the Bond rod mill grindability tests. The obtained curves show no clear correlation between BWI and P₁₀₀ sieve size. However, a parabolic curve was observed for the parameter $G$ with the change in comparative sieve size for all tested samples. The coefficients of determination for the parameter $G$ with P₁₀₀ were above 99.70% for all samples. They suggested that the parameter $G$ should be called the Maxson grindability index to recognise the value of the initial research in the field led by Walter Maxson, the mentor of Fred Bond at the beginning of his research career [22,23].

Again, García et al. [24] analysed the variability of the BWI test parameters, examining several variable factors resulting from the particle size distribution of the initial sample and the ground product. The variables selected to perform the variability analysis in the standard Bond ball mill test are as follows:

• Feed particle size, $F_{80}$ (μm).
• Closing circuit sieve (should coincide with maximum size in the closed-circuit product, $P_{100}$ (μm).
• Undersize percentage in the feed, u (%).

Table 6. Variables used for the formation of the synthetic feed samples [24].

Variables		Levels
		1	2	3
$F_{80}$ (µm)	D	2500	2000	1250
$P_{100}$ (µm)	C	500	400	200
u (%)	F	0	10	20

contains the variables used to create the synthetic feed samples for the BWI tests.

Table 7. Experimentally determined results [24].

	C1
	D1-F1	D1-F2	D1-F3	D2-F1	D2-F2	D2-F3	D3-F1	D3-F2	D3-F3
BWI (kWh/t)	7.82	8.54	8.96	8.69	9.09	9.50	11.25	11.95	12.13
G (g/rev)	6.552	6.008	5.668	6.432	6.265	5.809	6.110	6.046	5.773
	C2
	D1-F1	D1-F2	D1-F3	D2-F1	D2-F2	D2-F3	D3-F1	D3-F2	D3-F3
BWI (kWh/t)	8.07	8.39	8.45	8.49	8.84	8.80	10.16	10.79	10.69
G (g/rev)	5.427	5.220	4.995	5.504	5.383	5.332	5.506	5.377	5.241
	C3
	D1-F1	D1-F2	D1-F3	D2-F1	D2-F2	D2-F3	D3-F1	D3-F2	D3-F3
BWI (kWh/t)	8.85	9.15	9.29	9.24	9.33	9.46	10.93	11.01	10.50
G (g/rev)	3.300	3.157	3.044	3.264	3.235	3.121	3.087	3.082	3.121

shows the results of the BWI and the parameter G, which were determined after carrying out 27 standard Bond tests.

A formal analysis of the results was performed using an ANOVA test, which was applied to both the BWI and G. The results of the ANOVA test showed that, in the case of BWI, F₈₀ was the primary source of variability, followed by the binary interaction F₈₀ and undersize feed content (u%). The conclusion is that the variability of the BWI is more influenced by the granulometric composition of the initial sample ($F_{80}$ value), even to a greater extent than P₁₀₀. In the case of the$G$ parameter, the ANOVA test showed that the primary source of variability was P₁₀₀ and that the granulometric composition of the initial sample had almost no influence.

Levin [25] proposed a method for estimating the grindability of fine material, including an estimate of the energy required to grind fine material. For fine materials, a comparative grinding test must be performed in which the reference material from the mill is ground in a laboratory mill to determine the equivalent energy consumption per revolution of the laboratory mill. Since the Bond mill and the operating conditions are standardised, the equivalent energy consumption per revolution is constant and is referred to as $B$. Once the value of $B$ is determined, the mill can assess the grindability of fine material without the need for reference materials. The value of $B$ can be calculated from any Bond grindability test. The research concluded that the equivalent energy per revolution for the Bond grindability test is constant and close to $B=198·{10}^{-7}$ kWh/revolution and calculated values of $B$ that deviate from this value are from materials for which the Bond grindability test gives misleading or incorrect BWI values. The proposed grindability test for fine materials indicates the specific energy required to grind a given material from its initial size to a given size. The operating conditions defined for the Bond test are also applied to the grindability test for fine-size materials.

At the time this test was described, there was only one source of suitable material, which means that the few comparative data obtained from the test and energy consumption measurements in industrial plants cannot adequately assess the value of the test.

Magdalinovic et al. [26] estimated the BWI on samples with non-standard sizes (−3.327 + 0; −2.356 + 0; −1.651 + 0; −1.168 + 0; −0.833 + 0) mm. Based on the results obtained, rules were established for adjusting Bond’s equation parameters $G$ [g/rev], $P_{80}$ [μm] and $F_{80}$ [μm]. Adjustments were identified depending on the changes in particle size of the sample. Magdalinovic et al. [26] came to the following conclusion:

$$F_{80}=3327·k_{\mathrm{F}} , \left(ì\mathrm{m}\right)$$

(19)

where $k_{\mathrm{F}}$ is the coefficient ranging from 0.7 for softer materials to 0.8 for harder materials.

$$P_{80}=P_n$$

(20)

where $P_n$ is the grinding size of the product for a sample with non-standardised particle size.

$$G={\displaystyle \frac{G_n \ln F_n}{\ln F_{80}}}$$

(21)

where $G_n$ and $F_n$ are values estimating from the Bond test with the sample with non-standardised particle size and $G$ and $F_{80}$ are values corresponding to the standard particle size sample (−3.327 + 0) mm.

For a sample with a non-standardised particle size (smaller than −3.327 + 0 mm), the Bond test is first performed using a closing screen size of $P_c$ [μm] to obtain the parameters $F_n$ [μm], $P_n$ [μm] and $G_n$ [g/rev]. The following values are then calculated: $F_{80}$ (Equation (19)), $P_{80}$ (Equation (20)) and $G$ (Equation (21)), and finally, the BWI is calculated using Bond’s formula (Equation (1)).

Magdalinovic et al. [26] state that the most minor error is achieved with a coefficient value of$k_{\mathrm{F}}=0.75$. The comparative values of BWI obtained from the Bond test on samples with a standard particle size and the calculated values based on the results of the Bond test on samples with a non-standard particle size (−0.833 + 0 mm) for the coefficient value $k_{\mathrm{F}}=0.75$ are listed in

Table 8. Sample class (−0.833 + 0) mm, $k_{\mathrm{F}}=0.75$ [26].

	${\mathit{P}}_{\mathit{c}}=75 \mathsf{\mu }\mathbf{m}$			${\mathit{P}}_{\mathit{c}}=149 \mathsf{\mu }\mathbf{m}$
Sample	$\mathbf{BWI} \left(\mathbf{k}\mathbf{W}\mathbf{h}/\mathbf{t}\right)$		Error Δ (%)	$\mathbf{BWI} \left(\mathbf{k}\mathbf{W}\mathbf{h}/\mathbf{t}\right)$		Error Δ (%)
	Bond Test	Magdalinovic		Bond Test	Magdalinovic
Dolomite	12.70	12.86	1.26	9.82	9.82	0.00
Copper ore	15.67	15.86	1.21	15.32	15.10	−1.44
Quartzite	22.63	23.47	3.71	19.00	19.38	2.00

.

Nikolić and Trumić [27] developed a method for estimating the BWI for fine materials. Their tests were carried out with different size classes (−3.35 + 0 mm; −2.36 + 0 mm; −1.70 + 0 mm; −1.18 + 0 mm; −0.850 + 0 mm). Based on their results, they found that BWI for fine materials can be calculated using Equation (22), as shown below:

$$W_{Fm}=k{\displaystyle \frac{BWI}{{F_{80}}^{0.05}}}$$

(22)

where $W_{Fm}$ is the work index for fine materials (kWh/t); $BWI$ is the Bond Work Index [8] for a standard size sample (−3.35 + 0) mm, (kWh/t); $F_{80}$ is the 80% passing fine material particle size (μm) and $k$ is the coefficient ranging from 1.47 (soft–medium–hard ores) to 1.49 for hard ores.

The comparative results of the experimentally estimating BWI for fine material and by Equation (22) are listed in

Table 9. Comparative experimental vs. calculated results using Equation (22).

Sample	Size (mm)	${\mathbf{F}}_{80}$ (μm)	${\mathbf{P}}_{\mathbf{c}}=75 \mathsf{\mu }\mathbf{m}$$, \mathit{k}=1.47$
			$\mathit{B}\mathit{W}\mathit{I}$ (kWh/t)	${\mathit{W}}_{\mathit{F}\mathit{m}}$ (kWh/t)	Error Δ (%)
Zeolite	−3.35 + 0	2440	9.834	-	-
	−2.36 + 0	1652	10.010	9.980	+0.30
	−1.70 + 0	1090	10.197	10.190	+0.07
	−1.18 + 0	727	10.371	10.399	−0.27
	−0.850 + 0	544	10.572	10.550	+0.21

.

Nikolić et al. [28] presented a methodology for estimating the BWI when coarse or fine material is present in the initial sample, where $F_{100}\ne 3.35 \mathrm{mm}$. The Bond grindability test is first conducted for a non-standard feed size sample. The data obtained from this test are then used to estimate the Bond Work Index for a sample of standard feed size.

Figure 1 shows the relationship between ore grindability (ordinates) and the reduction ratio (abscises). The abscise value is calculated according to Equation (23), and the ordinate value according to Equation (24). The ordinate component contains the same exponent of 0.82 for the parameter $G$ as Bond specified in his equation. The relationship between the parameters${F_{80}}^{0.2}$ and ${P_{80}}^{0.6}$, i.e., coarse and fine samples, shows considerable variations in ore hardness for standard sizes. For the ordinates, the ratio values of $G^{\left(-0.82\right)}$ for the BWI ($W_i$) are presented for grindability degrees at a standard size for coarse and fine samples. The authors point out that the presented model is only valid for ores with a typical “Hukki exponent” (in the range of −0.4 to −0.7) and does not apply to some really “odd” ores.

$$X={\displaystyle \frac{{F_{80}}^{0.2}}{{P_{80}}^{0.6}}}$$

(23)

$$Y={\displaystyle \frac{G^{-0.82}}{W_i}}$$

(24)

The first condition for the model to apply to any coarse or fine material is to calculate the “X” and “Y” parameters using Equations (23) and (24) and check that they fall along the regression curve shown in Figure 1. If the first condition is met (i.e., the sample is close to the empirical curve), the corrected BWI for the standard particle size of the sample can be calculated using the models shown in Equations (25) and (26), as shown below:

$$Y_1=0.033·\ln \left(X\right)+0.0904$$

(25)

where $X$ is calculated according to Equation (23); $F_{80}$ is assumed to be 2440 µm ($F_{80}=2440 \mathsf{\mu }\mathrm{m}$); and $P_{80}$ is taken from the standard Bond test.

$$W{i}_{corr}={\displaystyle \frac{G^{-0.82}}{Y_1}}$$

(26)

The error determined by the authors ranges from 0.00% to 11.98%. The maximum error of 11.98% was observed in copper ore from Canada, which was significantly coarser than all other samples tested. Significantly lower errors were found for the other samples, confirming the accuracy and validity of the method presented. The technique is not restricted to a specific P₁₀₀; it was tested on five different closing screen size values: 75, 106, 150, 212 and 300 µm.

3. Discussions and Conclusions

The presented methods aim to demonstrate that the BWI can be estimated using alternative approaches from the standard method. Additionally, valuable information is provided to help avoid errors during the execution of the Bond test, highlighting which parameters have the most significant impact on the BWI estimating. Some methods yield substantial errors compared to the standard method, and such methods for estimating BWI should not be used. However, there are methods with 0% error (producing BWI values identical to the standard method), and these methods could be helpful for BWI estimation, especially considering the time required to perform a single Bond test.

This paper presents alternative modified methods for estimating the BWI that have been proposed through the years. The presented methods demonstrated how the BWI can be estimated using an alternative method rather than the standard Bond grindability test.

Table 10. Errors, advantages and disadvantages of the presented methods.

Authors	Methods	Errors, (%)		Advantages	Disadvantages
		Min	Max
Tüzün [11]	Wet method.	0.56	−5.70	No sample agglomeration.	The method takes longer than the standard Bond method. Filtration and drying of samples are required.
Deniz and Ozdag [12]	Estimating the BWI from dynamic elastic parameters.	−0.08	−32.4	/	The authors conducted tests only on soft and medium–hard samples. A significant error is obtained.
Deniz et al. [13]	Relationship between BWI, the circulating load (CL) and the closing screen size P100 (μm).	/	/	/	The BWI value increases with a lower circulating load for each sieve size, and the BWI value increases with the sieve size decreases.
Kaya et al. [14]	Repeatability of the Bond grindability test among three commercially available bond ball mills.	/	/	It has been proven that different BWI values are obtained for the same sample when using different Bond ball mills.	The tests were conducted on only one sample.
Ozkahraman [15]	The BWI [kWh/t] and the grindability index G [g/rev] can be estimated based on the brittleness value of the material.	/	/	To estimate BWI, the bond test is not necessary. The correlation coefficient is very high at 0.99.	The author did not specify the error obtained with this method or the number of samples used in the research.
Chandar et al. [16]	Estimating the BWI based on ore characteristics (density, Protodyakonov strength coefficient, and ore hardness).	−0.06	9.91	To estimate BWI, the bond test is not necessary.	The research was conducted on only three different samples, which belong to soft and medium–hard ores.
Menéndez et al. [17]	The authors proposed equations for estimating the P80 parameters.	0.08	3.42	Offers an indirect method of estimating P80.	It includes wet sieving when closing screen sizes of (90 and 63) µm are used, extending the grindability test time.
Menéndez et al. [18]	A corrected equation for estimating the BWI.	10.21	30.16	Considers the specific gravity of the sample.	It includes wet sieving when closing screen sizes of (90 and 63) µm are used, extending the grindability test time. Significant errors are obtained with this method.
Josefin and Doll [19]	Method for correcting the work index measured on a sample from one closing screen size P80 to another closing screen size P80 using a calibration sample.	0.0	2.9	Easy estimation of BWI for any closing screen size P80. It is not necessary to perform the Bond grindability test.	The method was applied to only one sample. It is necessary to perform the grindability test for the reference sample, increasing the time to complete the test.
Ciribeni et al. [20]	An alternative method for evaluating the BWI with practical advantages	1.1	−8.99	For estimating BWI, it is not necessary to perform the Bond grindability test. The test is conducted by grinding for 5 min, which reduces the testing time.	The tests were conducted on only two closing screen sizes of P80.
García et al. [24]	The analysis variability of the BWI test parameters	/	/	The variability of the BWI is more influenced by the granulometric composition of the initial sample (F80 value), even to a greater extent than P100.	/
Levin [25]	Method for estimating the grindability of fine material	/	/	This method allows for an immediate evaluation of the required energy for grinding fine materials.	When this test was described, only one source of the appropriate material was available, so the comparative data cannot be used to assess the value of the test.
Magdalinovic et al. [26]	Estimation of BWI on samples of non-standard sizes.	0.0	2.0	A simple method for estimating BWI on samples of non-standard sizes.	The method can only be used for closing screen sizes of 75 and 149 µm.
Nikolić and Trumić [27]	Estimation of BWI for finer samples.	0.07	0.30	A quick and simple method for estimating BWI for finer samples. Yielding very minimal error.	The method can only be used for closing screen sizes of 75 µm.
Nikolić et al. [28]	Method to obtain a corrected BWI valid with a non-standard feed size	0.00	11.98	It can be applied to estimating the BWI when coarse or fine material is present in the initial sample, with F100 ≠ 3.35 mm. The method is not restricted to a specific P100.	The model is only valid for ores with a typical “Hukki exponent” (in the range of -0.4 to −0.7) and does not apply to some really “odd” ores.

provides an overview of all the described methods, including their errors, advantages, and disadvantages.

A method for estimating BWI using a wet process was introduced [11]. Tests have shown that fine particles may agglomerate, so the wet process should be introduced. Other methods illustrate the impact of dynamic elastic parameters on estimating the BWI [12] and how increasing and decreasing the circulating load in the grinding process affects BWI values. It has been proven that the BWI value rises with a lower circulating load for each sieve size, and the BWI value increases with the sieve size decreases.

Another method shows how repeating the Bond grindability test affects the BWI value [14]. It has been proven that different BWI values are obtained for the same sample when using different Bond ball mills. A method is given for estimating the BWI [kWh/t] and the grindability index G [g/rev] based on the brittleness value of the material [15]. The author did not specify the error obtained with this method or the number of samples used in the research.

The BWI can also be estimated based on ore characteristics such as density, Protodyakonov strength coefficient, and ore hardness [16].

Another method [19] is also presented for correcting the work index measured on a sample from one closing screen size P₈₀ to another closing screen size P₈₀ using a calibration sample, and it can be applied to estimate the BWI for any P₈₀.

A method is given to estimate the BWI with only one grinding cycle of 5 min [20]. The technique can be applied on only two closing screen sizes P₈₀. Another approach [24] proves that the BWI variability is more influenced by the particle size distribution of the initial sample (F₈₀ value), even to a greater extent than P₁₀₀.

A method for evaluating the grindability of fine material is also presented [25]. This method allows for an immediate evaluation of the required energy for grinding fine materials. When this test was described, only one source of the appropriate material was available, so the comparative data cannot be used to assess the value of the test.

The method for evaluating the BWI on samples of non-standard sizes is given [26]. The procedure is straightforward and fast, but it can be applied only for closing screen sizes of (75 and 149) µm.

Another method for evaluating the BWI for finer samples is also presented [27]. The process is fast, and minimal error is obtained. The technique can only be used for closing screen sizes of 75 µm. Finally, another method is also given to obtain a corrected BWI valid for non-standard feed sizes [28]. It can be applied to evaluating the BWI when coarse or fine material is present in the initial sample, with F₁₀₀ ≠ 3.35 mm. The method is not restricted to a specific P₁₀₀. The model is only valid for ores with a typical “Hukki exponent” (−0.4 to −0.7).

All methods presented in this paper aim to assist practitioners and mining engineers in estimating BWI values as efficiently and accurately as possible. The described procedures may help in estimating BWI if problems similar to those faced by the authors of the presented papers are encountered. Many believe Bond’s work remains insufficiently defined regarding the standard Bond test [29,30], which is why many alternative modified methods for estimating BWI have been developed. Nevertheless, the Bond standard test is considered the industry standard. Therefore, the authors want to state that BWI should be determined using the standard Bond test whenever possible, so practitioners and mining engineers should use the other alternative methods in another case.