Linear Correlations of Gibbs Free Energy of REE Phosphates (Monazite, Xenotime, and Rhabdophane) and Internally Consistent Binary Mixing Properties
Abstract
1. Introduction
2. Mathematical Formulation
2.1. Linear Free Energy Correlation
2.2. Linear Correlation between Mixing Binaries
3. Data Availability and Formatting
3.1. Aqueous REE3+ Ion Parameters
3.2. REE Phosphate (Monazite, Xenotime, and Rhabdophane) Parameters
3.3. Available Margules Parameters for REE Phosphate End-Member Binaries
4. Results
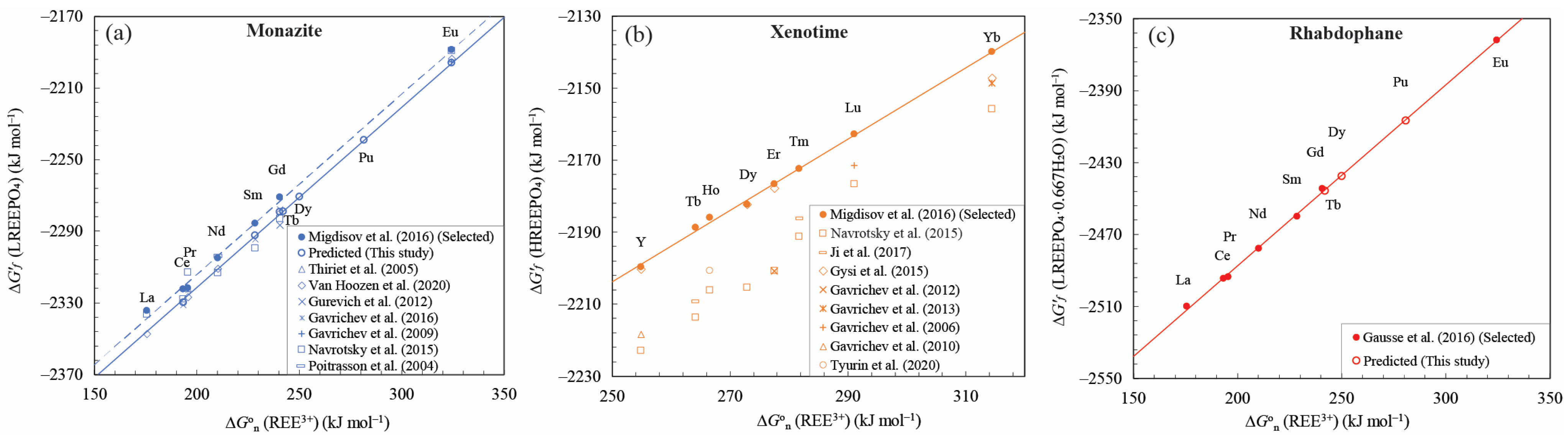
4.1. Linear Free Energy Relationships for REE Phosphates and Aqueous Ions
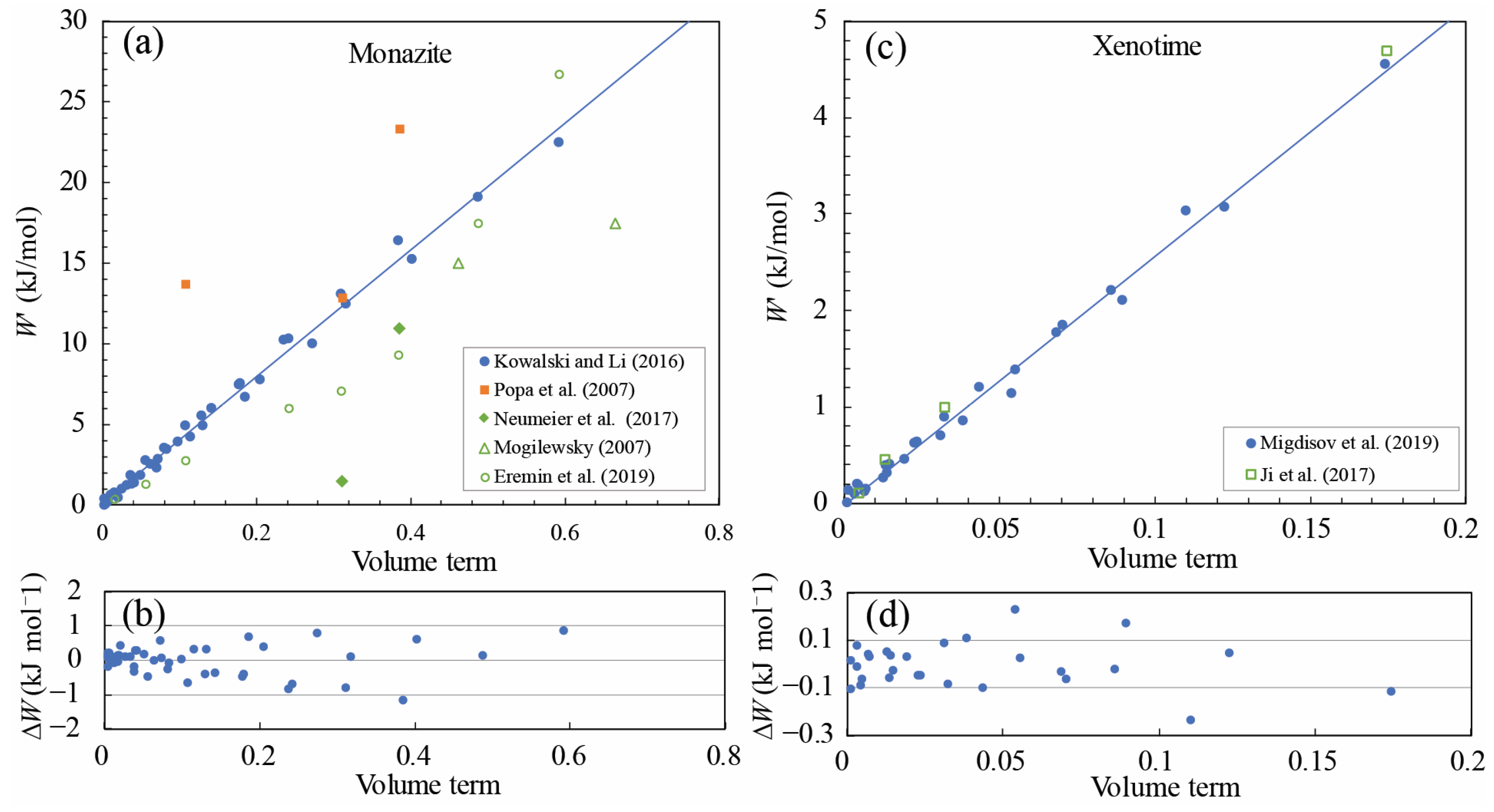
4.2. A Semi-Empirical Correlation for Margules Parameters of REE Phosphate End-Members
5. Discussion
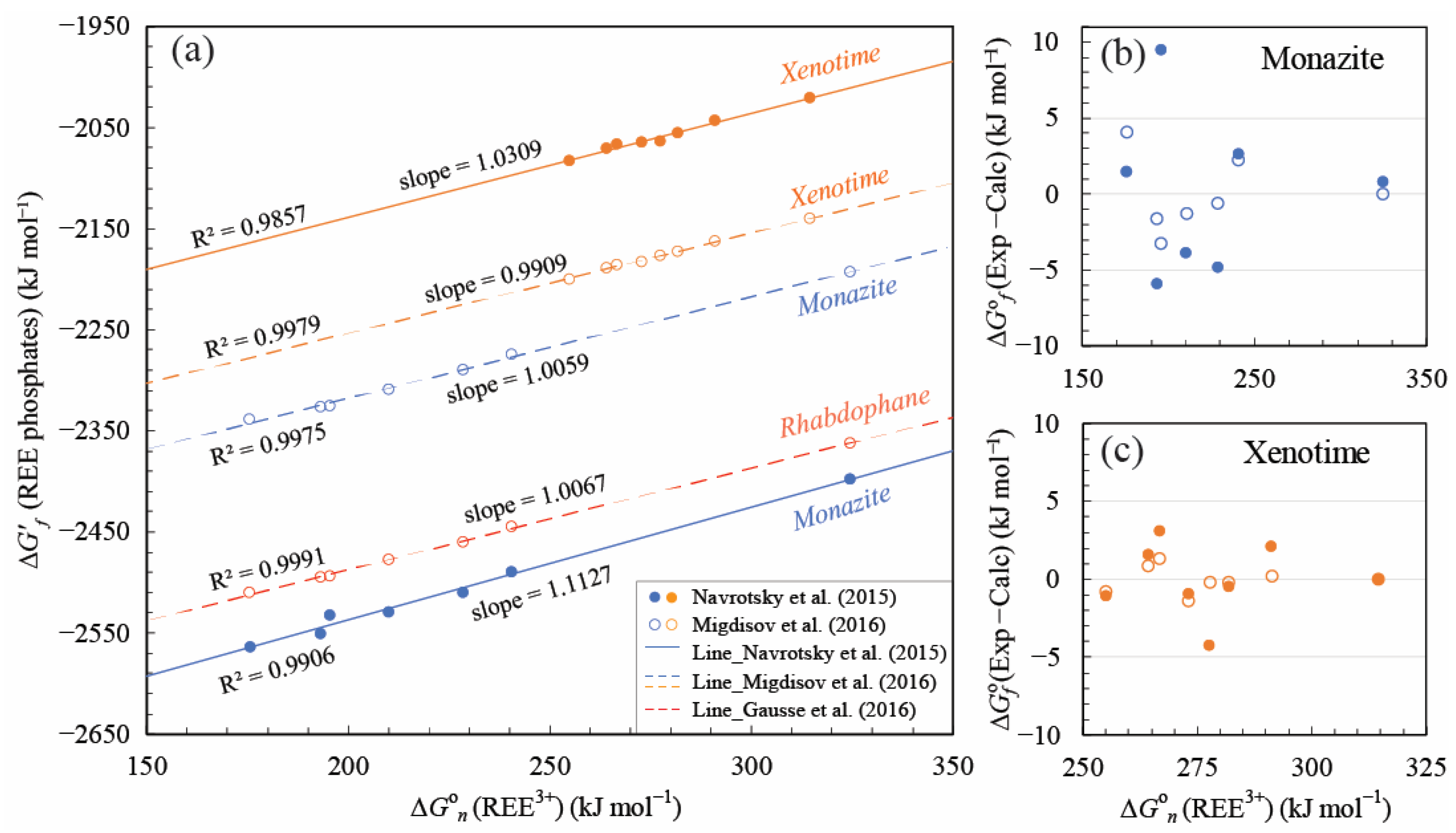
5.1. Comparisons with Previous Studies and Data Evaluation
5.1.1. Linear Correlation Calculated by Other ∆G°f Choice in the Literature
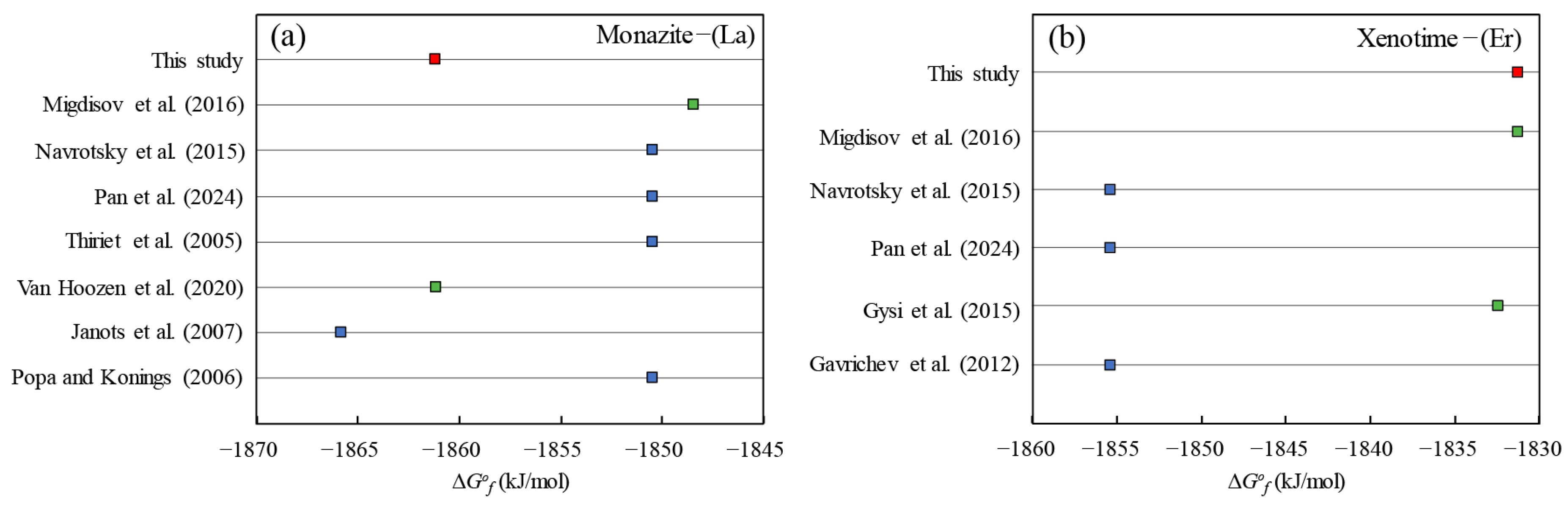
5.1.2. Comparisons of the Calculated ∆G°f Values with Other Data in the Literature
5.1.3. Comparisons of the Solubility Product (log Ksp) Performed in This Study using the Data in the Literature
5.2. Evaluation of Margules Parameter W and Comparisons with Previous Studies
6. Conclusions and Recommendations
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grandell, L.; Lehtilä, A.; Kivinen, M.; Koljonen, T.; Kihlman, S.; Lauri, L.S. Role of critical metals in the future markets of clean energy technologies. Renew. Energy 2016, 95, 53–62. [Google Scholar] [CrossRef]
- Goodenough, K.M.; Wall, F.; Merriman, D. The rare earth elements: Demand, global resources, and challenges for resourcing future generations. Nat. Resour. Res. 2018, 27, 201–216. [Google Scholar] [CrossRef]
- Smith, M.P.; Henderson, P.; Zhang, P. Reaction relationships in the Bayan Obo Fe-REE-Nb deposit Inner Mongolia, China: Implications for the relative stability of rare-earth element phosphates and fluorocarbonates. Contrib. Mineral. Petrol. 1999, 134, 294–310. [Google Scholar] [CrossRef]
- Smith, M.P.; Moore, K.; Kavecsánszki, D.; Finch, A.A.; Kynicky, J.; Wall, F. From mantle to critical zone: A review of large and giant sized deposits of the rare earth elements. Geosci. Front. 2016, 7, 315–334. [Google Scholar] [CrossRef]
- Harlov, D.E.; Meighan, C.J.; Kerr, I.D.; Samson, I.M. Mineralogy, Chemistry, and Fluid-Aided Evolution of the Pea Ridge Fe Oxide-(Y+REE) Deposit, Southeast Missouri, USA. Econ. Geol. 2016, 111, 1963–1984. [Google Scholar] [CrossRef]
- Dushyantha, N.; Batapola, N.; Ilankoon, I.; Rohitha, S.; Premasiri, R.; Abeysinghe, B.; Ratnayake, N.; Dissanayake, K. The story of rare earth elements (REEs): Occurrences, global distribution, genesis, geology, mineralogy and global production. Ore Geol. Rev. 2020, 122, 103521. [Google Scholar] [CrossRef]
- Migdisov, A.; Guo, X.; Nisbet, H.; Xu, H.; Williams-Jones, A.E. Fractionation of REE, U, and Th in natural ore-forming hydrothermal systems: Thermodynamic modeling. J. Chem. Thermodyn. 2019, 128, 305–319. [Google Scholar] [CrossRef]
- Migdisov, A.; Williams-Jones, A.E.; Brugger, J.; Caporuscio, F.A. Hydrothermal transport, deposition, and fractionation of the REE: Experimental data and thermodynamic calculations. Chem. Geol. 2016, 439, 13–42. [Google Scholar] [CrossRef]
- Gausse, C.; Szenknect, S.; Qin, D.W.; Mesbah, A.; Clavier, N.; Neumeier, S.; Bosbach, D.; Dacheux, N. Determination of the Solubility of Rhabdophanes LnPO4·0.667H2O (Ln = La to Dy). Eur. J. Inorg. Chem. 2016, 2016, 4615–4630. [Google Scholar] [CrossRef]
- Gysi, A.P.; Harlov, D.; Miron, G.D. The solubility of monazite (CePO4), SmPO4, and GdPO4 in aqueous solutions from 100 to 250 °C. Geochim. Et Cosmochim. Acta 2018, 242, 143–164. [Google Scholar] [CrossRef]
- Gysi, A.P.; Williams-Jones, A.E.; Harlov, D. The solubility of xenotime-(Y) and other HREE phosphates (DyPO4, ErPO4 and YbPO4) in aqueous solutions from 100 to 250 °C and p sat. Chem. Geol. 2015, 401, 83–95. [Google Scholar] [CrossRef]
- Gysi, A.P.; Harlov, D. Hydrothermal solubility of TbPO4, HoPO4, TmPO4, and LuPO4 xenotime endmembers at pH of 2 and temperatures between 100 and 250 °C. Chem. Geol. 2021, 567, 120072. [Google Scholar] [CrossRef]
- Pan, R.; Gysi, A.P.; Miron, G.D.; Zhu, C. Optimized thermodynamic properties of REE aqueous species (REE3+ and REEOH2+) and experimental database for modeling the solubility of REE phosphate minerals (monazite, xenotime, and rhabdophane) from 25 to 300 °C. Chem. Geol. 2024, 643, 121817. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, C.; Li, C.; Jiang, M. Separation and recovery of valuable metals from low-grade REE–Nb–Fe ore. Int. J. Miner. Process. 2016, 150, 16–23. [Google Scholar] [CrossRef]
- Popa, K.; Konings, R.J.M. High-temperature heat capacities of EuPO4 and SmPO4 synthetic monazites. Thermochim. Acta 2006, 445, 49–52. [Google Scholar] [CrossRef]
- Navrotsky, A.; Lee, W.; Mielewczyk-Gryn, A.; Ushakov, S.V.; Anderko, A.; Wu, H.; Riman, R.E. Thermodynamics of solid phases containing rare earth oxides. J. Chem. Thermodyn. 2015, 88, 126–141. [Google Scholar] [CrossRef]
- Thiriet, C.; Konings, R.J.M.; Javorský, P.; Magnani, N.; Wastin, F. The low temperature heat capacity of LaPO4 and GdPO4, the thermodynamic functions of the monazite-type LnPO4 series. J. Chem. Thermodyn. 2005, 37, 131–139. [Google Scholar] [CrossRef]
- Van Hoozen, C.J.; Gysi, A.P.; Harlov, D.E. The solubility of monazite (LaPO4, PrPO4, NdPO4, and EuPO4) endmembers in aqueous solutions from 100 to 250 °C. Geochim. Cosmochim. Acta 2020, 280, 302–316. [Google Scholar] [CrossRef]
- Janots, E.; Brunet, F.; Goffé, B.; Poinssot, C.; Burchard, M.; Cemič, L. Thermochemistry of monazite-(La) and dissakisite-(La): Implications for monazite and allanite stability in metapelites. Contrib. Mineral. Petrol. 2007, 154, 1–14. [Google Scholar] [CrossRef]
- Gavrichev, K.S.; Ryumin, M.A.; Tyurin, A.V.; Gurevich, V.M.; Khoroshilov, A.V.; Komissarova, L.N. Thermodynamic functions of erbium orthophosphate ErPO4 in the temperature range of 0–1600 K. Thermochim. Acta 2012, 535, 1–7. [Google Scholar] [CrossRef]
- Sverjensky, D.A.; Molling, P. A linear free energy relationship for crystalline solids and aqueous ions. Nature 1992, 356, 231–234. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A Cryst. Phys. Diffr. Theor. Gen. Crystallogr. 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Exner, O. Correlation Analysis of Chemical Data; Springer: New York, NY, USA, 1988. [Google Scholar]
- Xu, H.; Wang, Y. Use of linear free energy relationship to predict Gibbs free energies of formation of zirconolite phases (MZrTi2O7 and MHfTi2O7). J. Nucl. Mater. 1999, 275, 211–215. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Y. Use of linear free energy relationship to predict Gibbs free energies of formation of pyrochlore phases (CaMTi2O7). J. Nucl. Mater. 1999, 275, 216–220. [Google Scholar] [CrossRef]
- Xu, H.; Wang, Y. Use of linear free energy relationship to predict Gibbs free energies of formation of MUO4 phases. Radiochim. Acta 1999, 87, 37–40. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H. Prediction of trace metal partitioning between minerals and aqueous solutions: A linear free energy correlation approach. Geochim. Cosmochim. Acta 2001, 65, 1529–1543. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H. Thermodynamic stability of actinide pyrochlore minerals in deep geologic repository environments. MRS Online Proc. Libr. (OPL) 1999, 608, 367. [Google Scholar] [CrossRef]
- Zhu, C. Estimation of surface precipitation constants for sorption of divalent metals onto hydrous ferric oxide and calcite. Chem. Geol. 2002, 188, 23–32. [Google Scholar] [CrossRef]
- Ganguly, J.; Saxena, S.K. Mixtures and Mineral Reactions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1987; Volume 19. [Google Scholar]
- Urusov, V. Energetic theory of miscibility gaps in mineral solid solutions. Fortschr. Miner. 1975, 52, 141–150. [Google Scholar]
- Zhu, C. Coprecipitation in the barite isostructural family: 1. binary mixing properties. Geochim. Cosmochim. Acta 2004, 68, 3327–3337. [Google Scholar] [CrossRef]
- Helgeson, H.C.; Kirkham, D.H.; Flowers, G.C. Theoretical prediction of the thermodynamic behavior of aqueous electrolytes by high pressures and temperatures; IV, Calculation of activity coefficients, osmotic coefficients, and apparent molal and standard and relative partial molal properties to 600 degrees C and 5 kb. Am. J. Sci. 1981, 281, 1249–1516. [Google Scholar]
- Ni, Y.; Hughes, J.M.; Mariano, A.N. Crystal chemistry of the monazite and xenotime structures. Am. Mineral. 1995, 80, 21–26. [Google Scholar] [CrossRef]
- Mesbah, A.; Clavier, N.; Elkaim, E.; Gausse, C.; Kacem, I.B.; Szenknect, S.; Dacheux, N. Monoclinic form of the rhabdophane compounds: REEPO4·0.667H2O. Cryst. Growth Des. 2014, 14, 5090–5098. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Fernández, D.; Goodwin, A.; Sengers, J.L. Measurements of the relative permittivity of liquid water at frequencies in the range of 0.1 to 10 kHz and at temperatures between 273.1 and 373.2 K at ambient pressure. Int. J. Thermophys. 1995, 16, 929–955. [Google Scholar] [CrossRef]
- Shock, E.L.; Helgeson, H.C. Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: Correlation algorithms for ionic species and equation of state predictions to 5 kb and 1000 °C. Geochim. Cosmochim. Acta 1988, 52, 2009–2036. [Google Scholar] [CrossRef]
- Shannon, R.T.; Prewitt, C.T. Effective ionic radii in oxides and fluorides. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1969, 25, 925–946. [Google Scholar] [CrossRef]
- Liu, X.; Byrne, R.H. Rare earth and yttrium phosphate solubilities in aqueous solution. Geochim. Cosmochim. Acta 1997, 61, 1625–1633. [Google Scholar] [CrossRef]
- Ushakov, S.V.; Helean, K.B.; Navrotsky, A.; Boatner, L.A. Thermochemistry of rare-earth orthophosphates. J. Mater. Res. 2001, 16, 2623–2633. [Google Scholar] [CrossRef]
- Greenwood, H.J. Some linear and non-linear problems in petrology. Geochim. Cosmochim. Acta 1979, 43, 1873–1885. [Google Scholar] [CrossRef]
- Mesbah, A.; Clavier, N.; Elkaim, E.; Szenknect, S.; Dacheux, N. In pursuit of the rhabdophane crystal structure: From the hydrated monoclinic LnPO4·0.667H2O to the hexagonal LnPO4 (Ln = Nd, Sm, Gd, Eu and Dy). J. Solid State Chem. 2017, 249, 221–227. [Google Scholar] [CrossRef]
- Popa, K.; Konings, R.J.M.; Geisler, T. High-temperature calorimetry of (La1−xLnx)PO4 solid solutions. J. Chem. Thermodyn. 2007, 39, 236–239. [Google Scholar] [CrossRef]
- Neumeier, S.; Kegler, P.; Arinicheva, Y.; Shelyug, A.; Kowalski, P.M.; Schreinemachers, C.; Navrotsky, A.; Bosbach, D. Thermochemistry of La1−xLnxPO4-monazites (Ln= Gd, Eu). J. Chem. Thermodyn. 2017, 105, 396–403. [Google Scholar] [CrossRef]
- Strzelecki, A.C.; Reece, M.; Zhao, X.; Yu, W.; Benmore, C.; Ren, Y.; Alcorn, C.; Migdisov, A.; Xu, H.; Guo, X. Crystal chemistry and thermodynamics of HREE (Er, Yb) mixing in a xenotime solid solution. ACS Earth Space Chem. 2022, 6, 1375–1389. [Google Scholar] [CrossRef]
- Mogilevsky, P. On the miscibility gap in monazite–xenotime systems. Phys. Chem. Miner. 2007, 34, 201–214. [Google Scholar] [CrossRef]
- Kowalski, P.M.; Li, Y. Relationship between the thermodynamic excess properties of mixing and the elastic moduli in the monazite-type ceramics. J. Eur. Ceram. Soc. 2016, 36, 2093–2096. [Google Scholar] [CrossRef]
- Li, Y.; Kowalski, P.M.; Blanca-Romero, A.; Vinograd, V.; Bosbach, D. Ab initio calculation of excess properties ofLa1−x(Ln,An)xPO4solid solutions. J. Solid State Chem. 2014, 220, 137–141. [Google Scholar] [CrossRef]
- Eremin, N.N.; Marchenko, E.I.; Petrov, V.G.; Mitrofanov, A.A.; Ulanova, A.S. Solid solutions of monazites and xenotimes of lanthanides and plutonium: Atomistic model of crystal structures, point defects and mixing properties. Comput. Mater. Sci. 2019, 157, 43–50. [Google Scholar] [CrossRef]
- Gavrichev, K.S.; Gurevich, V.M.; Ryumin, M.A.; Tyrin, A.V.; Komissarova, L.N. Low-temperature heat capacity and thermodynamic properties of PrPO4. Geochem. Int. 2016, 54, 362–368. [Google Scholar] [CrossRef]
- Gavrichev, K.S.; Ryumin, M.A.; Tyurin, A.V.; Gurevich, V.M.; Komissarova, L.N. The heat capacity and thermodynamic functions of EuPO4 over the temperature range 0–1600 K. Russ. J. Phys. Chem. A 2009, 83, 901–906. [Google Scholar] [CrossRef]
- Gavrichev, K.S.; Smirnova, N.N.; Gurevich, V.M.; Danilov, V.P.; Tyurin, A.V.; Ryumin, M.A.; Komissarova, L.N. Heat capacity and thermodynamic functions of LuPO4 in the range 0–320 K. Thermochim. Acta 2006, 448, 63–65. [Google Scholar] [CrossRef]
- Gavrichev, K.S.; Ryumin, M.A.; Tyurin, A.V.; Gurevich, V.M.; Komissarova, L.N. Heat Capacity and Thermodynamic Functions of Xenotime YPO4(c) at 0–1600 K. Geochem. Int. 2010, 48, 932–939. [Google Scholar] [CrossRef]
- Gavrichev, K.S.; Ryumin, M.A.; Tyurin, A.V.; Gurevich, V.M.; Nikiforova, G.E.; Komissarova, L.N. Heat capacity and thermodynamic functions of YbPO4 from 0 to 1800 K. Inorg. Mater. 2013, 49, 701–708. [Google Scholar] [CrossRef]
- Gurevich, V.M.; Ryumin, M.A.; Tyurin, A.V.; Komissarova, L.N. Heat capacity and thermodynamic properties of GdPO4 in the temperature range 0–1600 K. Geochem. Int. 2012, 50, 702–710. [Google Scholar] [CrossRef]
- Poitrasson, F.; Oelkers, E.; Schott, J.; Montel, J.M. Experimental determination of synthetic NdPO4 monazite end-member solubility in water from 21 °C to 300 °C: Implications for rare earth element mobility in crustal fluids. Geochim. Cosmochim. Acta 2004, 68, 2207–2221. [Google Scholar] [CrossRef]
- Ji, Y.; Beridze, G.; Bosbach, D.; Kowalski, P.M. Heat capacities of xenotime-type ceramics: An accurate ab initio prediction. J. Nucl. Mater. 2017, 494, 172–181. [Google Scholar] [CrossRef]
- Tyurin, A.V.; Ryumin, M.A.; Khoroshilov, A.V.; Gurevich, V.M.; Gavrichev, K.S. Thermodynamic functions of holmium orthophosphate HoPO4 in the range 9–1370 K. Thermochim. Acta 2020, 683, 178459. [Google Scholar] [CrossRef]
- Ji, Y.; Beridze, G.; Li, Y.; Kowalski, P.M. Large Scale Simulation of Nuclear Waste Materials. Energy Procedia 2017, 127, 416–424. [Google Scholar] [CrossRef]
- Spear, F.S.; Pyle, J.M. Apatite, monazite, and xenotime in metamorphic rocks. Rev. Mineral. Geochem. 2002, 481, 293–335. [Google Scholar] [CrossRef]
- Zhu, X.; O’Nions, R. Monazite chemical composition: Some implications for monazite geochronology. Contrib. Mineral. Petrol. 1999, 137, 351–363. [Google Scholar] [CrossRef]
- Franz, G.; Andrehs, G.; Rhede, D. Crystal chemistry of monazite and xenotime from Saxothuringian-Moldanubian metapelites, NE Bavaria, Germany. Eur. J. Mineral. 1996, 8, 1097–1118. [Google Scholar] [CrossRef]
- Tananaev, I.V.O.; Orlovsky, V.P.; Kurbanov, J.M.; Halikov, B.S.; Osman, S.O.; Bulgakov, V.I. Reports of the Academy of Sciences of the Tajik SSR = Dokladhoi Akademiyai fanhoi RCC Tochikiston (USSR); USSR: Moscow, Russia, 1974; Volume 42. [Google Scholar]
- Shock, E.L.; Sassani, D.C.; Willis, M.; Sverjensky, D.A. Inorganic species in geologic fluids: Correlations among standard molal thermodynamic properties of aqueous ions and hydroxide complexes. Geochim. Cosmochim. Acta 1997, 61, 907–950. [Google Scholar] [CrossRef] [PubMed]
- Glynn, P. Solid-solution solubilities and thermodynamics: Sulfates, carbonates and halides. Rev. Mineral. Geochem. 2000, 40, 481–511. [Google Scholar] [CrossRef]
- Gavrichev, K.S.; Ryumin, M.A.; Khoroshilov, A.V.; Nikiforova, G.E.; Tyurin, A.V.; Gurevich, V.M.; Starykh, R.V. Thermodynamic properties and phase transitions of tetragonal modification of terbium orthophosphate. Phys. Chem. 2013, 4, 186–197. [Google Scholar]
- Gysi, A.P.; Harlov, D.; Filho, D.C.; Williams-Jones, A.E. Experimental determination of the high temperature heat capacity of a natural xenotime-(Y) solid solution and synthetic DyPO4 and ErPO4 endmembers. Thermochim. Acta 2016, 627–629, 61–67. [Google Scholar] [CrossRef]
- Nikiforova, G.E.; Ryumin, M.A.; Gavrichev, K.S.; Gurevich, V.M. High-temperature thermodynamic properties of LuPO4. Inorg. Mater. 2012, 48, 841–844. [Google Scholar] [CrossRef]
- Zimmer, K.; Zhang, Y.; Lu, P.; Chen, Y.; Zhang, G.; Dalkilic, M.; Zhu, C. SUPCRTBL: A revised and extended thermodynamic dataset and software package of SUPCRT92. Comput. Geosci. 2016, 90, 97–111. [Google Scholar] [CrossRef]


| Symbol | Definition |
|---|---|
| ∆G°f | Gibbs free energy of formation |
| ∆G°n | Non-solvation contribution to the Gibbs free energy of formation |
| ∆G°s | Solvation contribution to the Gibbs free energy of formation |
| ∆G’f | Adjusted Gibbs free energy of formation (∆G°f,REEPO4 − β rREE3+) |
| ΔS°f | Entropy of formation from the elements |
| S° | Absolute entropy |
| ΔHf | Enthalpy of formation from the elements |
| Cp | Heat capacity |
| V° | Molar volume |
| ∆V | Defined volume mismatch term in this study |
| dV | Mismatch of the cell volume values under the definition of Young’s moduli |
| R | Gas constant (8.314 J mol−1 K−1) |
| K | Equilibrium constant |
| Ksp | Solubility constants |
| W’ | Adjusted Margules parameter |
| W | Margules parameter |
| ω | Born coefficient of an ion |
| ωabs | Absolute Born coefficient of an ion |
| rREE3+ | Crystallographic radius of the aqueous REE3+ ion |
| Z | Charge number of an ion |
| α | Anion part of a mineral, such as PO4 |
| ψ | Effective bulk modulus |
| MX | Chemical formula of a solid |
| T3+ | Trace cation of REEPO4 with charge of 3+ |
| C3+ | Carrier cation of REEPO4 with charge of 3+ |
| REE | Rare Earth Elements |
| LREE | Light Rare Earth Elements |
| HREE | Heavy Rare Earth Elements |
| REE | r(REE3+) | r(REE3+) | V° (cm3 mol−1) | ∆G°s (kJ mol−1) | ∆G°f (kJ mol−1) | ∆G°n (kJ mol−1) | ∆G°f (kJ mol−1) 2 | ∆G°f (kJ mol−1) 3 |
|---|---|---|---|---|---|---|---|---|
| Å (CN9) 1 | Å (CN8) 1 | REEPO4(s) | REE3+(aq) | REE3+(aq) | REE3+(aq) | REEPO4(s) | REEPO4·0.667H2O(s) | |
| La | 1.216 | 1.160 | 46.03 | −861.74 | −686.18 | 175.56 | −1848.53 | −2004.00 |
| Ce | 1.196 | 1.143 | 45.16 | −869.35 | −676.13 | 193.22 | −1844.48 | −1997.00 |
| Pr | 1.179 | 1.126 | 44.45 | −875.89 | −680.32 | 195.57 | −1850.50 | −2003.00 |
| Nd | 1.163 | 1.109 | 43.86 | −882.09 | −671.95 | 210.14 | −1840.30 | −1994.00 |
| Pm | 1.144 | 1.093 | 43.26 | −889.51 | −661.07 | 228.44 | ||
| Sm | 1.132 | 1.079 | 42.81 | −894.24 | −665.67 | 228.57 | −1833.45 | −1989.00 |
| Eu | 1.120 | 1.066 | 42.40 | −899.00 | −574.46 | 324.54 | −1741.10 | −1896.00 |
| Gd | 1.107 | 1.053 | 42.01 | −904.19 | −663.58 | 240.60 | −1828.50 | −1984.00 |
| Tb | 1.095 | 1.040 | 41.53 4 | −909.00 | −667.35 | 241.65 | ||
| Dy | 1.083 | 1.027 | −913.85 | −664.00 | 249.85 | |||
| Tb | 1.095 | 1.040 | 43.90 | −931.47 | −667.35 | 264.12 | −1831.07 | |
| Dy | 1.083 | 1.027 | 43.35 | −936.87 | −664.00 | 272.87 | −1829.10 | |
| Y | 1.075 | 1.019 | 43.14 | −940.21 | −685.34 | 254.87 | −1849.12 | |
| Ho | 1.072 | 1.015 | 42.90 | −941.89 | −675.30 | 266.59 | −1836.79 | |
| Er | 1.062 | 1.004 | 42.37 | −946.52 | −669.02 | 277.50 | −1831.26 | |
| Tm | 1.052 | 0.994 | 42.00 | −950.75 | −669.02 | 281.73 | −1830.52 | |
| Yb | 1.042 | 0.985 | 41.64 | −954.58 | −640.15 | 314.43 | −1801.02 | |
| Lu | 1.032 | 0.977 | 41.22 | −958.00 | −666.93 | 291.07 | −1826.71 |
| REE Phosphate Lsostructural Type | Parameters | |||
|---|---|---|---|---|
| a | b (kJ mol−1) | β (kJ Å−1) | R2 | |
| Monazite | 1.0059 (0.0398) | −2515.31 (63.23) | 399.71 (48.33) | 0.9975 |
| Xenotime | 0.9909 (0.0325) | −2451.53 (35.58) | 344.08 (27.89) | 0.9979 |
| Rhabdophane | 1.0067 (0.0240) | −2688.86 (38.02) | 416.17 (29.06) | 0.9991 |
| REE Phosphate Lsostructural Type | Parameters | |||
|---|---|---|---|---|
| a (kJ V°−1) | b (kJ mol−1) | β | R2 | |
| Monazite | 39.3549 (0.5659) | 0.0641 (0.0958) | −0.0020 (0.0017) | 0.9939 |
| Xenotime | 25.4885 (0.5589) | −0.0062 (0.0269) | −0.0025 (0.0007) | 0.9931 |
| Monazite | Cation | La | Ce | Pr | Nd | Pm | Sm | Eu | Gd | Tb | Dy | Y1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| W (kJ/mol) | 0.76 | 2.32 | 4.36 | 7.14 | 9.70 | 12.6 | 15.3 | 19.4 | 23.6 | 26.4 | La | ||
| 0.52 | 1.61 | 3.41 | 5.21 | 7.40 | 9.46 | 12.7 | 16.0 | 18.3 | Ce | ||||
| 0.41 | 1.41 | 2.60 | 4.23 | 5.73 | 8.28 | 11.0 | 12.9 | Pr | |||||
| 0.43 | 1.12 | 2.28 | 3.33 | 5.32 | 7.50 | 9.02 | Nd | ||||||
| 0.25 | 0.95 | 1.56 | 2.98 | 4.64 | 5.83 | Pm | |||||||
| 0.42 | 0.69 | 1.69 | 2.96 | 3.89 | Sm | ||||||||
| 0.04 | 0.66 | 1.58 | 2.28 | Eu | |||||||||
| 0.33 | 0.93 | 1.41 | Gd | ||||||||||
| 0.26 | 0.49 | Tb | |||||||||||
| 0.06 | Dy | ||||||||||||
| Y | |||||||||||||
| Xenotime | Cation | Tb | Dy | Y | Ho | Er | Tm | Yb | Lu | ||||
| W (kJ/mol) | 0.19 | 0.46 | 0.59 | 1.44 | 2.23 | 3.25 | 4.50 | Tb | |||||
| 0.13 | 0.10 | 0.58 | 1.12 | 1.89 | 2.85 | Dy | |||||||
| −0.09 | 0.26 | 0.70 | 1.37 | 2.21 | Y | ||||||||
| 0.19 | 0.52 | 1.09 | 1.80 | Ho | |||||||||
| 0.09 | 0.41 | 0.85 | Er | ||||||||||
| 0.16 | 0.39 | Tm | |||||||||||
| 0.04 | Yb | ||||||||||||
| Lu | |||||||||||||
| Xenotime | Cation | La | Ce | Pr | Nd | Pm | Sm | Eu | Gd | ||||
| Fictive | W (kJ/mol) | 22.9 | 17.4 | 12.8 | 8.86 | 5.89 | 3.74 | 1.98 | 1.08 | Y1 |
| ΔG°f | ΔH°f | ΔS°f [16] | S° [16] | V°m [34] | Cp = a + bT + c/T2 + d/T0.5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| kJ mol−1 | kJ mol−1 | J mol−1 K−1 | J mol−1 K−1 | J mol−1 bar−1 | a | b*100 | c | d | Reference | |
| Monazite | ||||||||||
| LaPO4 | −1861.2 | −1980.46 | −400.0 | 108.3 | 46.03 | 121.13 | 3.0116 | −2,562,500 | - | [15] |
| CePO4 | −1851.7 | −1971.33 | −401.3 | 120.0 | 45.16 | 125.21 | 2.7894 | −2,408,500 | - | [15] |
| PrPO4 | −1855.6 | −1975.55 | −402.3 | 123.2 | 44.45 | 124.50 | 3.0374 | −2,449,500 | - | [15] |
| NdPO4 | −1846.2 | −1965.76 | −401.0 | 122.9 | 43.86 | 132.96 | 2.2541 | −3,100,900 | - | [15] |
| SmPO4 | −1840.7 | −1959.52 | −398.7 | 122.5 | 42.81 | 133.13 | 2.3468 | −3,068,700 | - | [15] |
| EuPO4 | −1748.3 | −1871.17 | −412.1 | 117.2 | 42.40 | 137.56 | 1.7693 | −2,785,400 | - | [15] |
| GdPO4 | −1835.7 | −1953.47 | −395.0 | 124.6 | 42.01 | 133.24 | 1.2793 | −3,097,200 | - | [15] |
| TbPO4 | −1841.7 | - | - | - | 41.53 1 | - | - | - | - | This study |
| DyPO4 | −1838.3 | - | - | - | 41.10 2 | - | - | - | - | This study |
| (YPO4) | −1859.7 | - | - | - | 40.82 2 | - | - | - | - | This study |
| (HoPO4) | −1849.6 | - | - | - | 40.71 2 | - | - | - | - | This study |
| (ErPO4) | −1843.1 | - | - | - | 40.37 2 | - | - | - | - | This study |
| (TmPO4) | −1843.0 | - | - | - | 40.03 2 | - | - | - | - | This study |
| (YbPO4) | −1813.8 | - | - | - | 39.68 2 | - | - | - | - | This study |
| (LuPO4) | −1859.7 | - | - | - | 39.34 2 | - | - | - | - | This study |
| Xenotime | ||||||||||
| (LaPO4) | −1857.1 | - | - | - | 49.35 2 | - | - | - | - | This study |
| (CePO4) | −1846.4 | - | - | - | 48.56 2 | - | - | - | - | This study |
| (PrPO4) | −1849.8 | - | - | - | 47.77 2 | - | - | - | - | This study |
| (NdPO4 | −1840.6 | - | - | - | 47.00 2 | - | - | - | - | This study |
| (SmPO4) | −1832.7 | - | - | - | 45.66 2 | - | - | - | - | This study |
| (EuPO4) | −1741.6 | - | - | - | 45.08 2 | - | - | - | - | This study |
| (GdPO4) | −1829.1 | - | - | - | 44.51 2 | - | - | - | - | This study |
| TbPO4 | −1831.1 | −1946.3 | −386.6 | 138.1 | 43.90 | 116.4 | 4.55 | −2,190,000 | - | [67] |
| DyPO4 | −1829.1 | −1945.0 | −388.6 | 138.1 | 43.35 | 185.5 | 0.00 | −3,261,000 | −751.900 | [68] |
| YPO4 | −1849.1 | −1964.4 | −386.8 | 108.8 | 43.14 | 131.3 | 1.992 | −3,563,700 | - | [54] |
| HoPO4 | −1836.8 | −1951.4 | −384.4 | 142.3 | 42.90 | 124.4 | 2.658 | −2,690,000 | - | [59] |
| ErPO4 | −1831.3 | −1952.8 | −407.7 | 116.6 | 42.37 | 205.5 | −0.076 | −859,073 | −1651.88 | [20] |
| TmPO4 | −1830.5 | −1945.9 | −387.1 | 138.1 | 42.00 | 128.8 | 1.904 | −3,090,000 | - | [12] |
| YbPO4 | −1801.0 | −1913.5 | −377.1 | 133.9 | 41.64 | 198.0 | 0.448 | −991,250 | −1506.38 | [55] |
| LuPO4 | −1826.7 | −1941.6 | −385.2 | 117.2 | 41.22 | 130.7 | 1.85 | −3,330,000 | - | [53,69] |
| Rhabdophane | ||||||||||
| LaPO4·0.667H2O | −2004.0 | −2151.3 | −494.0 | 170.0 | - | - | - | - | - | [9] |
| CePO4·0.667H2O | −1997.0 | −2147.3 | −504.0 | 175.0 | - | - | - | - | - | [9] |
| PrPO4·0.667H2O | −2003.0 | −2144.0 | −473.0 | 210.0 | - | - | - | - | - | [9] |
| NdPO4·0.667H2O | −1994.0 | −2142.8 | −499.0 | 180.0 | - | - | - | - | - | [9] |
| SmPO4·0.667H2O | −1989.0 | −2137.8 | −499.0 | 177.0 | - | - | - | - | - | [9] |
| EuPO4·0.667H2O | −1896.0 | −2056.4 | −538.0 | 149.0 | - | - | - | - | - | [9] |
| GdPO4·0.667H2O | −1984.0 | −2130.7 | −492.0 | 182.0 | - | - | - | - | - | [9] |
| TbPO4·0.667H2O | −1989.9 | - | - | - | - | - | - | - | - | This study |
| DyPO4·0.667H2O | −1986.6 | - | - | - | - | - | - | - | - | This study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, R.; Gysi, A.P.; Migdisov, A.; Gong, L.; Lu, P.; Zhu, C. Linear Correlations of Gibbs Free Energy of REE Phosphates (Monazite, Xenotime, and Rhabdophane) and Internally Consistent Binary Mixing Properties. Minerals 2024, 14, 305. https://doi.org/10.3390/min14030305
Pan R, Gysi AP, Migdisov A, Gong L, Lu P, Zhu C. Linear Correlations of Gibbs Free Energy of REE Phosphates (Monazite, Xenotime, and Rhabdophane) and Internally Consistent Binary Mixing Properties. Minerals. 2024; 14(3):305. https://doi.org/10.3390/min14030305
Chicago/Turabian StylePan, Ruiguang, Alexander P. Gysi, Artas Migdisov, Lei Gong, Peng Lu, and Chen Zhu. 2024. "Linear Correlations of Gibbs Free Energy of REE Phosphates (Monazite, Xenotime, and Rhabdophane) and Internally Consistent Binary Mixing Properties" Minerals 14, no. 3: 305. https://doi.org/10.3390/min14030305
APA StylePan, R., Gysi, A. P., Migdisov, A., Gong, L., Lu, P., & Zhu, C. (2024). Linear Correlations of Gibbs Free Energy of REE Phosphates (Monazite, Xenotime, and Rhabdophane) and Internally Consistent Binary Mixing Properties. Minerals, 14(3), 305. https://doi.org/10.3390/min14030305





_Migdisov.png)

