Moment Estimation from Time Domain Electromagnetic Data
Abstract
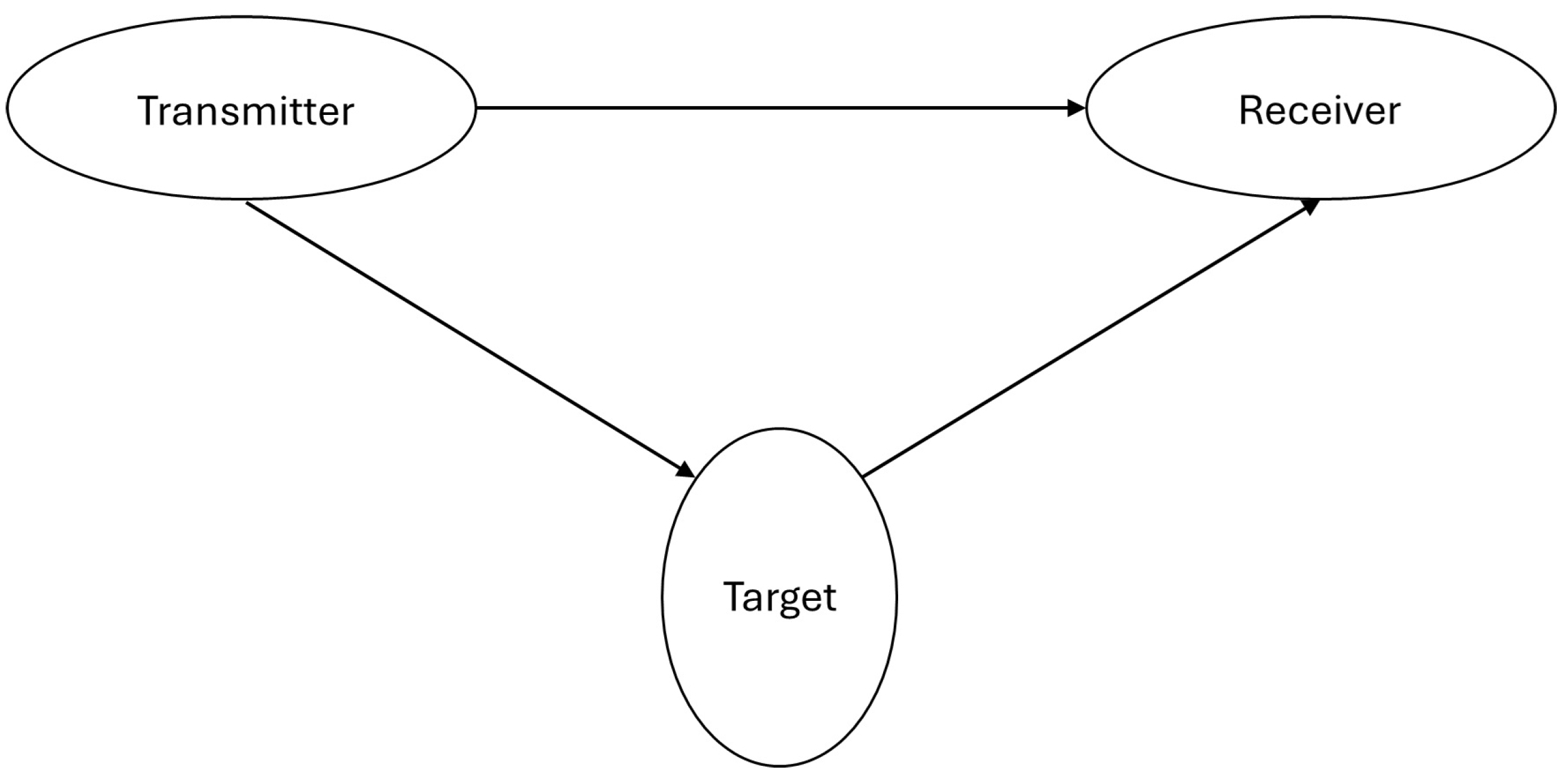
1. Introduction
2. Theory
2.1. Moment Estimation
2.2. MEGATEM
2.3. AeroTEM
2.4. Incomplete Moments
2.5. Normalization
2.6. Moment Estimation from Noisy Data
3. Results
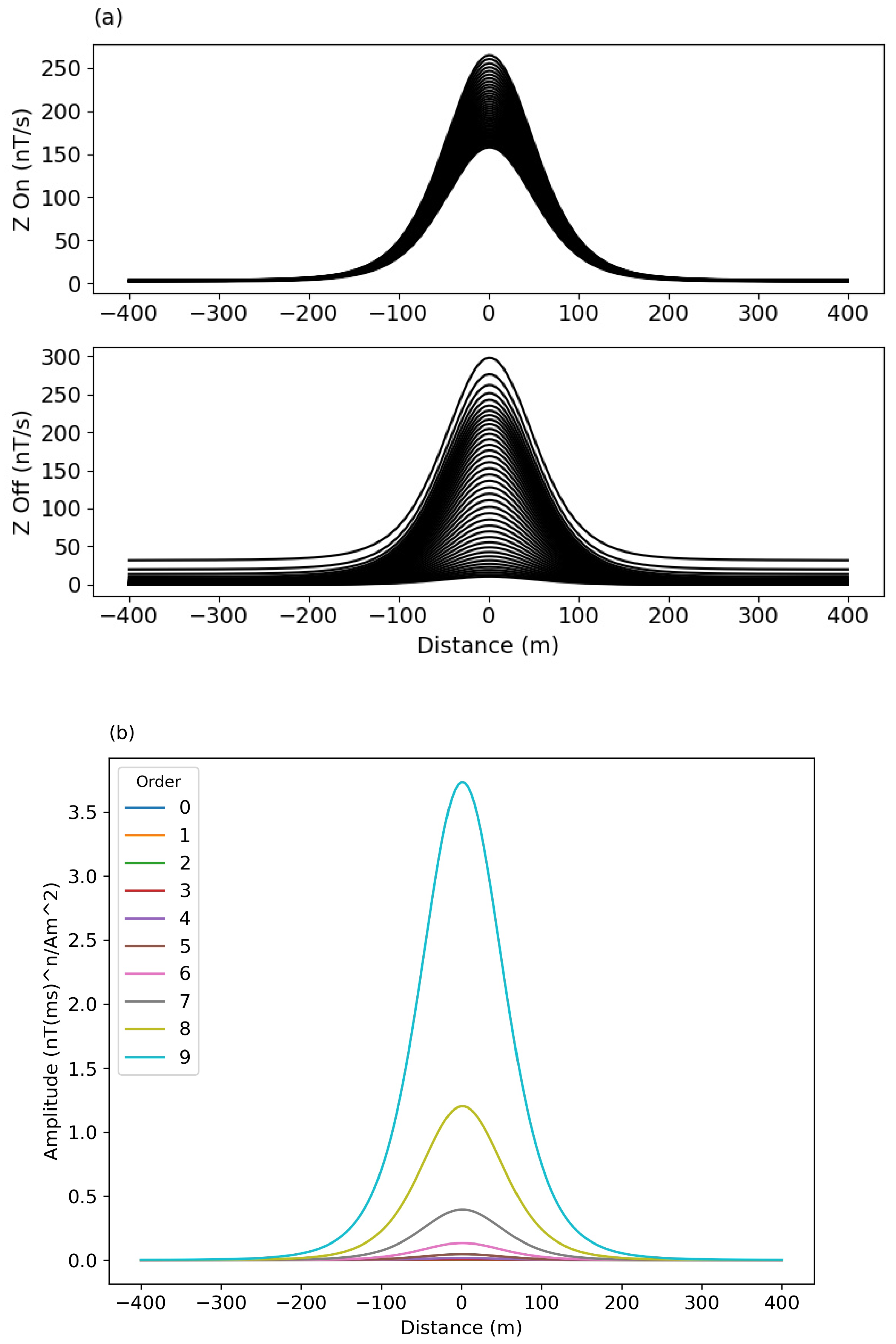
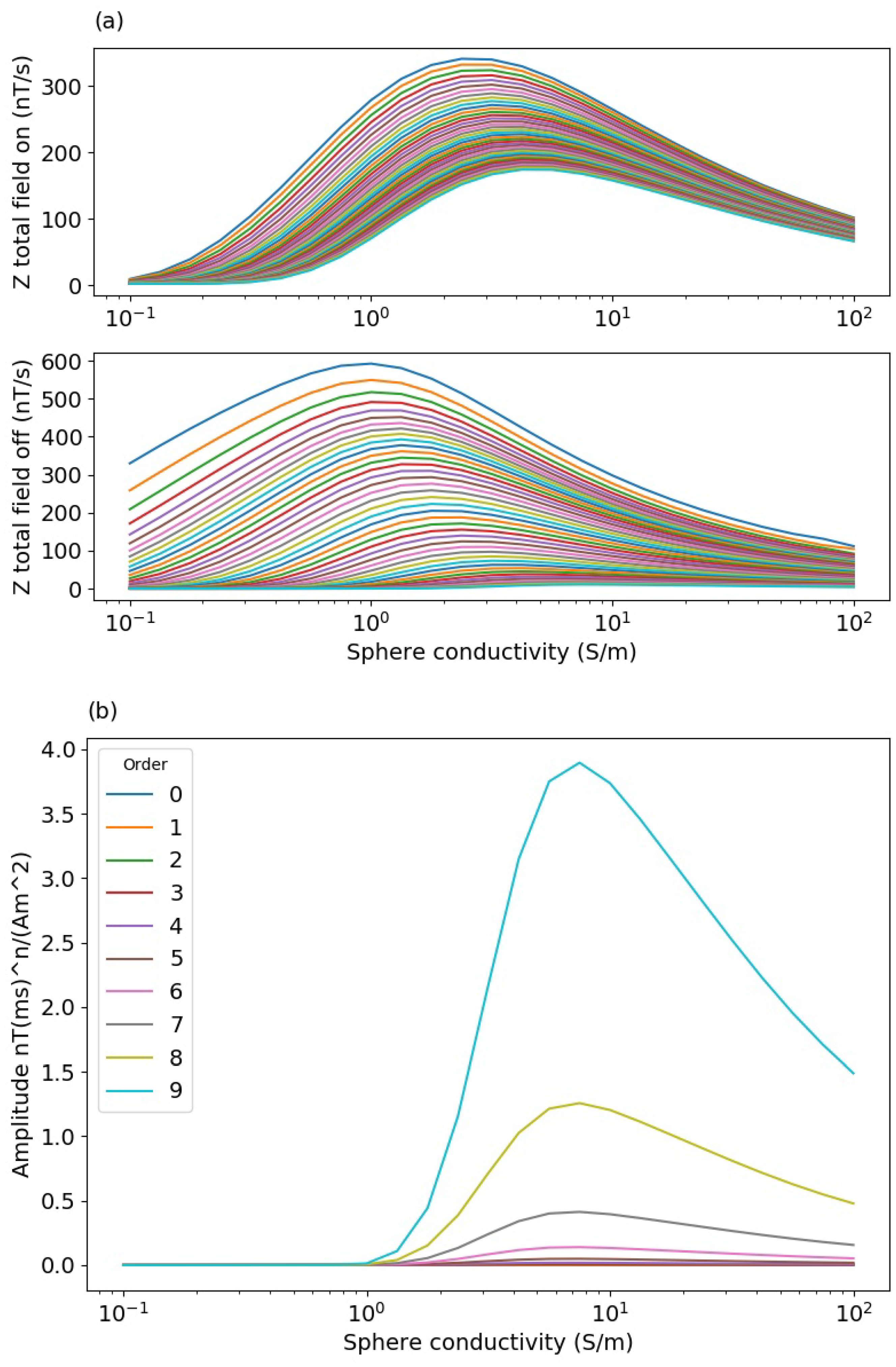
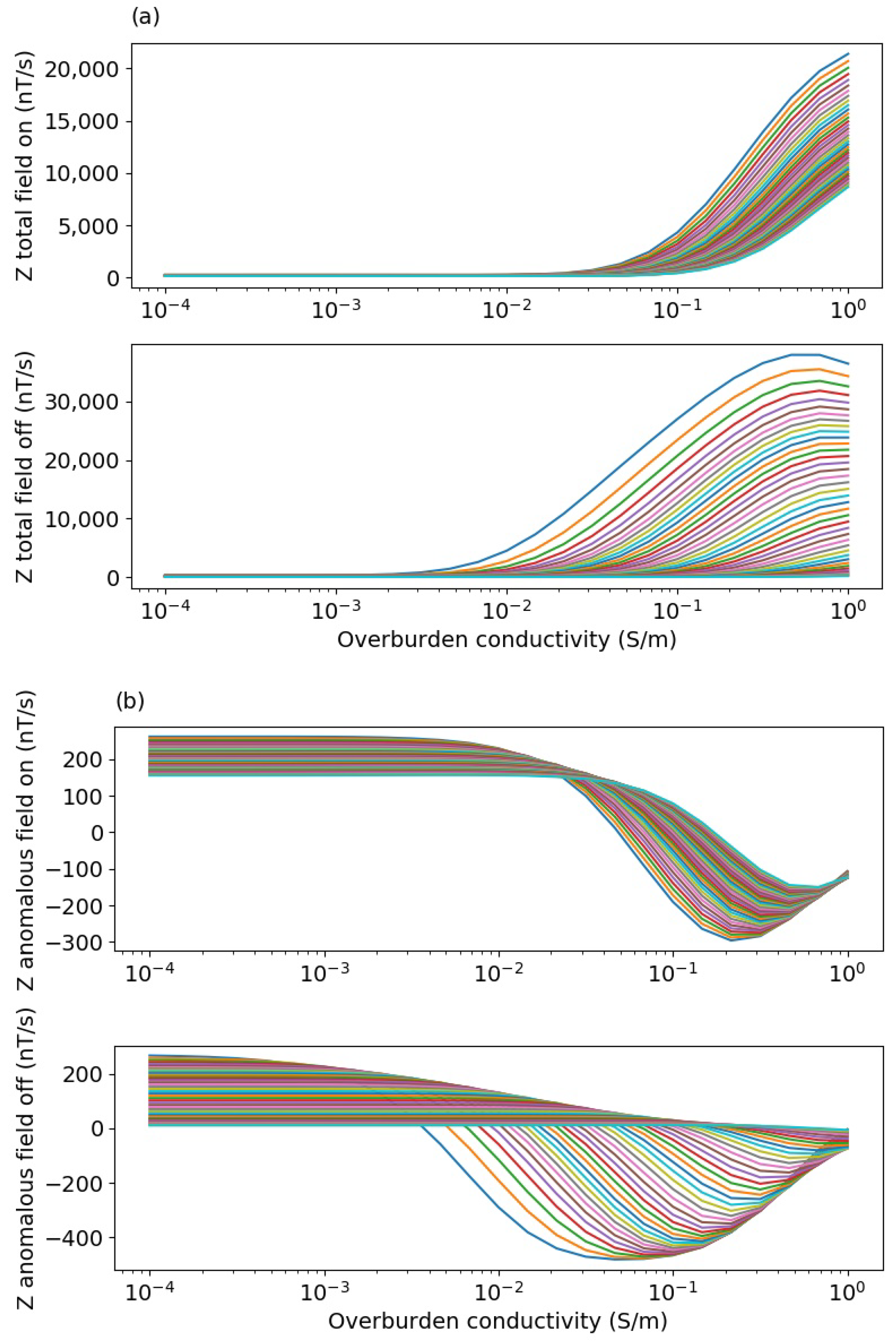
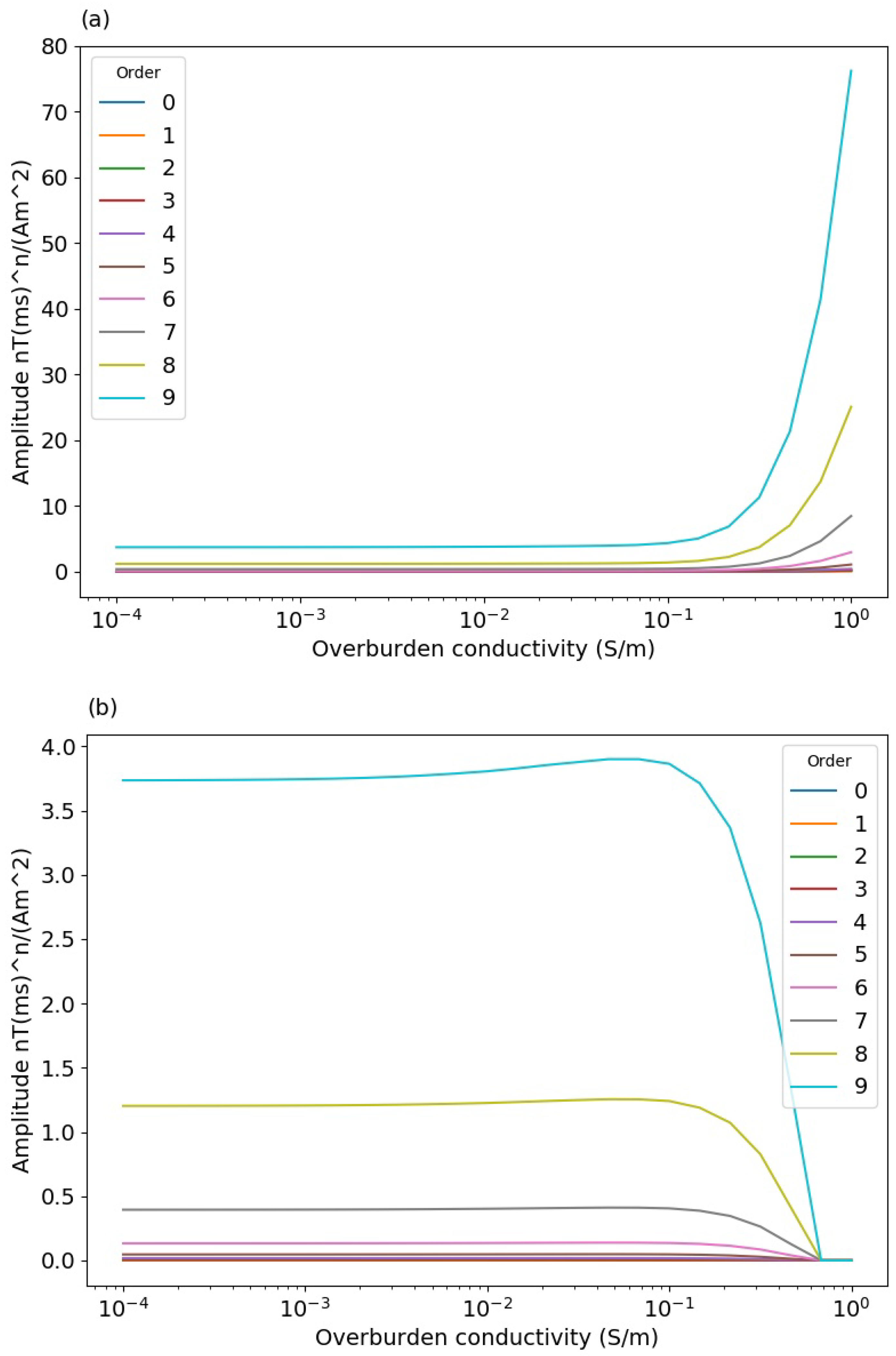
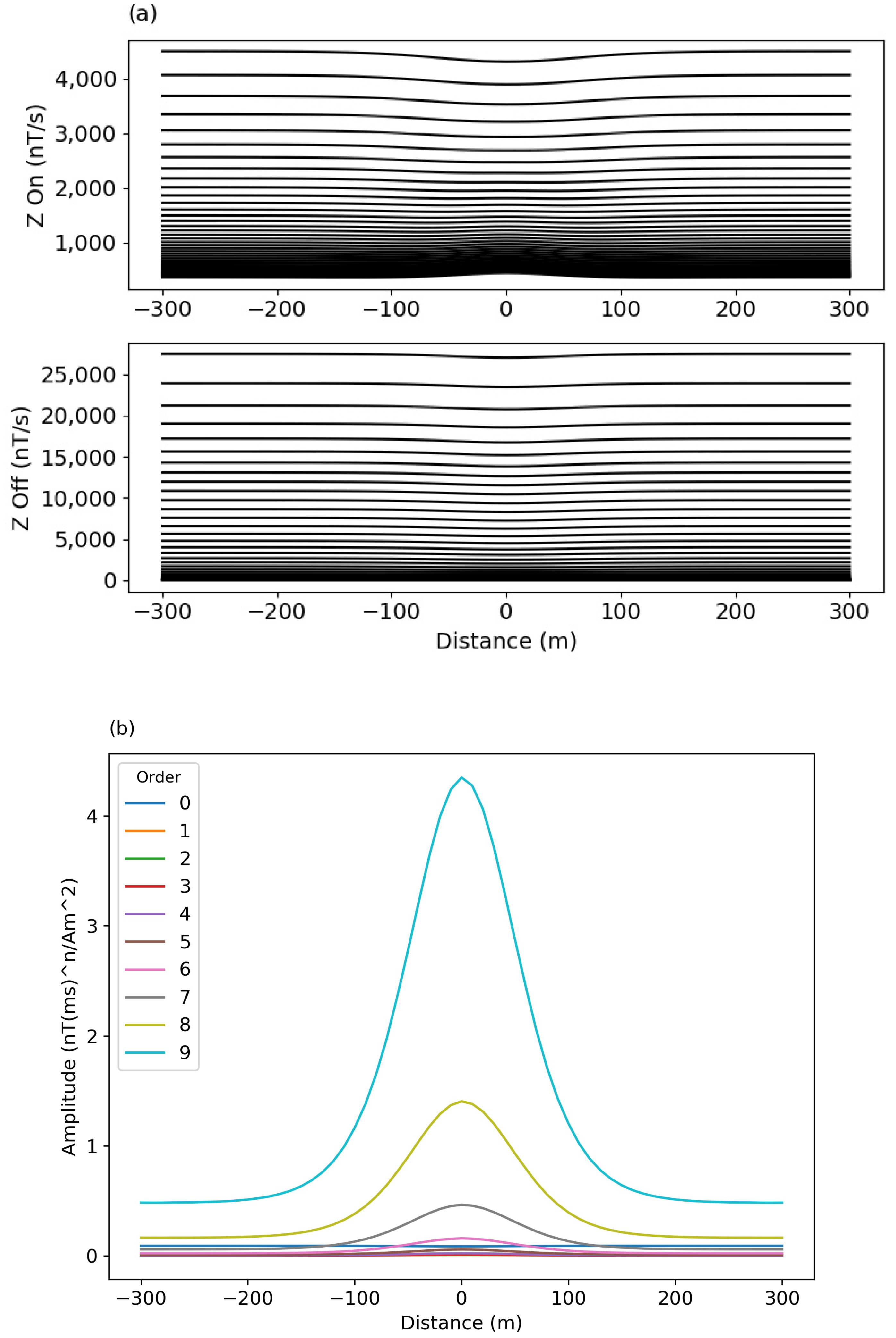
3.1. Synthetic Models
3.2. Field Data
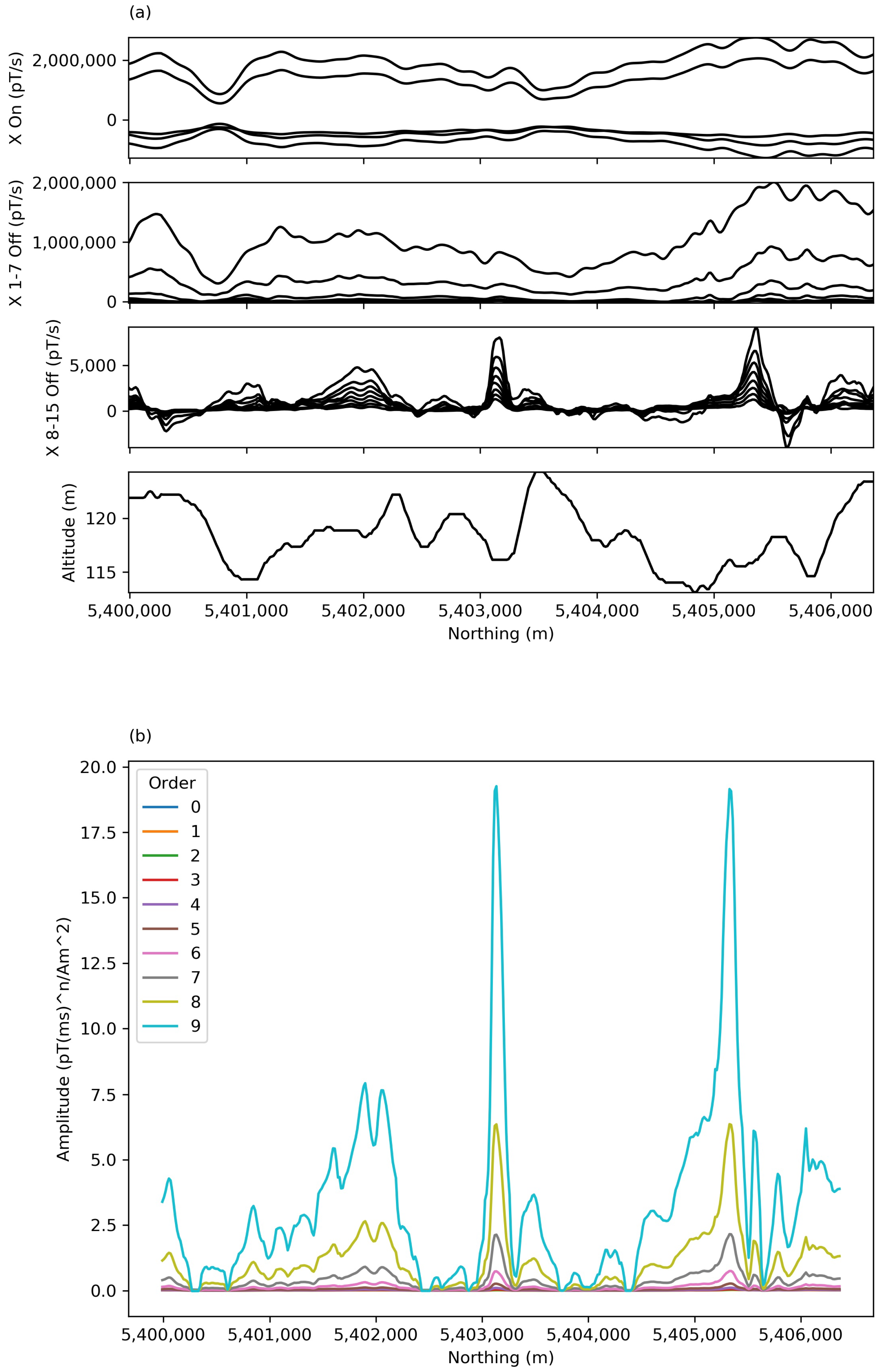
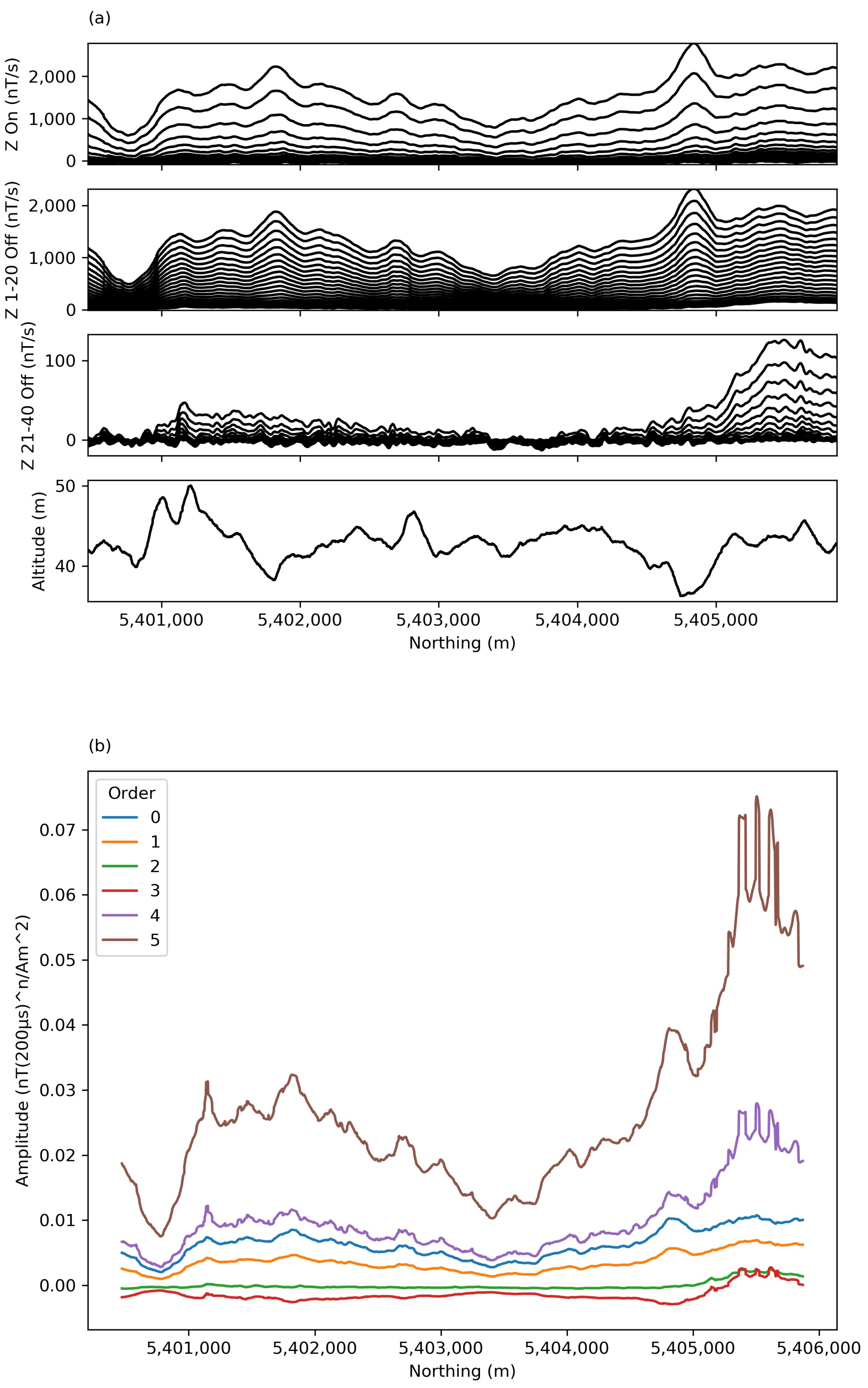
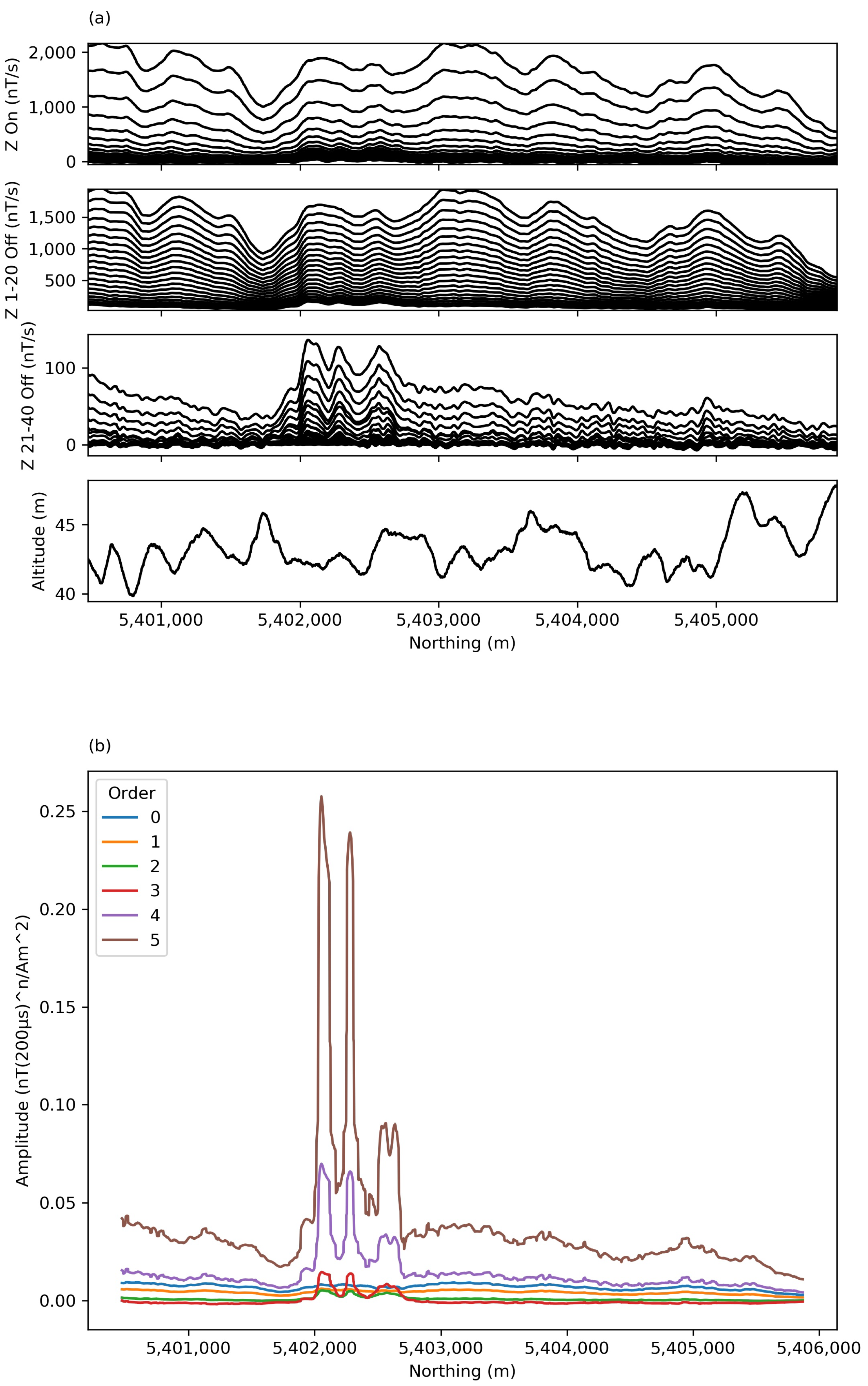
3.2.1. MEGATEM
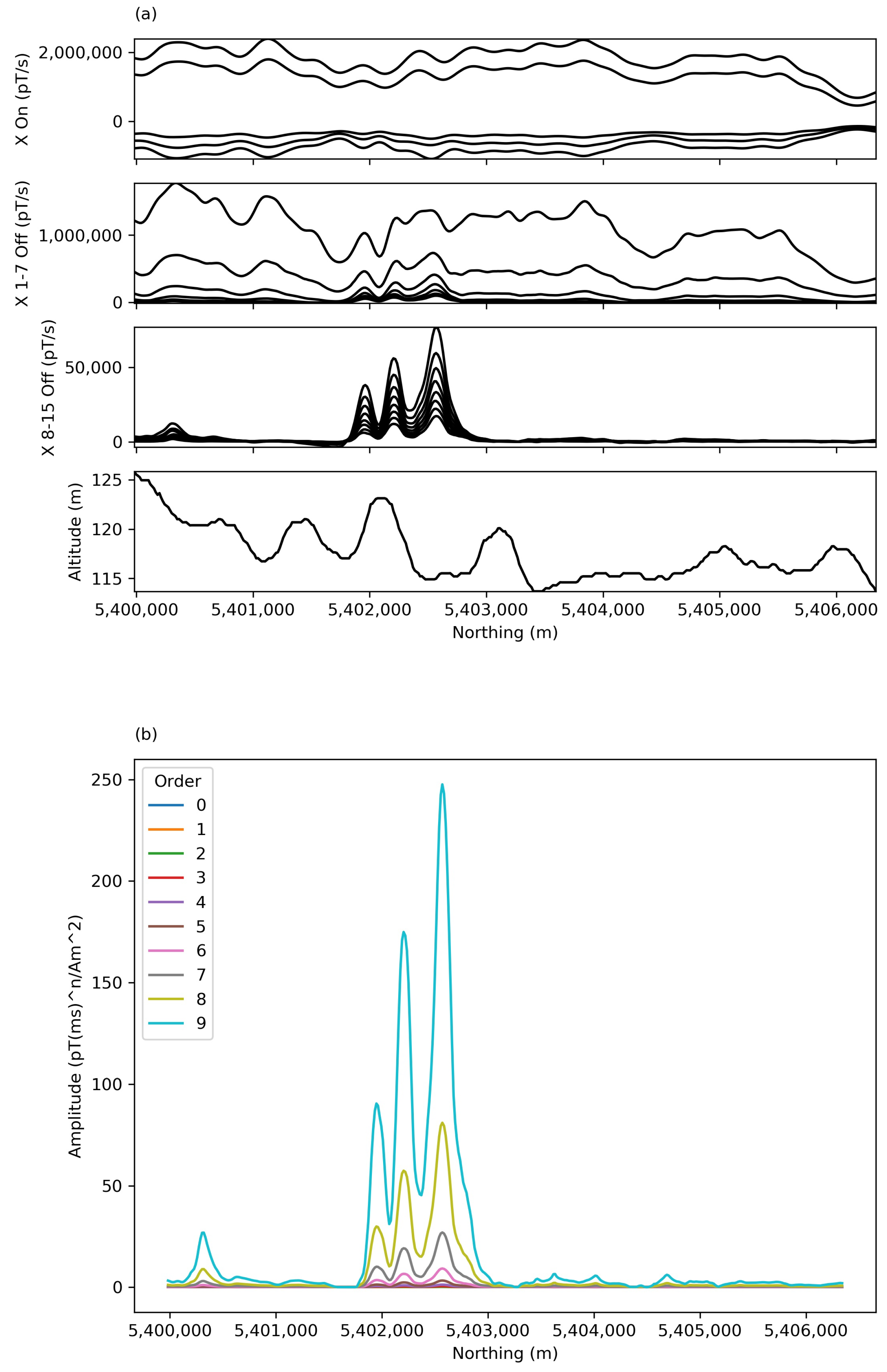
3.2.2. AirTEM
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grant, F.S.; West, G.F. Interpretation Theory in Applied Geophysics; McGraw-Hill Book Company: New York, NY, USA, 1965. [Google Scholar]
- Ward, S.H.; Hohmann, G.W. Electromagnetic theory for geophysical applications. In Electromagnetic Methods in Applied Geophysics: Volume I, Theory; Nabighian, M.N., Ed.; Society of Exploration Geophysicists: Tulsa, OK, USA, 1987; pp. 131–311. [Google Scholar]
- Kaufman, A.A.; Alekseev, D.; Oristaglio, M. Principles of Electromagnetic Methods in Surface Geophysics; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Palacky, G.J. Interpretation of INPUT AEM Measurements in Areas of Conductive Overburden. Geophysics 1975, 40, 490–502. [Google Scholar] [CrossRef]
- Keating, P.B.; Crossley, D.J. The inversion of time-domain airborne electromagnetic data using the plate model. Geophysics 1990, 55, 705–711. [Google Scholar] [CrossRef]
- Annan, A.P. The Equivalent Source Method for Electromagnetic Scattering Analysis and Its Geophysical Application. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 1974. [Google Scholar]
- Raiche, A.; Sugeng, F.; Wilson, G. Practical 3D AEM inversion—The P223F software suite. ASEG Ext. Abstr. 2007, 1, 1–5. [Google Scholar]
- Vallée, M.A. New developments in AEM discrete conductor modelling and inversion. Explor. Geophys. 2015, 46, 97–111. [Google Scholar] [CrossRef]
- Vallée, M.A.; Moussaoui, M. Modelling the electromagnetic response of a sphere located in a layered earth. Explor. Geophys. 2023, 54, 362–375. [Google Scholar] [CrossRef]
- Hauser, J.; Gunning, J.; Annetts, D. Probabilistic inversion of airborne electromagnetic data for basement conductors. Geophysics 2016, 81, E389–E400. [Google Scholar] [CrossRef]
- Macnae, J.; King, A.; Stolz, N.; Osmakoff, A.; Blaha, A. Fast AEM data processing and inversion. Explor. Geophys. 1998, 29, 163–169. [Google Scholar] [CrossRef]
- Macnae, J. Automated airborne EM anomaly picking and 3D model fitting. ASEG Ext. Abstr. 2015, 1, 1–4. [Google Scholar] [CrossRef]
- Sattel, D.; Reid, J. Modelling of Airborne Em Anomalies with Magnetic and Electric Dipoles Buried in a Layered Earth. Explor. Geophys. 2006, 37, 254–260. [Google Scholar] [CrossRef]
- Kolaj, M.; Smith, R.S. Inductive electromagnetic data interpretation using a 3D distribution of 3D magnetic or electric dipoles. Geophysics 2017, 82, E187–E195. [Google Scholar] [CrossRef]
- Cox, L.H.; Wilson, G.A.; Zhdanov, M.S. 3D inversion of airborne electromagnetic data. Geophysics 2012, 77, WB59–WB69. [Google Scholar] [CrossRef]
- Cox, L.H.; Zhdanov, M.S.; Pitcher, D.H.; Niemi, J. Three-Dimensional Inversion of Induced Polarization Effects in Airborne Time Domain Electromagnetic Data Using the GEMTIP Model. Minerals 2023, 13, 779. [Google Scholar] [CrossRef]
- Cox, L.H.; Zhdanov, M.S.; Prikhodko, A. Inversion for 3D Conductivity and Chargeability Models Using EM Data Acquired by the New Airborne TargetEM System in Ontario, Canada. Minerals 2024, 14, 237. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Haber, E.; Shekhtman, R. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics 2013, 78, E47–E57. [Google Scholar] [CrossRef]
- Ren, X.; Lai, M.; Wang, L.; Yin, C.; Liu, Y.; Su, Y.; Zhang, B.; Ben, F.; Huang, W. A fast 3-D inversion for airborne EM data using pre-conditioned stochastic gradient descent. Geophys. J. Int. 2023, 234, 737–754. [Google Scholar] [CrossRef]
- Fraser, D.C. Dighem resistivity techniques in airborne electro-magnetic mapping. In Airborne Resistivity Mapping; Palacky, G.J., Ed.; Geol. Surv. Canada Paper 86-22; Geological Survey of Canada: Ottawa, Canada, 1986; pp. 63–69. [Google Scholar]
- Annan, A.P.; Smith, R.S.; Lemieux, J.; O’Connell, M.D.; Pedersen, R.N. Resistive-limit, time-domain AEM apparent conductivity. Geophysics 1996, 61, 93–99. [Google Scholar] [CrossRef]
- Nelson, P.H.; Morris, D.B. Theoretical response of a time-domain, airborne, electromagnetic system. Geophysics 1969, 34, 729–738. [Google Scholar] [CrossRef]
- Martinez, J.M.; Smith, R.; Diaz Vazquez, D. On the time decay constant of AEM systems: A semi-heuristic algorithm to validate calculations. Explor. Geophys. 2020, 51, 94–107. [Google Scholar] [CrossRef]
- Macnae, J.; King, A.; Stolz, N.; Klinkert, P. 3-D EM Inversion to the Limit. In Three-Dimensional Electromagnetics; Oristaglio, M., Spies, B., Eds.; Society of Exploration Geophysicists: Tulsa, OK, USA, 1999; pp. 489–501. [Google Scholar]
- Schaa, R.; Fullagar, P.K. Rapid, approximate 3D inversion of transient electromagnetic (TEM) data. SEG Tech. Program Expand. Abstr. 2010, 650–654. [Google Scholar]
- Smith, R.S.; Lee, T.J. The impulse-response moments of a conductive sphere in a uniform field, a versatile and efficient electromagnetic model. Explor. Geophys. 2001, 32, 113–118. [Google Scholar] [CrossRef]
- Smith, R.S.; Lee, T.J. The moments of the impulse response: A new paradigm for the interpretation of transient electromagnetic data. Geophysics 2002, 67, 1095–1103. [Google Scholar] [CrossRef]
- Schaa, R.; Fullagar, P.K. Vertical and horizontal resistive limit formulas for a rectangular-loop source on a conductive half-space. Geophysics 2012, 77, E91–E99. [Google Scholar] [CrossRef]
- Fullagar, P.K.; Schaa, R. Analytic formulas for complete and incomplete first-order TEM moments below ground in a conductive half-space. Geophysics 2020, 86, E1–E11. [Google Scholar] [CrossRef]
- Smith, R.S.; Lee, T.J. Using the moments of a thick layer to map conductance and conductivity from airborne electromagnetic data. J. Appl. Geoph. 2002, 49, 173–183. [Google Scholar] [CrossRef]
- Lee, T.J.; Smith, R.S. Multiple-order moments of the transient electromagnetic response of a one-dimensional earth with finite conductance—Theory. Explor. Geophys. 2021, 52, 1–15. [Google Scholar] [CrossRef]
- Smith, R.; Hyde, C.; Lee, T.; Almond, R. Impulsive moments at work. ASEG Ext. Abstr. 2003, 1, 1–7. [Google Scholar] [CrossRef]
- Smith, R.S.; Fountain, D.; Allard, M. The MEGATEM fixed-wing transient EM system applied to mineral exploration: A discovery case history. First Break 2003, 21, 71–75. [Google Scholar] [CrossRef]
- Balch, S.J.; Boyko, W.P.; Paterson, N.R. The AeroTEM airborne electromagnetic system. Lead. Edge 2012, 22, 562–566. [Google Scholar] [CrossRef]
- Smith, R.S.; Lee, T.J. Multiple-order moments of the transient electromagnetic response of a one-dimensional earth with finite conductance—The Gaussian variation applied to a field example. Explor. Geophys. 2022, 53, 262–274. [Google Scholar] [CrossRef]
- Nash, J.E. Systematic Determination of Unit Hydrograph Parameters. J. Geoph. Res. 1959, 64, 111–115. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Xanthopoulos, T. On the Parametric Approach to Unit Hydrograph Identification. Water Resour. Manag. 1989, 3, 107–128. [Google Scholar] [CrossRef]
- Smith, R.S. On removing the primary field from fixed-wing time-domain airborne electromagnetic data: Some consequences for quantitative modelling, estimating bird position and detecting perfect conductors. Geophys. Prospect. 2001, 49, 405–416. [Google Scholar] [CrossRef]
- Balch, S.J.; Samson, C.; Sanchez, J.L. Correcting for HTEM altitude variations by transmitter mutual inductance normalization. SEG Tech. Program Expand. Abstr. 2016, 2139–2143. [Google Scholar]
- Christensen, N.B. Optimized fast Hankel transform filters. Geophys. Prospect. 1990, 38, 545–568. [Google Scholar] [CrossRef]
- Raiche, A. Modelling the time-domain response of AEM systems. Explor. Geophys. 1998, 29, 103–106. [Google Scholar] [CrossRef]
- Ku, H.H. Notes on the use of propagation of error formulas. J. Res. Natl. Bur. Stand. 1966, 70C, 262. [Google Scholar] [CrossRef]
- Witherly, K.; Irvine, R.; Godbout, M. Reid Mahaffy Test Site, Ontario Canada: An example of benchmarking in airborne geophysics. SEG Tech. Program Expand. Abstr. 2004, 1202–1204. [Google Scholar]
- Ontario Geological Survey. Ontario Airborne Geophysical Surveys, Magnetic and Electromagnetic Data, Timmins Area MEGATEM®; Ontario Geological Survey, Geophysical Data Set 1041; Ontario Geological Survey: Sudbury, ON, Canada, 2002. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallée, M.A.; Moussaoui, M. Moment Estimation from Time Domain Electromagnetic Data. Minerals 2024, 14, 888. https://doi.org/10.3390/min14090888
Vallée MA, Moussaoui M. Moment Estimation from Time Domain Electromagnetic Data. Minerals. 2024; 14(9):888. https://doi.org/10.3390/min14090888
Chicago/Turabian StyleVallée, Marc A., and Mouhamed Moussaoui. 2024. "Moment Estimation from Time Domain Electromagnetic Data" Minerals 14, no. 9: 888. https://doi.org/10.3390/min14090888
APA StyleVallée, M. A., & Moussaoui, M. (2024). Moment Estimation from Time Domain Electromagnetic Data. Minerals, 14(9), 888. https://doi.org/10.3390/min14090888






