Proposal of a Method for Calculating the Bond Work Index for Samples with Non-Standard Feed Particle Size Distribution

Abstract

Determining the Bond grindability test in a ball mill is one of the most commonly used methods in the mining industry for measuring the hardness of ores. The test is an essential part of the Bond work index methodology for designing and calculating the efficiency of mineral grinding circuits. The Bond ball mill grindability test has several restrictions, including the sample’s initial particle size distribution (PSD). This paper presents a method for calculating the Bond work index when the Bond ball mill grindability test is performed on samples with non-standard PSD. The presented equation includes a correction factor (k) and is applicable only for P₁₀₀ = 75 μm. The defined method is then compared with methods proposed by other researchers, and conclusions are drawn as to which method results in less deviation. The presented model resulted in a mean square error of 0.66%.

1. Introduction

To determine the required grinding power, Fred Bond [1] developed an approach that equipment manufacturers still use as the state-of-the-art design methodology [2]. The method’s theoretical basis is Bond’s Third Theory of Comminution, which introduced the Bond work index (w_i). The numerical input of w_i describes the energy (kWh/t) required for reducing ore size from an initial very large size to a specific particle size (e.g., 80% of the product passes through a 100 µm sieve) [3,4].

Notwithstanding its widespread use, the standard Bond test has certain limitations [5,6]. The test requires a specific sample preparation and a precisely defined initial sample PSD. A sample weighing 10 kg and, usually, the help of a professional technician is needed to perform one Bond test, which can last more than 8 hours. Based on the standard Bond test, w_i is determined by a simulation of batch dry grinding in a closed cycle in a Bond ball mill until a circulating mill charge of 250% is obtained [1,7,8]. The w_i is calculated after the mill product’s PSD.

These limitations prompted the proposal of alternative and faster methods and procedures for the Bond test simulation to determine the Bond w_i [9,10]. Alternative procedures presented by [11,12,13,14,15,16], faster procedures suggested by [17,18,19,20,21], and procedures for the Bond test simulation introduced by [22,23,24,25,26] were offered to shorten the Bond procedure duration. The procedures in [27,28,29,30,31,32,33,34,35] allowed estimating the w_i in other laboratory ball mills when the Bond laboratory mill was unavailable. All these procedures were based on Bond’s grinding theory and comparison with the determination of the work index. The authors [12,36,37] suggested that decreased closing screen size increased the Bond w_i. Josefin and Doll (2018) [38] introduced an equation that could correct the w_i obtained for a sample calculated with a P₈₀ value when the grinding operation is performed to a different P₈₀ using a calibration sample. Even though these procedures exist, the knowledge of the Bond standard test is constantly extended by new research [9,25,34,39,40,41,42,43,44,45].

Magdalinovic et al. [44] determined the Bond w_i on samples of non-standard PSD. The Bond test was performed on dolomite, copper ore, and quartzite samples of different size classes (−3.327 + 0; −2.356 + 0; −1.651 + 0; −1.168 + 0; −0.833 + 0) mm. Based on the obtained results, the rules for changing the parameters G [g/rev], P₈₀ [μm], and F₈₀ [μm] in the Bond equation were established. For calculating the Bond work index using this method, the authors have proposed three equations. The maximum error obtained by the authors Magdalinovic et al. [44] using this method was less than 5%. Nikolić and Trumić [42] provided the procedure for determining the Bond w_i for finer samples. The paper presents a method for assessing Bond’s w_i on samples showing a non-standard PSD.

The objective of this study was to demonstrate the theoretical and practical contribution to understanding the comminution process of non-standard particle size samples in a laboratory Bond ball mill. The research conducted in this study focused on the following:

• Monitoring the influence of the initial particle size of the sample on the Bond Work Index values during the execution of the standard Bond test;
• Defining a model for determining the Bond Work Index for standard particle size samples based on the known Bond Work Index value for a non-standard particle size sample;
• Testing the accuracy of the model using results from laboratory experiments and available data from the reviewed literature.

2. Materials and Methods

The samples used in this study were prepared with crushing in a jaw crusher and then sieved through a sieve with an opening size of −3.35 mm. Three mono-mineral-like ores were used in this study: zeolite, dacite, and basalt. The zeolite sample was taken from the “Jablanica” deposit near Kruševac [46]. The Jablanica zeolitized tuff deposit is located on the outskirts of the village of Jablanica, in the central part of the exploration area. The dacite sample was collected from the “Krš” open-pit mine near Ljubovija, which is a deposit of technical dacite stone of eruptive origin. The basalt sample was taken from the “Vrelo” basalt deposit, located in the vicinity of the village of Štava on the southeastern slopes of the central part of Mount Kopaonik. The samples had different resistance to comminution. Five 10 kg samples with different initial sizes (−3.35 + 0 mm; −2.36 + 0 mm; −1.70 + 0 mm; −1.18 + 0 mm; −0.850 + 0 mm) were formed for each type of raw material for a grinding test based on the standard Bond procedure. The PSDs of zeolite, dacite, and basalt are in

Table A1. Zeolite sample PSDs.

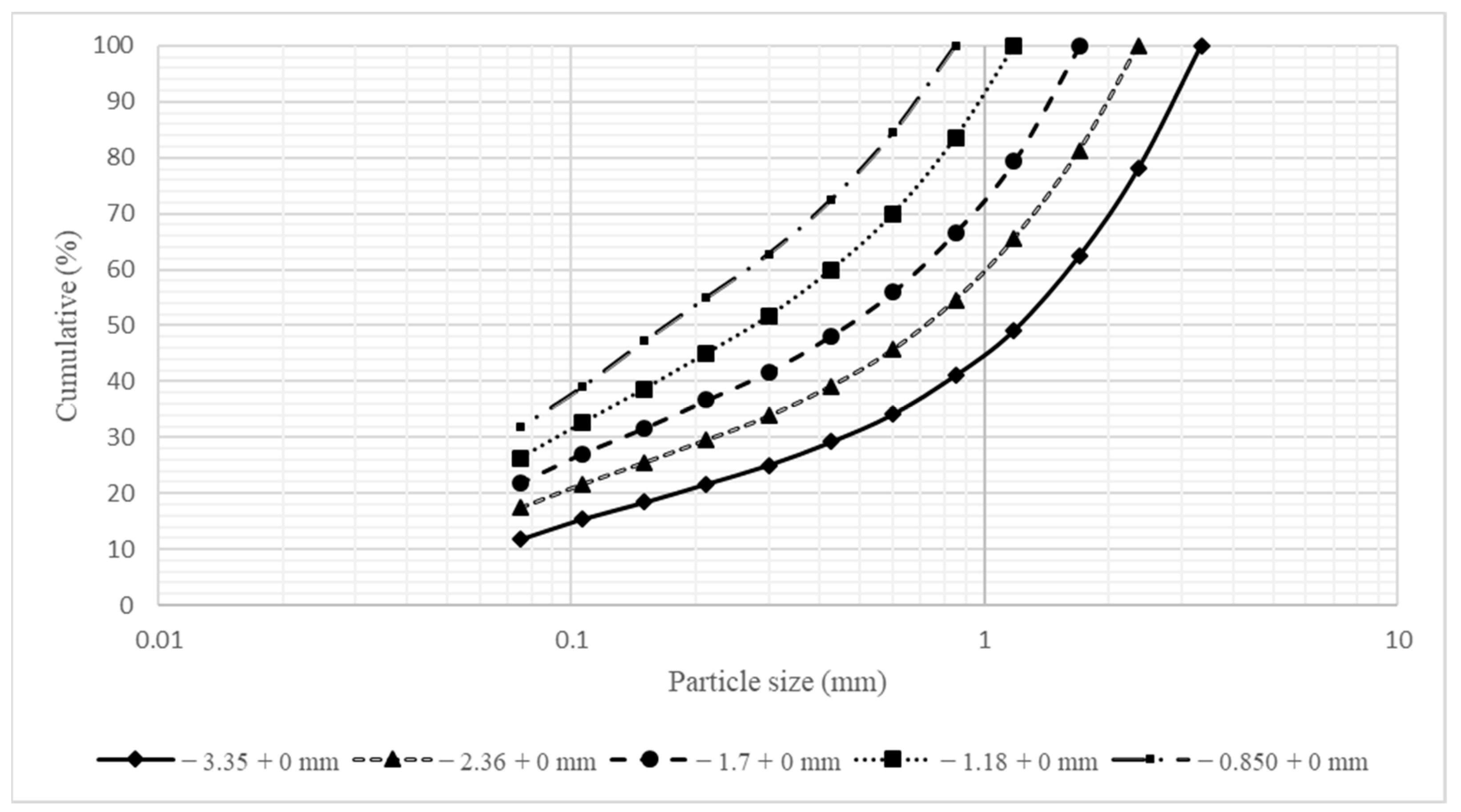
Particle Size (mm)	Class Size in mm (%)
	−3.35 + 0	−2.36 + 0	−1.70 + 0	−1.18 + 0	−0.850 + 0
−3.35 + 2.36	21.95
−2.36 + 1.70	15.55	18.74
−1.70 + 1.18	13.35	16.72	20.64
−1.18 + 0.850	8.10	9.99	12.74	16.42
−0.850 + 0.600	6.90	8.86	10.69	13.64	15.51
−0.600 + 0.425	4.95	6.51	7.80	9.99	12.02
−0.425 + 0.300	4.14	5.33	6.46	8.28	9.68
−0.300 + 0.212	3.37	4.26	5.02	6.66	7.82
−0.212 + 0.150	3.26	4.04	5.00	6.39	7.75
−0.150 + 0.106	3.01	3.87	4.56	6.07	8.23
−0.106 + 0.075	3.62	4.23	5.27	6.25	7.20
−0.075 + 0.00	11.80	17.45	21.82	26.30	31.79
∑	100.00	100.00	100.00	100.00	100.00

,

Table A2. Dacite sample PSDs.

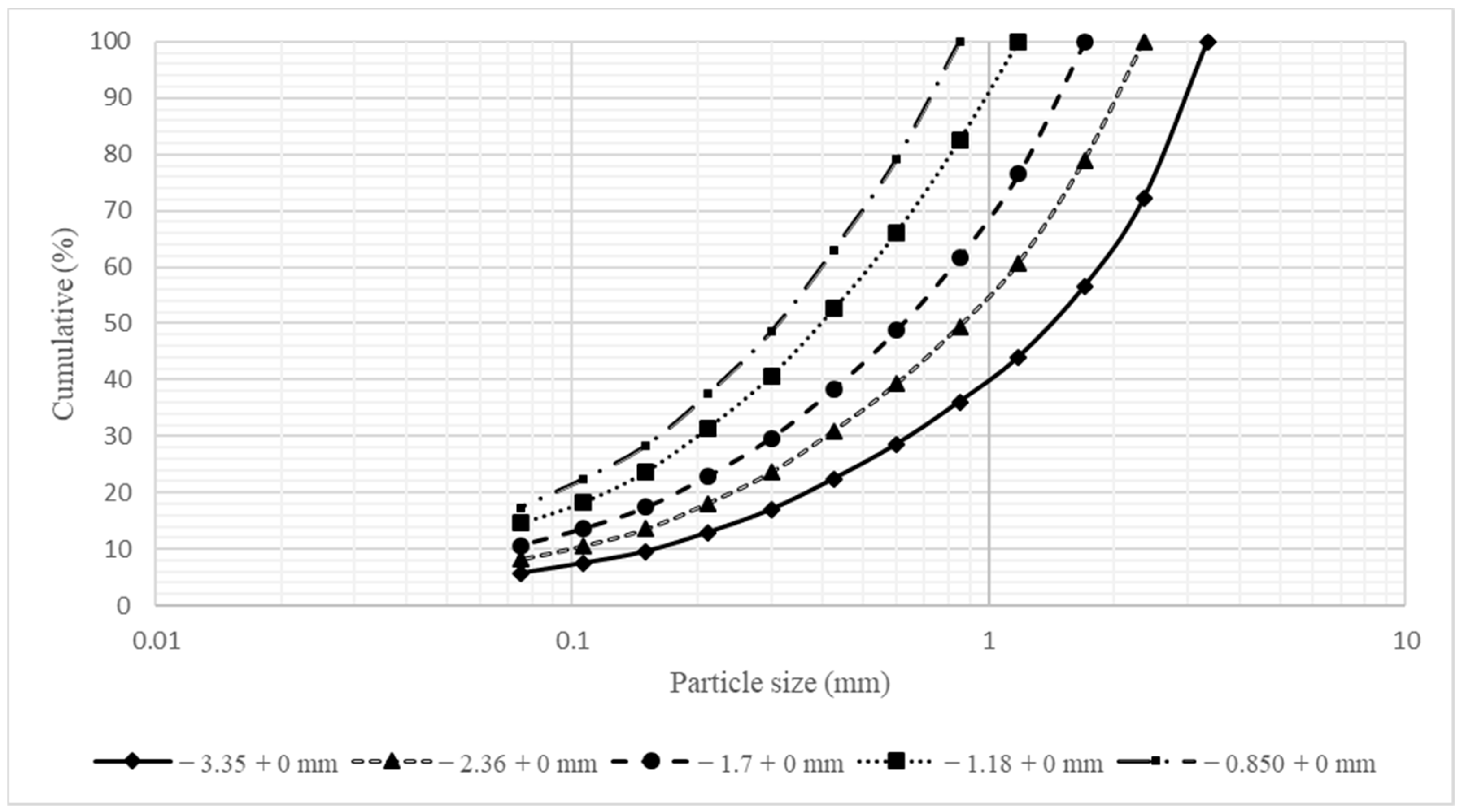
Particle Size (mm)	Class Size in mm (%)
	−3.35 + 0	−2.36 + 0	−1.70 + 0	−1.18 + 0	−0.850 + 0
−3.35 + 2.36	27.77
−2.36 + 1.70	15.60	21.08
−1.70 + 1.18	12.59	18.24	23.42
−1.18 + 0.850	7.99	11.28	14.83	17.54
−0.850 + 0.600	7.52	10.18	12.98	16.40	20.91
−0.600 + 0.425	6.10	8.28	10.36	13.47	16.02
−0.425 + 0.300	5.45	7.39	8.76	11.94	14.62
−0.300 + 0.212	4.05	5.46	6.73	9.21	10.95
−0.212 + 0.150	3.39	4.57	5.55	7.76	9.25
−0.150 + 0.106	2.08	3.00	3.78	5.46	5.93
−0.106 + 0.075	1.77	2.39	2.92	3.68	5.02
−0.075 + 0.00	5.69	8.13	10.67	14.54	17.30
∑	100.00	100.00	100.00	100.00	100.00

and

Table A3. Basalt sample PSDs.

Particle Size (mm)	Class Size in mm (%)
	−3.35 + 0	−2.36 + 0	−1.70 + 0	−1.18 + 0	−0.850 + 0
−3.35 + 2.36	29.92
−2.36 + 1.70	17.28	23.84
−1.70 + 1.18	14.10	19.64	24.71
−1.18 + 0.850	8.24	11.63	15.34	23.05
−0.850 + 0.600	7.38	10.22	13.14	18.60	23.14
−0.600 + 0.425	5.18	7.39	10.20	13.29	16.76
−0.425 + 0.300	4.33	6.19	8.32	10.45	13.55
−0.300 + 0.212	2.96	4.36	6.00	7.00	9.71
−0.212 + 0.150	2.44	3.76	4.84	6.00	8.04
−0.150 + 0.106	1.72	2.59	3.10	4.23	5.64
−0.106 + 0.075	1.47	2.28	3.14	3.79	4.98
−0.075 + 0.00	4.98	8.10	11.21	13.59	18.18
∑	100.00	100.00	100.00	100.00	100.00

and Figure 1, Figure 2 and Figure 3. Table A1, Table A2 and Table A3 are provided in Appendix A.

A standard Bond laboratory mill, with a grinding chamber 305 × 305 mm and a rotation speed of 70 rev/min, was used to determine the Bond work index. The mill was filled with 15.5 to 30.6 mm in diameter balls, and the total weight was 20.125 kg. Dry grinding was used, simulating a closed grinding cycle until a circulating load of 250% was established [7]. A 75 µm closing screen size (P₁₀₀) was used. The Bond work index was calculated with Equation (1).

$${\mathrm{w}}_{\mathrm{i}}=1.1·{\displaystyle \frac{44.5}{{{\mathrm{P}}_{100}}^{0.23}·{\mathrm{G}}^{0.82}·\left(\frac{10}{\sqrt{{\mathrm{P}}_{80}}}·\frac{10}{\sqrt{{\mathrm{F}}_{80}}}\right)}}[{\displaystyle \frac{\mathrm{k}\mathrm{W}\mathrm{h}}{\mathrm{t}}}]$$

(1)

wherein

P₁₀₀—closing screen size (μm);

G—net mass of undersize product per unit revolution of the mill, in g/rev;

P₈₀—the 80% passing product particle size (μm);

F₈₀—the 80% passing feed particle size (μm).

3. Results and Discussion

A single grindability test was performed on all samples, with no repetition of measurements. Therefore, the obtained results do not account for any potential experimental error that may arise from repeated measurements.

The obtained results for the Bond w_i for samples of zeolite, dacite, and basalt on non-standard size classes are shown in

Table A4. Parameters F₈₀ and value of w_i for samples of zeolite, dacite and basalt used on non-standard size classes.

Sample	Class Size (mm)	P100 = 75 µm
		F80 (μm)	wi (kWh/t)
Zeolite	−3.35 + 0	2440	9.834
	−2.36 + 0	1652	10.010
	−1.70 + 0	1090	10.197
	−1.18 + 0	727	10.371
	−0.850 + 0	544	10.572
Dacite	−3.35 + 0	2646	17.800
	−2.36 + 0	1729	18.130
	−1.70 + 0	1253	18.333
	−1.18 + 0	807	18.827
	−0.850 + 0	609	19.196
Basalt	−3.35 + 0	2609.1	21.098
	−2.36 + 0	1800.1	21.659
	−1.70 + 0	1278	21.951
	−1.18 + 0	892	22.352
	−0.850 + 0	633	22.874

and Figure 4. Table A4 is also included in Appendix A. The Bond work index was calculated using Equation (1) on samples with a standard particle size (F₁₀₀ = 3.35 mm) and non-standard particle size (F₁₀₀ ≤ 3.35 mm). A closing screen size (P₁₀₀) of 75 µm was used for all samples.

Based on the obtained results, it can be concluded that the Bond work index increases as the initial particle size of the sample decreases. The resistance of the raw material to comminution increases with decreasing particle size [44], which is one of the possible reasons for this phenomenon. An additional problem might be that feeds contain an excessive amount of finished product, which prolongs the attainment of a steady-state condition [30]. For practical purposes, a sample that contains 15% of the finished fraction or less is ideal [27]. However, in industrial practice, such a bulk material that has a higher ratio of fine fraction is not rare [30].

It is not unusual to receive at the laboratories samples to assess their w_i with a feed PSD differing from the standard PSD prescribed by Bond. The question arises as to whether it is possible to determine the Bond w_i if we obtain a sample of non-standard size. The presented method allows us to estimate the work index for a sample of standard size, although we do not have a sample of the size required by Bond. If we receive a sample of non-standard size, and we want to calculate the Bond w_i for a sample of standard PSD, the procedure is as follows:

• First, Bond’s standard test is performed on a sample of non-standard PSD;
• Then, the obtained parameters (w_i,ns and F_ns) from the Bond test on the non-standard PSD sample are used to estimate the w_i for the standard PSD sample, using Equation (2).

  $${\mathrm{w}}_{\mathrm{i},\mathrm{c}}={\displaystyle \frac{{\mathrm{w}}_{\mathrm{i},\mathrm{n}\mathrm{s}}·{{\mathrm{F}}_{\mathrm{n}\mathrm{s}}}^{0.05}}{\mathrm{k}}}$$

  (2)

where

w_i,ns—work index for a sample of non-standard PSD [kWh/t];

w_i,c—calculated work index for a sample of standard PSD [kWh/t];

F_ns—the 80% passing sample of non-standard PSD [μm];

k—coefficient that depends on the ore grindability (

Table 1. Value of coefficient k [42].

wi [kWh/t]	10–17	18–20	>21
k	1.47	1.48	1.49

).

Equation (2) was tested on samples of varying grindability, including zeolite, dacite, and basalt. The aim was to test the validity of the equation and check its accuracy and reliability. The results of testing Equation (2) on the samples of zeolite, dacite, and basalt are presented in

Table 2. Results obtained using Equation (2).

Sample	Class Size (mm)	Fns (μm)	P100 = 75 μm		wi (kWh/t)	wi,c (kWh/t)	Δ (%)
			wi,ns (kWh/t)	k
Zeolite	−2.36 + 0	1652	10.010	1.47	9.834	9.863	−0.29
	−1.70 + 0	1090	10.197			9.841	−0.07
	−1.18 + 0	727	10.371			9.827	+0.07
	−0.850 + 0	544	10.572			9.854	−0.20
Dacite	−2.36 + 0	1729	18.130	1.48	17.800	17.784	+0.09
	−1.70 + 0	1253	18.333			17.696	+0.58
	−1.18 + 0	807	18.827			17.777	+0.13
	−0.850 + 0	609	19.196			17.873	−0.41
Basalt	−2.36 + 0	1800.1	21.659	1.49	21.098	21.145	−0.22
	−1.70 + 0	1278	21.951			21.067	+0.15
	−1.18 + 0	892	22.352			21.069	+0.14
	−0.850 + 0	633	22.874			21.195	−0.46

. A search of the literature presented papers where researchers determined the Bond work index using samples of non-standard sizes. These results are added to the examination to confirm the validity and accuracy of the presented methodology for data not included in the empirical “training data” used to derive the model. In the continuation of the paper, the equation was tested on all other available data found in the literature.

The presented results show the Bond work index value that would be obtained for a sample with standard particle size (F₁₀₀ = 3.35 mm) if a sample with non-standard particle size (F₁₀₀ ≤ 3.35 mm) were present in the initial sample. Based on the results obtained using Equation (2), an error of less than 1% is obtained. Few researchers have addressed this issue because the preparation of samples and testing of the Bond test takes a very long time and usually requires the help of expert technical personnel. Equation (2) was tested on available data that could be found in the literature, and the results are shown in

Table 3. Comparative results of w_i obtained by Bond test and Equation (2).

Sample	Ref.	Class Size (mm)	Fns (μm)	P100 = 75 μm		wi (kWh/t)	wi,c (kWh/t)	Δ (%)	Δ2
				wi,ns (kWh/t)	k
Zeolite		−2.36 + 0	1652	10.01	1.47	9.834	9.86	−0.29	0.084
		−1.70 + 0	1090	10.20			9.84	−0.07	0.005
		−1.18 + 0	727	10.37			9.83	+0.07	0.0049
		−0.850 + 0	544	10.57			9.85	−0.20	0.040
Dolomite	[44]	−2.356 + 0	1662	12.91		12.70	12.72	−0.16	0.026
		−1.651 + 0	1090	13.16			12.70	0.00	0.000
		−1.168 + 0	727	13.38			12.65	+0.39	0.152
		−0.833 + 0	544	13.69			12.76	−0.47	0.221
Cu ore	[44]	−2.356 + 0	1729	15.70		15.67	15.51	+1.02	1.040
		−1.651 + 0	1253	15.84			15.39	+1.79	3.204
		−1.168 + 0	807	16.19			15.39	+1.79	3.204
		−0.833 + 0	609	16.79			15.74	−0.45	0.202
Dacite		−2.36 + 0	1729	18.13	1.48	17.80	17.78	+0.09	0.008
		−1.70 + 0	1253	18.33			17.70	+0.58	0.336
		−1.18 + 0	807	18.83			17.78	+0.13	0.017
		−0.850 + 0	609	19.20			17.87	−0.41	0.168
Basalt		−2.36 + 0	1800.1	21.66	1.49	21.10	21.14	−0.22	0.048
		−1.70 + 0	1278	21.95			21.07	+0.15	0.022
		−1.18 + 0	892	22.35			21.07	+0.14	0.020
		−0.850 + 0	633	22.87			21.20	−0.46	0.212
Quartzite	[44]	−2.356 + 0	1790	23.17		22.63	22.61	+0.09	0.001
		−1.651 + 0	1240	23.52			22.54	+0.40	0.160
		−1.168 + 0	870	24.14			22.73	−0.44	0.194
		−0.833 + 0	610	24.72			22.86	−1.02	1.040
Sum									10.4173
$\mathrm{Mean} \mathrm{square} \mathrm{error} \sqrt{{\displaystyle \frac{{∆}^2}{N=24}}}$									0.66

.

The results in Table 3 show that the mean square error is 0.66% when Equation (2) is used to calculate the w_i for a standard PSD sample. The application of Equation (2) in Table 3 was only tested for a 75 µm closing screen size. The presented method for determining the w_i for a sample with standard PSD when the value of the Bond w_i for a sample with non-standard particle size is known can only be applied when the Bond w_i is determined at P₁₀₀ = 75 µm. In their study, the authors Magdalinovic et al. [44] presented a method for determining the Bond (w_{i, cM}) for a sample with a standard PSD, where the value of the Bond w_i is known for a sample with a non-standard PSD and which can be used with a P₁₀₀ = 75 µm and P₁₀₀ = 149 µm. The idea was to compare these two methods, but only at a closing screen size of 75 µm, because the presented method is applicable only at a closing screen size of 75 µm, and to determine which model leads to a lower deviation. The comparative results obtained with Equation (2) and the model presented by Magdalinovic et al. in [44] are shown in

Table 4. Comparative results of the w_i obtained by the Bond test and the method in [44] (P₁₀₀ = 75 µm).

Sample	Ref.	Class Size (mm)	Fns (μm)	wi,ns (kWh/t)	wi (kWh/t)	wi,cM (kWh/t)	Δ (%)	Δ2
Zeolite		−2.36 + 0	1652	10.01	9.83	9.93	−0.98	0.96
		−1.70 + 0	1090	10.20		10.14	−3.11	9.67
		−1.18 + 0	727	10.37		10.12	−2.91	8.47
		−0.850 + 0	544	10.57		9.79	+0.45	0.20
Dolomite	[44]	−2.356 + 0	1662	12.91	12.70	12.91	−1.65	2.72
		−1.651 + 0	1090	13.16		13.04	−2.68	7.18
		−1.168 + 0	727	13.38		12.94	−1.89	3.57
		−0.833 + 0	544	13.69		12.85	−1.18	1.39
Cu ore	[44]	−2.356 + 0	1729	15.70	15.67	15.69	−0.13	0.02
		−1.651 + 0	1253	15.84		15.69	−0.13	0.02
		−1.168 + 0	807	16.19		15.72	−0.32	0.10
		−0.833 + 0	609	16.79		15.78	−0.70	0.49
Dacite		−2.36 + 0	1729	18.13	17.80	18.09	−1.63	2.66
		−1.70 + 0	1253	18.33		18.19	−2.19	4.80
		−1.18 + 0	807	18.83		18.35	−3.09	9.55
		−0.850 + 0	609	19.20		18.81	−5.67	32.15
Basalt		−2.36 + 0	1800.1	21.66	21.10	21.52	−2.00	4.00
		−1.70 + 0	1278	21.95		21.85	−3.56	12.67
		−1.18 + 0	892	22.35		22.05	−4.51	20.34
		−0.850 + 0	633	22.87		21.90	−3.80	14.44
Quartzite	[44]	−2.356 + 0	1790	23.17	22.63	23.16	−2.34	5.48
		−1.651 + 0	1240	23.52		23.39	−3.36	11.29
		−1.168 + 0	870	24.14		23.64	−4.46	19.89
		−0.833 + 0	610	24.72		23.46	−3.67	13.47
Sum								185.53
$\mathrm{Mean} \mathrm{square} \mathrm{error} \sqrt{{\displaystyle \frac{{∆}^2}{N=24}}}$								2.78

, respectively.

Table 5. Comparative results of the w_i obtained by the Bond test and the method in [44] (_P100 = 149 µm).

Sample	Ref.	Class Size (mm)	Fns (μm)	wi,ns (kWh/t)	wi (kWh/t)	wi,cM (kWh/t)	Δ (%)	Δ2
Dolomite	[44]	−2.356 + 0	1662	9.77	9.82	9.56	+2.65	7.023
		−1.651 + 0	1090	10.59		9.91	−0.92	0.846
		−1.168 + 0	727	11.44		9.94	−1.22	1.488
		−0.833 + 0	544	12.19		9.83	−0.10	0.010
Cu ore	[44]	−2.356 + 0	1729	15.86	15.32	15.43	−0.72	0.518
		−1.651 + 0	1253	16.46		15.43	−0.72	0.518
		−1.168 + 0	807	17.42		15.33	−0.07	0.005
		−0.833 + 0	609	18.93		15.11	+1.37	1.877
Quartzite	[44]	−2.356 + 0	1790	18.92	19.00	18.61	−2.05	4.203
		−1.651 + 0	1240	19.13		18.25	+3.95	15.603
		−1.168 + 0	870	20.61		18.67	+1.74	3.028
		−0.833 + 0	610	23.30		19.37	−1.95	3.803
Sum								38.922
$\mathrm{Mean} \mathrm{square} \mathrm{error} \sqrt{{\displaystyle \frac{{∆}^2}{N=25}}}$								1.80

presents the results obtained when using the model by Magdalinovic et al. in [44] for a closing screen size of 149 µm.

The results in Table 4 and Table 5 show that when testing the model presented by Magdalinovic et al. [44], the mean square error is 2.78% for a 75 µm closing screen size and 1.80% for a 149 µm closing screen size. Based on the results obtained, it can be concluded that when determining the w_i for a standard PSD sample, knowing the w_i for a non-standard PSD sample on a 75 µm closing screen size, Equation (2) poses a lower deviation than the model presented in [44]. Therefore, when determining the Bond w_i for a standard PSD sample, and knowing the Bond w_i for a non-standard particle size sample on a P₁₀₀ = 75 µm closing screen size, it should be recommended the use of Equation (2), while for a coarser grinding, P₁₀₀ = 149 µm, the model of Magdalinovic et al. [44] can be used, for it is currently the only model tested at this closing screen size.

4. Conclusions

The determination of the Bond work index is considered the most popular method used for calculating critical parameters of the grinding process, selecting equipment, and controlling the grinding process. The Bond test is regarded as a standard laboratory procedure for determining the parameter w_i. As an initial condition for conducting the Bond grindability test, the upper particle size limit of the raw material must be 3.35 mm (F₁₀₀ = 3.35 mm).

The determination of the Bond work index in a ball mill for raw materials with an initial particle size smaller than the standard size (−3.35 + 0 mm) has not received sufficient attention. Therefore, this study investigates the effect of raw material particle size, with an upper size limit smaller than 3.35 mm, on the Bond work index value. The experiments were conducted as a function of the initial sample size on raw materials with different mineral compositions and physical-mechanical properties (zeolite, dacite, and basalt).

Based on the experimentally obtained results from tests conducted on samples of zeolite, dacite, and basalt, as well as the analysis and discussion of the results, the following conclusions were drawn:

• The value of the Bond work index increases as the particle size of the raw material decreases. For samples with an upper size limit significantly smaller than the standard size, the Bond work index value is higher than the Bond work index value obtained for the standard-sized sample.
• A model for determining the Bond work index for standard-sized samples has been presented, provided the Bond work index for a non-standard-sized sample is known.
• The model is applicable only for a closing screen size (P₁₀₀) of 75 µm.
• The presented model was then tested on all available data found in the literature to verify the accuracy and validity of the model.

From the information presented, it can be concluded that the Bond work index for a standard particle size sample can be determined if the value of the Bond work index for a non-standard particle size sample is known. Applying Equation (2) to the tested samples to obtain wi resulted in a mean square error of −0.66%, which is within the limits of reproducibility of the standard Bond test. The results obtained with Equation (2) were compared with the results of Magdalinovic et al. (2012) [44], leading to the following conclusions:

• When determining the Bond work index for a standard particle size sample, if the Bond work index value for a non-standard particle size sample on a 75 µm closing screen size is known, Equation (2) should be used, as it provides more reliable results.
• When determining the Bond work index for a standard particle size sample, if the Bond work index value for a non-standard particle size sample on a closing screen size of 149 µm is known, the model of Magdalinovic et al. [44] should be used, as it is currently the only model tested on a closing screen size of 149 µm.

The low mean square error confirms the accuracy and validity of the presented method for determining the Bond work index on a standard particle size sample when the Bond work index value is known for a non-standard particle size sample. The presented method represents a practical contribution that will significantly help practitioners when planning a new plant or optimizing an existing one.