Next Article in Journal
Effect of the Occurrence State of Dodecylamine on the Adsorption Behavior of Calcium Sulfate Dihydrate and Silica
Previous Article in Journal
Unsupervised Anomaly Detection for Mineral Prospectivity Mapping Using Isolation Forest and Extended Isolation Forest Algorithms
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Minerals
Volume 15
Issue 4
10.3390/min15040412
minerals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Determining the Mechanical Properties of Shale Constituent Minerals Using Nanoindentation and a TESCAN Integrated Mineral Analyzer (TIMA)

by
Yongjun Xiao
1,2,
Qi Cheng
1,3,
Jiren Tang
1,3,* and
Shengyao Cai
1,3
1
State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400044, China
2
Sichuan Changning Natural Gas Development Co., Ltd., Chengdu 610051, China
3
State and Local Joint Engineering Laboratory of Methane Drainage in Complex Coal Gas Seam, Chongqing University, Chongqing 400044, China
*
Author to whom correspondence should be addressed.
Minerals 2025, 15(4), 412; https://doi.org/10.3390/min15040412
Submission received: 2 March 2025 / Revised: 8 April 2025 / Accepted: 10 April 2025 / Published: 14 April 2025
(This article belongs to the Section Mineral Exploration Methods and Applications)
Browse Figures
Versions Notes

Abstract

:
Understanding the mechanical properties of the constituent minerals of shales is of significance for gaining insight into the macroscopic mechanical behavior of shales. In this paper, a method combining nanoindentation with a TESCAN Integrated Mineral Analyzer (TIMA) was used to determine the mechanical properties of shale constituent minerals. The hardness and elastic modulus of five independent mineral phases and a mixed phase were detected. The order of the hardness of these five independent mineral phases is dolomite (4.90 ± 2.33 GPa) > wollastonite (4.84 ± 0.54 GPa) > ankerite (4.17 ± 1.37 GPa) > quartz (3.98 ± 0.67 GPa) > calcite (2.03 ± 0.29 GPa), and the order of the elastic modulus is dolomite (104.89 ± 11.25 GPa) > ankerite (103.70 ± 19.62 GPa) > wollastonite (100.78 ± 6.66 GPa) > quartz (88.04 ± 14.58 GPa) > calcite (78.20 ± 3.85 GPa). The mechanical properties of the shale mineral grain junctions are weaker than those inside the grains. When shale is subjected to an external load, it is more prone to intergranular failure. The proposed method in this study can rapidly and accurately probe the in situ mechanical properties of shale minerals. The results of this study enrich the database of in situ mechanical properties of shale minerals and provide a new insight into the macroscopy failure mode of shale.

Graphical Abstract

1. Introduction

The physical and chemical properties of black shale have attracted extensive attention with the global boom in shale gas development [1,2,3,4,5]. Mechanical parameters such as strength, elastic modulus, and hardness of shale have an important impact on well wall stability, fracture modification effectiveness, and stability of propped fractures during shale gas development, which in turn affects the efficiency and economy of shale gas development [6,7,8,9].
The mechanical parameters of shale are normally obtained through uniaxial or triaxial compression, Brazilian splitting, three-point bending, and ultrasonic measurement [10,11,12,13,14]. These methods enable the acquisition of bulk mechanical parameters of the shale. However, shale is a typical multiphase, multiscale composite material whose bulk mechanical behavior is determined by the mechanical properties of the constituent minerals. Obtaining the mechanical properties of constituent minerals is essential for gaining insight into the mechanical behaviors of shale and for developing physical prediction models [15]. The mechanical parameters of constituent minerals are the key input in the heterogeneous mechanical modeling of shale. In addition, the macroscopic failure of shale always starts with the sprouting of microcracks, and understanding the mechanical properties of the constituent minerals can help provide insight into the microscopic mechanisms of fracture initiation and propagation in shale. The particle sizes of the constituent mineral grains of shale are typically in the micron or submicron class size [16]. The conventional mechanical methods mentioned above cannot achieve the measurement of mechanical properties of shale constituent minerals.
The development of nanoindentation technology makes it possible to determine the mechanical properties of materials on the submicron scale. Nanoindentation was originally applied in the field of materials science and was recently introduced into the study of geological materials [17,18,19,20,21,22,23,24]. Liu et al. investigated the micromechanical properties of BaO-Sm2O3-5TiO2 ceramic based on nanoindentation [25,26]. Kang et al. investigated the mechanical behavior of polypropylene fiber-reinforced cement-based composites through nanoindentation [27]. Ulm et al. were the first to use nanoindentation to study the micromechanical properties of shale [28]. One of the advantages of nanoindentation is that only a small number of rock samples are needed to measure its mechanical parameters, which are friendly for reservoir rocks that are difficult to sample. Liu et al. [29] used nanoindentation to study the micromechanical properties of Bakken reservoir shale, and Lu et al. [30] used nanoindentation to compare the mechanical properties of Longmaxi and Yanchang reservoir shales and analyzed the effect of diagenesis on the mechanical properties of the reservoir shale. In addition to shale, nanoindentation was widely used to characterize the micromechanical properties of other geological materials, such as coal, mudstone, sandstone, etc. [31,32,33,34,35].
Only mechanical parameters can be obtained through nanoindentation, and any information related to the composition of the specimen cannot be obtained directly through nanoindentation. Combining nanoindentation with other techniques enables the correlation of mechanical parameters with their corresponding compositional information. The multivariate clustering analysis technique enables the assignment of the results of nanoindentation to different mechanical phases. Both Gaussian mixture models and k-means have proven to be successful tools for analyzing nanoindentation data of composite materials [28,36,37,38]. Prior studies showed that the micromechanical parameters of shale can be classified into soft, intermediate, and hard phases. However, the mechanical phase is an abstract concept; it cannot be directly equated with the mineral phase. It is empirical to determine which mechanical phase the constituent minerals belong to. Clay minerals and organic matter are generally considered to correspond to the soft phase, while quartz and feldspar correspond to the hard phase [36,39]. Some researchers have analyzed mineralogical information corresponding to each indentation via microscopic observation of the nanoindentation area. Yang et al. [40] used high magnification optical microscopy to determine the mineral composition corresponding to the indentation. However, it is very challenging to determine the mineral composition only relying on optical microscopes. Some researchers tried to determine the mineral composition corresponding to each indentation via the scanning electron microscopy–energy dispersive spectroscopy (SEM-EDS) method [15,41,42]. EDS can obtain the spatial distribution of elements within the indentation area, which helps in mineral composition analysis. For example, regions containing only Si and O elements can be identified as quartz. However, it is still difficult to accurately identify minerals with complex elemental compositions (e.g., feldspar and clay minerals).
The TESCAN Integrated Mineral Analyzer (TIMA, TESCAN Co,. Ltd, Brno, Czech Republic) is an automated mineral analysis system consisting of a field emission scanning electron microscope, a backscattering probe, four sets of energy spectrum probes, analysis software, and a standard minerals database. The main principle of the system is to rapidly collect BSE and EDS data from the sample surface and determine the boundaries of the different mineral phases in the sample based on the differences in mineral composition reflected by BSE and EDS. The mineral species are then confirmed by comparing and matching the measured EDS data with the information in the mineral database [43]. With the support of the powerful software and database, TIMA can accurately quantify the mineral composition of micro-areas and has been widely used in the research of geology, mineral processing, and smelting fields [44,45,46].
In general, efforts to correlate shale micromechanical properties with corresponding mineralogy are still limited. In this study, a new attempt was made to combine nanoindentation with TIMA to obtain in situ mechanical parameters of shale constituent minerals. Firstly, nanoindentation tests were carried out on shale samples to obtain the micromechanical parameters of the samples. Then, the location of the indentation was found in the scanning electron microscope. The indentation areas were scanned and analyzed by TIMA to identify the minerals corresponding to each indentation. This method enables direct correlation of shale micromechanical properties with mineralogy, which helps to deepen the understanding of shale macromechanical performance and develop multi-scale geomechanical models of shale.

2. Material and Method

2.1. Sample Material and Preparation

The experimental samples were collected from an outcrop of Lower Silurian Longmaxi shale formation in the Fuling District, Chongqing Municipality, China. The bulk specimens were sectioned into cubic samples (10 × 10 × 10 mm3) using a precision wire-slicing apparatus to preserve structural integrity. A multi-stage surface finishing protocol was implemented on bedding-plane-parallel surfaces to achieve submicron-level flatness. Initial surface planarization involved sequential mechanical abrasion with silicon carbide papers (P800 to P5000 grit). Subsequently, argon ion-beam etching was performed using a Leica EM-RES 102 precision ion polisher (Leica Co., Ltd, Wetzlar, Germany). The final surface refinement phase consisted of 4-h ion milling at optimized parameters (4 kV acceleration voltage, 3° incident angle). The resultant ultra-low surface roughness satisfied the stringent topography requirements for both TIMA mineralogical analysis and nanoindentation mechanical characterization.

2.2. Nanoindentation

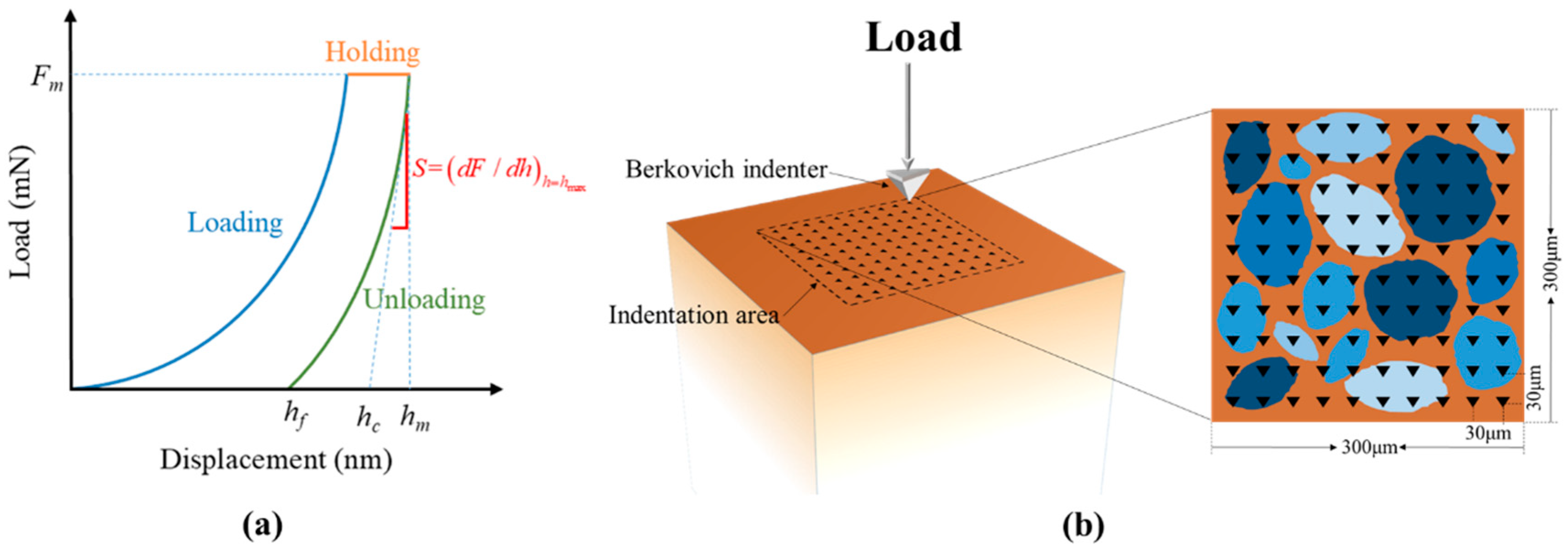
2.2.1. Nanoindentation Theory

Nanoindentation quantifies micromechanical properties through controlled contact mechanics between a geometrically defined diamond indenter and the specimen surface. The technique executes a predefined loading–unloading cycle where the indenter applies a controlled normal force until reaching either target penetration depth (hmax) or peak load (Fmax), followed by quasi-static retraction. The resultant characteristic load versus penetration depth profile enables extraction of two fundamental mechanical parameters: material hardness (H) and reduced elastic modulus (Er), which are derived through analytical models from the unloading curve’s slope and contact projection area [18]:
H = F max A c
E = 1 − ν 2 1 E r − 1 − ν i 2 E i − 1
where H is the hardness, Fmax is the peak load, and Ac is the projected contact area. E and Ei are elastic moduli of the sample and indenter, respectively, and ν and ν i are the Poisson’s ratios of the sample and indenter, respectively. Ei = 1141 GPa, ν i = 0.07, and ν is set to be 0.3. Er is the reduced modulus, and is given by:
E r = π S 2 η A c
where S is the contact stiffness, which is calculated by the initial stages of the unloading curve, S = d F / d h h = h max . η is a constant related to the indenter geometry for a Berkovich indenter, η = 1.034 [47]. A more detailed calculation procedure can be found in the literature [17,41].

2.2.2. Determination of the Representative Elementary Area (REA)

Given the intrinsic heterogeneity of shale formations, grid-based nanoindentation has been widely adopted to acquire statistically significant micromechanical measurements. The indentation test area must exceed the representative elementary area (REA), which is defined as the minimum sampling area required for statistically stable measurements that accurately reflect bulk material properties [36]. The mineral map-based box counting method was employed to determine the REA of the shale sample. A point was randomly selected on the mineral map and a series of concentric boxes were determined with that point as the center. The fraction of minerals in each box was calculated. Mineral fractions gradually stabilized with box size increasing. REA was determined as the size of the box when the mineral fraction reached stability [48]. Therefore, the mineral map of the sample was obtained using TIMA before nanoindentation, and the REA of the sample was determined using the box counting method (Figure 1). The REA of the sample was determined to be 250 × 250 µm.

2.2.3. Nanoindentation Design

The nanoindentation testing protocol employed a 10 × 10 array spanning 300 μm × 300 μm, exceeding the representative elementary area (REA) dimensions. Adjacent indentation sites were spatially offset by 30 μm to prevent stress field interactions. The indentation matrix was set in a pre-engraved box on the sample surface so that it could be quickly found for subsequent electron microscopy observations (Figure 2b).
Factors such as loading rate and indenter type in nanoindentation tests may affect measurement results. Shi et al. conducted nanoindentation experiments on Longmaxi shale samples within a loading rate range of 5–30 mN/s [49]. The results showed that the hardness and elastic modulus of the samples slightly increased with increasing loading rate. In order to avoid dynamic disturbances caused by excessively high loading rates, this study adopted a quasi-static loading scheme and set the loading rate to 5 mN/s. The individual indents were performed in quasi-static constant loading rate mode with a trapezoidal loading profile (20 s loading, 15 s hold, 20 s unloading) and a maximum load of 100 mN. Common nanoindentation indenter types include Berkovich (three-sided pyramid, 142.3° face angle), Vickers (four-sided pyramid, 136° face angle), spherical (5–200 μm radii), and cube-corner (35.1° face angle) geometries. Indenter selection critically influences contact mechanics: Berkovich/Vickers indenters generate well-defined plastic zones for hardness calculations but exhibit 3%–7% modulus discrepancies due to differing projected contact areas. Spherical indenters enable elastic–plastic transition studies through Hertzian contact mechanics, while cube-corner geometries enhance strain gradient sensitivity at shallower depths (<100 nm) but increase substrate effect errors. For shale characterization, Berkovich indenters are preferred due to their standardized area function (ISO 14577 [50]) and reduced anisotropy artifacts. The trigonal symmetry minimizes orientation-dependent errors in layered media compared to Vickers indenters, while maintaining sufficient acuity (effective strain ~8%) to probe individual mineral phases. This geometry also facilitates direct comparison with geological materials literature, where most of the reported shale nanoindentation data derives from Berkovich tests, ensuring methodological consistency across studies. A NanoTest Vantage system (Micro Materials Co., Ltd, Wrexham, UK) was applied for the nanoindentation tests.

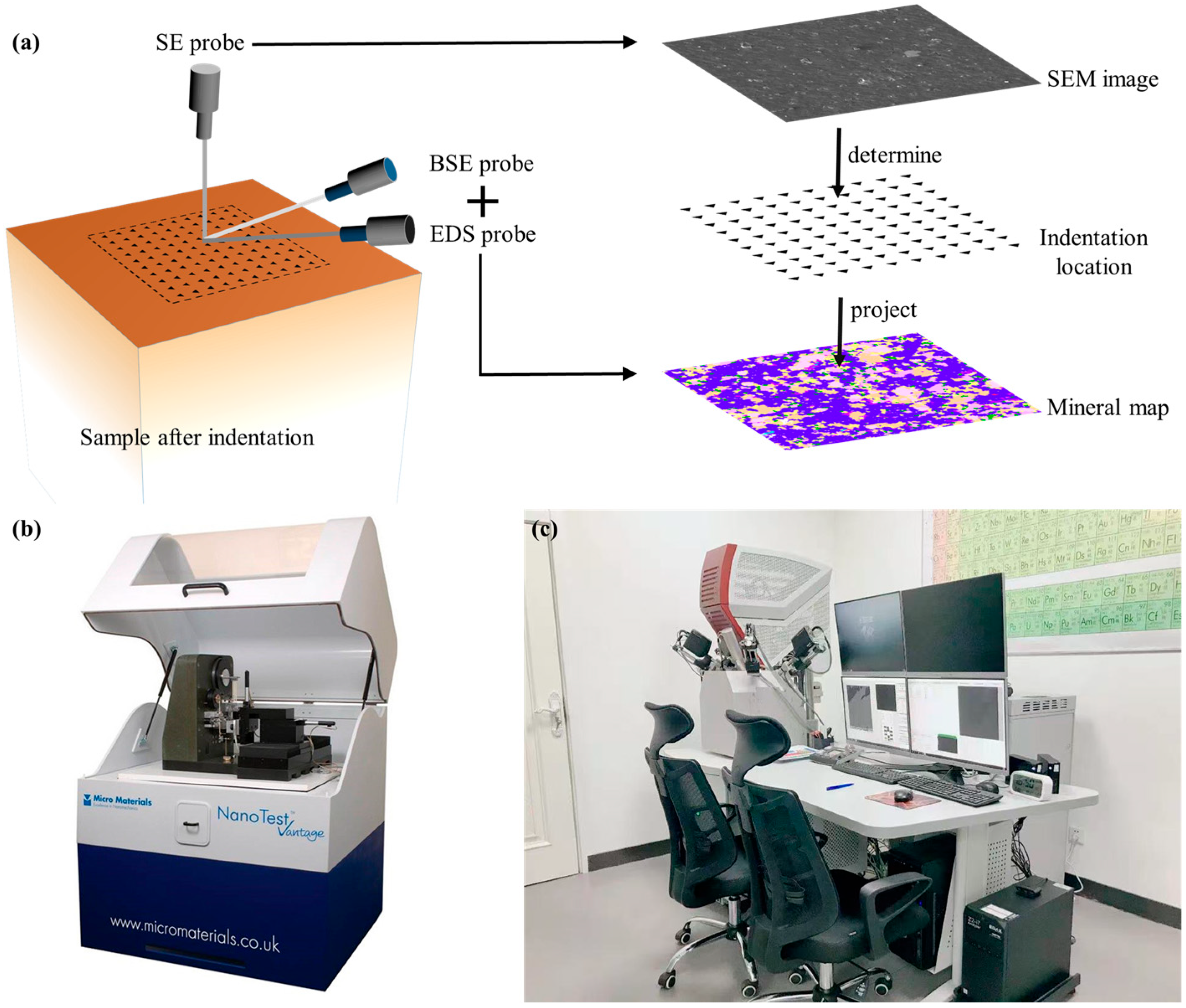
2.3. SEM Observation and TIMA

In addition to mineral analysis, TIMA can also perform all the functions of a conventional field emission scanning electron microscope. The sample after the nanoindentation test was sprayed with a thin carbon conductive layer. First, the location of the indentation matrix was determined in the secondary electron (SE) mode and the microscopic morphology of the residual indentation marks was observed. Then, the TIMA scan and analysis is performed on the area where the indentation matrix is located to obtain the mineral map of the area. The positions of the indentations in the secondary electron map were then projected onto the mineral map to obtain the mineralogical information corresponding to each indentation (Figure 3a). When observed in secondary electronic mode, the acceleration voltage was 10 kV, and the working distance was 9 mm. During the TIMA scanning, the working distance is 15 mm, the BSE scanning step is 3 μm, and the EDS scanning step is 1 μm. The TIMA test was conducted in the geological laboratory of Xi’an Kuangpu Geological Survey Technology Co., Ltd (Xi’an, China). Figure 3b,c demonstrated the photo of the NanoTest Vantage system and the TIMA system.

3. Result and Discussion

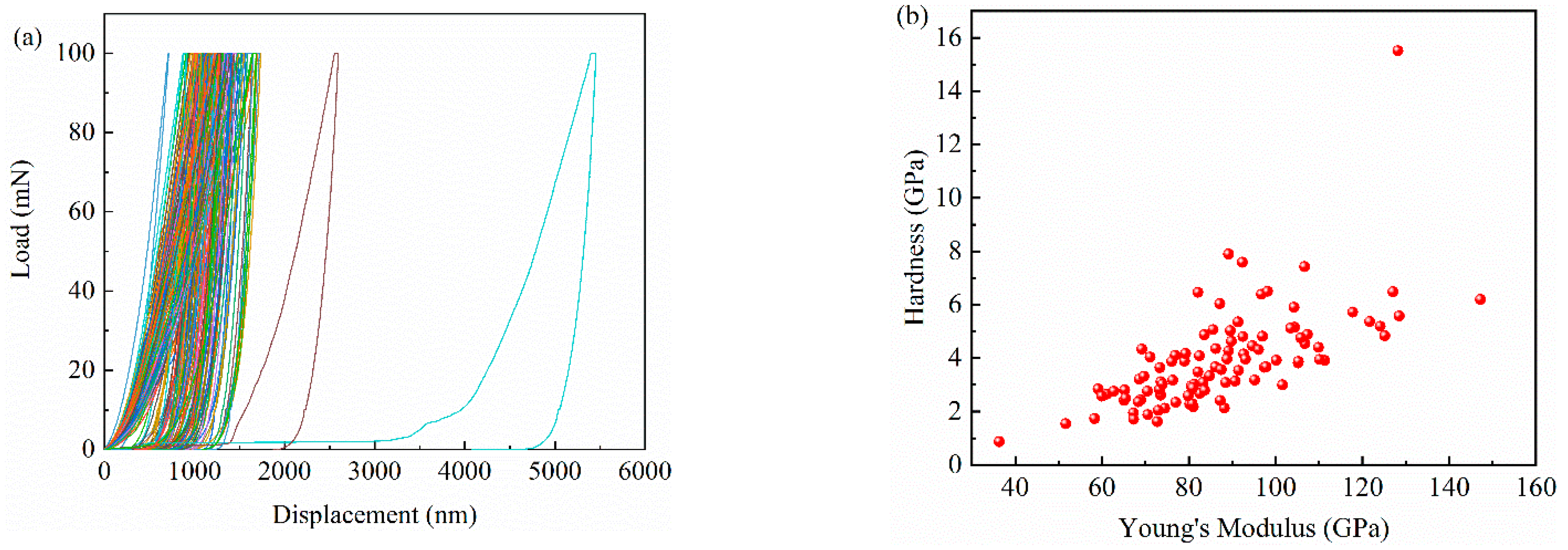
3.1. Micromechanical Result

Figure 4a shows the load-displacement curves obtained from the nanoindentation test. The majority of the indentations have a maximum displacement of less than 2600 nm, and only one indentation has a maximum displacement of more than 2600 nm. The anomalous curves may be related to localized defects on the sample surface. Figure 4b shows the mechanical parameters obtained from the nanoindentation test. The hardness of the sample ranges from 0.87 to 15.51 GPa with an average value of 3.91 GPa, and the elastic modulus ranges from 36.30 to 147.23 GPa with an average value of 87.08 GPa. The spatial distribution of the mechanical parameters of the samples is shown in Figure 5. It can be found that the micromechanical properties of the sample are highly heterogeneous.

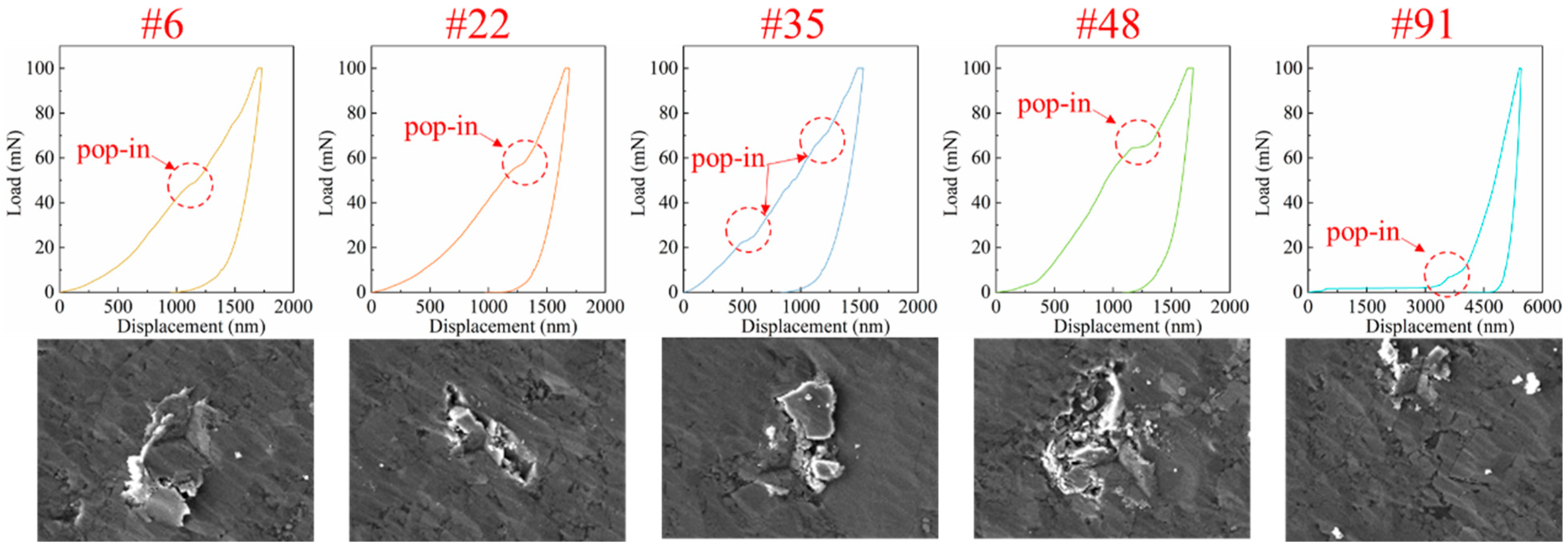
3.2. Micromorphology of the Indentation Area

The location of the indentation area was found, and the morphology of the indentation residue imprints was observed in the secondary electron mode of the TIMA system. The indentation residual imprints show two types of morphology. Type Ⅰ is the pit that matches the shape of the Berkovich indenter, as marked by the yellow circle in Figure 6. Type Ⅱ is the pit with local fracture damage and mineral particle ejection nearby, as marked by the red circle in Figure 6.
Comparing the morphology and mechanical parameters of the indentations, it can be found that the hardness and elastic modulus of the type Ⅱ indentations are smaller than the average value of the whole sample (Figure 7). Moreover, all the load-displacement curves corresponding to type II indentations have unsmooth displacement jumps, which are called pop-in [51,52] (Figure 8). This gives visual evidence that the pop-in is caused by local fracture damage on the sample surface, and that the mechanical properties of the location where the pop-in occurs are relatively weak.

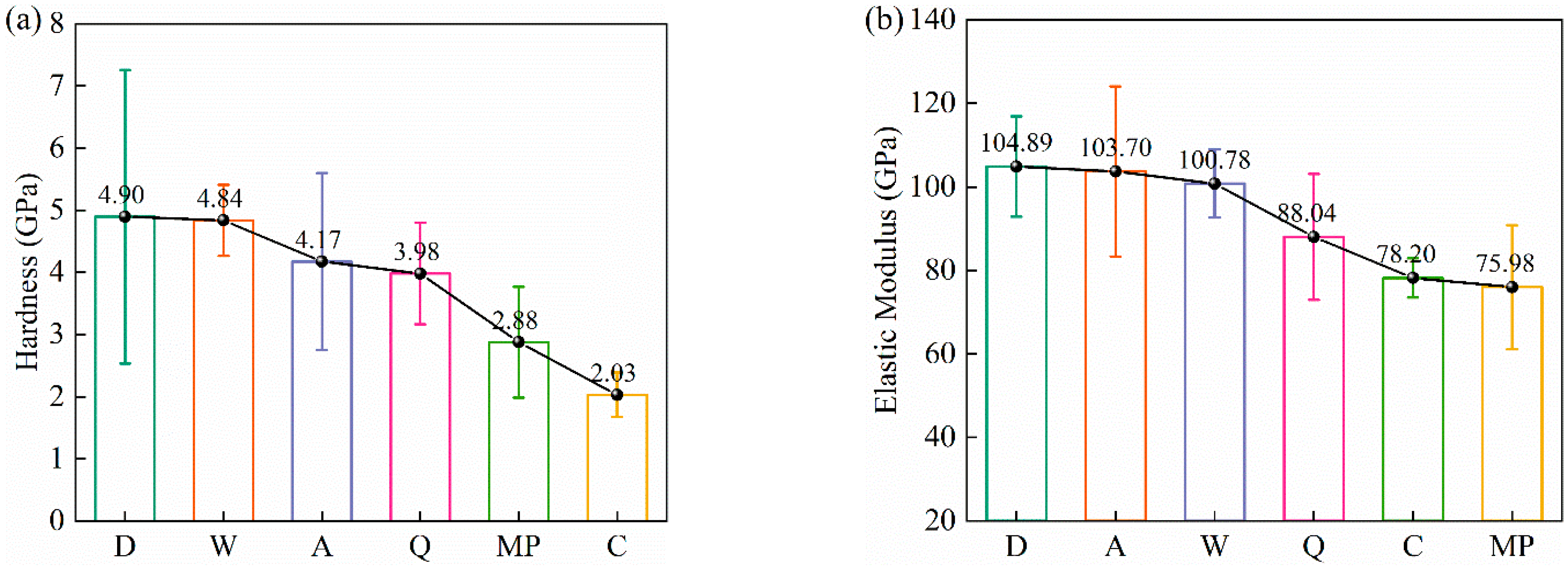
3.3. The Mechanical Properties of Shale Constituent Mineral

The indentation area was found in SE mode and the position of each indentation was marked. TIMA was performed, and a mineral map of the indentation area was obtained. The mineral content of the indentation area is shown in Table 1. The position of each indentation was projected onto the mineral map, and the corresponding mineral of each indentation was identified (Figure 9). The indentation detected 5 independent mineral phases (quartz, ankerite, calcite, dolomite, wollastonite) and a mixed phase (indentation located at the junction of mineral grains). The order of the hardness of these five mineral phases is dolomite (4.90 ± 2.33 GPa) > wollastonite (4.84 ± 0.54 GPa) > ankerite (4.17 ± 1.37 GPa) > quartz (3.98 ± 0.67 GPa) > calcite (2.03 ± 0.29 GPa), and the order of the elastic modulus is dolomite (104.89 ± 11.25 GPa) > ankerite (103.70 ± 19.62 GPa) > wollastonite (100.78 ± 6.66 GPa) > quartz (88.04 ± 14.58 GPa) > calcite (78.20 ± 3.85 GPa) (Figure 10). The main mineral compositions of the shale sample used in this study are quartz and carbonate. The mechanical properties of minerals with content more than 5% were all detected, and the elastic moduli of quartz, calcite, and dolomite in this study were compared with those in the literature (Table 2). It can be seen that the results of this study are in good agreement with the prior studies, which shows the reliability of the proposed method in this paper.
The mechanical properties of the samples, particularly hardness, exhibit relatively large standard deviations, which are likely attributed to multiple coupled factors. Firstly, the anisotropic nature of shale-forming minerals implies that the varying grain orientations of minerals may influence the test results [16]. Secondly, variations in crystallinity and trace elements could affect nanoindentation hardness and elastic modulus. Highly crystalline minerals demonstrate elevated and stable mechanical properties due to ordered atomic arrangements and strong bonding forces, while crystallographic defects (e.g., dislocations, amorphous phases) induce localized plastic flow and increase data scatter. Trace elements (e.g., Mg2+, Fe2+) weaken interatomic bonding via lattice substitution-induced distortions, systematically reducing hardness and modulus. Additionally, substrate effects may contribute to data dispersion. This effect occurs when the indentation depth exceeds 1/10 of the mineral grain size, where surrounding matrix materials distort stress fields during measurement. Specifically, a hard substrate (e.g., quartz) may lead to overestimated hardness, whereas a soft substrate (e.g., clay) could induce anomalous plastic deformation and systematic underestimation of modulus [16,40].
Based on hardness and elastic modulus, additional derived parameters can be derived to characterize distinct mechanical properties. According to Xu et al., H/E represents the yield strain or the limit of non-permanent deformation of material, (H/E)2 is a factor controlling the elastic–plastic contact transition, H2/2E stands for resilience modulus or elastic strain capacity, and H3/E2 represents the resistance to the plastic indentation [59]. The derived parameters of deferent mineral phases are listed in Table 3.

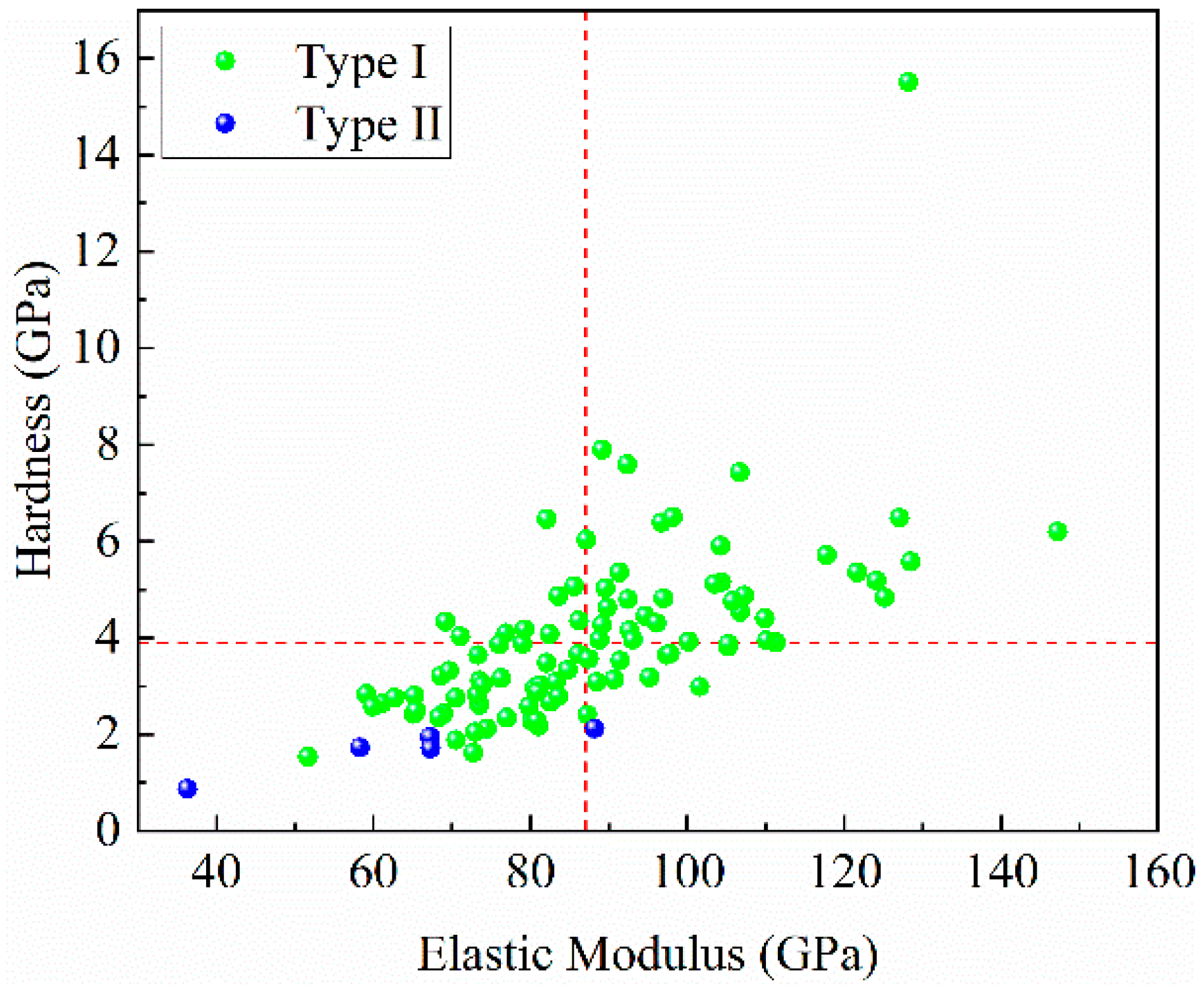
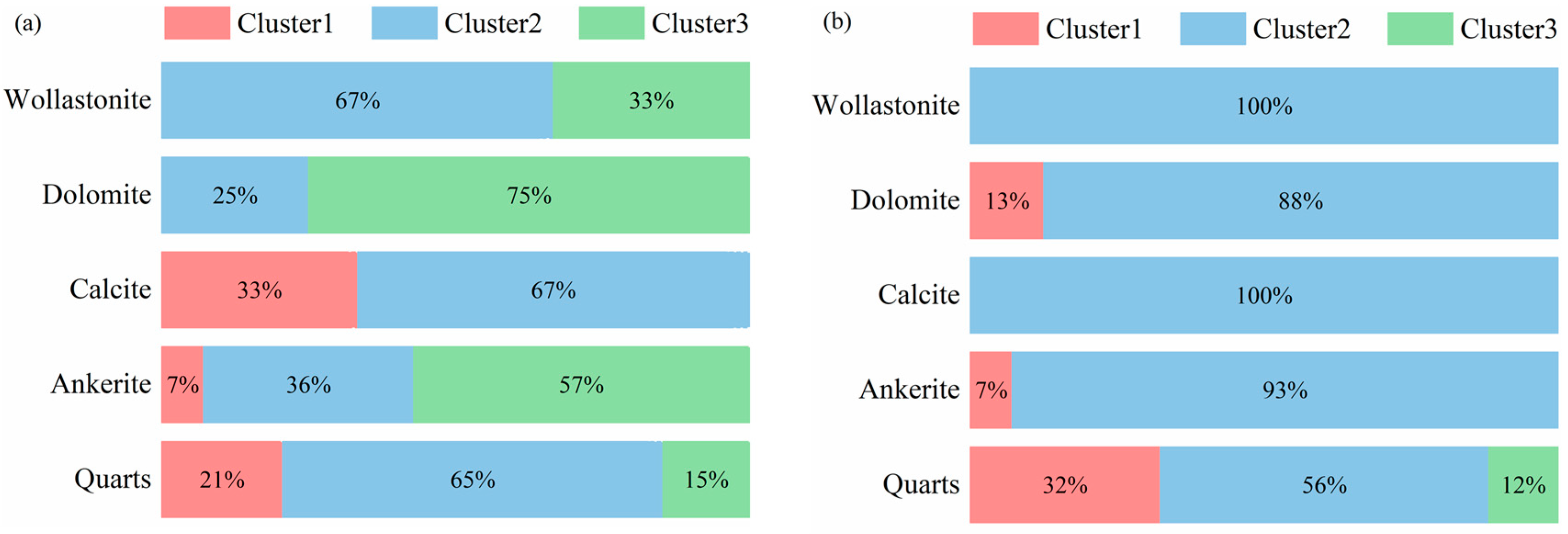
3.4. Clustering Analysis of the Nanoindentation Data Set

Clustering analysis is a commonly used method to obtain the mechanical properties of different phases in composite materials. The k-means algorithm and Gaussian mixture model (GMM) were applied for the clustering analysis of the mechanical data set, respectively. The k-means is an unsupervised clustering algorithm that partitions data through an iterative optimization process. Users first specify the target cluster count (k), after which the algorithm assigns data points to the nearest centroid—the geometric mean of each cluster. This process cycles between recalculating centroids and reassigning points until achieving convergence, defined by minimized within-cluster variance (sum of squared point-to-centroid distances) and stabilized cluster membership [38,60]. Gaussian Mixture Model deconvolution assumes that the observed data arises from a superposition of multiple independent Gaussian distributions. It employs maximum likelihood estimation (e.g., the EM algorithm) to estimate the mean, covariance, and weight parameters of each Gaussian component. This method statistically decomposes the mixed signal into sub-distributions with distinct probability densities, enabling the separation of different phases within the data set. The commercial software XLSTAT was employed to perform k-means and GMM clustering. According to prior studies, the micromechanical dataset of shale can usually be divided into three clusters [1,36]. The number of clusters k was set to three. The clustering results are shown in Figure 11.
By analyzing the mineral phases corresponding to the indentations and the clustering results, it can be found that the mechanical data of the same mineral type may be assigned to multiple clusters. The assignments of the mechanical data corresponding to each mineral in the three clusters are shown in Figure 12. The mechanical phase derived from cluster analysis represents an abstract construct that does not precisely align with the actual mineral phase. On one hand, two distinct minerals may be misclassified as a single mechanical phase when their mechanical properties exhibit high similarity. On the other hand, when a mineral exhibits significant variability in its mechanical properties, it may be misclassified into multiple mechanical phases.

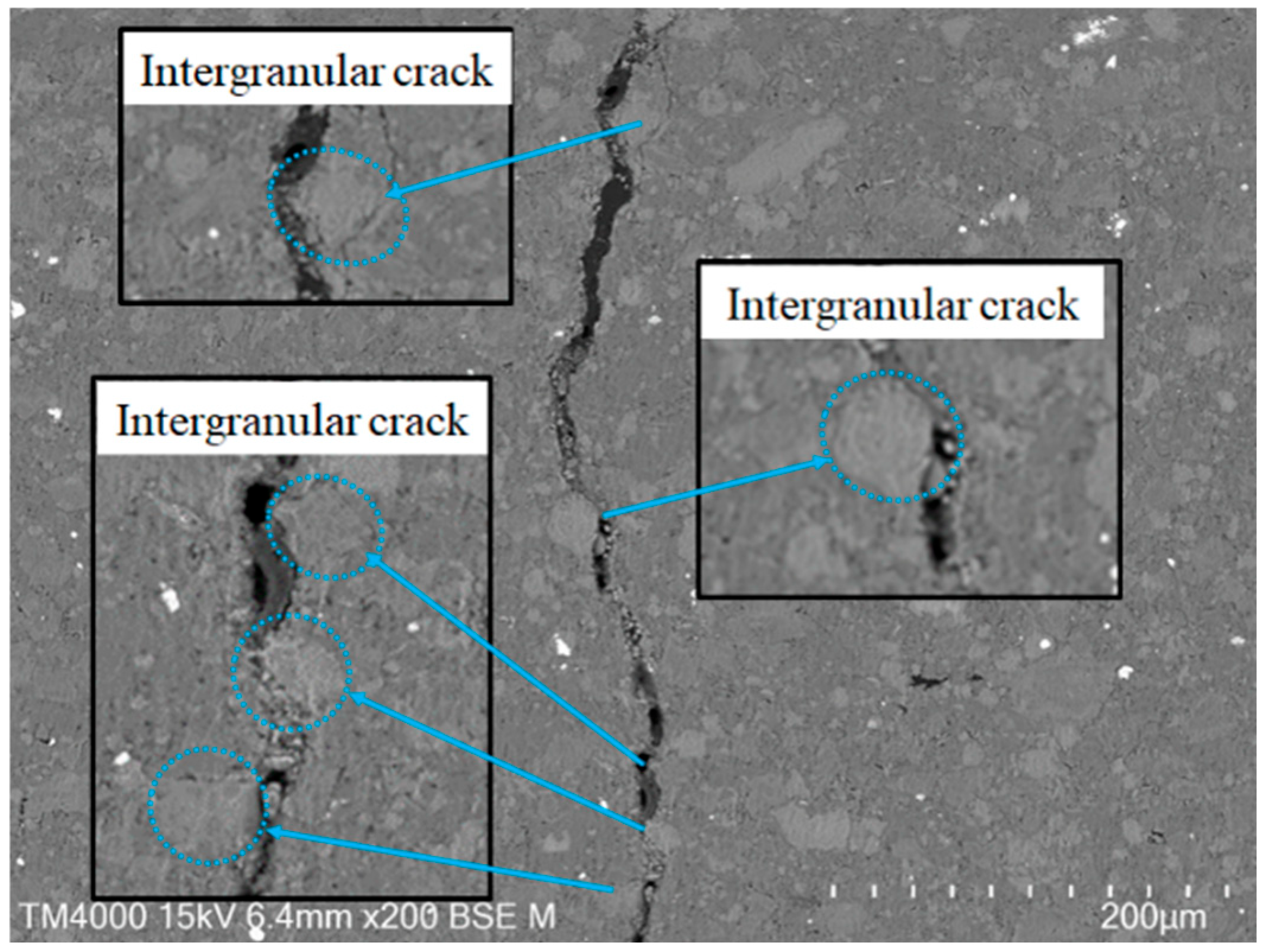
3.5. Influence of Micromechanical Properties on Macroscopic Failure Form of Shale

The mixed phase means that the indentation falls near the junction of mineral particles. As can be seen in Figure 10, the mixed phases have lower hardness and elastic modulus than most of the independent mineral phases. In addition, the type II indentations defined in Section 3.2 (with local fracture damage nearby) all correspond to the mixed phase (Figure 13). This indicates that the mechanical properties of the shale mineral grain junctions are weaker than those inside the grains, and that the mineral grain junctions are more prone to fracture damage. It can be deduced that when shale is subjected to external loading, microcracks always tend to sprout at the junction of mineral grains and propagate along the boundary of mineral grains to become macroscopic cracks, i.e., so-called intergranular failure. In our earlier study, three-point bending loading was carried out on shales of the same origin as in this study, and the morphology of the cracks was observed by scanning electron microscopy (Figure 14) [14]. It was found that macroscopic cracks always propagate along the boundary of mineral grains, which is consistent with the inference of this study.

4. Conclusions

In this paper, a method combining nanoindentation with a TESCAN Integrated Mineral Analyzer (TIMA) was used to determine the mechanical parameters of shale constituent minerals. The mechanical properties of minerals with content more than 5% were all detected, and the results of this study are in good agreement with the prior studies.
  • The mechanical properties of 5 independent mineral phases (quartz, ankerite, calcite, dolomite, wollastonite) and a mixed phase (indentation located at the junction of mineral grains) were detected. The order of the hardness of these five mineral phases is dolomite (4.90 ± 2.33 GPa) > wollastonite (4.84 ± 0.54 GPa) > ankerite (4.17 ± 1.37 GPa) > quartz (3.98 ± 0.67 GPa) > calcite (2.03 ± 0.29 GPa), and the order of the elastic modulus is dolomite (104.89 ± 11.25 GPa) > ankerite (103.70 ± 19.62 GPa) > wollastonite (100.78 ± 6.66 GPa) > quartz (88.04 ± 14.58 GPa) > calcite (78.20 ± 3.85 GPa).
  • The pop-in phenomenon is caused by local fracture damage on the sample surface, and the mechanical properties of the location where the pop-in occurs are relatively weak.
  • The mechanical properties of the shale mineral grain junctions are weaker than those inside the grains, and the mineral grain junctions are more prone to fracture damage. When shale is subjected to external loading, microcracks always tend to sprout at the junction of mineral grains and propagate along the boundary of mineral grains to become macroscopic cracks, i.e., so-called intergranular failure.

Author Contributions

Conceptualization, Q.C. and J.T.; methodology, Q.C.; formal analysis, Y.X. and S.C.; investigation, Y.X. and S.C.; writing—original draft preparation, Y.X. and Q.C.; writing—review and editing, Y.X. and Q.C.; visualization, Y.X. and Q.C.; supervision, J.T.; project administration, J.T.; funding acquisition, J.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by [National Natural Science Foundation of China] grant number [U21A2030] and [Excellent Youth Team Project for the Central Universities] grant number (2023CDJYXTD-00). And The APC was funded by [Excellent Youth Team Project for the Central Universities].

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).

Acknowledgments

This work is financially supported by the National Natural Science Foundation of China (NSFC) (No. U21A2030) and the Excellent Youth Team Project for the Central Universities (No. 2023CDJYXTD-00), which are gratefully acknowledged. In addition, this study received technical support from Zhang Bin of the Analytical Testing Center of Chongqing University, for which we are grateful.

Conflicts of Interest

The authors declare no conflicts of interest. Among them, the author Yongjun Xiao is employee of Sichuan Changning Natural Gas Development Co., Ltd. The paper reflects the views of the scientists and not the company.

References

  1. Kasyap, S.S.; Senetakis, K. Characterization of two types of shale rocks from Guizhou China through micro-indentation, statistical and machine-learning tools. J. Pet. Sci. Eng. 2022, 208, 109304. [Google Scholar] [CrossRef]
  2. Soeder, D.J. The successful development of gas and oil resources from shales in North America. J. Pet. Sci. Eng. 2018, 163, 399–420. [Google Scholar] [CrossRef]
  3. Castro-Alvarez, F.; Marsters, P.; Ponce de León Barido, D.; Kammen, D.M. Sustainability lessons from shale development in the United States for Mexico and other emerging unconventional oil and gas developers. Renew. Sustain. Energy Rev. 2018, 82, 1320–1332. [Google Scholar] [CrossRef]
  4. Prpich, G.; Coulon, F.; Anthony, E.J. Review of the scientific evidence to support environmental risk assessment of shale gas development in the UK. Sci. Total Environ. 2016, 563–564, 731–740. [Google Scholar] [CrossRef]
  5. McMahon, T.P.; Larson, T.E.; Zhang, T.; Shuster, M. Geologic characteristics, exploration and production progress of shale oil and gas in the United States: An overview. Pet. Explor. Dev. 2024, 51, 925–948. [Google Scholar] [CrossRef]
  6. Wang, L.; Guo, Y.; Zhou, J.; Yang, H.; Yang, C.; Xiao, J. Rock mechanical characteristics of deep marine shale in southern China, a case study in Dingshan block. J. Pet. Sci. Eng. 2021, 204, 108699. [Google Scholar] [CrossRef]
  7. Katende, A.; O’Connell, L.; Rich, A.; Rutqvist, J.; Radonjic, M. A comprehensive review of proppant embedment in shale reservoirs: Experimentation, modeling and future prospects. J. Nat. Gas Sci. Eng. 2021, 95, 104143. [Google Scholar] [CrossRef]
  8. Zhang, X.; Lu, Y.; Tang, J.; Zhou, Z.; Liao, Y. Experimental study on fracture initiation and propagation in shale using supercritical carbon dioxide fracturing. Fuel 2017, 190, 370–378. [Google Scholar] [CrossRef]
  9. Bryson, L.S.; Mahmoodabadi, M.; Gomez-Gutierrez, I.C. Mechanical Behavior of Weathered Compacted Shales. Geotechnol. Geol. Eng. 2024, 42, 1993–2009. [Google Scholar] [CrossRef]
  10. Jin, Z.; Li, W.; Jin, C.; Hambleton, J.; Cusatis, G. Anisotropic elastic, strength, and fracture properties of Marcellus shale. Int. J. Rock Mech. Min. Sci. 2018, 109, 124–137. [Google Scholar] [CrossRef]
  11. Fjær, E.; Nes, O.-M. The Impact of Heterogeneity on the Anisotropic Strength of an Outcrop Shale. Rock Mech. Rock Eng. 2014, 47, 1603–1611. [Google Scholar] [CrossRef]
  12. Li, H.; Lai, B.; Liu, H.-H.; Zhang, J.; Georgi, D. Experimental Investigation on Brazilian Tensile Strength of Organic-Rich Gas Shale. SPE J. 2016, 22, 148–161. [Google Scholar] [CrossRef]
  13. Lu, Y.; Xu, Z.; Li, H.; Tang, J.; Chen, X. The influences of super-critical CO2 saturation on tensile characteristics and failure modes of shales. Energy 2021, 221, 119824. [Google Scholar] [CrossRef]
  14. Xu, Z.; Lu, Y.; Tang, J.; Xiao, J.; Li, H.; Jia, Y.; Chen, X.; Cheng, Q. The mode I fracture toughness alternation and crack propagation behavior evolution due to long-term Sc-CO2 saturation. Eng. Fract. Mech. 2022, 263, 108259. [Google Scholar] [CrossRef]
  15. Liu, Y.; Liu, A.; Liu, S.; Kang, Y. Nano-scale mechanical properties of constituent minerals in shales investigated by combined nanoindentation statistical analyses and SEM-EDS-XRD techniques. Int. J. Rock Mech. Min. Sci. 2022, 159, 105187. [Google Scholar] [CrossRef]
  16. Wu, Y.; Li, Y.; Luo, S.; Lu, M.; Zhou, N.; Wang, D.; Zhang, G. Multiscale elastic anisotropy of a shale characterized by cross-scale big data nanoindentation. Int. J. Rock Mech. Min. Sci. 2020, 134, 104458. [Google Scholar] [CrossRef]
  17. Ma, Z.; Pathegama Gamage, R.; Zhang, C. Application of nanoindentation technology in rocks: A review. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 60. [Google Scholar] [CrossRef]
  18. Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
  19. Cao, Z.; Zhang, X. Nanoindentation creep of plasma-enhanced chemical vapor deposited silicon oxide thin films. Scr. Mater. 2007, 56, 249–252. [Google Scholar] [CrossRef]
  20. Wang, Y.; Zhang, J.; Wu, K.; Liu, G.; Kiener, D.; Sun, J. Nanoindentation creep behavior of Cu–Zr metallic glass films. Mater. Res. Lett. 2018, 6, 22–28. [Google Scholar] [CrossRef]
  21. Liu, Y.; Liu, Q.; Feng, G.; Lyu, Q.; Liu, S.; Wang, Y.; Tang, X. Upscaling mechanical properties of shale obtained by nanoindentation to macroscale using accurate grain-based modeling (AGBM). Energy 2025, 314, 134126. [Google Scholar] [CrossRef]
  22. Liu, Y.; Liu, Q.; Wu, Z.; Liu, S.; Kang, Y.; Tang, X. Cross-scale mechanical softening of Marcellus shale induced by CO2-water–rock interactions using nanoindentation and accurate grain-based modeling. Undergr. Space 2024, 19, 26–46. [Google Scholar] [CrossRef]
  23. Liu, Y.; Zhang, G.; Qiao, J.; Tang, X. Micromechanical testing and property upscaling of planetary rocks: A critical review. Int. J. Min. Sci. Technol. 2024, 34, 1217–1241. [Google Scholar] [CrossRef]
  24. Rahman, M.J.; Lebedev, M.; Mondol, N.H. Nanoscale mechanical properties of organic-rich Draupne caprock shale using nano-indentation method, offshore Norway. Int. J. Greenh. Gas Control 2024, 132, 104073. [Google Scholar] [CrossRef]
  25. Liu, M.; Xu, Z. Micromechanical characterization of microwave dielectric ceramic BaO–Sm2O3–5TiO2 by indentation and scratch methods. J. Adv. Ceram. 2023, 12, 1136–1165. [Google Scholar]
  26. Liu, M.; Xu, Z.; Fu, R. Micromechanical and microstructure characterization of BaO-Sm2O3–5TiO2 ceramic with addition of Al2O3. Ceram. Int. 2022, 48, 992–1005. [Google Scholar] [CrossRef]
  27. Kang, R.; Kong, X.; Liu, M.; Zhang, M.; Qiao, W. Influence of graphene oxide on mechanical behavior of polypropylene fibers reinforced cement-based composites from a macro-to-micro perspective. Constr. Build. Mater. 2025, 472, 140902. [Google Scholar] [CrossRef]
  28. Ulm, F.-J.; Abousleiman, Y. The nanogranular nature of shale. Acta Geotechnol. 2006, 1, 77–88. [Google Scholar] [CrossRef]
  29. Liu, K.; Ostadhassan, M.; Bubach, B. Applications of nano-indentation methods to estimate nanoscale mechanical properties of shale reservoir rocks. J. Nat. Gas Sci. Eng. 2016, 35, 1310–1319. [Google Scholar] [CrossRef]
  30. Lu, Y.; Cheng, Q.; Tang, J.; Liu, W.; Li, H.; Liu, J.; Xu, Z.; Tian, R.; Sun, X. Differences in micromechanical properties of shales from different depositional environment: A case study of Longmaxi marine shale and Yanchang continental shale using nanoindentation. J. Nat. Gas Sci. Eng. 2022, 107, 104727. [Google Scholar] [CrossRef]
  31. Liu, A.; Liu, S.; Liu, Y.; Liu, B.; Liu, T. Characterizing mechanical heterogeneity of coal at nano-to-micro scale using combined nanoindentation and FESEM-EDS. Int. J. Coal Geol. 2022, 261, 104081. [Google Scholar] [CrossRef]
  32. Zhang, Y.; Lebedev, M.; Al-Yaseri, A.; Yu, H.; Xu, X.; Sarmadivaleh, M.; Barifcani, A.; Iglauer, S. Nanoscale rock mechanical property changes in heterogeneous coal after water adsorption. Fuel 2018, 218, 23–32. [Google Scholar] [CrossRef]
  33. Sun, C.; Li, G.; Elgharib Gomah, M.; Xu, J.; Rong, H. Meso-scale mechanical properties of mudstone investigated by nanoindentation. Eng. Fract. Mech. 2020, 238, 107245. [Google Scholar] [CrossRef]
  34. Li, Y.; Luo, S.; Lu, M.; Wu, Y.; Zhou, N.; Wang, D.; Lu, Y.; Zhang, G. Cross-scale characterization of sandstones via statistical nanoindentation: Evaluation of data analytics and upscaling models. Int. J. Rock Mech. Min. Sci. 2021, 142, 104738. [Google Scholar] [CrossRef]
  35. Ma, Z.; Zhang, C.; Pathegama Gamage, R.; Zhang, G. Uncovering the creep deformation mechanism of rock-forming minerals using nanoindentation. Int. J. Min. Sci. Technol. 2022, 32, 283–294. [Google Scholar] [CrossRef]
  36. Liu, K.; Ostadhassan, M.; Bubach, B.; Ling, K.; Tokhmechi, B.; Robert, D. Statistical grid nanoindentation analysis to estimate macro-mechanical properties of the Bakken Shale. J. Nat. Gas Sci. Eng. 2018, 53, 181–190. [Google Scholar] [CrossRef]
  37. Li, C.; Ostadhassan, M.; Abarghani, A.; Fogden, A.; Kong, L. Multi-scale evaluation of mechanical properties of the Bakken shale. J. Mater. Sci. 2018, 54, 2133–2151. [Google Scholar] [CrossRef]
  38. Vranjes-Wessely, S.; Misch, D.; Kiener, D.; Cordill, M.; Frese, N.; Beyer, A.; Horsfield, B.; Wang, C.; Sachsenhofer, R. High-speed nanoindentation mapping of organic matter-rich rocks: A critical evaluation by correlative imaging and machine learning data analysis. Int. J. Coal Geol. 2021, 247, 103847. [Google Scholar] [CrossRef]
  39. Li, C.; Wang, D.; Kong, L. Mechanical response of the Middle Bakken rocks under triaxial compressive test and nanoindentation. Int. J. Rock Mech. Min. Sci. 2021, 139, 104660. [Google Scholar] [CrossRef]
  40. Yang, C.; Xiong, Y.; Wang, J.; Li, Y.; Jiang, W. Mechanical characterization of shale matrix minerals using phase-positioned nanoindentation and nano-dynamic mechanical analysis. Int. J. Coal Geol. 2020, 229, 103571. [Google Scholar] [CrossRef]
  41. Shi, X.; Jiang, S.; Wang, Z.; Bai, B.; Xiao, D.; Tang, M. Application of nanoindentation technology for characterizing the mechanical properties of shale before and after supercritical CO2 fluid treatment. J. CO2 Util. 2020, 37, 158–172. [Google Scholar] [CrossRef]
  42. Du, J.; Whittle, A.J.; Hu, L.; Divoux, T.; Meegoda, J.N. Characterization of meso-scale mechanical properties of Longmaxi shale using grid microindentation experiments. J. Rock Mech. Geotechnol. Eng. 2021, 13, 555–567. [Google Scholar] [CrossRef]
  43. Hrstka, T.; Gottlieb, P.; Skála, R.; Breiter, K.; Motl, D. Automated mineralogy and petrology—Applications of TESCAN Integrated Mineral Analyzer (TIMA). J. Geosci. 2018, 63, 47–63. [Google Scholar] [CrossRef]
  44. Li, Y.; Tang, G.-Q.; Liu, Y.; He, S.; Chen, B.; Li, Q.-L.; Li, X.-H. Revisiting apatite SIMS oxygen isotope analysis and Qinghu-AP reference material. Chem. Geol. 2021, 582, 120445. [Google Scholar] [CrossRef]
  45. Wang, X.-J.; Chen, L.-H.; Hanyu, T.; Zhong, Y.; Shi, J.-H.; Liu, X.-W.; Kawabata, H.; Zeng, G.; Xie, L.-W. Magnesium isotopic fractionation during basalt differentiation as recorded by evolved magmas. Earth Planet. Sci. Lett. 2021, 565, 116954. [Google Scholar] [CrossRef]
  46. Du, D.-H.; Wang, X.-L.; Wang, S.; Miller, C.F.; Xu, X.; Chen, X.; Zhang, F.-F. Deciphering Cryptic Multi-Stage Crystal-Melt Separation during Construction of the Tonglu Volcanic–Plutonic Complex, SE China. J. Petrol. 2022, 63, egab098. [Google Scholar] [CrossRef]
  47. Pharr, G.M.; Oliver, W.C.; Brotzen, F.R. On the generality of the relationship among contact stiffness, contact area, and elastic modulus during indentation. J. Mater. Res. 2011, 7, 61. [Google Scholar] [CrossRef]
  48. Klaver, J.; Desbois, G.; Urai, J.L.; Littke, R. BIB-SEM study of the pore space morphology in early mature Posidonia Shale from the Hils area, Germany. Int. J. Coal Geol. 2012, 103, 12–25. [Google Scholar] [CrossRef]
  49. Shi, X.; He, Z.; Long, S.; Peng, Y.; Li, D.; Jiang, S. Loading rate effect on the mechanical behavior of brittle longmaxi shale in nanoindentation. Int. J. Hydrogen Energy 2019, 44, 6481–6490. [Google Scholar] [CrossRef]
  50. ISO 14577-1:2015; Metallic Materials—Instrumented Indentation Test for Hardness and Materials Parameters—Part 1: Test Method. ISO: Geneva, Switzerland, 2015.
  51. Liu, K.; Ostadhassan, M. Microstructural and geomechanical analysis of Bakken shale at nanoscale. J. Pet. Sci. Eng. 2017, 153, 133–144. [Google Scholar] [CrossRef]
  52. Schuh, C.A.; Nieh, T.G.; Kawamura, Y. Rate Dependence of Serrated Flow During Nanoindentation of a Bulk Metallic Glass. J. Mater. Res. 2002, 17, 16. [Google Scholar] [CrossRef]
  53. Mavko, G.; Dvorkin, J.; Mukerji, T. The Rock Physics Handbook: Tools for Seismic Analysis of Porous Media, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
  54. Lu, Y.; Li, Y.; Wu, Y.; Luo, S.; Jin, Y.; Zhang, G. Characterization of Shale Softening by Large Volume-Based Nanoindentation. Rock Mech. Rock Eng. 2020, 53, 1393–1409. [Google Scholar] [CrossRef]
  55. Kumar, V.; Sondergeld, C.H.; Rai, C.S. Nano to Macro Mechanical Characterization of Shale. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012. SPE-159804-MS. [Google Scholar]
  56. Zhao, J.; Zhang, D.; Wu, T.; Tang, H.; Xuan, Q.; Jiang, Z.; Dai, C. Multiscale Approach for Mechanical Characterization of Organic-Rich Shale and Its Application. Int. J. Geomech. 2019, 19, 04018180. [Google Scholar] [CrossRef]
  57. Zhu, W.; Hughes, J.J.; Bicanic, N.; Pearce, C.J. Nanoindentation mapping of mechanical properties of cement paste and natural rocks. Mater. Charact. 2007, 58, 1189–1198. [Google Scholar] [CrossRef]
  58. Chen, C.-C.; Lin, C.-C.; Liu, L.-G.; Sinogeikin, S.V.; Bass, J.D. Elasticity of single-crystal calcite and rhodochrosite by Brillouin spectroscopy. Am. Mineral. 2001, 86, 1525–1529. [Google Scholar] [CrossRef]
  59. Xu, Z.; Yuktanan, N.; Liu, M.; Gu, T.; Shi, M. Characterization of microstructures and micromechanical properties of Ti6Al4V powders. Powder Technol. 2024, 448, 120352. [Google Scholar] [CrossRef]
  60. Hartigan, J.A.; Wong, M.A. Algorithm AS136: A k-means clustering algorithm. J. R. Stat. Soc. 1979, 28, 100–108. [Google Scholar]
Minerals 15 00412 g001
Figure 1. (a) Schematic diagram of box counting method. (b) Results of representative elementary area (REA) calculations for shale samples.
Figure 1. (a) Schematic diagram of box counting method. (b) Results of representative elementary area (REA) calculations for shale samples.
Minerals 15 00412 g001
Minerals 15 00412 g002
Figure 2. (a) Schematic diagram of a nanoindentation load-displacement curve. (b) Schematic diagram of indentation matrix design. The orange part represents clay matrix, and the blue polygons represents mineral particles.
Figure 2. (a) Schematic diagram of a nanoindentation load-displacement curve. (b) Schematic diagram of indentation matrix design. The orange part represents clay matrix, and the blue polygons represents mineral particles.
Minerals 15 00412 g002
Minerals 15 00412 g003
Figure 3. (a) Flow chart for identifying minerals corresponding to indentation. (b) NanoTest Vantage system. (c) TIMA system.
Figure 3. (a) Flow chart for identifying minerals corresponding to indentation. (b) NanoTest Vantage system. (c) TIMA system.
Minerals 15 00412 g003
Minerals 15 00412 g004
Figure 4. (a) Load-displacement curves obtained from the nanoindentation test. (b) Mechanical parameters obtained from the nanoindentation test.
Figure 4. (a) Load-displacement curves obtained from the nanoindentation test. (b) Mechanical parameters obtained from the nanoindentation test.
Minerals 15 00412 g004
Minerals 15 00412 g005
Figure 5. The spatial distribution of the mechanical parameters: (a) hardness and (b) elastic modulus.
Figure 5. The spatial distribution of the mechanical parameters: (a) hardness and (b) elastic modulus.
Minerals 15 00412 g005
Minerals 15 00412 g006
Figure 6. The two types of morphology of the indentation residue imprints. Type Ⅰ is the pit that matches the shape of the Berkovich indenter, as marked by the yellow circle. Type Ⅱ is the local fracture damage and mineral particle ejection near the pit, as marked by the red circle.
Figure 6. The two types of morphology of the indentation residue imprints. Type Ⅰ is the pit that matches the shape of the Berkovich indenter, as marked by the yellow circle. Type Ⅱ is the local fracture damage and mineral particle ejection near the pit, as marked by the red circle.
Minerals 15 00412 g006
Minerals 15 00412 g007
Figure 7. The mechanical parameters of type Ⅰ and type Ⅱ indentations. The red dotted line represents the average value of the whole sample.
Figure 7. The mechanical parameters of type Ⅰ and type Ⅱ indentations. The red dotted line represents the average value of the whole sample.
Minerals 15 00412 g007
Minerals 15 00412 g008
Figure 8. SEM morphology and corresponding load-displacement curves of the type Ⅱ indentations. All the load-displacement curves corresponding to type II indentations show pop-in phenomena.
Figure 8. SEM morphology and corresponding load-displacement curves of the type Ⅱ indentations. All the load-displacement curves corresponding to type II indentations show pop-in phenomena.
Minerals 15 00412 g008
Minerals 15 00412 g009
Figure 9. (a) The position of each indentation was marked. (b) The position of each indentation was projected onto the mineral map.
Figure 9. (a) The position of each indentation was marked. (b) The position of each indentation was projected onto the mineral map.
Minerals 15 00412 g009
Minerals 15 00412 g010
Figure 10. The mechanical parameters of the five mineral phases: (a) hardness and (b) elastic modulus. D, W, A, Q, C, and MP refer to dolomite, wollastonite, ankerite, quartz, calcite, and mixed phase, respectively.
Figure 10. The mechanical parameters of the five mineral phases: (a) hardness and (b) elastic modulus. D, W, A, Q, C, and MP refer to dolomite, wollastonite, ankerite, quartz, calcite, and mixed phase, respectively.
Minerals 15 00412 g010
Minerals 15 00412 g011
Figure 11. The clustering results of the micromechanical dataset. (a) k-means clustering. (b) Gaussian mixture model clustering.
Figure 11. The clustering results of the micromechanical dataset. (a) k-means clustering. (b) Gaussian mixture model clustering.
Minerals 15 00412 g011
Minerals 15 00412 g012
Figure 12. The assignments of the mechanical data corresponding to each mineral in the three clusters. (a) k-means clustering. (b) GMM clustering.
Figure 12. The assignments of the mechanical data corresponding to each mineral in the three clusters. (a) k-means clustering. (b) GMM clustering.
Minerals 15 00412 g012
Minerals 15 00412 g013
Figure 13. The SEM morphology (a) and mineral map (b) of the representative of type II indentations (#35), which are located at the junction of mineral.
Figure 13. The SEM morphology (a) and mineral map (b) of the representative of type II indentations (#35), which are located at the junction of mineral.
Minerals 15 00412 g013
Minerals 15 00412 g014
Figure 14. The morphology of the cracks induced by three-point bending. The blue arrows and circles indicate intergranular cracks [14].
Figure 14. The morphology of the cracks induced by three-point bending. The blue arrows and circles indicate intergranular cracks [14].
Minerals 15 00412 g014
Table 1. The mineral content of the indentation area.
Table 1. The mineral content of the indentation area.
Content (%)
Quartz58.94
Ankerite15.45
Calcite9.33
Dolomite7.46
Clay3.14
Wollastonite2.45
Anorthite1.91
Others1.32
Table 2. Literature elastic property values for quartz, calcite, and dolomite.
Table 2. Literature elastic property values for quartz, calcite, and dolomite.
ReferenceElastic Modulus (GPa)Method
QuartzCalciteDolomite
This study88.0478.2104.89Nanoindentation
[53]77–9674–83116Acoustic Methods
[40]94–14367–8497–155Nanoindentation
[54]92.253 ± 6-Nanoindentation
[55]98–10078–88-Nanoindentation
[56]87.255.7-Nanoindentation
[57]101--Nanoindentation
[15]77.4--Nanoindentation
[58]-76.1-Acoustic Methods
[58]-86-Brillouin spectroscopy
Table 3. Derived parameters of deferent mineral phases.
Table 3. Derived parameters of deferent mineral phases.
ParameterMineral
QuartzCalciteDolomiteWollastoniteAnkeriteMP
H/E0.04520.02600.04670.04800.04020.0379
(H/E)20.00200.00070.00220.00230.00160.0014
H2/2E (GPa)0.09000.02630.11450.11620.08380.0546
H3/E2 (GPa)0.00810.00140.01070.01120.00670.0041
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Xiao, Y.; Cheng, Q.; Tang, J.; Cai, S. Determining the Mechanical Properties of Shale Constituent Minerals Using Nanoindentation and a TESCAN Integrated Mineral Analyzer (TIMA). Minerals 2025, 15, 412. https://doi.org/10.3390/min15040412

AMA Style

Xiao Y, Cheng Q, Tang J, Cai S. Determining the Mechanical Properties of Shale Constituent Minerals Using Nanoindentation and a TESCAN Integrated Mineral Analyzer (TIMA). Minerals. 2025; 15(4):412. https://doi.org/10.3390/min15040412

Chicago/Turabian Style

Xiao, Yongjun, Qi Cheng, Jiren Tang, and Shengyao Cai. 2025. "Determining the Mechanical Properties of Shale Constituent Minerals Using Nanoindentation and a TESCAN Integrated Mineral Analyzer (TIMA)" Minerals 15, no. 4: 412. https://doi.org/10.3390/min15040412

APA Style

Xiao, Y., Cheng, Q., Tang, J., & Cai, S. (2025). Determining the Mechanical Properties of Shale Constituent Minerals Using Nanoindentation and a TESCAN Integrated Mineral Analyzer (TIMA). Minerals, 15(4), 412. https://doi.org/10.3390/min15040412

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop