Abstract
This study systematically investigated the extraction and separation of ytterbium (Yb) and nickel (Ni) from manganese (Mn)- and calcium (Ca)-containing heavy metal solutions using 2-ethylhexyl phosphoric acid mono-2-ethylhexyl ester (HEHEHP) in nitric acid media. Results demonstrated that the logarithms of distribution ratios for Yb, Ni, Mn, and Ca exhibited positive correlations with both solution pH and the logarithm of extractant concentration, consistent with theoretical models. Elevated initial metal concentrations reduced distribution ratios for all elements, indicating extraction inhibition. Ytterbium back-extraction efficiency increased proportionally with hydrochloric acid concentration and the number of back-extraction stages. Optimization of key extraction parameters established predictive equilibrium relationships: Yb/Ni and Mn/Ca separation coefficients increased with decreasing acidity and extractant concentration, whereas Mn/Ni and Ca/Ni coefficients rose under higher acidity and extractant conditions. Infrared spectroscopy confirmed HEHEHP-Yb complexation mechanisms, with extractant stability retained through multiple reuse cycles. Optimized cascade processing parameters (3 extraction stages, 3 washing stages, 4 back-extraction stages) achieved >99.9% purity for both Yb and Ni. This validated methodology provides a robust technical framework for heavy metal waste treatment and high-value element recovery.
1. Introduction
Ytterbium, a heavy rare earth element, is widely used in fields such as optical fiber materials, laser technology, electronics, medical devices, and alloys, making it a material of significant application value [1,2,3,4]. Similarly, nickel plays a critical role in various industries, including catalysis, battery materials, and high-temperature alloys. With the rapid advancement in new energy technologies, the demand for nickel is increasing [5,6,7]. As the failed ytterbium-nickel alloy components dissolve in acid, the elements are transferred into the solution, which contains not only ytterbium and nickel but also calcium and manganese. Therefore, multi-element extraction and separation experiments are necessary to achieve the selective recovery of ytterbium and nickel.
The primary separation methods for metal elements in solution include precipitation and extraction methods [8,9,10]. The precipitation method involves adding reagents such as ammonia, ammonium sulfide, or oxalic acid to selectively precipitate elements. However, this method is typically used for coarse separation due to challenges in controlling the precipitation endpoint and issues with sediment adsorption, which can negatively affect the purity and yield of the product [11,12]. Extraction, on the other hand, uses differences in the solubility of elements in insoluble solvents to achieve separation [13,14,15]. The HEHEHP extractant is known for its low equilibrium acidity, good selectivity, and high stability, making it widely used in the preparation of single high-purity rare earth elements [16,17,18]. In [16], a mixture of HEHEHP and Cyanex 272 was used to extract rare earth elements from chloride solutions, and partition ratios and separation factors were experimentally determined, leading to the proposal of an extraction process for rare earth elements. In [19], the selectivity of a hydrophobic deep eutectic solvent composed of HEHEHP and menthol for extracting Cu, Co, and Ni from acid leaching solutions was studied. The separation coefficients for Cu, Co, and Ni were 2150 and 305, respectively, demonstrating the successful selective separation of these elements. In [20], the feasibility of separating lutetium and ytterbium using a 10% volume fraction HEHEHP extraction system in nitric acid was investigated. At 3 mol/L nitric acid concentration, the separation factor β(Lu/Yb) ranged from 1.4 to 1.6. In [21], the kinetics of HEHEHP extraction of V(IV) and Fe(II) in sulfuric acid solution were studied using a self-designed cylindrical constant interface cell. Results showed that increasing the stirring speed and extraction temperature led to higher extraction rates for both V(IV) and Fe(II), and the apparent activation energies of V(IV) and Fe(II) extraction were 48.68 kJ/mol and 135.11 kJ/mol, respectively. It was indicated that HEHEHP is more likely to extract V(IV) in sulfuric acid solutions, thus facilitating the efficient separation of V(IV) and Fe(II).
Overall, existing research primarily focuses on the separation of either rare earth elements or non-rare earth elements, and is not directly applicable to the separation of ytterbium, nickel, manganese, and calcium. Therefore, it is essential to investigate the equilibrium modeling of multi-element extraction and separation in nitric acid systems, explore the distribution ratios and changes in separation coefficients of ytterbium, nickel, manganese, and calcium, analyze the reaction mechanisms of these elements in the HEHEHP extraction system, and design and validate the cascade extraction process to enhance the technical framework for ytterbium and nickel recovery.
2. Materials and Methods
2.1. Materials
2-ethylhexyl-2-ethylhexyl phosphate, n-dodecane, nitric acid, hydrochloric acid, ytterbium nitrate, nickel nitrate, manganese nitrate, calcium nitrate, and ammonia solution were analytically pure, not purified again, and purchased from Shanghai Alding Biochemical Technology Co., Ltd. (Shanghai, China).
The samples were derived from the special alloy components used in the nuclear industry. After being retired, they were dissolved by 7 mol/L nitric acid to obtain the resulting solution.
2.2. Experimental Methods
The extractant was prepared by mixing n-dodecane and HEHEHP in a specific ratio according to experimental requirements. The HEHEHP extractant was then saponified using a 2 mol/L ammonia solution to achieve a saponification rate of 50%. For the extraction experiment, 50 mL of the heavy metal solution and 50 mL of the saponified HEHEHP extractant were added to a 250 mL separatory funnel. The mixture was agitated for 15 min using a mechanical shaker (manufactured by Sichuan Shubo Co., Ltd., Chengdu, China) and allowed to settle for phase separation. The raffinate (aqueous phase) was collected and analyzed for metal ion concentrations using inductively coupled plasma mass spectrometry (ICP-MS, Agilent 7900, Santa Clara, CA, USA). The purpose of washing and back-extraction experiments was to remove the impurity elements from the organic phase loaded with metal elements and collect the target elements. For the washing and stripping experiments, the metal-loaded organic phase was mixed with hydrochloric acid solutions of varying acidities and agitated for 15 min. After phase separation, the aqueous phase was collected and analyzed for elemental concentration. Furthermore, the spectra of the extractant were obtained by using a Fourier Transform Infrared Spectrometer (FT-IR, Thermo Fisher IS50, Waltham, MA, USA), with the wavelength range of 400 to 4000 cm−1 and a scanning speed of 4 cm−1.
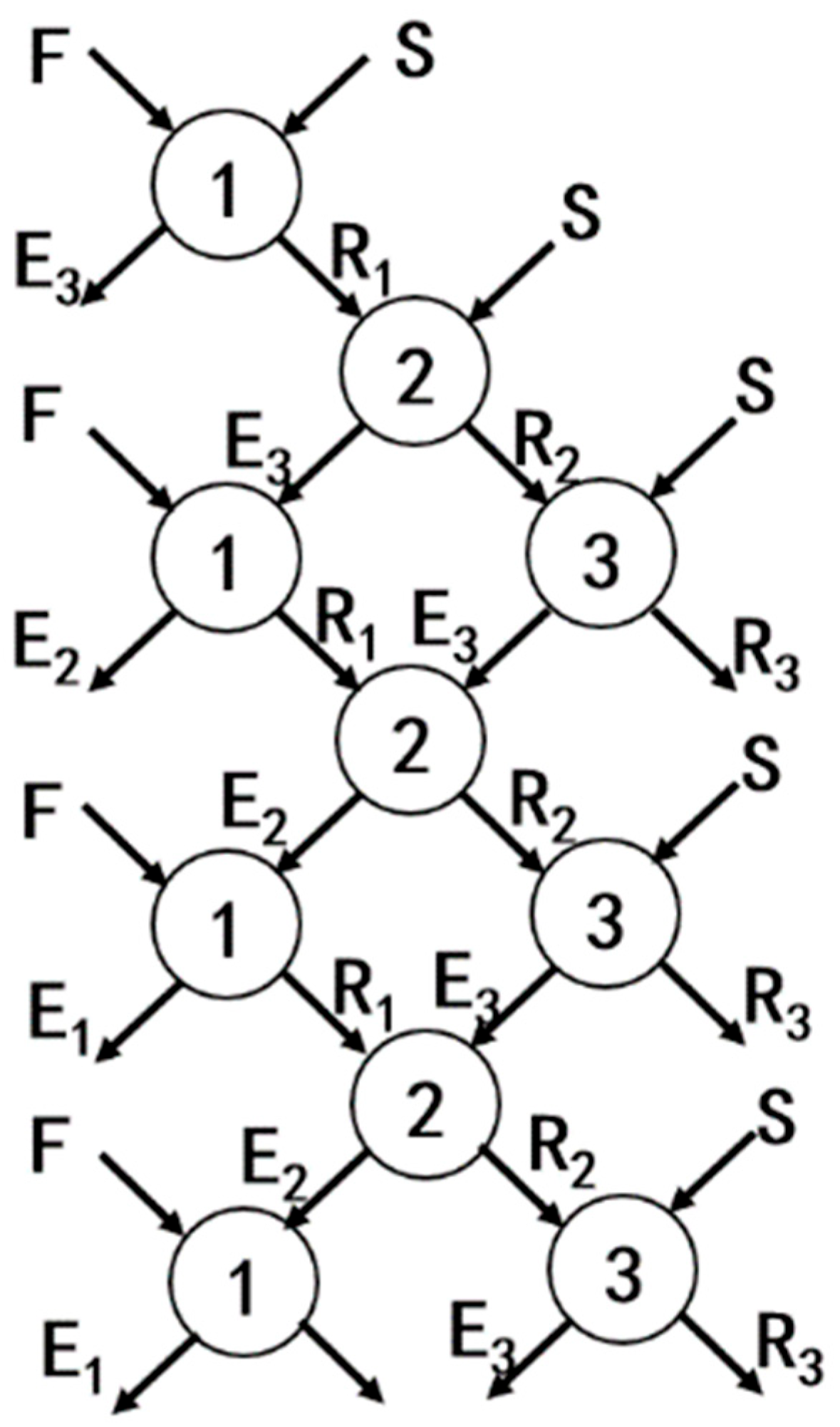
The schematic diagram of the countercurrent extraction process is illustrated in Figure 1. In this process, the feed solution (F) and the organic phase (S) were mixed to produce the extract phase (E) and the raffinate phase (R). The raffinate phase was then mixed with a fresh organic phase for further extraction, while the extract phase was mixed with a fresh feed solution for additional extraction. The numbers in the diagram represent the extraction stages.
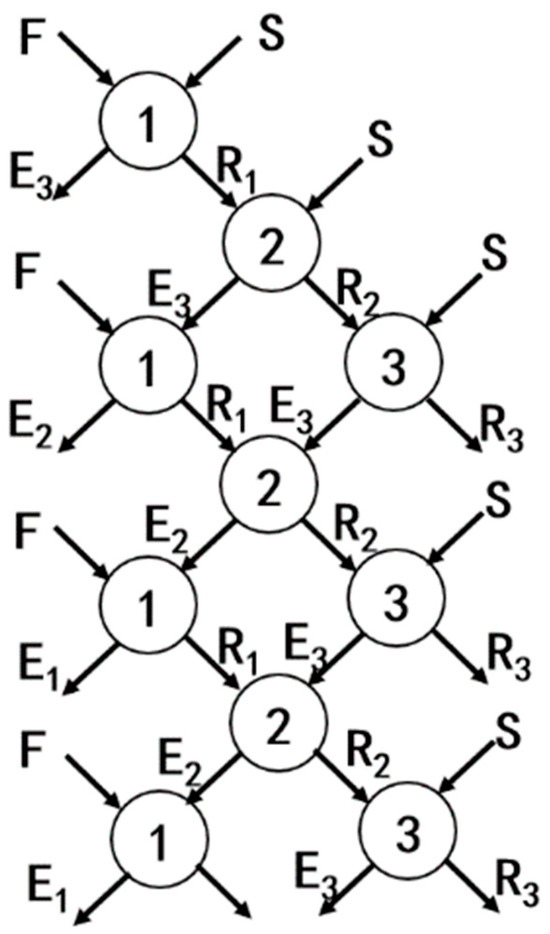
Figure 1.
Schematic diagram of the countercurrent extraction process.
2.3. Calculation Methods
The distribution ratio (D) is defined as the ratio of the solute concentration in the organic phase (co) to that in the aqueous phase (cw). It quantifies the extraction capacity of the extractant for a specific solute under given conditions. The distribution (β), on the other hand, is the ratio of the partition ratios of two solutes(D1 and D2), reflecting the relative difficulty of separating them under identical conditions. These relationships are expressed as follows:
In the design of cascade countercurrent extraction processes, it was assumed that the flow rates of the organic and aqueous phases were equal (1:1 ratio). The extraction efficiency (E) and back-extraction efficiency (St) were calculated based on the partition ratio (D) of each element. The corresponding formulas are as follows:
where ne refers to the extraction series; nx refers to the back-extraction series.
3. Results and Discussion
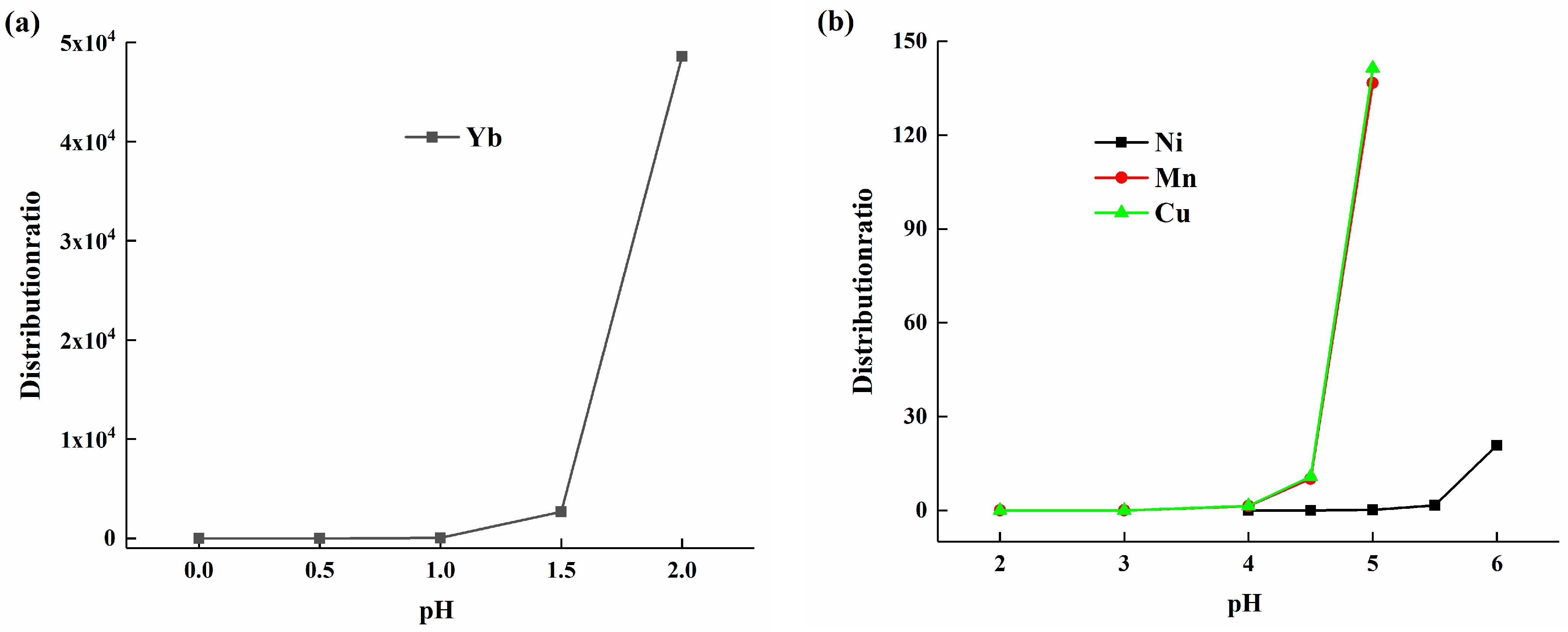
The extraction principle of the HEHEHP extractant for metal ions is based on cation exchange. Metal ions exchange with hydrogen ions in the extractant, and the concentration of hydrogen ions in the solution significantly impacts the reaction equilibrium [22]. Research was conducted on the effect of solution acidity on the distribution coefficient of elements. Distribution coefficient tests were performed using a 50% volume fraction HEHEHP extraction system at varying acidities. The results are shown in Figure 2a, where the x-axis represents the pH value of the solution, and the y-axis represents the element distribution ratio. As the pH increased from 0 to 2, the distribution ratio of ytterbium increased slowly at first, then the rate of increase accelerated with higher pH values. The observed behavior was consistent with the cation exchange mechanism of HEHEHP, where the extraction efficiency of metal ions is highly dependent on solution pH. The slow initial increase in the distribution ratio of ytterbium at low pH (0–2) can be attributed to the competition between hydrogen ions and ytterbium ions for binding sites on the extractant. As the pH increases, the concentration of H+ decreases, reducing this competition and allowing for a more efficient exchange of Yb3+ ions, which explains the accelerated increase in the distribution ratio at higher pH values, and which is also consistent with previous research [20].
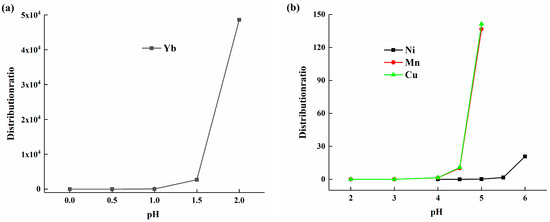
Figure 2.
(a) The distribution ratio of ytterbium in the pH range of 0 to 2; (b) The distribution ratios of manganese, calcium, and nickel in the pH range of 2 to 6.
The distribution ratio data for elements such as manganese, nickel, and calcium are shown in Figure 2b. Their distribution ratios were close to 0 when the pH was below 4, indicating a significant difference in the distribution ratios of ytterbium and these elements at pH 2. In the pH range of 4 to 6, the distribution ratios of manganese and calcium gradually increased as the pH rose, while the distribution ratio of nickel started to increase only when the pH reached 5. In conclusion, different elements exhibited distinct distribution ratio patterns at different acidities, and by controlling the acidity of the feed solution, effective separation of elements could be achieved.
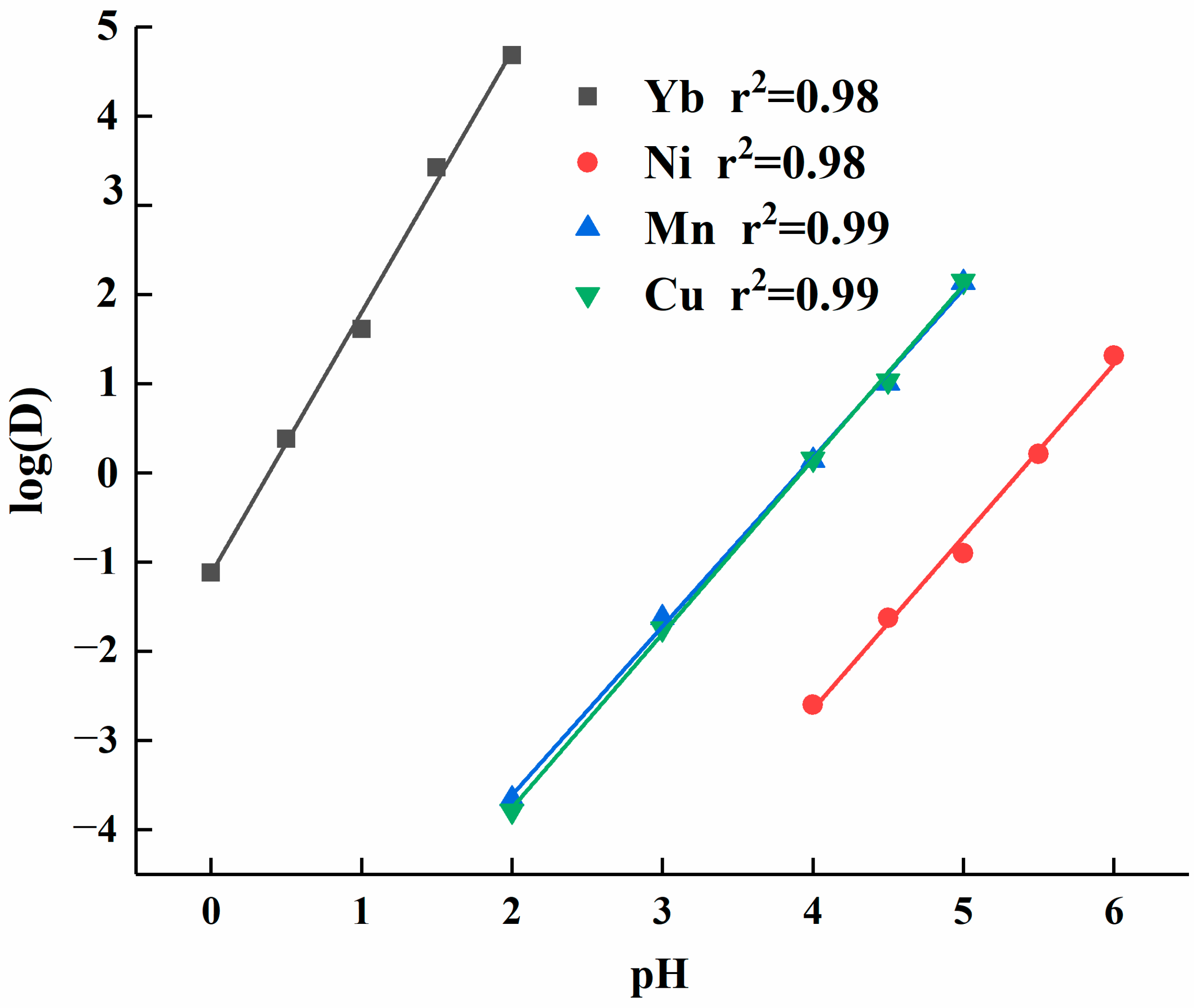
To further understand the impact of solution acidity on the extraction efficiency of elements, data processing was conducted on the distribution ratio of each element. The log(D) values were plotted as the dependent variable (y-axis) and pH values as the independent variable (x-axis), yielding linear equations for each element’s log(D) as a function of pH. As shown in Figure 3, the slope of the linear equation for ytterbium’s log(D) versus pH was 2.93, which was significantly higher than the slopes for other elements. The linear equations for calcium and manganese were similar, with their log(D) values falling within the same range. The slope of the linear equation for manganese was 1.91, slightly lower than the slope of 1.93 for calcium. Nickel had a slope of 1.95, but its log(D) value was lower overall than that of the other elements.
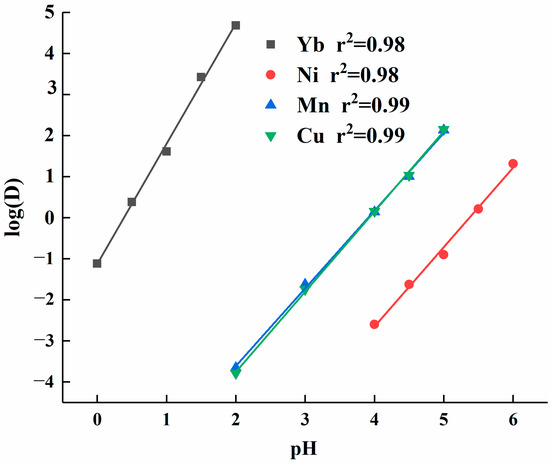
Figure 3.
Element partition ratios fitted to the linear equation of acidity.
To understand the significance of the slope of the linear equation of log(D) for each element with respect to pH, the extraction mechanism of metal ions by HEHEHP was analyzed. HEHEHP exists in a dimeric (H2A2) form in n-dodecane solution [23], and the reaction equations between HEHEHP and each element are shown in Formulas (5) to (8):
In addition, the equilibrium constant KYb Equation (9) for ytterbium and the equilibrium constant KX Equation (10) for manganese, calcium, and nickel were derived from the reaction equation.
Additionally, the equilibrium constant KYb for ytterbium (Equation (9) and the equilibrium constant KX for manganese, calcium, and nickel (Equation (10) were derived from the corresponding reaction equations:
where X refers to either Mn, Ca, or Ni.
Taking the logarithm of both sides of the ytterbium equilibrium constant equation yields Equation (11):
Similarly, applying the logarithm to the equilibrium constant equation for nickel, manganese, and calcium results in Equation (12):
In the acidity partition ratio test, both the extractant concentration and equilibrium constant were held constant, making log(D) and logc(H+) the variables. Therefore, the slope corresponded to the valence state of the metal ions. Based on the dynamic fitting results of the experimental data, the slope for ytterbium was 2.93, which was close to the theoretical value of 3. The slight discrepancy may be attributed to measurement system errors. Additionally, the slopes for the equations of nickel, manganese, and calcium aligned closely with the theoretical calculations, confirming the accuracy of the test data.
The relationship between the separation coefficient and solution acidity for ytterbium, manganese, calcium, and nickel was further analyzed, and the test data were substituted for correction. The separation coefficient between ytterbium and other elements is given by Formula (13):
where is the slope of the equation for element X with respect to acidity. The separation coefficient for manganese, calcium, and nickel is expressed in Formula (14):
In this equation, Y represents either Mn or Ca, and is the slope of the equation for element X with respect to acidity.
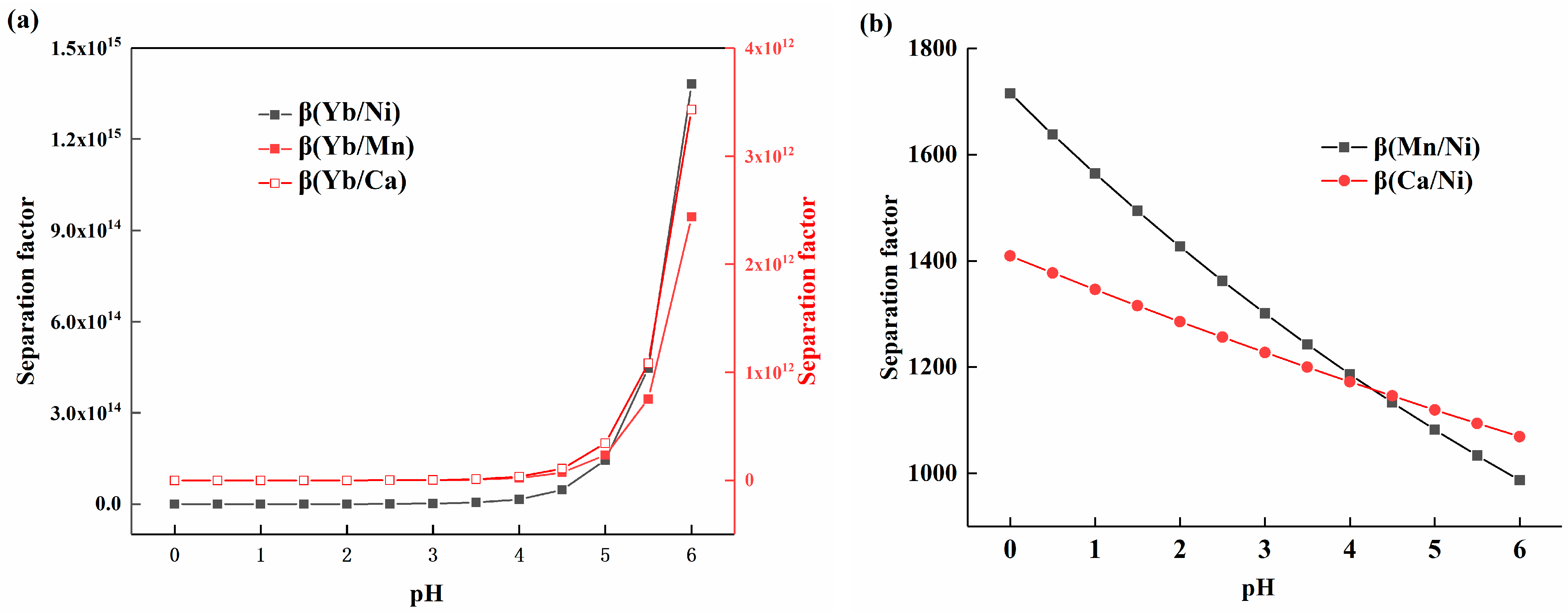
The corresponding K values were calculated based on the experimental data for the distribution ratio of each element, and Equations (9) and (10) were used to obtain Figure 4a,b. As shown in Figure 4a, the separation coefficients of ytterbium and other elements all increased with the rise in pH, with their growth rates following a similar trend, as the equations for the distribution ratios exhibited comparable slopes. The value of β(Yb/Ni) was higher than that of β(Yb/Mn) and β(Yb/Ca), which can be attributed to the relatively lower distribution of nickel at the same pH value. Figure 4b shows the variation trends of the separation coefficients β(Mn/Ni) and β(Ca/Ni) with acidity. It can be observed that the separation coefficients ranged from 987 to 1715, displaying a slow decreasing trend. The reduction rate of β(Mn/Ni) was faster than that of β(Ca/Ni), which was due to the differences in the slopes of their respective equations.
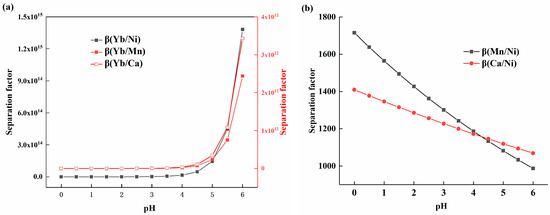
Figure 4.
(a) The relationship between the separation coefficient of ytterbium, manganese, calcium, and nickel and solution acidity; (b) The relationship between the separation coefficients of manganese, calcium, and nickel and solution acidity.
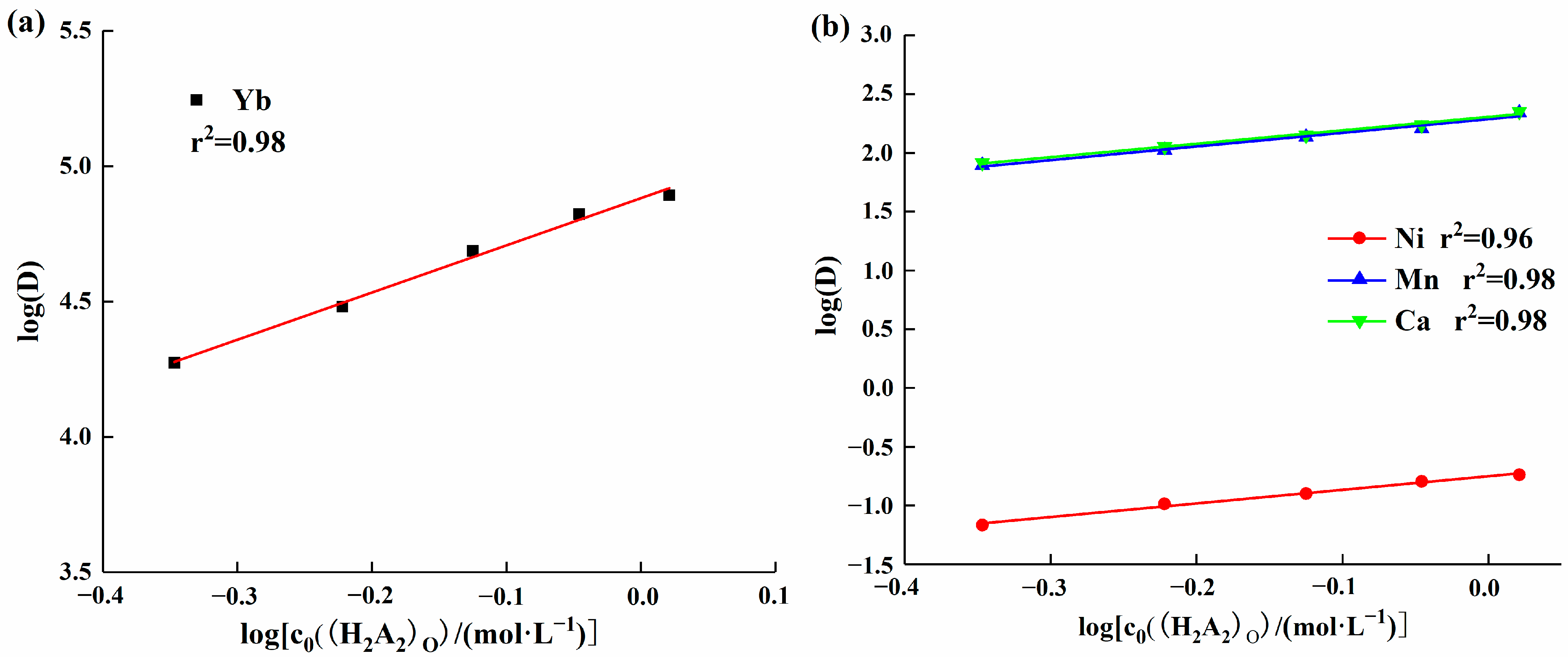
To investigate the influence of extractant concentration on the distribution ratio and separation coefficient of each element, additional experiments were conducted to examine how changes in extractant concentration affect the distribution ratio of each element. Under experimental conditions with a solution pH of 2, the effect of HEHEHP concentration changes in the range of 30% to 70% on the distribution ratio of ytterbium was studied. The results are shown in Figure 5a. As the extractant concentration increased, the distribution ratio of ytterbium gradually rose. A linear equation was fitted to the data, and the slope was found to be 1.74, which was lower than the theoretical slope value of 3. This discrepancy may be due to the fact that HEHEHP not only forms the Yb((H2A)3) structure with ytterbium ions but also possibly exists in the form of YbA3·HA or YbA3 complexes [24]. Under experimental conditions with a solution pH of 5, further experiments were conducted to examine the effect of extractant concentration on manganese, calcium, and nickel. Figure 5b shows the equations of the distribution ratios of manganese, calcium, and nickel with respect to extractant concentration. The slopes were 1.16, 1.14, and 1.16, respectively, which were also lower than the theoretical slope value of 2. This can be attributed to the same cause as for ytterbium, where nitrate ions in the aqueous phase are also extracted in large quantities by HEHEHP, resulting in a decrease in the concentration of free ligands. This, in turn, affects the interaction ratio between the extractant and metal ions, causing changes in the structure of the complex molecules.
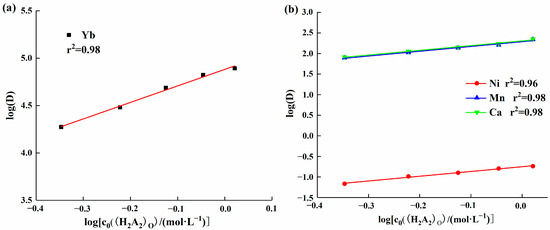
Figure 5.
(a) Effect of extractant concentration on the ytterbium partition ratio; (b) Effect of extractant concentration on the distribution ratios of manganese, nickel, and calcium.
By substituting the experimental data for extractant concentration into Equations (11) and (8), the partition ratio equations with acidity and extractant concentration as variables were derived. The partition ratio equation for ytterbium is shown in Formula (15):
Similarly, the equilibrium constant equation for nickel, manganese, and calcium with respect to acidity and extractant concentration is given by Equation (16):
where is the slope of the extraction agent concentration equation.
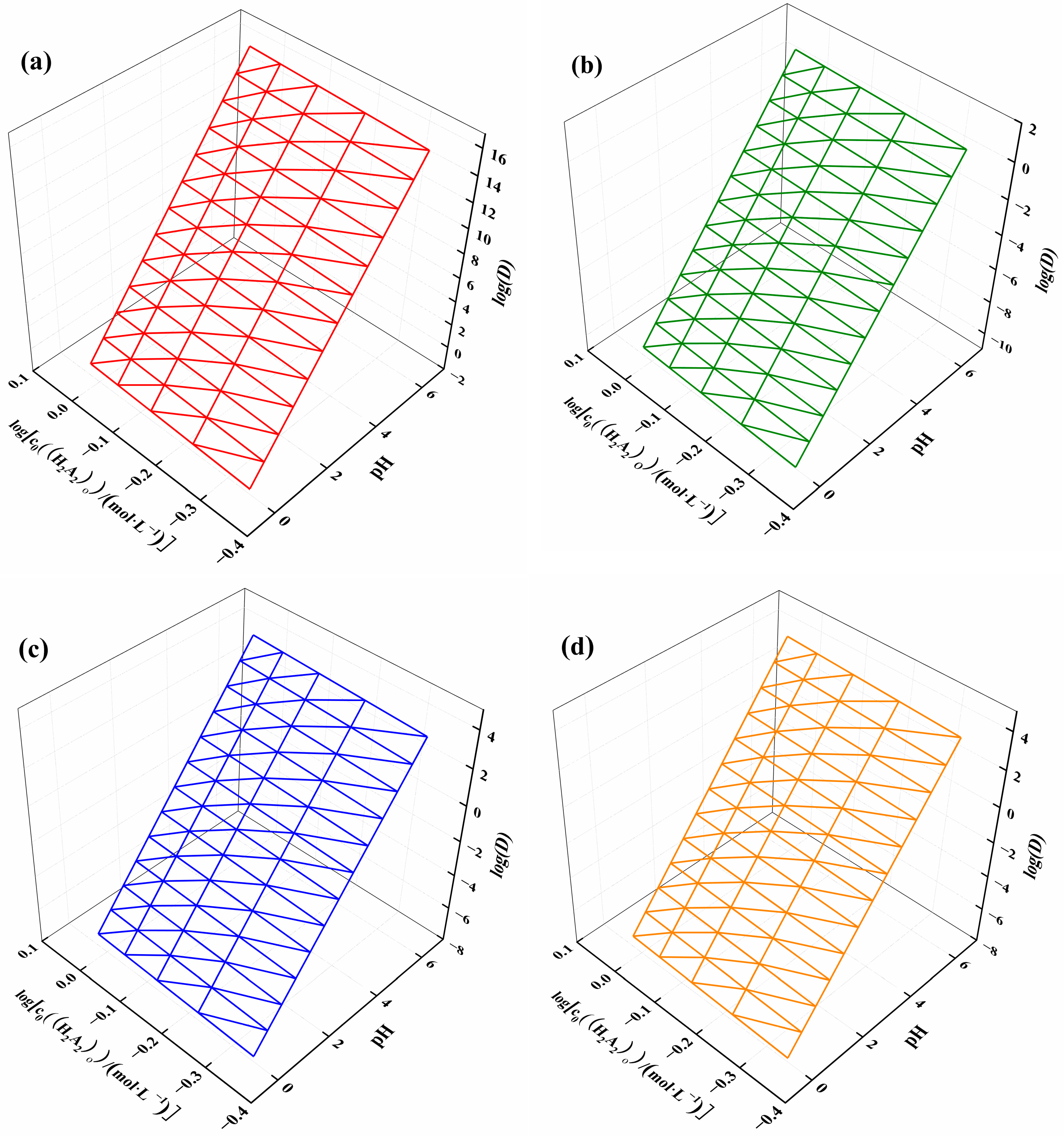
Using Formulas (15) and (16), the distribution ratios of ytterbium, nickel, manganese, and calcium were derived with respect to the changing solution acidity and extractant concentration, as shown in Figure 6. Figure 6a illustrates that the log(D) of ytterbium increased with both increasing pH and extractant concentration, with acidity having a greater influence on the ytterbium partition ratio, consistent with the slope results. Figure 6b–d show the relationships between the log(D) of nickel, manganese, and calcium and the acidity of the solution and extractant concentration, displaying a trend similar to that of ytterbium. However, the log(D) interval for ytterbium ranged from 2 to 16, while for nickel it ranged from −10 to 2, and for manganese and calcium, it ranged from −8 to 4. This indicates that solution acidity and extractant concentration can be controlled to achieve the separation of different elements.
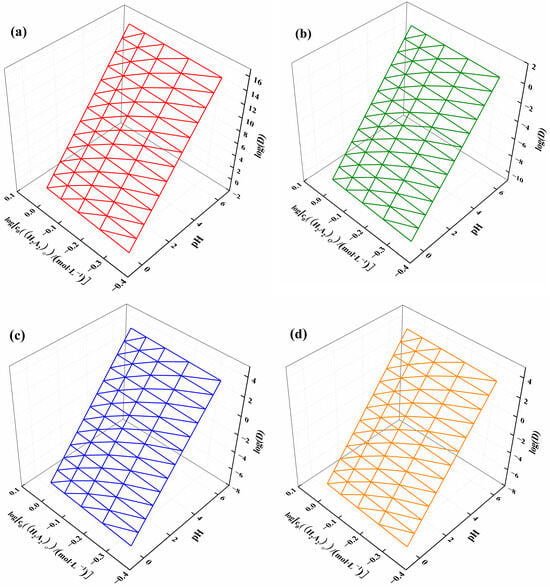
Figure 6.
(a) Ytterbium, (b) nickel, (c) manganese, and (d) calcium distribution ratios as a function of solution acidity and extractant concentration variation.
The effect of extractant concentration changes on the separation coefficient between ytterbium and manganese, calcium, and nickel was further analyzed. The test data were substituted for correction, and the separation coefficient between ytterbium and other elements is given by Formula (17):
The separation coefficients for manganese, calcium, and nickel are expressed in Formula (18):
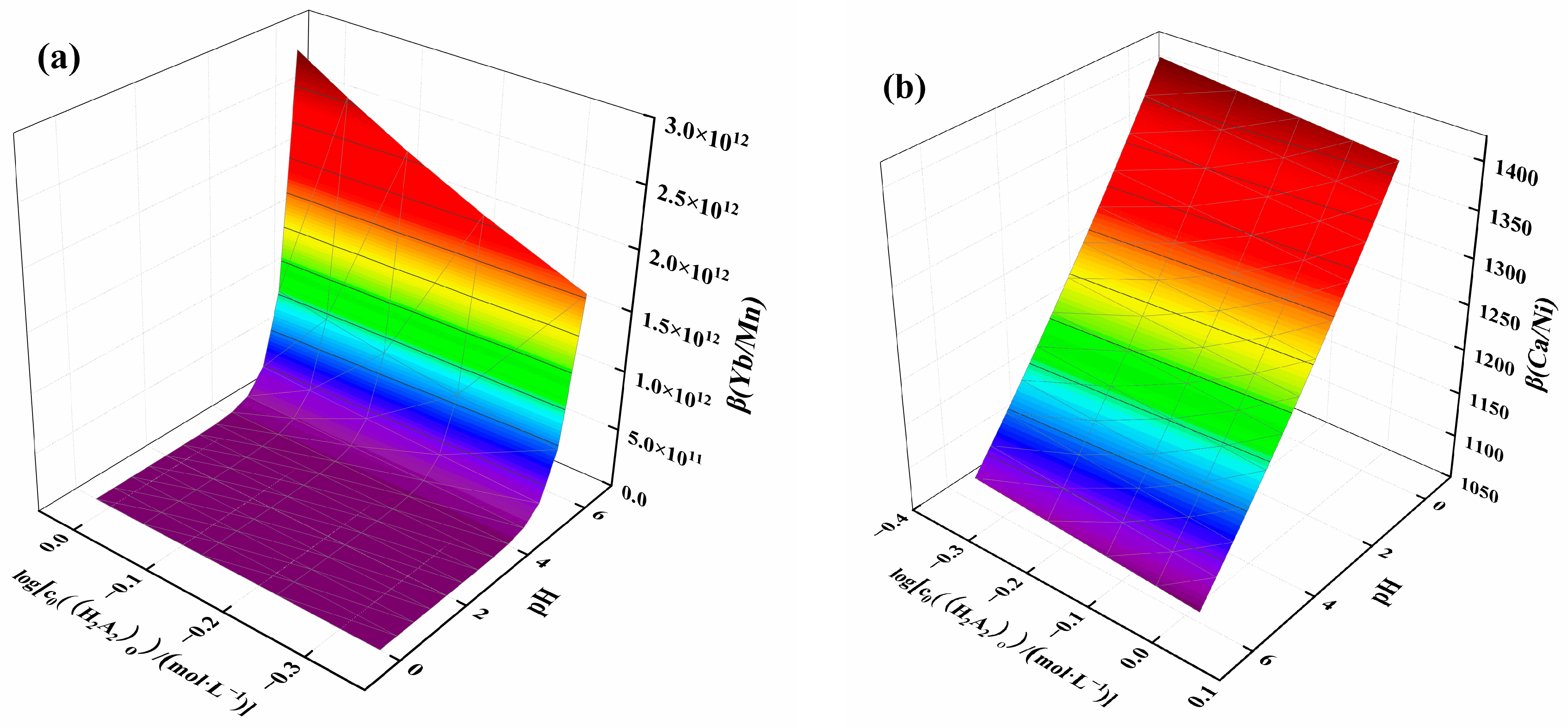
β(Yb/Mn) and β(Ca/Ni) were selected for plotting, as shown in Figure 7. Figure 7a illustrates the effect of acidity and extractant concentration on β(Yb/Mn). It can be observed that β(Yb/Mn) increased with decreasing solution acidity and extractant concentration. The separation coefficient increased slowly before pH 5, but after pH exceeded 5, the separation coefficient rose more rapidly. This rapid increase in the separation coefficient indicated that acidity is the key factor affecting the separation. Figure 7b shows the effect of acidity and extractant concentration on β(Ca/Ni), with the separation coefficient ranging from 1062 to 1424. This coefficient increased with increasing solution acidity and extractant concentration, with acidity being the dominant factor. Based on the results of the separation coefficient, it can be concluded that the extraction of ytterbium, manganese, and calcium can be achieved by adjusting the pH. Further, the separation of ytterbium from manganese and calcium can be achieved by using a washing solution with higher acidity, facilitating the distribution of ytterbium in the organic phase and nickel in the raffinate phase.
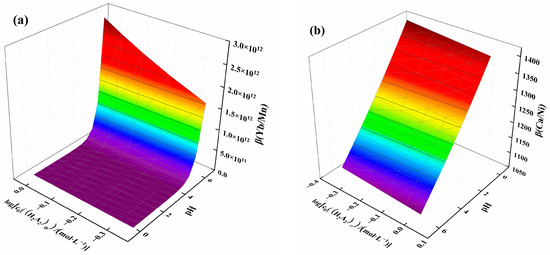
Figure 7.
Effect of acidity and extractant concentration on (a) β(Yb/Mn) and (b) β(Ca/Ni).
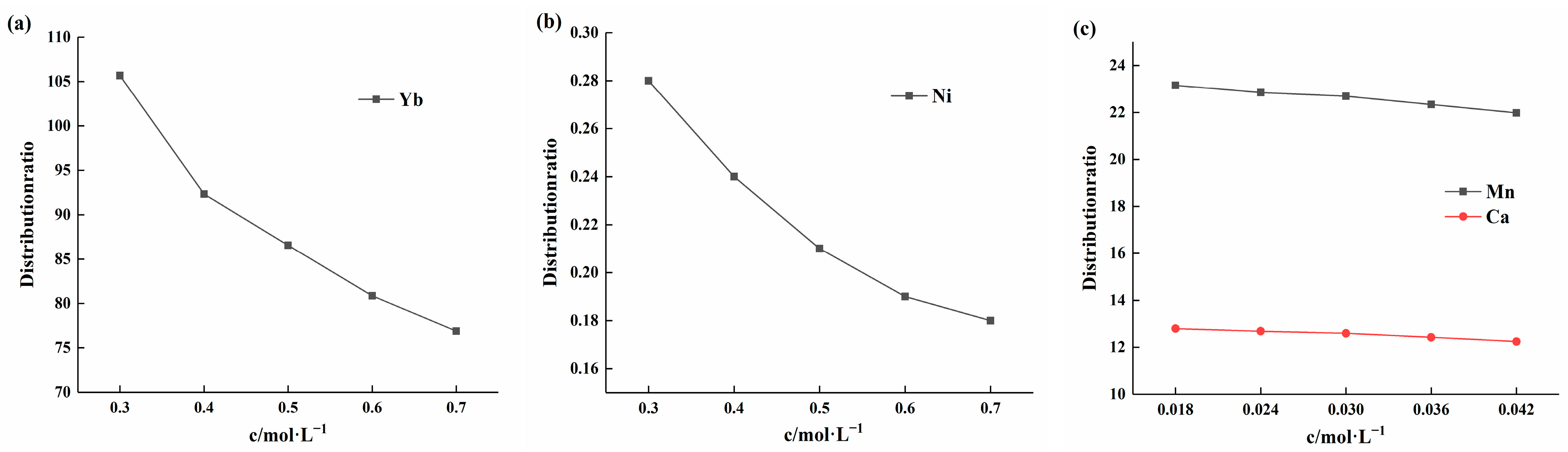
To further understand the influence of factors other than acidity and extractant concentration on the distribution data, experiments were conducted to examine the effect of different element concentrations in the solution on the distribution ratio. Ytterbium was tested at pH 2, while nickel, manganese, and calcium were tested at pH 5. The results of the influence of changes in ytterbium concentration are shown in Figure 8a. As the ytterbium concentration increased in the range of 0.3 to 0.7 mol/L, the distribution ratio gradually decreased. Figure 8b illustrates the effect of nickel concentration changes on the distribution ratio. As nickel concentration increased within the range of 0.3 to 0.7 mol/L, the distribution ratio also decreased, showing a trend similar to that of ytterbium. Figure 8c shows the influence of changes in manganese and calcium ion concentrations on the partition ratio. When the concentration of manganese and calcium ions increased from 0.018 to 0.042 mol/L, the partition ratio exhibited a slow decrease. In summary, as the initial element concentration increases, the element partition ratio gradually decreases. This can be attributed to the fact that an increase in element concentration in the solution inhibits the chemical reaction process. Additionally, the extractant’s saturation capacity limit and the reduction in the concentration of free extractant ions in the organic phase have significant effects.
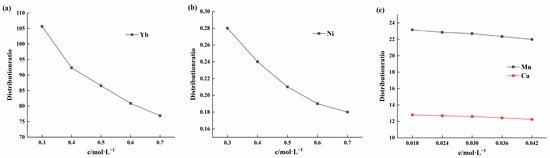
Figure 8.
(a) Effect of ytterbium concentration on the distribution ratio at a solution pH of 2; (b) Effect of nickel concentration on the distribution ratio at a solution pH of 5; (c) Effect of manganese and calcium concentrations on the distribution ratio at a solution pH of 5.
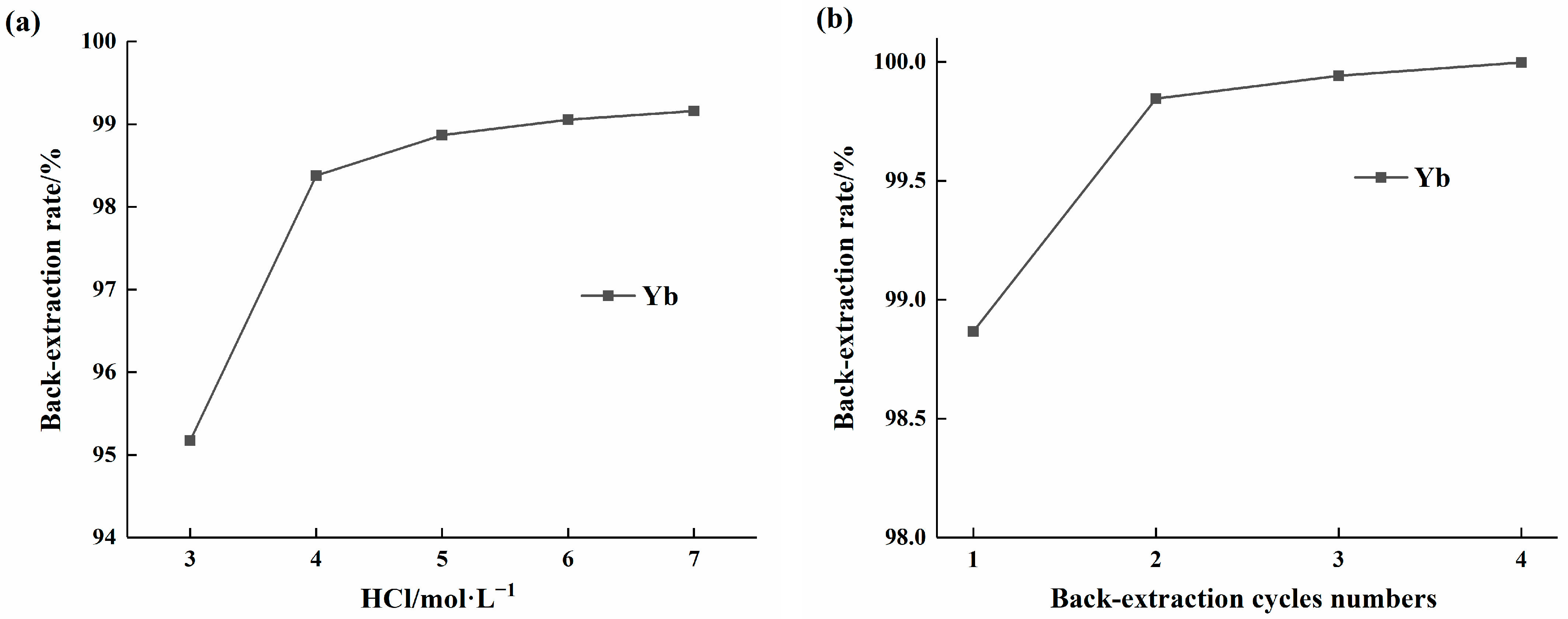
Given the strong affinity of HEHEHP extractant for ytterbium, the influence of HCl concentration on ytterbium back-extraction efficiency was investigated. Single-stage back-extraction experiments were conducted using HCl concentrations ranging from 3 to 7 mol/L. The results, as shown in Figure 9a, indicated that the ytterbium back-extraction efficiency increased with higher HCl concentrations, but the rate of increase gradually slowed. At an HCl concentration of 5 mol/L, the stripping efficiency reached 98.92%. Since further increases in acid concentration beyond 5 mol/L did not significantly improve the stripping efficiency, 5 mol/L was selected for subsequent experiments to study the effect of stripping stages. As illustrated in Figure 9b, the stripping efficiency increased progressively with the number of stripping stages. After four stripping stages, the stripping efficiency exceeded 99.99%.
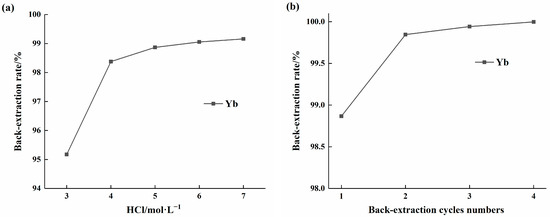
Figure 9.
(a). Effect of HCL concentration on the back-extraction rate of ytterbium in HEHEHP extractant; (b) Effect of extraction times on the extraction rate of ytterbium in HEHEHP extractant.
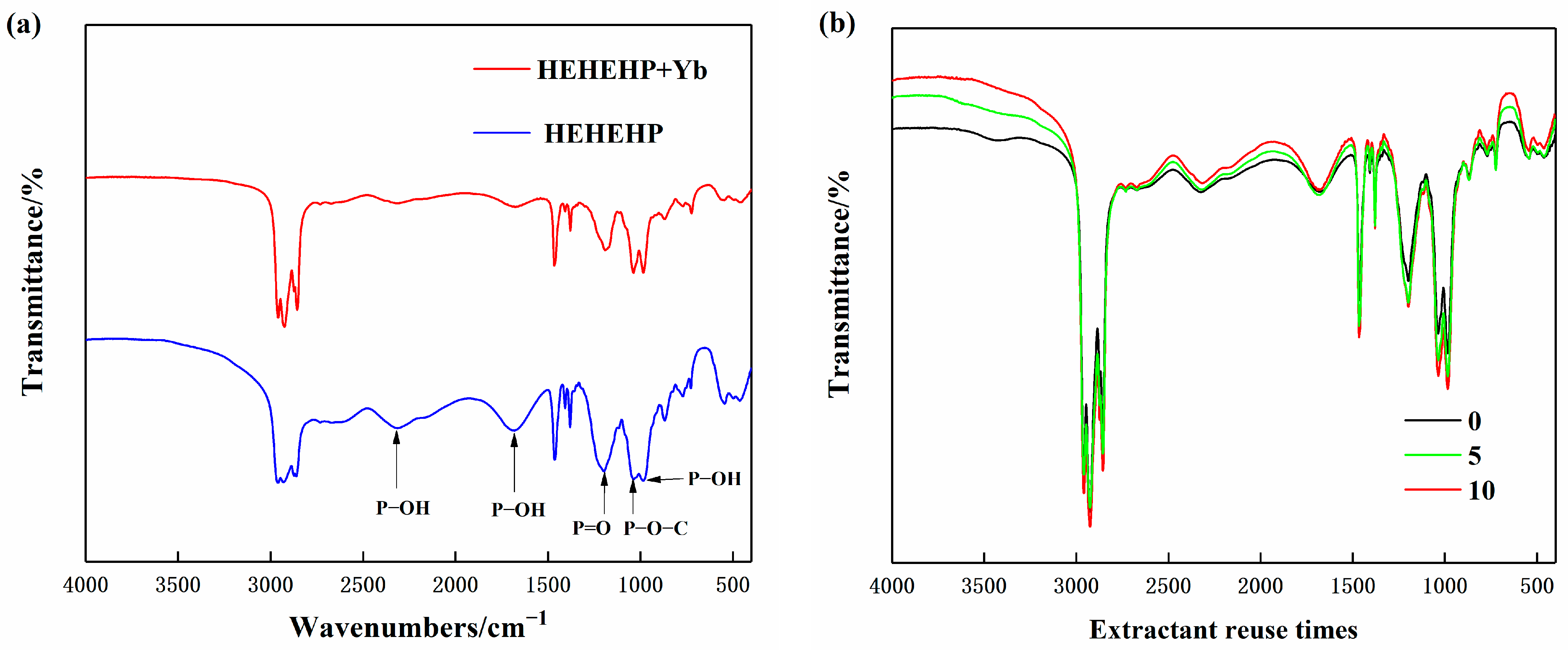
To further investigate the binding state between HEHEHP extractant and Yb, FT-IR was performed on both the pure extractant and the extractant phase after Yb extraction. The results are shown in Figure 10a. For the pure HEHEHP extractant, the peaks at 2316 cm−1 and 984 cm−1 corresponded to the stretching vibrations of P−OH groups, while the peak at 1682 cm−1 represented the bending vibration of P−OH, indicating the hydrogen bonding absorption frequency of HEHEHP dimers. The peak at 1197 cm−1 was attributed to the stretching vibration of the P=O double bond, and the peak at 1035 cm−1 corresponded to the stretching vibration of P−O−C [25].
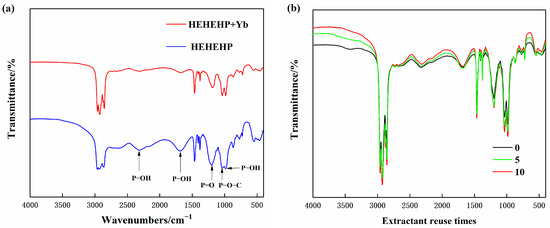
Figure 10.
(a) Comparison of FT-IR spectra of pure HEHEHP extractant and extractant after extracting ytterbium. (b) Comparison of infrared spectra of different repeated usage times of HEHEHP Extractant.
Comparing the spectra before and after extraction, the following results were found. The peaks at 2316 cm−1 and 984 cm−1 significantly weakened, indicating that the H+ in the P−OH groups was replaced by Yb3+ during the extraction process, leading to the formation of new chemical groups. The peak at 1682 cm−1 also showed a notable reduction, suggesting that the HEHEHP dimers gradually disappeared as Yb3+ formed chelate complexes with the extractant molecules. The P=O double bond peak shifted to a lower frequency by 8 cm−1, moving from 1197 cm−1 to 1189 cm−1 after extraction. This shift indicated the formation of a new P=O:Yb coordination bond, which weakened the electron density of the P=O group. The P−O−C peak at 1032 cm−1 remained almost unchanged, further confirming that the extraction reaction primarily involved cation exchange at the P−OH sites [26]. In conclusion, it is demonstrated that the extraction mechanism of HEHEHP and yttrium follows the cation exchange reaction.
To investigate the impact of reuse cycles on the stability of the HEHEHP extractant, FT-IR spectroscopy was performed on the extractant after different numbers of reuse cycles. As shown in Figure 10b, the FT-IR spectra of the freshly prepared extractant and the extractant reused 5 and 10 times exhibited nearly identical characteristic peaks, indicating that the chemical structure of HEHEHP remained unchanged even after multiple reuse cycles. However, slight variations in the intensity of some peaks were observed, which could be attributed to the presence of water or partial loss of extractant components, leading to changes in concentration.
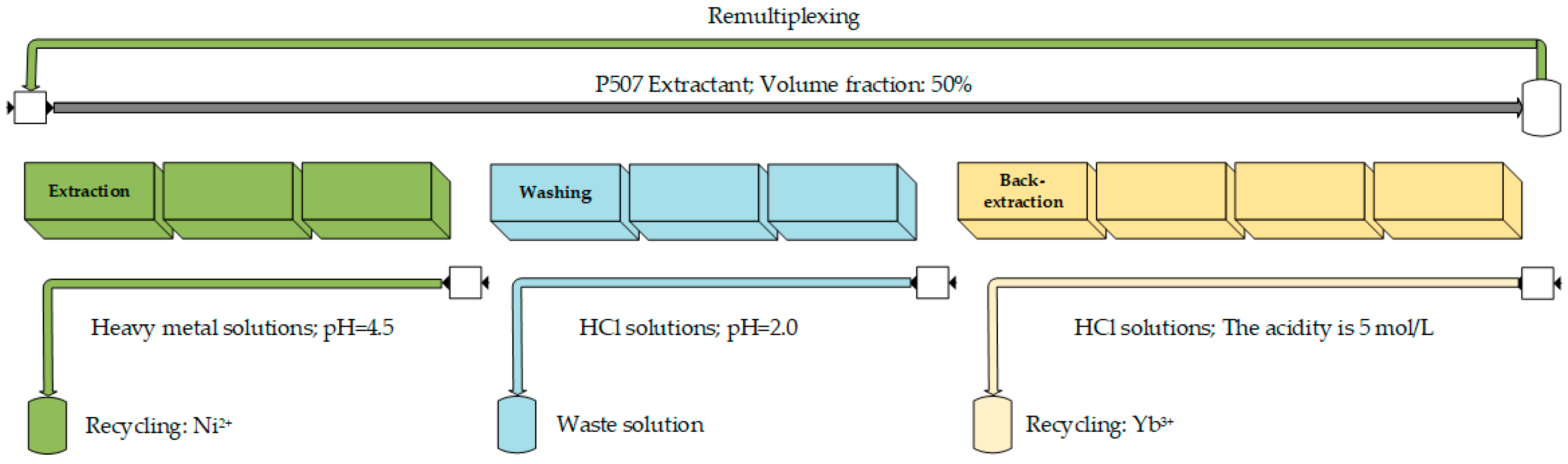
To verify the separation of ytterbium and nickel from manganese and calcium, a cascade countercurrent extraction process was designed. In the extraction phase, the elements Yb, Mn, and Ca were predominantly extracted into the organic phase, while nickel remained in the raffinate. Assuming a 1:1 flow ratio between the organic and aqueous phases, a solution pH of 4.5, and three extraction stages, the extraction rates for Yb, Mn, and Ca exceeded 99.9%, while the extraction rate for Ni was 3.7%. To remove non-rare-earth impurities from the organic phase, washing was carried out using an HCl solution with a pH of 2. Theoretical calculations suggested that impurities can be effectively removed in two washing stages, resulting in a Yb purity of 99.9% in the organic phase.
The process was tested with the following conditions: a solution pH of 4.5, a washing solution pH of 2, a 50% volume fraction of extractant, concentrations of 0.3 mol/L for Yb and Ni, and 0.02 mol/L for Mn and Ca, with three extraction and washing stages each. In addition, 5 mol/L hydrochloric acid, equal to the volume of organic, was used for stage 4 back-extraction to ensure that ytterbium was recovered to the water phase as much as possible. The process diagram is shown in Figure 11.
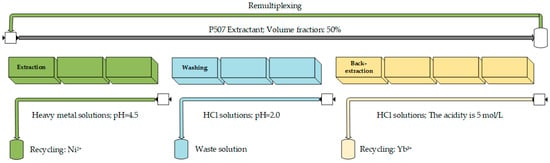
Figure 11.
Diagram of series flow extraction process.
The verification results are presented in Table 1. The primary component of the raffinate was Ni, with a concentration of 16.8 × 103 μg/mL, while the concentrations of other elements were minimal. The calculated absolute purity of Ni was 99.97%. The main constituents of the washing solution were Mn and Ca, suggesting that Yb can be effectively separated during the washing process. Finally, the concentration of ytterbium in the back extract was 39.1 × 103 μg/mL, with an absolute purity of 99.99%.

Table 1.
Concentration of elements in the experimental raffinate, washing solution, and back-extraction solution separated by cascade countercurrent extraction.
To evaluate the economic feasibility of the designed extraction process, the reagent consumption per mole of Yb and Ni obtained was statistically analyzed. The results are summarized in Table 2. Under countercurrent extraction conditions, the amount of metal ions extracted by each unit of extractant was approximately equal. Assuming that the extractant could be reused 10 times (in fact, the extractant stability is still good after 10 times), experimental calculations indicated that the consumption of HEHEHP extractant and the diluent n-dodecane was approximately 1.6 mol and 2.2 mol, respectively, per mole of ytterbium or nickel recovered. In the washing stage, a 0.01 mol/L hydrochloric acid (HCl) solution was used, with cumulative consumption of pure water and HCl amounting to approximately 12 L and 0.12 mol, respectively. In the back-extraction stage, a 5 mol/L HCl solution was employed, with cumulative consumption of pure water and HCl reaching approximately 7.6 L and 65 mol, respectively. The detailed reagent consumption per mole of ytterbium and nickel product is presented in Table 2.

Table 2.
Statistical tables show the amount of sample solution consumed per mol of ytterbium and nickel product obtained by extraction.
4. Conclusions
Through extraction and separation tests of Yb, Ni, Mn, and Ca in nitric acid solutions, it was determined that the logarithm of the distribution ratio (log(D)) for each element showed a positive correlation with both the pH of the solution and the logarithm of extractant concentration. The pH slopes were 2.93, 1.95, 1.91, and 1.93, respectively, which closely aligned with the theoretical calculation values. The slopes for extractant concentration were 1.74, 1.16, 1.15, and 1.16, which were lower than the theoretical values due to the formation of multiple complexes between extractant and ytterbium ions, including Yb((H2A)3) and potentially YbA3·HA or YbA3 structures. Additionally, the distribution ratios of the elements were negatively correlated with the initial metal ion concentrations, indicating that the extraction process was inhibited at higher metal concentrations. Using a 5 mol/L hydrochloric acid solution for four back-extraction stages, the ytterbium extraction efficiency from the HEHEHP extractant exceeded 99.99%. The ion exchange reaction mechanism between HEHEHP and ytterbium was confirmed through FT-IR spectroscopy, and the stability of the HEHEHP extractant was validated.
The equation for the separation coefficients between Yb and the other elements, in relation to solution acidity and extractant concentration, was optimized based on experimental data. The separation coefficient equation for Yb and the other elements is given by:
A cascade countercurrent extraction process was designed with the following optimized parameters: a solution pH of 4.5, a washing solution pH of 2, a 5 mol/L hydrochloric acid back-extraction solution, three extraction and washing stages, and four back-extraction stages. The process successfully achieved the separation of Yb and Ni with purities of 99.99% and 99.97%, respectively. This outcome is significant for both the recovery of high-value elements and the treatment of contaminated wastewater.
Author Contributions
B.Z. was responsible for the research scheme design and manuscript writing; Y.H. was responsible for the test; G.Z. was responsible for the dynamic analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by China National Nuclear Corporation Limited, first grant number GW-JTWZ-2023-013, second grant number GZ-JTWZ-2023-02.
Data Availability Statement
The data that support the findings of this study are available from the authors upon reasonable request.
Acknowledgments
Qingkai Liu and Xiaojiao An for ICP characterization.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, Y.; Miao, S.H.; Liang, Y.J.; Liang, C.; Chen, D.X.; Shan, X.H.; Sun, K.N.; Wang, X.J. Blue LED-pumped intense short-wave infrared luminescence based on Cr3+-Yb3+-co-doped phosphors. Light Sci. Appl. 2022, 11, 136. [Google Scholar] [CrossRef]
- Kir’yanov, A.; Sholokhov, E. 35 W highly effective Ytterbium-Erbium-Thulium tandem all-fiber 1.947 µm laser system at 975 nm diode pumping. Laser Phys. Lett. 2023, 20, 105102. [Google Scholar] [CrossRef]
- Liao, J.S.; Wang, M.H.; Lin, F.L.; Han, Z.; Fu, B.; Tu, D.T.; Chen, X.Y.; Qiu, B.; Wen, H.R. Thermally boosted upconversion and downshifting luminescence in Sc2(MoO4)3:Yb/Er with two-dimensional negative thermal expansion. Nat. Commun. 2022, 13, 2090. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, J.W. Ytterbium (III) Fluoride in Dental Materials. Inorganics 2023, 11, 449. [Google Scholar] [CrossRef]
- Magnier, L.; Cossard, G.; Martin, V.; Pascal, C.; Roche, V.; Sibert, E.; Shchedrina, I.; Bousquet, R.; Parry, V.; Chatenet, M. Fe–Ni-based alloys as highly active and low-cost oxygen evolution reaction catalyst in alkaline media. Nat. Mater. 2024, 23, 252–261. [Google Scholar] [CrossRef]
- Maximov, J.; Duncheva, G.; Anchev, A.; Dunchev, V.; Anastasov, K.; Argirov, Y. Sustainable Diamond Burnishing of Chromium–Nickel Austenitic Stainless Steels: Effects on Surface Integrity and Fatigue Limit. Appl. Sci. 2024, 14, 9031. [Google Scholar] [CrossRef]
- Ren, Y.; Zhou, Q.; Hua, D.P.; Huang, Z.B.; Li, Y.L.; Jia, Q.; Gumbsch, P.; Greiner, C.; Wang, H.F.; Liu, W.M. Wear-resistant CoCrNi multi-principal element alloy at cryogenic temperature. Sci. Bull. 2024, 69, 227–236. [Google Scholar] [CrossRef]
- Li, W.Y.; Wang, N.; Lu, F.H.; Chai, H.Y.; Gu, H.N. Selective separation of aluminum, silicon, and titanium from red mud using oxalic acid leaching, iron precipitation and pH adjustments with calcium carbonate. Hydrometallurgy 2024, 223, 106221. [Google Scholar] [CrossRef]
- Lee, S.I.; Kim, H.R.; Park, J.K.; Oh, W.; Kim, J.; Kim, C.; Lee, J.; Kim, K.-C.; Lee, B.-C. Precipitation of Ferrous Oxalate from Ferrous Ammonium Sulfate in Oxalic Acid Solution. Processes 2022, 10, 2420. [Google Scholar] [CrossRef]
- Satpathy, S.; Mishra, S. Kinetics and mechanisms of solvent extraction and separation of La(III) and Ni(II) with DEHPA in petrofin. Trans. Nonferrous Met. Soc. China 2019, 29, 1538–1548. [Google Scholar] [CrossRef]
- Wang, Y.; Ziemkiewicz, P.; Noble, A. A Hybrid Experimental and Theoretical Approach to Optimize Recovery of Rare Earth Elements from Acid Mine Drainage Precipitates by Oxalic Acid Precipitation. Minerals 2022, 12, 236. [Google Scholar] [CrossRef]
- Li, S.; Hu, P.C.; Zhang, Y.M.; Xue, N.N.; Huang, J.Y.; He, Y.; Zhang, Z.Y.; Ye, S.Y. Comprehensive recovery of valuable elements from vanadium precipitation liquor using selective impurity removal-reduction precipitation process. J. Clean. Prod. 2024, 467, 143013. [Google Scholar] [CrossRef]
- Labb, S.A.; Despotopulos, J.D.; Kmak, K.N.; Hoffman, D.R. Extraction and separation of rare earth elements using LN resins in hydrochloric acid. J. Radioanal. Nucl. Chem. 2024, 333, 6525–6531. [Google Scholar] [CrossRef]
- Zeng, Z.Y.; Gao, Y.; Ni, S.N.; Fu, X.Y.; Sun, X.Q. Efficient separation for yttrium and heavy rare earth elements using functionalized quaternary ammonium ionic liquids. J. Ind. Eng. Chem. 2024, 136, 577–588. [Google Scholar] [CrossRef]
- Kostanyan, A.E.; Belova, V.V.; Tsareva, Y.V.; Petyaeva, M.M. Separation of Rare Earth Elements in Multistage Extraction Columns in Chromatography Mode: Experimental Study and Mathematical Simulation. Processes 2023, 11, 1757. [Google Scholar] [CrossRef]
- Afonin, M.A.; Nechaev, A.V.; Yakimenko, I.A.; Belova, V.V. Extraction of Rare Earth Elements from Chloride Solutions Using Mixtures of P507 and Cyanex 272. Compounds 2024, 4, 172–181. [Google Scholar] [CrossRef]
- Zheng, X.H.; Zhang, J.P.; Shen, J.D.; Guo, J.W.; Jiang, X.W.; Lei, Y.; Li, S.W. Synergistic extraction of zinc from spent acid using P507-P204: A novel approach for efficient separation. J. Environ. Chem. Eng. 2024, 12, 114515. [Google Scholar] [CrossRef]
- Zhu, X.B.; Liu, Y.; Ma, C.; Li, W. Effective separation of V (IV) and Fe (III) from sulfuric acid solution by solvent extraction with P507 and N235. Hydrometallurgy 2024, 224, 106228. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, H.X.; Zhu, S. Study on Cu(II) extraction process optimization and mechanism from acidic leaching solution using the deep eutectic solvent P507/Menthol. J. Mol. Liq. 2024, 396, 11. [Google Scholar] [CrossRef]
- Ambul, E.; Goletskii, N.; Medvedeva, A.; Naumov, A.; Puzikov, E.; Afonin, M.; Shishkin, D. Separation of Ytterbium And Lutetium with Solutions of (2-Ethylhexyl) Phosphonic Acid Mono-2-Ethylhexyl Ester in Hydrocarbons from Nitric Acid Solutions and its Simulation. Radiochemistry 2022, 64, 300–307. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Zhu, X.B.; Liu, Y. Study on the Kinetics of Extracting Vanadium and Iron from Sulfuric Acid Solution with P507. Rare Met. Cem. Carbides 2024, 52, 1. [Google Scholar]
- Pan, J.; Zhao, X.; Zhou, C.C.; Yang, F.; Ji, W.S. Study on Solvent Extraction of Rare Earth Elements from Leaching Solution of Coal Fly Ash by P204. Minerals 2022, 12, 1547. [Google Scholar] [CrossRef]
- Zheng, X.D.; Zhao, L.S.; Li, Z.; Zhang, H.Y.; Wei, W.S.; Huang, X.W.; Feng, Z.Y. Selective separation of rare earths and aluminum from low-concentration rare earth solution via centrifugal extraction. Sep. Purif. Technol. 2024, 351, 9. [Google Scholar] [CrossRef]
- Tan, C.M.; Cao, S.W.; Huang, Q.G.; Chen, D.S.; Qin, Z. Extraction and Separation of Lanthanum and Actinium by Non-Saponification P507 System. J. Nucl. Radiochem. 2024, 46, 221–230. [Google Scholar]
- Zhang, Y.; Li, X.; Wang, H. Mechanism of rare earth extraction using acidic organophosphorus extractants: Insights from spectroscopy and DFT calculations. J. Mol. Liq. 2022, 345, 118234. [Google Scholar]
- Wang, L.; Sun, Y.; Zhao, X. Advances in the understanding of rare earth extraction mechanisms using advanced spectroscopic techniques. Coord. Chem. Rev. 2021, 437, 213852. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).