1. Introduction
With the rising of “artificial intelligence” technology, the mining industry is paying more and more attention to intelligent mining. In this framework, a preliminary step to intelligent mining is the automatic building and quick updating of mineral resource models. However, for the existing three-dimensional mining software (e.g., Vulcan, Datamine, Surpac, MineSight, Micromine, Dimine, QuantyMine, 3Dmine, etc.), the contour tiling approach is generally adopted for the three-dimensional model building for ore body. For this approach, there is much man–machine interaction, low efficiency, low geometric quality, difficult partial update and other problems, which make it difficult to satisfy the actual mine production demands [
1]. Only rare mining software (e.g., SKUA/Gocad, Mira Suite, GeoModeler) offer implicit modeling facility since more than 10 years.
For implicit modeling, based on the geological exploration data processing in combination with actual engineering demands, corresponding spatial interpolation function is selected to establish the implicit equation of a surface to represent the geometrical morphology and grade distribution of the ore body and the surface model pick-up algorithm is introduced for its drawing [
2,
3,
4,
5,
6]. For implicit modeling, there is no much man–machine interaction; moreover, due to a high degree of modeling automatization and quick partial update, it is getting more and more wide attention in the field of three-dimensional modeling for ore body.
For the common implicit modeling methods, there is the triangulation with linear interpolation [
7], nearest neighbor [
8], distance power inverse ratio method [
9], linear interpolation [
10], local polynomial [
11], interpolation of radial basis function [
12], spline interpolation [
13], ordinary Kriging [
14], indicator Kriging [
15], universal Kriging [
16], etc. Implicit modeling methods have been focused on and studied in the fields of digital terrain modeling [
17,
18], geological structure modeling [
19,
20], reservoir modeling [
21], hydrogeological modeling [
22] and ore body modeling [
23,
24,
25], etc. Among them, three-dimensional implicit modeling of the ore body has become a research hotspot of mining scholars all over the world in recent years. For example, Mallet [
23] proposed a geological modeling based on the discrete smooth interpolation algorithm, which is often applied to the stratified geologic body modeling. Therefore, there are certain limitations in the application scenarios. Calcagno et al. [
24] proposed the potential field method for three-dimensional geologic modeling and the universal Co-Kriging method to solve the interface between different rock stratums. Under the rock stratum constraints, the Kriging interpolation is used for the ore body modeling. However, this method needs interpretation based on original data in practical use. Moreover, the complex algorithm, heavy calculation burden and weak geometric domain constraint result in considerable difference between the ore body distribution and the actual morphology. Jiateng et al. [
25] adopted the Hermite interpolation method and Marching Cubes (MC) algorithm to build the implicit surface model, where the radial basis function is used as the kernel function. However, for this method, the unit vector pointing to high grade in the drilling direction is directly taken as the normal direction of the boundary point, which is inaccurate. Because the shape of the ore body is extremely complex or extremely irregular, the borehole cannot be exactly perpendicular to the ore body. Moreover, in view of the sparse and scattered geological drilling, the implicit model built directly with this method presents problems such as weak continuity and boundary closure failure. Therefore, despite the fruitful research findings, there are still the following defects in the selection of algorithms and solution: (1) It is hard for the implicit modeling algorithm to satisfy the modeling of various complex ore bodies, i.e., this algorithm lacks general applicability; (2) There is high degree of algorithm complexity, heavy calculation burden and slow solving speed; (3) For the implicit model built based on the original geological borehole data, there are problems such as weak continuity and boundary closure failure; and (4) The point-cloud normal solution is inaccurate.
Therefore, this paper takes the Hermite radial basis function algorithm as the core, which can better meet the construction of implicit surface of the ore body with various complex topological structures and geometric features. Secondly, the virtual borehole densification is used to improve the borehole data intensity, which can solve the problems of poor continuity and non-closure of the boundary of ore body model easily caused by sparse original geological boreholes. In addition, the calculation of point-cloud normal direction based on the adjacent hole-drilling method is proposed to ensure the accuracy of the point-cloud normal direction, and the inaccurate problem of the point cloud normal solution is solved. Moreover, the least-squares Householder-QR decomposition method is adopted to solve the HRBF coefficient matrix to improve the solving speed and solve the problem that the algorithm complexity is high and the calculation amount is large, which causes the solution speed to be slow. Finally, the Marching Cubes (MC) algorithm is introduced for the discretization of model space and the iso-surface is extracted to realize the visualization of the implicit surface, so as to ultimately realize the accurate building of three-dimensional model for complex ore body.
2. Hermite Radial Basis Function Principle
The radial basis function (RBF) interpolation only requires sampling point coordinates, and the shape of the surface is controlled by adding the zero points on the surface and the constraint points inside and outside the surface. However, it is hard to determine the distance from the constraint points inside and outside the surface to the surface. Moreover, the shape of the surface is usually extremely complicated, and it is easy to cause the cross phenomenon. Therefore, Macedo et al. [
26,
27,
28] combined the Hermite interpolation theory with the radial basis function and proposed the Hermite radial basis function (HRBF) implicit surface building method, the core concept of which is to build an implicit function and enable it to interpolate the position and normal direction of the sampling point.
The mathematical formulation of HRBF surface reconstruction algorithm is given as follows: For the given sampling point set
, where
xi represents the position of the sampling point and
ni represents the normal direction of the sampling point, the constructor function
f:
R3→
R meets the following conditions:
Suppose function f(
x) is a series of base functions by means of linear combination:
In combination with Equation (1), this system is regularized in accordance with the optimization theory:
In Equation(3),
C1 > 0 and
C2 > 0 are weights used to account for fitting errors wit samples (
f(
xi)), and measures errors from imposed gradient directions parallel to the normal;
is the coefficient to measure the fitting degree of the function to the sampling point;
is to measure the fitting degree of the function gradient to the normal direction of the sampling point;
is the regularization term of the function, and the smaller the value is, the smoother the surface will be; and H is the reproducing Hilbert space of the kernel function. According to the derivation of Steinke et al. [
29], with the minimum
E(f) and
∂E(f)/∂f = 0, there is:
where
,
.
In order to guarantee the positive definiteness of the solving system as well as the continuity of the surface, one first-order polynomial is generally added, i.e.,
At this point, additional constraint conditions are needed for the one-first polynomial:
During the three-dimensional surface reconstruction, the radial basis function ensures satisfactory point cloud data processing results, with high algorithm robustness, few independent variables and high-order continuity, being applicable to the multivariate scattered and sparse data. Therefore, the radial basis function is used for the kernel function. According to Equation (1), this solving system is:
Based on the sampling point set , αi, βi as well as γ (the coefficient of the first-order polynomial) are obtained by establishing the linear system of equations in accordance with the above-mentioned method. They are put in Equation (5) to obtain the implicit function f(x) for the surface where the characterization sampling point set is.
This algorithm presents the advantages of the radial basis function in the implicit surface building, being applicable to the description of sparse and non-uniform sampling surface and guaranteeing satisfactory fitting of the surface with complex topological structure as well as geometrical characteristics. Meanwhile, for this algorithm, the implicit function gradient being equal to the normal vector of the sampling point is taken as the constraint condition and there is no need to choose the offset distance. However, it also has disadvantages, such as discontinuity of derivatives at the border of the neighborhood, and only deterministic solution, not possible to account for uncertainty.
3. Implicit Modeling Approach and Process
For the three-dimensional implicit modeling approach for ore body based on the geological borehole data proposed in this paper, with the geological borehole data as the basis, the position and depth of the virtual borehole as well as the sample length is determined based on the Delaunay triangulation; the virtual borehole containing the mineral and rock information is determined based on the Support Vector Machine (SVM); the borehole data are subject to sample length combination to form the ore block based on the cut-off grade, minimum mining thickness, band rejected thickness as well as the “low-grade ore to the delineation of ore body” thought; the upper-lower demarcation point (i.e., the boundary point, referring to the mineral and rock demarcation point under the minimum cut-off grade requirements) of each ore block is extracted and the normal direction of the boundary point is calculated with the adjacent hole-drilling method, so as to obtain the Hermite point cloud data set; the HRBF method is introduced for interpolation and accelerating the solving process to obtain the implicit surface of the ore body model; and the MC algorithm is introduced for the discretization of the model space and the iso-surface is extracted to finally realize the visualization of the implicit surface of the ore body. More details are given as follows (
Figure 1).
(1) Based on the borehole position given by the original geological borehole data, the position of the virtual borehole is obtained with the Delaunay triangulation; the depth and sample length of the virtual borehole is determined based on that of the existing geological borehole; and the midpoint of each sample length is extracted.
(2) The midpoint of each sample length in compliance with the cut-off grade in the original geological borehole data is extracted, and is used to the SVM training and testing, so as to obtain the optimal classification function to predict the mineral and rock information of each sample length of the virtual borehole. The detailed determination method is given in
Section 4 of this paper.
(3) The geological borehole data and the virtual borehole data constitute the borehole database; the borehole data are subject to sample length combination to form the ore block based on the cut-off grade, minimum mining thickness, band rejected thickness as well as the “low-grade ore to the delineation of ore body” thought; and the upper-lower demarcation point, i.e., the boundary point, of each ore block is extracted.
(4) Based on the boundary point so obtained as well as its corresponding borehole, the neighbour borehole of each borehole as well as its corresponding boundary point is obtained with the Delaunay triangulation; and the normal direction of such point is obtained with Principal Component Analysis (PCA) method. The normal direction of the upper boundary point of some borehole can be obtained by identifying the upper boundary point of its adjacent borehole with the PCA method. The detailed solving process is given in
Section 5 of this paper.
(5) The boundary points as well as their corresponding normal directions constitute the Hermite point cloud data set; and the implicit function equation for the three-dimensional mode for ore body is obtained through the interpolation approximation based on HRBF as well as accelerating the solving process based on the least-squares Householder-QR decomposition method [
30].
(6) The model space corresponding to the implicit function surface of the three-dimensional model for ore body is discretized with the MC algorithm [
31] and the vertex value of each cube discretized is calculated to extract the iso-surface, so as to finally build the three-dimensional model for the ore body.
(7) In case of any change in the cut-off grade or any new borehole data with the productive exploration, the above (3)–(6) will be re-executed to quickly realize the update of the three-dimensional model for the ore body.
4. Determination of the Virtual Borehole and Extraction of Its Boundary Point
For the geological borehole, there is high drilling cost and generally a long distance between two boreholes. According to the mathematical features of kernel function in the HRBF algorithm, the bigger the distance between two points is, the larger the kernel function value attenuation of the two points will be. In this case, there will be scattered ore body, with weak continuity. Therefore, in order to improve the continuity of the ore body model and ensure the accuracy of the ore body model, the virtual borehole [
32,
33] are added between boreholes, i.e., the position of the virtual borehole is determined with the Delaunay triangulation based on the original geological borehole and the mineral and rock information on the virtual borehole is obtained with the SVM classification method.
4.1. SVM Principle
The SVM (Support Vector Machines) [
34,
35,
36] mechanism is to find the optimal separating hyperplane in the sample characteristic space which not only meets the classification accuracy requirement, but also maximizes the classification interval. The optimal separating hyperplane so obtained is used to predict the unknown data.
The separating hyperplane is expressed as (w and b is respectively the normal vector and offset of the hyperplane). Suppose the given data set is , map the data from the low-dimensional sample space Rd to the high-dimensional characteristic space H, i.e., , choose a proper kernel function to make , and introduce the slack variable and penalty factor C.
For the SVM solution, the Lagrangian multiplier
as well as
is introduced to establish the Lagrangian function and transform the original convex quadratic programming problem into the dual problem, obtaining the optimal
and the support vector
S = {
i∣
αi > 0,
i = 1, 2, …,
n} in the original sample set. The optimal weight vector
and the optimal offset
are calculated. The optimal classification function is finally given as follows:
4.2. Determination of the Optimal Classification Function
(1) Determination of the Borehole Position
For the determination of the borehole position, the position of each original geological borehole is mapped onto the XY plane; the two-dimensional borehole point mapped onto the XY plane is subject to the Delaunay triangulation and the borehole index is established based on the structured grid relationship; after each triangular patch in the above Delaunay grid is traversed, the borehole positions corresponding to the three vertexes of the existing triangular patches are extracted. The position coordinates of the virtual borehole are the average coordinates of the three borehole points (
Figure 2).
(2) Sample Set Building
Before the SVM model training, the sample set is built based on the known boreholes around the virtual borehole. After the borehole position is determined, three boreholes corresponding to the existing virtual borehole to be solved as well as those connected to these three borehole points on the XY plane by the Delaunay side are extracted to constitute the adjacent borehole set D’ of the existing virtual borehole. The midpoint of the sample length of each borehole is taken as the sampling point. After the sampling points of each borehole in the set are traversed, the coordinate
x is extracted as the characteristic value. Tag y is set based on its grade value in accordance with Equation (9). Furthermore, in this paper, in order to improve the rate of convergence and classification accuracy of the SVM model during training and simplify the data inner product calculation, the characteristic values are mapped with the z-score standardized method to a range of [−1, +1]. The calculation equation is given as Equation (10).
In the above formula, and are respectively the feature vector before and after the normalization; is the sample mean; and is the sample standard deviation.
(3) SVM Training
Before training, the kernel function of the SVM model needs to be determined. The common kernel functions include the linear kernel function, polynomial kernel function, radial basis kernel function, Sigmoid kernel function, etc. The radial basis kernel function could implicitly transform the nonlinear data into the linear separable data in high-dimensional space, which greatly enhances the nonlinear data processing performance. Meanwhile, there are few parameters, reducing the model complexity [
37]. The radial basis kernel function is given as follows:
For the parameter
γ,
C+ and
C−, the grid search method [
38] is introduced. In each parameter range, the coarse search is first adopted, and the K-fold cross validation method is used to calculate the precision ratio (acc
+, acc
−) of positive and negative samples corresponding to each group of parameters. The geometric mean (g-means) of the two is taken as the evaluation criterion to further determine the local optimal parameter. The fine search is then adopted within the surrounding area to solve the optimal classification forecasting function.
4.3. Determination of the Virtual Borehole and Extraction of the Boundary Point
The mineral and rock information of each sample length of the existing virtual borehole is predicted in accordance with the optimal classification function solved in
Section 4.2 and the sample lengths are combined to form the ore block before the boundary point of each ore block is extracted. The detailed process is given as follows:
- (1)
Suppose the existing virtual borehole point coordinate is , the maximum hole depth is h and the sample length is l.
- (2)
Extract the midpoint of all sample lengths of the virtual borehole as the predicted sampling point in accordance with Equation (13), constituting the sampling point set to be measured
P.
where
pi is the midpoint coordinate of the sample length of the
i-th segment;
n is a natural number.
- (3)
Calculate the function value of each point in the point set P based on the optimal function solved. If less than 0, the point indicates rock, written as −1; otherwise, it indicates mineral, written as +1.
- (4)
Rank the points in the point set P from biggest to smallest in accordance with the Z coordinate value and combine the sample lengths of which the point is written as +1 to form the ore block in accordance with the constraint conditions, such as the minimum mining thickness and band rejected thickness.
- (5)
Extract the upper-lower demarcation point, i.e., the boundary point, of each ore block of the borehole to realize the extraction of the boundary point of the virtual borehole.
5. Point-Cloud Normal Vector Calculation
The normal direction information of the boundary point set is of vital importance for the implicit modeling of the ore body. It is not only a basic element of the HRBF algorithm, but also one of the important mediums for the control of the curved surface model. For surface reconstruction, the PCA (Principal Component Analysis) [
39] is generally adopted to calculate the point-cloud normal direction. However, for this method, the dense and uniform point cloud is the precondition, while the geological borehole is sparse and scattered, with a complex topological structure. Therefore, during the selection of neighbourhood points, there is often confusion, leading to the normal solution error. Although it is impossible to obtain the neighbourhood points with the conventional method, the borehole adjacent to that where this boundary point is located may be determined. Between adjacent boreholes, the corresponding neighbourhood points can be determined based on the corresponding relationship between the upper and lower boundary points and then the normal direction can be determined. Therefore, based on the PCA algorithm, this paper proposes the point-cloud normal direction calculation method based on the adjacent borehole. More details are given as follows:
- (1)
The boundary point as well as the data set {D1, D2, …, Dl} of the corresponding borehole is given, and the coordinates of opening point for each borehole is extracted and mapped onto the XY two-dimensional plane.
- (2)
As shown in
Figure 3, the two-dimensional borehole point is subject to the Delaunay triangulation; all points connected to the existing borehole points by the Delaunay side are defined as the neighbourhood points of the existing points and the corresponding borehole is the neighbourhood borehole. The neighbourhood borehole search tree is therefore established based on the structured grid relationship.
- (3)
All boreholes in the data set are traversed. For the existing borehole
Di, the neighbourhood borehole set is {
Dm}. As shown in
Figure 4, each boundary point
pj in the
Di is traversed. If the point is the upper boundary point, the upper boundary point of each borehole
Dm in the neighbourhood borehole set is extracted. If the number of the upper boundary points of
Dm is
n > 1, the dip angle of the rock stratum or ore body obtained during exploration is taken as the basis for the selection of the neighbourhood point, i.e., the boundary point
pj is connected to each upper boundary point of
Dm and the included angle of their respective projection line on the horizontal plane and the connection line to the boundary point is calculated. The upper boundary point nearest to the dip angle of the rock stratum or ore body is selected as the neighbourhood point of
pj. When
pj is the lower boundary point, it can be obtained in a similar way. The neighbourhood point set {
Ot} of each boundary point
pj in the
Di is therefore obtained.
- (4)
As shown in
Figure 5, two adjacent boundary points
Oi and
Oi+1 are taken from the {
Ot} and the local plane is solved based on the three points of {
pj,
Oi,
Oi+1}, and finally the normal direction set
n of the local plane is obtained.
- (5)
The set for normal n is traversed. If the current normal direction is ni, the next is nj. If , nj is inverted.
- (6)
All normal averages in the set n are the normal N of pj.
6. Experiments and Results
The VC++ development tools are used for the secondary development on the DIMINE three-dimensional mining software platform, with the experiment operating environment of Windows7, CPU of Intel (R) Core (TM) i5-4590
[email protected] and memory of 8GB. The mine engineering cases I and II are subject to the ore body modeling experiment.
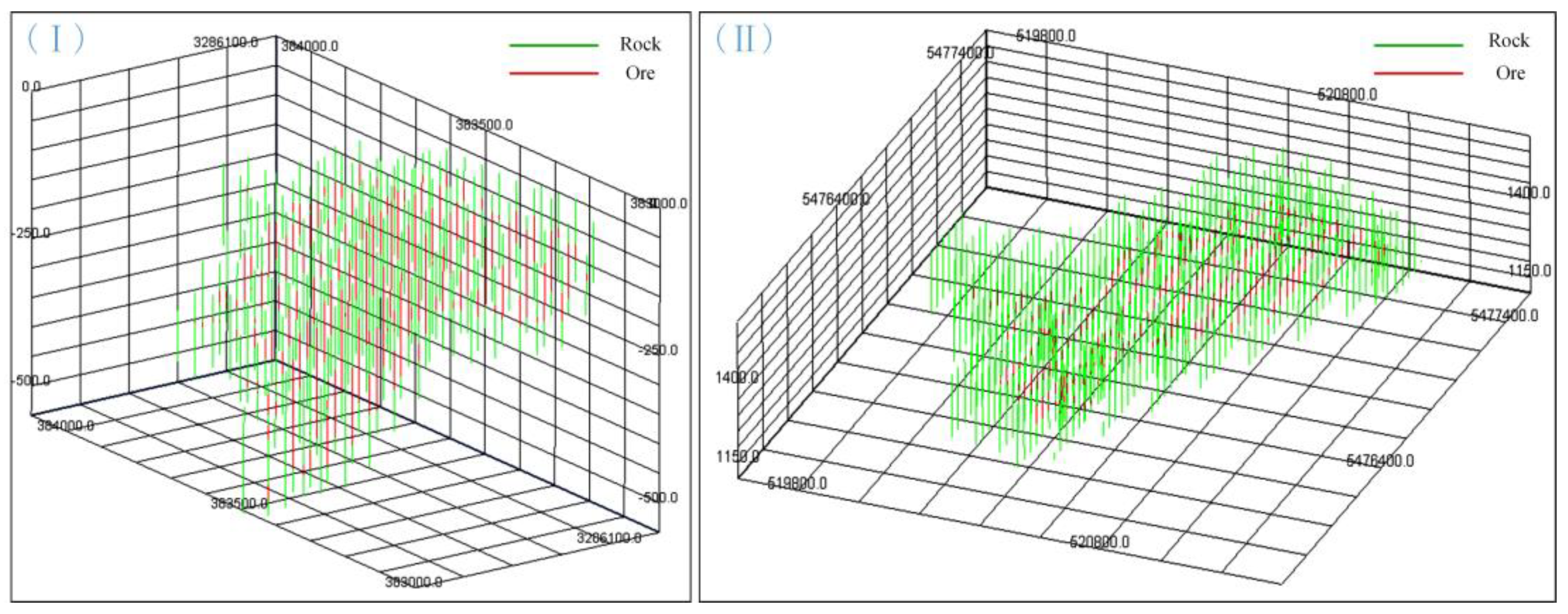
Figure 6 shows the borehole data of Case I and Case II, including the geological borehole and virtual borehole, where the red line segment represents the mineral that is higher than the cut-off grade and the green part represents the rock that is lower than the cut-off grade.
Figure 7 shows the boundary point cloud extracted based on the borehole data for Case I and Case II as well as the point-cloud normal direction calculated based on the adjacent borehole method, where the blue line represents the point-cloud normal direction.
Figure 8 shows the automatic modeling rendering based on HRBF for Case I and Case II, respectively including 101,465 and 7,982 triangular patches, with smooth and natural surface and high geometric quality. For Case I and Case II, the solving time for the HRBF coefficient matrix based on the Householder-QR decomposition is about 1s.
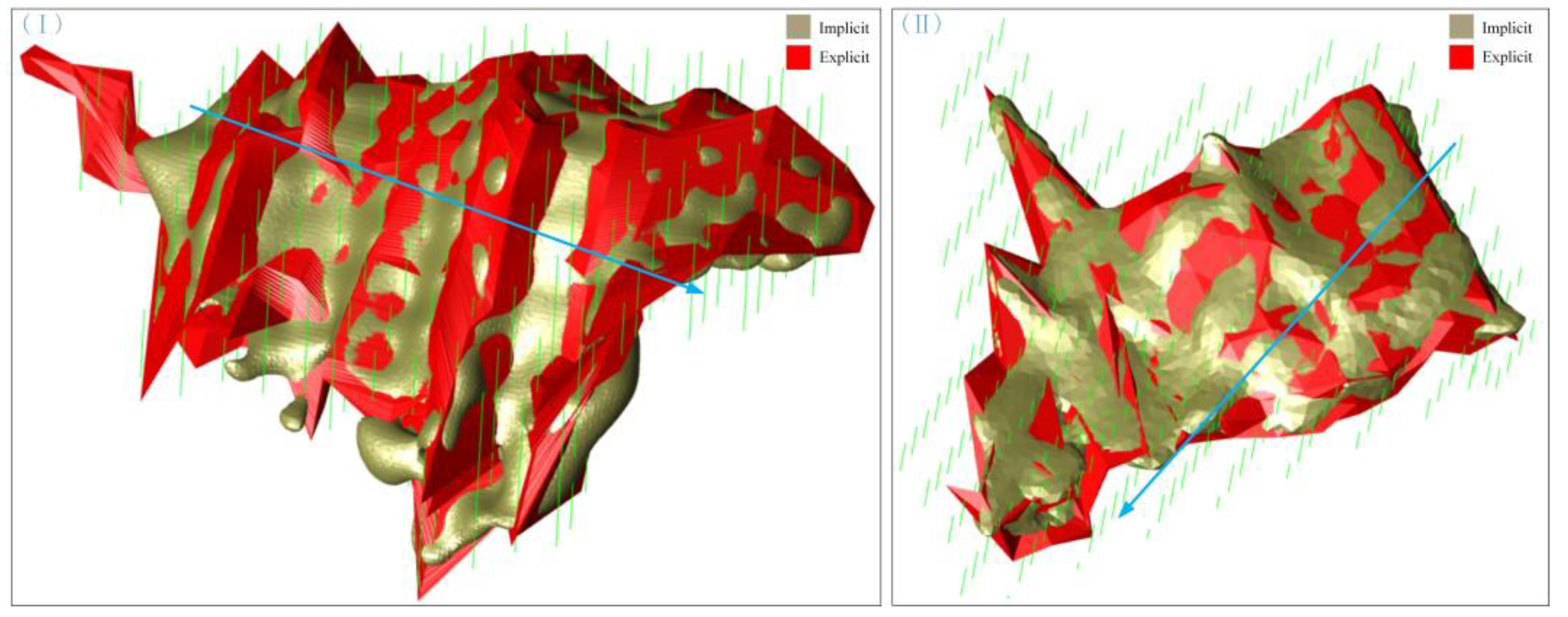
Figure 9 shows the three-dimensional model explicitly built with the contour tiling approach as well as the man-machine interaction mode based on the ore body contour line after geological interpretation for Case I and Case II. The comparison between
Figure 8 and
Figure 9 shows that the explicit ore body model is characterized by a rough surface, sharp edges, unsatisfactory visualization effects, etc., while the implicit model is obviously more natural and smoother. The implicit model for ore body in
Figure 8 and the explicit model in
Figure 9 are overlapped and shown in
Figure 10. The ore body model so overlapped and shown in
Figure 10 is sectioned in any direction, where the blue arrow direction is the sectioning direction. The ore body contour line so obtained is shown in
Figure 11. From
Figure 10 and
Figure 11, we can see that the implicit model automatically built based on HRBF and the explicit model built based on the contour tiling approach are basically the same; however, there is still a certain difference between boreholes as well as the boundary part. The main reason is that there is estimation to some extent during the explicit modeling in combination with the experience of the prospectors and geologists, while the implicit model is obtained with the spatial interpolation method. Therefore, with the ore body contour line unchanged, affected by specialized knowledge and experience, the explicit models built by different modellers are inconsistent; while with the geological and virtual borehole data and radial function unchanged, the implicit models finally built are the same. Furthermore, as the productive exploration data increase or the cut-off grade changes, the model needs continuous update. Obviously, it is quite difficult for the explicit modeling based on the contour tiling approach, while for the automatic implicit modeling based on HRBF, only the spatial interpolation and visualization again are needed, guaranteeing fast update speed and a high degree of automation.
7. Discussion
In order to realize the automatic building and quick update of the three-dimensional model for the ore body, first of all, the HRBF algorithm is used as the core of 3D implicit modeling of the ore body. Secondly, the Delaunay triangulation and SVM algorithm are introduced to determine the virtual borehole position and the mineral and rock information. Thirdly, the adjacent borehole method based on the PCA algorithm is proposed to calculate the point-cloud normal direction. Fourthly, this paper accelerates the solution of the HRBF coefficient matrix by use of the least-squares Householder-QR method and adopts the MC algorithm for the discretization of the modeling space and the iso-surface extraction to visualize the 3D model of the ore body. Finally, the verification through two engineering cases and the comparison with the explicit modeling results show that the models built through the two methods are basically consistent.
Due to the sparse and scattered geological borehole data, the bigger the distance between the boundary points of two adjacent boreholes is, the faster the attenuation of the kernel function value in the HRBF will be. Especially for the ore body with the large fluctuation of the form or narrow vein, there might be scattered distribution and weak continuity.
Figure 12 shows an extremely thin ore body area in the west (Case I).
Figure 12a shows the point cloud as well as its normal direction, indicating that the boundary point of the west is far away from the midpoint. The implicit model built with the approach given in this paper is shown in
Figure 12b, where the two isolated points along the boundary are directly pinched out. The comparison between the explicit model built based on the contour line and the implicit model built with the approach under this paper is shown in
Figure 12c. Therefore, in case of a bigger distance between the boundary points, a large fluctuation of the form of the ore body, narrow vein, etc., the building of the ore body model with satisfactory continuity and higher degree of accuracy requires the borehole data densification based on the Delaunay and SVM algorithm.
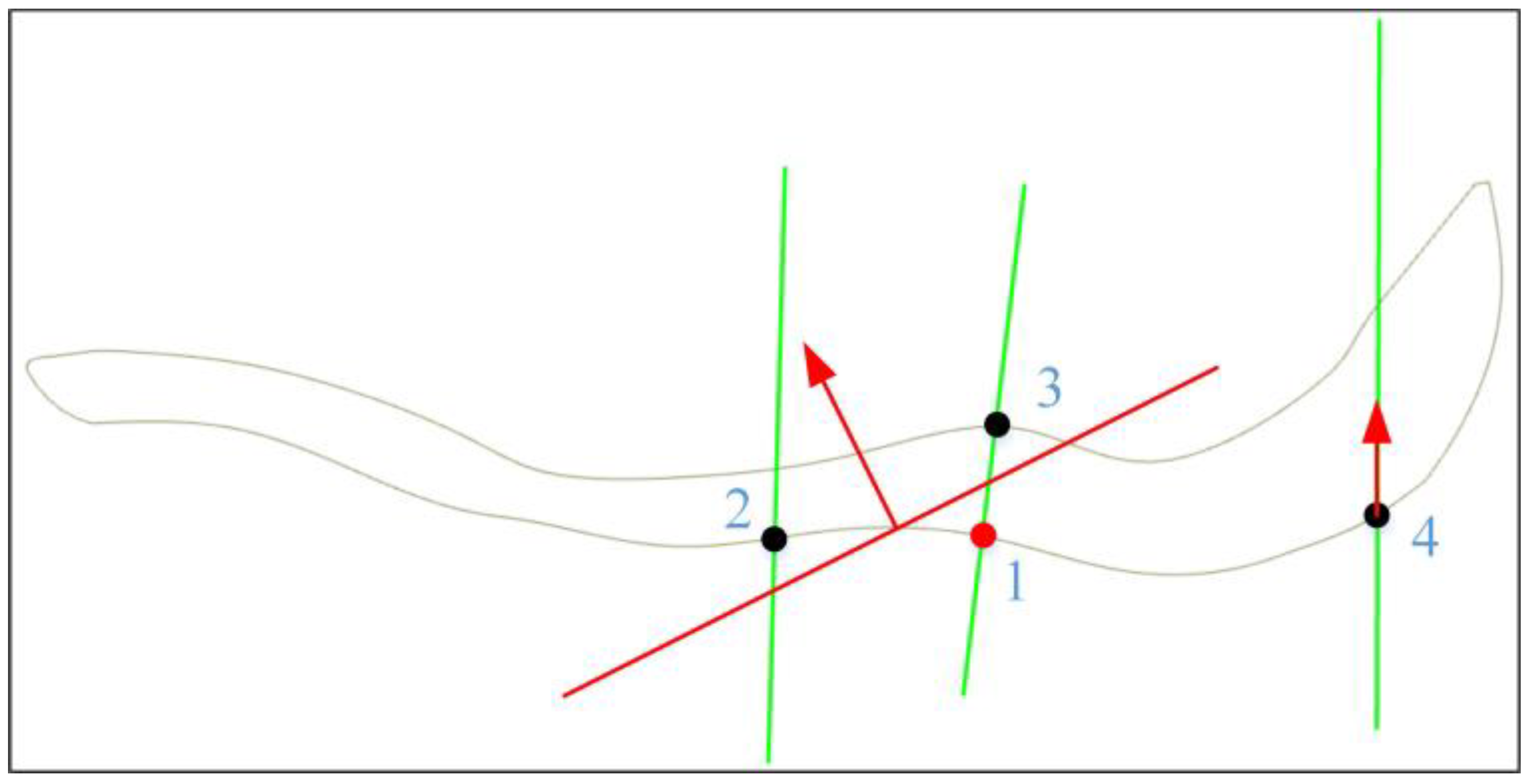
The solution of the implicit surface equation with the HRBF algorithm requires the solution of the normal direction of the boundary point. However, the boundary points between the boreholes are quite sparsely distributed. When the thickness of the ore body is smaller than the distance between the boreholes, the traditional PCA method is used for solving, with the neighbourhood points solved including the boundary points of the same borehole, which will lead to the normal solution error. As shown in
Figure 13, for the solution of the normal direction of Point 1, the PCA method is introduced, with Point 2 and Point 3 selected as the neighbourhood points, and the normal direction of Point 1 so obtained is roughly the red arrow direction in the middle of Point 1, Point 2 and Point 3, which is obviously incorrect. When solving the point-cloud normal direction, Jiateng et al. [
25] directly took the unit vector pointing to high grade in the drilling direction of the point as the normal direction of this point (Point 4 in
Figure 13). Obviously, it is incorrect to take the red arrow direction at Point 4 as its normal direction. Therefore, based on the PCA algorithm, this paper proposes the point-cloud normal vector calculation on the basis of the adjacent borehole. As shown in
Figure 13, for the solution of the normal direction of the Lower Boundary Point 1, the adjacent borehole of the borehole where Point 1 is located may be first identified and then the Lower Boundary Point 2 and 4 of the adjacent borehole may be correspondingly identified. Finally, the normal direction of Point 1 can be accurately calculated.
Despite certain research achievements in the borehole densification, point-cloud normal direction calculation as well as the automatic building of three-dimensional model for ore body in this paper, the following three aspects still need to be considered for improvement and further research: (1) Due to the relatively large computer resources consumed by 3D interpolation, it usually leads to a high computational cost. This paper has used the least squares Householder-QR decomposition method to perform matrix decomposition and achieve certain effects. However, the HRBF algorithm can still be optimized and other methods and techniques such as parallel computing can be used to reduce the computational cost and speed up the calculation time. (2) During the implicit modeling, the solution of the implicit function equation is one of the key problems, however, subject to the sparse borehole data, there is insufficient data set available for calculation, which lowers the quality and precision of the implicit surface. Although the virtual borehole may be introduced for data densification, the interpolation algorithm commonly used will produce new errors in the system. Meanwhile, the interpolation algorithm consumes relatively more computing resources. Therefore, the transformation of the space where the point cloud data is may be considered. For example, the compression, rotation, function mapping, etc. may be introduced to reduce the distance between data and finally restore the model calculated reversely to the original space. (3) The implicit surface building is obtained based on the original data interpolation, which only considers its mathematical characteristics but neglects the geological information contained in the geological exploration data. In this case, the model so built sometimes fails to meet the actual requirements. Due to the quick update of the implicit modeling, the priori geological knowledge from geologist may be properly introduced during the modeling and quantized into the corresponding geometric constraints, such as the point, line and surface so added, so as to better control the geometrical morphology of the ore body and ensure the three-dimensional model so built for the ore body could better satisfy the actual requirements.
8. Conclusions
In this paper, the Hermite radial basis function is used to directly interpolate the boundary points of the geological borehole data and its normal direction to realize the construction of the implicit 3D model of the ore body. On this basis, the paper also improves in the following aspects: First, the combination of Delaunay triangulation and SVM is used to increase the virtual borehole to improve the fit of the scarce sampling area. Second, the adjacent borehole method based on the PCA algorithm is proposed to calculate the normal vector direction of the boundary point accurately. Final, the least squares Householder-QR method is used to speed up the solution, and Marching Cubes (MC) is used to visualize the implicit 3D model of the ore body. The method has a high degree of automation, high geometrical quality of the model and fast update speed. Therefore, it has certain guiding significance and practical value for the construction of the ore body three-dimensional model.