Rock Sample Surface Preparation Influences Thermal Infrared Spectra
Abstract
:1. Introduction
Surface Roughness and Reflectivity of Light
2. Materials and Methods
2.1. Sample Description
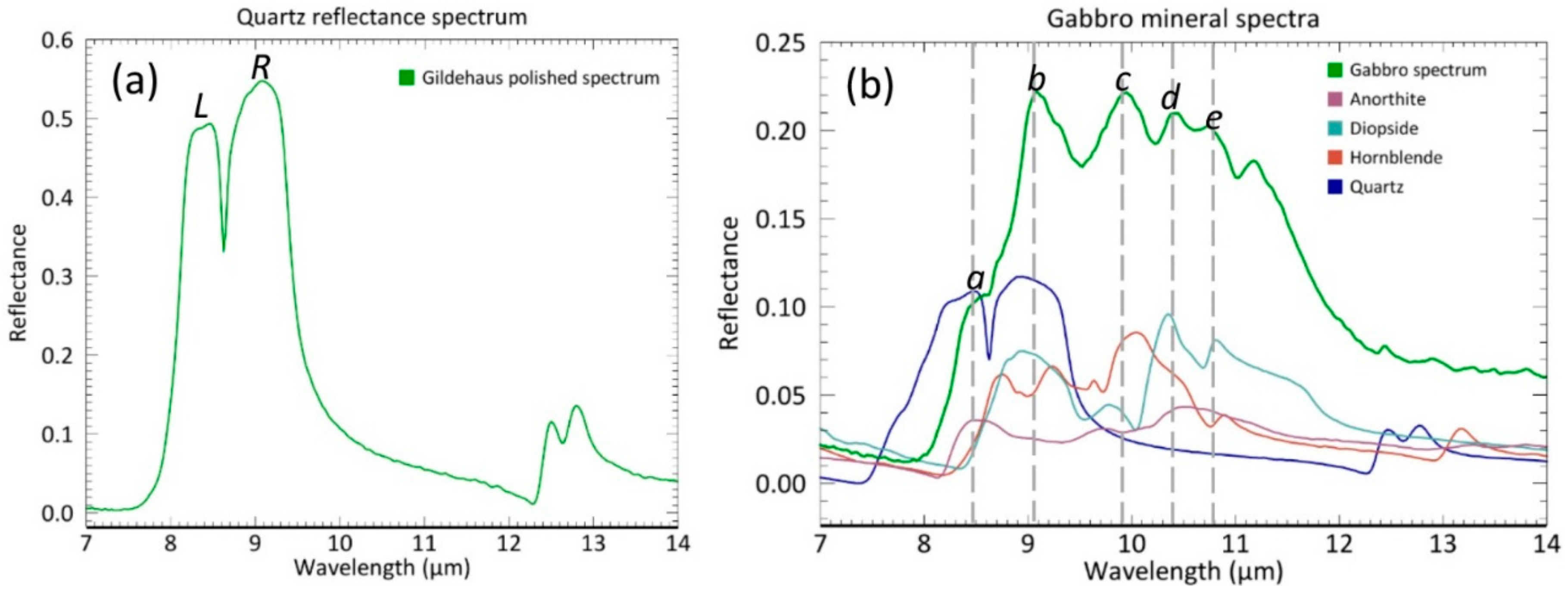
2.1.1. Sample Selection
2.1.2. Sample Preparation
2.2. Spectral Measurements and Data Processing
2.2.1. Directional-Hemispherical Reflectance (DHR) Measurements
2.2.2. Bidirectional Reflectance (BDR) Images
2.2.3. Emissivity Measurements
2.3. Surface Analyses
2.3.1. Scanning Electron Microscopy (SEM)
2.3.2. Profilometer Measurements
- The arithmetic average roughness (Ra): the arithmetical mean of the absolute values of the profile deviations from the mean line of the roughness profile;
- The root-mean-square roughness (Rq): the geometric average roughness of the area;
- The maximum peak height (Rp): the highest peak measured from the mean line;
- The maximum valley depth (Rv): the deepest valley measured from the mean line; and
- The maximum height of profile (Rt): the range of the total set of data points.
2.4. X-ray Diffraction
3. Results
3.1. Spectral Measurements
3.1.1. Directional-Hemispherical Reflectance (DHR) Spectra
3.1.2. Bidirectional Reflectance (BDR) Images
- For the Gildehaus sandstone: Highest spectral contrast for the sawed surface, followed by the split and the polished surface.
- For the Fontainebleau sandstone: An equal spectral contrast for the sawed and the split surface followed by the polished surface.
- For the Gabbro: The highest spectral contrast for the split surface, followed by the sawed and the polished surface.
3.1.3. Emissivity Spectra
3.2. Surface Analyses
3.2.1. Scanning Electron Microscopy
3.2.2. Profilometer Analyses
4. Discussion
4.1. Influence of Sample Preparation Method on Spectral Contrast
4.2. Influence of Sample Preparation Method on Spectral Shape
4.3. Practical Implications
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lyon, R.J.P.; Tuddenham, W.M.; Thompson, C.S. Quantitative mineralogy in 30 minutes. Econ. Geol. 1959, 54, 1047–1055. [Google Scholar] [CrossRef]
- Lyon, R.J.P.; Burns, E.A. Analysis of rocks and minerals by reflected infrared radiation. Econ. Geol. 1963, 58, 274–284. [Google Scholar] [CrossRef]
- Hunt, G.R. Visible and near-infrared spectra of minerals and rocks: I silicate minerals. Mod. Geol. 1970, 1, 283–300. [Google Scholar]
- Hunt, G.R.; Salisbury, J.W.; Lenhoff, C.J. Visible and near infrared spectra of minerals and rocks: IX. Basic and ultrabasic igneous rocks. Mod. Geol. 1974, 5, 15–22. [Google Scholar]
- Hunt, G.R.; Salisbury, J.W. Mid-Infrared Spectral Behavior of Metamorphic Rocks; Air Force Cambrigde Research Labs Hanscom AFB: Bedford MA, USA, 1976. [Google Scholar]
- Lyon, R.J.P. Analysis of rocks by spectral infrared emission (8 to 25 microns). Econ. Geol. 1965, 60, 715–736. [Google Scholar] [CrossRef]
- Vincent, R.K.; Hunt, G.R. Infrared reflectance from mat surfaces. Appl. Opt. 1968, 7, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Riley, D.N.; Hecker, C.A. Mineral mapping with airborne hyperspectral thermal infrared remote sensing at Cuprite, Nevada, USA. In Thermal Infrared Remote Sensing; Springer: Dordrecht, The Netherlands, 2013; pp. 495–514. [Google Scholar]
- Kuosmanen, V.; Arkimaa, H.; Tiainen, M.; Bärs, R. Hyperspectral close-range LWIR imaging spectrometry–3 case studies. In Geophysical Signatures of Mineral Deposit Types in Finland; Airo, M.-L., Ed.; Geological Survey of Finland: Espoo, Finland, 2015; Volume 58, pp. 117–144. [Google Scholar]
- Martini, B.A. Personal communication 2017. Corescan Pty Ltd.: Denver, CO, USA.
- Salisbury, J.W.; Walter, L.S. Thermal infrared (2.5–13.5 µm) spectroscopic remote sensing of igneous rock types on particulate planetary surfaces. J. Geophys. Res. Solid Earth 1989, 94, 9192–9202. [Google Scholar] [CrossRef]
- Lyon, R.J.P. Evaluation of infrared Spectrophotometry for Composition Analysis Lunar and Planetary Soils: Rough and Powdered Surfaces; Stanford Research Institute: Menlo Park, CA, USA, 1964; Part I1, Contract NASR 49. [Google Scholar]
- Hunt, G.R.; Logan, L.M. Variation of single particle mid-infrared emission spectrum with particle size. Appl. Opt. 1972, 11, 142–147. [Google Scholar] [CrossRef] [PubMed]
- Salisbury, J.W.; Eastes, J.W. The effect of particle size and porosity on spectral contrast in the mid-infrared. Icarus 1985, 64, 586–588. [Google Scholar] [CrossRef]
- Salisbury, J.W.; Walter, L.S.; Vergo, N. Mid-Infrared (2.1–25 um) Spectra of Minerals; US Geological Survey: Reston, VA, USA, 1987; pp. 87–263. [Google Scholar]
- Salisbury, J.W.; D’Aria, D.M. Emissivity of terrestrial materials in the 3–5 μm atmospheric window. Remote Sens. Environ. 1994, 47, 345–361. [Google Scholar] [CrossRef]
- Schodlok, M.C.; Whitbourn, L.; Huntington, J.; Mason, P.; Green, A.; Berman, M.; Coward, D.; Conner, P.; Wright, W.; Jolivet, M.; et al. HyLogger-3, A visible to shortwave and thermal infrared reflectance spectrometer system for drill core logging: Functional description. Aust. J. Earth Sci. 2016, 63, 929–940. [Google Scholar]
- Hardgrove, C.J.; Rogers, A.D.; Glotch, T.D.; Arnold, J.A. Thermal emission spectroscopy of microcrystalline sedimentary phases: Effects of natural surface roughness on spectral feature shape. J. Geophys. Res. Planets 2016, 121, 542–555. [Google Scholar] [CrossRef]
- Kirkland, L.; Herr, K.; Keim, E.; Adams, P.; Salisbury, J.; Hackwell, J.; Treiman, A. First use of an airborne thermal infrared hyperspectral scanner for compositional mapping. Remote Sens. Environ. 2002, 80, 447–459. [Google Scholar] [CrossRef] [Green Version]
- Ramsey, M.S.; Fink, J.H. Estimating silicic lava vesicularity with thermal remote sensing: A new technique for volcanic mapping and monitoring. Bull. Volcanol. 1999, 61, 32–39. [Google Scholar] [CrossRef]
- Osterloo, M.M.; Hamilton, V.E.; Anderson, F.S. A laboratory study of the effects of roughness on the thermal infrared spectra of rock surfaces. Icarus 2012, 220, 404–426. [Google Scholar] [CrossRef]
- Bedford, R.E.; Ma, C.K.; Chu, Z.; Sun, Y.; Chen, S. Emissivities of diffuse cavities. 4: Isothermal and nonisothermal cylindro-inner-cones. Appl. Opt. 1985, 24, 2971–2980. [Google Scholar] [CrossRef] [PubMed]
- Giancoli, D.C. Physics: Principles with Applications; Pearson: Nerw York, NY, USA, 2005. [Google Scholar]
- Kirkland, L.E.; Herr, K.C.; Adams, P.M. Infrared stealthy surfaces: Why TES and THEMIS may miss some substantial mineral deposits on Mars and implications for remote sensing of planetary surfaces. J. Geophys. Res. Planets 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Aronson, J.R.; Emslie, A.G. Spectral reflectance and emittance of particulate materials. 2: Application and results. Appl. Opt. 1973, 12, 2573–2584. [Google Scholar] [CrossRef] [PubMed]
- Salisbury, J.W.; Wald, A. The role of volume scattering in reducing spectral contrast of reststrahlen bands in spectra of powdered minerals. Icarus 1992, 96, 121–128. [Google Scholar] [CrossRef]
- Salisbury, J.W.; Wald, A.; D’Aria, D.M. Thermal-infrared remote sensing and Kirchhoff’s law: 1. Laboratory measurements. J. Geophys. Res. Solid Earth 1994, 99, 11897–11911. [Google Scholar] [CrossRef]
- Fraden, J. AlP Handbook of Modern Sensors; American Institute of Physics, Springer: New York, NY, USA, 1993. [Google Scholar]
- Hapke, B. Theory of Reflectance and Emittance Spectroscopy; Cambridge University Press: Cambrige, UK, 1993. [Google Scholar]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER Spectral Library Version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Salisbury, J.W.; D’Aria, D.M. Emissivity of terrestrial materials in the 8–14 μm atmospheric window. Remote Sens. Environ. 1992, 42, 83–106. [Google Scholar] [CrossRef]
- Bourbie, T.; Zinszner, B. Hydraulic and acoustic properties as a function of porosity in Fontainebleau sandstone. J. Geophys. Res. Solid Earth 1985, 90, 11524–11532. [Google Scholar] [CrossRef]
- Reyer, D.; Philipp, S.L. Empirical relations of rock properties of outcrop and core samples from the Northwest German Basin for geothermal drilling. Geotherm. Energy Sci. 2014, 2, 21–37. [Google Scholar] [CrossRef] [Green Version]
- Hecker, C.; Hook, S.; Meijde, M.V.D.; Bakker, W.; Werff, H.V.D.; Wilbrink, H.; van Ruitenbeek, F.; de Smeth, B.; van der Meer, F. Thermal infrared spectrometer for earth science remote sensing applications—Instrument modifications and measurement procedures. Sensors 2011, 11, 10981–10999. [Google Scholar] [CrossRef] [PubMed]
- Hecker, C.; Dilles, J.H.; Meijde, M.; Meer, F.D. Thermal infrared spectroscopy and partial least squares regression to determine mineral modes of granitoid rocks. Geochem. Geophys. Geosyst. 2012, 13. [Google Scholar] [CrossRef] [Green Version]
- Korb, A.R.; Dybwad, P.; Wadsworth, W.; Salisbury, J.W. Portable Fourier transform infrared spectroradiometer for field measurements of radiance and emissivity. Appl. Opt. 1996, 35, 1679–1692. [Google Scholar] [CrossRef] [PubMed]
- Reichelt, R. Scanning electron microscopy. In Science of Microscopy; Springer: New York, NY, USA, 2007; pp. 133–272. [Google Scholar]
- Dong, W.P.; Sullivan, P.J.; Stout, K.J. Comprehensive study of parameters for characterizing three-dimensional surface topography: IV: Parameters for characterizing spatial and hybrid properties. Wear 1994, 178, 45–60. [Google Scholar] [CrossRef]
- Dinnebier, R.E.; Billinge, S.J.L. (Eds.) Powder Diffraction: Theory and Practice; Royal Society of Chemistry: London, UK, 2008. [Google Scholar]
- Larson, A.C.; Von Dreele, R.B. Gsas. General Structure Analysis System; LANSCE: Los Alamos, NM, USA, 1994. [Google Scholar]
- Toby, B.H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 2001, 34, 210–213. [Google Scholar] [CrossRef]
- Hunt, S.D.; Sierra, H. Spectral oversampling in hyperspectral imagery. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery IX. Int. Soc. Opt. Photonics 2003, 5093, 643–651. [Google Scholar]
- Maturilli, A.; Helbert, J.; Ferrari, S.; D’Amore, M. On the effect of emergence angle on emissivity spectra: Application to small bodies. Earth Planets Space 2016, 68, 84. [Google Scholar] [CrossRef]
- Mustard, J.F.; Hays, J.E. Effects of hyperfine particles on reflectance spectra from 0.3 to 25 μm. Icarus 1997, 125, 145–163. [Google Scholar] [CrossRef]









| Sample | Mineral | Composition |
|---|---|---|
| Fontainebleau | Quartz | 100% |
| Gildehaus | Quartz | 99% |
| Kaolinite | 1% | |
| Gabbro | Anorthite | 57% |
| Diopside | 28% | |
| Quartz | 6% | |
| Hornblende | 6% | |
| Zoisite | 1% | |
| Biotite | 0.08% | |
| Ilmenite | 0.03% |
| Polished | Sawed | Split | |
|---|---|---|---|
| Gildehaus | 0.54 | 0.45 | 0.39 |
| Fontainebleau | 0.70 | 0.54 | 0.62 |
| Gabbro | 0.22 | 0.17 | 0.16 |
| Polished | Sawed | Split | |
|---|---|---|---|
| Gildehaus | 0.37 | 0.47 | 0.42 |
| Fontainebleau | 0.37 | 0.45 | 0.43 |
| Gabbro | 0.07 | 0.12 | 0.23 |
| Polished | Sawed | Split | |
|---|---|---|---|
| Gildehaus | 0.36 | 0.50 | 0.51 |
| Fontainebleau | 0.32 | 0.35 | 0.24 |
| Gabbro | 0.75 | 0.81 | 0.81 |
| Gildehaus | Fontainebleau | Gabbro | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pol | Saw | Split | Pol | Saw | Split | Pol | Saw | Split | |||
| Ra | 20.5 | 11.2 | 32.4 | Ra | 17.3 | 33.1 | 18.3 | Ra | 28.9 | 28.9 | 144.1 |
| Rq | 22.9 | 17.1 | 50.1 | Rq | 21.1 | 39.5 | 35.1 | Rq | 34.3 | 35.1 | 200.7 |
| Rp | 51.5 | 93.3 | 559.7 | Rp | 27.3 | 115.6 | 361.5 | Rp | 68.6 | 72.2 | 1061.0 |
| Rv | −113.2 | −103.4 | −186.2 | Rv | −106.9 | −88.0 | −141.0 | Rv | −83.1 | −81.9 | −223.1 |
| Rt | 164.7 | 196.7 | 745.9 | Rt | 134.3 | 203.6 | 502.5 | Rt | 151.7 | 154.0 | 1284.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rost, E.; Hecker, C.; Schodlok, M.C.; Van der Meer, F.D. Rock Sample Surface Preparation Influences Thermal Infrared Spectra. Minerals 2018, 8, 475. https://doi.org/10.3390/min8110475
Rost E, Hecker C, Schodlok MC, Van der Meer FD. Rock Sample Surface Preparation Influences Thermal Infrared Spectra. Minerals. 2018; 8(11):475. https://doi.org/10.3390/min8110475
Chicago/Turabian StyleRost, Evelien, Christoph Hecker, Martin C. Schodlok, and Freek D. Van der Meer. 2018. "Rock Sample Surface Preparation Influences Thermal Infrared Spectra" Minerals 8, no. 11: 475. https://doi.org/10.3390/min8110475
APA StyleRost, E., Hecker, C., Schodlok, M. C., & Van der Meer, F. D. (2018). Rock Sample Surface Preparation Influences Thermal Infrared Spectra. Minerals, 8(11), 475. https://doi.org/10.3390/min8110475





