Hydrodynamic and Flotation Kinetic Analysis of a Large Scale Mechanical Agitated Flotation Cell with the Typical Impeller and the Arc Impeller
Abstract
:1. Introduction
2. Model Description
2.1. Hydrodynamic Numbers of Flotation Cells
2.2. Flotation Kinetics
2.3. Geometry and CFD Model
3. Results and Discussion
3.1. Hydrodynamics of the Large Flotation Cell
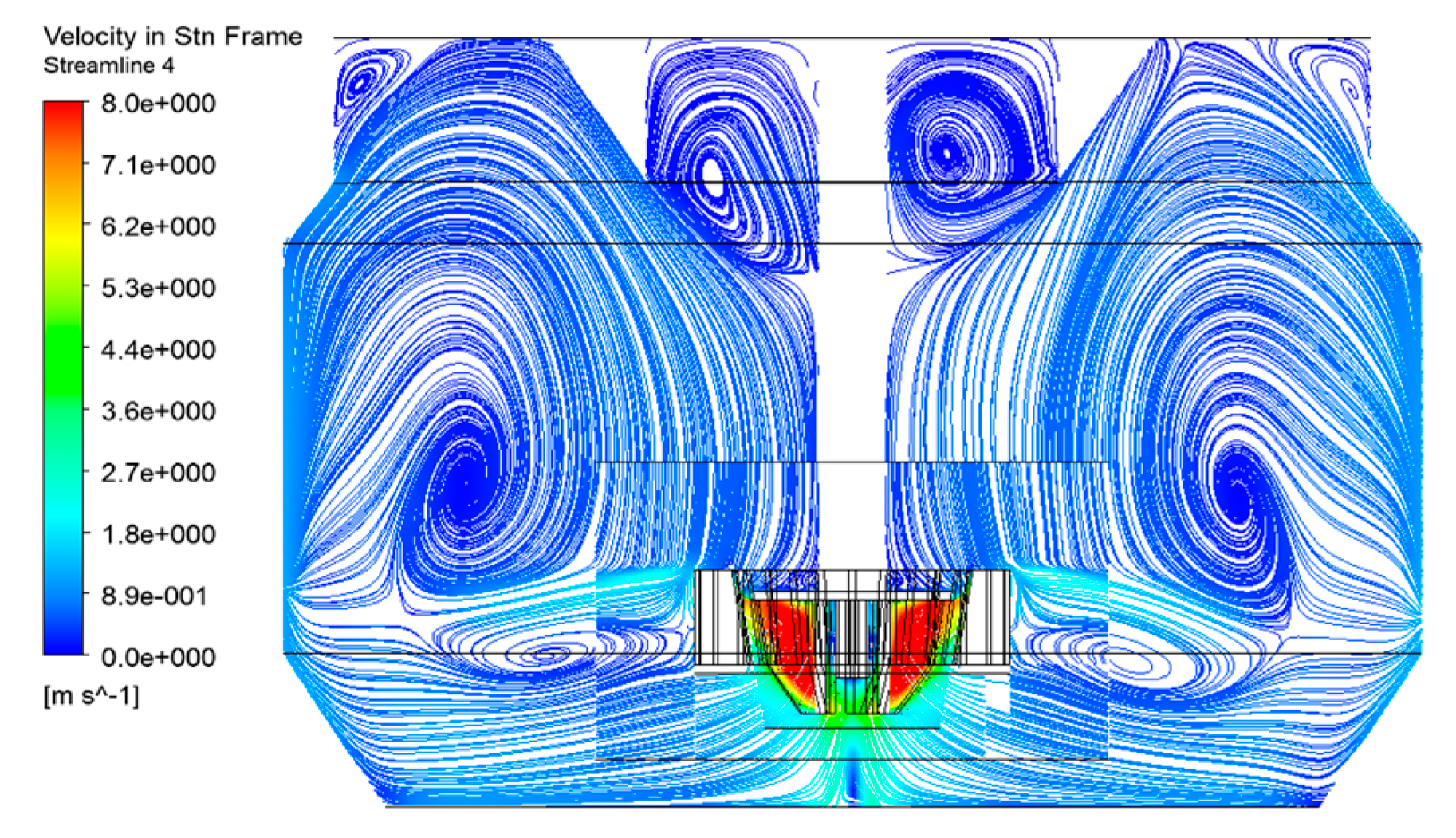
3.1.1. Flow Pattern
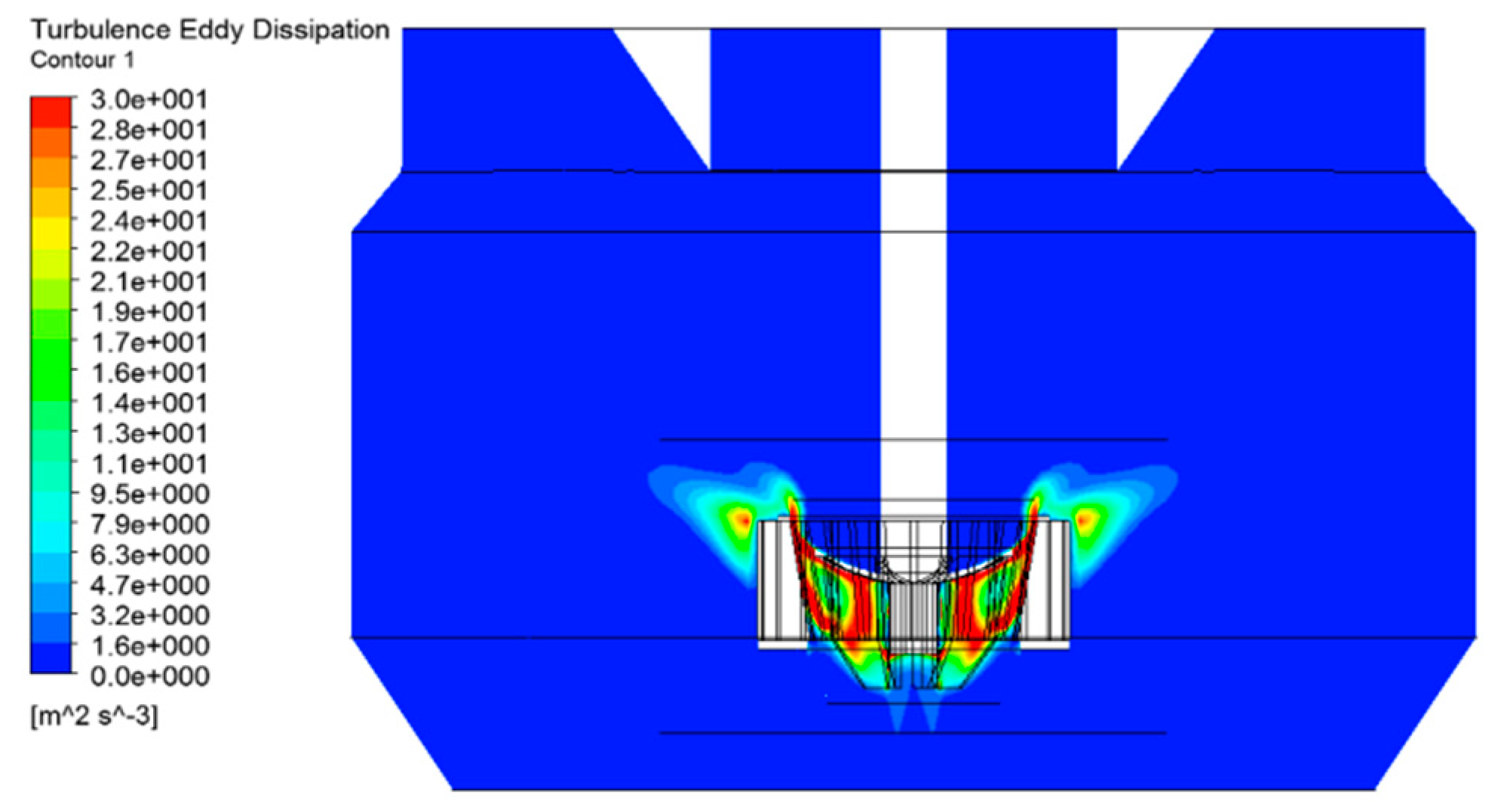
3.1.2. Gas Dispersion and Solid Suspension
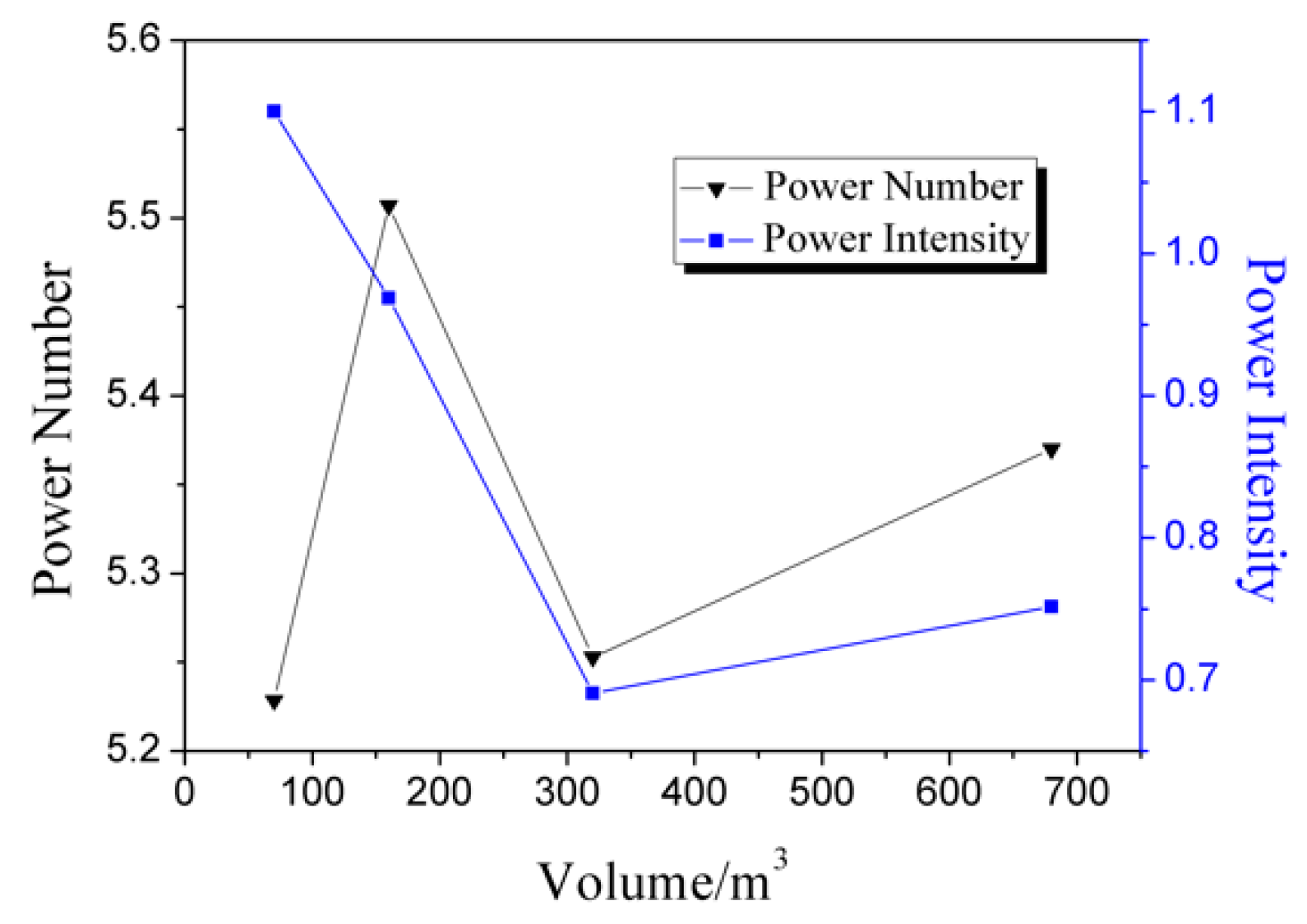
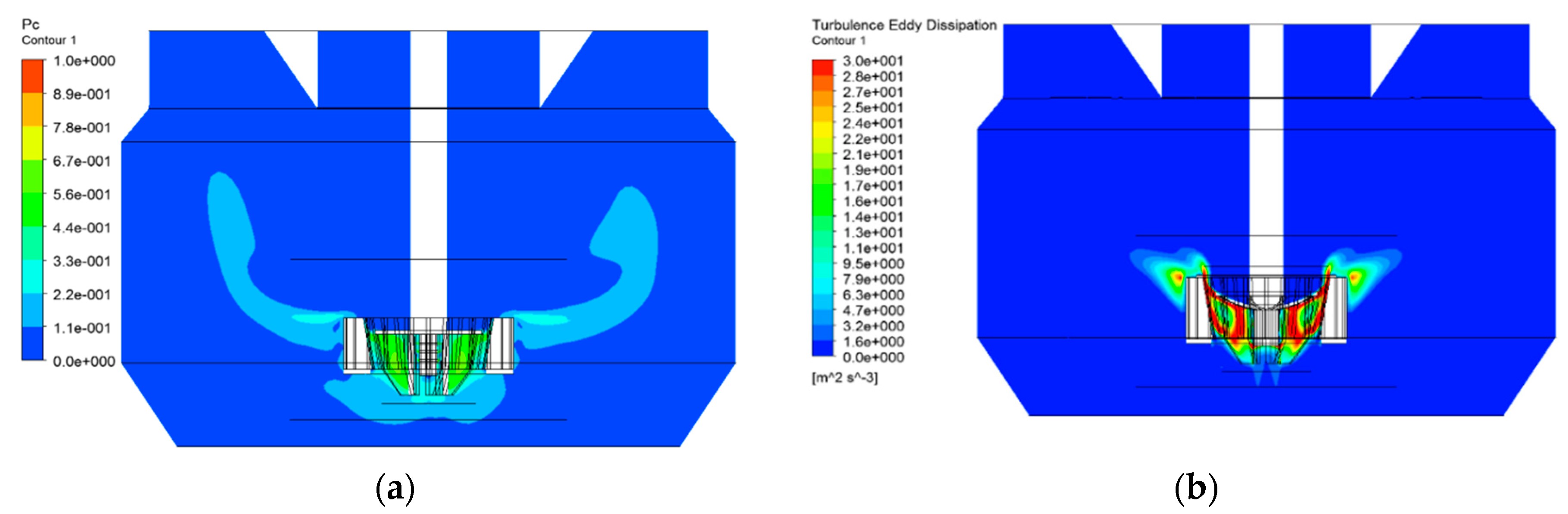
3.1.3. Analysis of Hydrodynamics Performances
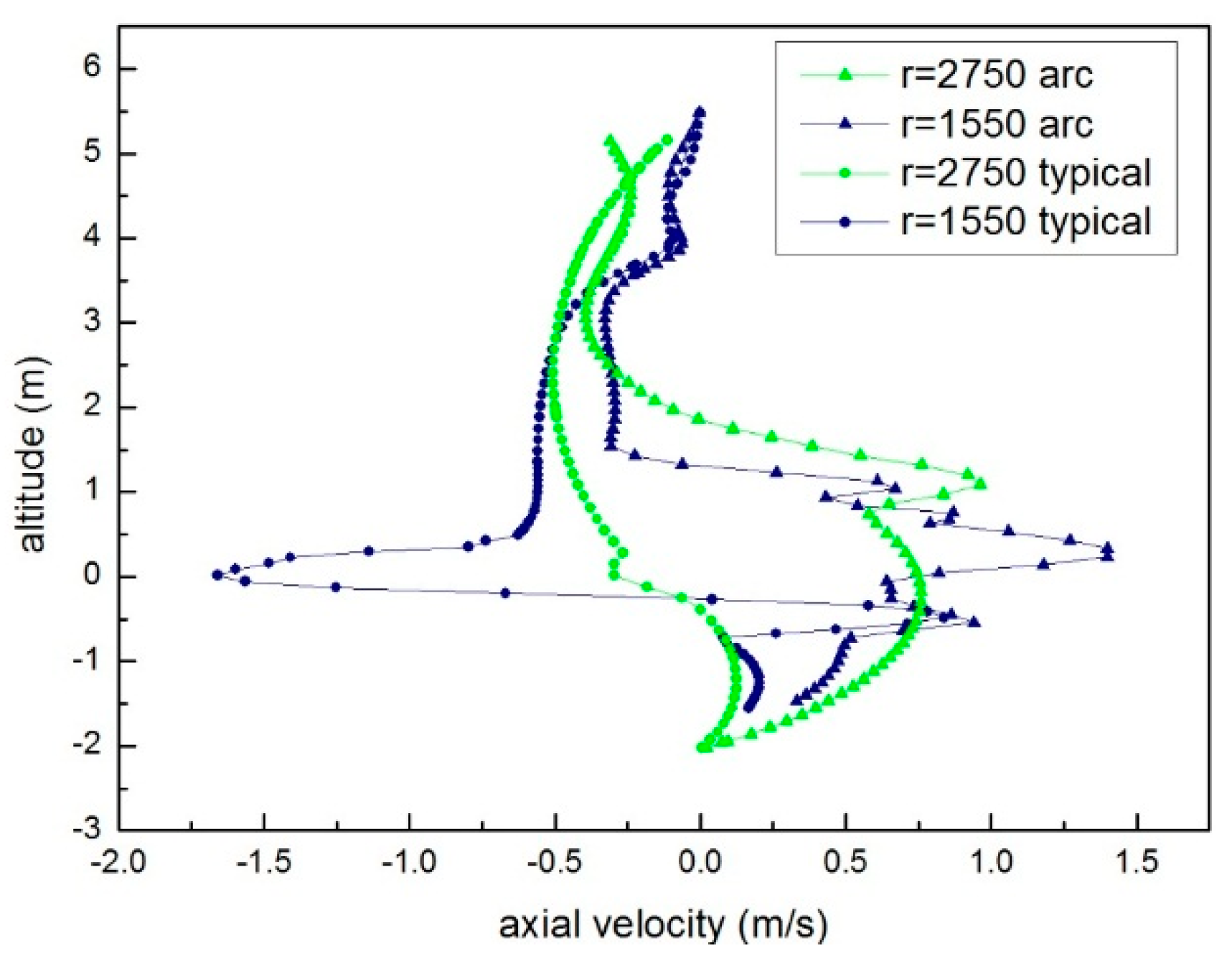
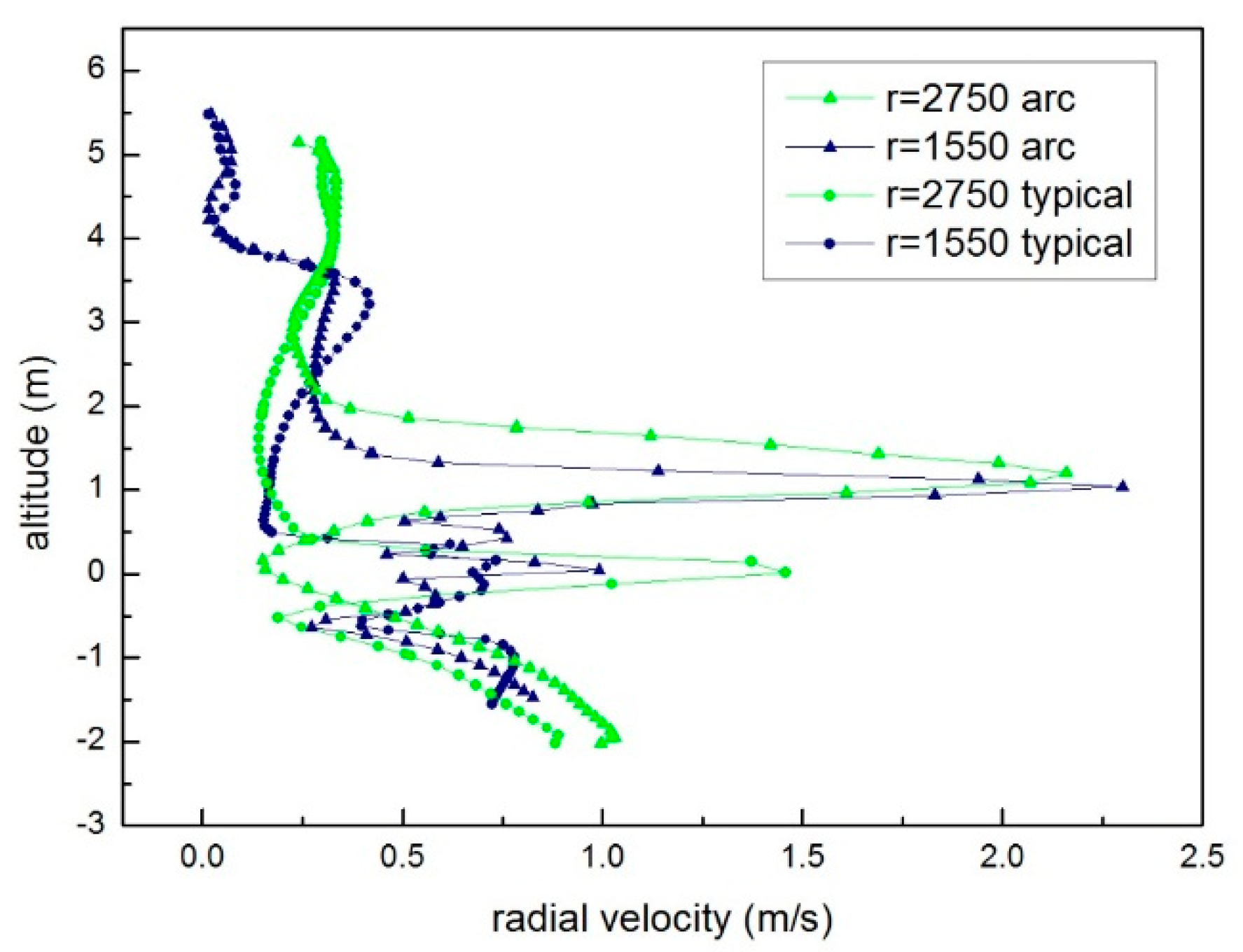
3.2. Comparison of the Typical Impeller and the Arc Impellers
3.2.1. Comparison of Flow Pattern
3.2.2. Comparison of Flotation Kinetics
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yianatos, J.B.; Larenas, J.M.; Moys, M.H.; Diaz, F.J. Short time mixing response in a big flotation cell. Int. J. Miner. Process. 2008, 89, 1–8. [Google Scholar] [CrossRef]
- Murphy, B.; Miettinen, T.; Yanez, A. Proceedings of the 27th International Mineral Processing Congress, IMPC 2014, Santiago, Chile, 20–24 October 2014; p. 265.
- Shen, Z.; Lu, S.; Yang, L. R&D and application of KYF large scale flotation cells developed by BGRIMM. Nonferrous Met. 2008, 4, 115–119. (In Chinese) [Google Scholar]
- Graul, R.; Nousiainen, M.; Yanez, A. Gas dispersion measurements in three outotec flotation cells: TankCell 1, e300 and e500. In Proceedings of the 27th International Mineral Processing Congress, IMPC 2014, Santiago, Chile, 20–24 October 2014; p. 265. [Google Scholar]
- Lelinski, D.; Yang, Y.; Caldwell, K.; Rahal, K.; Traczyk, F.; Olson, T.; Jespersen, M. Advances in FLSmidth flotation. In Proceedings of the 11th International Mineral Processing Conference, Santiago, Chile, 21–23 October 2015; p. 176. [Google Scholar]
- Mesa, D.; Brito-Parada, P.R. Scale-Up in Froth Flotation: A State-of-the-Art Review. Sep. Purif. Technol. 2019, 210, 950–962. [Google Scholar]
- Koh, P.T.L.; Manickam, M.; Schwarz, M.P. CDF simulation of bubble-particle collisions in mineral flotation cells. Miner. Eng. 2000, 13, 1455–1463. [Google Scholar] [CrossRef]
- Wang, G.; Ge, L.; Mitra, S.; Evans, G.M.; Joshi, J.B.; Chen, S. A review of CFD modelling studies on the flotation process. Miner. Eng. 2018, 127, 153–177. [Google Scholar] [CrossRef]
- Koh, P.T.L.; Schwarz, M.P. CFD modelling of bubble–particle collision rates and efficiencies in a flotation cell. Miner. Eng. 2003, 16, 1055–1059. [Google Scholar] [CrossRef]
- Xia, J.; Rinne, A.; Grönstrand, S. Effect of turbulence models on prediction of fluid flow in an Outotec flotation cell. Miner. Eng. 2009, 22, 880–885. [Google Scholar] [CrossRef]
- Salem-Said, A.-H.; Fayed, H.; Ragab, S. Numerical simulations of two-phase flow in a Dorr-Oliver flotation cell model. Minerals 2013, 3, 284–303. [Google Scholar] [CrossRef]
- Tiitinen, J.; Koskinen, K.; Ronkainen, S. Numerical modeling of an Outokumpu flotation cell. In Proceedings of the Centenary of Flotation Symposium, Brisbane, Australia, 6–9 June 2005; pp. 271–275. [Google Scholar]
- Shi, S.; Zhang, M.; Fan, X.; Chen, D. Experimental and computational analysis of the impeller angle in a flotation cell by PIV and CFD. Int. J. Miner. Process. 2015, 142, 2–9. [Google Scholar] [CrossRef]
- Koh, P.T.L.; Smith, L.K. The effect of stirring speed and induction time on flotation. Miner. Eng. 2011, 24, 442–448. [Google Scholar] [CrossRef]
- Nelson, M.G.; Lelinski, D. Hydrodynamic design of self-aerating flotation machines. Miner. Eng. 2000, 13, 991–998. [Google Scholar] [CrossRef]
- Arbiter, N.; Harris, C.C. Design and Operating Characteristics for Large Flotation Cells; SME Inc.: Littleton, CO, USA, 1979; p. 8. [Google Scholar]
- Brander, B. Dimensional analysis and scale-up in chemical engineering. Von m. Zlokarnik. Springer verlag, berlin 1991. 176 S., 51 Abb., geb., DM 38,–. Chem. Ing. Tech. 1993, 65, 457. [Google Scholar] [CrossRef]
- Yianatos, J.B.; Henríquez, F.D. Short-cut method for flotation rates modelling of industrial flotation banks. Miner. Eng. 2006, 19, 1336–1340. [Google Scholar] [CrossRef]
- Yianatos, J.; Contreras, F.; Morales, P.; Coddou, F.; Elgueta, H.; Ortíz, J. A novel scale-up approach for mechanical flotation cells. Miner. Eng. 2010, 23, 877–884. [Google Scholar] [CrossRef]
- Yianatos, J.; Carrasco, C.; Bergh, L.; Vinnett, L.; Torres, C. Modelling and simulation of rougher flotation circuits. Int. J. Miner. Process. 2012, 112, 63–70. [Google Scholar] [CrossRef]
- Yianatos, J.B. Fluid flow and kinetic modelling in flotation related processes columns and mechanically agitated cells—A review. Chem. Eng. Res. Des. 2007, 85, 1591–1603. [Google Scholar] [CrossRef]
- Yianatos, J. Flotation rate distribution in the collection zone of industrial cells. Miner. Eng. 2010, 23, 1030–1035. [Google Scholar] [CrossRef]
- Shen, Z. Principle and Technology of Flotation Machine; Metallurgical Industrial Press: Beijing, China, 2012. [Google Scholar]
- Shen, Z.; Zhang, Y.; Han, D.; Feng, T. Application of KYF-320 flotation cell. In Proceedings of the 27th International Mineral Processing Congress, IMPC 2014, Santiago, Chile, 20–24 October 2014; p. 178. [Google Scholar]
- Garcfa-Zuniga, H. Flotation recovery is an exponential function of its rate. In Proceedings of the 11th International Mineral Processing Conference, Santiago, Chile, 21–23 October 2015; Volume 47, pp. 83–86. [Google Scholar]
- Finch, J.A. Column flotation: A selected review—Part IV: Novel flotation devices. Miner. Eng. 1995, 8, 587–602. [Google Scholar] [CrossRef]
- Ahmed, N.; Jameson, G.J. Flotation kinetics. Miner. Process. Extr. Metall. Rev. 1989, 5, 77–99. [Google Scholar] [CrossRef]
- Salem-Said, A.; Fayed, H.; Ragab, S. CFD simulation of a Dorr-Oliver flotation cell. In Proceedings of the SME Annual Meeting and Exhibit, Denver, CO, USA, 24–27 February 2011. [Google Scholar]
- Tiitinen, J. Numerical modeling of a OK rotor-stator mixing device. In Proceedings of the European Symposium on Computer Aided Process Engineering, Kunming, China, 1–4 June 2003; Kraslawski, A., Turunen, I., Eds.; Volume 14, pp. 959–964. [Google Scholar]
- Shen, Z.; Chen, J. Flow Field Simulation and Its Applications; Science Press: Beijing, China, 2012. [Google Scholar]
- Fayed, H.; Ragab, S. Numerical simulations of two-phase flow in a self-aerated flotation machine and kinetics modeling. Minerals 2015, 5, 164–188. [Google Scholar] [CrossRef]
- Verrelli, D.I.; Koh, P.T.L.; Nguyen, A.V. Particle–bubble interaction and attachment in flotation. Chem. Eng. Sci. 2011, 66, 5910–5921. [Google Scholar] [CrossRef]
- Koh, P.T.L.; Schwarz, M.P. Modelling attachment rates of multi-sized bubbles with particles in a flotation cell. Miner. Eng. 2008, 21, 989–993. [Google Scholar] [CrossRef]
- Koh, P.T.L.; Schwarz, M.P. CFD modelling of bubble–particle attachments in flotation cells. Miner. Eng. 2006, 19, 619–626. [Google Scholar] [CrossRef]
- Koh, P.T.L.; Schwarz, M.P. CFD model of a self-aerating flotation cell. Int. J. Miner. Process. 2007, 85, 16–24. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Song, T.; Shen, Z. CFD simulation of gas-liquid flow in a large scale flotation cell. J. Comput. Multiph. Flows 2010, 2, 145–150. [Google Scholar] [CrossRef]
- Abrahamson, J. Collision rates of small particles in a vigorously turbulent fluid. Chem. Eng. Sci. 1975, 30, 1371–1379. [Google Scholar] [CrossRef]
- Schubert, H.; Bischofberger, C. On the optimization of hydrodynamics in flotation processes. In Proceedings of the 13th International Mineral Processing Congress, Warsaw, Poland, 4–9 June 1979; Volume 2, pp. 1261–1285. [Google Scholar]
- Yoon, R.H.; Luttrell, G.H. The effect of bubble size on fine particle flotation. Miner. Process. Extr. Metall. Rev. 1989, 5, 101–122. [Google Scholar] [CrossRef]
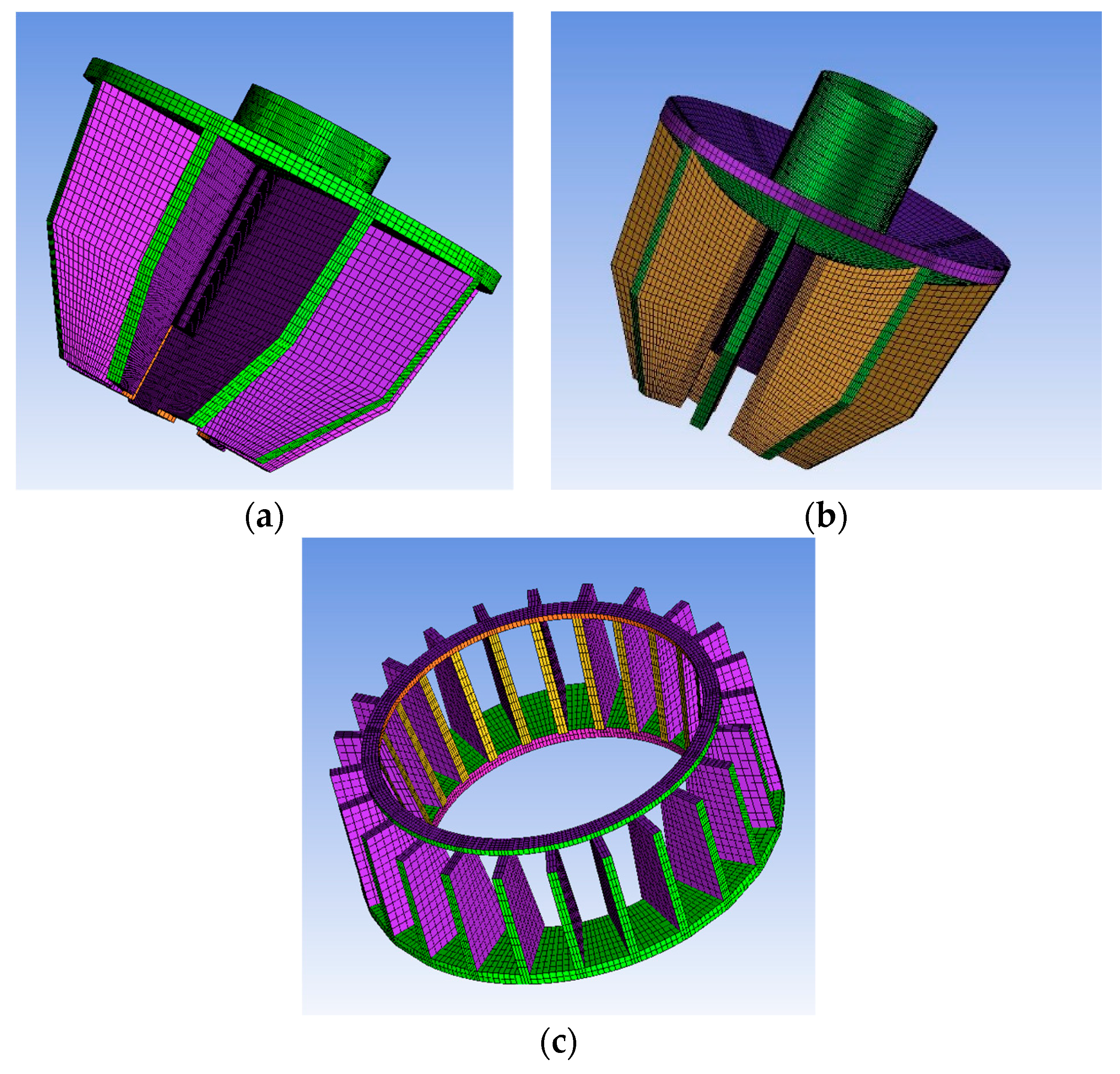











| Research | Comment | Author/Organization |
|---|---|---|
| Large flotation application | Tank cell flotation cells scale-up from 60–620 m3 in 1960s–now; The new flotation force impeller was developed | Outotec company |
| Dorroliver/Wemco flotation cells scale up to 660 m3/300 m3. The next step impeller and stator was developed | FLSmidth company | |
| KFY/JJF flotation cells scale up to 680 m3/320 m3 from 1990–2018. The arc impeller and other newly designed impeller are developing | BGRIMM company | |
| Scale-up method of flotation cell | hydrodynamic numbers are established to analyze the hydrodynamics characteristics in Wemco flotation cell | Nelson [15] |
| Propose seven important hydrodynamic numbers to scaling up | Arbiter [16] | |
| summarized 24 dimensionless numbers for mineral processing and chemical engineering | Zlokarnik [17] | |
| Based on the RTD research to scale up and optimize large flotation cell | Yianatos et al. [18,19,20,22] | |
| Scale-up method of BGRIMM flotation cell based on four scale-up numbers | Shen et al. [23,24] | |
| Kinetic model | R(t) = Rmax(1 − e−kt) | Garcfa-Zuniga [25] |
| Dobby & Finch [26] | ||
| Yianatos [1,21] | ||
| Ahmed and Jameson [27] | ||
| CFD model | Single phase: Continuity: Momentum: | Wang et al. [8] |
| Euler-Euler: Continuity: Monentum: | ||
| Euler-Lagrangian: Continuity: Monentum: Continuity: Monentum: Particle or bubble motion: | ||
| CFD simulation | Flow pattern research including mixing, air bubbles dispersion and so on, such as air forced flotation cell of TankCell, KYF, Dorr-Oliver flotation cell | Salem-Said et al. [28]; Tiitinen [12,29]; Xia et al. [10]; Shen et al. [30]; |
| Self-induced flotation cell research on air suction, flow pattern | Fayed and Ragab [31] | |
| Particle-air bubbles collision, adherin, detachment research predict the metallurgical performance | Koh and Schwarz [7,32,33,34,35] | |
| Recovery simulation would be compared with experiment | Koh and Schwarz [14] | |
| CFD model verification using experimental data | Shi et al. [13] | |
| Optimized of flotation cell of structure | Zhou et al. [36] |
| Parameter | Definition |
|---|---|
| Power Number, Np | P/ρN3D5 |
| Power intensity | P/V |
| Circulation Intensity | Qr/ND3 |
| Froude Number, Fr | N2D/g |
| Air Capacity Number, Ca | Q/ND3 |
| Air Flow Number, Na | Q/AcVt |
| Constant | Cμ | C1ε | C2ε | C3ε | k | σε |
|---|---|---|---|---|---|---|
| Value | 0.09 | 1.44 | 1.92 | 1.0 | 0.4187 |
| Single Phase | Multiphase |
|---|---|
| Mesh type | Structure mesh |
| Analysis type | Steady stead |
| Phase | Water for continous fluid; air for dispersion fluid; solid for dispersion solid |
| Model | K–ε model for liquid; dispersed phase zero equation for liquid |
| Multiple zone | The Multiple Reference Frame model (MFR) |
| Single Phase | Multiphase | |
|---|---|---|
| Mesh zone | Move zone with rotating of 90 rpm including impeller; stationary zone including stator and tank | |
| Interface | Connecting move zone and stationary zone with GGI | |
| Materials | Water; air bubbles of 2 mm, particles of 0.074 mm, 2650 kg/m3, 3 mPa·s | |
| Boundary | Wall at the top of tank; others as wall | Degassing at the top of tank as air outlet; Air inlet at the impeller; others as wall |
| Initial | 100% of water; Pressure 1 atm; velocity 0; Turbluence: medium (intensity 5%) | The simulation result of the single phase; Gas liquid simulation: the volume fraction of water 1, the volume fraction of gas 0; Gas–liquid–solid simulation: 15% of solid, 85% of water, no air for initial |
| Solution | High resolution in CFX software | |
| Volume Average of TED in Rotor Zone, m2/s3 | Volume Average of z1 in Rotor Zone | Volume Average of Pc in Rotor Zone, % | Torque of Rotor Zone, N·m | ||||
|---|---|---|---|---|---|---|---|
| Typical | Arc | Typical | Arc | Typical | Arc | Typical | Arc |
| 33.0 | 17.2 | 2.4 × 10−5 | 1.9 × 10−5 | 31.9 | 25.4 | 54,280.6 | 46,859.3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Z.; Zhang, M.; Fan, X.; Shi, S.; Han, D. Hydrodynamic and Flotation Kinetic Analysis of a Large Scale Mechanical Agitated Flotation Cell with the Typical Impeller and the Arc Impeller. Minerals 2019, 9, 79. https://doi.org/10.3390/min9020079
Shen Z, Zhang M, Fan X, Shi S, Han D. Hydrodynamic and Flotation Kinetic Analysis of a Large Scale Mechanical Agitated Flotation Cell with the Typical Impeller and the Arc Impeller. Minerals. 2019; 9(2):79. https://doi.org/10.3390/min9020079
Chicago/Turabian StyleShen, Zhengchang, Ming Zhang, Xuesai Fan, Shuaixing Shi, and Dengfeng Han. 2019. "Hydrodynamic and Flotation Kinetic Analysis of a Large Scale Mechanical Agitated Flotation Cell with the Typical Impeller and the Arc Impeller" Minerals 9, no. 2: 79. https://doi.org/10.3390/min9020079




