A Spherical Fuzzy Analytic Hierarchy Process (SF-AHP) and Combined Compromise Solution (CoCoSo) Algorithm in Distribution Center Location Selection: A Case Study in Agricultural Supply Chain

Abstract

Logistics is an important service sector, contributing to improving the competitiveness of the economy. Therefore, along with increasing the application of technology and effective business models, it is necessary to increase the connectivity of the infrastructure systems of industrial parks, roads, and seaports of regions and the country. Over the past decades, Vietnamese businesses have been step-by-step going through many stages from production, packaging, quality, hygiene, and safety to grasping new stages in the domestic and global value chain. In many industries, businesses are increasing the content of their own designs, exploiting brands, and approaching consumption networks in the target market. The role of the distribution center is becoming more and more important in ensuring a seamless and flawless supply chain. In particular, the distribution center is the most sensitive contact point between supply and demand in each enterprise. Therefore, the key mission of a distribution center is to reconcile supply and demand requirements. Distribution center location selection problems usually involve multiple quantitative and qualitative criteria that the decision maker must take into account for assessing the symmetrical impact of the criteria to reach the most accurate result. In this study, the authors propose a hybrid MCDM model based on Spherical Fuzzy Analytic Hierarchy Process (SF-AHP) and Combined Compromise Solution (CoCoSo) Algorithm to support the distribution location selection problem of perishable agricultural products. The proposed model is then applied to the numerical case study of the sweet potato product of the Mekong Delta region of Vietnam to demonstrate the feasibility of the model. The contribution of this research is to propose an MCDM model for improving the efficiency of the agricultural supply chain through selecting a location distribution center. This proposed model can be applied to the agricultural supply chain around the world.

1. Introduction

Most perishable supply chains in the Mekong Delta Region of Vietnam are inefficient, which contributes to low production and productivity of the agricultural sector of the region as a whole. Among many agriculture products of the region, sweet potato is considered as one of the major products. However, the majority of sweet potato growers are small-scale farmers who are not able to produce and distribute their produce efficiently due to the inefficiency of the current supply chain [1]. 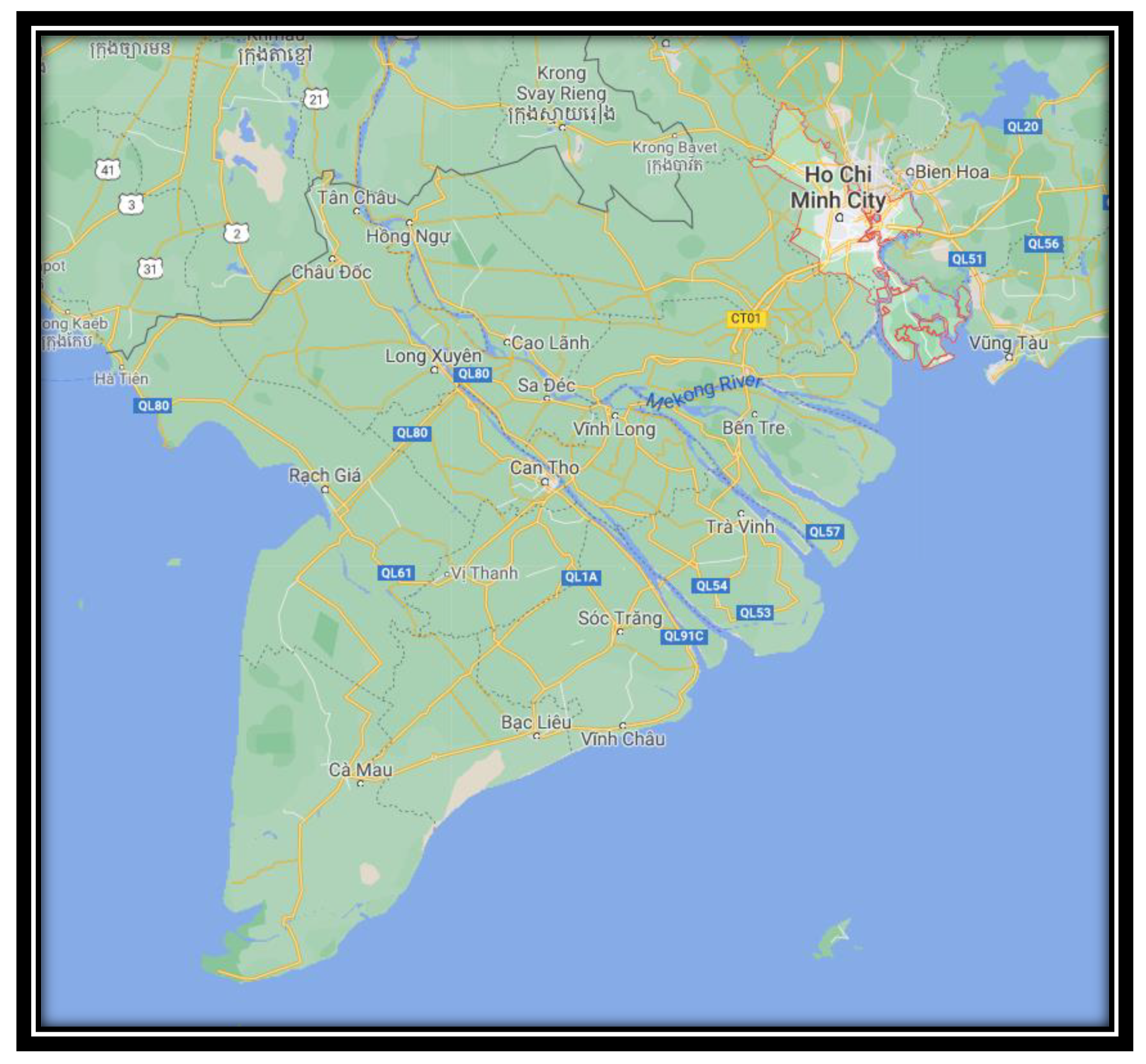One of the reasons is the lack of a proper distribution center to service the largest domestic market region and international logistics gateway of the country—the metropolitan part of the South East region of Vietnam [2]. As the local government has put a focus on improving the livelihood of the small-scale farmers by improving the inefficiency, by improving the design of the current supply chain, the problem of choosing the optimal location for a dedicated distribution center is becoming an important question to solve in order to improve these farmers′ livelihood, as well as the overall profitability of the whole sweet potato supply chain. Multiple criteria in both quantitative and qualitative forms must be considered in a systematic approach in order to ensure the efficiency of the final design of the supply chain. Therefore, the distribution center location selection problem can be considered as a multicriteria decision-making problem under uncertain environments. Mekong Delta Region and South East Region of Vietnam is shown in Figure 1.

Distribution center location selection problems usually involve multiple quantitative and qualitative criteria. A feasible approach to such problems is the use of multicriteria decision-making (MCDM) methods to develop specialized MCDM models. These models differ from each other by having different criteria or employing different MCDM methods. There are multiple MCDM methods that can be employed to support the decision makers such as Analytical Hierarchy Process (AHP), Analytical Network Process (ANP), Multicriteria Optimization and Compromise Solution (VIKOR), Technique for Order Preference Similarity to the Ideal Solution (TOPSIS), etc. In the cases where the decision-making problem involves an uncertain decision-making environment, fuzzy theory is employed in combination with MCDM methods to create fuzzy MCDM models to effectively solve the problems. In this study, the authors propose a hybrid MCDM model based on Spherical Fuzzy Analytic Hierarchy Process (SF-AHP) and Combined Compromise Solution (CoCoSo) Algorithm to support the distribution location selection problem of perishable agricultural products. The proposed model is then applied to the numerical case study of the sweet potato product of the Mekong Delta region of Vietnam to demonstrate the feasibility of the model.

2. Literature Review

Over the years, many decision support systems based on MCDM methods have been developed to assist decision makers in solving complex decision-making problems in different sectors, such as computer science, environmental science, manufacturing engineering, energy and fuels, etc. Among these, supply chain management is an increasingly frequent topic of research with numerous MCDM models developed to support the optimization of different supply chains. Common decision-making problems in the supply chain management field include sustainable supplier selection, sustainable innovation selection, facility location selection, and many more.

Supplier selection is one of the most demanding multicriteria decision-making problems, especially in cases where sustainability is a concern. Fallahpour et al. [4] proposed a fuzzy AHP-TOPSIS method to support the supplier ranking and selection process. The author applied the fuzzy preference programming technique to calculate the relative fuzzy weights of the ranking criteria, while fuzzy TOPSIS is employed to determine the ranking of the potential suppliers. Govidan et al. [5] introduced the fuzzy TOPSIS-based MCDM model to support the sustainable supplier evaluation process. Dai and Blackhurst [6] utilized the AHP and Quality Function Deployment (QFD) methods to develop a MCDM model for the sustainable supplier selection problem. Luthra et al. [7] introduced a sustainable supplier selection method based on AHP and VIKOR methods. The proposed model has 22 criteria for the three pillars of sustainability. Wang et al. [8] developed a hybrid fuzzy ANP-PROMETHEE II to assist the supplier evaluation and selection process in the textile industry. The selection criteria of the proposed model are based on the popular Supply Chain Operation Reference (SCOR) model.

Sustainable innovation is also an important part of supply chain management where MCDM models are frequently employed. Gupta and Sarkis [9] introduced a Best-Worst Method based theoretical framework for ranking sustainable assessment criteria. Entezaminia et al. [10] developed an AHP-based decision support system to assist the evaluation of potential products of the supply chain based on sustainability criteria. Facility location selection is another aspect of supply chain management where MCDM methods are frequently applied to support the decision makers. Chien et al. [11] proposed a hybrid fuzzy ANP-TOPSIS model to support the location selection problem of hydroelectric plant projects. The model is applied to a hydroelectric plant development project in Vietnam to verify its feasibility. Tadić et al. [12] utilized the Delphi method, AHP, and Combinative Distance-based Assessment (CODAS) to develop a decision support system under grey environment to support the location selection process of a dry port terminal. Budak et al. [13] utilized Interval-valued Intuitionistic Fuzzy sets theory in combination with the Decision-Making Trial and Evaluation Laboratory (DEMATEL) method to create a real-time location system (RTLSs) to support the asset location management problem of humanitarian relief efforts. Deveci et al. [14] combined a fuzzy COPRAS-based MCDM model with Geographical Information Systems (GIS) to solve a factory location selection problem. In order to solve a stacker’s selection problem in a logistics system, Ulutaş et al. [15] employed correlation coefficient and the standard deviation to determine the objective weights of criteria, the Indifference Threshold-based Attribute Ratio Analysis (ITARA) method to calculate the semi-objective weights of criteria. Finally, the compromise solution method (MARCOS) is applied to calculate the alternative ranking. The proposed model provided a comprehensive and easy approach to the problem. Ulutaş et al. [16] developed a novel MULTIMOOSRAL approach to the supplier selection problem. Ulutaş [17] developed a grey MCDM model based on grey Step-wise Weight Assessment Ratio Analysis (SWARA) and Multi-Objective Optimization Method by Ratio Analysis (MOORA) to evaluate the logistics performance of transition economies. The model suggests that the most influential criterion is “infrastructure” and Serbia is the country with the best logistics performance among the transition economies.

There are multiple literatures on the development of MCDM models supporting distribution center (DC) location selection problems. Yilmaz and Kabak [18] developed a type—2 fuzzy AHP-TOPSIS approach to identify the criteria for a disaster response distribution center. Liu and Li [19] developed a MCDM model utilizing 2-dimensional linguistic (2DL) information to ensure the effective decision-making process under uncertain environments to support a DC location selection problem. Quynh et al. [20] developed a fuzzy TOPSIS-based model to assist the DC location selection process. Kuo [21] introduced a utilized fuzzy AHP/ANP and fuzzy DEMATEL to support the international DC selection problem. The proposed approach is employed to solve an international DC selection problem in Pacific Asia to demonstrate the model and its feasibility. Yang et al. [22] proposed a novel MCDM-based approach to solve the logistics center location selection process for FMCG supply chains in China.

While the application of MCDM methods in solving DC selection problems of various supply chains has been studied in multiple literatures, only a few focus on solving the problem under uncertain decision-making environments by incorporating fuzzy theory to existing MCDM methods. Among these models, none are dedicated to the DC selection problem of agriculture perishable supply chains. Therefore, this research aims to develop a comprehensive MCDM model to support the DC selection process of agricultural supply chains under uncertain decision-making environments. The proposed model is based on a hybrid SF-AHP and CoCoSo approach and is applied to a real-world case study of sweet-potato produced in the Mekong Delta Region of Vietnam.

3. Methodology

3.1. Research Graph

Distribution center location selection is an important decision-making issue that has a profound impact on the performance of any supply chains. However, the decision-making process usually involves not only quantitative criteria but also qualitative ones, which increases the complexity of the process. Thus, fuzzy set theory is frequently integrated into MCDM models, which allows the ambiguity of the decision-making process to be reflected. While there are multiple methods to calculate the weighting of the criteria, such as BWM, LBWA, FAHP, FUCOM, and FANP. There are few applications of three dimensions fuzzy sets on the developments of MCDM modes. Therefore, this paper aims to create a hybrid MCDM model based on SF-AHP and CoCoSo methods to solve the DC location selection problem.

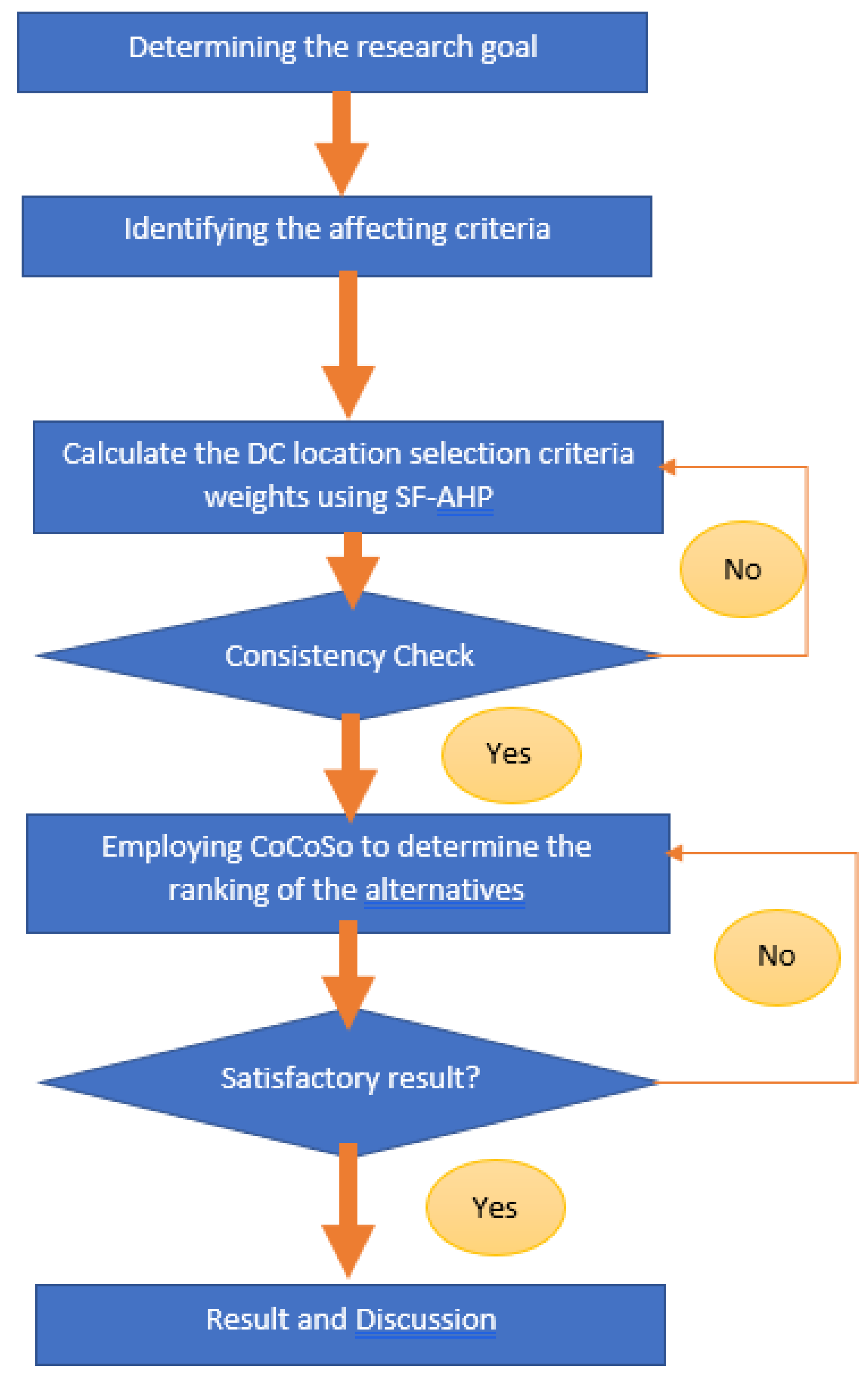
The application of the proposed approach includes four steps shown in Figure 2 below:

Step 1: Analyzing the current statuses of the product distribution system. Next, the decision-making criteria set, and sub-criteria set are established based on the relevant literatures and industry expert interviews.

Step 2: Applying the SF-AHP method to calculate the weights of the criteria. The weight of the criteria is also the input data of CoCoSo method in Step 4.

Step 3: Checking the consistency of the results of the SF-AHP model.

Step 4: Employing the CoCoSo method to calculate the ranking of the alternatives based on the criteria weights calculated using the SF-AHP model.

3.2. Theoretical Basis

3.2.1. Spherical Fuzzy Sets Theory

The spherical fuzzy sets theory has been applied in multiple MCDM models. Sharaf [23] applied spherical fuzzy sets in combination with the VIKOR method to solve a supplier selection problem. The implementation of spherical fuzzy sets provides the decision makers with a larger preference domain [23]. Otay and Atik [24] created an MCDM model to solve a real-world oil station location evaluation problem using spherical fuzzy sets and the WASPAS method. Sensitivity analysis showed that the proposed model is robust [24]. Gül [25] developed a spherical fuzzy extension of the DEMATEL method. The proposed model was applied to a building contractor selection problem [25]. In this research, a hybrid SF-AHP and CoCoSo approach is developed to solve a DC location selection problem.

Spherical fuzzy sets theory was introduced recently by Gundogdu and Kahraman [26] as a synthesis of Pythagorean fuzzy sets [27] and Neutrosophic sets theories [28]. Pythagorean fuzzy sets′ membership functions are defined by membership, non-membership, and hesitancy parameters; Neutrosophic fuzzy sets membership functions are also composed of truthiness, falsity, and indeterminacy parameters. Spherical fuzzy sets theory is based on the idea that by defining a membership function on a spherical surface, decision makers can generalize different types of fuzzy sets [26].

The membership function of a spherical fuzzy set is defined by three parameters: the degree of membership, the degree of non-membership, and the degree of hesitancy. Each of these parameters can have a value between 0 and 1 independently and the sum of the squared values of these parameters is at most 1.

A spherical fuzzy set ${\tilde{A}}_S$ of the universe of $U_1$ is defined as:

$${\tilde{A}}_S=\left\{x,\left({\mu }_{{\tilde{A}}_S}\left(x\right),v_{{\tilde{A}}_S}\left(x\right),{\pi }_{{\tilde{A}}_S}\left(x\right)\right)|xϵU_1\right\}$$

(1)

with:

$${\mu }_{{\tilde{A}}_S}\left(x\right):U_1\to \left[0,1\right],v_{{\tilde{A}}_S}\left(x\right):U_1\to \left[0,1\right],\mathrm{and}{\pi }_{{\tilde{A}}_S}\left(x\right):U_1\to \left[0,1\right]$$

and

$$0\le {\mu }_{{\tilde{A}}_S}^2\left(x\right)+v_{{\tilde{A}}_S}^2\left(x\right)+{\pi }_{{\tilde{A}}_S}^2\left(x\right)\le 1$$

(2)

with $\forall x\in U_1$, ${\mu }_{{\tilde{A}}_S}\left(x\right)$ as the degree of membership, $v_{{\tilde{A}}_S}\left(x\right)$ as the degree of non-membership, and ${\pi }_{{\tilde{A}}_S}\left(x\right)$ as the hesitancy of $x$ to ${\tilde{A}}_S$.

Basic arithmetic operations—such as union, intersection, addition, multiplication, and power—of spherical fuzzy sets are defined and demonstrated in the work of Gundogdu and Kahraman [29]. For these spherical fuzzy sets ${\tilde{A}}_S=({\mu }_{{\tilde{A}}_S},v_{{\tilde{A}}_S},{\pi }_{{\tilde{A}}_S}$) and ${\tilde{B}}_S=({\mu }_{{\tilde{B}}_S},v_{{\tilde{B}}_S},{\pi }_{{\tilde{B}}_S}$), basic arithmetic operations are performed as follows:

$${\tilde{A}}_S{\displaystyle \cup }{\tilde{B}}_S=\left\{max\left\{{\mu }_{{\tilde{A}}_S},{\mu }_{{\tilde{B}}_S}\right\},min\left\{v_{{\tilde{A}}_S},v_{{\tilde{B}}_S}\right\},min\left\{{\left[1-\left({\left(max\left\{{\mu }_{{\tilde{A}}_S},{\mu }_{{\tilde{B}}_S}\right\}\right)}^2+{\left(min\left\{v_{{\tilde{A}}_S},v_{{\tilde{B}}_S}\right\}\right)}^2\right)\right]}^{0.5},max\left\{{\pi }_{{\tilde{A}}_S},{\pi }_{{\tilde{B}}_S}\right\}\right\}\right\}$$

(3)

• Intersection of ${\tilde{A}}_S\mathrm{and}{\tilde{B}}_S$:

  $$\begin{array}{cc}\hfill {\tilde{A}}_S{\displaystyle \cap }{\tilde{B}}_S& =\{min\left\{{\mu }_{{\tilde{A}}_S},{\mu }_{{\tilde{B}}_S}\right\},max\left\{v_{{\tilde{A}}_S},v_{{\tilde{B}}_S}\right\},max\left\{\right[1\hfill \\ & -({\left(min\left\{{\mu }_{{\tilde{A}}_S},{\mu }_{{\tilde{B}}_S}\right\}\right)}^2+{\left(max\left\{v_{{\tilde{A}}_S},v_{{\tilde{B}}_S}\right\}\right)}^2){]}^{0.5},min\left\{{\pi }_{{\tilde{A}}_S},{\pi }_{{\tilde{B}}_S}\right\}\}\}\hfill \end{array}$$

  (4)
• Addition of ${\tilde{A}}_S\mathrm{and}{\tilde{B}}_S$:

  $${\tilde{A}}_S+{\tilde{B}}_S=\left\{{\left({\mu }_{{\tilde{A}}_S}^2+{\mu }_{{\tilde{B}}_S}^2-{\mu }_{{\tilde{A}}_S}^2{\mu }_{{\tilde{B}}_S}^2\right)}^{0.5},v_{{\tilde{A}}_S}{v}_{{\tilde{B}}_S},{\left(\left(1-{\mu }_{{\tilde{B}}_S}^2\right){\pi }_{{\tilde{A}}_S}^2+\left(1-{\mu }_{{\tilde{A}}_S}^2\right){\pi }_{{\tilde{B}}_S}^2-{\pi }_{{\tilde{A}}_S}^2{\pi }_{{\tilde{B}}_S}^2\right)}^{0.5}\right\}$$

  (5)
• Multiplication of ${\tilde{A}}_S\mathrm{and}{\tilde{B}}_S$:

  $${\tilde{A}}_S\times {\tilde{B}}_S=\left\{{\mu }_{{\tilde{A}}_S}{\mu }_{{\tilde{B}}_S},{\left(v_{{\tilde{A}}_S}^2+v_{{\tilde{B}}_S}^2-v_{{\tilde{A}}_S}^2{v}_{{\tilde{B}}_S}^2\right)}^{0.5},{\left(\left(1-v_{{\tilde{B}}_S}^2\right){\pi }_{{\tilde{A}}_S}^2+\left(1-v_{{\tilde{A}}_S}^2\right){\pi }_{{\tilde{B}}_S}^2-{\pi }_{{\tilde{A}}_S}^2{\pi }_{{\tilde{B}}_S}^2\right)}^{0.5}\right\}$$

  (6)
• Multiplication of ${\tilde{A}}_S\mathrm{and}\mathrm{a}\mathrm{scalar}\left(\lambda >0\right):$

  $$\lambda \times {\tilde{A}}_S=\left\{{\left(1-{\left(1-{\mu }_{{\tilde{A}}_S}^2\right)}^{\lambda }\right)}^{0.5},v_{{\tilde{A}}_S}^{\lambda },{\left({\left(1-{\mu }_{{\tilde{A}}_S}^2\right)}^{\lambda }-{\left(1-{\mu }_{{\tilde{A}}_S}^2-{\pi }_{{\tilde{A}}_S}^2\right)}^{\lambda }\right)}^{0.5}\right\}$$

  (7)
• Power of ${\tilde{A}}_S$, with $\lambda >0$:

  $${\tilde{A}}_S^{\lambda }=\left\{{\mu }_{{\tilde{A}}_S}^{\lambda },{\left(1-{\left(1-v_{{\tilde{A}}_S}^2\right)}^{\lambda }\right)}^{0.5},{\left({\left(1-v_{{\tilde{A}}_S}^2\right)}^{\lambda }-{\left(1-v_{{\tilde{A}}_S}^2-{\pi }_{{\tilde{A}}_S}^2\right)}^{\lambda }\right)}^{0.5}\right\}$$

  (8)

3.2.2. Spherical Fuzzy Analytic Hierarchy Process (SF-AHP) Model

The SF-AHP method is introduced by Gundogdu and Kahraman [29] is an extension of AHP with spherical fuzzy sets. In this paper, SF-AHP is employed to determine the DC selection criteria weights. The SF-AHP method has seven steps [29]:

Step 1: Build the model hierarchical structure.

A hierarchical structure with three levels is constructed. Level 1 is the goal of the model based on a score index. The score index is determined with n criteria, which is represented in Level 2 of the structure. A set of m alternative A ($m\ge 2$), is defined in Level 3 of the structure.

Step 2: Build pairwise comparison matrices of the criteria using spherical fuzzy judgement based on linguistic terms (

Table 1. Linguistic measures of importance [29].

Definition	$\left(\mathit{\mu },\mathit{v},\mathit{\pi }\right)$	Score Index
Absolutely more importance (AM)	(0.9, 0.1, 0.0)	9
Very high importance (VH)	(0.8, 0.2, 0.1)	7
High importance (HI)	(0.7, 0.3, 0.2)	5
Slightly more importance (SM)	(0.6, 0.4, 0.3)	3
Equally importance (EI)	(0.5, 0.4, 0.4)	1
Slightly lower importance (SL)	(0.4, 0.6, 0.3)	1/3
Low importance (LI)	(0.3, 0.7, 0.2)	1/5
Very low importance (VL)	(0.2, 0.8, 0.1)	1/7
Absolutely low importance (AL)	(0.1, 0.9, 0.0)	1/9

):

Equation (9) and (10) are applied to calculate the score indices (SI) of each alternative.

$$\mathrm{SI}=\sqrt{\left|100*\left[{\left({\mu }_{{\tilde{A}}_s}-{\pi }_{{\tilde{A}}_s}\right)}^2-{\left(v_{{\tilde{A}}_s}-{\pi }_{{\tilde{A}}_s}\right)}^2\right]\right|}$$

(9)

for AM, VH, HI, SM, and EI.

$$\frac{1}{\mathrm{SI}}=\frac{1}{\sqrt{\left|100*\left[{\left({\mu }_{{\tilde{A}}_s}-{\pi }_{{\tilde{A}}_s}\right)}^2-{\left(v_{{\tilde{A}}_s}-{\pi }_{{\tilde{A}}_s}\right)}^2\right]\right|}}$$

(10)

for SL, LI, VL, and AL.

Step 3: Check the consistency of each pairwise comparison matrix.

The classical consistency check is applied with the threshold of the Consistency Ratio (CR) value of 10%:

$$CR=\frac{CI}{RI}$$

(11)

With CI as Consistency Index calculated as:

$$CI=\frac{{\lambda }_{max}-n}{n-1}$$

(12)

where ${\lambda }_{max}$ is the maximum eigenvalue of the matrix, and $n$ is the number of criteria.

The Random Index (RI) is determined based on the number of criteria.

Step 4: Obtain the fuzzy weights of criteria and alternatives.

Each alternative′s weight with respect to each criterion is obtained using the following equation:

$$\begin{array}{cc}\hfill SW{M}_w\left({\tilde{A}}_{S_{i1}}, \dots , {\tilde{A}}_{S_{in}}\right)& =w_1{\tilde{A}}_{S_{i1}}+\cdots + w_n{\tilde{A}}_{S_{in}}\hfill \\ & =‹{\left[1-{\displaystyle \prod _{j=1}^n}{\left(1-{\mu }_{{\tilde{A}}_{s_{ij}}}^2\right)}^{w_j}\right]}^{0.5}, {\displaystyle \prod _{j=1}^n}{V}_{{\tilde{A}}_{s_{ij}}}^{w_j}, {\left[{\displaystyle \prod _{j=1}^n}{\left(1-{\mu }_{{\tilde{A}}_{s_{ij}}}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^n}{\left(1-{\mu }_{{\tilde{A}}_{s_{ij}}}^2-{\pi }_{{\tilde{A}}_{s_{ij}}}^2\right)}^{w_j}\right]}^{0.5}›\hfill \end{array}$$

(13)

where $w=1/n$.

Step 5: Obtain the global weights using hierarchical layer sequencing.

The final ranking of the alternatives is estimated by aggregating the spherical weights at each level of the hierarchical structure. There are two feasible ways to perform the computation at this point.

The first way is using the score function in Equation (14) to defuzzify the criteria weights:

$$S\left({\tilde{w}}_j^S\right)=\sqrt{\left|100*\left[{\left(3{\mu }_{{\tilde{A}}_s}-\frac{{\pi }_{{\tilde{A}}_s}}{2}\right)}^2-{\left(\frac{v_{{\tilde{A}}_s}}{2}-{\pi }_{{\tilde{A}}_s}\right)}^2\right]\right|}$$

(14)

Then, the criteria weights are normalized using Equation (15) and spherical fuzzy multiplication in Equation (16) is applied:

$${\overline{w}}_j^s=\frac{S\left({\tilde{w}}_j^s\right)}{{{\displaystyle \sum }}_{j=1}^{n}S\left({\tilde{w}}_j^s\right)}.$$

(15)

$${\tilde{A}}_{S_{ij}}={\overline{w}}_j^s*{\tilde{A}}_{S_i}={‹\left(1-{\left(1-{\mu }_{{\tilde{A}}_{S_i}}^2\right)}^{{\overline{w}}_j^s}\right)}^{1/2},v_{{\tilde{A}}_{S_i}}^{{\overline{w}}_j^s},{\left({\left(1-{\mu }_{{\tilde{A}}_{S_i}}^2\right)}^{{\overline{w}}_j^s}-{\left(1-{\mu }_{{\tilde{A}}_{S_i}}^2-{\pi }_{{\tilde{A}}_{S_i}}^2\right)}^{{\overline{w}}_j^s}\right)}^{1/2}›$$

(16)

The final ranking score ($\tilde{F}$) for each alternative $A_i$ is calculated using Equation (17):

$$\tilde{F}={\displaystyle \sum }_{j=1}^n{\tilde{A}}_{S_{ij}}={\tilde{A}}_{S_{i1}}+{\tilde{A}}_{S_{i2}}+\cdots +{\tilde{A}}_{S_{in}}$$

(17)

Another option is to continue the calculation without the defuzzification of the criteria weights. The spherical fuzzy global weights are calculated as:

$${\displaystyle \prod }_{j=1}^n{\tilde{A}}_{S_{ij}}={\tilde{A}}_{S_{i1}}*{\tilde{A}}_{S_{i2}}*\dots *{\tilde{A}}_{S_{in}}$$

(18)

Then, the final ranking score ($\tilde{F}$) of each alternative is calculated using Equation (17).

3.2.3. Combined Compromise Solution (CoCoSo)

CoCoSo is an MCDM method developed by Yazdani et al. [30], combining simple additive weighting method and exponentially weighted product model. In this research, the CoCoSo method is used to obtain the ranking of the potential DC locations. A typical CoCoSo model with m alternatives and n criteria has 5 steps:

Step 1: Determine the decision-making matrix $X={\left(x_{ij}\right)}_{m\times n}$ for the ith alternative and the jth criterion:

$$x_{ij}=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \dots & x_{1n}\\ x_{21}& x_{22}& \dots & x_{2n}\\ \dots & \dots & \dots & \dots \\ x_{m1}& x_{m2}& \dots & x_{mn}\end{array}\right]$$

(19)

With $i=1,2,\dots ,m$ and $j=1,2,\dots ,n$.

Step 2: Normalizing the decision-making matrix [30]:

For beneficial criterion:

$$r_{ij}=\frac{x_{ij}-\begin{array}{c}min{x}_{ij}\\ i\end{array}}{\begin{array}{c}max{x}_{ij}\\ i\end{array}-\begin{array}{c}min{x}_{ij}\\ i\end{array}}$$

(20)

For non-beneficial criterion:

$$r_{ij}=\frac{\begin{array}{c}max{x}_{ij}\\ i\end{array}-x_{ij}}{\begin{array}{c}max{x}_{ij}\\ i\end{array}-\begin{array}{c}min{x}_{ij}\\ i\end{array}}$$

(21)

Step 3: The power weight of comparability ($S_i$) and the total of the power weight of comparability ($P_i$) sequence for each alternative is calculated using Equation (22) and (23):

$$S_i={\displaystyle \sum }_{j=1}^n\left(w_j{r}_{ij}\right)$$

(22)

$$P_i={\displaystyle \sum }_{j=1}^n\left(r_{ij}{}^{w_j}\right)$$

(23)

Step 4: Calculate three aggregated performance scores. With $k_{ia}$ as the relative performance scores of the ith alternative calculated as the arithmetic mean of sums of $S_i$ and $P_i$ scores:

$$k_{ia}=\frac{P_i+S_i}{{{\displaystyle \sum }}_{i=1}^m{\left(P_i+S_i\right)}^{,}}$$

(24)

$k_{ib}$ is the relative performance scores of the ith alternative calculated as the sum of relative scores of $S_i$ and $P_i$ scores in comparison to the ideal performance values.

$$k_{ib}=\frac{S_i}{\begin{array}{c}min{S}_i\\ i\end{array}}+\frac{P_i}{\begin{array}{c}min{P}_i\\ i\end{array}}$$

(25)

$k_{ic}$ is the relative performance scores of the ith alternative calculated as the compromise of $S_i$ and $P_i$ performance scores. In Equation (20), the $\lambda$ value is selected by the decision makers and has a value between 0 and 1 (usually $\lambda =0.5)$.

$$k_{ic}=\frac{\lambda (S_i)+\left(1-\lambda \right)P_i}{\begin{array}{c}\lambda max{S}_i\\ i\end{array}+\begin{array}{c}\left(1-\lambda \right)max{P}_i\\ i\end{array}}$$

(26)

Step 5: Obtain each alternative′s performance score ($k_i)$:

$$k_i={(k_{ia}{k}_{ib}{k}_{ic})}^{\frac{1}{3}}+\frac{1}{3}(k_{ia}+k_{ib}+k_{ic})$$

(27)

The final ranking of the alternatives is based on the calculated performance scores with the optimal alternative having the highest score.

4. Case Study

4.1. Model Application

In order to increase the objectivity for the determination of the location of the distribution center, as well as to match the actual situation and the socio-economic development of the region, interviews were conducted to ask for opinions of experts, including scientists, managers, and local representative leaders, who are directly involved in the DC development project, for options according to the criteria as well as the importance between the criteria. Then, a list of DC location selection criteria is identified as shown in

Table 2. List of DC location selection criteria.

Criteria	Symbol	Sub Criteria
Cost	A	Land Cost (A1)
		Logistics Cost (A2)
Available Infrastructure	B	Proximity to Airport (B2)
		Proximity to Highway (B3)
		Proximity to Railway (B4)
Service Level	C	Transportation Time (C1)
		Distance to Markets (C2)
		Distance to Manufacturers(C3)
Sustainability Factors	D	Distance to forest area (D1)
		Distance to surface water (D2)
		Ethical Factors (D3)

:

In the first stage of this research, the author applied the Spherical Fuzzy Analytic Hierarchy Process (SF-AHP) for determining the weight of eleven criteria. The results are shown in

Table 3. Results from the SF-AHP model.

Spherical Fuzzy Weights			Crisp Weights
Degree of Membership	Degree of Non-Membership	Degree of Hesitancy
0.433	0.540	0.318	0.067
0.325	0.660	0.254	0.049
0.422	0.589	0.241	0.067
0.443	0.583	0.229	0.071
0.472	0.554	0.229	0.076
0.564	0.459	0.219	0.092
0.634	0.390	0.182	0.106
0.667	0.343	0.202	0.111
0.705	0.302	0.174	0.118
0.707	0.295	0.196	0.118
0.741	0.256	0.177	0.125

.

Then, Combined Compromise Solution (CoCoSo) Algorithm is applied at this step to calculate the ranking of the potential locations of the DC. The normalized matrix, weighted comparability sequence and Si, and exponentially weighted comparability sequence and Pi, are shown in

Table 4. Normalized matrix.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11
A1	0.6667	1.0000	1.0000	0.0000	0.3333	0.5000	0.0000	1.0000	0.5000	0.5000	0.8000
A2	1.0000	0.0000	0.5000	0.5000	0.0000	0.0000	0.3333	0.7500	0.0000	0.0000	0.0000
A3	0.0000	0.0000	0.5000	0.5000	1.0000	0.5000	0.6667	0.0000	1.0000	1.0000	0.6000
A4	0.6667	0.5000	0.0000	1.0000	0.3333	1.0000	0.6667	0.2500	0.5000	0.0000	1.0000
A5	1.0000	0.0000	1.0000	1.0000	0.0000	1.0000	1.0000	0.2500	0.5000	0.0000	0.8000

,

Table 5. Weighted comparability sequence and Si value.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11
A1	0.0447	0.0490	0.0670	0.0000	0.0253	0.0460	0.0000	0.1110	0.0590	0.0590	0.1000
A2	0.0670	0.0000	0.0335	0.0355	0.0000	0.0000	0.0353	0.0833	0.0000	0.0000	0.0000
A3	0.0000	0.0000	0.0335	0.0355	0.0760	0.0460	0.0707	0.0000	0.1180	0.1180	0.0750
A4	0.0447	0.0245	0.0000	0.0710	0.0253	0.0920	0.0707	0.0278	0.0590	0.0000	0.1250
A5	0.0670	0.0000	0.0670	0.0710	0.0000	0.0920	0.1060	0.0278	0.0590	0.0000	0.1000

and

Table 6. Exponentially weighted comparability sequence and Pi values.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11
A1	0.9732	1.0000	1.0000	0.0000	0.9199	0.9382	0.0000	1.0000	0.9215	0.9215	0.9725
A2	1.0000	0.0000	0.9546	0.9520	0.0000	0.0000	0.8901	0.9686	0.0000	0.0000	0.0000
A3	0.0000	0.0000	0.9546	0.9520	1.0000	0.9382	0.9579	0.0000	1.0000	1.0000	0.9381
A4	0.9732	0.9666	0.0000	1.0000	0.9199	1.0000	0.9579	0.8574	0.9215	0.0000	1.0000
A5	1.0000	0.0000	1.0000	1.0000	0.0000	1.0000	1.0000	0.8574	0.9215	0.0000	0.9725

.

In the final stage, an aggregated multiplication rule is employed to release the ranking of the alternatives and end the decision process. As the results from

Table 7. Final Aggregation and Ranking.

Alternatives	Ka	Ranking	Kb	Ranking	Kc	Ranking	Ki
								A1	0.2301	1	4.0181	1	0.9969	1	2.7215
A2	0.1254	5	2.0000	5	0.5435	5	1.4043
A3	0.2077	4	3.8739	4	0.9001	4	2.5586
A4	0.2283	2	3.9248	3	0.9892	2	2.6747
A5	0.2084	3	3.9432	2	0.9031	3	2.5903

, alternative A₁ (location A₁) is the optimal location. Findings: the authors described a real case of choosing optimal location for distribution center in Mekong Delta, Vietnam from an agricultural supply chain project.

4.2. Sensitivity Analysis

In this section, a sensitivity analysis is performed to validate the result of the model. A sensitivity analysis can allow the decision makers to validate the outcome of their decision-making process by changing parameters of the original model. In this study, different $\lambda$ values between 0 and 1 are used to perform the sensitivity test. The performance scores of each alternative with different λ values are shown in

Table 8. Final performance score (Ki) with different λ values.

Alternative	Final Performance Score (Ki)
	λ = 0.1	λ = 0.2	λ = 0.3	λ = 0.4	λ = 0.5	λ = 0.6	λ = 0.7	λ = 0.8	λ = 0.9	λ = 0.10
A1	2.72	2.72	2.72	2.72	2.72	2.72	2.72	2.72	2.71	2.69
A2	1.41	1.41	1.41	1.41	1.40	1.40	1.40	1.39	1.38	1.33
A3	2.56	2.56	2.56	2.56	2.56	2.56	2.56	2.57	2.57	2.61
A4	2.68	2.68	2.68	2.68	2.67	2.67	2.67	2.67	2.66	2.65
A5	2.59	2.59	2.59	2.59	2.59	2.59	2.60	2.60	2.61	2.63

.

Based on the result of Table 8, the rankings of each alternative with different λ values are unchanged as shown in Figure 3 below:

According to Table 8 and Figure 3, the result of the proposed model is robust with different values of λ. Alternative 1 (A1) is consistently the optimal location for the given DC selection problem. Therefore, it can be concluded that the proposed model’s performance is adequate and can be applied to real-world cases.

Distribution center (DC) location evaluation and selection process is a crucial issue in modern supply chain design and management. An effective DC location selection method, which allows the decision makers to consider multiple quantitative and qualitative criteria, can help improve the performance of supply chains. In this research, a comprehensive MCDM-based approach is proposed. After the relevant criteria are identified and evaluated, the SF-AHP method is employed to calculate the weights of the criteria. Then, the CoCoSo method is applied to calculate the ranking of the alternative. The proposed model is verified by applying to a DC location selection problem of a sweet potato supply chain in Southern Vietnam. A sensitivity analysis is also performed to verify the reliability of the model. The results show that the optimal location is Alternative 1 (A1) and the model performs consistently with different values of the parameter λ. Therefore, it can be concluded that the proposed model is feasible and can be applied to real-world DC location selection problems.

5. Conclusions

In recent years, the global market has been volatile in order to survive and grow, companies must focus on building business strategies that help reduce costs, continually improve quality, and increase satisfaction customer performance and on-time delivery. Therefore, the identification of an optimal location for the construction of a distribution center is one of the most important decision-making problems. This decision requires achieving all the above objectives. In this research, the authors propose a MCDM-based approach, utilizing spherical fuzzy analytic hierarchy process (SF-AHP) and Combined Compromise Solution (CoCoSo) Algorithm to support the distribution location selection problem of perishable agricultural products.

A real problem of distribution center’s assessment in Vietnam is handled to examine the performance of the proposed algorithm. By some comparative analysis and through the evidence, the stability of the CoCoSo algorithm is also approved. The proposed model can be applied to the agricultural supply chain around the world. Implementing and applying this new-born technique not only increases the accuracy of the decision-making system, but also aids company policies, accredits the global objectives, and delivers the beneficial consequences to the management control.

The future scope of this research can be extended by comparing the relative performance of the other MCDM methods, like Multi-attributive Ideal-Real Comparative Analysis (MAIRCA), Complex Proportional Assessment (COPRAS), and Linear Programming Technique for Multi-dimensional Analysis of Preference (LINMAP) while solving the facility location selection problems.