Dynamical Analysis and Finite-Time Synchronization for a Chaotic System with Hidden Attractor and Surface Equilibrium
Abstract
:1. Introduction
2. Dynamical Properties
2.1. Equilibria and Stability
2.2. Dynamical Behaviors Analysis
2.2.1. Phase Orbits
2.2.2. Poincaré Section
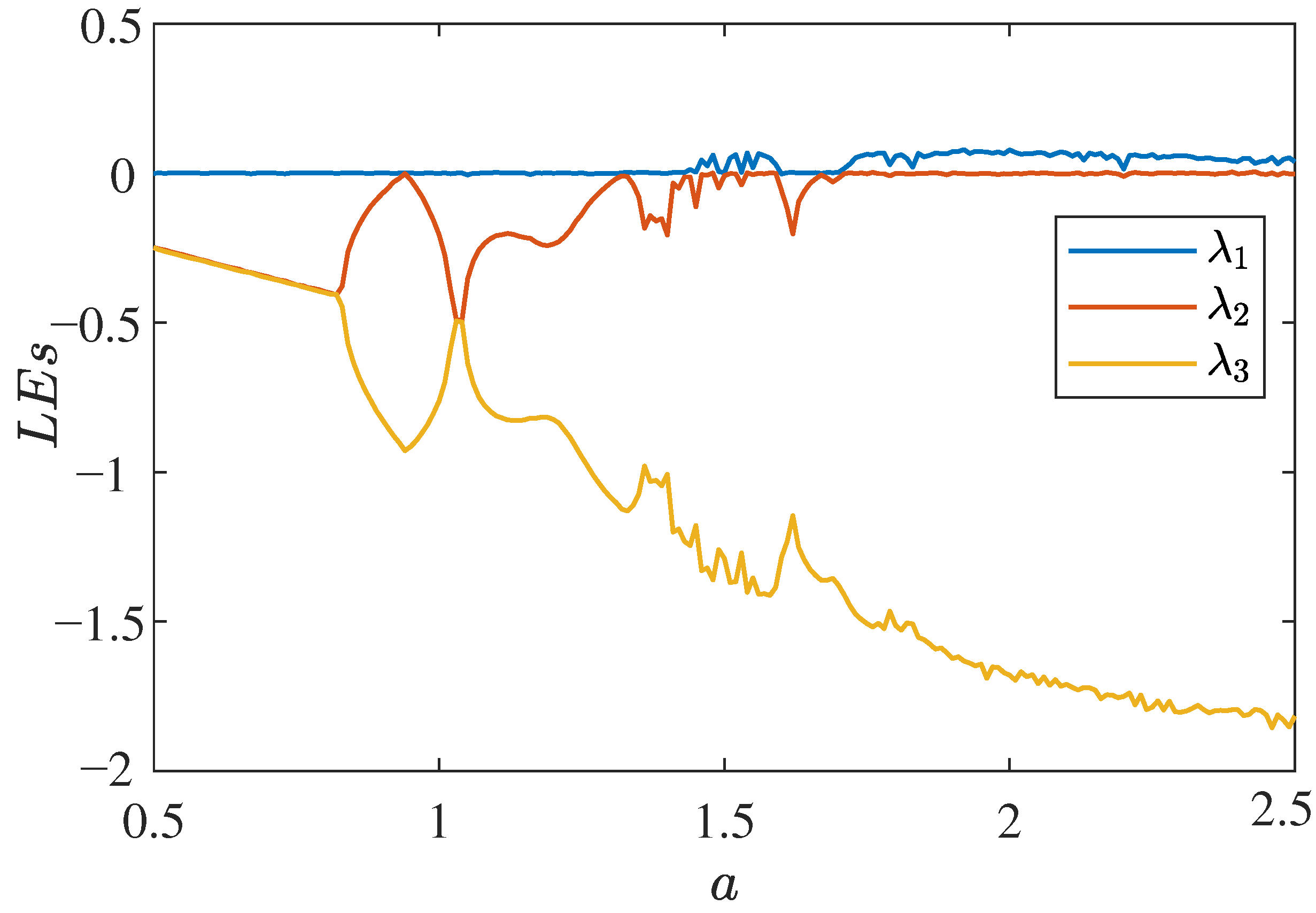
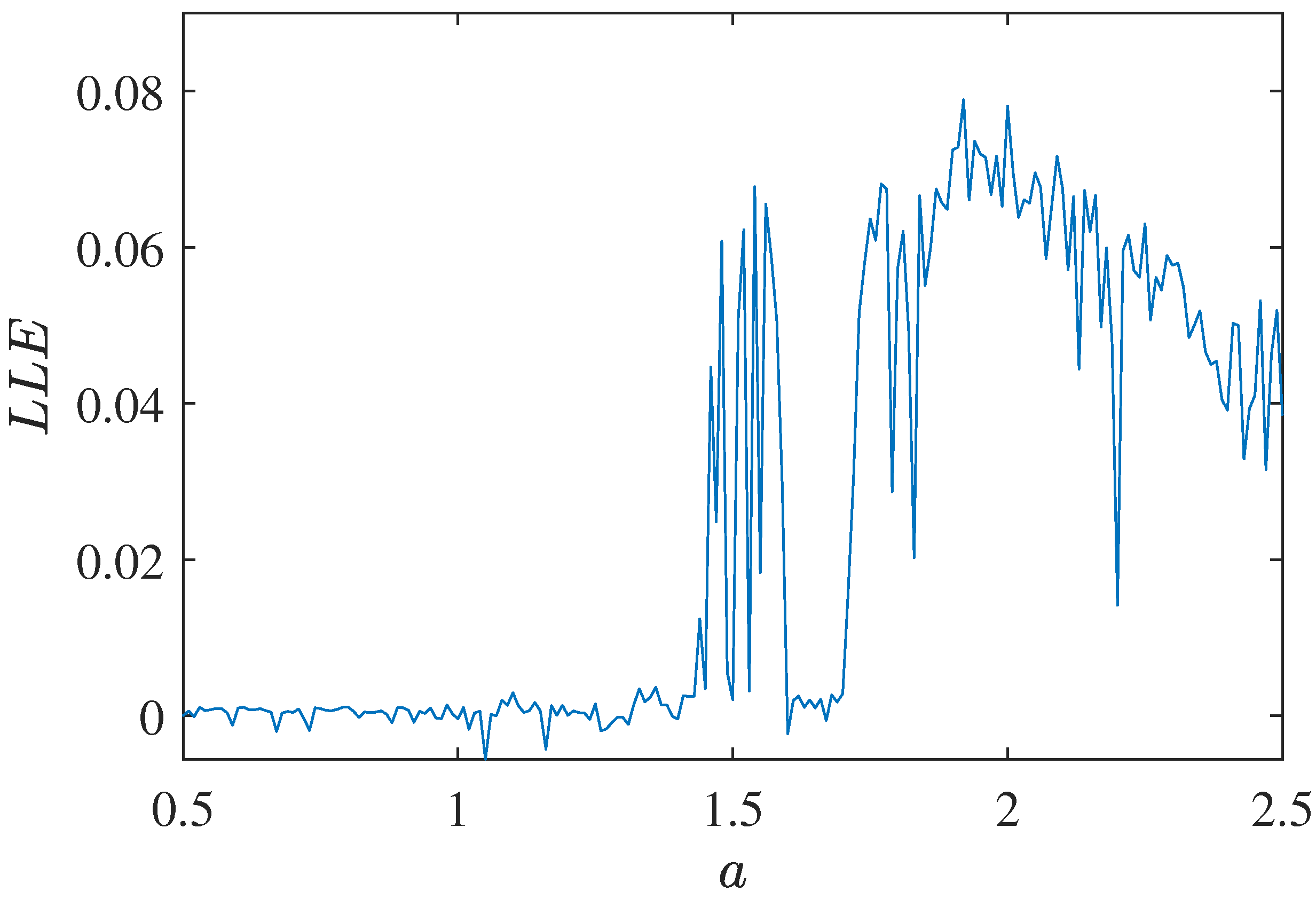
2.2.3. Lyapunov Exponent
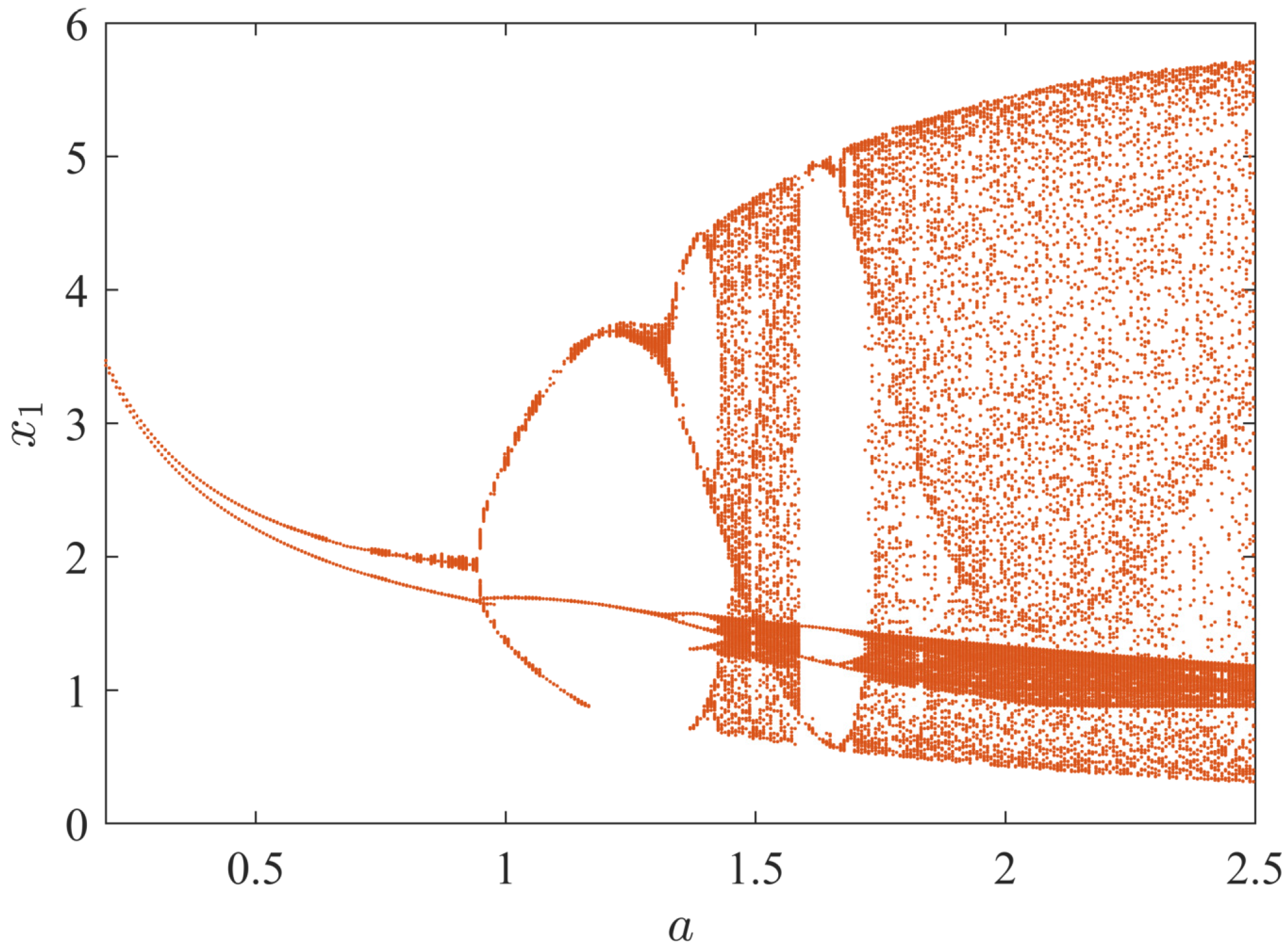
2.2.4. Bifurcation
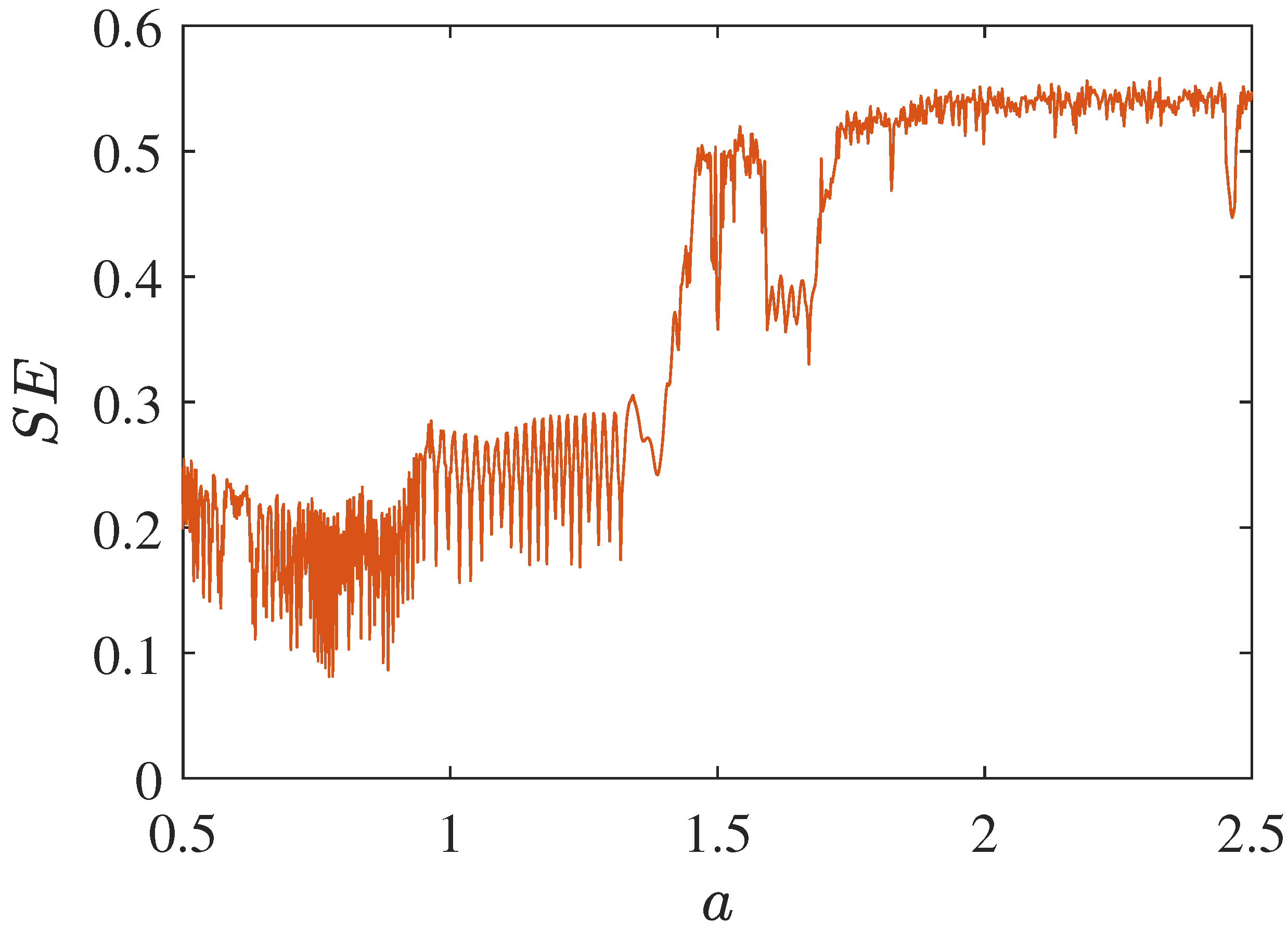
2.2.5. Complexity Resolution
3. Design of Feedback Controller
3.1. Implementation of Robust Controller
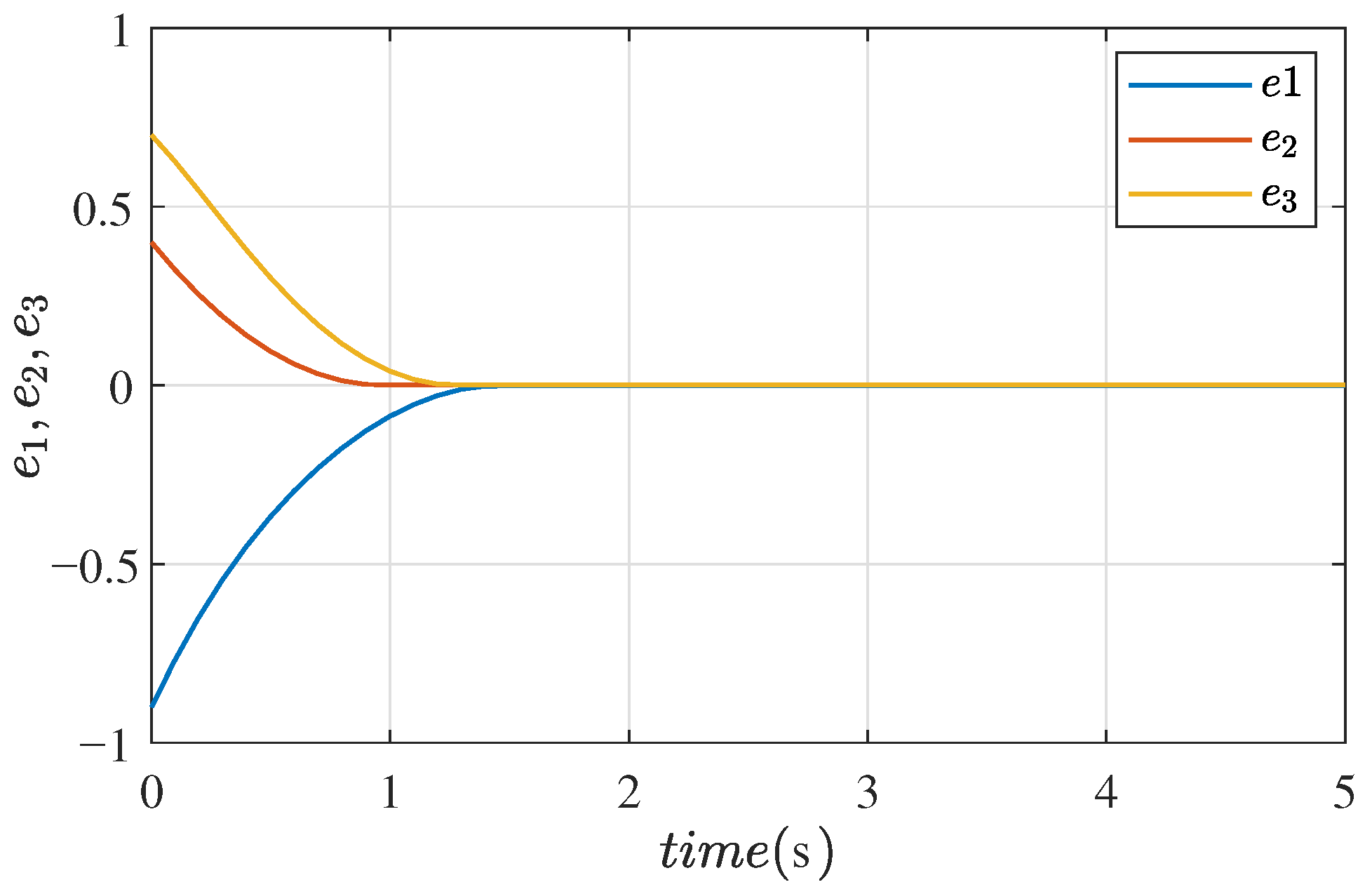
3.2. Performance of Robust Feedback Controller
3.3. Numerical Simulation
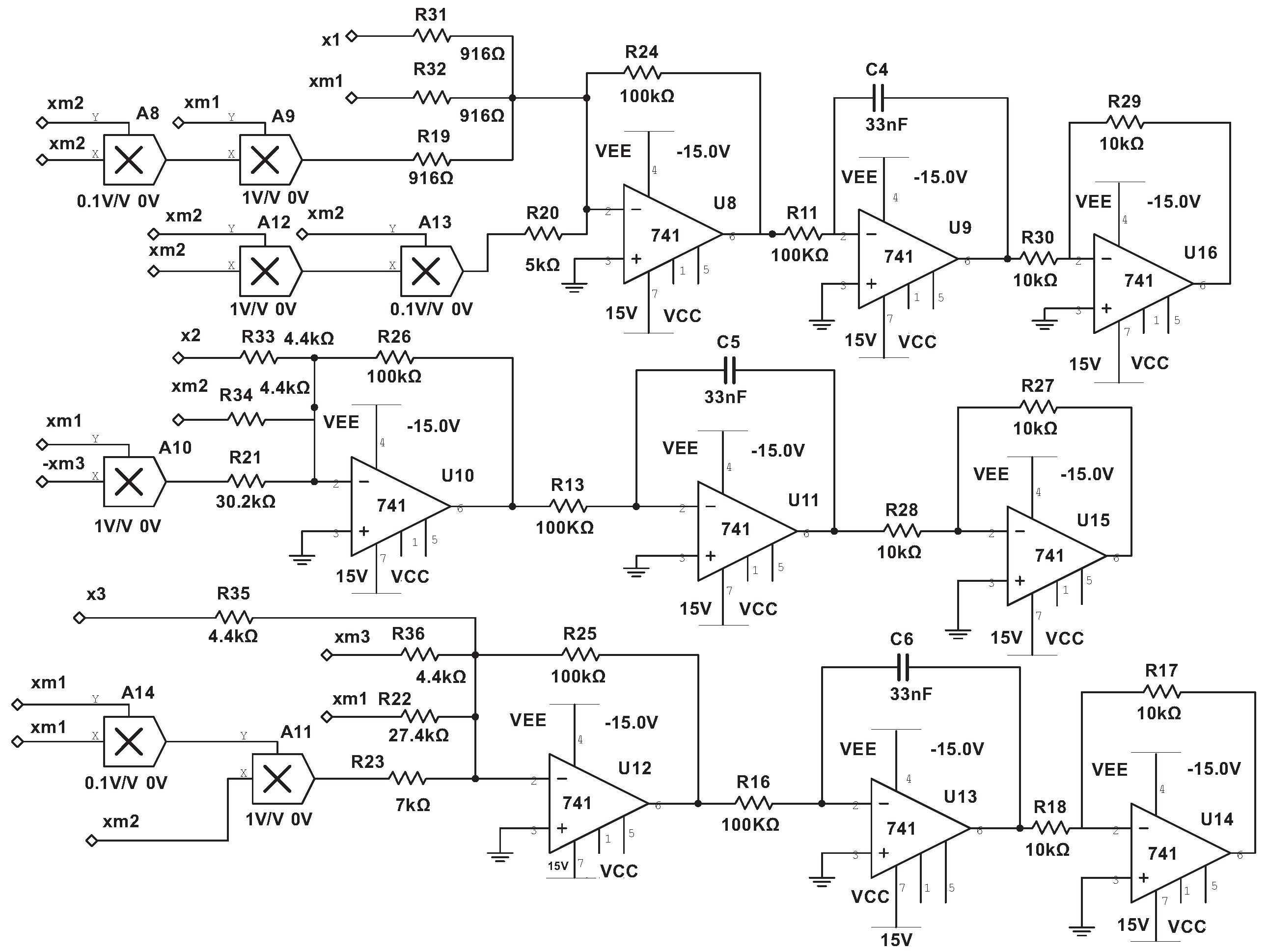
4. Circuit Implementation and Numerical Simulation
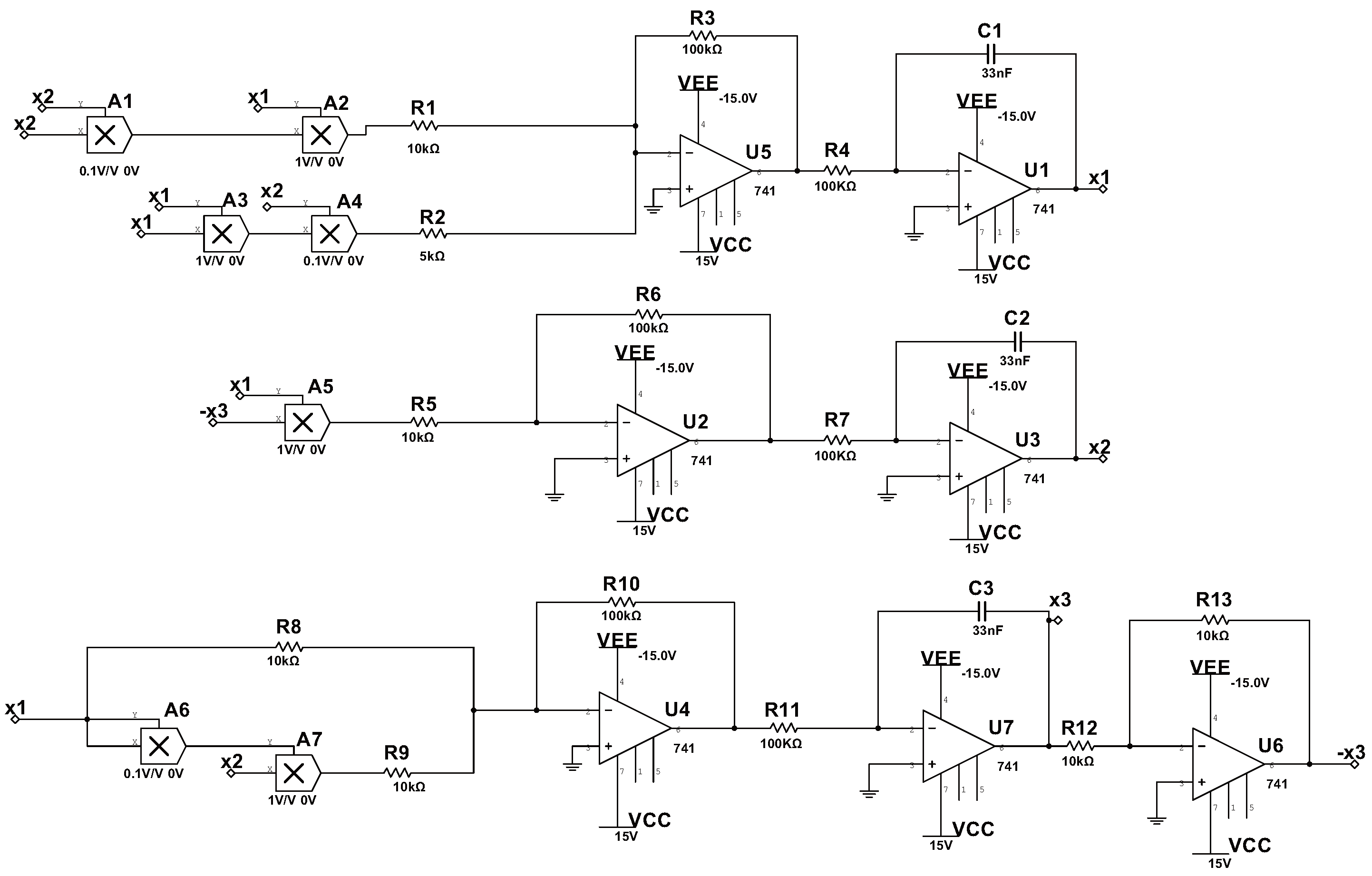
4.1. Circuit Implementation
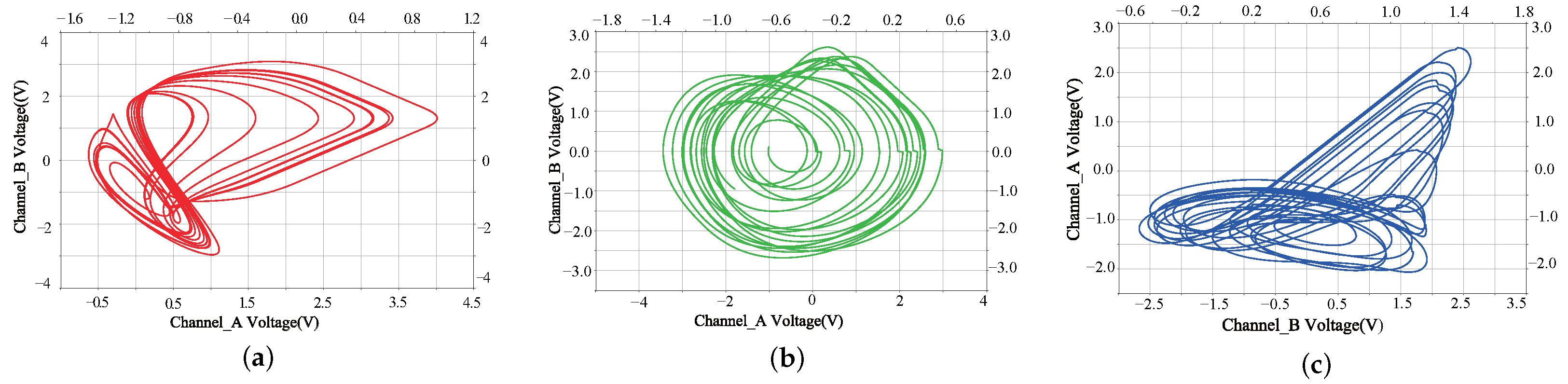
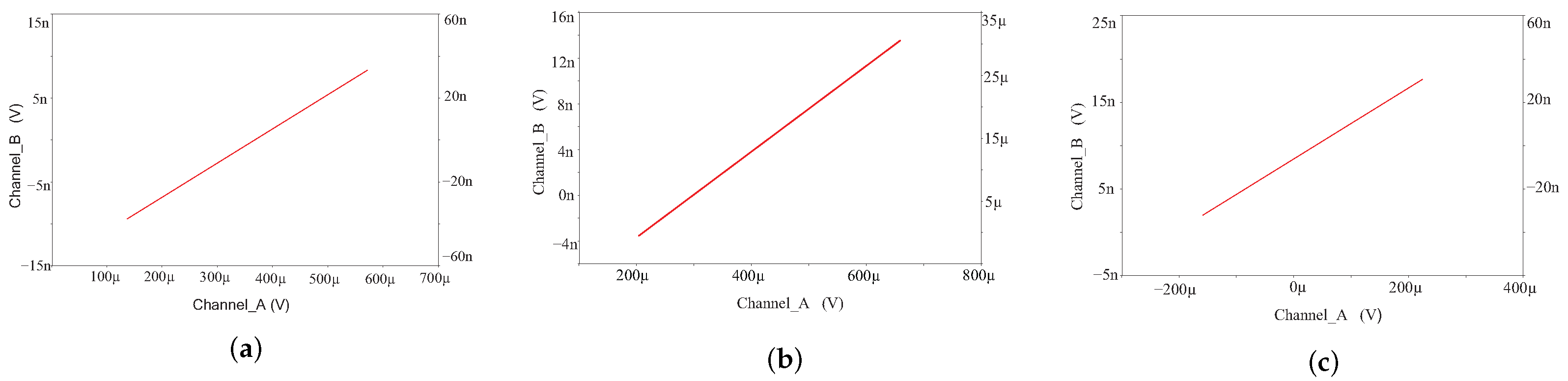
4.2. Circuit Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kapitaniak, T.; Jafari, S. Nonlinear effects in life sciences. Eur. Phys. J. Spec. Top. 2018, 227, 693–696. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Sprott, J.C. Some simple chaotic flows. Phys. Rev. E 1994, 50, R647. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Lü, J.; Chen, G. A new chaotic attractor coined. Int. J. Bifurc. Chaos 2002, 12, 659–661. [Google Scholar] [CrossRef] [Green Version]
- Leonov, G.A.; Kuznetsov, N.V. Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Tian, H.; Wang, Z.; Zhang, H.; Cao, Z.; Zhang, P. Dynamical analysis and fixed-time synchronization of a chaotic system with hidden attractor and a line equilibrium. Eur. Phys. J. Spec. Top. 2022, 231, 2455–2466. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert–Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurc. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef] [Green Version]
- Dudkowski, D.; Jafari, S.; Kapitaniak, T.; Kuznetsov, N.V.; Leonov, G.A.; Prasad, A. Hidden attractors in dynamical systems. Phys. Rep. 2016, 637, 1–50. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, Z.; Sun, K.; He, S.; Wang, H.; Xu, Q.; Chen, M. Chaotic flows with special equilibria. Eur. Phys. J. Spec. Top. 2020, 229, 905–919. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G. A chaotic system with only one stable equilibrium. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1264–1272. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, C.; Yang, L. Four-wing hidden attractors with one stable equilibrium point. Int. J. Bifurc. Chaos 2020, 30, 2050086. [Google Scholar] [CrossRef]
- Wei, Z. Dynamical behaviors of a chaotic system with no equilibria. Phys. Lett. A 2011, 376, 102–108. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Golpayegani, S.M.R.H. Elementary quadratic chaotic flows with no equilibria. Phys. Lett. A 2013, 377, 699–702. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Thio, W. Bistability in a hyperchaotic system with a line equilibrium. J. Exp. Theor. Phys. 2014, 118, 494–500. [Google Scholar] [CrossRef]
- Li, Q.; Hu, S.; Tang, S.; Zeng, G. Hyperchaos and horseshoe in a 4D memristive system with a line of equilibria and its implementation. Int. J. Circuit Theory Appl. 2014, 42, 1172–1188. [Google Scholar] [CrossRef]
- Kingni, S.T.; Pham, V.T.; Jafari, S.; Kol, G.R.; Woafo, P. Three-dimensional chaotic autonomous system with a circular equilibrium: Analysis, circuit implementation and its fractional-order form. Circuits, Syst. Signal Process. 2016, 35, 1933–1948. [Google Scholar] [CrossRef]
- Kapitaniak, T.; Leonov, G.A. Multistability: Uncovering hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1405–1408. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Zhang, G.; Kuznetsov, N.V.; Bao, H. Hidden attractors and multistability in a modified Chua’s circuit. Commun. Nonlinear Sci. Numer. Simul. 2021, 92, 105494. [Google Scholar] [CrossRef]
- Yang, Y.; Qi, G.; Hu, J.; Faradja, P. Finding method and analysis of hidden chaotic attractors for plasma chaotic system from physical and mechanistic perspectives. Int. J. Bifurc. Chaos 2020, 30, 2050072. [Google Scholar] [CrossRef]
- Wang, Z.; Baruni, S.; Parastesh, F.; Jafari, S.; Ghosh, D.; Perc, M.; Hussain, I. Chimeras in an adaptive neuronal network with burst-timing-dependent plasticity. Neurocomputing 2020, 406, 117–126. [Google Scholar] [CrossRef]
- Wang, Z.; Parastesh, F.; Rajagopal, K.; Hamarash, I.I.; Hussain, I. Delay-induced synchronization in two coupled chaotic memristive Hopfield neural networks. Chaos Solitons Fractals 2020, 134, 109702. [Google Scholar] [CrossRef]
- Liang, H.; Wang, Z.; Yue, Z.; Lu, R. Generalized synchronization and control for incommensurate fractional unified chaotic system and applications in secure communication. Kybernetika 2012, 48, 190–205. [Google Scholar]
- Xi, X.; Mobayen, S.; Ren, H.; Jafari, S. Robust finite-time synchronization of a class of chaotic systems via adaptive global sliding mode control. J. Vib. Control 2018, 24, 3842–3854. [Google Scholar] [CrossRef]
- Ghosh, D. Nonlinear-observer–based synchronization scheme for multiparameter estimation. EPL (Europhys. Lett.) 2008, 84, 40012. [Google Scholar] [CrossRef]
- Chaudhary, H.; Khan, A.; Nigar, U.; Kaushik, S.; Sajid, M. An Effective Synchronization Approach to Stability Analysis for Chaotic Generalized Lotka–Volterra Biological Models Using Active and Parameter Identification Methods. Entropy 2022, 24, 529. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Wang, Y.; Shen, Y. Finite-time synchronization between two complex-variable chaotic systems with unknown parameters via nonsingular terminal sliding mode control. Nonlinear Dyn. 2016, 85, 1105–1117. [Google Scholar] [CrossRef]
- Deng, Y.; Hu, H.; Xiong, W.; Xiong, N.N.; Liu, L. Analysis and design of digital chaotic systems with desirable performance via feedback control. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 1187–1200. [Google Scholar] [CrossRef]
- Ghosh, D.; Banerjee, S. Adaptive scheme for synchronization-based multiparameter estimation from a single chaotic time series and its applications. Phys. Rev. E 2008, 78, 056211. [Google Scholar]
- Ghosh, D.; Frasca, M.; Rizzo, A.; Majhi, S.; Rakshit, S.; Alfaro-Bittner, K.; Boccaletti, S. The synchronized dynamics of time-varying networks. Phys. Rep. 2022, 949, 1–63. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, R.; Zhao, L.; Wang, H.; Wei, Z. Control of chaos in vehicle lateral motion using the sliding mode variable structure control. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2019, 233, 776–789. [Google Scholar] [CrossRef]
- Wang, C.; Tang, J.; Jiang, B.; Wu, Z. Sliding-mode variable structure control for complex automatic systems: A survey. Math. Biosci. Eng. 2022, 19, 2616–2640. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Chen, M.; Zhang, P.; Yang, R.; Yang, B. Chaotic system dynamics analysis and synchronization circuit realization of fractional-order memristor. Eur. Phys. J. Spec. Top. 2022, 1–13. [Google Scholar] [CrossRef]
- Tian, H.; Wang, Z.; Zhang, P.; Chen, M.; Wang, Y. Dynamic analysis and robust control of a chaotic system with hidden attractor. Complexity 2021, 2021, 8865522. [Google Scholar] [CrossRef]
- Haimo, V.T. Finite time controllers. SIAM J. Control Optim. 1986, 24, 760–770. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Zhihong, M. Robust global terminal sliding mode control of SISO nonlinear uncertain systems. In Proceedings of the 39th IEEE Conference on Decision and Control (Cat. No. 00CH37187), Sydney, Australia, 12–15 December 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 3, pp. 2198–2203. [Google Scholar]
- Amato, F.; Ariola, M.; Dorato, P. Finite-time control of linear systems subject to parametric uncertainties and disturbances. Automatica 2001, 37, 1459–1463. [Google Scholar] [CrossRef]
- Li, S.; Tian, Y. Finite time synchronization of chaotic systems. Chaos Solitons Fractals 2003, 15, 303–310. [Google Scholar] [CrossRef]
- Perruquetti, W.; Floquet, T.; Moulay, E. Finite-time observers: Application to secure communication. IEEE Trans. Autom. Control 2008, 53, 356–360. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Ye, J.; Miao, Z.; Jonckheere, E.A. Robust finite-time chaos synchronization of time-delay chaotic systems and its application in secure communication. Trans. Inst. Meas. Control 2018, 40, 1177–1187. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Pham, V.T.; Volos, C.; Li, C. Simple chaotic 3D flows with surfaces of equilibria. Nonlinear Dyn. 2016, 86, 1349–1358. [Google Scholar] [CrossRef]
- Aghababa, M.P.; Khanmohammadi, S.; Alizadeh, G. Finite-time synchronization of two different chaotic systems with unknown parameters via sliding mode technique. Appl. Math. Model. 2011, 35, 3080–3091. [Google Scholar] [CrossRef]


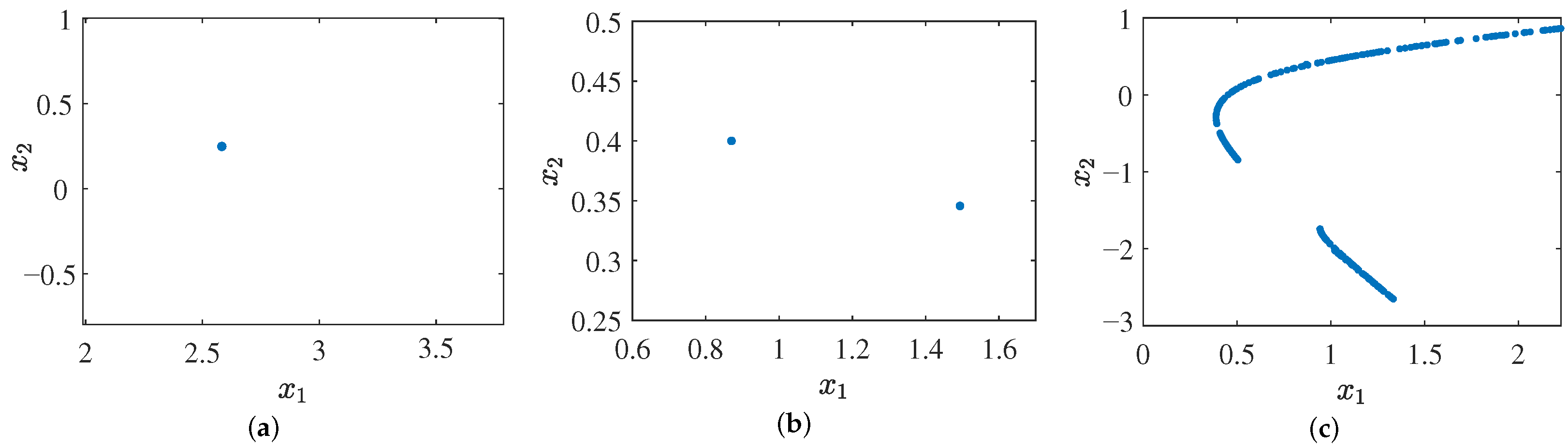


| PVs | Dynamics | LES | PPs | Ps |
|---|---|---|---|---|
| Periodic-1 | [0, −0.1728, −0.1786] | Figure 2a,d,g | Figure 3a | |
| Periodic-2 | [0, −0.0217, −0.1945] | Figure 2b,e,h | Figure 3b | |
| Chaotic | [0.0661, 0, −1.664] | Figure 2c,f,i | Figure 3c |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Xi, X.; Tian, H.; Wang, Z. Dynamical Analysis and Finite-Time Synchronization for a Chaotic System with Hidden Attractor and Surface Equilibrium. Axioms 2022, 11, 579. https://doi.org/10.3390/axioms11110579
Zhang R, Xi X, Tian H, Wang Z. Dynamical Analysis and Finite-Time Synchronization for a Chaotic System with Hidden Attractor and Surface Equilibrium. Axioms. 2022; 11(11):579. https://doi.org/10.3390/axioms11110579
Chicago/Turabian StyleZhang, Runhao, Xiaojian Xi, Huaigu Tian, and Zhen Wang. 2022. "Dynamical Analysis and Finite-Time Synchronization for a Chaotic System with Hidden Attractor and Surface Equilibrium" Axioms 11, no. 11: 579. https://doi.org/10.3390/axioms11110579
APA StyleZhang, R., Xi, X., Tian, H., & Wang, Z. (2022). Dynamical Analysis and Finite-Time Synchronization for a Chaotic System with Hidden Attractor and Surface Equilibrium. Axioms, 11(11), 579. https://doi.org/10.3390/axioms11110579









