1. Introduction
The concept of Population Monotonic Allocation Scheme (PMAS) in cooperative games was introduced by [
1] as a refinement of the core. The concept of core is one way to describe stability of the grand coalition. According to the definition of the core, no player has an incentive to deviate from the grand coalition under a core allocation. A PMAS selects a core distribution for every subgame of a game in such a way that the payoff of any player cannot decrease as the coalition to which he belongs enlarges. As a consequence, a game with a PMAS has a nonempty core (i.e., is balanced).
Sprumont showed that all convex games (defined formally in the next section) have a PMAS and opened a new area of research for game theorists; we mention some of that work next. Conditions for determining whether a game has a PMAS or not was provided by [
2]. For instance, a characteristic function of a four-player game must satisfy sixty inequalities for the game to have a PMAS. Ref. [
3] introduced a new class of totally balanced cost games that consists of all non-negative cost games allowing for PMASes, and called the members of that class PMAS-games. Recently, Ref. [
4] introduced a new notion of convexity that guarantees the existence of PMAS for games with externalities.
As all convex games have a PMAS, PMAS can be proposed for many well-known models; we list here just a few examples. Ref. [
5] applied PMAS to the problem of cost-sharing of public goods and developed a theoretical characterization of the class of games with a PMAS, while Ref. [
6] studied PMAS in bankruptcy problems. More recently, Ref. [
7] studied newsvendor games and showed that when the demands faced by the newsvendors are independent, log-concavity of their distributions is sufficient to guarantee the existence of a PMAS. Ref. [
8] provided a necessary and sufficient characterization for the existence of PMAS in matching games.
Being a member of a larger coalition in a profit game with PMAS implies that your profit cannot decrease if you join a larger coalition, hence it implies nonemptiness of the core. A natural question is how does this monotonicity property impact stability (in the sense of the core) of other coalition structures, and how does it impact stability of various coalition structures under different solution concepts. In this work, we study what are some additional properties that such games may possess because of their structure. More specifically, we are studying the following questions:
Does the special feature of PMAS games (population monotonicity) help in identifying additional stable coalition structures (besides the grand coalition) under different stability concepts in cooperative games—namely, core partitions, the von Neumann–Morgenstern (vNM) stable set, the largest consistent set, and the equilibrium process of coalition formation (EPCF)?
Does the special feature of PMAS games (population monotonicity) help in developing relationships between coalition structures that are stable under these different stability concepts?
To the best of our knowledge, these questions have not yet been studied in literature. Most of the work related to PMAS games, as we indicated above, focused on providing conditions for the existence of PMAS for different classes of games or applying PMAS to some well-known problems. Moreover, while several authors studied relationships between stable outcomes under different solution concepts for general TU games (see, for instance, [
9,
10,
11,
12]; we discuss their work later in the paper when we introduce relevant concepts), none of them focused on specific features of PMAS games. Thus, we believe that our work is novel in exploring the abovementioned questions. We address the first question in
Section 3, and the second one in
Section 4. Our main results can be summarized as follows:
We define two special classes of players for PMAS profit games—extreme and strong players—and use them, along with the notion of weak top-coalition, to develop an algorithm for construction of stable (core) partitions.
We use extreme players to identify absorbing states for equilibrium processes of coalition formation with high level of farsightedness.
We obtain results on stability of the grand coalition and on relationships between stable coalition structures under different stability notions that are consistent with the existing body of knowledge, and establish that, in general, population monotonicity is not sufficient for strengthening of the existing results.
We show that, for general cooperative TU profit games, the members of vNM farsighted stable sets are core partitions, and that core partitions are members of vNM stable sets. Moreover, we show that the members of vNM farsighted stable sets are EPCF-stable partitions.
Thus, with respect to our first question, we were able to reach a positive answer and we used features of PMAS profit games to identify stable coalition structures. With respect to the second question, the answer is mixed–while population monotonicity is, indeed, a nice and desirable feature, it does not provide additional insights into relationship between stable coalition structures under different stability concepts. However, for general cooperative TU profit games, we were able to provide a relationship between EPCF-stable partitions and vNM farsighted stable sets that strengthens the result obtained by [
9], and a relationship between vNM stable sets, core partitions, and vNM farsighted stable sets that we believe is a novel result.
The structure of the paper is as follows. We first introduce some preliminaries in
Section 2, and show how to identify stable coalition structures under different stability concepts in
Section 3.
Section 4 explores relationship between stable coalition structures under different stability concepts, and we conclude in
Section 5. All the proofs can be found in the
Appendix A.
2. Preliminaries
We start with some basic concepts from cooperative game theory. A transferable utility (TU) game is a pair , where N is a finite set (also called the grand coalition) and v is a map that assigns to every a real number with . A game is said to be superadditive if for each such that , it holds that . Thus, as the value of two disjoint coalitions after merger is never less than the sum of their values before merger, when a game is superadditive, it is reasonable to expect formation of the grand coalition. A particular class of superadditive games is the class of convex games. A game is said to be convex if for each it holds that It can be shown that this condition is equivalent to for all . The convexity property provides us with additional information about the game: the marginal contribution of an agent increases as a coalition grows.
One of the main issues treated in cooperative game theory is how to divide the benefits from cooperation if the players act together, that is, if the grand coalition has formed. We are interested in providing a distribution of the total value,
, so that no coalition has an incentive to leave the grand coalition and receive less. One way to share these benefits is according to an allocation in the core. A vector
such that
is called an
efficient allocation. The allocation
x is
coalitionally stable if it satisfies condition
The
core of
is denoted by
and is the set of all efficient allocations that are coalitionally stable, that is
when an element of the core (henceforth, a core allocation) in which player
i receives the payoff
is proposed, every coalition
S of players should receive at least the amount they can generate on their own. A game is balanced if and only if it has a non-empty core (see [
13,
14]), and it is called totally balanced (see [
15]) if each subgame
is balanced, where
, for all
. In addition, Ref. [
16] shows that convex profit games are always balanced.
A refinement of the core is the set of allocations of the total benefit that can be reached through a Population Monotonic Allocation Scheme; in short, PMAS. These schemes were introduced in [
1] and defined as follows.
Definition 1. A vector is a PMAS of the game (N,v) if and only if satisfies the following two conditions:
- (i)
for all non empty coalitions , and
- (ii)
for all nonempty coalitions and for all players , implies .
It was also showed in [
1] that a core allocation,
, is reached through a PMAS of the game if there exists a PMAS
such that
. Moreover, every game with PMAS is totally balanced and thus superadditive, but there exist totally balanced games without PMAS. Finally, a vector
is a Strong PMAS (SPMAS) if the second condition is satisfied strictly; that is,
implies
, for all
.
The class of non-negative TU cost games that possess a PMAS was studied in [
3] and referred to as PMAS-games. The authors showed a direct relationship between PMAS-games and Production Inventory games. In this paper, we analyze profit games with PMAS and refer to them as [
3], can be easily adapted to this setting by replacing the cost function with its negative counterpart.
As being a member of a larger coalition implies that your profit cannot decrease, the grand coalition is always stable in PMAS profit games. However, this does not imply that other partitions of players cannot be stable. In this paper, we study stability of partitions of the set of all players when a PMAS is used.
We identify two separate groups of players, strong and weak players, and a sub-group of strong players, called extreme players, which have important roles in our further analysis.
Definition 2. Let be a TU game with a PMAS
Player i is a strong player for N in coalition if , and he is a weak player for N in Sif for all .
Player i is strong for Nif there exists a coalition such that i is a strong player for N in coalition S.
Coalition is a strong coalition for Nif there exists a strong player for N in S.
Player i is an extreme player for Nif is a strong coalition for N.
Coalition is an extreme coalition for Nif all its members are strong players for N in S.
Note that if i is a strong player for some , then i is a strong player for all T such that . In addition, if S is an extreme coalition, all members of S receive their highest payoffs in all sets that contain S.
We next introduce the definition of coalition structures. Consider TU game with finite set of players . A coalition structure is a collection of subsets which partitions N; that is, . The subsets are called coalitions. We will use to denote the set of all coalition structures (partitions) of N. For a given , we denote by the coalition in partition that player i belongs to; that is . Each player has preferences over possible coalition structures, which are determined by the coalition that he belongs to. We represent these preferences by a complete, reflexive, and transitive binary relation defined on the set , and we use to denote associated asymmetric relation of strict preferences. If for all , we write . A TU game with preferences, , is described by the TU game and corresponding preferences ⪰.
As mentioned above, our focus in this paper are PMAS profit games. Let vector be a PMAS of the game . Then, we know that for all . Consider two arbitrary coalitions such that . We define , and we say that is a PMAS profit game with preferences. By definition of PMAS, we have . We denote the set of strong players for this game by ; we shorten this notation to when the underlying game is obvious.
Next, we describe some well-known stability concepts and their related properties. We start with static/myopic stability concepts (the core and the von Neumann–Morgenstern stable set), and then move to dynamic/farsighted concepts of stability (the largest consistent set, the von Neumann–Morgenstern farsighted stable set, and the equilibrium process of coalition formation).
2.1. Myopic Stability
Most of the stability concepts studied in the literature presuppose myopia of the players, in the sense that the players do not take into account how their decisions affect future decisions of other players. Myopic stability is also called static stability because it assumes that the agents who consider possible deviations from stable coalition structures look only at immediate consequences of their actions and not at the potential reactions by other coalitions that may be triggered by their move.
Two well-known myopic stability concepts are the core and the von Neumann–Morgenstern (vNM) stable set. The core was introduced by [
17] as the set of allocations that lead to stability of the grand coalition. Several researchers afterwards extended the concept of the core to stability of arbitrary partitions/coalition structures. In this paper, we adopt the definition proposed by [
18,
19].
Definition 3. Let be a TU game with preferences. Given a coalition structure , if there is a coalition such that for all , we say that T blocks . If which blocks , we say that coalition structure is a core partition.
This definition is consistent with the definition of the core, as no coalition can benefit from defecting from the status quo coalition structure.
Several authors studied properties that a game should possess in order to have a nonempty core; we introduce some of these properties as they will be useful in our characterization of stable core partitions. The notion of the common ranking property was introduced in [
20]: A game
satisfies
the common ranking property if for any
and any
,
, we have
. They showed that this condition ensures nonemptiness of the core, but it can be difficult to satisfy in arbitrary games. Two relaxations of the common ranking property were considered in [
18], as follows.
Definition 4. Let be a TU game with preferences.
Given a non-empty set of players , a non-empty subset is a top-coalition of V if and only if for any and any with , we have .
satisfies the top-coalition property if and only if for any non-empty set of players , there exists a top-coalition of V.
This condition requires that, for any group of players V there is a subgroup that is mutually the best for all its members. This can be a rather strong requirement which does not hold in many situations, so they introduced a following weaker condition.
Definition 5. Let be a TU game with preferences.
Given a non-empty set of players , a non-empty subset is a weak top-coalition of V if and only if S has an ordered partition such that
for any and any with , we have and
for any , and any with , we have .
satisfies the weak top-coalition property if and only if for any non-empty set of players , there exists a weak top-coalition of V.
This definition implies that a coalition
S is a weak top-coalition of
V if it has a partition
such that any agent in
prefers
S to any subset of
V, any agent in
needs cooperation of at least one agent in
in order to form a better coalition than
S, any agent in
needs cooperation of at least one agent in
in order to form a better coalition than
S, and so on. Ref. [
18] showed that every game that satisfies the weak top-coalition property has a nonempty core, and that every game that satisfies the top-coalition property with strict preferences has a unique core partition. We will use these two concepts, top-coalition and weak top-coalition property, in
Section 3.1 to establish some theoretical results for PMAS games that will be used in the algorithm for construction of core partitions.
Let us now move to the stable set as introduced by [
21]. Given a TU game
, denote by
the following relation:
if the coalition structure
is obtained when
S deviates from the coalition structure
and
S is a coalition in
. The following definition shows the concepts of direct and indirect dominance.
Definition 6. Let be a TU game.
We say that is directly dominated by , denoted by , if there exists an S such that , and .
We say that is indirectly dominated by , denoted by , if there exist and such that and for .
Note that we can use the concept of direct dominance to restate our definition of core partitions—a partition of the set of all players,
N, is a core partition if there is no other partition that dominates it directly. We can now define stable sets as introduced by [
21].
Definition 7. Let be a TU game and the set of all coalition structures of N. A set is called von Neumann–Morgenstern (vNM) stable set if it satisfies:
- (i)
Internal stability—there are no such that ;
- (ii)
External stability—for every there is a such that .
Note that core partitions satisfy internal stability as they cannot be directly dominated by other coalition structures.
We next consider some dynamic/farsighted concepts of stability.
2.2. Farsighted Stability
As discussed above, myopic stability only takes into account the immediate consequences of possible players’ deviations without considering potential reactions from other coalitions that may be triggered by such moves. However, it may very well happen that an initial deviation is followed by a sequence of other defections before some sort of stability is reached. Notions of stability that capture some of these dynamics and prove to be of great theoretical and practical value include the largest consistent set, vNM farsighted stable set, and equilibrium process of coalition formation.
We begin with the consistent set, introduced by [
9].
Definition 8. Let be a TU game and the set of all coalition structures of N. A set is called consistent if if and only if for all and S, such that , there is a , where or , such that .
In fact, Ref. [
9] proved the existence, uniqueness, and non-emptiness of the largest consistent set (henceforth LCS). Since every coalition considers the possibility that, once it reacts, another coalition may react, and then yet another, and so on, the LCS incorporates
farsighted or
dynamic coalitional stability. Some members of the LCS can directly dominate other members, so internal stability generally does not hold for the LCS. In fact, the LCS and the vNM stable set can make very different predictions about potentially stable coalition structures. However, if we replace direct dominance with indirect dominance, we can establish relationship between the LCS and the vNM stable set. Let us first introduce the following definition.
Definition 9. Let be a TU game and the set of all coalition structures of N. A set is called vNM farsighted stable set if it satisfies:
- (i)
Internal stability—there are no such that ;
- (ii)
External stability—for every there is a such that .
We note here that Ref. [
9] studied sets that satisfied internal and external with respect to direct and indirect dominance. Ref. [
11] referred to sets that satisfied internal and external stability with respect to indirect dominance as vNM farsighted stable sets. On the other hand, Ref. [
12] referred to such sets as Harsanyi stable sets, as Ref. [
22] proposed a modification of the dominance concept from Ref. [
20] in order to account for farsighted behavior.
It was showed by [
9] that vNM farsighted stable sets belong to the LCS; thus, while the relationship between the LCS and the vNM stable sets cannot be established with respect to direct dominance, we can do it with respect to the indirect dominance. Note that core partitions satisfy internal stability with respect to direct dominance, but not necessarily with respect to indirect dominance.
A criticism of the LCS is that it may be too inclusive. As a result, Ref. [
10] proposed an alternate dynamic approach to stability of coalition structures, which they called the
equilibrium process of coalition formation (henceforth EPCF), and established a possible link between the LCS and the limit states of absorbing deterministic EPCFs.
Before we define the EPCF we need to introduce some notation. For each player , let denote its discount factor. Then, i’s payoff from a sequence of coalition structures may be written as , where is the payoff that player i receives in coalition structure . Clearly, a larger value of implies higher a level of farsightedness.
Definition 10. Let be a TU game and the set of all coalition structures of N. A process of coalition formation (PCF) is a transition probability , so that .
A PCF
p induces a value function
for each player
i, which represents the infinite horizon discounted payoff to a player starting from any coalition structure
under the Markov process
p and is the unique solution to the equation
We say that coalition
S has a profitable move from
under
p if there exists
such that
We say that coalition S has a strictly profitable move from under p if the last inequality is strict. Now, we can define an EPCF, as follows.
Definition 11. Let be a TU game and the set of all coalition structures of N. A PCF is an equilibrium PCF (EPCF) if:
whenever for some , , then there is a coalition S such that is a profitable move for S from
if there is a strictly profitable move from then and there is a strictly profitable move with .
Thus, a deviation from one coalition structure to another occurs only if all members of the deviating coalition agree to move. In addition, the deviation from a coalition structure must occur if there is a strictly profitable move. Notice that this definition does not require that every strictly profitable move has a positive probability.
A PCF is called deterministic if . A coalition structure is said to be absorbing if , while a PCF is absorbing if, for every coalition structure there is some absorbing coalition structure such that , where denotes the k-step transition probability. Konishi and Ray (2003) showed that, when the discount factor is large enough, the set of all absorbing states under all deterministic EPCFs is a subset of the LCS. Thus, absorbing states may provide a refinement of the LCS. To simplify the exposition, we will refer to absorbing states of deterministic EPCFs as EPCF-stable partitions.
3. Stability under PMAS Allocations
We are now ready to identify some stable coalition structures under abovementioned stability concepts for PMAS profit games. Consider a PMAS profit game with preferences, . We know that the grand coalition is always a core structure for such allocations, hence a PMAS game has a nonempty core. We next show that strong players play an important role in achieving stability under PMAS allocations. More specifically, we demonstrate how strong players in PMAS profit games can be used to identify stable coalition structures beyond the grand coalition.
Let us first assume that the game does not possess strong players. The following result is straightforward.
Proposition 1. Let be a PMAS profit game with preferences. If , then the grand coalition is the only core partition. In addition, it is the unique EPCF-stable partition and the unique member of the LCS.
Indeed, we can see that from any coalition structure a joint defection by all players strictly benefits all players; thus, partitions of players into smaller groups cannot be stable. As a result, in this scenario the core partitions, the EPCF-stable partitions, and the LCS coincide. Of more interest are examples in which we have strong players; that is, games in which some players receive their highest payoffs in both the grand coalition and some of its strict subcoalitions.
The following example illustrates that, for PMAS profit games with strong players, the grand coalition ceases to be the only stable structure. At the same time, it also shows that even for PMAS profit games, core partitions may fail to satisfy other notions of stability.
Example 1. Consider the PMAS profit game with preferences, , where , and the characteristic function and the PMAS are given in Table 1. It is easily checked that players 1, 2, and 3 are strong players for N but not extreme; that is, . We next identify a coalition structure that belongs to the core partition set and the LCS but is not EPCF-stable.
Consider coalition structure ; it is a core structure because we cannot find a blocking coalition T. To see this, observe that player 2 is a strong player for N who cannot improve upon its payoff, so any blocking coalition cannot include player 2. At the same time, the payoff of player 4 only increases in the grand coalition, which requires participation of all players, including player 2, so 4 cannot belong to a blocking coalition as well. Lastly, any blocking coalition containing player 1 and/or player 3 would require participation of players 2 and/or 4 in order to increase their payoffs.
To see that
is in the LCS, observe that player 2 generates its highest payoff in
, so 2 does not want to defect. If player 4 defects on its own from
in order to potentially induce player 2 to join the grand coalition, it may trigger the sequence
in which player 4 would be worse off. Similar conclusions can be made for joint defections in which 4 is joined by 1 and/or 3, so player 4 does not want to defect either. The only defections that players 1 and/or 3 can make without players 2 and 4 would not change their profit, hence
is in the LCS.
To see that cannot be EPCF-stable, suppose that the current status quo is the grand coalition. Players 1, 3, and 4 do not want to make a move from the grand coalition that eventually leads to , as represents strictly lower payoff for them. This leaves us with player 2, whose profit in corresponds to its profit in the grand coalition. If 2 made the move from the grand coalition alone, it would reduce its payoff during one period from 3 to 1. As 3 is the highest profit for 2, making such a move would strictly reduce its infinite horizon discounted payoff. Consequently, we cannot find profitable moves from the grand coalition that eventually lead to , and is not EPCF-stable.
The grand coalition should belong to a vNM farsighted stable set, if it exists, as it is not dominated by any other coalition structure. It is easy to see that the grand coalition dominates
indirectly:
hence internal stability prevents
to be a member of a vNM farsighted stable set.
Thus, in this example joins the grand coalition as a core structure. It belongs to the LCS, but is not EPCF-stable or a member of a vNM farsighted stable set. Observe that coalition is a strong coalition for N that is also a weak top-coalition; we will show next how these properties can be used to construct core partitions.
3.1. Core Partitions
First, we explore relationships between PMAS profit games and top-coalition properties. The following proposition shows that PMAS profit games with preferences always satisfy top-coalition property.
Proposition 2. Every PMAS profit game with preferences, , satisfies the top-coalition property.
It was shown in [
18] that every ordered coalition structure
such that
is a weak top-coalition of
is a member of the core. Next, we study the composition of weak top-coalitions in PMAS profit games and use it to describe core coalition structures.
Lemma 1. Let be PMAS profit game with preferences. If , then every set consisting of only extreme players represents a top-coalition of N.
This result is straightforward, as extreme players do not benefit by defecting from any coalition. We continue by considering more general structures of top-coalitions.
Lemma 2. Let be PMAS profit game with preferences and . Let S be a weak top-coalition of N with ordered partition as introduced in Definition 5. Then, every is a strong player for N in coalition S, and cannot be a strong player for N in coalition S.
We use these results to construct an algorithm for finding core partitions for PMAS profit games. Namely, for each strong coalition S of N we check if it satisfies weak top-coalition property; if that is the case, S is an element of a core partitions.
Algorithm for finding core partitions
Consider PMAS profit game with preferences . The grand coalition is always a core partition.
- Step 1:
If , then the grand coalition is the only core partition.
- Step 2:
If every player is an extreme player, then all partitions are core partitions.
- Step 3:
If and the game has strong players who are not extreme, let be the set of all strong coalitions of N. For each , denote by the set of all strong players for N in S.
If there is a player and set such that and , then S is not a weak top-coalition. Move to the next element of .
If the above does not hold, then S is a weak top-coalition and a member of a core partition. To identify the remaining elements of this core partition, repeat the steps of the algorithm by replacing N with .
We now use the algorithm to find the core partitions for our previous example. We can observe that the presence of strong players makes the core partition set grow beyond the grand coalition.
Example 2. We return to the game described in Example 1. We know that 1, 2, and 3 are strong players that are not extreme, and that .
We can easily verify that whenever S is a three-player strong coalition in N, then S is a weak top-coalition, so by Step 3.2 is a core partition.
is not a weak top-coalition because , hence, by Step 3.1, is not a part of a core partition for N.
When , we showed in Example 1 that it cannot be dominated, so is a member of a core partition by Step 3.2. We replace by and repeat the steps of the algorithm.
Observe that both 1 and 3 are extreme players for , so by Step 2 all partitions are core partitions for . Thus, both and are core partitions for N.
As a result, all the core partitions for the original game are
It is easy to verify that this set also satisfies external and internal stability with respect to direct dominance—all partitions that are not core partitions are directly dominated either by the grand coalition or by while internal stability holds by definition of core partitions. Thus, this set is also a vNM stable set.
3.2. EPCF-Stable Partitions
We first note that in arbitrary games a player can have a strict preference for an arbitrary coalition structure over the grand coalition. Thus, a defection from the grand coalition that reduces its payoff during one round can be offset by increased payoffs in subsequent rounds when the discount factor is large enough. However, this is never the case with PMAS profit games, in which the grand coalition is the most preferred (although in some instances this preference is weak) coalition structure for all players. Thus, when considering EPCF-stable partitions, it is important to consider possible defections from the grand coalition. In order for such defection to lead to stable coalition structures, they need to be conducted by extreme coalitions (that is, coalitions S that consist only of strong players for N in S). However, once such an initial defection is made, subsequent moves can be taken by coalitions which are not extreme.
Example 3. We return again to the game described in Example 1. Note that is the only extreme coalition for N for this example. Following our discussion above, we can verify that only and are EPCF-stable. To that point, consider any other partition as the candidate for stability and assume that the grand coalition is the status quo. Any defection from the grand coalition other than would reduce payoff of the defecting members in at least one cycle, hence it would be deterred.
We can also easily verify that the set of EPCF-stable partitions, , satisfies both external and internal stability with respect to indirect dominance. While we can easily observe that neither of the two EPCF-stable partitions indirectly dominates the other one as is the extreme coalition for N, we need to verify external stability:
shows .
shows .
shows .
shows
.
shows
.
shows .
All other partitions that are not EPCF-stable are directly dominated by the grand coalition. Thus, the set of EPCF-stable partitions is vNM farsighted stable.
While Example 3 shows that an extreme coalition for N is a member of an EPCF-stable partition, the example below shows that we can have EPCF-stable partitions in which all coalitions contain players that are not strong for N in their respective coalitions. In other words, there exist EPCF-stable partitions that do not contain extreme coalitions for N.
Example 4. Consider again the game described in Example 1. While the original game did not contain extreme players, we now assume that player 3 is an extreme player for N; that is, for all , while all the remaining allocations to all other players remain unchanged. Once again, 1, 2, and 3 are strong players for N, but the set of strong coalitions now contains all coalitions containing player 3; in other words, it increases toHowever, of all new members of only satisfies weak top-coalition property. As a result, core partitions for the new game are the same as the ones obtained for the original game. Note that the vNM stable set in this case contains all core partitions and partition , as is directly nominated only by , which is dominated by and cannot be in a vNM stable set. Now, if we consider the EPCF, our results differ from the ones in Example 3; in this case the EPCF-stable partitions coincide with core partitions, and some coalitions contain members that are not strong for N in their respective coalitions. To see this, first observe that is an extreme coalition for N in this case. If we consider the set , we can observe that is an extreme coalition for . Let us denote We want to show that and are EPCF-stable.
First, in order to show that is EPCF-stable, consider the following PCF:The payoff for players in S does not change if they defect from N. Furthermore, note that the move in (
2c)
takes players in coalition S to the state in which their payoff is the highest. Finally, the move by players in in (
2d)
cannot reduce their payoff as they are ending up in a larger set. Players from S have no incentive to move from S, and players in cannot increase their payoff on their own. Thus, is an absorbing state. To show that is EPCF-stable, we replace (
2b)
byAs S is an extreme coalition, joint defection with T does not impact payoffs of its members, while the payoff of players in T is the same in T and in , and joining players in S can only increase their payoff. To show that is EPCF-stable, we replace (
2b)
byAs T is an extreme coalition for , defection from does not change payoffs of its members. In the second sequence, joining the players in S can only improve the payoffs of players in . Finally, to show that is EPCF-stable, we replace (
2b)
by
Thus, in this example all core partitions are also EPCF-stable.
We can also easily verify that the set of EPCF-stable partitions satisfies both external and internal stability with respect to indirect dominance. As player 2 is strong player for N in and in all three-player coalitions it belongs to, we can easily show that internal stability holds. To show external stability, first observe that sequenceshows . In addition, it is easy to verify that directly dominates all other partitions that are not EPCF-stable, as it is a more preferred coalition structure for players 2 and 4. Thus, the set of EPCF-stable partitions is vNM farsighted stable. Moreover, note that none of the coalitions in partitions
or
is extreme.
We can now state a Theorem that characterizes the EPCF-stable partitions in PMAS profit games.
Theorem 1. Consider a PMAS profit game with preferences, . Then,
For any and for any absorbing deterministic EPCF, the grand coalition is EPCF-stable. The grand coalition is the only EPCF-stable partition if and only if N has no extreme coalitions.
If is an extreme coalition for N, then is EPCF-stable. Moreover, if is an extreme coalition for , then and are also EPCF-stable.
To complete our analysis of stability under PMAS, we next study the LCS.
3.3. The LCS
We start this section with an example that illustrates the inclusive nature of the LCS for PMAS profit games without extreme coalitions.
Example 5. Consider the following PMAS profit game with preferences, , where , and the characteristic function and the PMAS are given in Table 2. We can observe that all players are strong for N, but none of them is extreme. In addition, players have circular preferences for coalition structures containing two-player coalitions:
In this example, the grand coalition is the only core structure. If, for instance, we consider coalition structure and , it is easy to see that and , hence T is blocking for .
It is easy to verify that no vNM stable set exists as , hence because of internal stability the stable set could contain only one partition with a two-player coalition. Suppose that is in a vNM stable set. Then, cannot be in that vNM stable set because it is dominated by , and cannot be in that vNM stable set because it dominates . But this implies that there is no element of that vNM stable set that dominates , which would violate external stability. Because of symmetry, the same reasoning can be applied to all partitions with a two-player coalition, hence no vNM stable set exists.
The grand coalition is the only EPCF-stable partition—if any player deviates from the grand coalition alone, its payoff is reduced in one period, and if any two-player coalition defects, the player of one coalition member decreases. As payoff in no other coalition dominates the payoff in the grand coalition, no player or coalition have a profitable move from the grand coalition.
However, the LCS contains, besides the grand coalition, all coalition structures containing a two-player coalition; that is,
Indeed, consider, for example, coalition structure
. As coalition
is strong for
N with player 1 as a strong player, this player does not want to defect, and player 3 cannot defect alone. Thus, possible defections are either by player 2 alone, or a joint defection by players 2 and 3. Consider the following sequence of defections:
It is easy to see that
, and that
, so player 2 does not want to initiate a joint defection with player 3 that may eventually make it worse off. Similar conclusions can be obtained by considering the following sequence of defections:
Thus, is in the LCS. As the payoffs are symmetric, the same is true for the remaining two coalition structures containing two-player coalitions.
The vNM farsighted stable set coincides with the EPCF-stable partitions and contains only the grand coalition.
Note that in the Example 5 we do not have any extreme coalitions. However, unlike in the case with the EPCF, wherein the lack of extreme coalitions implies that the grand coalition is the only stable coalition structure, the LCS has multiple elements. The following proposition shows that the LCS may contain other coalition structures in addition to the grand coalition.
Proposition 3. The grand coalition is always in the LCS for a PMAS profit game with preferences, . The LCS can contain multiple coalition structures even if the the game does not possess extreme coalitions.
The result follows directly from Example 5 and the fact that no player’s profit in an arbitrary coalition can dominate its payoff in the grand coalition.
In this section, we have addressed our first research question and used population monotonicity to help in identifying stable coalition structures. More precisely, we have defined two special classes of players for PMAS profit games—extreme and strong players—and used them, along with the notion of weak top-coalition, to develop an algorithm for construction of stable (core) partitions. Furthermore, we used extreme players to identify EPCF-stable partitions. Next, we focus on our second question and study the relationships between coalition structures that are stable under different solution concepts.
4. Comparison of Stable Coalition Structures
In this section we compare stable coalition structures under different stability concepts studied above. We start by comparing EPCF-stable partitions with core partitions in PMAS profit games.
Theorem 2. Consider a PMAS profit game with preferences, . Then,
There exists a threshold such that for any collection of discount factors and for any absorbing deterministic EPCF, the set of all EPCF-stable partitions is contained in the set of core partitions of .
Core partitions of do not need to be EPCF-stable.
For general games, we note that Ref. [
10] compared the EPCF-stable partitions with stable coalition structures under other stability concepts. They used the notions of weak and strong core states, wherein weak core states coincided with our core partitions, and strong core states represented a subset of weak core states. Theorem 4.2 from [
10] corresponds to our Theorem 2.1, and their Theorem 4.1 established the relationship between strong core states and EPCF-stable states, which is consistent with our Theorem 2.2. Thus, our results about the relationships between core structures and EPCF-stable partitions for PMAS profit games are consistent with results from [
10] for general games, and the introduction of PMAS did not bring additional insights. However, in the previous section we were able to show how to easily identify EPCF-stable partitions in PMAS profit games with extreme coalitions.
Next, we compare core partitions and EPCF-stable partitions with vNM stable sets. In this part of our analysis, we do not use the existence of PMAS. Hence, we are able to obtain some general results for any TU profit game with preferences. We start by looking at core partitions and vNM stable sets.
Theorem 3. Consider a TU profit game with preferences, . Then,
Any vNM stable set contains the set of core partitions of . A vNM stable set can contain non-core partitions as well.
Any vNM farsighted stable set is contained in the set of core partitions of . The set of core partitions can contain other elements as well.
Thus, we are able to obtain an interesting result that is more general and does not apply only to PMAS profit games. Namely, we show how the relationship between core partitions and vNM stable sets changes when we replace myopic stability with farsighted stability—vNM stable sets contain core partitions, and core partitions contain vNM farsighted stable sets. Next, we consider EPCF-stable partitions and vNM farsighted stable sets.
Theorem 4. Consider a TU profit game with preferences, .Then,
There exists a threshold such that for any collection of discount factors and for any absorbing deterministic EPCF, the set of all EPCF-stable partitions satisfies external stability with respect to indirect dominance.
For any vNM farsighted stable set there exists a threshold such that for any collection of discount factors in and for any absorbing deterministic EPCF, is the set of EPCF-stable partitions.
Thus, when comparing EPCF-stable partitions with vNM farsighted stable sets, we show that the set of all EPCF-stable partitions satisfies external stability with respect to farsighted dominance. Moreover, we are able to show that we can always find a discount factor large enough so that each member of a set that satisfies internal and external farsighted stability is an EPCF-stable partition. This result is interesting as it links two rather different concepts of stability. Recall that EPCF-stability implies that we consider possible profitable moves from any partition to an EPCF-stable partition, while vNM farsighted stable set implies that stable partitions satisfy internal and external stability with respect to indirect dominance, the concept related to the LCS. Yet, the partitions identified as being stable under the vNM farsighted stability are also stable under the EPCF-stability.
In Theorem 2 we showed that EPCF-stable partitions are core partitions for PMAS profit games. However, the results are different when we consider the LCS, as illustrated in Example 5, which showed that we can have elements of the LCS that are not core partitions. In our next example, we show that the opposite is also true—not all core partitions are contained in the LCS.
Example 6. Consider the following PMAS profit game with preferences,
, where
, and the characteristic function and the PMAS are given in
Table 3. Observe that player 1 is the only strong player for
N, and there are no extreme players.
Consider coalition structure . It is a core structure because of the following. Player 1 is a strong player who cannot improve upon its payoff, so any blocking coalition cannot contain player 1. The payoff of players 3 and 4 increases only in the grand coalition, so the only blocking coalition containing players 3 and 4 could be the grand coalition, which is eliminated because of player 1. Finally, player 2 by itself cannot be the blocking coalition.
Now, consider a possible joint defection by players 2, 3 and 4:
For to be in the LCS, we have to show that there is a , such that and . Now, implies that for any defecting from we must have . The only set in which players 2, 3 and 4 receive higher payoff than in is the grand coalition, so any defection that contains any of these three players must have . As player 1 cannot make any moves on its own (without including some of the remaining players), the only possible defection from leads to N, and . Thus, we have found such that and for every in the LCS such that we have , hence is not in the LCS.
Examples 5 and 6 lead to the last result in this paper.
Proposition 4. Let be a PMAS profit game with preferences.
The LCS can contain elements that are not core partitions of .
The core partitions of do not need to be contained in the LCS.
Recall that [
9] showed that both the EPCF-stable set and the vNM farsighted stable set belong to the LCS for general profit games, so we do not need to analyze the relationship between the LCS and the vNM farsighted stable set.
In this section, we have studied our second research question, which focuses on relationships between coalition structures that are stable under different solution concepts. Most of our results on stability of the grand coalition and on relationships between stable coalition structures under different stability notions are consistent with the existing body of knowledge, which implies that, unfortunately, population monotonicity is not sufficient for strengthening of the existing results. However, we were able to show several results that apply to more general cooperative TU profit games, namely that the members of vNM farsighted stable sets are core partitions, that core partitions are members of vNM stable sets, and that members of vNM farsighted stable sets are EPCF-stable partitions.
5. Conclusions
In this paper we used the monotonicity property of PMAS to address two research questions: can we identify stable coalition structures other than the grand coalition under different stability concepts in cooperative games, and can we understand the relationship between stable coalition structures under different stability concepts.
To address the first question, we first identify two special classes of players for PMAS profit games, strong players and extreme players, and we show that whenever a PMAS profit game does not possess a strong player, the grand coalition is the unique core partition, the unique EPCF-stable partition and the unique member of the LCS. However, in the presence of strong players, the sets of stable coalition structures are likely to grow and include other partitions as well. More precisely, for general PMAS profit games (which may allow for strong players), we develop an algorithm that uses strong players and the notion of weak top-coalition to completely characterize the set of core partitions. In addition, we show the importance of extreme players in determining EPCF-stable partitions, and we show how to identify EPCF-stable partitions in the presence of such players.
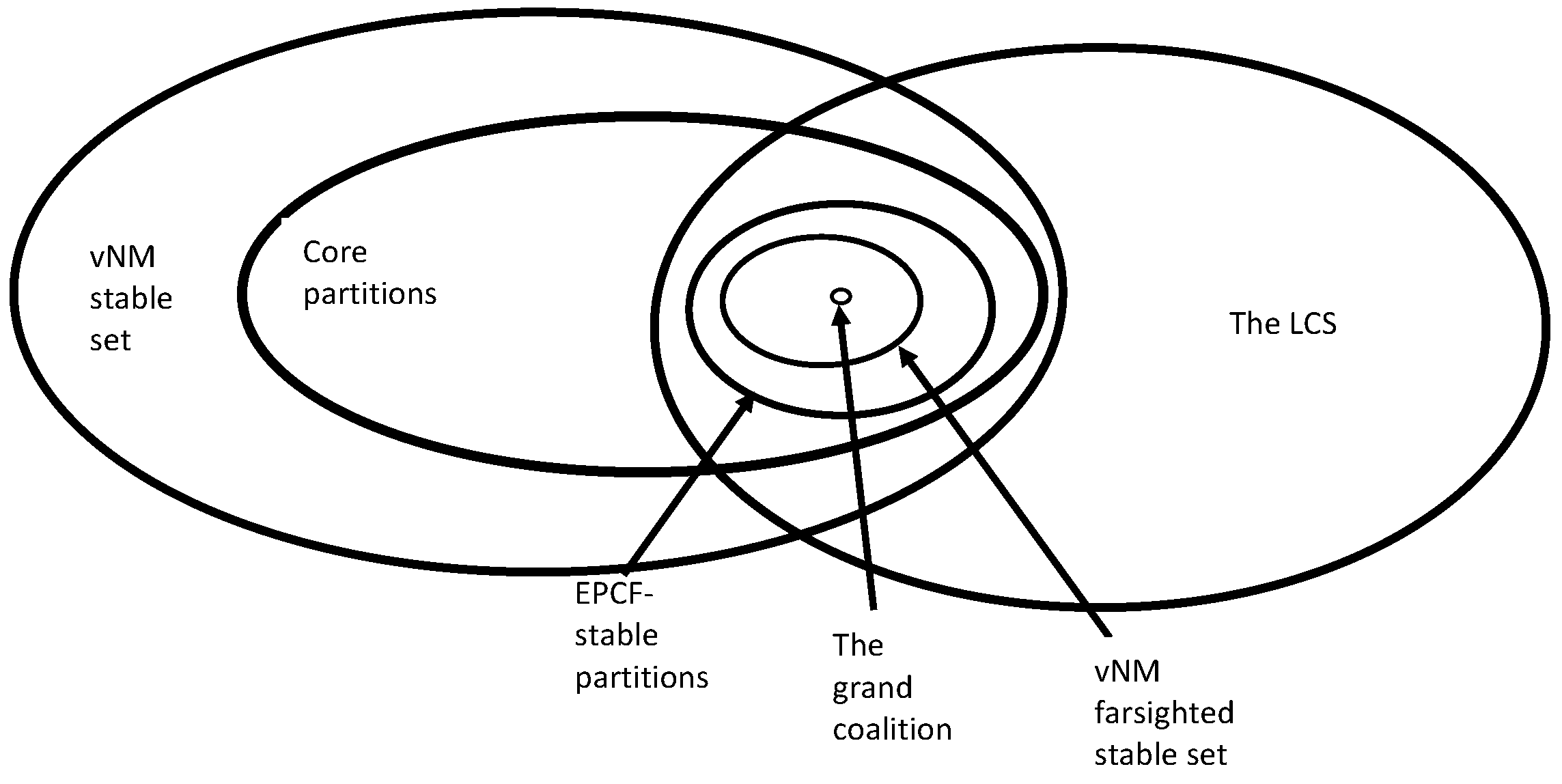
To address our second research question, we have compared stable coalition structures for PMAS profit games under different stability concepts to see if monotonicity can strengthen different relationships that hold between them. The results of our analysis are represented in
Figure 1.
The answer to the second research question is mixed. That is, while our results for PMAS profit games are consistent with existing results for general cooperative games established in literature, we have found that monotonicity does not add enough for strengthening of the relationships between stable coalition structures under different notions of stability. We plan to see if adding additional structure and/or constraints to PMAS profit games would help in obtaining additional insights.
However, on the positive side, we were able to show a couple of interesting results for general TU cooperative profit games. First, we show how the relationship between stable coalition structures depends on the level of farsightedness as vNM stable set contains core partitions, and the set of core partitions contains the vNM farsighted stable set. To the best of our knowledge, this is a novel result. Next, we show that the members of vNM farsighted stable sets are EPCF-stable partitions. While Ref. [
9] showed that both vNM farsighted stable sets and EPCF-stable partitions belong to the LCS, our result further narrows the relationship between these different stability concepts and is thus expanding our understanding of these two rather different concepts of stability.
As the next step in our investigation of PMAS games, we intend to study how our results can be applied in some practical settings and to identify areas that may benefit from application of our work. For instance, Ref. [
7] studied stability of collaboration among all players (that is, formation of the grand coalition) in newsvendor games and analyzed conditions for existence of a PMAS in such games, but they did not address stability of different partitions. As we discussed above, while the grand coalition is always stable for PMAS games, it needs not be the only stable coalition structure. Our results can be applied to newsvendor games studied in [
7] to check if partitions other than the grand coalition may emerge as stable. For instance, Example 1 from [
7] has no strong players, hence our Proposition 1 implies that the grand coalition is the only stable coalition structure. On the other hand, two out of three players in Example 4 from [
7] are extreme, and
N itself is an extreme coalition, so our results indicate that all partitions of players are potentially stable.