Score-Guided Generative Adversarial Networks
Abstract
:1. Introduction
- The score-guided GAN (ScoreGAN) that uses the evaluation metric as an additional target is proposed.
- The proposed ScoreGAN circumvents the overfitting problem by using MobileNet as an evaluator.
- Evaluated by the Inception score and cross-validated through the FID, ScoreGAN demonstrates state-of-the-art performance on the CIFAR-10 dataset and CIFAR-100 dataset, where its Inception score in the CIFAR-10 is 10.36 ± 0.15, and the FID in the CIFAR-100 is 13.98.
2. Background
2.1. Controllable Generative Adversarial Networks
2.2. The Inception Score
2.3. The Fréchet Inception Distance
3. Methods
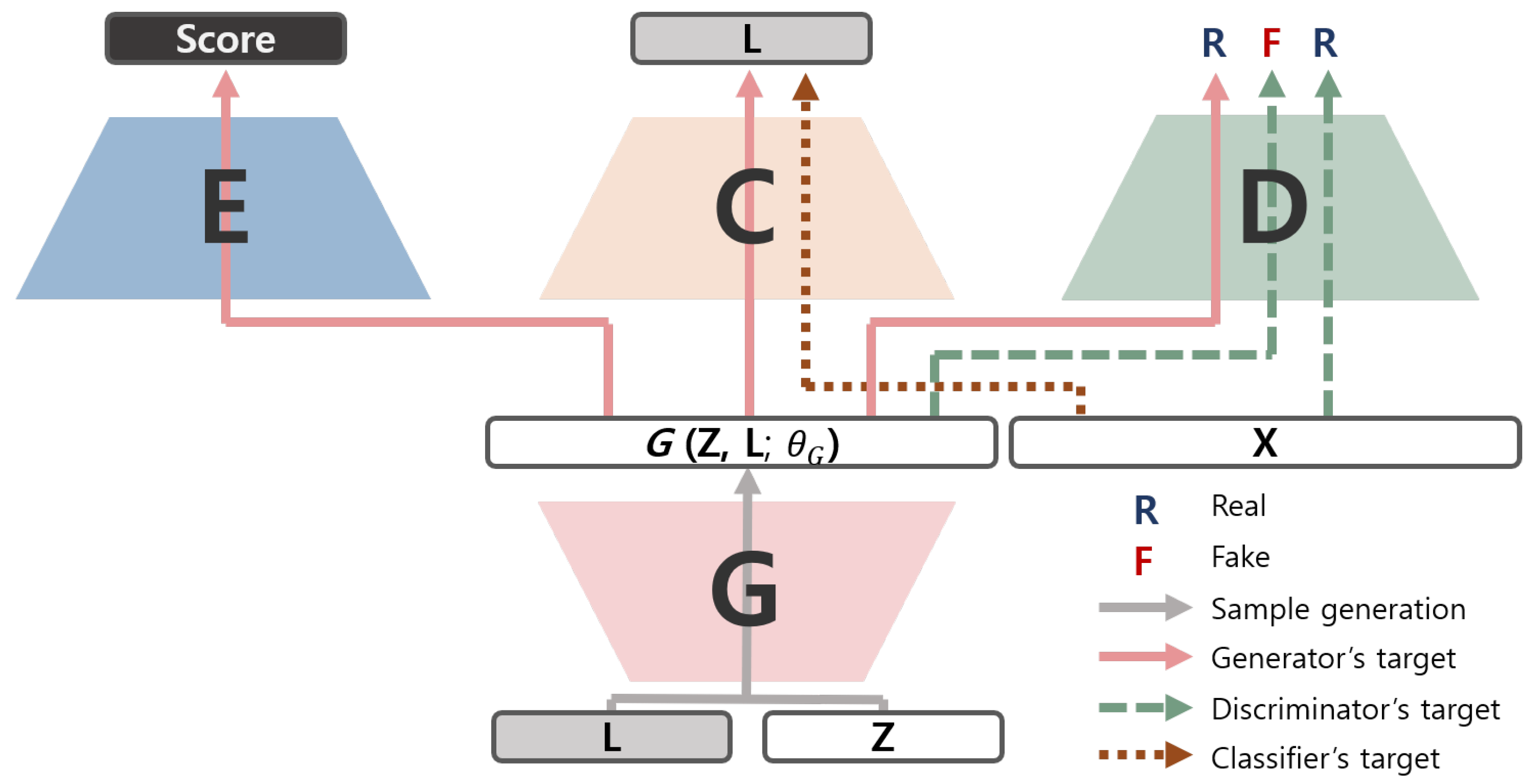
3.1. Score-Guided Generative Adversarial Network
3.1.1. The Auxiliary Costs Using the Evaluation Metrics
3.1.2. The Evaluator Module with MobileNet
3.2. Network Structures and Regularization
4. Results
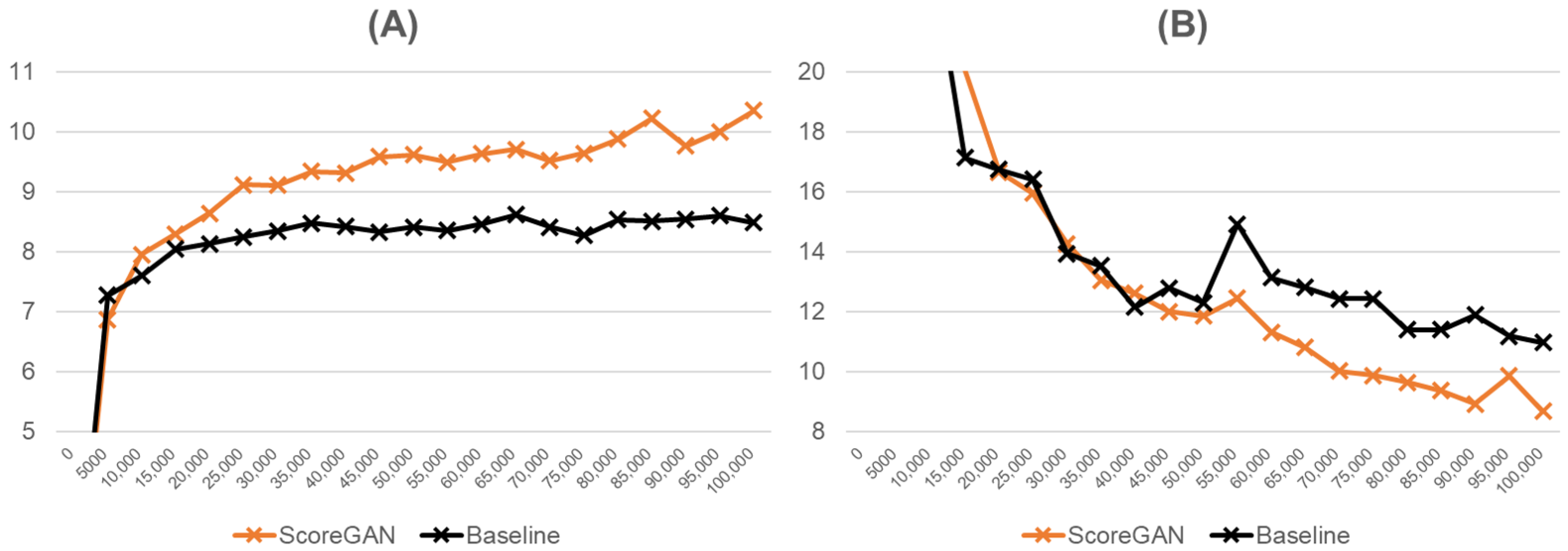
4.1. Image Generation with CIFAR-10 Dataset
4.2. Image Generation with CIFAR-100 Dataset
4.3. Image Generation with LSUN Dataset
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Neural Network Architectures of ScoreGAN for the CIFAR-100 Dataset
| Generator | Discriminator | Classifier |
|---|---|---|
| Dense | ResBlock Downsample | ResBlock |
| ResBlock Downsample | ||
| ResBlock Upsample | ResBlock Downsample | ResBlock |
| ResBlock Downsample | ||
| ResBlock Upsample | ResBlock | ResBlock |
| ResBlock Downsample | ||
| ResBlock Upsample | ResBlock | ResBlock |
| cBN; ReLU; Conv ; Tanh | ReLU; Global Pool; Dense | LN; ReLU; Global Pool; Dense |
References
- Ramesh, A.; Dhariwal, P.; Nichol, A.; Chu, C.; Chen, M. Hierarchical text-conditional image generation with clip latents. arXiv 2022, arXiv:2204.06125. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Aggarwal, A.; Mittal, M.; Battineni, G. Generative adversarial network: An overview of theory and applications. Int. J. Inf. Manag. Data Insights 2021, 1, 100004. [Google Scholar] [CrossRef]
- Kim, W.; Kim, S.; Lee, M.; Seok, J. Inverse design of nanophotonic devices using generative adversarial networks. Eng. Appl. Artif. Intell. 2022, 115, 105259. [Google Scholar] [CrossRef]
- Park, M.; Lee, M.; Yu, S. HRGAN: A Generative Adversarial Network Producing Higher-Resolution Images than Training Sets. Sensors 2022, 22, 1435. [Google Scholar] [CrossRef]
- Lee, M.; Tae, D.; Choi, J.H.; Jung, H.Y.; Seok, J. Improved recurrent generative adversarial networks with regularization techniques and a controllable framework. Inf. Sci. 2020, 538, 428–443. [Google Scholar]
- Cai, Z.; Xiong, Z.; Xu, H.; Wang, P.; Li, W.; Pan, Y. Generative adversarial networks: A survey toward private and secure applications. ACM Comput. Surv. (CSUR) 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Brock, A.; Donahue, J.; Simonyan, K. Large scale GAN training for high fidelity natural image synthesis. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Karras, T.; Laine, S.; Aila, T. A style-based generator architecture for generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 4401–4410. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Kim, S.W.; Zhou, Y.; Philion, J.; Torralba, A.; Fidler, S. Learning to simulate dynamic environments with GameGAN. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Lee, M.; Seok, J. Estimation with uncertainty via conditional generative adversarial networks. Sensors 2021, 21, 6194. [Google Scholar] [CrossRef]
- Yi, X.; Walia, E.; Babyn, P. Generative adversarial network in medical imaging: A review. Med. Image Anal. 2019, 58, 101552. [Google Scholar]
- Zhang, H.; Goodfellow, I.; Metaxas, D.; Odena, A. Self-attention generative adversarial networks. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019; pp. 7354–7363. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training GANs. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Barcelona, Spain, 5–10 December 2016; pp. 2234–2242. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs trained by a two time-scale update rule converge to a local nash equilibrium. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 6626–6637. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Yuan, X.; He, P.; Zhu, Q.; Li, X. Adversarial examples: Attacks and defenses for deep learning. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2805–2824. [Google Scholar] [CrossRef] [Green Version]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Barratt, S.; Sharma, R. A note on the inception score. arXiv 2018, arXiv:1801.01973. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Zhu, Y.; Wu, Y.; Olszewski, K.; Ren, J.; Tulyakov, S.; Yan, Y. Discrete contrastive diffusion for cross-modal and conditional generation. arXiv 2022, arXiv:2206.07771. [Google Scholar]
- Song, J.; Meng, C.; Ermon, S. Denoising Diffusion Implicit Models. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Miyato, T.; Koyama, M. cGANs with projection discriminator. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Ni, Y.; Song, D.; Zhang, X.; Wu, H.; Liao, L. CAGAN: Consistent adversarial training enhanced GANs. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Stockholm, Sweden, 13–19 July 2018; pp. 2588–2594. [Google Scholar]
- Odena, A.; Olah, C.; Shlens, J. Conditional image synthesis with auxiliary classifier GANs. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 2642–2651. [Google Scholar]
- Lee, M.; Seok, J. Controllable generative adversarial network. IEEE Access 2019, 7, 28158–28169. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M. Imagenet large scale visual recognition challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Chen, H.Y.; Su, C.Y. An enhanced hybrid MobileNet. In Proceedings of the International Conference on Awareness Science and Technology (iCAST), Fukuoka, Japan, 19–21 September 2018; pp. 308–312. [Google Scholar]
- Qin, Z.; Zhang, Z.; Chen, X.; Wang, C.; Peng, Y. FD-MobileNet: Improved MobileNet with a fast downsampling strategy. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 1363–1367. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved training of wasserstein GANs. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5767–5777. [Google Scholar]
- Lee, M.; Seok, J. Regularization methods for generative adversarial networks: An overview of recent studies. arXiv 2020, arXiv:2005.09165. [Google Scholar]
- Miyato, T.; Kataoka, T.; Koyama, M.; Yoshida, Y. Spectral normalization for generative adversarial networks. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Lim, J.H.; Ye, J.C. Geometric GAN. arXiv 2017, arXiv:1705.02894. [Google Scholar]
- Dumoulin, V.; Shlens, J.; Kudlur, M. A learned representation for artistic style. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Kavalerov, I.; Czaja, W.; Chellappa, R. cGANs with Multi-Hinge Loss. arXiv 2019, arXiv:1912.04216. [Google Scholar]
- Wang, D.; Liu, Q. Learning to draw samples: With application to amortized mle for generative adversarial learning. arXiv 2016, arXiv:1611.01722. [Google Scholar]
- Grinblat, G.L.; Uzal, L.C.; Granitto, P.M. Class-splitting generative adversarial networks. arXiv 2017, arXiv:1709.07359. [Google Scholar]
- Shmelkov, K.; Schmid, C.; Alahari, K. How good is my GAN? In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 213–229. [Google Scholar]
- Tran, N.T.; Tran, V.H.; Nguyen, B.N.; Yang, L. Self-supervised GAN: Analysis and improvement with multi-class minimax game. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019; pp. 13232–13243. [Google Scholar]
- Yu, F.; Seff, A.; Zhang, Y.; Song, S.; Funkhouser, T.; Xiao, J. Lsun: Construction of a large-scale image dataset using deep learning with humans in the loop. arXiv 2015, arXiv:1506.03365. [Google Scholar]



| Generator | Discriminator | Classifier |
|---|---|---|
| Dense | ResBlock Downsample | ResBlock |
| ResBlock Downsample | ||
| ResBlock Upsample | ResBlock Downsample | ResBlock |
| ResBlock Downsample | ||
| ResBlock Upsample | ResBlock | ResBlock |
| ResBlock Downsample | ||
| ResBlock Upsample | ResBlock | ResBlock |
| cBN; ReLU; Conv ; Tanh | ReLU; Global Pool; Dense | LN; ReLU; Global Pool; Dense |
| Name | Image Res. | No. of Samples | Descriptions |
|---|---|---|---|
| CIFAR-10 | 32 × 32 | 50,000 | 10 classes of small objects 5000 images per class |
| CIFAR-100 | 32 × 32 | 50,000 | 100 classes of small objects 500 images per class |
| LSUN | down-sampled to 128 × 128 | around 10 million | 10 classes of indoor and outdoor scenes around 120,000 to 3,000,000 per class |
| Methods | IS | FID |
|---|---|---|
| Real data | 11.23 ± 0.20 | - |
| ControlGAN [29] | 8.61 ± 0.10 | - |
| ControlGAN (w/Table 1; baseline) | 8.60 ± 0.09 | 10.97 |
| Conditional DCGAN [40] | 6.58 | - |
| AC-WGAN-GP [33] | 8.42 ± 0.10 | - |
| CAGAN [27] | 8.61 ± 0.12 | - |
| Splitting GAN [41] | 8.87 ± 0.09 | - |
| BigGAN [8] | 9.22 | 14.73 |
| MHingeGAN [39] | 9.58 ± 0.09 | 7.50 |
| ScoreGAN | 10.36 ± 0.15 | 8.66 |
| Methods | IS | FID |
|---|---|---|
| Real data | 14.79 ± 0.18 | - |
| ControlGAN (baseline) | 9.32 ± 0.11 | 18.42 |
| MSGAN [43] | - | 19.74 |
| SNGAN [42] | 9.30 ± 0.08 | 15.6 |
| MHingeGAN [39] | 14.36 ± 0.09 | 17.30 |
| ScoreGAN | 13.11 ± 0.16 | 13.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.; Seok, J. Score-Guided Generative Adversarial Networks. Axioms 2022, 11, 701. https://doi.org/10.3390/axioms11120701
Lee M, Seok J. Score-Guided Generative Adversarial Networks. Axioms. 2022; 11(12):701. https://doi.org/10.3390/axioms11120701
Chicago/Turabian StyleLee, Minhyeok, and Junhee Seok. 2022. "Score-Guided Generative Adversarial Networks" Axioms 11, no. 12: 701. https://doi.org/10.3390/axioms11120701
APA StyleLee, M., & Seok, J. (2022). Score-Guided Generative Adversarial Networks. Axioms, 11(12), 701. https://doi.org/10.3390/axioms11120701







