Bargaining-Based Profit Allocation Model for Fixed Return Investment Water-Saving Management Contract

Abstract

Fixed Return Investment (FRI) is one of the main operating modes of a Water-Saving Management Contract (WSMC). Aiming at the critical profit allocation of FRI WSMC projects, a new profit allocation model based on bargaining theory is proposed. First, the net present value is adopted to determine the profit interval to be allocated. Second, the bargaining process is divided into two levels. The first-level bargaining process is between a water user and an alliance, which consists of a Water Service Company (WSCO) and a financial institution. The second-level bargaining process is between the WSCO and the financial institution. Given the imbalance caused by offering first, the number of bargaining stages and sunk cost are introduced, and the equilibrium offers of the two parties in different bargaining stages are determined by using backward induction and mathematical induction. According to the feature that the number of bargaining stages is an integer in practice, the deterrence discount factors are introduced to redistribute the remaining part, and sixteen situations of profit allocation among participants are given. Third, the model analysis shows that the profit allocation of participants is closely related to the minimum profit requirements, deterrence discount factors, the number of bargaining stages, and sunk cost. Finally, the effectiveness of the model and the influence of various factors on profit allocation are verified by an example. The example shows that in the early stage of FRI WSMC, the water users enjoy more profits.

1. Introduction

Water shortage is aggravated by the worsening of environmental pollution and the modernization of the human process. Climate change, population growth, and mismanagement have led to severe water shortages for at least one month yearly for about 4 billion people [1,2]. The global water demand is expected to increase by 55%, and around 25% of large cities are currently experiencing varying levels of water stress [3]. Water issues in the 21st century are not just about resources; water scarcity can lead to national and domestic interbasin water conflicts [4]. Thus, water shortages place tremendous pressure on the sustainable and peaceful development of humanity and reasonable measures to alleviate the dilemma need to be taken.

China faces severe water scarcity and has taken various measures to improve the situation, such as carrying out the South-to-North Water Diversion [5] and establishing a progressive pricing scheme for water use [6]. Both of these initiatives have alleviated regional water shortages and wastage, but they still fall short. The South-to-North Water Diversion is costly to build and maintain, and open-air evaporation results in serious water wastage. The progressive pricing scheme for water use may be effective for residential users but may not be useful for collective or public users. Therefore, the Water-Saving Management Contract (WSMC) was proposed based on the Energy Performance Contracting in 2014.

WSMC is a pattern of investment that involves Water Service Companies (WSCOs) participating in water-saving projects [7]. This pattern involves the WSCOs and the water users agreeing on water-saving targets in the form of contracts and sharing the water-saving benefits. The current research on WSMC focuses on risk assessment [8,9] and investment pricing [10]. Fixed Return Investment (FRI) is an operational model of WSMC [7]. In the FRI model, the WSCOs and water users agree on the main elements, such as the amount of water-saving benefits, total investment, and return, before implementing the retrofit and financing by the WSCOs. This model is suitable for projects where the effects of water savings are not easy to measure accurately or the water-saving benefits are uncertain or arduous to assess quantitatively. Profit allocation is an important part of FRI WSMC’s promotion and implementation. What is more, the profit allocation for the FRI WSMC projects has not been studied at present; therefore, our aim was to study the profit allocation of FRI WSMC projects.

According to the number of stakeholders, profit allocation methods were divided into two categories: (1) Profit allocation schemes for three stakeholders are discussed based on the Shapley value [11,12,13]. The Shapley value method compares the results of cooperation and noncooperation between participants and is suitable for a cooperative game. However, for a noncooperative game, the Shapley value method is powerless. (2) Profit allocation schemes for two stakeholders are used based on risk-profit mechanisms [14] or bargaining theory [15,16]. The risk-profit mechanisms mainly consider the impact of risk. When determining profit based on risk, due to cognitive differences, participants’ subjective risk and objective risk may differ, resulting in an unfair allocation. Bargaining theory applies to noncooperative games. The business model of FRI WSMC is that the WSCOs are responsible for financing from financial institutions, therefore, the WSCOs and financial institutions are in alliance. Then, the profits are divided between the water users and the WSCOs. In the end, the WSCOs share the proceeds with the financial institutions. Therefore, this paper solves the profit allocation of the three stakeholders in FRI WSMC projects based on bargaining theory.

Rubinstein developed an infinite-term full-information rotating offer bargaining model in 1982 [17]. Backward induction can solve the finite-term bargaining model. The infinite-term bargaining model cannot be solved since there is no definite term. In 1984, Shaked and Sutton transformed the infinite-term bargaining process into a finite-term bargaining process by assuming that the game starting from time t is identical to the game starting from time t − 2, which is then solved based on the backward induction method [18]. However, with the introduction of new factors such as the sunk cost in this paper, Shaked and Sutton’s solution is no longer applicable.

Scholars introduced different factors to the Rubinstein bargaining game and re-considered. Based on Rubinstein’s two-person alternating-offer bargaining model, a dynamic multi-person bargaining game model with veto players was constructed by adding constraints to the bargaining process [19]. Feng et al. introduced altruism and malice into the Rubinstein bargaining game [20]. Xiao and Li redefined the discount factor as the deterrence discount factor and proposed a trading model with three participants deterring each other [21]. However, none of these studies considered sunk costs, such as travel and venue fees, in the bargaining process.

Rubinstein bargaining is widely used to solve allocation in various fields. Zhang and Wang investigated a sustainable supply chain under the Rubinstein game model [22]. Zhang and Kong proposed a method to determine the transaction price and quantity of emergency supply procurement based on the Rubinstein bargaining game [23]. Xue et al. studied the equilibrium returns of host countries and oil companies in international oil and gas development projects based on the bargaining theory [24]. Isaaks and Colby developed a bilateral water trading model based on Rubenstein’s bargaining theory to inform water trading in the western US [25]. From the above literature, it is clear that the Rubinstein bargaining game is an effective way to deal with profit allocation.

Therefore, the Rubinstein bargaining game is also applicable to the profit allocation of FRI WSMC projects. However, the existing studies based on bargaining theory still have some aspects to be modified in the relevant literature. First, the measurable sunk cost is not taken into account, which does not fully reflect the intrinsic nature of bargaining. Second, for the bargaining model with the introduction of sunk cost, the sunk cost varies with the number of bargaining stages, and the solution based on Shaked and Sutton’s assumptions is not valid. Moreover, there are situations where the water-saving benefits are not exactly shared out in the bargaining process. Therefore, this paper improves the existing model based on the above shortcomings and further applies the improved model to FRI WSMC projects. The research shows that the amount of profit allocation of participants is closely related to the minimum profit requirements, the deterrence discount factors, the number of bargaining stages, and the sunk cost. Moreover, in the early stage of FRI WSMC, water users enjoy more benefits because their deterrence discount factor is higher than others.

The remainder of this paper is organized as follows. Section 2 determines the interval of the amount of water-saving benefits to be allocated, establishes a deterrence bargaining model that introduces the number of bargaining stages and sunk costs, and provides the method of profit redistribution. Section 3 gives the profit distribution results according to the established model. Section 4 presents a numerical experiment on the profit allocation for an FRI WSMC project to verify the validity of the model. In Section 5, the model is analyzed and discussed, and the correlation between affecting factors and profit allocation is explored. Finally, Section 6 discusses the conclusions of this paper and makes suggestions for further work.

2. Materials and Methods

There are four main parts in this section. First, the interval of the amount of profit to be allocated under the premise of meeting the minimum profit requirements of each participant is determined, that is, the bargaining interval is determined. Second, the deterrence discount factor is introduced. Next, the first-level bargaining process takes place, where an alliance of a WSCO and a financial institution bargain with a water user over the water-saving benefits to be allocated. Finally, the second-level bargaining process takes place, where the WSCO and the financial institution bargain over the alliance’s share of the water-saving benefits in the first-level bargaining process. The basic framework of this section is shown in Figure 1.

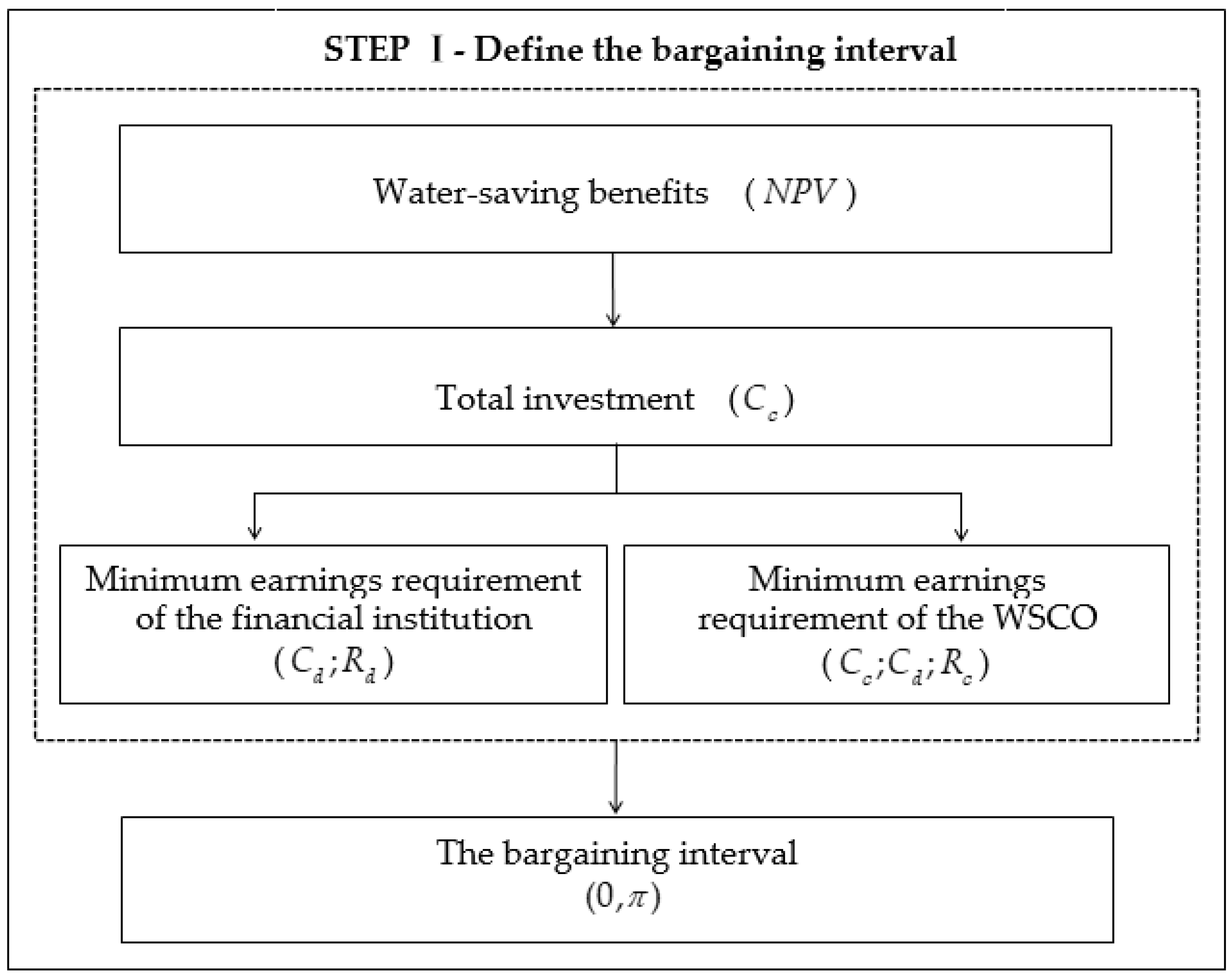
2.1. The Bargaining Interval

The bargaining interval in this paper is the range of water-saving benefits to be distributed on the premise of meeting the minimum earnings requirement of each participant. This paper considers three parties: water users, WSCOs, and financial institutions. Water users are customers in high water-consuming industries. WSCOs are specialized companies with the ability to integrate water-saving technology, financing, and project management. Financial institutions provide central financial support for projects. It is assumed that each participant is risk neutral. The basic framework of STEP Ⅰ is shown in Figure 2.

Before the profit allocation, the amount of water-saving benefits to be allocated is determined. The net present value used to determine the water-saving benefits over the contract period is

$$NPV(T)={\displaystyle \sum _{t=0}^T\frac{E(A_t)}{{(1+r)}^t}}-C_c,$$

(1)

where $T$ represents the contract period of a WSMC project, $A_t$ represents the water-saving benefits in year $t$, $E(A_t)$ represents the expected water-saving benefits in year $t$, $r$ represents the risk-free discount rate, and $C_c$ represents the total investment in a WSMC project agreed upon by the participants.

It follows from (1) that

$${\displaystyle \sum _{t=0}^T\frac{E(A_t)}{{(1+r)}^t}}=NPV(T)+C_c.$$

(2)

The water-saving benefits meet the cost investment first. Then, the competition focuses on the $NPV(T)$ of the project.

The FRI WSMC projects require significant financial support due to one-time investments and long-term returns. To reduce their own risk, WSCOs do not rely entirely on their funds to accomplish water-saving improvements, even if they have the capital to complete a water-saving project [9]. As a result, WSCOs receive financial support through financial institutions. We assume that the amount of contribution of the financial institution is $C_d$ ($C_d\le C_c$) and the minimum investment return required on the project is $R_d$. This means that the financial institution participates in the partnership if the return is not less than

$$C_d{R}_d.$$

(3)

In the FRI model, WSCOs focus on the input–output relationship of the project. The average return on investment in the water-saving service sector is $R_0$. We assume the WSCO requires a profit margin of $\begin{array}{cc}{R}_c& (R_c\ge R_0)\end{array}$ for water-saving projects. The WSCO participates in the partnership when the amount of the return is not less than

$$(C_c-C_d)R_c.$$

(4)

As a result, the total profit to be distributed is

$$\pi =NPV(T)-C_d{R}_d-(C_c-C_d)R_c.$$

(5)

Since each player benefits from $\pi$, there is no case where one side benefits by $0$. This means that the bargaining interval is $(0,\pi )$.

2.2. The Deterrence Discount Factor

The ability of one party to cause harm to the other participants is referred to as deterrence capacity, and is directly reflected in the bargaining power in the negotiation process and indirectly in the scale of operation of the participants and the degree of substitutability in the project. The first bidder in the first stage of the bargaining process is not affected by the deterrence capacity of others. There is a deterrence coefficient between 0 and 1, as the deterrence capacity may not be fully effective due to the external environment. At the same time, the ability of one side to resist the deterrence of the other is referred to as the withstand deterrence capacity.

Each participant can deter and resist deterrence. $y_i,y_j$, and $y_k$ are the deterrence capabilities of participants $i,j$, and $k$, respectively. $x_i,x_j$, and $x_k$ are the withstand deterrence capacities of participants $i,j$, and $k$, respectively. Deterrence and withstand deterrence capabilities may not be fully functional due to environmental and other factors. Therefore, corresponding degree factors exist. In this paper, only the deterrence degree coefficients are considered, not the withstand deterrence degree coefficients. The deterrence degree coefficients of participants $i,j$, and $k$ are ${\alpha }_i,{\alpha }_j$, and ${\alpha }_k$, respectively. Each of the above parameters is between 0 and 1. The deterrence discount factor [21] caused by participant $i$ to participant $j$ is

$${\delta }_{i,j}=\frac{x_j}{x_j+y_i\times {\alpha }_i}.$$

(6)

The deterrence discount factor [21] caused by participant $i$ to the alliance formed by participants $j$ and $k$ is

$${\delta }_{i,jk}=\frac{x_j+x_k}{x_j+x_k+y_i\times {\alpha }_i}.$$

(7)

The deterrence discount factor caused by the alliance formed by participants $j$ and $k$ to participant $i$ is

$${\delta }_{jk,i}=\frac{x_i}{x_i+y_j\times {\alpha }_j+y_k\times {\alpha }_k}.$$

(8)

From the above equations, the deterrence discount factor of each participant is between 0 and 1.

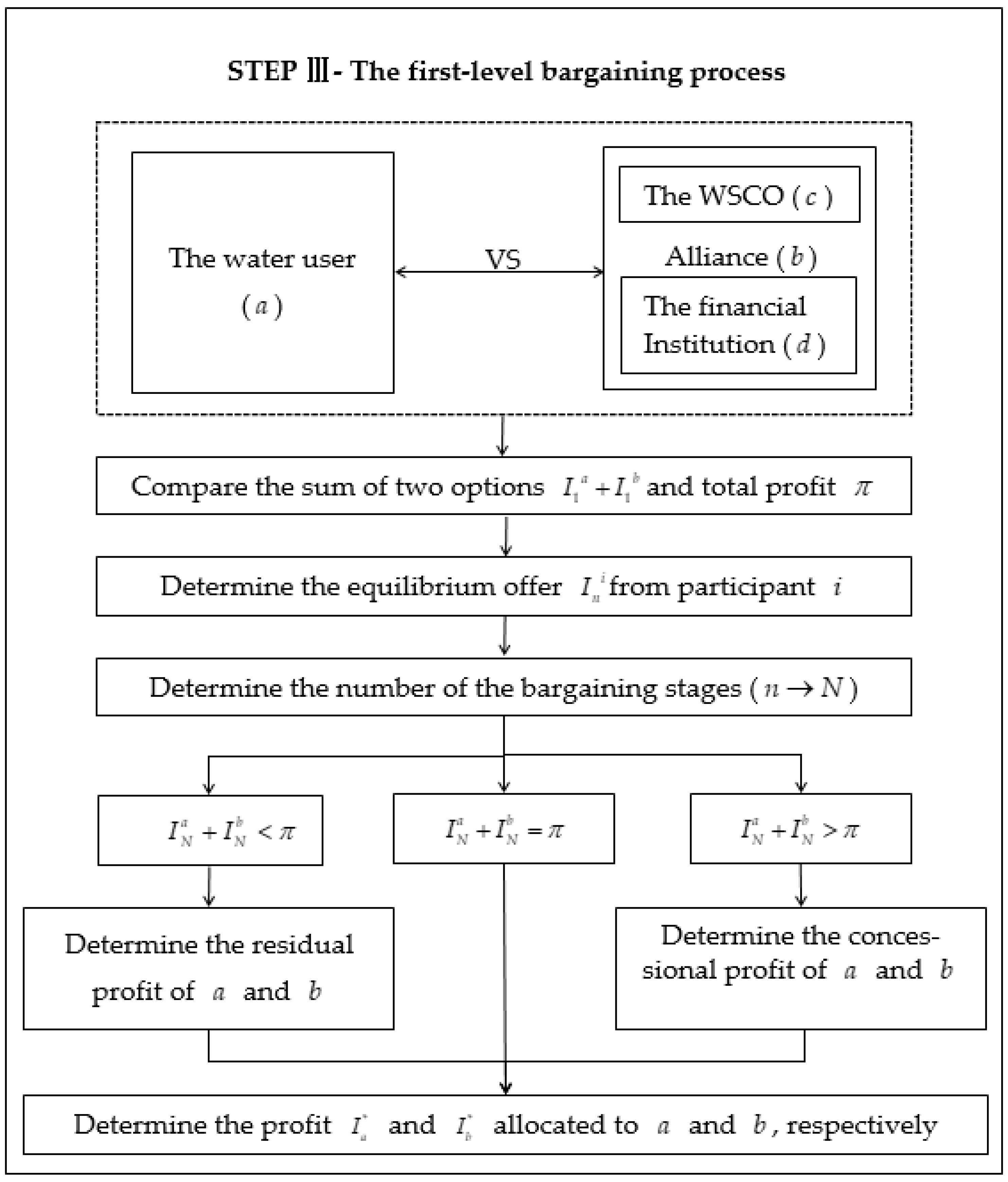
2.3. The First-Level Bargaining Process

After determining the bargaining interval and the deterrence discount factor, the first-level bargaining process is implemented. Due to the business model of FRI, the WSCO and the financial institution form a profit allocation alliance. The first-level bargaining process is between the alliance and the water user. There is one stage in the bargaining process where one party makes an offer, then the other party accepts or rejects it. Assuming both parties in the game are rational economic agents, there is no case that one party benefits by 0 [26]. Thus, the bargaining process ends when one party’s offer is accepted by the other party. The basic framework of STEP Ⅲ is shown in Figure 3.

2.3.1. Comparison of the Sum of the Two Options and the Total Profit

As the number of bargaining stages increases, the sunk cost also increases, resulting in less profit for each participant. Each participant is a rational economic agent and will play as few stages as possible. Therefore, we assume that the bargaining process has one stage.

Each party makes the first offer, and each offer is accepted by the other. The water-saving benefits are allocated according to their first offer, overcoming the effect of the first-mover advantage.

Supposing the bargaining process has one stage, the sum of the expected earnings of the water user and the alliance with the total profit to be distributed are compared. We assume that $M_i$ and $m_i$ are the maximum and minimum expected earnings, respectively, for offers starting with participant $\begin{array}{cc}i& (i=a,b)\end{array}$, and $f_i$ is the sunk cost of participant $\begin{array}{cc}i& (i=a,b)\end{array}$. Each participant’s expected earnings are sufficient to cover its total sunk cost. The argument breaks down into two cases.

Case 1: The water user makes the first offer, and the alliance accepts the water user’s offer.

If the alliance rejects the first offer from the water user and counters, the alliance has to pay the sunk cost of $f_b$. At this point, the maximum expected earnings for the alliance are

$${\delta }_{a,b}(M_b-f_b),$$

and the minimum expected earnings are

$${\delta }_{a,b}(m_b-f_b).$$

The water user should give the alliance an earnings interval of

$$[{\delta }_{a,b}(m_b-f_b),{\delta }_{a,b}(M_b-f_b)]$$

in addition to paying the sunk cost of $f_a$ on the first offer to avoid the alliance counteroffer.

Under this strategy, the maximum expected earnings of the water user are

$$(\pi -f_a)-{\delta }_{a,b}(m_b-f_b),$$

and the minimum expected earnings are

$$(\pi -f_a)-{\delta }_{a,b}(M_b-f_b).$$

Thus, we have

$$M_a-f_a\le (\pi -f_a)-{\delta }_{a,b}(m_b-f_b),$$

(9)

$$m_a-f_a\ge (\pi -f_a)-{\delta }_{a,b}(M_b-f_b).$$

(10)

Case 2: The alliance makes the first offer, and the water user accepts the alliance’s offer.

If the water user rejects the alliance’s initial offer and makes a counteroffer, the water user has to pay the sunk cost of $f_a$. At this time, the maximum expected earnings for the water user are

$${\delta }_{b,a}(M_a-f_a),$$

and the minimum expected earnings are

$${\delta }_{b,a}(m_a-f_a).$$

To avoid counteroffers by the water user, the alliance should give the water user an earnings interval of

$$[{\delta }_{b,a}(m_a-f_a),{\delta }_{b,a}(M_a-f_a)]$$

in addition to paying the sunk cost of $f_b$ in the first offer.

Under this strategy, the maximum expected earnings of the alliance are

$$(\pi -f_b)-{\delta }_{b,a}(m_a-f_a),$$

and the minimum expected earnings are

$$(\pi -f_b)-{\delta }_{b,a}(M_a-f_a).$$

Thus, we have

$$M_b-f_b\le (\pi -f_b)-{\delta }_{b,a}(m_a-f_a),$$

(11)

$$m_b-f_b\ge (\pi -f_b)-{\delta }_{b,a}(M_a-f_a).$$

(12)

Based on the above two cases, the equilibrium offers for the water user and the alliance are given and compared with the total profit. The specific steps are as follows.

By (13) and (12), we have

$$M_a\le \frac{(1-{\delta }_{a,b})\pi -{\delta }_{b,a}{\delta }_{a,b}{f}_a+{\delta }_{a,b}{f}_b}{1-{\delta }_{b,a}{\delta }_{a,b}}.$$

(13)

By (10) and (11), we have

$$m_a\ge \frac{(1-{\delta }_{a,b})\pi -{\delta }_{b,a}{\delta }_{a,b}{f}_a+{\delta }_{a,b}{f}_b}{1-{\delta }_{b,a}{\delta }_{a,b}}.$$

(14)

By (13) and (14), we have

$$I_1^a=\frac{(1-{\delta }_{a,b})\pi -{\delta }_{b,a}{\delta }_{a,b}{f}_a+{\delta }_{a,b}{f}_b}{1-{\delta }_{b,a}{\delta }_{a,b}},$$

where $I_1^a$ is the equilibrium offer of the water user when $n=1$.

By (10) and (11), we have

$$M_b\le \frac{(1-{\delta }_{b,a})\pi -{\delta }_{b,a}{\delta }_{a,b}{f}_b+{\delta }_{b,a}{f}_a}{1-{\delta }_{b,a}{\delta }_{a,b}}.$$

(15)

By (9) and (12), we have

$$m_b\ge \frac{(1-{\delta }_{b,a})\pi -{\delta }_{b,a}{\delta }_{a,b}{f}_b+{\delta }_{b,a}{f}_a}{1-{\delta }_{b,a}{\delta }_{a,b}}.$$

(16)

By (15) and (16), we have

$$I_1^b=\frac{(1-{\delta }_{b,a})\pi -{\delta }_{b,a}{\delta }_{a,b}{f}_b+{\delta }_{b,a}{f}_a}{1-{\delta }_{b,a}{\delta }_{a,b}},$$

where $I_1^b$ is the equilibrium offer of the alliance when $n=1$.

We then compare the sum of the equilibrium offer of the water user and the alliance with the total profit. That is,

$$\begin{array}{l}(I_1^a+I_1^b)-\pi \\ =\frac{(1-{\delta }_{a,b})\pi -{\delta }_{b,a}{\delta }_{a,b}{f}_a+{\delta }_{a,b}{f}_b}{1-{\delta }_{b,a}{\delta }_{a,b}}+\frac{(1-{\delta }_{b,a})\pi -{\delta }_{b,a}{\delta }_{a,b}{f}_b+{\delta }_{b,a}{f}_a}{1-{\delta }_{b,a}{\delta }_{a,b}}-\pi \\ =\frac{(1-{\delta }_{b,a})(1-{\delta }_{a,b})\pi +(1-{\delta }_{a,b}){\delta }_{b,a}{f}_a+(1-{\delta }_{b,a}){\delta }_{a,b}{f}_b}{1-{\delta }_{b,a}{\delta }_{a,b}}\\ >0\end{array}$$

Hence,

$$I_1^a+I_1^b>\pi .$$

(17)

When both parties make the first offer in the first phase of the bargaining process, the sum of their share of the profit is always greater than the total profit. This means that the total profit is not enough to share.

Scholars have studied bargaining theory based on the assumption that the sum of the two options is not greater than the total benefits [27]. If the sum of the two options is greater than the total benefits, the only Nash equilibrium outcome $I_n^i$ is zero. Therefore, the number of bargaining stages and sunk costs were introduced to reduce the options for both parties.

2.3.2. Equilibrium Offers from Participants

Theorem 1.

In the first-level bargaining process with $n$bargaining stages, the equilibrium offer of participant $i$ is

$$I_n^i=\{\begin{array}{l}\frac{(1-{\delta }_{i,j})\pi -(\frac{n+1}{2}{\delta }_{j,i}{\delta }_{i,j}-\frac{n-1}{2}{\delta }_{i,j})f_i+(\frac{n+1}{2}{\delta }_{i,j}-\frac{n-1}{2})f_j}{1-{\delta }_{j,i}{\delta }_{i,j}},n=1,3,5,\dots \\ \frac{(1-{\delta }_{i,j})\pi -(\frac{n}{2}{\delta }_{j,i}{\delta }_{i,j}-\frac{n}{2}{\delta }_{i,j})f_i+(\frac{n}{2}{\delta }_{i,j}-\frac{n}{2})f_j}{1-{\delta }_{j,i}{\delta }_{i,j}},n=2,4,6,\dots \end{array}$$

(18)

where$i=a,b$;$j=a,b$; and$i\ne j$.

Proof of Theorem 1.

To prove Theorem 1, it is necessary to discuss the equilibrium offers of participant $\begin{array}{cc}i& (i=a,b)\end{array}$ when the number of bargaining phases is odd or even. □

Step 1: The argument breaks down into two cases when $n=1,3,5,\dots$

Case 1: The water user makes the first offer, and then the alliance rejects the water user’s offer and makes a counteroffer. The first-level bargaining process does not end until the water user makes an offer at stage $n$ and the alliance accepts the water user’s offer.

For the backward induction to the water user’s first offer, the water user considered the following question. The alliance offers $\frac{n+1}{2}$ times and pays a cumulative sunk cost of

$$\frac{n+1}{2}{f}_b.$$

The maximum expected earnings for the alliance are

$${\delta }_{a,b}(M_b-\frac{n+1}{2}{f}_b),$$

and the minimum expected earnings are

$${\delta }_{a,b}(m_b-\frac{n+1}{2}{f}_b).$$

To avoid a counteroffer by the alliance, the water user should give the alliance an earnings interval of

$$[{\delta }_{a,b}(m_b-\frac{n+1}{2}{f}_b),{\delta }_{a,b}(M_b-\frac{n+1}{2}{f}_b)].$$

In the $n$ stages of the bargaining process, the alliance accumulated $\frac{n-1}{2}$ offers at the total sunk cost of

$$\frac{n-1}{2}{f}_b,$$

and the water user accumulated $\frac{n-1}{2}+1$ offers at the total sunk cost of

$$\frac{n+1}{2}{f}_a.$$

At this point, the total profit is

$$\pi -\frac{n+1}{2}{f}_a-\frac{n-1}{2}{f}_b.$$

The maximum expected earnings for the water user are

$$(\pi -\frac{n+1}{2}{f}_a-\frac{n-1}{2}{f}_b)-{\delta }_{a,b}(m_b-\frac{n+1}{2}{f}_b),$$

and the minimum expected earnings are

$$(\pi -\frac{n+1}{2}{f}_a-\frac{n-1}{2}{f}_b)-{\delta }_{a,b}(M_b-\frac{n+1}{2}{f}_b).$$

Thus, we have

$$M_a-\frac{n+1}{2}{f}_a\le (\pi -\frac{n+1}{2}{f}_a-\frac{n-1}{2}{f}_b)-{\delta }_{a,b}(m_b-\frac{n+1}{2}{f}_b),$$

(19)

$$m_a-\frac{n+1}{2}{f}_a\ge (\pi -\frac{n+1}{2}{f}_a-\frac{n-1}{2}{f}_b)-{\delta }_{a,b}(M_b-\frac{n+1}{2}{f}_b).$$

(20)

Case 2: The alliance makes the first offer; then, the water user rejects the alliance’s offer and makes a counteroffer. The first-level bargaining process does not end until the alliance makes an offer at stage $n$ and the water user accepts the alliance’s offer.

Similar to Case 1, we have

$$M_b-\frac{n+1}{2}{f}_b\le (\pi -\frac{n+1}{2}{f}_b-\frac{n-1}{2}{f}_a)-{\delta }_{b,a}(m_a-\frac{n+1}{2}{f}_a),$$

(21)

$$m_b-\frac{n+1}{2}{f}_b\ge (\pi -\frac{n+1}{2}{f}_b-\frac{n-1}{2}{f}_a)-{\delta }_{b,a}(M_a-\frac{n+1}{2}{f}_a).$$

(22)

By (19) and (22), we have

$$M_a\le \frac{(1-{\delta }_{a,b})\pi -(\frac{n+1}{2}{\delta }_{b,a}{\delta }_{a,b}-\frac{n-1}{2}{\delta }_{a,b})f_a+(\frac{n+1}{2}{\delta }_{a,b}-\frac{n-1}{2})f_b}{1-{\delta }_{b,a}{\delta }_{a,b}}.$$

(23)

By (20) and (21), we have

$$m_a\ge \frac{(1-{\delta }_{a,b})\pi -(\frac{n+1}{2}{\delta }_{b,a}{\delta }_{a,b}-\frac{n-1}{2}{\delta }_{a,b})f_a+(\frac{n+1}{2}{\delta }_{a,b}-\frac{n-1}{2})f_b}{1-{\delta }_{b,a}{\delta }_{a,b}}.$$

(24)

By (23) and (24), we have

$$I_n^a=\frac{(1-{\delta }_{a,b})\pi -(\frac{n+1}{2}{\delta }_{b,a}{\delta }_{a,b}-\frac{n-1}{2}{\delta }_{a,b})f_a+(\frac{n+1}{2}{\delta }_{a,b}-\frac{n-1}{2})f_b}{1-{\delta }_{b,a}{\delta }_{a,b}},$$

where $I_n^a$ is the equilibrium offer of the water user first offer when $n=1,3,5,\dots$

By (20) and (21), we have

$$M_b\le \frac{(1-{\delta }_{b,a})\pi -(\frac{n+1}{2}{\delta }_{b,a}{\delta }_{a,b}-\frac{n-1}{2}{\delta }_{b,a})f_b+(\frac{n+1}{2}{\delta }_{b,a}-\frac{n-1}{2})f_a}{1-{\delta }_{b,a}{\delta }_{a,b}}.$$

(25)

By (19) and (22), we have

$$m_b\ge \frac{(1-{\delta }_{b,a})\pi -(\frac{n+1}{2}{\delta }_{b,a}{\delta }_{a,b}-\frac{n-1}{2}{\delta }_{b,a})f_b+(\frac{n+1}{2}{\delta }_{b,a}-\frac{n-1}{2})f_a}{1-{\delta }_{b,a}{\delta }_{a,b}}.$$

(26)

By (25) and (26), we have

$$I_n^b=\frac{(1-{\delta }_{b,a})\pi -(\frac{n+1}{2}{\delta }_{b,a}{\delta }_{a,b}-\frac{n-1}{2}{\delta }_{b,a})f_b+(\frac{n+1}{2}{\delta }_{b,a}-\frac{n-1}{2})f_a}{1-{\delta }_{b,a}{\delta }_{a,b}},$$

where $I_n^b$ is the equilibrium offer of the alliance’s first offer when $n=1,3,5,\dots$

Thus, the equilibrium offers of the water user and the alliance that offers first, respectively, satisfy (18) when $n=1,3,5,\dots$

Step 2: The argument breaks down into two cases when $n=2,4,6,\dots$

Case 1: The water user makes the first offer, and the alliance then rejects the water user’s offer and makes a counteroffer. The first-level bargaining process does not end until the alliance makes an offer at stage $n$ and the water user accepts the alliance’s offer.

For the backward induction to the water user’s first offer, the water user considered the following question. The alliance offers $\frac{n}{2}$ times and pays the cumulative sunk cost of

$$\frac{n}{2}{f}_b.$$

The maximum expected earnings for the alliance are

$${\delta }_{a,b}(M_b-\frac{n}{2}{f}_b),$$

and the minimum expected earnings are

$${\delta }_{a,b}(m_b-\frac{n}{2}{f}_b).$$

To avoid a counteroffer by the alliance, the water user should give the alliance an earnings interval of

$$[{\delta }_{a,b}(m_b-\frac{n}{2}{f}_b),{\delta }_{a,b}(M_b-\frac{n}{2}{f}_b)].$$

In the $n$ stages of the bargaining process, the alliance accumulated $\frac{n}{2}$ offers at the total sunk cost of

$$\frac{n}{2}{f}_b,$$

and the water user accumulated $\frac{n}{2}$ offers at the total sunk cost of

$$\frac{n}{2}{f}_a.$$

At this point, the total profit is

$$\pi -\frac{n}{2}{f}_b-\frac{n}{2}{f}_a.$$

The maximum expected earnings for the water user are

$$(\pi -\frac{n}{2}{f}_b-\frac{n}{2}{f}_a)-{\delta }_{a,b}(m_b-\frac{n}{2}{f}_b),$$

and the minimum expected earnings are

$$(\pi -\frac{n}{2}{f}_b-\frac{n}{2}{f}_a)-{\delta }_{a,b}(M_b-\frac{n}{2}{f}_b).$$

Thus, we have

$$M_a-\frac{n}{2}{f}_a\le (\pi -\frac{n}{2}{f}_b-\frac{n}{2}{f}_a)-{\delta }_{a,b}(m_b-\frac{n}{2}{f}_b),$$

(27)

$$m_a-\frac{n}{2}{f}_a\ge (\pi -\frac{n}{2}{f}_b-\frac{n}{2}{f}_a)-{\delta }_{a,b}(M_b-\frac{n}{2}{f}_b).$$

(28)

Case 2: The alliance makes the first offer, and the water user rejects the alliance’s offer and makes a counteroffer. The first-level bargaining process does not end until the water user makes an offer at stage $n$ and the alliance accepts the water user’s offer.

Similar to Case 1, we have

$$M_b-\frac{n}{2}{f}_b\le (\pi -\frac{n}{2}{f}_a-\frac{n}{2}{f}_b)-{\delta }_{b,a}(M_a-\frac{n}{2}{f}_a),$$

(29)

$$m_b-\frac{n}{2}{f}_b\ge (\pi -\frac{n}{2}{f}_a-\frac{n}{2}{f}_b)-{\delta }_{b,a}(M_a-\frac{n}{2}{f}_a).$$

(30)

By (27) and (30), we have

$$M_a\le \frac{(1-{\delta }_{a,b})\pi -(\frac{n}{2}{\delta }_{b,a}{\delta }_{a,b}-\frac{n}{2}{\delta }_{a,b})f_a+(\frac{n}{2}{\delta }_{a,b}-\frac{n}{2})f_b}{1-{\delta }_{b,a}{\delta }_{a,b}}.$$

(31)

By (28) and (29), we have

$$m_a\ge \frac{(1-{\delta }_{a,b})\pi -(\frac{n}{2}{\delta }_{b,a}{\delta }_{a,b}-\frac{n}{2}{\delta }_{a,b})f_a+(\frac{n}{2}{\delta }_{a,b}-\frac{n}{2})f_b}{1-{\delta }_{b,a}{\delta }_{a,b}}.$$

(32)

By (31) and (32), we have

$$I_n^a=\frac{(1-{\delta }_{a,b})\pi -(\frac{n}{2}{\delta }_{b,a}{\delta }_{a,b}-\frac{n}{2}{\delta }_{a,b})f_a+(\frac{n}{2}{\delta }_{a,b}-n)f_b}{1-{\delta }_{b,a}{\delta }_{a,b}},$$

where $I_n^a$ is the equilibrium offer of the water user first offer when $n=2,4,6,\dots$

By (28) and (29), we have

$$M_b\le \frac{(1-{\delta }_{b,a})\pi -(\frac{n}{2}{\delta }_{b,a}{\delta }_{a,b}-\frac{n}{2}{\delta }_{b,a})f_b+(\frac{n}{2}{\delta }_{b,a}-\frac{n}{2})f_a}{1-{\delta }_{b,a}{\delta }_{a,b}}.$$

(33)

By (27) and (30), we have

$$m_b\ge \frac{(1-{\delta }_{b,a})\pi -(\frac{n}{2}{\delta }_{b,a}{\delta }_{a,b}-\frac{n}{2}{\delta }_{b,a})f_b+(\frac{n}{2}{\delta }_{b,a}-\frac{n}{2})f_a}{1-{\delta }_{b,a}{\delta }_{a,b}}.$$

(34)

By (33) and (34), we have

$$I_n^b=\frac{(1-{\delta }_{b,a})\pi -(\frac{n}{2}{\delta }_{b,a}{\delta }_{a,b}-\frac{n}{2}{\delta }_{b,a})f_b+(\frac{n}{2}{\delta }_{b,a}-\frac{n}{2})f_a}{1-{\delta }_{b,a}{\delta }_{a,b}},$$

where $I_n^b$ is the equilibrium offer of the alliance’s first offer when $n=2,4,6,\dots$

Hence, the equilibrium offers of the water user and the alliance that offers first, respectively, satisfy (18) when $n=2,4,6,\dots$

Thus, the equilibrium offers of the water user and the alliance that offer first, respectively, satisfy Theorem 1 when $n=1,3,5,\dots$ or $n=2,4,6,\dots$ 0.

2.3.3. The Number of Bargaining Stages

As the number of bargaining stages increases, the sunk cost to be paid by both sides increases, and $I_n^a+I_n^b$ decreases. Thus, by increasing the number of game stages, the sum of the earnings of both sides of the game is equal to the amount of water savings to be distributed. When $I_n^a+I_n^b=\pi$, the number of bargaining stages can be determined.

The profit shared by both parties to the game is related to whether the number of stages is odd or even. According to Theorem 1, the number of bargaining stages is divided into two cases: $n=1,3,5,\dots$ or $n=2,4,6,\dots$.

Case 1: $n=1,3,5,\dots$

By

$$I_n^i+I_n^j=\pi ,$$

where $i=a,b$; $j=a,b$; and $i\ne j$, we have

$$n=\frac{2({\delta }_{j,i}-1)(1-{\delta }_{i,j})\pi +({\delta }_{i,j}-1)(1+{\delta }_{j,i})f_i+({\delta }_{j,i}-1)(1+{\delta }_{i,j})f_j}{({\delta }_{j,i}-1)(1-{\delta }_{i,j})(f_i+f_j)}.$$

Analysis of the solved $n$.

• If n is an odd integer, then the number of bargaining stages is N = n. At this point,

  $$I_N^i+I_N^j=\pi ,$$

  where $i=a,b$; $j=a,b$; and $i\ne j$, the water-saving benefits to be distributed are exactly divided.
• If n is not an integer and the integer part is odd, the operation INT(n) is performed; n is rounded down to the nearest integer, and the number of bargaining stages is N = INT(n). At this point,

  $$I_N^i+I_N^j>\pi ,$$

  where $i=a,b$; $j=a,b$; and $i\ne j$. The parties to the game need to make concessions on their expected water-saving benefits.
• If n is not an integer and the integer part is even, the operation ODD(n) is performed; $n$ is rounded up to the nearest odd integer, and the number of bargaining stages is N = ODD(n). At this point,

  $$I_N^i+I_N^j<\pi ,$$

  where $i=a,b$; $j=a,b$; and $i\ne j$, the parties to the game need to redistribute the undistributed water-saving benefits.
• If n is an even integer, the number of bargaining stages can be either $N=n-1$ or $N=n+1$. If $N=n-1$, we have

  $$I_N^i+I_N^j>\pi ,$$

  where $i=a,b$; $j=a,b$; and $i\ne j$; the parties to the game need to make concessions on their expected water-saving benefits. If $N=n+1$, we have

  $$I_N^i+I_N^j<\pi ,$$

  where $i=a,b$; $j=a,b$; and $i\ne j$; the parties to the game need to redistribute the undistributed water-saving benefits.

Case 2: $n=2,4,6,\dots$

By

$$I_n^i+I_n^j=\pi ,$$

where $i=a,b$; $j=a,b$; and $i\ne j$, we have

$$n=\frac{2\pi }{f_i+f_j}.$$

Analysis of the solved $n$.

• If n is an integer and even, then the number of bargaining stages is $N=n$. At this point,

  $$I_N^i+I_N^j=\pi ,$$

  where $i=a,b$; $j=a,b$; and $i\ne j$, the water-saving benefits to be distributed are exactly divided.
• If n is not an integer and the integer part is even, the operation $INT(n)$ is performed; $n$ is rounded down to the nearest integer, and the number of bargaining stages is $N=INT(n)$. At this point,

  $$I_N^i+I_N^j>\pi ,$$

  where $i=a,b$; $j=a,b$; and $i\ne j$, the parties to the game need to make concessions on their expected water-saving benefits.
• If n is not an integer and the integer part is odd, the operation $EVEN(n)$ is performed; $n$ is rounded up to the nearest even integer and the number of bargaining stages is $N=EVEN(n)$. At this point,

  $$I_N^i+I_N^j<\pi ,$$

  where $i=a,b$; $j=a,b$; and $i\ne j$, the parties to the game need to redistribute the undistributed benefits of water savings.
• If n is an odd integer, the number of bargaining stages can be either $N=n-1$ or $N=n+1$. If $N=n-1$, we have

  $$I_N^i+I_N^j>\pi ,$$

  where $i=a,b$; $j=a,b$; and $i\ne j$; the parties to the game need to make concessions on their expected water-saving benefits. If $N=n+1$, we have

  $$I_N^i+I_N^j<\pi ,$$

  where $i=a,b$; $j=a,b$; and $i\ne j$; the parties to the game need to redistribute the undistributed water-saving benefits.

2.3.4. Distribution of Residual or Concessional Benefits

When $N=n$, the water-saving benefits are exactly distributed; conversely, the benefits that are not exactly distributed need to be redistributed. The redistribution of water-saving benefits is divided into the following three cases.

Case 1: If $I_N^i+I_N^j=\pi$ ($i=a,b$; $j=a,b$; and $i\ne j$), the water-saving benefits to be distributed are exactly divided.

Case 2: If $I_N^i+I_N^j<\pi$ ($i=a,b$; $j=a,b$; and $i\ne j$), the total profit has an unfinished part, namely, residual benefits

$$w_1=\pi -(I_N^i+I_N^j).$$

The allocation to $w_1$ is determined based on the deterrence discount factor of participants $i$ and $j$. The residual benefits received by participant $i$ are

$$w_1^i=\frac{{\delta }_{j,i}}{{\delta }_{j,i}+{\delta }_{i,j}}{w}_1.$$

The residual benefits received by participant $j$ are

$$w_1^j=\frac{{\delta }_{i,j}}{{\delta }_{i,j}+{\delta }_{j,i}}{w}_1.$$

Case 3: If $I_N^i+I_N^j>\pi$ ($i=a,b$; $j=a,b$; and $i\ne j$), then the total profit has a missing part, namely, concessional benefits

$$w_2=(I_N^i+I_N^j)-\pi .$$

The allocation to $w_2$ is determined based on the deterrence discount factor of participants $i$ and $j$. The concession benefits shared by participant $i$ are

$$w_2^i=\frac{{\delta }_{i,j}}{{\delta }_{j,i}+{\delta }_{i,j}}{w}_2.$$

The concession benefits shared by participant $j$ are

$$w_2^j=\frac{{\delta }_{j,i}}{{\delta }_{i,j}+{\delta }_{j,i}}{w}_2.$$

2.3.5. Profit Allocation Scheme

In the first-level bargaining process, the equilibrium earnings for each party are

$$I_i^{*}=\{\begin{array}{l}\frac{({\delta }_{j,i}^2+{\delta }_{i,j})(1-{\delta }_{i,j})\pi -({\delta }_{{}_{i,j}}^2+{\delta }_{j,i})(\frac{N+1}{2}{\delta }_{j,i}-\frac{N-1}{2})f_i+({\delta }_{i,j}+{\delta }_{j,i}^2)(\frac{N+1}{2}{\delta }_{i,j}-\frac{N-1}{2})f_j}{(1-{\delta }_{j,i}{\delta }_{i,j})({\delta }_{j,i}+{\delta }_{i,j})},\\ N=1,3,5,\dots \\ \frac{({\delta }_{j,i}^2+{\delta }_{i,j})(1-{\delta }_{i,j})\pi -({\delta }_{{}_{i,j}}^2+{\delta }_{j,i})(\frac{N}{2}{\delta }_{j,i}-\frac{N}{2})f_i+({\delta }_{i,j}+{\delta }_{j,i}^2)(\frac{N}{2}{\delta }_{i,j}-\frac{N}{2})f_j}{(1-{\delta }_{j,i}{\delta }_{i,j})({\delta }_{j,i}+{\delta }_{i,j})},\\ N=2,4,6,\dots \end{array}$$

where $N\ge n$; $i=a,b$; $j=a,b$; and $i\ne j$.

$$I_i^{*}=\{\begin{array}{l}\frac{{\delta }_{j,i}(1-{\delta }_{{}_{i,j}}^2)\pi -{\delta }_{i,j}(1+{\delta }_{j,i})(\frac{N+1}{2}{\delta }_{j,i}-\frac{N-1}{2})f_i+{\delta }_{j,i}(1+{\delta }_{i,j})(\frac{N+1}{2}{\delta }_{i,j}-\frac{N-1}{2})f_j}{(1-{\delta }_{j,i}{\delta }_{i,j})({\delta }_{j,i}+{\delta }_{i,j})},\\ N=1,3,5,\dots \\ \frac{{\delta }_{j,i}(1-{\delta }_{{}_{i,j}}^2)\pi -{\delta }_{i,j}(1+{\delta }_{j,i})(\frac{N}{2}{\delta }_{j,i}-\frac{N}{2})f_i+{\delta }_{j,i}(1+{\delta }_{i,j})(\frac{N}{2}{\delta }_{i,j}-\frac{N}{2})f_j}{(1-{\delta }_{j,i}{\delta }_{i,j})({\delta }_{j,i}+{\delta }_{i,j})},\\ N=2,4,6,\dots \end{array}$$

where $N<n$; $i=a,b$; $j=a,b$; and $i\ne j$.

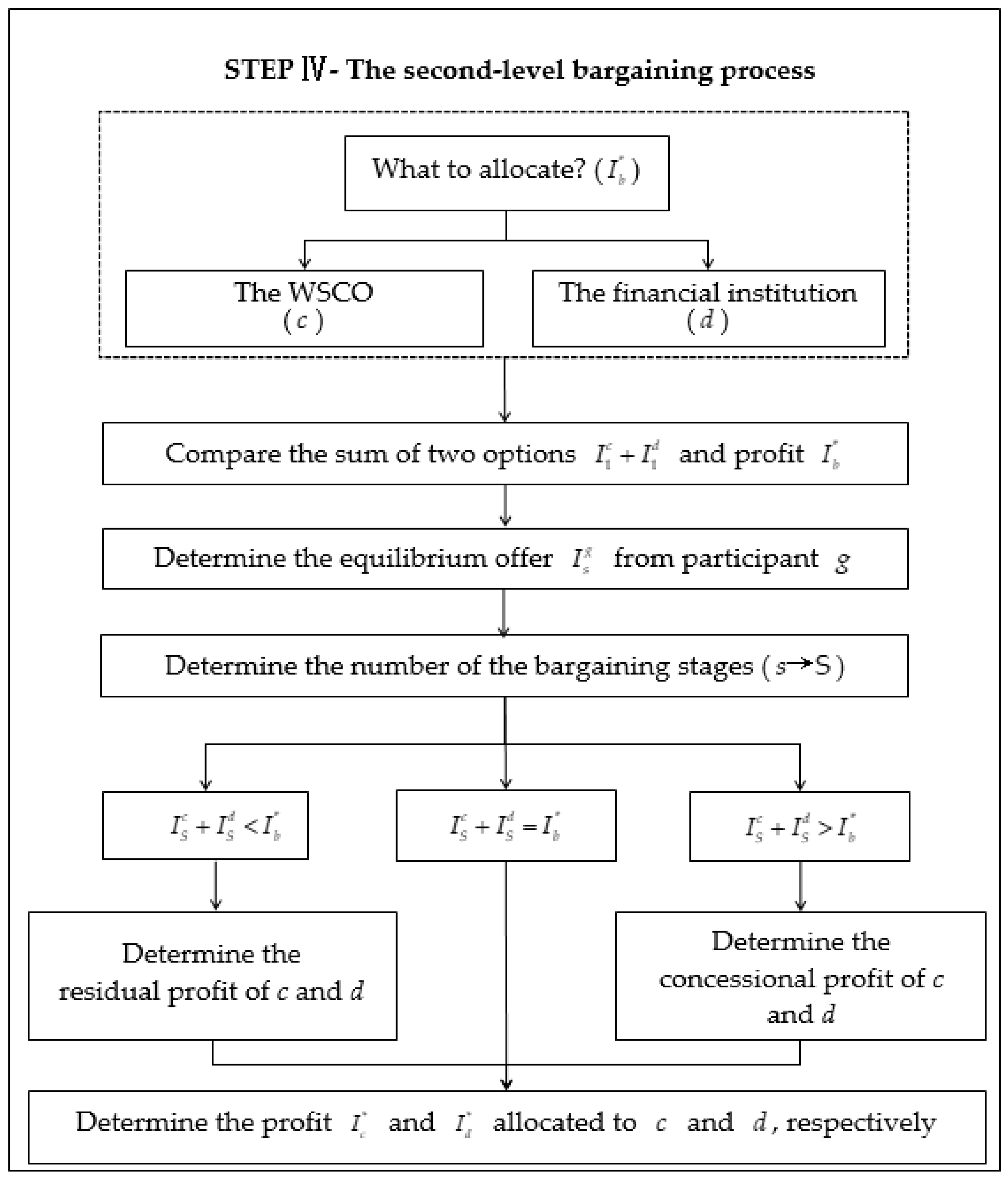
2.4. The Second-Level Bargaining Process

The second-level bargaining process is between the WSCO and the financial institution over the alliance’s share of the benefits $I_b^{*}$ in the first-level bargaining process. The basic framework of STEP Ⅳ is shown in Figure 4.

We assume that $M_g$ and $m_g$ are the maximum and minimum expected earnings, respectively, of the offers starting with participant $\begin{array}{cc}g& (g=c,d)\end{array}$ and $f_g$ is the sunk cost of participant $g$. Each participant’s expected earnings are sufficient to cover its total sunk cost. In the second-level bargaining process, the WSCO and the financial institution make the first offer, respectively. Similar to the first-level bargaining process, there is

$$I_1^c+I_1^d>I_b^{*},$$

where $I_1^c$ is the equilibrium offer of the WSCO in the second-level bargaining process with one stage and $I_1^d$ is the financial institution’s equilibrium offer in the second-level bargaining process with one stage. The sum of the WSCO’s expected earnings and the financial institution’s expected earnings are always greater than $I_b^{*}$, namely, $I_b^{*}$ is not enough to share.

Theorem 2.

In the second-level bargaining process with$s$bargaining stages, the equilibrium offer of participant$g$ is

$$I_s^g=\{\begin{array}{c}\frac{(1-{\delta }_{g,h})I_b^{*}-(\frac{s+1}{2}{\delta }_{h,g}{\delta }_{g,h}-\frac{s-1}{2}{\delta }_{g,h})f_g+(\frac{s+1}{2}{\delta }_{g,h}-\frac{s-1}{2})f_h}{1-{\delta }_{h,g}{\delta }_{g,h}},s=1,3,5,\dots \\ \frac{(1-{\delta }_{g,h})I_b^{*}-(\frac{s}{2}{\delta }_{h,g}{\delta }_{g,h}-\frac{s}{2}{\delta }_{g,h})f_g+(\frac{s}{2}{\delta }_{g,h}-\frac{s}{2})f_h}{1-{\delta }_{h,g}{\delta }_{g,h}},s=2,4,6,\dots \end{array}$$

(35)

where$g=c,d$;$h=c,d$; and$g\ne h$.

Proof of Theorem 2.

Similar to the proof of Theorem 1, Theorem 2 can be proved. □

Similar to Section 2.3.3, the number of bargaining stages of the second-level bargaining process $S$ can be determined.

Similar to Section 2.3.4, the residual or concessional benefits of participants in the second-level bargaining process are as follows.

The residual benefits received by participant $g$ are

$$w_3^g=\frac{{\delta }_{h,g}}{{\delta }_{h,g}+{\delta }_{g,h}}{w}_3.$$

The residual benefits received by participant $h$ are

$$w_3^h=\frac{{\delta }_{g,h}}{{\delta }_{g,h}+{\delta }_{h,g}}{w}_3.$$

The concession benefits shared by participant $g$ are

$$w_4^g=\frac{{\delta }_{g,h}}{{\delta }_{h,g}+{\delta }_{g,h}}{w}_4.$$

The concession benefits shared by participant $h$ are

$$w_4^h=\frac{{\delta }_{h,g}}{{\delta }_{g,h}+{\delta }_{h,g}}{w}_4.$$

In the second-level bargaining process, the equilibrium earnings for each party are

$$I_S^g=\{\begin{array}{l}\frac{({\delta }_{h,g}^2+{\delta }_{g,h})(1-{\delta }_{g,h})I_b^{*}-({\delta }_{g,h}^2+{\delta }_{h,g})(\frac{S+1}{2}{\delta }_{h,g}-\frac{S-1}{2})f_g+({\delta }_{g,h}+{\delta }_{h,g}^2)(\frac{S+1}{2}{\delta }_{g,h}-\frac{S-1}{2})f_h}{(1-{\delta }_{h,g}{\delta }_{g,h})({\delta }_{h,g}+{\delta }_{g,h})},\\ S=1,3,5,\dots \\ \frac{({\delta }_{h,g}^2+{\delta }_{g,h})(1-{\delta }_{g,h})I_b^{*}-({\delta }_{g,h}^2+{\delta }_{h,g})(\frac{S}{2}{\delta }_{h,g}-\frac{S}{2})f_g+({\delta }_{g,h}+{\delta }_{h,g}^2)(\frac{S}{2}{\delta }_{g,h}-\frac{S}{2})f_h}{(1-{\delta }_{h,g}{\delta }_{g,h})({\delta }_{h,g}+{\delta }_{g,h})},\\ S=2,4,6,\dots \end{array}$$

where $S\ge s$; $g=c,d$; $h=c,d$; and $g\ne h$.

$$I_S^g=\{\begin{array}{l}\frac{{\delta }_{h,g}(1-{\delta }_{g,h}^2)I_b^{*}-{\delta }_{g,h}(1+{\delta }_{h,g})(\frac{S+1}{2}{\delta }_{h,g}-\frac{S-1}{2})f_g+{\delta }_{h,g}(1+{\delta }_{g,h})(\frac{S+1}{2}{\delta }_{g,h}-\frac{S-1}{2})f_h}{(1-{\delta }_{h,g}{\delta }_{g,h})({\delta }_{h,g}+{\delta }_{g,h})},\\ S=1,3,5,\dots \\ \frac{{\delta }_{h,g}(1-{\delta }_{g,h}^2)I_b^{*}-{\delta }_{g,h}(1+{\delta }_{h,g})(\frac{S}{2}{\delta }_{h,g}-\frac{S}{2})f_g+{\delta }_{h,g}(1+{\delta }_{g,h})(\frac{S}{2}{\delta }_{g,h}-\frac{S}{2})f_h}{(1-{\delta }_{h,g}{\delta }_{g,h})({\delta }_{h,g}+{\delta }_{g,h})},\\ S=2,4,6,\dots \end{array}$$

where $S<s$; $g=c,d$; $h=c,d$; and $g\ne h$.

3. Results

Since each participant has four possible equilibrium offers in the first-level and the second-level bargaining process, there are sixteen situations of profit allocation among the three participants—the water user, the WSCO, and the financial institutions—in the two-level bargaining process. Considering the minimum earnings requirement of participants, the profit allocation results of each participant are shown in

Table 1. The sixteen situations of the profit allocation schemes among the three participants.

Situation	${\mathit{I}}_{\mathit{a}}^{\mathbf{*}}$										${\mathit{I}}_{\mathit{c}}^{\mathbf{*}}$											${\mathit{I}}_{\mathit{d}}^{\mathbf{*}}$
	B1	B2	−D1	−D2	−D3	−D4	E1	E2	E3	E4	B3	B4	−D5	−D6	−D7	−D8	E5	E6	E7	E8	L1	B5	B6	−E5	−E6	−E7	−E8	D5	D6	D7	D8	L2
1	√ *		√				√				√		√				√				√	√		√				√				√
2	√		√				√				√			√				√			√	√			√				√			√
3	√		√				√					√			√				√		√		√			√				√		√
4	√		√				√					√				√				√	√		√				√				√	√
5	√			√				√			√		√				√				√	√		√				√				√
6	√			√				√			√			√				√			√	√			√				√			√
7	√			√				√				√			√				√		√		√			√				√		√
8	√			√				√				√				√				√	√		√				√				√	√
9		√			√				√		√		√				√				√	√		√				√				√
10		√			√				√		√			√				√			√	√			√				√			√
11		√			√				√			√			√				√		√		√			√				√		√
12		√			√				√			√				√				√	√		√				√				√	√
13		√				√				√	√		√				√				√	√		√				√				√
14		√				√				√	√			√				√			√	√			√				√			√
15		√				√				√		√			√				√		√		√			√				√		√
16		√				√				√		√				√				√	√		√				√				√	√

* √ denotes that in case $\begin{array}{cc}u& (u=1,2,\dots ,16)\end{array}$, participant $\begin{array}{cc}v& (v=a,c,d)\end{array}$ has a certain profit. In the case $\begin{array}{cc}u& (u=1,2,\dots ,16)\end{array}$, the total profit of participant $\begin{array}{cc}v& (v=a,c,d)\end{array}$ is the sum of the profit of √.

. $I_a^{*}$ is the benefits of the water user; $I_c^{*}$ is the benefits of the WSCO; and $I_d^{*}$ is the benefits of the financial institution. To observe the differences between the various cases, the following assumptions are made.

$$B_1==\frac{({\delta }_{b,a}^2+{\delta }_{a,b})(1-{\delta }_{a,b})\pi }{(1-{\delta }_{b,a}{\delta }_{a,b})({\delta }_{b,a}+{\delta }_{a,b})}$$

$$B_2==\frac{{\delta }_{b,a}(1-{\delta }_{a,b}^2)\pi }{(1-{\delta }_{b,a}{\delta }_{a,b})({\delta }_{b,a}+{\delta }_{a,b})}$$

$$B_3==\frac{({\delta }_{d,c}^2+{\delta }_{c,d})(1-{\delta }_{c,d})I_N^b}{(1-{\delta }_{d,c}{\delta }_{c,d})({\delta }_{d,c}+{\delta }_{c,d})}$$

$$B_4=\frac{{\delta }_{d,c}(1-{\delta }_{c,d}^2)I_N^b}{(1-{\delta }_{d,c}{\delta }_{c,d})({\delta }_{d,c}+{\delta }_{c,d})}$$

$$B_5=\frac{({\delta }_{c,d}^2+{\delta }_{d,c})(1-{\delta }_{d,c})I_N^b}{(1-{\delta }_{c,d}{\delta }_{d,c})({\delta }_{c,d}+{\delta }_{d,c})}$$

$$B_6=\frac{{\delta }_{c,d}(1-{\delta }_{d,c}^2)I_N^b}{(1-{\delta }_{c,d}{\delta }_{d,c})({\delta }_{c,d}+{\delta }_{d,c})}$$

$$D_1=\frac{({\delta }_{{}_{a,b}}^2+{\delta }_{b,a})(\frac{N+1}{2}{\delta }_{b,a}-\frac{N-1}{2})f_a}{(1-{\delta }_{b,a}{\delta }_{a,b})({\delta }_{b,a}+{\delta }_{a,b})}$$

$$D_2=\frac{({\delta }_{a,b}^2+{\delta }_{b,a})(\frac{N}{2}{\delta }_{b,a}-\frac{N}{2})f_a}{(1-{\delta }_{b,a}{\delta }_{a,b})({\delta }_{b,a}+{\delta }_{a,b})}$$

$$D_3=\frac{{\delta }_{a,b}(1+{\delta }_{b,a})(\frac{N+1}{2}{\delta }_{b,a}-\frac{N-1}{2})f_a}{(1-{\delta }_{b,a}{\delta }_{a,b})({\delta }_{b,a}+{\delta }_{a,b})}$$

$$D_4=\frac{{\delta }_{a,b}(1+{\delta }_{b,a})(\frac{N}{2}{\delta }_{b,a}-\frac{N}{2})f_a}{(1-{\delta }_{b,a}{\delta }_{a,b})({\delta }_{b,a}+{\delta }_{a,b})}$$

$$D_5=\frac{({\delta }_{c,d}^2+{\delta }_{d,c})(\frac{S+1}{2}{\delta }_{d,c}-\frac{S-1}{2})f_c}{(1-{\delta }_{d,c}{\delta }_{c,d})({\delta }_{d,c}+{\delta }_{c,d})}$$

$$D_6=\frac{({\delta }_{c,d}^2+{\delta }_{d,c})(\frac{S}{2}{\delta }_{d,c}-\frac{S}{2})f_c}{(1-{\delta }_{d,c}{\delta }_{c,d})({\delta }_{d,c}+{\delta }_{c,d})}$$

$$D_7=\frac{{\delta }_{c,d}(1+{\delta }_{d,c})(\frac{S+1}{2}{\delta }_{d,c}-\frac{S-1}{2})f_c}{(1-{\delta }_{d,c}{\delta }_{c,d})({\delta }_{d,c}+{\delta }_{c,d})}$$

$$D_8=\frac{{\delta }_{c,d}(1+{\delta }_{d,c})(\frac{S}{2}{\delta }_{d,c}-\frac{S}{2})f_c}{(1-{\delta }_{d,c}{\delta }_{c,d})({\delta }_{d,c}+{\delta }_{c,d})}$$

$$E_1=\frac{({\delta }_{a,b}+{\delta }_{b,a}^2)(\frac{N+1}{2}{\delta }_{a,b}-\frac{N-1}{2})f_b}{(1-{\delta }_{b,a}{\delta }_{a,b})({\delta }_{b,a}+{\delta }_{a,b})}$$

$$E_2=\frac{({\delta }_{a,b}+{\delta }_{b,a}^2)(\frac{N}{2}{\delta }_{a,b}-\frac{N}{2})f_b}{(1-{\delta }_{b,a}{\delta }_{a,b})({\delta }_{b,a}+{\delta }_{a,b})}$$

$$E_3=\frac{{\delta }_{b,a}(1+{\delta }_{a,b})(\frac{N+1}{2}{\delta }_{a,b}-\frac{N-1}{2})f_b}{(1-{\delta }_{b,a}{\delta }_{a,b})({\delta }_{b,a}+{\delta }_{a,b})}$$

$$E_4=\frac{{\delta }_{b,a}(1+{\delta }_{a,b})(\frac{N}{2}{\delta }_{a,b}-\frac{N}{2})f_b}{(1-{\delta }_{b,a}{\delta }_{a,b})({\delta }_{b,a}+{\delta }_{a,b})}$$

$$E_5=\frac{({\delta }_{c,d}+{\delta }_{d,c}^2)(\frac{S+1}{2}{\delta }_{c,d}-\frac{S-1}{2})f_d}{(1-{\delta }_{d,c}{\delta }_{c,d})({\delta }_{d,c}+{\delta }_{c,d})}$$

$$E_6=\frac{({\delta }_{c,d}+{\delta }_{d,c}^2)(\frac{S}{2}{\delta }_{c,d}-\frac{S}{2})f_d}{(1-{\delta }_{d,c}{\delta }_{c,d})({\delta }_{d,c}+{\delta }_{c,d})}$$

$$E_7=\frac{{\delta }_{d,c}(1+{\delta }_{c,d})(\frac{S+1}{2}{\delta }_{c,d}-\frac{S-1}{2})f_d}{(1-{\delta }_{d,c}{\delta }_{c,d})({\delta }_{d,c}+{\delta }_{c,d})}$$

$$E_8=\frac{{\delta }_{d,c}(1+{\delta }_{c,d})(\frac{S}{2}{\delta }_{c,d}-\frac{S}{2})f_d}{(1-{\delta }_{d,c}{\delta }_{c,d})({\delta }_{d,c}+{\delta }_{c,d})}$$

$$L_1=(C_c-C_d)R_c$$

$$L_2=C_d{R}_d$$

The sixteen situations of profit allocation among the three participants are listed in Table 1.

The amount of profit allocation of participants is closely related to the minimum profit requirements, the deterrence discount factors, the number of bargaining stages, and the sunk cost. When $N\ge n$, the water user has a profit of $B_1$; conversely, it has a profit of $B_2$. When $S\ge s$, the WSCO has the benefits of $B_3$, and the financial institution has the benefits of $B_5$; conversely, they have a return of $B_4$ and $B_6$, respectively. In any case, the WSCO has the benefits of $L_1$ and the financial institution has the benefits of $L_2$. When the three participants lose $D_h$ or $E_h$ ($h=1,2,\dots ,8$), they will gain $E_h$ or $D_h$.

4. Numerical Analysis

In this section, numerical simulations demonstrate the theoretical results obtained and provide further management insights for participants.

A WSCO adopts the FRI WSMC model to implement water-saving technology on a golf course. The WSCO is responsible for financing from a bank. Under the business model, the WSCO is allied with the bank. Detailed project characteristics are illustrated in

Table 2. Project details.

Property	Details
Investment cost	The WSCO invested a total of CNY 12 million in the project, including CNY 8 million in financing from the bank
The water price	CNY 160 per cubic meter
Savings	The annual average water saving is 200.000 cubic meters
Contract period	5 years
Risk-free discount rate	3.0%

. The average return on investment in the water services sector is 12.0%. Detailed information on each participant is shown in

Table 3. Participant details.

Parameters	Details
Return on investment	The WSCO requires an excess return on investment of 15%; the bank requires a minimum return on investment of 4.4%
Sunk cost	CNY 10.000 per bid
The deterrence capacity	The deterrence capacity of the golf course, the WSCO, and the bank is 0.7, 0.4, and 0.4, respectively
The withstand deterrence capacity	The withstand deterrence capacity of the golf course, the WSCO, and the bank is 0.8, 0.3, and 0.4, respectively
The deterrence degree coefficient	The deterrence degree coefficient of the golf course, the WSCO, and the bank is 0.8, 0.9, and 0.7, respectively

.

Table 2 shows that the average annual water cost savings are CNY 32 million. By (1), the net present value during the project contract is CNY 134.5506 million.

The following information can be obtained in Table 3. The bank has a minimum profit requirement of CNY 352.000 by (3). The WSCO has a minimum profit requirement of CNY 600.000 by (4). The total benefits to be distributed are CNY 133.5986 million by (5). The deterrence discount factor caused by the golf course to the alliance is 0.56 by (7). The deterrence discount factor caused by the alliance with the golf course is 0.56 by (8). The deterrence discount factor caused by the bank to the WSCO is 0.52, and the deterrence discount factor caused by the WSCO to the bank is 0.53 by (6).

Based on the above data and the proposed methodology, the benefits distributed by the golf course, the WSCO, and the bank are shown in

Table 4. Profit allocation.

Situations	Number of Bargaining Stage (Odd/Even)		Profit (CNY Million)
	The First-Level Bargaining Process	The Second-Level Bargaining Process	The Golf Course	The WSCO	The Bank
1	odd	odd	66.79930	33.99990	33.75140
2	odd	even	66.79930	33.99965	33.75165
3	even	odd	66.79930	33.99990	33.75140
4	even	even	66.79930	33.99965	33.75165

.

Whether the number of bargaining stages at the first-level is odd or even, the water-saving profits shared by the golf course are CNY 66.79930 million. If the number of bargaining stages at the second-level is odd, the WSCO obtains CNY 33.99990 million, and the bank achieves CNY 33.75140 million. If the number of bargaining stages in the second-level is even, the WSCO obtains CNY 33.99965 million, and the bank earns CNY 33.75165 million. At the early stage of FRI WSMC, the golf course received the largest share of the water-saving benefits, the WSCO received the second largest, and the bank received the smallest.

5. Discussion

In order to study the influence of various factors on the results of profit allocation, the following discussion is made.

5.1. The First-Level Bargaining Process

The results of the first-level bargaining process are analyzed as follows.

• Factors such as the amount of water-saving benefits to be allocated, the deterrence discount factor, the number of game stages, and the sunk cost are closely related to the equilibrium earnings of the participants.
• $\begin{array}{cc}\frac{({\delta }_{j,i}^2+{\delta }_{i,j})(1-{\delta }_{i,j})\pi }{(1-{\delta }_{j,i}{\delta }_{i,j})({\delta }_{j,i}+{\delta }_{i,j})}& (N\ge n)\end{array}$ and $\begin{array}{cc}\frac{{\delta }_{j,i}(1-{\delta }_{{}_{i,j}}^2)\pi }{(1-{\delta }_{j,i}{\delta }_{i,j})({\delta }_{j,i}+{\delta }_{i,j})}& (N<n)\end{array}$ as the major benefits of participant $\begin{array}{cc}i& (i=a,b)\end{array}$ with

  $$\frac{\partial \frac{({\delta }_{j,i}^2+{\delta }_{i,j})(1-{\delta }_{i,j})\pi }{(1-{\delta }_{j,i}{\delta }_{i,j})({\delta }_{j,i}+{\delta }_{i,j})}}{\partial {\delta }_{j,i}}>0(N\ge n),$$

  and

  $$\frac{\partial \frac{({\delta }_{j,i}^2+{\delta }_{i,j})(1-{\delta }_{i,j})\pi }{(1-{\delta }_{j,i}{\delta }_{i,j})({\delta }_{j,i}+{\delta }_{i,j})}}{\partial {\delta }_{i,j}}<0(N\ge n),$$

  or

  $$\frac{\partial \frac{{\delta }_{j,i}(1-{\delta }_{{}_{i,j}}^2)\pi }{(1-{\delta }_{j,i}{\delta }_{i,j})({\delta }_{j,i}+{\delta }_{i,j})}}{\partial {\delta }_{j,i}}>0(N<n),$$

  and

  $$\frac{\partial \frac{{\delta }_{j,i}(1-{\delta }_{{}_{i,j}}^2)\pi }{(1-{\delta }_{j,i}{\delta }_{i,j})({\delta }_{j,i}+{\delta }_{i,j})}}{\partial {\delta }_{i,j}}<0(N<n).$$

The major benefits of participant $i$ are positively correlated with the deterrence discount factor of participant $i$ and negatively correlated with the deterrence discount factor of participant $\begin{array}{cc}\begin{array}{cc}j& (j=a,b;\end{array}& i\ne j\end{array})$. If participant $i$ has a larger deterrence discount factor, it will gain more of the major benefits in the bargaining process. Conversely, it will gain fewer of the major benefits.

3.

If

$$-({\delta }_{{}_{i,j}}^2+{\delta }_{j,i})(\frac{N+1}{2}{\delta }_{j,i}-\frac{N-1}{2})f_i+({\delta }_{i,j}+{\delta }_{j,i}^2)(\frac{N+1}{2}{\delta }_{i,j}-\frac{N-1}{2})f_j>0(N\ge n,N=1,3,5,\dots )$$

or

$$-({\delta }_{{}_{i,j}}^2+{\delta }_{j,i})(\frac{N}{2}{\delta }_{j,i}-\frac{N}{2})f_i+({\delta }_{i,j}+{\delta }_{j,i}^2)(\frac{N}{2}{\delta }_{i,j}-\frac{N}{2})f_j>0(N\ge n,N=2,4,6,\dots )$$

or

$$-{\delta }_{i,j}(1+{\delta }_{j,i})(\frac{N+1}{2}{\delta }_{j,i}-\frac{N-1}{2})f_i+{\delta }_{j,i}(1+{\delta }_{i,j})(\frac{N+1}{2}{\delta }_{i,j}-\frac{N-1}{2})f_j>0(N<n,N=1,3,5,\dots )$$

or

$$-{\delta }_{i,j}(1+{\delta }_{j,i})(\frac{N}{2}{\delta }_{j,i}-\frac{N}{2})f_i+{\delta }_{j,i}(1+{\delta }_{i,j})(\frac{N}{2}{\delta }_{i,j}-\frac{N}{2})f_j>0(N<n,N=2,4,6,\dots )$$

it will promote the first-mover advantage of participant $i$; conversely, the first-mover advantage of participant $i$ will be suppressed.

4.

For $w_1^i$, we have

$$\frac{\partial w_1^i}{\partial {\delta }_{j,i}}>0,$$

and

$$\frac{\partial w_1^i}{\partial {\delta }_{i,j}}<0.$$

The residual benefits of participant $i$ increase with the increase in ${\delta }_{j,i}$ and decrease with the increase in ${\delta }_{i,j}$.

For $w_2^i$, we have

$$\frac{\partial w_2^i}{\partial {\delta }_{i,j}}>0,$$

and

$$\frac{\partial w_2^i}{\partial {\delta }_{j,i}}<0.$$

The concession benefits of participant $i$ increase with the increase in ${\delta }_{i,j}$ and decrease with the increase in ${\delta }_{j,i}$.

Thus, a party with a larger deterrence discount factor gains more, and a party with a smaller deterrence discount factor gains less.

Participant $j$ is influenced by the first-mover advantage and the deterrence discount factor in the same way as participant $i$.

The immature development of the FRI WSMC and the dominant position of water users in the market, which resulted in a greater deterrence discount factor for water users, were the main reasons for the golf course receiving the greatest share of water-saving benefits.

5.2. The Second-Level Bargaining Process

Similar to Section 5.1, the results of the second-level bargaining process are analyzed as follows.

• Factors such as the benefits of the alliance in the first-level bargaining process, the deterrence discount factor, the number of game stages, and the sunk cost are closely related to the equilibrium earnings of the participants.
• The major benefits of participant $\begin{array}{cc}g& (g=a,b)\end{array}$ are positively correlated with the deterrence discount factor of participant $g$ and negatively correlated with the deterrence discount factor of participant $\begin{array}{cc}\begin{array}{cc}h& (h=c,d;\end{array}& g\ne h\end{array})$. If participant $g$ has a larger deterrence discount factor, it will gain more of the major benefits. Conversely, it will gain fewer of the major benefits.
• If

  $$-({\delta }_{g,h}^2+{\delta }_{h,g})(\frac{S+1}{2}{\delta }_{h,g}-\frac{S-1}{2})f_g+({\delta }_{g,h}+{\delta }_{h,g}^2)(\frac{S+1}{2}{\delta }_{g,h}-\frac{S-1}{2})f_h>0(S\ge s,S=1,3,5,\dots ),$$

  or

  $$-({\delta }_{g,h}^2+{\delta }_{h,g})(\frac{S}{2}{\delta }_{h,g}-\frac{S}{2})f_g+({\delta }_{g,h}+{\delta }_{h,g}^2)(\frac{S}{2}{\delta }_{g,h}-\frac{S}{2})f_h>0(S\ge s,S=2,4,6,\dots )$$

  or

  $$-{\delta }_{g,h}(1+{\delta }_{h,g})(\frac{S+1}{2}{\delta }_{h,g}-\frac{S-1}{2})f_g+{\delta }_{h,g}(1+{\delta }_{g,h})(\frac{S+1}{2}{\delta }_{g,h}-\frac{S-1}{2})f_h>0(S<s,S=1,3,5,\dots )$$

  or

  $$-{\delta }_{g,h}(1+{\delta }_{h,g})(\frac{S}{2}{\delta }_{h,g}-\frac{S}{2})f_g+{\delta }_{h,g}(1+{\delta }_{g,h})(\frac{S}{2}{\delta }_{g,h}-\frac{S}{2})f_h>0(S<s,S=2,4,6,\dots )$$

  it will promote the first-mover advantage of participant $g$; conversely, the first-mover advantage of participant $g$ will be suppressed.
• The residual benefits of participant $g$ increase with increasing ${\delta }_{h,g}$ and decrease with increasing ${\delta }_{g,h}$. The concession benefits of participant $g$ increase with the increase in ${\delta }_{g,h}$ and decrease with the increase in ${\delta }_{h,g}$.

Thus, a party with a larger deterrence discount factor gains more, and a party with a smaller deterrence discount factor gains less.

Participant $h$ is influenced by the first-mover advantage and the deterrence discount factor in the same way as participant $g$.

The lower minimum profit requirement of the bank is the main reason for its smaller share of water-saving benefits. With the development and widespread use of the FRI WSMC, WSCOs and financial institutions can improve their position in the market to obtain more water-saving benefits. Financial institutions can also raise their minimum profit requirements to a certain extent to obtain more profit.

6. Conclusions

WSMC is an emerging method of water conservation that is important for improving the global water resource situation. FRI WSMC is an effective way to address water shortages, so it has considerable potential for application. However, profit allocation has become a major obstacle to its implementation. It is important to solve the profit allocation of FRI WSMC projects. Therefore, the main contributions of this paper are as follows:

• A new profit allocation model is established based on the bargaining theory to create the distribution scheme. The two sides of the game offer first, respectively, and allocate the profit according to their offers to overcome the first-mover advantage. The number of bargaining stages and sunk cost are introduced into the model so that the sum of the options of both sides is not greater than the profit to be allocated, redistributing the remaining profit according to the deterrence discount factor of the players.
• It improves the theoretical mechanism of FRI WSMC and has guiding significance for the profit distribution of FRI WSMC projects in practice. Sixteen profit allocation results of the three participants were proposed and applied in the FRI WSMC projects. The relationship between profit and influencing factors was explored. The profit allocation of participants is closely related to the minimum profit requirements, deterrence discount factors, the number of bargaining stages, and sunk cost. Participants’ major benefits and residual benefits are positively correlated with their deterrence discount factors and negatively correlated with the other side’s deterrence discount factors. The concessional benefits of the participants are negatively correlated with its deterrence discount factors and positively correlated with the other side’s deterrence discount factors. At the same time, the effect of major benefits on first-mover advantage was also explored.

While the proposed methodology considers practicalities as much as possible, some limitations should be noted. First, the methodology only considers the impact of the water-saving profit to be allocated, the deterrence discount factor, the number of bargaining stages, and the sunk cost of the allocation of water-saving benefits. However, the factors affecting profit allocation are likely to be more numerous. There are complex relationships between the factors, all of which need to be extensively considered. Second, when determining the interval of the amount of water-saving benefits to be allocated, the amount of investment is static. There may be other factors affecting fluctuations in investment volumes that are not mentioned in our study. Third, the sunk cost of each offer is the same fixed value, and its volatility is worth considering. Finally, this paper only discusses the water-saving benefit allocation scheme when each participant is risk neutral. There may be participants that are risk-averse. In general, addressing the above limitations would make the methodology more rigorous and practical.

In the future, the profit allocation of participants with risk-averse and risk-preference in FRI WSMC projects will be studied and the profit of participants with different risk attitudes will be compared, so as to allocate the profit reasonably.