Proximal Linearized Iteratively Reweighted Algorithms for Nonconvex and Nonsmooth Optimization Problem
Abstract
:1. Introduction
2. Background
2.1. Mathematical Preliminary
- ω is a regular subgradient of f at , denoted by , if
- v is a (limiting) subgradient of f at , denoted by , if there are sequences , with .
- 1.
- If f is convex, the regular and limiting subdifferentials are same sets, which is the subdifferential in the convex analysis:
- 2.
- If f is continuously differentiable on a neighborhood of , then .
- 3.
- If g is a l.s.c. function and f is continuously differentiable on a neighborhood of , then we can obtain the subdifferential of as follows:
- 4.
- If a proper and l.s.c. function has a local minimum at , then . Furthermore, if f is convex, then this condition is also sufficient for a global minimum.
- (i)
- ;
- (ii)
- ϕ is differentiable in ;
- (iii)
- for all ;
- (iv)
- For any ,
2.2. Iterative Convex Majorization–Minimization Method
| Algorithm 1 Iterative Convex Majorization–Minimization Method (ICMM). |
Initialization Choose a starting point with and define a suitable family of convex surrogate functions such that for all , holds, where
repeat until The algorithm satisfies a stopping condition |
3. Proposed Algorithm
3.1. Proximal Linearized Iteratively Convex Majorization–Minimization Method
| Algorithm 2 Proximal Linearized Iteratively Convex Majorization–Minimization Method (PL-ICMM). |
Conditions
Initialization Choose a starting point with and define a suitable family of convex surrogate functions such that for all , holds, where
repeat Solve
until The algorithm satisfies a stopping condition. |
| Algorithm 3 Proximal linearized iteratively reweighted algorithm (PL-IRL1). |
Conditions
Initialization Choose a starting point with . repeat . Solve
until The algorithm satisfies a stopping condition |
| Algorithm 4 Proximal Linearized Iterative Reweighted Least Square Algorithm (PL-IRLS). |
Conditions
Initialization Choose a starting point with . repeat . , . Solve
until The algorithm satisfies a stopping condition |
3.2. Convergence Analysis of the PL-ICMM
- h has a locally Lipschitz gradient on a compact set containing the sequence , and majorizers have a Lipschitz gradient on a compact set containing the sequence with a common Lipschitz constant.
- 1.
- For all ,
- 2.
- For all ,
4. Numerical Experiments and Discussion
4.1. Numerical Results for PL-IRL1
4.2. Numerical Results for PL-IRLS
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| l.s.c. | Lower semicontinuous |
| ICMM | Iterative convex majorization–minimization method |
| KL | Kurdyka–Łojasiewicz |
| PL-ICMM | Proximal linearized iterative convex majorization–minimization method |
| PL-IRL1 | Proximal linearized iteratively reweighted algorithm |
| PL-IRLS | Proximal linearized iteratively reweighted least square algorithm |
| IRL1 | Iteratively reweighted algorithm |
| DCT | discrete cosine transform |
References
- Curry, H.B. The method of steepest descent for non-linear minimization problems. Q. Appl. Math. 1944, 2, 258–261. [Google Scholar] [CrossRef] [Green Version]
- Nesterov, Y.E. A method for solving the convex programming problem with convergence rate O . Dokl. Akad. Nauk Sssr 1983, 269, 543–547. [Google Scholar]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef] [Green Version]
- Rockafellar, R.T. Monotone operators and the proximal point algorithm. SIAM J. Control Optim. 1976, 14, 877–898. [Google Scholar] [CrossRef] [Green Version]
- Kaplan, A.; Tichatschke, R. Proximal point methods and nonconvex optimization. J. Glob. Optim. 1998, 13, 389–406. [Google Scholar] [CrossRef]
- Gong, P.; Zhang, C.; Lu, Z.; Huang, J.; Ye, J. A general iterative shrinkage and thresholding algorithm for non-convex regularized optimization problems. In Proceedings of the 30th International Conference on Machine Learning. PMLR 2013, 28, 37–45. [Google Scholar]
- Attouch, H.; Bolte, J.; Redont, P.; Soubeyran, A. Proximal alternating minimization and projection methods for nonconvex problems: An approach based on the Kurdyka-Łojasiewicz inequality. Math. Oper. Res. 2010, 35, 438–457. [Google Scholar] [CrossRef] [Green Version]
- Candes, E.J.; Wakin, M.B.; Boyd, S.P. Enhancing sparsity by reweighted ℓ1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Lai, M.J.; Xu, Y.; Yin, W. Improved iteratively reweighted least squares for unconstrained smoothed ℓq minimization. SIAM J. Numer. Anal. 2013, 51, 927–957. [Google Scholar] [CrossRef]
- Ochs, P.; Dosovitskiy, A.; Brox, T.; Pock, T. On iteratively reweighted algorithms for nonsmooth nonconvex optimization in computer vision. SIAM J. Imaging Sci. 2015, 8, 331–372. [Google Scholar] [CrossRef]
- Łojasiewicz, S. Sur la géométrie semi-et sous-analytique. Ann. l’Institut Fourier 1993, 43, 1575–1595. [Google Scholar] [CrossRef]
- Łojasiewicz, S. Une propriété topologique des sous-ensembles analytiques réels. Les Équations aux Dérivées Partielles 1963, 117, 87–89. [Google Scholar]
- Bolte, J.; Daniilidis, A.; Lewis, A.; Shiota, M. Clarke subgradients of stratifiable functions. SIAM J. Optim. 2007, 18, 556–572. [Google Scholar] [CrossRef] [Green Version]
- Bolte, J.; Daniilidis, A.; Lewis, A. The Lojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J. Optim. 2007, 17, 1205–1223. [Google Scholar] [CrossRef]
- Bolte, J.; Combettes, P.L.; Pesquet, J.C. Alternating proximal algorithm for blind image recovery. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 1673–1676. [Google Scholar] [CrossRef] [Green Version]
- Attouch, H.; Bolte, J. On the convergence of the proximal algorithm for nonsmooth functions involving analytic features. Math. Program. 2009, 116, 5–16. [Google Scholar] [CrossRef]
- Ochs, P.; Chen, Y.; Brox, T.; Pock, T. iPiano: Inertial proximal algorithm for nonconvex optimization. SIAM J. Imaging Sci. 2014, 7, 1388–1419. [Google Scholar] [CrossRef]
- Attouch, H.; Bolte, J.; Svaiter, B.F. Convergence of descent methods for semi-algebraic and tame problems: Proximal algorithms, forward–backward splitting, and regularized Gauss–Seidel methods. Math. Program. 2013, 137, 91–129. [Google Scholar] [CrossRef]
- Osher, S.; Mao, Y.; Dong, B.; Yin, W. Fast linearized Bregman iteration for compressive sensing and sparse denoising. Commun. Math. Sci. 2010, 8, 93–111. [Google Scholar]
- Bolte, J.; Sabach, S.; Teboulle, M. Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 2014, 146, 459–494. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Wets, R.J.B. Variational Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009; Volume 317. [Google Scholar]
- Mordukhovich, B.S.; Nam, N.M.; Yen, N. Fréchet subdifferential calculus and optimality conditions in nondifferentiable programming. Optimization 2006, 55, 685–708. [Google Scholar] [CrossRef] [Green Version]
- Bochnak, J.; Coste, M.; Roy, M.F. Real Algebraic Geometry; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 36. [Google Scholar]
- Wilkie, A.J. Model completeness results for expansions of the ordered field of real numbers by restricted Pfaffian functions and the exponential function. J. Am. Math. Soc. 1996, 9, 1051–1094. [Google Scholar] [CrossRef]
- Dries, L.P.D.v.d. Tame Topology and O-Minimal Structures; Cambridge University Press: Cambridge, UK, 1998; Volume 248. [Google Scholar]
- Kang, M. Approximate versions of proximal iteratively reweighted algorithms including an extended IP-ICMM for signal and image processing problems. J. Comput. Appl. Math. 2020, 376, 112837. [Google Scholar] [CrossRef]
- Combettes, P.L.; Wajs, V.R. Signal recovery by proximal forward-backward splitting. Multiscale Model. Simul. 2005, 4, 1168–1200. [Google Scholar] [CrossRef] [Green Version]
- Chartrand, R.; Yin, W. Iteratively reweighted algorithms for compressive sensing. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 3869–3872. [Google Scholar]
- Daubechies, I.; DeVore, R.; Fornasier, M.; Güntürk, C.S. Iteratively reweighted least squares minimization for sparse recovery. Commun. Pure Appl. Math. 2010, 63, 1–38. [Google Scholar] [CrossRef] [Green Version]
- Needell, D. Noisy signal recovery via iterative reweighted L1-minimization. In Proceedings of the 2009 Conference Record of the Forty-Third Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–4 November 2009; pp. 113–117. [Google Scholar]
- Sun, T.; Jiang, H.; Cheng, L. Global convergence of proximal iteratively reweighted algorithm. J. Glob. Optim. 2017, 68, 815–826. [Google Scholar] [CrossRef]
- Ji, Y.; Yang, Z.; Li, W. Bayesian sparse reconstruction method of compressed sensing in the presence of impulsive noise. Circuits Syst. Signal Process. 2013, 32, 2971–2998. [Google Scholar] [CrossRef]
- Javaheri, A.; Zayyani, H.; Figueiredo, M.A.; Marvasti, F. Robust sparse recovery in impulsive noise via continuous mixed norm. IEEE Signal Process. Lett. 2018, 25, 1146–1150. [Google Scholar] [CrossRef]
- Wen, F.; Liu, P.; Liu, Y.; Qiu, R.C.; Yu, W. Robust Sparse Recovery in Impulsive Noise via ℓp-ℓ1 Optimization. IEEE Trans. Signal Process. 2016, 65, 105–118. [Google Scholar] [CrossRef]
- Wen, J.; Weng, J.; Tong, C.; Ren, C.; Zhou, Z. Sparse signal recovery with minimization of 1-norm minus 2-norm. IEEE Trans. Veh. Technol. 2019, 68, 6847–6854. [Google Scholar] [CrossRef]
- Wen, F.; Pei, L.; Yang, Y.; Yu, W.; Liu, P. Efficient and robust recovery of sparse signal and image using generalized nonconvex regularization. IEEE Trans. Comput. Imaging 2017, 3, 566–579. [Google Scholar] [CrossRef] [Green Version]
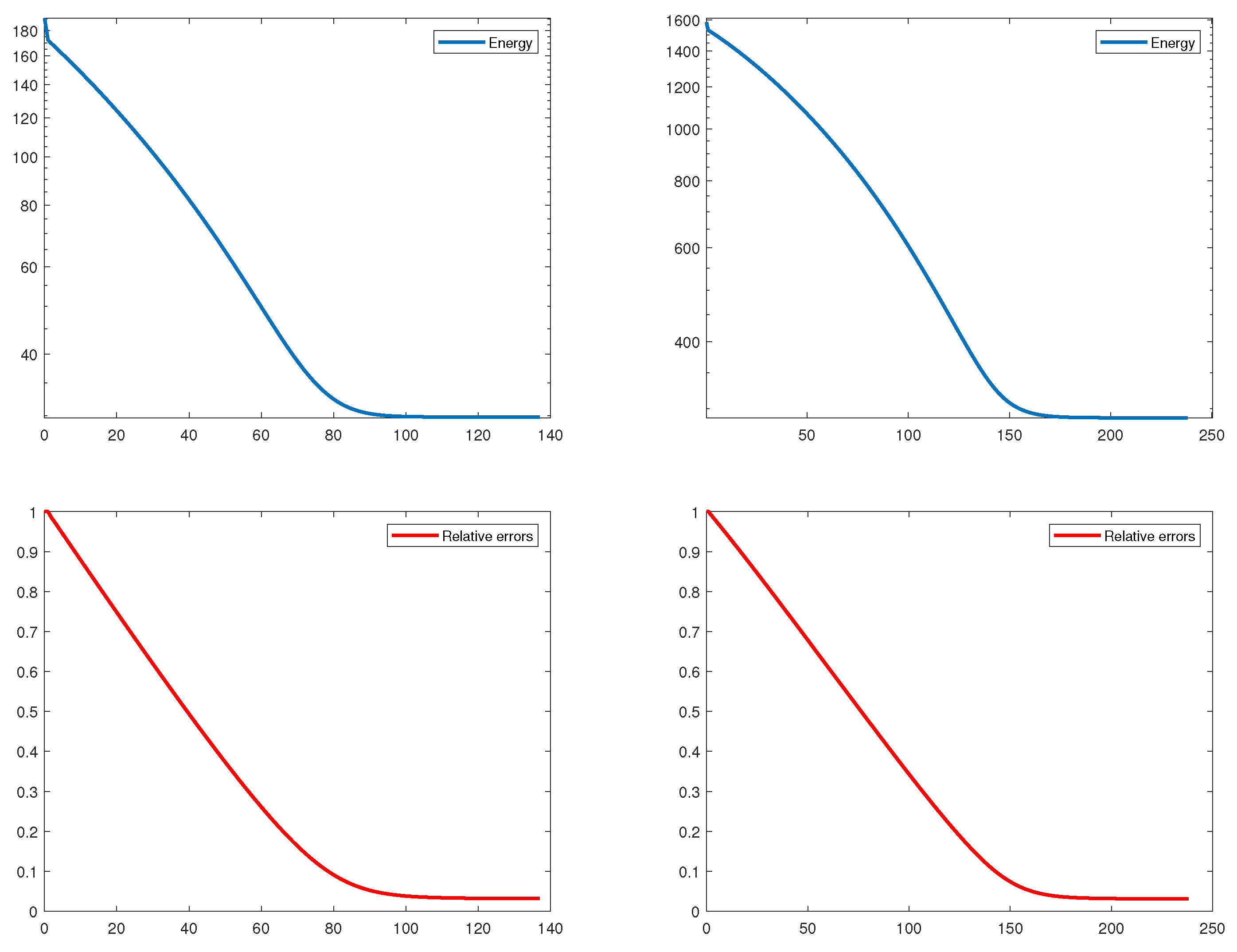
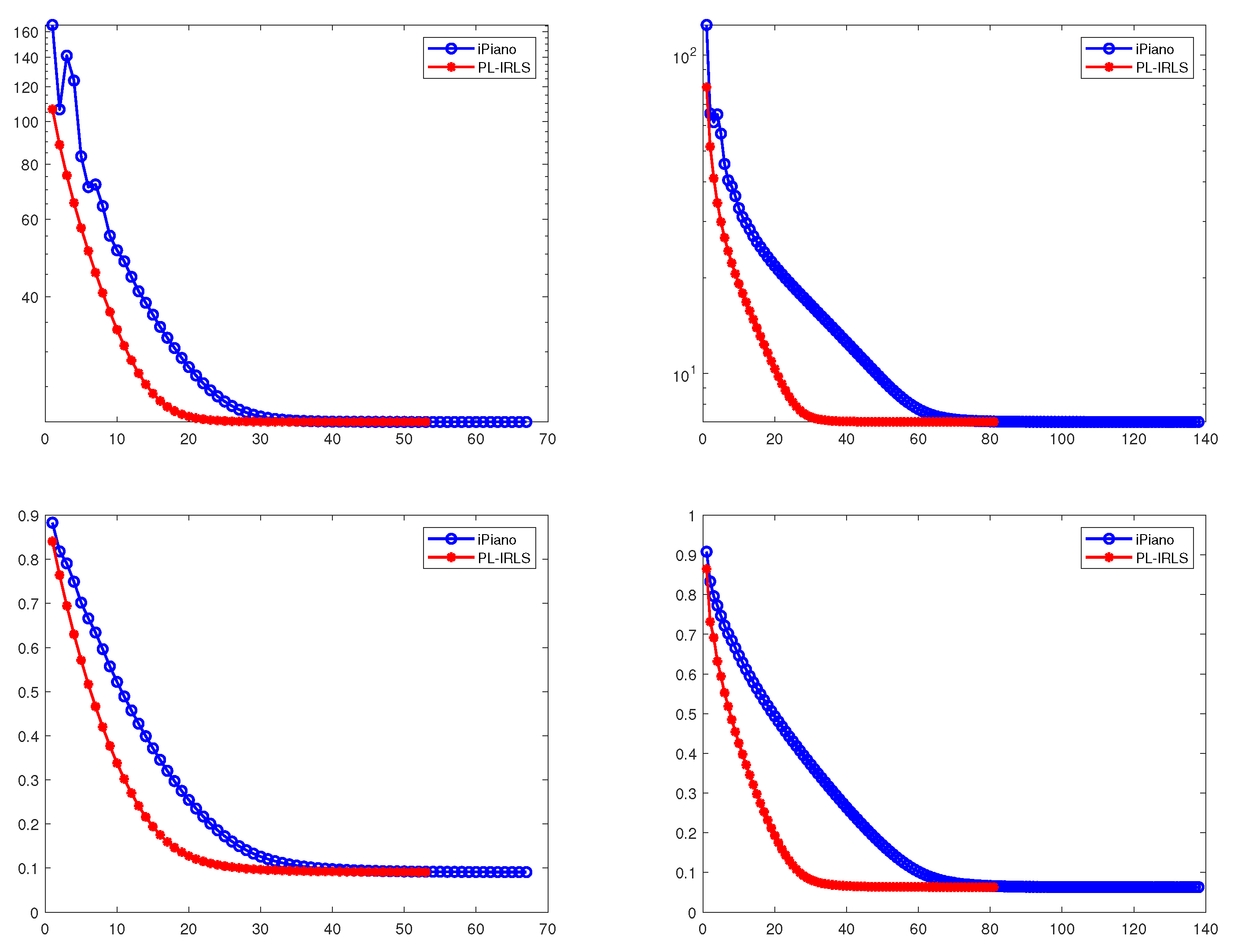
| Model | Computing Time (s) | Iterations | Energy | Relative Error | |
|---|---|---|---|---|---|
| Problem (14) | mean | 5.437452 | 142 | 34.1832 | |
| std | 0.293790 | 8 | 2.1721 | ||
| Problem (15) | mean | 8.960141 | 236 | 282.1852 | |
| std | 0.563042 | 15 | 13.0279 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeo, J.; Kang, M. Proximal Linearized Iteratively Reweighted Algorithms for Nonconvex and Nonsmooth Optimization Problem. Axioms 2022, 11, 201. https://doi.org/10.3390/axioms11050201
Yeo J, Kang M. Proximal Linearized Iteratively Reweighted Algorithms for Nonconvex and Nonsmooth Optimization Problem. Axioms. 2022; 11(5):201. https://doi.org/10.3390/axioms11050201
Chicago/Turabian StyleYeo, Juyeb, and Myeongmin Kang. 2022. "Proximal Linearized Iteratively Reweighted Algorithms for Nonconvex and Nonsmooth Optimization Problem" Axioms 11, no. 5: 201. https://doi.org/10.3390/axioms11050201
APA StyleYeo, J., & Kang, M. (2022). Proximal Linearized Iteratively Reweighted Algorithms for Nonconvex and Nonsmooth Optimization Problem. Axioms, 11(5), 201. https://doi.org/10.3390/axioms11050201





