Krein’s Theorem in the Context of Topological Abelian Groups ^†

Abstract

A topological abelian group G is said to have the quasi-convex compactness property (briefly, qcp) if the quasi-convex hull of every compact subset of G is again compact. In this paper we prove that there exist locally quasi-convex metrizable complete groups G which endowed with the weak topology associated to their character groups $G^{\wedge }$, do not have the qcp. Thus, Krein’s Theorem, a well known result in the framework of locally convex spaces, cannot be fully extended to locally quasi-convex groups. Some features of the qcp are also studied.

1. Introduction

Krein’s Theorem is a key result in the classical theory of topological vector spaces. It admits different formulations with varying degrees of generality; for instance the one presented in [1] (5.3, Theorem 4) reads as follows:

Theorem 1.

Let E be a locally convex space and let A be a weakly compact subset of E. Then the closed convex hull of A is weakly compact if and only if it is complete for the given topology.

From this result it immediately follows that the weak topology of a complete locally convex space has the convex compactness property (we recall the relevant notions below). In this paper we deal with the extension of Krein’s Theorem to topological abelian groups, in the natural form, which consists of replacing classical objects of the theory of topological vector spaces by corresponding objects of the theory of topological abelian groups. For instance, the natural substitution of continuous linear forms is realized by continuous characters, the notion of convexity by that of quasi-convexity etc. This process may result in natural counterparts of important theorems of Functional Analysis for the class of topological abelian groups. Our main result Theorem 6 confirms that this is not always the case.

We first deal with the quasi-convex compactness property (qcp), a convenient notion which mimics the convex compactness property as defined in [2]. In Section 2 and Section 3 some aspects of the qcp are outlined, including the description of classes of abelian topological groups which have the qcp, the hereditary behaviour and some obstructions to the qcp. In Section 4 we study the relation between the qcp and the convex compactness property in topological vector spaces. With these instruments at hand, in Section 5 we prove that a counterpart of Krein’s Theorem holds for the class of locally convex spaces considered as topological abelian groups. However, it cannot be extended to the bigger class of locally quasi-convex groups. We provide a family of locally quasi-convex metrizable groups G which endowed with their weak topology $\sigma (G,G^{\wedge })$ do not have the qcp. The groups in this family can be considered as counterexamples to the version of Krein’s Theorem for topological groups.

In Section 6 we study some interactions between the qcp and other properties like being g-barrelled, or the Glicksberg property.

The many ways in which completeness-like properties relate to convexity in topological vector spaces have been studied for a long time and Krein’s theorem is just an important milestone in this ongoing exploration. As suggested by one of the referees of this paper, it would make sense to look for relevant topological group counterparts of other concepts and results which have arisen in connection with this topic, e.g., those concerning the metric convex compactness property, or Mackey completeness.

Preliminaries

Define $\mathbb{T}$ as $\mathbb{R}/\mathbb{Z}$ and denote by $\pi :\mathbb{R}\to \mathbb{T}$ the canonical projection. On $\mathbb{T}$ we consider the group norm $\left|\pi \left(r\right)\right|=d_{\mathbb{R}}(r+\mathbb{Z},0).$ Note that $\left|\pi \right(r\left)\right|\le min\left\{\right|r|,1/2\}$ for every $r\in \mathbb{R},$ and $\left|\pi \right(r\left)\right|=\left|r\right|$ whenever $\left|r\right|\le 1/2.$ We put ${\mathbb{T}}_{+}=\pi \left([-1/4,1/4]\right).$

A character of an abelian group X is a homomorphism $\chi :X\to \mathbb{T}$. We denote by $\mathrm{Hom}(X,\mathbb{T})$ the group of all characters of X with pointwise sum.

If X is a topological abelian group, we write $X^{\wedge }$ for the subgroup of $\mathrm{Hom}(X,\mathbb{T})$ whose elements are the continuous characters of X. A topological abelian group X is said to be MAP (an abbreviation of “maximally almost periodic”) if for every $x\ne 0$ in X there exists $\chi \in X^{\wedge }$ with $\chi \left(x\right)\ne 0.$ Two group topologies on an abelian group are called compatible if they give rise to the same family of continuous characters.

If U is a subset of the topological abelian group X, the set $U^{▹}:=\{\chi \in X^{\wedge }:\chi \left(U\right)\subseteq {\mathbb{T}}_{+}\}$ is called the polar of U. Note that a subset of $X^{\wedge }$ is equicontinuous if and only if it is a subset of the polar of a neighborhood of zero in X. If B is a subset of $X^{\wedge }$, where X is clear from the context, we will sometimes denote by $B^{◃}$ the set $\{x\in X:B\left(x\right)\subseteq {\mathbb{T}}_{+}\}$. Note that $U^{▹◃}={\bigcap }_{\chi \in U^{▹}}{\chi }^{-1}\left({\mathbb{T}}_{+}\right)$ for every $U\subseteq X.$ We will say that U is quasi-convex if $U=U^{▹◃}$. For an arbitrary $U\subseteq X,$ the set $U^{▹◃}$ is the smallest quasi-convex subset of X which contains U; we call it the quasi-convex hull of U in X and denote it usually by ${\mathrm{qc}}_X\left(U\right).$

A topological abelian group is called locally quasi-convex if it has a basis of neighborhoods of zero formed by quasi-convex sets. Given a topological abelian group X with topology $\tau$, the quasi-convex neighborhoods of zero in X form a basis of neighborhoods of zero for the finest topology among the group topologies on X which are coarser than $\tau$ and locally quasi-convex. We call $X_{lqc}$ the group X endowed with this locally quasi-convex modification of its original topology. The groups X and $X_{lqc}$ have the same continuous characters. Moreover, $X_{lqc}$ is Hausdorff if and only if X is MAP. See ([3], Proposition 6.18) for details on this construction.

Given an abelian group X and a subgroup H of $\mathrm{Hom}(X,\mathbb{T})$, we denote by $\sigma (X,H)$ the initial topology on X with respect to the characters in H. The topological group $(X,\sigma (X,H\left)\right)$ is precompact and its dual group is exactly H. In what follows X will often carry a group topology and H will be taken as $X^{\wedge };$ also, for a MAP topological group X we will sometimes consider the weak topology $\sigma (X^{\wedge },X)$ where X is regarded as a subgroup of $\mathrm{Hom}(X^{\wedge },\mathbb{T})$ in the natural way.

A topological abelian group $(X,\tau )$ is said to satisfy the Glicksberg property if every $\sigma (X,{(X,\tau )}^{\wedge })–$compact subset of X is $\tau –$compact. The classical Glicksberg Theorem establishes that all locally compact abelian groups have the Glicksberg property.

If X is a topological abelian group, we denote by ${\mathcal{T}}_c$ the topology on $X^{\wedge }$ of uniform convergence on compact subsets of X. We will often write $X_c^{\wedge }$ as a shorthand for $(X^{\wedge },{\mathcal{T}}_c)$. The topology ${\mathcal{T}}_c$ admits as a basis of neighborhoods of zero the family of all sets of the form $K^{▹}$ where K runs over all compact subsets of X.

For any topological abelian group X we define the homomorphism ${\alpha }_X:X\to {\left(X_c^{\wedge }\right)}_c^{\wedge }$ by ${\alpha }_X\left(x\right)\left(\chi \right)=\chi \left(x\right)$. We say that X is semi-reflexive if ${\alpha }_X$ is onto. We say that X is reflexive if ${\alpha }_X$ is a topological isomorphism. The classical Pontryagin-van Kampen theorem asserts that every locally compact abelian group is reflexive.

Let H be a subgroup of a topological abelian group X, and let $ı:H\to X$ be the inclusion mapping. We say that H is dually embedded in X if every continuous character of H can be extended to X, i.e., if the restriction mapping ${ı}^{\wedge }:X^{\wedge }\to H^{\wedge }$ is onto. It is clear that ${ı}^{\wedge }:X_c^{\wedge }\to H_c^{\wedge }$ is always continuous; we say that H is strongly dually embedded in X if it is actually a quotient mapping (i.e., it is onto and open). Every open subgroup is strongly dually embedded ([4], Lemma 2.2). Assume that H is dense in X; then clearly H is strongly dually embedded in X if and only if ${ı}^{\wedge }:X_c^{\wedge }\to H_c^{\wedge }$ is a topological isomorphism. We say in this case that Hdetermines X. A metrizable group is determined by all of its dense subgroups (see ([3], Theorem 4.3) and ([5], Theorem 2)).

The $k–$refinement or k-modification of a topological space $(X,t)$ is the topological space $(X,kt)$ where $kt$ is the family formed by those $U\subseteq X$ with $U\cap K\in t{\upharpoonright }_K$ for every $t–$compact set $K\subseteq X.$ The topology $kt$ is the finest topology on X among those which induce $t{\upharpoonright }_K$ on every $t–$compact $K\subseteq X.$ If t is a Hausdorff topology, $kt$ admits the following characterization: a subset $C\subseteq X$ is $kt–$closed if and only if $C\cap K$ is $t–$compact for every $t–$compact subset $K\subseteq X.$ The space $(X,t)$ is a $k–$space if $kt=t.$ Metrizable spaces and locally compact spaces are $k–$spaces. If an abelian topological group X is a $k–$space, then all compact subsets of $X_c^{\wedge }$ are equicontinuous, i.e., the homomorphism ${\alpha }_X:X\to {\left(X_c^{\wedge }\right)}_c^{\wedge }$ is continuous.

We say that the topological abelian group X is locally precompact if it admits a nonempty precompact open subset or, equivalently if it is a subgroup of a locally compact group.

A topological group is almost metrizable if it contains a compact subset of countable character. As proved in ([3], 2.20), an abelian Hausdorff topological group X is almost metrizable if and only if it has a compact subgroup K such that $X/K$ is metrizable.

We only consider vector spaces over $\mathbb{R}.$ A subset A of a topological vector space E is said to be balanced if $[-1,1]A\subseteq A.$ A subset of E is absolutely convex if it is both convex and balanced. For any subset $A\subseteq E,$ we denote by ${\mathrm{acc}}_E\left(A\right)$ the closure of the absolutely convex hull of A. A topological vector space E is said to have the convex compactness property (ccp in what follows) if ${\mathrm{acc}}_E\left(A\right)$ is compact for every compact subset $A\subseteq E.$

If E is a topological vector space, we denote by $E^{\ast }$ the dual space of E, i.e., the space of all linear continuous functionals defined on E. We say that E is dually separated if for every $x\ne 0$ in E there exists $x^{\ast }\in E^{\ast }$ with $x^{\ast }\left(x\right)\ne 0.$ We denote by $\omega (E,E^{\ast })$ the initial vector space topology on E with respect to all linear functionals in $E^{\ast }.$

The symbol $E_c^{\ast }$ stands for the space $E^{\ast }$ endowed with the topology of uniform convergence on compact subsets of E. For any topological abelian group E the mapping

$$T_E:E_c^{\ast }⟶E_c^{\wedge }, T_E\left(f\right)=\pi \circ f$$

(1)

is an isomorphism of topological abelian groups (see [6] or ([7], Proposition 2.3)).

If U is a subset of a topological vector space E, we put $U^{\circ }:=\{f\in E^{\ast }:f\left(U\right)\subseteq [-1,1]\}.$ We call the set ${\bigcap }_{f\in U^{\circ }}{f}^{-1}\left([-1,1]\right)$ the bipolar of U and denote it by $U^{\circ \circ }.$ The well-known Bipolar Theorem asserts ([8], II.4, Corollary 1) that $U^{\circ \circ }={\mathrm{acc}}_E\left(U\right)$ for any subset U of a locally convex space E.

Every topological vector space has a topological abelian group structure which arises from its internal operation and its topology. The topological vector spaces whose underlying topological groups are MAP (resp. locally quasi-convex) are exactly the dually separated (resp. locally convex) ones ([7], Proposition 2.4). Other aspects of topological vector spaces considered as abelian groups are studied in the book [9].

2. Generalities on the Quasi-Convex Compactness Property

We start by formulating the natural group counterpart of the convex compactness property:

Definition 1.

Let X be a topological abelian group. We say that X satisfies the quasi-convex compactness property (qcp) if ${\mathrm{qc}}_X\left(K\right)$ is a compact subset of X for any compact subset $K\subseteq X.$

The qcp was defined for the first time in [10]. In the next Proposition we collect some (mostly known) information regarding this property.

Proposition 1.

(a) 

Every semi-reflexive locally quasi-convex group has the qcp.

(b) 

Every complete locally quasi-convex group has the qcp.

(c) 

A locally quasi-convex group with the qcp can fail to be semi-reflexive. Actually there exists a complete, metrizable, locally quasi-convex group which is not semi-reflexive.

(d) 

A locally quasi-convex group with the qcp can fail to be complete.

(e) 

A metrizable, locally quasi-convex group with the qcp is necessarily complete.

(f) 

If X is a topological abelian group such that ${\alpha }_X:X\to {\left(X_c^{\wedge }\right)}_c^{\wedge }$ is continuous, then $X_c^{\wedge }$ has the qcp.

(g) 

If σ and τ are compatible locally quasi-convex group topologies on an abelian group X where $\sigma \le \tau ,$ and $(X,\sigma )$ has the qcp, then $(X,\tau )$ has the qcp too.

Proof. 

(a) and (b) are proved in ([11], Proposition 3.1).

(c) 

Such an example can be found in ([3], Corollary 11.15). Note that this group has the qcp by (a).

(d) 

Let G be any locally compact, noncompact abelian group. Put $X=(G,\sigma (G,G^{\wedge })).$ By Glicksberg’s Theorem, $X_c^{\wedge }=G_c^{\wedge }.$ This implies, on the one hand, that ${\left(X_c^{\wedge }\right)}^{\wedge }=G,$ that is, X is semi-reflexive and by (a) has the qcp. On the other hand, X is not complete since otherwise it would be compact and in particular ${\left(X_c^{\wedge }\right)}_c^{\wedge }={\left(G_c^{\wedge }\right)}_c^{\wedge }\cong G$ would be compact as well, a contradiction.

(e) 

(f) and (g) are Theorem 3.6, Proposition 3.4 and Proposition 3.3 in [11], respectively. A different proof of (e) can be found in ([12], Theorem 2).

□

It makes sense to ask whether local quasi-convexity can be relaxed to the MAP property in Proposition 1 (a), (b) and (e). The answer is negative in the case of (b) (see Example 3 below) and positive in the case of (e); actually within the class of MAP metrizable groups the qcp already implies local quasi-convexity (see Theorem 2).

Lemma 1.

Let X be a metrizable, MAP topological abelian group. The identity mapping ${\left(X_{lqc}\right)}_c^{\wedge }\to X_c^{\wedge }$ is a topological isomorphism.

Proof. 

See ([3], Proposition 6.18). □

The following result is included in the preprint [13] as Theorem I.34. We provide a different, very natural proof.

Theorem 2.

Let X be a metrizable, MAP topological abelian group with the qcp. Then X is locally quasi-convex and complete.

Proof. 

Call $\tau$ the given metrizable topology on X and ${\tau }_{lqc}$ its locally quasi-convex modification. We are going to show that $\tau ={\tau }_{lqc}.$ Since ${\tau }_{lqc}\le \tau$ and ${\tau }_{lqc}$ (being metrizable) is a $k–$space topology, it is enough to show that every ${\tau }_{lqc}–$compact set is $\tau –$compact. Fix a ${\tau }_{lqc}–$compact set K. The set $K^{▹}$ is a neighborhood of zero in ${\left(X_{lqc}\right)}_c^{\wedge }.$ By Lemma 1$K^{▹}$ is also a neighborhood of zero in $X_c^{\wedge }$. Hence there exists a $\tau –$compact set C with $C^{▹}\subseteq K^{▹}.$ This implies $K\subseteq K^{▹◃}\subseteq C^{▹◃}$. Since $C^{▹◃}$ is $\tau –$compact by hypothesis, and K is ${\tau }_{lqc}–$closed, we deduce that K is actually $\tau –$compact.

This implies that X is locally quasi-convex. The fact that it is also complete follows from Proposition 1(e). □

Problem 1.

Is it possible to extend Theorem 2 to the class $\mathcal{K}$ of MAP topological groups which are k-spaces? Is the dual group of any group X in $\mathcal{K}$ a k-space?

Note that if X is a metrizable topological vector space, we can even remove the restriction of being MAP from Theorem 2 (see Proposition 7 below). A non-metrizable topological vector space with the qcp does not need to be locally (quasi-)convex; see ([14], Example 2) and Section 4 below.

In order to give a characterization of the qcp in terms of topologies of uniform convergence on the dual group, we need the following result:

Lemma 2.

Let X be an abelian group. Let ${\tau }_1$ and ${\tau }_2$ be group topologies on X such that ${\tau }_1<{\tau }_2$ and ${\tau }_2$ has a basis of neighborhoods of zero formed by ${\tau }_1$-closed sets. If $L\subset X$ is ${\tau }_1–$complete, then it is ${\tau }_2–$complete, too.

Proof. 

Assume that L is ${\tau }_1$-complete. Let ${\left\{x_{\alpha }\right\}}_{\alpha }\subseteq L$ be a Cauchy net in ${\tau }_2$. The inequality ${\tau }_1<{\tau }_2$ implies that ${\left\{x_{\alpha }\right\}}_{\alpha }$ is a Cauchy net in ${\tau }_1$, thus we can find $x\in L$ such that $x_{\alpha }\stackrel{{\tau }_1}{⟶}x\in L$.

Let V be a zero neighborhood in ${\tau }_2$, which is ${\tau }_1$-closed. Since ${\left\{x_{\alpha }\right\}}_{\alpha }$ is a Cauchy net in ${\tau }_2$ there is an index ${\alpha }_0$ such that $x_{\alpha }-x_{\beta }\in V$ for all $\alpha ,\beta >{\alpha }_0$. For a fixed $\alpha$, $x_{\alpha }-x_{\beta }\stackrel{{\tau }_1}{⟶}{x}_{\alpha }-x$ and $x_{\alpha }-x\in V$ since V is ${\tau }_1$-closed. This is true for all $\alpha >{\alpha }_0$, thus $x_{\alpha }\in x+V$ for all $\alpha >{\alpha }_0$. In other words, $x_{\alpha }\stackrel{{\tau }_2}{⟶}x$. □

Recall that for any topological abelian group X we denote by ${\mathcal{T}}_c$ the topology on $X^{\wedge }$ of uniform convergence on compact subsets of X. In what follows we also denote by ${\mathcal{T}}_{\sigma qc}$ the topology on $X^{\wedge }$ of uniform convergence on $\sigma (X,X^{\wedge })–$compact, quasi-convex subsets of X.

Proposition 2.

For a Hausdorff locally quasi-convex topological group $(X,\tau )$ the following statements are equivalent:

(a) 

X has the qcp.

(b) 

${\mathcal{T}}_c\le {\mathcal{T}}_{\sigma qc}$.

Proof. 

$\left(a\right)\Rightarrow \left(b\right)$ A basic ${\mathcal{T}}_c$-neighborhood of zero has the form $K^{▹}$ for some compact $K\subset X$. Fix such a subset $K.$ By (a) the quasi-convex hull ${\mathrm{qc}}_{X}K$ of K is compact in $\tau$, and hence also in the weaker topology $\sigma (X,X^{\wedge })$. Now ${\left({\mathrm{qc}}_{X}K\right)}^{▹}=K^{▹}$ is a neighborhood of zero in ${\mathcal{T}}_{\sigma qc}$.

$\left(b\right)\Rightarrow \left(a\right)$ Let $K\subset X$ be $\tau$-compact. By (b) we can find a $\sigma (X,X^{\wedge })$-compact, quasi-convex $C\subset X$ such that $C^{▹}\subseteq K^{▹}$. This implies ${\mathrm{qc}}_{X}K\subseteq {\mathrm{qc}}_{X}C=C$. Since ${\mathrm{qc}}_{X}K$ is a $\sigma (X,X^{\wedge })$-closed subset of C, it is $\sigma (X,X^{\wedge })$-compact, therefore complete with respect to $\sigma (X,X^{\wedge })$. By Lemma 2, ${\mathrm{qc}}_{X}K$ is also complete with respect to $\tau$ (note that quasi-convex subsets of X are $\sigma (X,X^{\wedge })–$closed). On the other hand it is $\tau$- precompact, being the quasi-convex hull of a $\tau$-compact set ([3], Theorem 7.12). Thus ${\mathrm{qc}}_{X}K$ is $\tau$-compact and $(X,\tau )$ has the qcp.   □

3. The qcp on Subgroups

In this section we analyze the hereditary behavior of the quasi-convex compactness property. Clearly, the qcp is not preserved by proper dense subgroups in general. Actually a noncomplete metrizable group cannot have the qcp (Proposition 1(e)). This can be generalized to proper dense, determining subgroups of groups that are $k–$spaces (Corollary 2).

The following result gives a quite general condition under which a subgroup inherits the qcp from its ambient group.

Proposition 3.

Let X be a topological abelian group with the qcp. Let H be a subgroup of X which is closed in the $k–$modification of X. Then H also has the qcp.

Proof. 

Since H is closed in the k-modification of X, the set $C\cap H$ is compact for any compact subset C in X. By hypothesis for every compact subset K of H the set ${\mathrm{qc}}_{X}K$ is compact. Hence $\left({\mathrm{qc}}_{X}K\right)\cap H$ is compact as well. Since ${\mathrm{qc}}_{H}K$ is closed in H and is clearly a subset of $\left({\mathrm{qc}}_{X}K\right)\cap H$, the result follows.   □

Corollary 1.

Let X be a topological abelian group with the qcp. Let H be a closed subgroup of X. Then H has the qcp.

The following result is a partial converse of Proposition 3. Note that the qcp of the group X is not required.

Theorem 3.

Let X be a Hausdorff topological abelian group and let H be a strongly dually embedded subgroup of X. If H has the qcp, then H is closed in the $k–$modification of $X.$

Proof. 

Fix a compact subset C in X. We need to show that $C\cap H$ is compact. Since $C\cap H$ is closed in H, it suffices to find a compact subset of H which contains it. Let us denote by $r:X_c^{\wedge }\to H_c^{\wedge }$ the restriction mapping given by $r\left(\chi \right)=\chi {\upharpoonright }_H;$ this is an open mapping by hypothesis, so there exists a compact subset K of H such that $K^{▸}\subseteq r\left(C^{▹}\right)$. (The symbol ▸ denotes a polar set computed in the dual pair $⟨H,H^{\wedge }⟩$.) Since clearly $r\left(K^{▹}\right)=K^{▸}$, we deduce that $K^{▹}\subseteq C^{▹}+H^{\perp }$, where $H^{\perp }$ denotes the subgroup of $X^{\wedge }$ formed by those characters which are identically zero on H. This implies ${\mathrm{qc}}_{X}K\supseteq {(C^{▹}+H^{\perp })}^{◃}$ and consequently

$$C\cap H\subseteq {(C^{▹}+H^{\perp })}^{◃}\cap H\subseteq \left({\mathrm{qc}}_{X}K\right)\cap H={\mathrm{qc}}_{H}K$$

which is compact by hypothesis. (The identity $\left({\mathrm{qc}}_{X}K\right)\cap H={\mathrm{qc}}_{H}K$ follows easily from the fact that H is dually embedded in X.) □

As expressed in Section 1, the notion of strongly dually embedded subgroup directly leads to that of determining subgroup. Thus, Theorem 3 yields the following results:

Corollary 2.

Let X be a Hausdorff topological abelian group which is a $k–$space. If H is a proper dense subgroup of X which determines X, then H fails to have the qcp.

Note that Corollary 2 implies (e) in Proposition 1, since every metrizable group determines its completion. An analogous consequence in a different context follows:

Corollary 3.

If a topological abelian group H is (locally) precompact, has the qcp and determines its completion, then it is actually (locally) compact.

It is known ([3], Theorem 7.11) that the quasi-convex hull of a finite subset of a MAP group is again finite. This gives the following

Corollary 4.

If H is a precompact non-compact topological group whose compact subsets are finite, then H does not determine its completion.

We prove below (Theorem 6) that the locally precompact groups X which determine their completions can be characterized by means of the joint continuity of the evaluation mapping $e_X:X_c^{\wedge }\times X\to \mathbb{T}$, defined by $e_X(\varphi ,x)=\varphi \left(x\right)$. Previously we establish a few results related with the weaker condition of continuity of the associated mapping ${\alpha }_X$.

The following result has a straightforward proof.

Lemma 3.

Let X be a topological abelian group. If $e_X:X_c^{\wedge }\times X\to \mathbb{T}$ is continuous then ${\alpha }_X:X\to {\left(X_c^{\wedge }\right)}_c^{\wedge }$ is continuous.

Lemma 4.

Let H be a dense subgroup of a topological abelian group X, $r:X^{\wedge }\to H^{\wedge }$ the restriction mapping, and $L\subset H^{\wedge }$ equicontinuous with respect to H. Then $r^{-1}\left(L\right)$ is equicontinuous with respect to X.

Proof. 

Let V be an open zero neighborhood in H with $\varphi \left(V\right)\subseteq {\mathbb{T}}_{+}$ for every $\varphi \in L.$ Let W be an open zero neighborhood in X such that $V=W\cap H$. We next check that $r^{-1}\left(L\right)\subset W^{▹}$. If $\varphi \in L$ and $\tilde{\varphi }=r^{-1}\left(\varphi \right)$ is its unique extension to a continuous character on X, we have $\tilde{\varphi }(W\cap H)\subset {\mathbb{T}}_{+}$. Since $\tilde{\varphi }$ is continuous, also $\tilde{\varphi }\left(\overline{W\cap H}\right)\subset {\mathbb{T}}_{+}$ where the closure is taken in X. The density of H implies $\overline{W\cap H}=\overline{W}$. Thus $\tilde{\varphi }\in {\overline{W}}^{▹}=W^{▹}$. □

Proposition 4.

Let H be a dense subgroup of a topological abelian group X and let $r:X^{\wedge }\to H^{\wedge }$ be the restriction mapping. If ${\alpha }_H$ is continuous then the inverse image $r^{-1}\left(K\right)$ of any compact subset $K\subset H_c^{\wedge }$ is compact in $X_c^{\wedge }$.

Proof. 

This is Theorem I.19(b) in the preprint [13]. We provide the reader with a proof anyway. Pick $K\subset H_c^{\wedge }$ compact. Since ${\alpha }_H$ is continuous, K is equicontinuous with respect to H and by Lemma 4, $r^{-1}\left(K\right)$ is equicontinuous with respect to X. On the other hand, $r^{-1}\left(K\right)$ is closed in $X_c^{\wedge }$ by the continuity of r. By Ascoli’s Theorem ([15], Theorem 9), $r^{-1}\left(K\right)$ is compact in $X_c^{\wedge }$. □

Proposition 5.

Let H be a dense subgroup of a topological abelian group X. If ${\alpha }_H$ is continuous (in particular, if H is a k-space) and $H_c^{\wedge }$ is a $k–$space, then H determines X.

Proof. 

The restriction mapping $r:X_c^{\wedge }\to H_c^{\wedge }$ is a continuous isomorphism whenever H is a dense subgroup. Thus it is only left to prove that r is open, equivalently closed. Pick a closed $C\subset X_c^{\wedge }$. We must prove that $r\left(C\right)\cap K$ is compact in $H_c^{\wedge }$ for every compact $K\subset H_c^{\wedge }$. Since $r^{-1}(r\left(C\right)\cap K)=C\cap r^{-1}\left(K\right)$ and $r^{-1}\left(K\right)$ is compact by Proposition 4, we obtain that $r^{-1}(r\left(C\right)\cap K)$ is compact. Now r continuous implies that $r\left(C\right)\cap K$ is compact.   □

The continuity of ${\alpha }_H$ in Proposition 5 cannot be removed as the following example shows.

Example 1.

Let L be a locally compact, non-compact abelian group and let $H:=(L,\sigma (L,L^{\wedge }))$. By Glicksberg’s theorem $H_c^{\wedge }=L_c^{\wedge }$, therefore $H_c^{\wedge }$ is even locally compact. However H does not determine its completion X: clearly, $X_c^{\wedge }$ is discrete whereas $H_c^{\wedge }$ is non-discrete. Observe further that H has the qcp (see the proof of Proposition 1(d)).

Under the more restrictive assumption that $e_H:H_c^{\wedge }\times H\to \mathbb{T}$ is continuous, it is easily obtained that $H_c^{\wedge }$ is locally compact, ([16], Proposition 1.2). We claim the following:

Theorem 4.

Let H be a locally quasi-convex, Hausdorff group. The following conditions are equivalent:

(i) 

$e_H:H_c^{\wedge }\times H\to \mathbb{T}$ is continuous.

(ii) 

H is locally precompact and determines its completion.

Proof. 

$\left(ii\right)\Rightarrow \left(i\right):$ Let X be the completion of H and $ı:H\to X$ be the inclusion mapping. By hypothesis X is locally compact and the restriction mapping $r:X_c^{\wedge }\to H_c^{\wedge }$ is a topological isomorphism. The diagram

is commutative and $e_X$ is clearly continuous. The assertion follows.

$\left(i\right)\Rightarrow \left(ii\right):$ By Prop. 1.2 in [16], $H_c^{\wedge }$ is locally compact, and in particular a $k–$space. The homomorphism ${\alpha }_H:H\to {\left(H_c^{\wedge }\right)}_c^{\wedge }$ is an embedding: take into account that H is Hausdorff, locally quasi-convex and apply Lemma 3 and ([7], Lemma 14.3). Since ${\left(H_c^{\wedge }\right)}_c^{\wedge }$ is locally compact, we deduce that H is locally precompact.

From Proposition 5 we obtain that H determines X.   □

Corollary 5.

Let X be a locally compact abelian group and let H be a dense subgroup of X. Then H determines X if and only if $e_H:H_c^{\wedge }\times H\to \mathbb{T}$ is continuous.

Remark 1.

In the class of reflexive groups, continuity of $e_X$ implies local compactness of X, as proved in [17]. On the other hand, a reflexive noncomplete group does not determine its completion ([18], Theorem 5.2). For a general topological group X, continuity of $e_X$ is equivalent to continuity of ${\alpha }_X$ plus local compactness of $X_c^{\wedge }$ [19].

Example 1 shows that a topological group which is a k-space may have dense subgroups which are not k-spaces. In particular, H does not determine X in the mentioned example. The following are natural questions:

Problem 2. 

(i) 

If a topological group X contains a dense subgroup which is a k-space and determines X, must X be a k-space?

(ii) 

If a topological group X contains a dense subgroup H which is a k-space, does H determine X?

Corollary 6.

Let H be a dense subgroup of X. If H is almost metrizable, then H determines X.

Proof. 

If H is almost metrizable, then H is a k-space ([3], Proposition 1.24) therefore ${\alpha }_H$ is continuous and $H_c^{\wedge }$ is a k-space (Proposition 5.20 in the same reference). Thus H satisfies the hypothesis of Proposition 5.   □

Remark 2.

If H is a dense subgroup of X and H is almost metrizable, then X is almost metrizable too. In fact, if K is a compact subgroup of H such that $H/K$ is metrizable, clearly K is also a compact subgroup of X. On the other hand $H/K$ is dense in $X/K$, therefore $H/K$ metrizable implies $X/K$ metrizable. Thus, X is almost metrizable.

In the preceding Remark “almost metrizable” cannot be replaced by “$k–$space”, as the following example shows:

Example 2.

Let $X:={\mathbb{R}}^{\beta }$, where β is any uncountable ordinal, and let H be the corresponding Σ-product (i.e., the subgroup formed by those $x\in {\mathbb{R}}^{\beta }$ with countable support). If X is endowed with its usual product topology, H is Fréchet-Urysohn ([20], Theorem 2.1), therefore it is a k-space ([21], 1.6.14, 3.3.20). Clearly H is dense in X. However X is not a k-space. ([22], Chapter 7, Ex. J(b)).

In ([23], Theorem 4.8) it is proved that any compact abelian group X contains an almost metrizable proper dense subgroup which determines X. Our Corollary 6 shows that the fact that H determines X is a consequence of the remaining hypothesis. The following question arises naturally:

Problem 3.

Does every almost metrizable (resp. k-space) X contain an almost metrizable (resp. k-space) proper dense subgroup which determines X?

4. The qcp in Topological Vector Spaces

In this section we study the relationship between the ccp and the qcp on a topological vector space.

The next result is a slight improvement of Proposition 4.5 in [11] (see also ([7], Proposition 15.1)). In its proof we will need the following fact: If E is any dually separated topological vector space, $\omega (E,E^{\ast })–$compact subsets and $\sigma (E,E^{\wedge })–$compact subsets coincide. This result is proved in ([24], Lemma 1.2) in the locally convex case but it can be easily generalized since it only involves weak topologies.

Proposition 6.

Let E be a topological vector space. Consider the following properties:

(a) 

For every compact subset K of E, the set ${\mathrm{qc}}_E\left(K\right)$ is compact (i.e., E has the qcp).

(a′) 

For every compact subset K of E, the set ${\mathrm{qc}}_E\left(K\right)$ is $\sigma (E,E^{\wedge })–$compact.

(b) 

For every compact subset K of E, the set $K^{\circ \circ }$ is compact.

(b′) 

For every compact subset K of E, the set $K^{\circ \circ }$ is $\omega (E,E^{\ast })–$compact.

(c) 

For every compact subset K of E, the set ${\mathrm{acc}}_E\left(K\right)$ is compact (i.e., E has the ccp).

(d) 

The natural mapping ${\alpha }_E:E\to {\left(E_c^{\wedge }\right)}^{\wedge }$ defined by ${\alpha }_E\left(x\right)\left(\chi \right)=\chi \left(x\right)$ is onto (i.e., E is semi-reflexive as a topological abelian group).

(e) 

The natural mapping ${\gamma }_E:E\to {\left(E_c^{\ast }\right)}^{\ast }$ defined by ${\gamma }_E\left(x\right)\left(f\right)=f\left(x\right)$ is onto.

Then the following implications hold:

If E is locally convex then all these properties are equivalent.

Proof. 

$\left(a\right)\iff \left(b\right):$ Note that if $B\subseteq E$ is balanced and nonempty then ${\mathrm{qc}}_{E}B=B^{\circ \circ }$ ([25], Prop. 1.11(c)). Since $[-1,1]K$ is compact for every compact $K\subseteq E,$ and quasi-convex hulls are closed sets, it is clear that (a) holds if and only if ${\mathrm{qc}}_E\left([-1,1]K\right)$ is compact for every compact set $K\subseteq E.$ Now ${\mathrm{qc}}_E\left([-1,1]K\right)={\left([-1,1]K\right)}^{\circ \circ }=K^{\circ \circ }$ and the equivalence is proved.

$\left(a^{\prime }\right)\iff \left(b^{\prime }\right):$ Again, since $[-1,1]K$ is compact for every compact $K\subseteq E,$ and quasi-convex hulls are $\sigma (E,E^{\wedge })–$closed sets, it is clear that (a′) holds if and only if ${\mathrm{qc}}_E\left([-1,1]K\right)=K^{\circ \circ }$ is $\sigma (E,E^{\wedge })–$compact for every compact set $K\subseteq E.$ It only remains to apply that $\omega (E,E^{\ast })–$compact subsets and $\sigma (E,E^{\wedge })–$compact subsets coincide.

$\left(a\right)\Rightarrow \left(a^{\prime }\right)$ and $\left(b\right)\Rightarrow \left(b^{\prime }\right)$ are trivial.

$\left(b\right)\Rightarrow \left(c\right)$: Let K be a compact subset of E. The set ${\mathrm{acc}}_{E}K$ is closed and a subset of $K^{\circ \circ },$ which is compact by hypothesis. Hence it is compact, too.

$\left(d\right)\iff \left(e\right)$: As we have mentioned (1), the mapping

$$T_E:E_c^{\ast }⟶E_c^{\wedge }, T_E\left(f\right)=\pi \circ f$$

is an isomorphism of topological abelian groups. Hence its adjoint mapping

$$T_E^{\wedge }:{\left(E_c^{\wedge }\right)}^{\wedge }⟶{\left(E_c^{\ast }\right)}^{\wedge }, T_E^{\wedge }\left(\kappa \right)=\kappa \circ T_E$$

is an isomorphism of abelian groups.

Analogously, the mapping

$$T_{E^{\ast }}:{\left(E_c^{\ast }\right)}^{\ast }⟶{\left(E_c^{\ast }\right)}^{\wedge }, T_{E^{\ast }}\left(\lambda \right)=\pi \circ \lambda$$

is an isomorphism of abelian groups.

It is easy to check that $T_{E^{\ast }}^{-1}\circ T_E^{\wedge }\circ {\alpha }_E={\gamma }_E.$ This shows that (d) and (e) are equivalent.

$\left(c\right)\Rightarrow \left(b\right)$ if E is locally convex: This is an immediate consequence of the Bipolar Theorem.

$\left(c\right)\iff \left(e\right)$ if E is locally convex: This is known ([26], Theorem 9.2.12).

$\left(a^{\prime }\right)\Rightarrow \left(a\right)$ if E is locally convex: Fix a compact subset $K\subseteq E.$ By hypothesis the set ${\mathrm{qc}}_E\left(K\right)$ is $\sigma (E,E^{\wedge })–$compact. Since E is a locally quasi-convex group, ${\mathrm{qc}}_E\left(K\right)$ is both complete (Lemma 2) and precompact ([3], 7.12), hence compact.   □

The equivalence between qcp and ccp holds for metrizable spaces, and actually these properties characterize Fréchet spaces within this class:

Proposition 7.

Let E be a metrizable topological vector space. The following properties are equivalent:

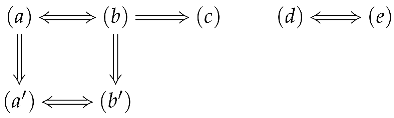
(a) 

E has the qcp.

(b) 

E has the ccp.

(c) 

E is locally convex and complete.

Proof. 

$\left(a\right)\Rightarrow \left(b\right)$ follows from Proposition 6.

$\left(b\right)\Rightarrow \left(c\right)$: If E has the ccp then it is locally convex by ([27], 1.642). Hence it is also complete ([2], Theorem 2.3).

$\left(c\right)\Rightarrow \left(a\right)$: This is true for locally quasi-convex complete groups ([11], Proposition 3.1). □

Local convexity in (c) plays an essential role. Below we present an example of a metrizable complete topological vector space which does not have the qcp.

Example 3.

Consider the space ${\ell }_p$ (with $0<p<1$) endowed with the p-norm ${\parallel x\parallel }_p={\sum }_{k=1}^{\infty }{\left|x_k\right|}^p.$ It is known that ${\ell }_p$ is a non locally convex, complete metric linear space. Its dual space is ${\ell }_{\infty }$ (in the usual sense for sequence spaces), and in particular ${\ell }_p$ is a MAP group. (Details can be found for instance in Chapter 2.3 of [28].) The fact that ${\ell }_p$ does not have the ccp follows from $\left(b\right)\Rightarrow \left(c\right)$ in Proposition 7. Let us give a concrete example of a compact subset of this space whose absolutely convex closure is not compact. Define the sequence $\left\{x_n\right\}\in {\ell }_p$ by

$$x_n\left(n\right)=n^{p-1}\hspace{1em}\mathrm{and}\hspace{1em}{x}_n\left(m\right)=0\hspace{1em}\mathrm{if}\hspace{1em}n\ne m.$$

The sequence $\left\{x_n\right\}$ converges to 0 in the space ${\ell }_p$, since

$$\parallel x_n{\parallel }_p=x_n{\left(n\right)}^p=n^{(p-1)p}\to 0.$$

However, the convex hull of the compact subset $K:=\left\{0\right\}\cup \{x_n:n\in \mathbb{N}\}$ is unbounded with respect to the p-norm ${\parallel ·\parallel }_p$. Indeed, define

$$y_N={\displaystyle \frac{x_1+\cdots +x_N}{N}}=\left(\frac{1}{N},\frac{2^{p-1}}{N},\cdots ,\frac{N^{p-1}}{N},0,0,\cdots \right)$$

for each $N\in \mathbb{N}.$ This sequence is clearly contained in the convex hull of K. We have

$$\parallel y_N{\parallel }_p=\sum _{k=1}^N\frac{k^{(p-1)p}}{N^p}\ge \sum _{k=1}^N\frac{N^{(p-1)p}}{N^p}=N^{{(p-1)}^2}$$

which goes to infinity as $N\to \infty$. Thus $\left\{y_N\right\}$ is unbounded in ${\ell }_p$ and consequently, the closed convex hull of K is not compact.

Let us now analyze the presence of the qcp in weak vector space topologies.

Proposition 8.

Let E be a dually separated topological vector space. The following properties are equivalent:

(a) 

The group $(E,\sigma (E,E^{\wedge }))$ has the qcp.

(b) 

The space $(E,\omega (E,E^{\ast }))$ has the ccp.

(c) 

$(E,\sigma (E,E^{\wedge }))$ is a semi-reflexive group.

Proof. 

It is known that for any dually separated topological vector space E, the dual space of $(E,\omega (E,E^{\ast }))$ is $E^{\ast }$ (see for instance ([29], Chapter IV, 1.2)). Moreover, as we have mentioned above, given any topological vector space F the natural group homomorphism $F^{\ast }\to F^{\wedge }$ given by $f\mapsto \pi \circ f$ is actually an isomorphism. These facts clearly imply that

$${(E,\omega (E,E^{\ast }))}^{\wedge }=E^{\wedge }={(E,\sigma (E,E^{\wedge }))}^{\wedge }$$

(2)

From (2) and the above mentioned fact that $\omega (E,E^{\ast })–$compact subsets and $\sigma (E,E^{\wedge })–$compact subsets coincide, we deduce on the one hand that (a) is equivalent to

(a′) 

$(E,\omega (E,E^{\ast }))$ has the qcp and on the other hand that

$${(E,\omega (E,E^{\ast }))}_c^{\wedge }={(E,\sigma (E,E^{\wedge }))}_c^{\wedge }$$

(3)

By $\left(a\right)\iff \left(c\right)$ in Proposition 6 applied to the locally convex space $(E,\omega (E,E^{\ast })),$ (b) is equivalent to (a′). Since (a′) is equivalent to (a), we have proved $\left(a\right)\iff \left(b\right).$

By $\left(c\right)\iff \left(d\right)$ in Proposition 6 applied to the locally convex space $(E,\omega (E,E^{\ast })),$ (b) is equivalent to

(b′) 

$(E,\omega (E,E^{\ast }))$ is semi-reflexive as a topological abelian group.

From (3) we deduce that (b′) is equivalent to (c). This shows $\left(b\right)\iff \left(c\right)$. □

5. The Krein Property for Topological Abelian Groups

In the sequel we will call Krein’s Theorem the following statement which is an immediate consequence of Theorem 1:

Theorem 5.

If E is a complete locally convex space, then the space $(E,\omega (E,E^{\ast }))$ has the ccp.

We will see below that Krein’s Theorem cannot be totally extended to the class of locally quasi-convex groups, but some approach is possible and we first study positive results in this line. For convenience we introduce the Krein property:

Definition 2.

Let X be a MAP topological abelian group. We say that X has the Krein property if $(X,\sigma (X,X^{\wedge }))$ has the qcp.

By Proposition 1(g), any locally quasi-convex group with the Krein property has the qcp.

Denote by ${\mathcal{T}}_{\sigma c}$ the topology on $X^{\wedge }$ of uniform convergence on $\sigma (X,X^{\wedge })–$compact subsets of a topological abelian group X. Proposition 2 yields the following:

Proposition 9.

Let X be a MAP topological abelian group. The following conditions are equivalent:

(a) 

X has the Krein property.

(b) 

The topologies ${\mathcal{T}}_{\sigma c}$ and ${\mathcal{T}}_{\sigma qc}$ coincide on $X^{\wedge }.$

We denote by $bX$ the completion of the group $(X,\sigma (X,X^{\wedge }))$, where X is a MAP topological abelian group. The compact group $bX$ can be realized as $\mathrm{Hom}(X^{\wedge },\mathbb{T})$ with the topology it carries as a subgroup of ${\mathbb{T}}^{X^{\wedge }}.$ The following result is an immediate consequence of Corollary 3:

Proposition 10.

Let X be a MAP topological abelian group. If X has the Krein property then either $(X,\sigma (X,X^{\wedge }))=bX$ or $(X,\sigma (X,X^{\wedge }))$ does not determine $bX$.

The following result follows at once from Proposition 8. It shows that the Krein property, as we have just defined it, generalizes its natural vector-space counterpart in a satisfactory way.

Proposition 11.

Let $(X,\tau )$ be a dually separated topological vector space. Then its underlying group has the Krein property if and only if $(X,\omega (X,X^{\ast }))$ has the ccp.

Hence Krein’s (Theorem 5 above) can be restated as the fact that all complete locally convex spaces have the Krein property as groups. In order to show that Krein’s Theorem does not remain true for complete locally quasi-convex groups, we present a family of counterexamples considered in [30] with a different purpose.

We follow the notation of the mentioned paper, and outline the parts that allow us to reach our conclusion.

Notation 1.

For a Hausdorff topological abelian group X, let u and p be, respectively, the uniform and the product topology on $X^{\mathbb{N}}$. A basis of zero neighborhoods for u is given by the family $\{U^{\mathbb{N}},U\in \mathcal{N}\left(X\right)\}$ where $\mathcal{N}\left(X\right)$ stands for a zero-neighborhood basis at X. Denote by $c_0\left(X\right)$ the subgroup of $(X^{\mathbb{N}},u)$ formed by the null sequences of X, by $u_0$ the topology induced by u in $c_0\left(X\right)$ and by $p_0$ the topology induced by p in $c_0\left(X\right)$.

Theorem 6.

Let X be an infinite compact, connected metrizable topological abelian group, and let $G:=(c_0\left(X\right),u_0)$. Then G is a complete metrizable group. However, G does not have the Krein property.

Proof. 

Straightforward calculations show that $c_0\left(X\right)$ is closed in $(X^{\mathbb{N}},u)$. Therefore G is complete and metrizable.

The important fact is that its dual group $G^{\wedge }$ is countable, and this is obtained in [30], after several steps that include the definition of a subclass of the locally generated abelian groups. A steady reasoning leads to the fact that ${(c_0\left(X\right),u_0)}^{\wedge }={(c_0\left(X\right),p_0)}^{\wedge }$, whenever X is a nontrivial compact connected metrizable group ([30], Theorem 7.3).

Now it is easy to prove that ${(c_0\left(X\right),p_0)}^{\wedge }$ is countable. Taking into account that $c_0\left(X\right)$ is dense in $(X^{\mathbb{N}},p)$, ${(c_0\left(X\right),p_0)}^{\wedge }$ can be identified with the dual group of $(X^{\mathbb{N}},p)$ which is the direct sum of countably many copies of $X^{\wedge }$, say ${\left(X^{\wedge }\right)}^{\left(\mathbb{N}\right)}$. Since X is a compact metrizable group, $X^{\wedge }$ is countable. Thus, $G^{\wedge }={\left(X^{\wedge }\right)}^{\left(\mathbb{N}\right)}$ is also countable.

The topology $\sigma (G,G^{\wedge })$ coincides with $p_0$, so we have that $(G,\sigma (G,G^{\wedge }))$ is metrizable. The fact that G does not have the Krein property follows by contradiction: had $(G,\sigma (G,G^{\wedge }))$ the qcp, by Proposition 1(e), it would be complete. But this is not the case since $(G,\sigma (G,G^{\wedge }))=(c_0\left(X\right),p_0)$ and $c_0\left(X\right)$ is a proper dense subgroup of the complete group $(X^{\mathbb{N}},p)$. □

6. The Krein and the Glicksberg Properties in the Context of Duality

There is some interaction between these properties as we present below.

Proposition 12.

Let X be a locally quasi-convex topological group with the Krein property. The following statements are equivalent:

(a) 

X has the Glicksberg property.

(b) 

${\mathcal{T}}_c={\mathcal{T}}_{\sigma c}={\mathcal{T}}_{\sigma qc}$.

Proof. 

$\left(a\right)\Rightarrow \left(b\right)$ derives from the equality ${\mathcal{T}}_c={\mathcal{T}}_{\sigma c}$ and from Proposition 9.

$\left(b\right)\Rightarrow \left(a\right):$ Let $K\subset X$ be $\sigma (X,X^{\wedge })$-compact. Thus $K^{▹}$ is a ${\mathcal{T}}_{\sigma c}$-neighborhood of zero, and since ${\mathcal{T}}_c={\mathcal{T}}_{\sigma c}$ we can find a compact subset C of $(X,\tau )$ such that $C^{▹}\subset K^{▹}$. This implies $K\subset {\mathrm{qc}}_{X}C$. Since, by Proposition 1 (g), $(X,\tau )$ also has the qcp, we obtain that ${\mathrm{qc}}_{X}C$ is compact in $\tau$. Consequently, K is $\tau$-compact. □

We recall that a topological abelian group $(X,\tau )$ is g-barrelled if every $\sigma ({(X,\tau )}^{\wedge },X)–$compact subset of $X^{\wedge }$ is $\tau –$equicontinuous. For reflexive groups, the “Glicksberg property” and “being g-barrelled” are dual to each other as shown below (Corollary 7).

Proposition 13.

Let $(X,\tau )$ be a Hausdorff locally quasi-convex group. Consider the assertions:

(a) 

$X_c^{\wedge }$ is g-barrelled.

(b) 

X has the Glicksberg property.

Then $\left(a\right)\Rightarrow \left(b\right)$. If $(X,\tau )$ is further semi-reflexive, then $\left(b\right)\Rightarrow \left(a\right)$.

Proof. 

$\left(a\right)\Rightarrow \left(b\right)$ Let $S\subset X$ be $\sigma (X,X^{\wedge })$-compact. Through the natural embedding

$$\beta :(X,\sigma (X,X^{\wedge }))\hookrightarrow ({\left(X_c^{\wedge }\right)}^{\wedge },\sigma ({\left(X_c^{\wedge }\right)}^{\wedge },X^{\wedge }))$$

we obtain that $\beta \left(S\right)$ is a $\sigma ({\left(X_c^{\wedge }\right)}^{\wedge },X^{\wedge })$-compact subset of ${\left(X_c^{\wedge }\right)}^{\wedge }$. By $\left(a\right)$ there is a zero-neighborhood V in $X_c^{\wedge }$ such that $\beta \left(S\right)\subset V^{▹}$. Since $V^{▹}$ is a compact subset of ${\left(X_c^{\wedge }\right)}_c^{\wedge }$ and $\beta \left(S\right)$ is closed, we obtain that $\beta \left(S\right)$ is also compact in ${\left(X_c^{\wedge }\right)}_c^{\wedge }$. From the assumption that X is locally quasi-convex, we have that $\alpha :(X,\tau )\to {\left(X_c^{\wedge }\right)}_c^{\wedge }$ is relatively open, thus ${\alpha }^{-1}\left(\beta \left(S\right)\right)=S$ is compact in $\tau$, which ends the proof.

Assume now that $(X,\tau )$ is semi-reflexive. In order to prove $\left(b\right)\Rightarrow \left(a\right)$ observe that $\beta :(X,\sigma (X,X^{\wedge }))\to ({\left(X_c^{\wedge }\right)}^{\wedge },\sigma ({\left(X_c^{\wedge }\right)}^{\wedge },X^{\wedge }))$ is a topological isomorphism. Thus, if $K\subset {\left(X_c^{\wedge }\right)}^{\wedge }$ is $\sigma ({\left(X_c^{\wedge }\right)}^{\wedge },X^{\wedge })$-compact, ${\beta }^{-1}\left(K\right)$ is a $\sigma (X,X^{\wedge })$-compact subset of X. By $\left(b\right)$ it is also $\tau$-compact, therefore ${\left({\beta }^{-1}\left(K\right)\right)}^{▹}=K^{◃}$ is a neighborhood of zero in $X_c^{\wedge }$ such that $K\subset {\left({\beta }^{-1}\left(K\right)\right)}^{▹▹}$. Thus, K is equicontinuous. Consequently, $X_c^{\wedge }$ is g-barrelled. □

Corollary 7.

Let $(X,\tau )$ be a reflexive group. The following two properties are equivalent:

(a) 

$X_c^{\wedge }$ is g-barrelled.

(b) 

X has the Glicksberg property.

Remark 3.

$\left(a\right)\Rightarrow \left(b\right)$ of Corollary 7 is a generalization of ([25], Proposition 1.7). In [31] it was wrongly stated that every reflexive group satisfies $\left(b\right)$. A counterexample can be seen in [24]. Thus, we conclude that the dual of a reflexive group is not necessarily g-barreled.

Corollary 7 can also be obtained from Proposition 5.3 of [32], where several notions of barreledness for groups are considered.

Melting Proposition 12 and Corollary 7, we obtain:

Corollary 8.

Let X be a reflexive group with the Krein property. The following statements are equivalent:

(i) 

$X_c^{\wedge }$ is g-barrelled.

(ii) 

X has the Glicksberg property.

(iii) 

The topologies ${\mathcal{T}}_c$ and ${\mathcal{T}}_{\sigma qc}$ coincide on $X^{\wedge }.$

Example 4.

(i) 

Banach spaces provide examples of reflexive topological groups with the Krein property. Just take into account that a Banach space is a reflexive topological group ([6]), and Theorem 5 and Proposition 11 of the present paper.

(ii) 

A reflexive group $(G,\tau )$ with the Krein property, such that $G_c^{\wedge }$ is not g-barrelled: Let G be an infinite dimensional, reflexive Banach space (in the ordinary sense of reflexivity for Banach spaces). It does not have the Glicksberg property: in fact, the unit ball B is $\omega (G,G^{\ast })$-compact and by [24] also $\sigma (G,G^{\wedge })$-compact. Clearly B is not compact in the norm topology of G. Thus, Corollary 8 applies to obtain that $G_c^{\wedge }$ is not g-barrelled.

(iii) 

A non reflexive group with Krein and Glicksberg properties such that $G_c^{\wedge }$ is g-barrelled: Let $G:=(E,\omega (E,E^{\ast }))$ where E is an infinite dimensional Banach space and $\omega (E,E^{\ast })$ is its weak topology. The group G is locally quasi-convex nonreflexive (${\alpha }_G$ is not continuous) and by (i) it has the Krein property. Since the $\omega (E,E^{\ast })$-compact subsets of E coincide with the $\sigma (E,E^{\wedge })$-compact subsets ([24], Lemma 1.2), G has the Glicksberg property. By Proposition 12, the compact-open topology on $G^{\wedge }$ coincides with ${\mathcal{T}}_{\sigma qc}$.

By Proposition 8, G is semi-reflexive and Proposition 13 proves that $G_c^{\wedge }$ is g-barrelled. Observe also that G itself is not g-barrelled.