Application of Deep Learning and Neural Network to Speeding Ticket and Insurance Claim Count Data
Abstract
:1. Introduction
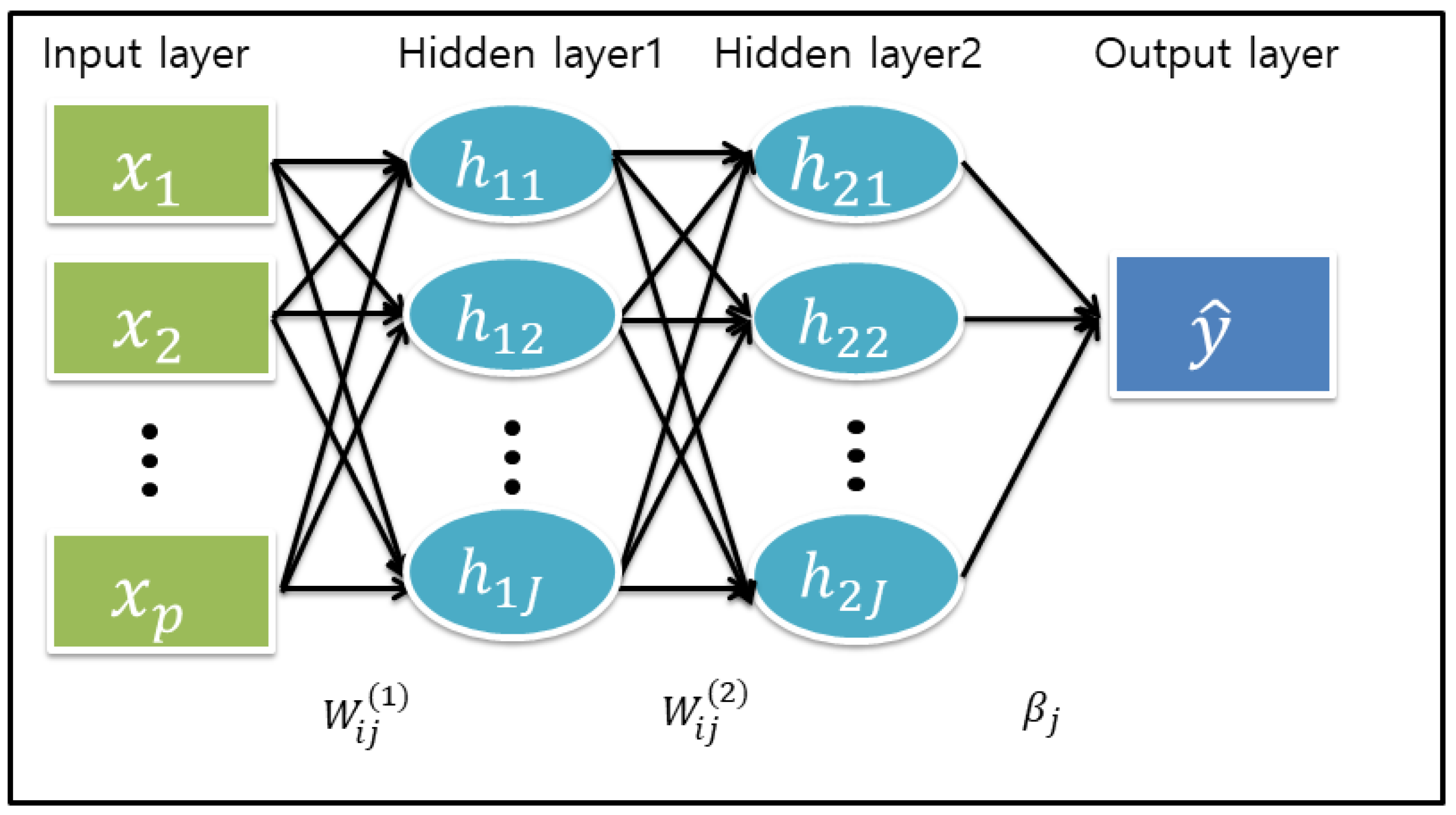
2. Statistical Methods
3. Simulation Study
3.1. Simulation Setup
3.2. Simulation Results
4. Illustrated Data Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. R Codes for Data Analysis








References
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Ma, C.; Zhong, Y. A selective overview of deep learning. Stat. Sci. 2021, 36, 264–290. [Google Scholar] [CrossRef] [PubMed]
- Farrell, M.H.; Liang, T.; Misra, S. Deep neural networks for estimation and inference. Econometrica 2021, 89, 181–213. [Google Scholar] [CrossRef]
- Sun, T.; Wei, Y.; Chen, W.; Ding, Y. Genome-wide association study-based deep learning for survival prediction. Stat. Med. 2020, 39, 4605–4620. [Google Scholar] [CrossRef] [PubMed]
- Montesinos-Lopez, O.A.; Montesinos-Lopez, J.C.; Salazar, E.; Barron, J.A.; Montesinos-Lopez, A.; Buenrostro-Marisca, l.R.; Crossa, J. Application of a Poisson deep neural network model for the prediction of count data in genome-based prediction. Plant Genome 2021, 14, e20118. [Google Scholar] [CrossRef]
- Polson, N.G.; Sokolov, V. Deep learning: A Bayesian perspective. Bayesian Anal. 2017, 12, 1275–1304. [Google Scholar] [CrossRef]
- Tran, M.-N.; Nguyen, N.; Nott, D.; Kohn, R. Bayesian deep net GLM and GLMM. J. Comput. Graph. Stat. 2020, 29, 97–113. [Google Scholar] [CrossRef]
- Rai, R.; Tiwari, M.K.; Ivanov, D.; Dolgui, A. Machine learning in manufacturing and industry 4.0 applications. Int. Prod. Res. 2021, 59, 4773–4778. [Google Scholar] [CrossRef]
- Kim, J.-M.; Liu, Y.; Wang, N. Multi-stage change point detection with copula conditional distribution with PCA and functional PCA. Mathematics 2020, 8, 1777. [Google Scholar] [CrossRef]
- Kim, J.-M.; Wang, N.; Liu, Y.; Park, K. Residual Control Chart for Binary Response with Multicollinearity Covariates by Neural Network Model. Symmetry 2020, 12, 381. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.-M.; Ha, I.D. Deep Learning-Based Residual Control Chart for Binary Response. Symmetry 2021, 13, 1389. [Google Scholar] [CrossRef]
- Skinner, K.R.; Montgomery, D.C.; Runger, G.C. Process monitoring for multiple count data using generalized linear model-based control charts. Int. J. Prod. Res. 2003, 41, 1167–1180. [Google Scholar] [CrossRef]
- Park, K.; Kim, J.-M.; Jung, D. GLM-based statistical control r-charts for dispersed count data with multicollinearity between input variables. Qual. Reliab. Eng. Int. 2018, 34, 1103–1109. [Google Scholar] [CrossRef]
- Park, K.; Kim, J.-M.; Jung, D. Control Charts Based on Randomized Quantile Residuals. Appl. Stoch. Model. Bus. Ind. 2020, 36, 716–729. [Google Scholar] [CrossRef]
- Kim, J.M.; Ha, I.D. Deep Learning-Based Residual Control Chart for Count Data. Qual. Eng. 2022, 34. [Google Scholar] [CrossRef]
- Sakthivel, K.M.; Rajitha, C.S. A Comparative Study of Zero-inflated, Hurdle Models with Artificial Neural Network in Claim Count Modeling. Int. J. Stat. Syst. 2017, 12, 265–276. [Google Scholar]
- Sakthivel, K.M.; Rajitha, C.S. Artificial Intelligence for Estimation of Future Claim Frequency in Non-Life Insurance. Glob. J. Pure Appl. Math. 2017, 13, 1701–1710. [Google Scholar]
- Sakthivel, K.M.; Rajitha, C.S. Model selection for count data with excess number of zero counts. Am. J. Appl. Math. Stat. 2019, 7, 43–51. [Google Scholar] [CrossRef]
- Goundar, S.; Prakash, S.; Sadal, P.; Bhardwaj, A. Health Insurance Claim Prediction Using Artificial Neural Networks. Int. J. Syst. Dyn. Appl. 2020, 9, 40–56. [Google Scholar] [CrossRef]
- Haghani, S.; Sedehi, M.; Kheiri, S. Artificial neural network to modeling zero-inflated count data: Application to predicting number of return to blood donation. J. Res. Health Sci. 2017, 17, 1–4. [Google Scholar]
- Rodrigo, H.; Tsokos, C. Bayesian modelling of nonlinear Poisson regression with artificial neural networks. J. Appl. Stat. 2020, 47, 757–774. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models; Chapman and Hall: New York, NY, USA, 1989. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Agatonovic-Kustrin, S.; Beresford, R. Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J. Pharm. Biomed. Anal. 2000, 22, 717–727. [Google Scholar] [CrossRef]
- Hassabis, D.; Kumaran, D.; Summerfield, C.; Botvinick, M. Neuroscience-inspired artificial intelligence. Neuron 2017, 95, 245–258. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Masood, I.; Hassan, A. Pattern Recognition for Bivariate Process Mean Shifts Using Feature-Based Artificial Neural Network. Int. J. Adv. Manuf. Technol. 2013, 66, 1201–1218. [Google Scholar] [CrossRef] [Green Version]
- Addeh, A.; Khormali, A.; Golilarz, N.A. Control Chart Pattern Recognition Using RBF Neural Network with New Training Algorithm and Practical Features. ISA Trans. 2018, 79, 202–216. [Google Scholar] [CrossRef]
- Zan, T.; Liu, Z.; Su, Z.; Wang, M.; Gao, X.; Chen, D. Statistical Process Control with Intelligence Based on the Deep Learning Model. Appl. Sci. 2020, 10, 308. [Google Scholar] [CrossRef] [Green Version]
- Fritsch, S.; Günther, F.; Wright, M.N.; Suling, M.; Mueller, S.M. Training of Neural Networks; R Package, neuralnet; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Kim, J.-M. A Review of Copula Methods for Measuring Uncertainty in Finance and Economics. Quant. Bio-Sci. 2020, 39, 81–90. [Google Scholar]
- Alexey, N.; Alois, K. Gradient boosting machines, a tutorial. Front. Neurorobotics 2013, 7, 21. [Google Scholar] [CrossRef] [Green Version]
- Makowsky, M.D.; Stratmann, T. Political Economy at Any Speed: What Determines Traffic Citations? Am. Econ. 2009, 99, 509–527. [Google Scholar] [CrossRef]
- Wolny-Dominiak, A.; Trzesiok, M. A Collection of Insurance Datasets Useful in Risk Classification in Non-life Insurance; R Package, insuranceData; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Frees, E.W.; Valdez, E.A. Hierarchical Insurance Claims Modeling. J. Am. Stat. 2008, 103, 1457–1469. [Google Scholar] [CrossRef] [Green Version]


| Multivariate Normal Distribution | |||||||
| Model | Min | Q1 | Median | Mean | Q3 | Max | IQR |
| DL | 0.0005 | 0.3295 | 0.6544 | 0.8707 | 1.1626 | 8.2775 | 0.8331 |
| NN | 0.0020 | 0.3393 | 0.6406 | 0.7988 | 1.1279 | 7.1339 | 0.7886 |
| DLk | 0.0026 | 0.2834 | 0.6127 | 0.7987 | 1.0401 | 8.4060 | 0.7567 |
| GBM | 0.0017 | 0.2519 | 0.5293 | 0.6418 | 0.9370 | 2.6102 | 0.6850 |
| POI | 0.0015 | 0.3999 | 0.8425 | 0.9949 | 1.4125 | 4.0888 | 1.0125 |
| ZIP | 0.0001 | 0.3584 | 0.7742 | 0.9225 | 1.3505 | 3.8733 | 0.9920 |
| NB | 0.0016 | 0.4000 | 0.8425 | 0.9949 | 1.4215 | 4.0888 | 1.0125 |
| Multivariate Normal, Binary and Clayton Copula | |||||||
| Model | Min | Q1 | Median | Mean | Q3 | Max | IQR |
| DL | 0.0002 | 0.5277 | 0.9982 | 1.2227 | 1.7328 | 4.7735 | 1.2052 |
| NN | 0.0009 | 0.4935 | 1.0258 | 1.2163 | 1.7223 | 4.6658 | 1.2288 |
| DLk | 0.0014 | 0.5083 | 1.0752 | 1.2591 | 1.8047 | 5.1306 | 1.2964 |
| GBM | 0.0007 | 0.5039 | 1.0827 | 1.2773 | 1.8091 | 5.4367 | 1.3052 |
| POI | 0.0024 | 0.4939 | 1.0077 | 1.2108 | 1.6895 | 4.8488 | 1.1957 |
| ZIP | 0.0019 | 0.5055 | 1.0290 | 1.2227 | 1.7382 | 4.9925 | 1.2327 |
| NB | 0.0023 | 0.4939 | 1.0077 | 1.2108 | 1.6895 | 4.8488 | 1.1957 |
| Variable | Description |
|---|---|
| Amount | Amount of fine (in dollars) assessed for speeding |
| Age | Age of speeding driver (in years) |
| MPHover | Miles per hour over the speed limit |
| Black | Dummy = 1 if driver was black, =0 if not |
| Hispanic | Dummy = 1 if driver was Hispanic, =0 if not |
| Female | Dummy = 1 if driver was female, =0 if not |
| OutTown | Dummy = 1 if driver was not from local town, =0 if not |
| OutState | Dummy = 1 if driver was not from local state, =0 if not |
| StatePol | Dummy = 1 if driver was stopped by State Police, =0 if stopped by other (local) |
| Variable | Description |
|---|---|
| Female | 1 if female, 0 otherwise |
| PC | 1 if private vehicle, 0 otherwise |
| Clm Exp Count | Number of claims during the year |
| Exp weights | Exposure weight or the fraction of the year that the policy is in effect |
| LNWEIGHT | Logarithm of exposure weight |
| NCD | NoClaims Discount. This is based on the previous accident record of the policyholder. |
| The higher the discount, the better the prior accident record. | |
| AgeCat | The age of the policyholder, in years grouped into seven categories. |
| 0–6 indicate age groups 21 and younger, 22–25, 26–35, 36–45, 46–55, 56–65, 66 and over. | |
| VAgeCat | The age of the vehicle, in years, grouped into seven categories. |
| 0–6 indicate groups 0, 1, 2, 3–5, 6–10, 11–15, 16 and older, respectively | |
| AutoAge0 | 1 if private vehicle and VAgeCat = 0, 0 otherwise |
| AutoAge1 | 1 if private vehicle and VAgeCat = 1, 0 otherwise |
| AutoAge2 | 1 if private vehicle and VAgeCat = 2, 0 otherwise |
| AutoAge | 1 if Private vehicle and VAgeCat = 0, 1 or 2, 0 otherwise |
| VAgecat1 | VAgeCat with categories 0, 1, and 2 combined |
| Speeding Tickets | |||||||
| Model | Min | Q1 | Median | Mean | Q3 | Max | IQR |
| DL | 0.0587 | 19.9503 | 39.9615 | 47.9565 | 69.4222 | 182.4835 | 49.4719 |
| NN | 0.0243 | 19.9641 | 40.0596 | 47.8394 | 67.8350 | 184.3338 | 47.8709 |
| DLk | 0.0259 | 19.4476 | 41.1430 | 49.5775 | 71.4395 | 192.8575 | 51.9919 |
| GBM | 0.0470 | 22.1840 | 42.1820 | 48.6240 | 68.9000 | 183.6440 | 46.7166 |
| POI | 0.0157 | 27.5435 | 63.1032 | 73.2054 | 104.4818 | 363.6643 | 76.9383 |
| ZIP | 0.0306 | 19.3467 | 41.3465 | 48.8347 | 72.2811 | 191.3155 | 52.9344 |
| NB | 0.0168 | 27.6735 | 63.0762 | 73.2649 | 104.8259 | 364.1900 | 77.1524 |
| Singapore Automobile Claims | |||||||
| Model | Min | Q1 | Median | Mean | Q3 | Max | IQR |
| DL | 0.0005 | 0.0924 | 0.2022 | 0.2375 | 0.3471 | 1.0236 | 0.2547 |
| NN | 0.0001 | 0.1045 | 0.1997 | 0.2380 | 0.3397 | 1.0111 | 0.2352 |
| DLk | 0.0001 | 0.0964 | 0.2025 | 0.2466 | 0.3636 | 1.0991 | 0.2672 |
| GBM | 0.0004 | 0.0089 | 0.2035 | 0.2436 | 0.3428 | 1.0895 | 0.2529 |
| POI | 0.0013 | 0.0932 | 0.1985 | 0.2349 | 0.3398 | 0.9863 | 0.2465 |
| ZIP | 0.0001 | 0.0891 | 0.1987 | 0.2353 | 0.3436 | 0.9699 | 0.2545 |
| NB | 0.0001 | 0.0937 | 0.1997 | 0.2350 | 0.3400 | 0.9865 | 0.2463 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-M.; Kim, J.; Ha, I.D. Application of Deep Learning and Neural Network to Speeding Ticket and Insurance Claim Count Data. Axioms 2022, 11, 280. https://doi.org/10.3390/axioms11060280
Kim J-M, Kim J, Ha ID. Application of Deep Learning and Neural Network to Speeding Ticket and Insurance Claim Count Data. Axioms. 2022; 11(6):280. https://doi.org/10.3390/axioms11060280
Chicago/Turabian StyleKim, Jong-Min, Jihun Kim, and Il Do Ha. 2022. "Application of Deep Learning and Neural Network to Speeding Ticket and Insurance Claim Count Data" Axioms 11, no. 6: 280. https://doi.org/10.3390/axioms11060280
APA StyleKim, J. -M., Kim, J., & Ha, I. D. (2022). Application of Deep Learning and Neural Network to Speeding Ticket and Insurance Claim Count Data. Axioms, 11(6), 280. https://doi.org/10.3390/axioms11060280







