The Influence of Multiplicative Noise and Fractional Derivative on the Solutions of the Stochastic Fractional Hirota–Maccari System
Abstract
1. Introduction
2. Wave Equation for SFSHMs
3. The Analytical Solutions of the SFSHMs
3.1. Method Description
3.2. Solutions of SFSHMs
| Case | |||||
|---|---|---|---|---|---|
| 1 | 2 | 1 | |||
| 2 | 2 | 1 | 0 | sech | sech |
| 3 | 2 | 1 | 0 | csch | csch |
| 4 | |||||
| 5 | 2 | 0 | 0 |
| Case | |||||
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 |
| Case | |||||
|---|---|---|---|---|---|
| 1 | 1 | 0 | |||
| 2 | 2 | 0 |
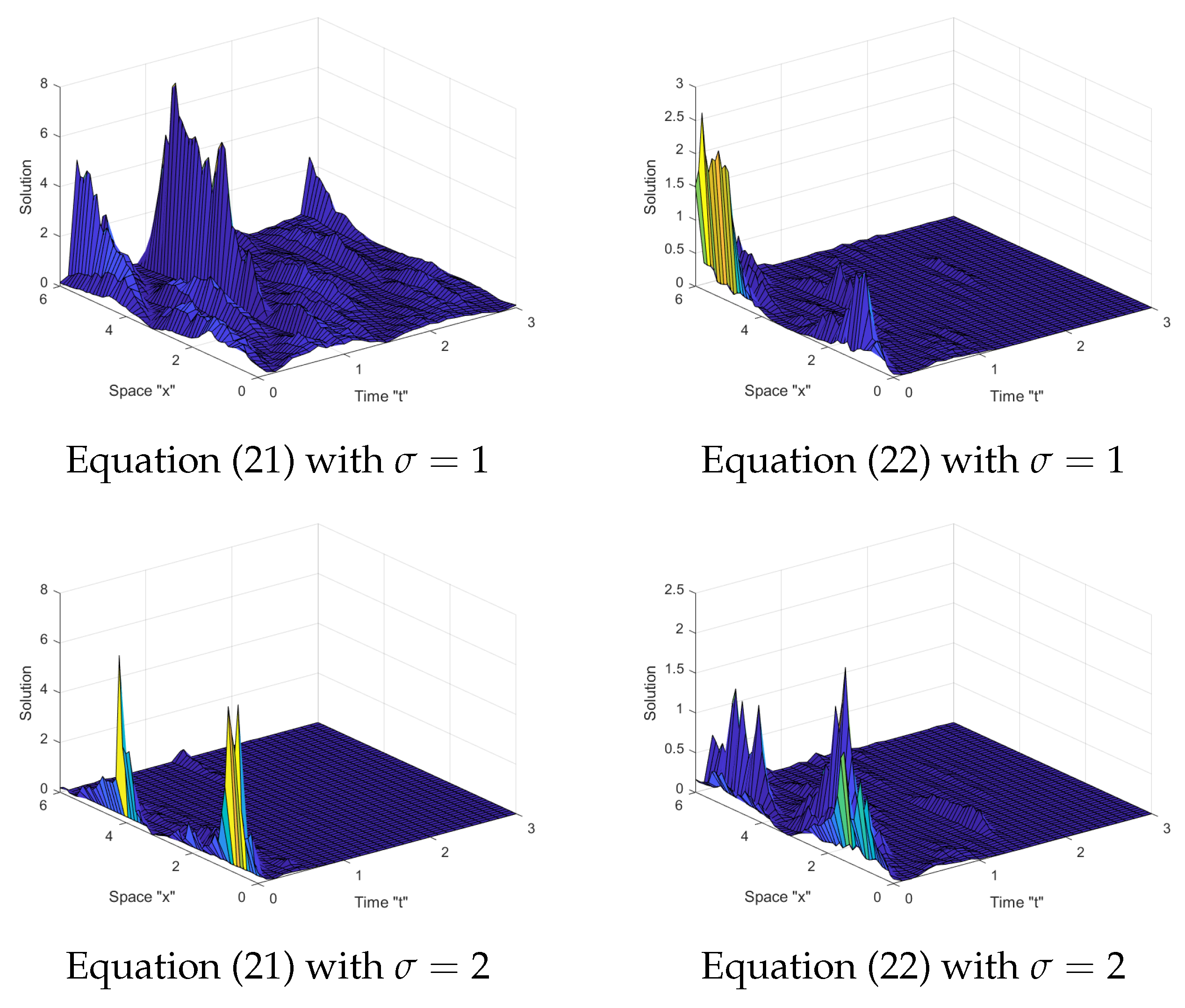
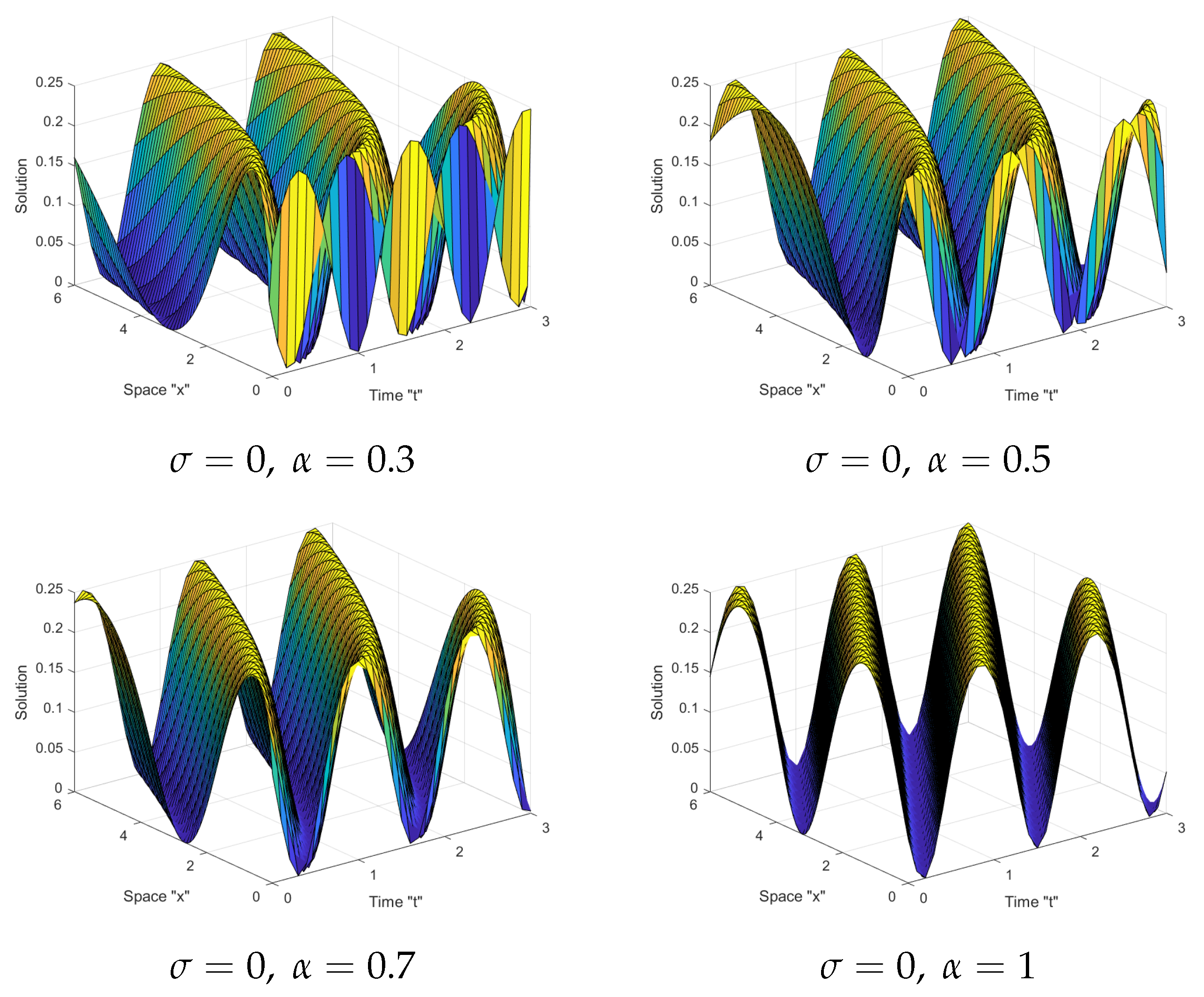
4. The Effect of Noise and Fractional Derivative on Solutions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuste, S.B.; Acedo, L.; Lindenberg, K. Reaction front in an A+B→C reaction–subdiffusion process. Phys. Rev. E 2004, 69, 036126. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, W.W.; Iqbal, N.; Botmart, T. Additive noise effects on the stabilization of fractional-space diffusion equation solutions. Mathematics 2022, 10, 130. [Google Scholar] [CrossRef]
- Benson, D.A.; Wheatcraft, S.W.; Meerschaert, M.M. The fractional-order governing equation of Lévy motion. Water Resour. 2000, 36, 1413–1423. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Aly, E.S.; Matouk, A.E.; Albosaily, S.; EM Elabbasy, E.M. An analytical study of the dynamic behavior of Lotka-Volterra based models of COVID-19. Phys. Rev. Lett. 2001, 87, 118301. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, W.W.; Bazighifan, O.; Al-Sawalha, M.M.; Almatroud, A.O.; Aly, E.S. The influence of noise on the exact solutions of the stochastic fractional-space chiral nonlinear schrdinger equation. Fractal Fract. 2021, 5, 262. [Google Scholar] [CrossRef]
- Barkai, E.; Metzler, R.; Klafter, J. From continuous time random walks to the fractional Fokker–Planck equation. Phys. Rev. 2000, 61, 132–138. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Blömker, D. Fast-diffusion limit for reaction-diffusion equations with multiplicative noise. J. Math. Anal. Appl. 2021, 496, 124808. [Google Scholar] [CrossRef]
- Weinan, E.; Li, X.; Vanden-Eijnden, E. Some recent progress in multiscale modeling. Multiscale Model. Simul. 2004, 39, 3–21. [Google Scholar]
- Imkeller, P.; Monahan, A.H. Conceptual stochastic climate models. Stoch. Dynam. 2002, 2, 311–326. [Google Scholar] [CrossRef]
- Mohammed, W.W. Modulation equation for the stochastic Swift–Hohenberg equation with cubic and quintic nonlinearities on the Real Line. Mathematics 2020, 6, 1217. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Mirzazadeh, M.; Mirhosseini-Alizamini, S.M.; Neirameh, A.; Eslami, M.; Zhou, Q. Optical solitons of Lakshmanan–Porsezian–Daniel model with a couple of nonlinearities. Optik 2018, 164, 414–423. [Google Scholar] [CrossRef]
- Arshed, S.; Raza, N.; Alansari, M. Soliton solutions of the generalized Davey-Stewartson equation with full nonlinearities via three integrating schemes. Ain Shams Eng. J. 2021, 12, 3091–3098. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The ()-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Mirzazadeh, M.; Eslami, M.; Milovic, D.; Biswas, A. Topological solitons of resonant nonlinear Schödinger’s equation with dual-power law nonlinearity by ()-expansion technique. Optik 2014, 125, 5480–5489. [Google Scholar] [CrossRef]
- Biswas, A.; Zhou, Q.; Moshokoa, S.P.; Triki, H.; Belic, M.; Alqahtani, R. Resonant 1-soliton solution in anti-cubic nonlinear medium with perturbations. Optik 2017, 145, 14–17. [Google Scholar] [CrossRef]
- Savescu, M.; Bhrawy, A.H.; Hilal, E.M.; Alshaery, A.A.; Biswas, A. Optical Solitons in Birefringent Fibers with Four-Wave Mixing for Kerr Law Nonlinearity. Rom. J. Phys. 2014, 59, 582–589. [Google Scholar]
- Blömker, D.; Mohammed, W.W. Amplitude equations for SPDEs with cubic nonlinearities. Stochastics Int. J. Probability Stoch. Process. 2013, 85, 181–215. [Google Scholar] [CrossRef][Green Version]
- Mohammed, W.W. Amplitude equation with quintic nonlinearities for the generalized Swift-Hohenberg equation with additive degenerate noise. Adv. Differ. Equ. 2016, 1, 1–18. [Google Scholar] [CrossRef]
- Wen-Xiu, M.; Sumayah, B. A binary darboux transformation for multicomponent NLS equations and their reductions. Anal. Math. Phys. 2021, 11, 44. [Google Scholar]
- Al-Askar, F.M.; Mohammed, W.W.; Albalahi, A.M.; El-Morshedy, M. The Impact of the Wiener process on the analytical solutions of the stochastic (2+ 1)-dimensional breaking soliton equation by using tanh–coth method. Mathematics 2022, 10, 817. [Google Scholar] [CrossRef]
- Malfliet, W.; Hereman, W. The tanh method. I. Exact solutions of nonlinear evolution and wave equations. Phys. Scr. 1996, 54, 563–568. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A. The exp(-Φ(ς))-expansion method for finding travelling wave solutions of Vakhnenko-Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 2014, 5, 72–83. [Google Scholar]
- Yan, Z.L. Abunbant families of Jacobi elliptic function solutions of the-dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Mohammed, W.W.; FM Al-Askar, F.M.; Cesarano, C.; El-Morshedy, M. The Optical Solutions of the Stochastic Fractional Kundu-Mukherjee-Naskar Model by Two Different Methods. Mathematics 2020, 10, 1465. [Google Scholar] [CrossRef]
- Khalil, R.; Horani, M.A.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: New York, NY, USA, 1995. [Google Scholar]
- Maccari, A. A generalized Hirota equation in (2+1) dimensions. J. Math. Phys. 1998, 39, 6547–6551. [Google Scholar] [CrossRef]
- Demiray, S.T.; Pandir, Y.; Bulut, H. All exact travelling wave solutions of Hirota equation and Hirota-Maccari system. Opt. Int. J. Light Electron Opt. 2016, 127, 1848–1859. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Abundant soliton and periodic wave solutions for the coupled Higgs eld equation, the Maccari system and the Hirota-Maccari system. Phys. Scr. 2012, 85, 1–10. [Google Scholar] [CrossRef]
- Malik, A.; Chand, F.; Khatri, H. Exact solutions of some physical models using the (G′/G)-expansion method. Pramana 2012, 78, 513. [Google Scholar] [CrossRef]
- Yu, X.; Gao, Y.T.; Sun, Z.Y.; Meng, X.H.; Liu, Y.; Feng, Q.; Wang, M.Z. N-soliton solutions for the (2+1)-dimensional Hirota-Maccari equation in fluids, plasmas and optical bers. J. Math. Anal. Appl. 2011, 378, 519–527. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, Z. The Weierstrass elliptic function expansion method and its applications in nonlinear wave equations. Chaos Solitons Fractals 2006, 29, 948–964. [Google Scholar] [CrossRef]
- Liang, Z.F.; Tang, X.Y. Modulational instability and variable separation solution for a generalized (2+1)-dimensional Hirota equation. Chin. Phys. Lett. 2010, 27, 1–4. [Google Scholar]
- Xu, G.Q.; Li, Z.B. The Painleve test of nonlinear partial differential equations and its implementation using Maple. Comput. Algebr. Geom. Algebra Appl. 2005, 3519, 179–190. [Google Scholar]
- Raza, N.; Jhangeery, A.; Rezazadehz, H.; Bekir, A. Explicit solutions of the (2 + 1)-dimensional Hirota-Maccarisystem arising in nonlinear optics. Int. J. Mod. Phys. B 2019, 33, 1950360. [Google Scholar] [CrossRef]
- Bai, C.L.; Zhao, H. Complex hyperbolic-function method and its applications to nonlinear equations. Phys. Lett. A 2006, 355, 32–38. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Ahmad, H.; Boulares, H.; Khelifi, F.; El-Morshedy, M. Exact solutions of Hirota–Maccari system forced by multiplicative noise in the Itô sense. Journal of Low Frequency Noise. Vib. Act. Control 2022, 41, 74–84. [Google Scholar]
- Peng, Y.Z. Exact solutions for some nonlinear partial differential equations. Phys. Lett. A 2013, 314, 401–408. [Google Scholar] [CrossRef]

| Case | ||||
|---|---|---|---|---|
| 1 | 1 | |||
| 2 | 2 | |||
| 3 | 2 | |||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ) | |||
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | 2 | 0 | 0 | |
| 13 | 0 | 1 | 0 |
| Case | |||||
|---|---|---|---|---|---|
| 1 | 2m | 1 | |||
| 2 | 2 | ||||
| 3 | 2 | ||||
| 4 | or | ||||
| 5 | |||||
| 6 | |||||
| 7 | 2 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Askar, F.M.; Mohammed, W.W.; Cesarano, C.; El-Morshedy, M. The Influence of Multiplicative Noise and Fractional Derivative on the Solutions of the Stochastic Fractional Hirota–Maccari System. Axioms 2022, 11, 357. https://doi.org/10.3390/axioms11080357
Al-Askar FM, Mohammed WW, Cesarano C, El-Morshedy M. The Influence of Multiplicative Noise and Fractional Derivative on the Solutions of the Stochastic Fractional Hirota–Maccari System. Axioms. 2022; 11(8):357. https://doi.org/10.3390/axioms11080357
Chicago/Turabian StyleAl-Askar, Farah M., Wael W. Mohammed, Clemente Cesarano, and M. El-Morshedy. 2022. "The Influence of Multiplicative Noise and Fractional Derivative on the Solutions of the Stochastic Fractional Hirota–Maccari System" Axioms 11, no. 8: 357. https://doi.org/10.3390/axioms11080357
APA StyleAl-Askar, F. M., Mohammed, W. W., Cesarano, C., & El-Morshedy, M. (2022). The Influence of Multiplicative Noise and Fractional Derivative on the Solutions of the Stochastic Fractional Hirota–Maccari System. Axioms, 11(8), 357. https://doi.org/10.3390/axioms11080357