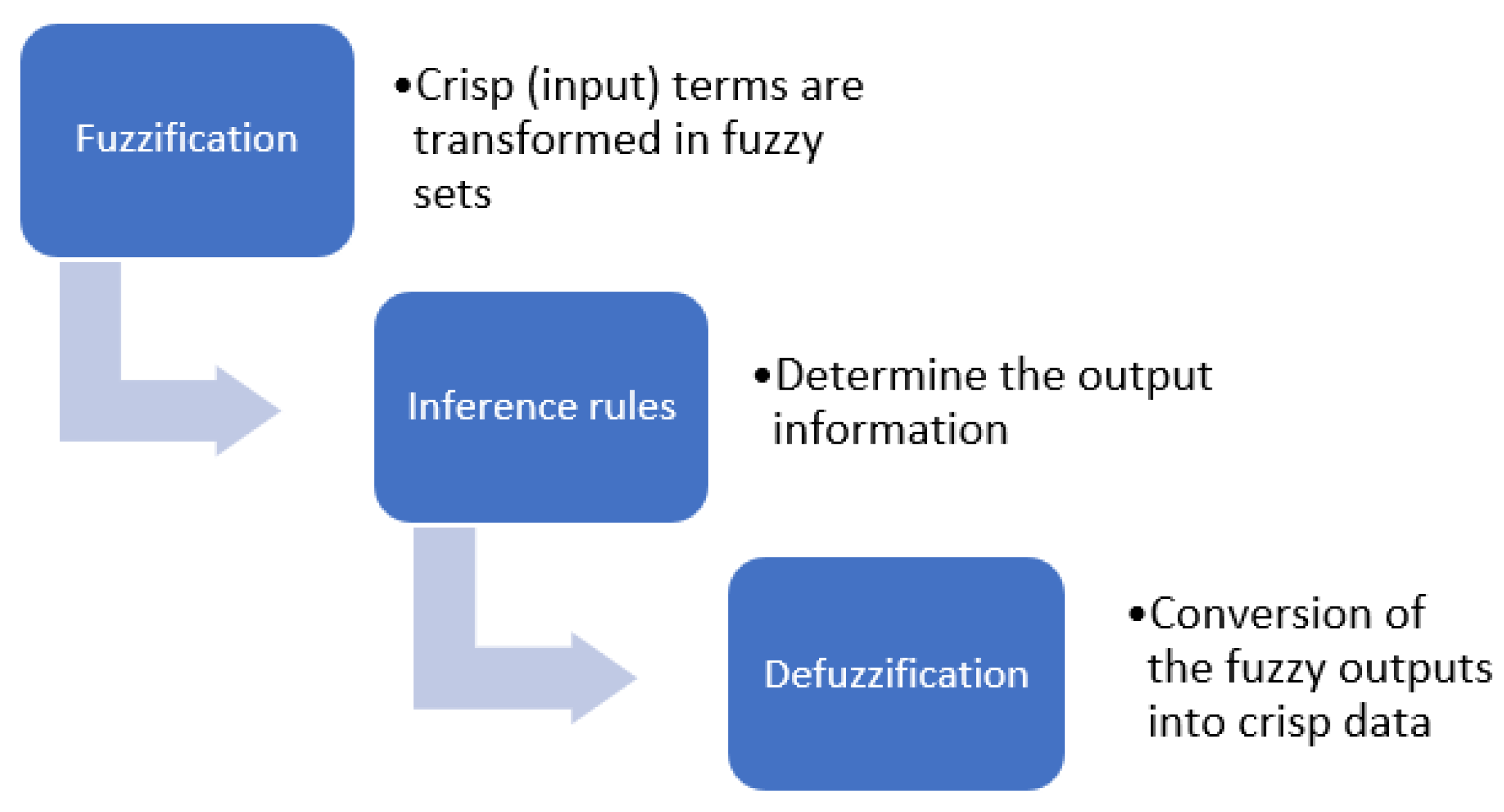
1. Introduction
The assessment of students’ knowledge is one of the most important components of the pedagogical process [
1], as it provides educators, students, and their parents with important feedback information on learners’ knowledge, skills, and competencies [
2]. In recent decades, several researchers [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14] have studied the possibility of evaluating students’ knowledge with fuzzy logic.
Fuzzy logic is based on the fuzzy set theory introduced by the Iranian mathematician Lofti A. Zadeh in 1965 [
15]. This type of logic provides a significant addition to standard logic since its applications are wide-ranging and it offers the possibility of modeling under conditions of imprecision [
3,
4], for example in engineering [
16], science [
17], economics [
18], medicine [
19], and psychology [
20]. Despite its name, which may recall an imprecise, hazy, or even false mathematical theory, fuzzy logic operates on the basis of precise and rigorous mathematical rules [
21]. In real-life situations, fuzzy logic could be used to construct mathematical solutions of problems, which are expressed in natural language and characterized by a degree of vagueness and/or uncertainty [
3]. Fuzzy logic refers to the ability to calculate with words; additionally, it provides mathematical strength to emulate several linguistic attributes associated with human cognition [
4].
Precisely because fuzzy logic tackles operating with inaccurate data, some research [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14] has proposed its use for the purpose of assessing students’ knowledge and competencies. In particular, teacher-given grades are usually based on verbal judgements. For instance, in Italy, where grades range from 1 to 10, grade “10” corresponds to “excellent”, while grade “6” means “sufficient”. In addition, teacher-given grades can include several factors that contribute to the final grading, such as students’ academic knowledge [
5], their class attendance [
8], achievements obtained in different exams [
7], students’ lab work [
6], etc. Fuzzy logic, therefore, represents a mathematical tool which educators and researchers can use to combine multiple verbal and imprecise variables.
The present paper aims to explore how fuzzy logic can be used to evaluate students’ mathematical knowledge, specifically by combining their school grades (i.e., teacher-given grades) with their achievements on a standardized mathematics test, namely the Italian National Assessment of Mathematical knowledge INVALSI. The topic on how to combine teacher-given grades with their performance on standardized tests is still developing. Therefore, with the present paper, we want to contribute to the literature by comparing the traditional method of assessing students’ mathematical knowledge (i.e., teacher-given grades) with the fuzzy logic model.
In the paper, we will first present some basic definitions regarding fuzzy logic and then a review of the literature on using fuzzy logic for student’s evaluation. A detailed description of the adopted methodology and the obtained results will follow. Finally, the results will be discussed and implication for practice will be presented.
5. Discussion
The idea of evaluating students’ knowledge with fuzzy logic is not entirely new, as it has been studied by several researchers [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
22,
26,
27], mainly because the grades awarded by teachers are based on verbal descriptions of students’ knowledge. Moreover, students’ assessment is an imprecise construct and fuzzy logic seems to be suitable for such variables [
3,
4]. The international literature has proposed different models for assessing students’ knowledge, i.e., combining test scores and the time taken to solve them [
4], combining two or more test/exam outcomes [
6,
7], combining student achievement and class attendance [
9], etc. Among those studies which investigated the difference between traditional assessing method and fuzzy logic based one, the findings are relatively inconsistent: some researchers found no difference between fuzzy grades and traditional grades [
4,
9,
26], while others found that fuzzy grades were lower or higher than those of the teachers [
6,
7,
27].
Therefore, the main aim of the present work was to clarify these inconsistencies by comparing the traditional (based on teacher-given grades) math knowledge assessing method to the fuzzy logic one, which combines teacher-assigned grades with students’ performance on a standardized math test (i.e., the INVALSI). Moreover, extending previous literature, we were interested in exploring whether there are differences in the fuzzy logic evaluation method among different school levels (grades 8, 10, and 13).
To answer the first research question, we compared traditional grades to the fuzzy ones in students attending the 8th, 10th, and 13th grade in Italy. In all school levels, students’ traditional grades were statistically higher than their fuzzy grades; the effect sizes were medium to large, suggesting that the fuzzy logic evaluation method yields lower overall ratings. Therefore, combining teacher-given grades with students’ results obtained from the national assessment using fuzzy logic reduces their final grades. This result is consistent with previous research [
27]; we have shown that the affirmation is valid for all considered school levels.
A deeper look at the distribution of fuzzy grades across categories of teacher-assigned grades reveals that fuzzy grades within the same teacher-assigned grades are sparse. This consequently means that students with the same grade assigned by the teacher could get a different grade when assessed with the proposed fuzzy model. This finding also raises questions regarding the validity and reliability of teachers’ grades [
2]: students who have excellent academic results could get lower grades if the INVALSI standardized test is also considered. This could have important consequences, especially considering the labor market [
58] and the possibility of being accepted to higher education institutions, such as universities. For example, the present study showed that 5 students who had an excellent grade on their report cards (i.e., a 10), would obtain a lower grade (i.e., a 6), if evaluated by the fuzzy logic method proposed. On the other hand, there have been some students who received an insufficient grade by the teacher (e.g., 5), but would have obtained a sufficient grade (e.g., 6 or more) if evaluated with the system of logic fuzzy. Therefore, although the academic results of some excellent students may indeed be excellent, their results on the INVALSI test could demonstrate that these students do not master all the mathematics topics assessed by the national standardized test. In the document ref. [
37] it is stated that the INVALSI test cannot evaluate the non-cognitive and metacognitive factors involved in math learning, such as the students’ attitude toward the subject, therefore, considering merely the students’ performance on the INVALSI test might not give a complete picture of students’ math competencies. Thus, the proposed fuzzy logic method for assessing students’ mathematical knowledge and skills could provide educators, students, and their parents with a clearer picture of students’ mathematical skills [
2].
The importance of predicting students’ grades and developing a sustainable learning environment was recently studied by Kanetaki and colleagues [
59]. They identified and quantified the factors affecting mechanical engineering students’ outcomes (e.g., classroom fatigue, understanding of the concept of planes, insecurity, computer skills, etc.,) when classes were held online or in a hybrid learning environment due to the COVID-19 outbreak. The proposed model is a valid model that can be used to predict students’ failure of promotion in a hybrid or online learning environment. Although the model predicted the promotion of some students who then failed (and therefore, the model overestimated their achievements), the model still has a non-negligible importance from an educational point of view, as it could help educators and especially learners to have a clearer picture of students’ knowledge and competencies. Our work can be placed within the effort made by Kanetaki et al. [
59] and could be used by educators to implement sustainable assessment, i.e., giving students skills to become lifelong learners [
60]. In particular, students would gain self-awareness and would be able to self-assess [
60], since they might constantly monitor their performances by receiving additional feedback information from the standardized INVALSI tests. Future research could seek to develop a model for predicting the grades that students would receive if the INVALSI test results were also considered, so that students could self-assess their mathematics knowledge, improving and possibly changing their way of learning mathematics. The model could be tested as suggested by [
59] and used by students to obtain real-time feedback on their knowledge and competencies in mathematics.
The second aim of the research was to explore possible differences in fuzzy scores between 8th, 10th, and 13th grade students. We found that among high school students (i.e., grades 10 and 13), there are no significant differences in fuzzy scores, while there are some significant differences between secondary (i.e., grade 8) and high school students. However, the differences found have an almost negligible effect size, meaning that the proposed method produces similar results at all levels of education. This fact therefore underlines that the evaluation method with fuzzy logic is solid and produces very similar outcomes, even when used at different educational levels. Further research could extend the proposed model to primary schools and verify whether the fuzzy logic assessment model produces comparable grades to those found in this study. In particular, the fact that the obtained results do not significantly differ among school levels contributes to a further validation of the model proposed in the present study.
The present study has some relevant implications for educators. For instance, the assessment method based on teacher-assigned grades and performance on standardized tests (such as national assessment) has been suggested by some authors as a possible solution to grade inflation [
61], i.e., the phenomenon of assigning students higher grades than they deserve or that they would obtain if they were evaluated with a sort of standardized evaluation [
62]. The proposed fuzzy logic method could serve the purpose of lowering excessively high mathematics grades while also offering a clearer picture of students’ mathematical knowledge. Furthermore, as already mentioned, the model could help students develop self-assessment skills and therefore, sustainable learning and assessment [
59,
60]. In addition, the existence of different evaluation methodologies can influence the improvement of teaching policies. In particular, teachers who consider other methods of assessing students’ knowledge and competencies can verify how much their grades differ from students’ achievements in other forms of assessment, such as standardized tests [
63]. Additionally, educators need to know about different data sources [
64] and use multiple assessment strategies, including criterion-referenced methods and standardized tests [
65]. Recent research on the impacts the INVALSI test has on teachers’ practices [
66] has shown that some teachers (1) enhanced activities aimed at improving students’ skills in problem-solving and critical thinking; (2) changed the teaching method by using more examples of the applications of mathematics to reality; and (3) implemented the curriculum by anticipating the order of the topics covered. Another aspect that was highlighted in the same research is the fact that a critical analysis of the INVALSI tests has led teachers to reflect on their teaching methodologies and try developing argumentative skills in students. Moreover, some argued that standardized tests are promising tools for the evaluation of the effectiveness of different instructional practices [
67], therefore, by using the fuzzy logic model teachers would be able to monitor the effectiveness of their teaching practices and implement them.
The present empirical research should be considered in light of some limitations. First, the results obtained through fuzzy logic depend on the techniques used, on fuzzification, on the definition and the granularity of fuzzy rules, and on defuzzification. Membership functions and inferential rules were chosen by the researchers based on previous studies [
7] and based on their experiences as educators [
25]. Changing the functions and inference rules would lead to potentially very different results. Future research should address the question of how fuzzy grades would change if different membership functions or defuzzification methods were used. Second, in the present work, we assumed the proposed model to be better than considering solely teacher-given grades. In particular, teacher-given grades and standardized assessment scores measure slightly different aspects of achievement and achievement-related behavior [
68]. Considering both measures of students’ knowledge and competencies is important to improve student achievement [
69] and give educators, students, and parents more complete information regarding students’ achievements [
2]. However, we did not compare the proposed model with other assessing models. Future studies could therefore evaluate the validity of the proposed model by comparing it with other methods. Lastly, in this study, we did not consider some factors which could affect students’ achievement, such as their gender, socio-economic status, and geographic origin. Future studies could therefore explore the role these factors play in the fuzzy logic model proposed in this paper. There are also practical limitations in applying the methodology described in this work. Indeed, teachers may not be familiar with fuzzy logic, so the transition from traditional to fuzzy assessing model may not be smooth. Teachers should thus receive specific training and knowledge on the fuzzy logic itself before the model could be used in everyday teaching practice.
6. Conclusions
Although teacher-given grades are often reported numerically, the grades awarded by teachers are based on verbal descriptions of students’ knowledge and competencies. To work with variables that are based on descriptions and verbal judgments and characterized by a degree of vagueness, it is recommended to use the fuzzy logic [
3]. Moreover, the teachers’ approach to evaluation in classrooms may not coincide with the approach taken in INVALSI tests. Indeed, in classrooms, the tests have a concentrated focus on the subject content which is studied (e.g., tests assess solely students’ knowledge of equations), while in the INVALSI tests, the focus is usually more multidisciplinary (i.e., several mathematics topics are assessed). The aim of the present work was to investigate how to combine teacher-given grades with students’ results in the standardized INVALSI test in order to create a novel assessing method, based on fuzzy logic, and how it differs from the traditional assessment method.
From the obtained results we can deduce that in the considered samples, the fuzzy assessment method reduces students’ grades. Therefore, the evaluation method with fuzzy logic is stricter than the traditional one. Furthermore, we have shown that the level of schooling has an almost negligible effect on students’ fuzzy grades.
Although this research has considered solely secondary and high school students, future research is needed to test the possibility of evaluating students’ mathematical knowledge also in lower schools, namely elementary schools. Therefore, more research is needed to explore the possibility of extending the proposed model of assessing students’ mathematical knowledge across grades. In the present research, we used students’ achievement on the Italian national assessment of mathematics knowledge INVALSI, while future research could investigate the combination of student grades with their results in other standardized tests, such as the PISA or TIMSS. Additionally, the proposed model, although it has been tested only for mathematics, can also be extended to other subjects, for which there are standardized national or international tests (e.g., the INVALSI institute also assesses the knowledge of Italian and English language).