Complex Dynamics Analysis of a Discrete Amensalism System with a Cover for the First Species
Abstract
:1. Introduction
- (1)
- If , then is globally stable.
- (2)
- If , then is globally stable.
2. Dynamics and Bifurcation of System (3)
2.1. Analysis of Fixed Points
- (1)
- It always has three boundary fixed points, which are , and
- (2)
- It has only one interior fixed point if
- (1)
- a sink if and and it is locally asymptotically stable;
- (2)
- a source if and and it is unstable;
- (3)
- a saddle if and (or and
- (4)
- non-hyperbolic if either or .
- (1)
- It is a source if and only if
- (2)
- It is a saddle if and only if
- (3)
- It is non-hyperbolic if
- (1)
- It is a sink if and only if
- (2)
- It is a saddle if and only if or
- (3)
- It is a source if and only if
- (4)
- It is non-hyperbolic if and only if or
2.2. Permanence
- (1)
- If , then .
- (2)
- If , then
2.3. Global Stability of Interior Fixed Point
2.4. Bifurcation Analysis
2.4.1. Flip Bifurcation at and
2.4.2. Flip Bifurcation at
3. Dynamics and Bifurcation of System (4)
3.1. Analysis of Fixed Points
- (1)
- It is a sink if and only if
- (2)
- It is a source if and only if
- (3)
- It is non-hyperbolic if and only if or
- (4)
- It is a saddle for the other values of parameters except for those values in (1)–(3).
3.2. Permanence
3.3. Global Stability of Interior Fixed Point
3.4. Bifurcation Analysis
3.5. Chaos Control
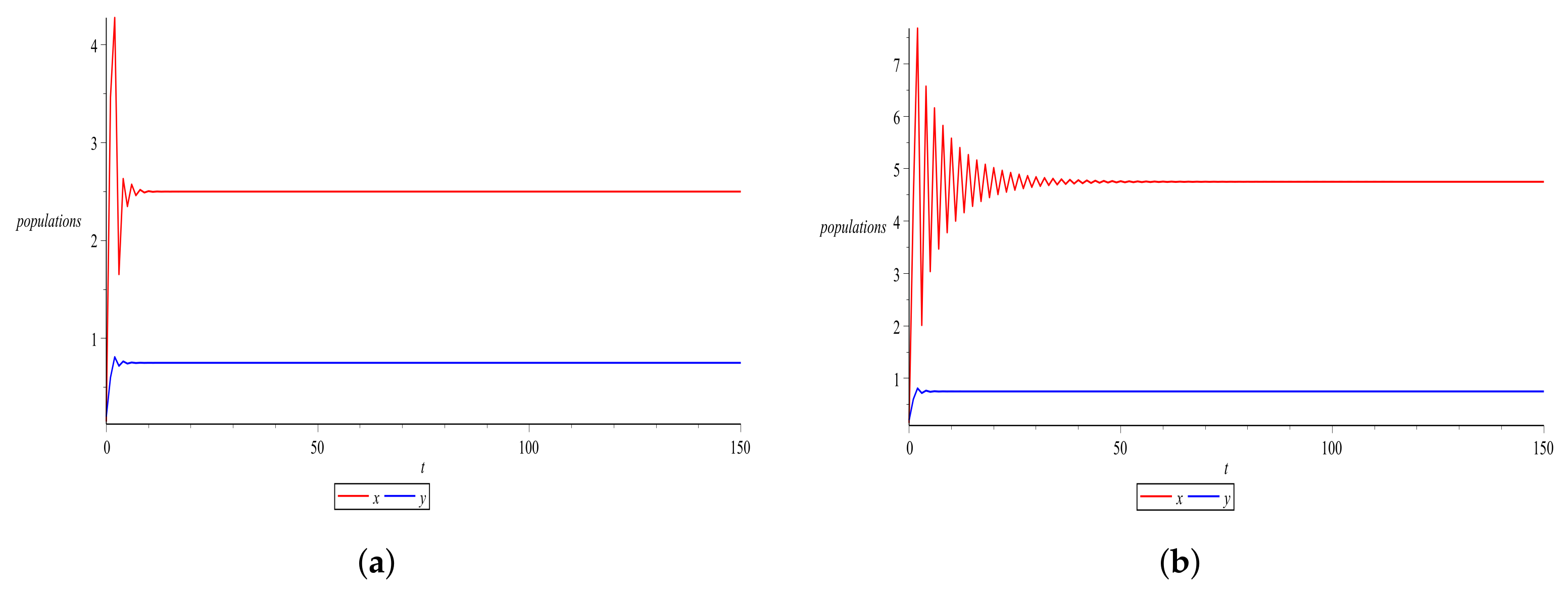
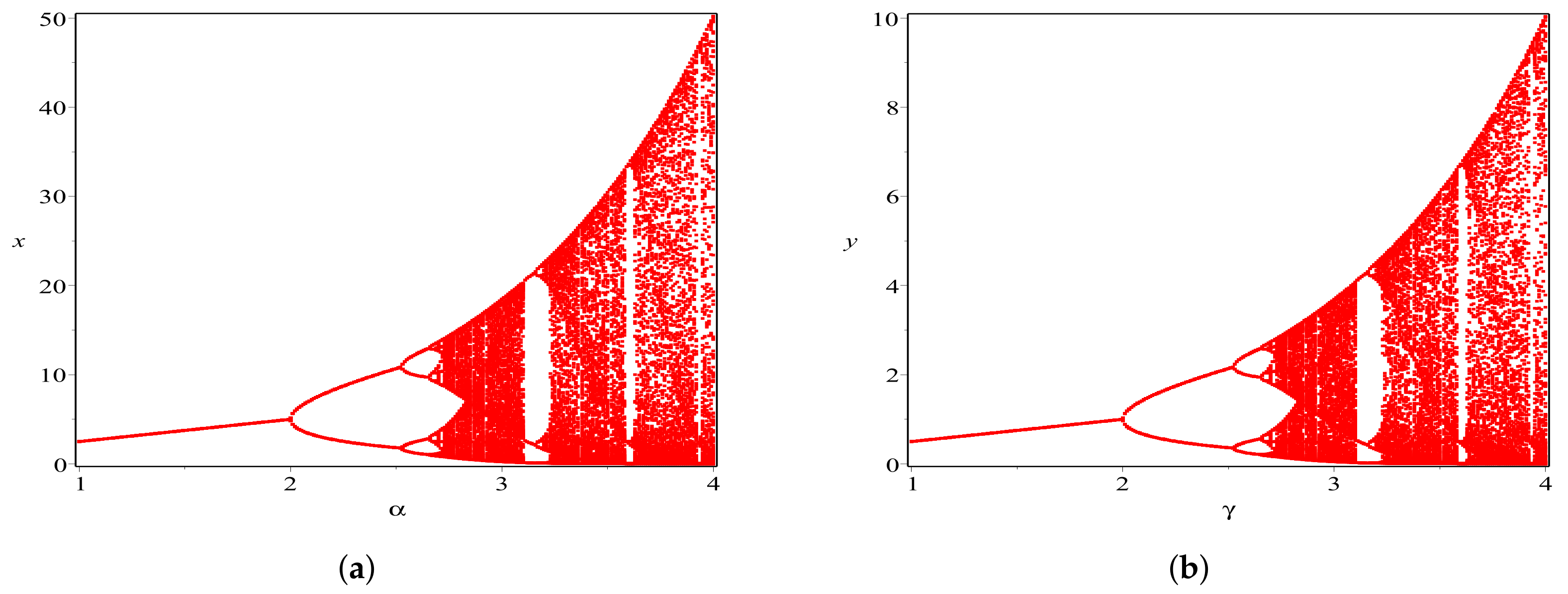
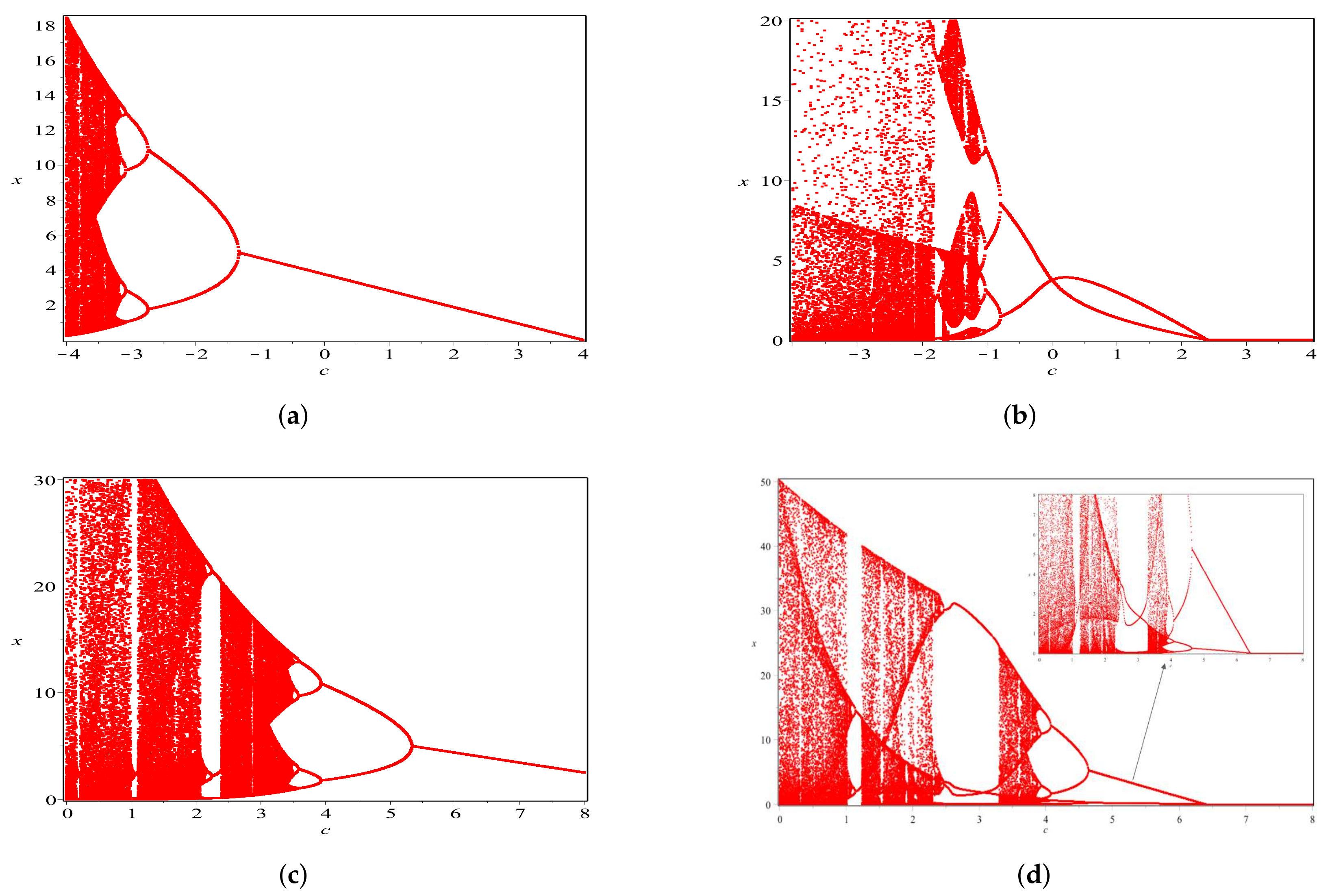
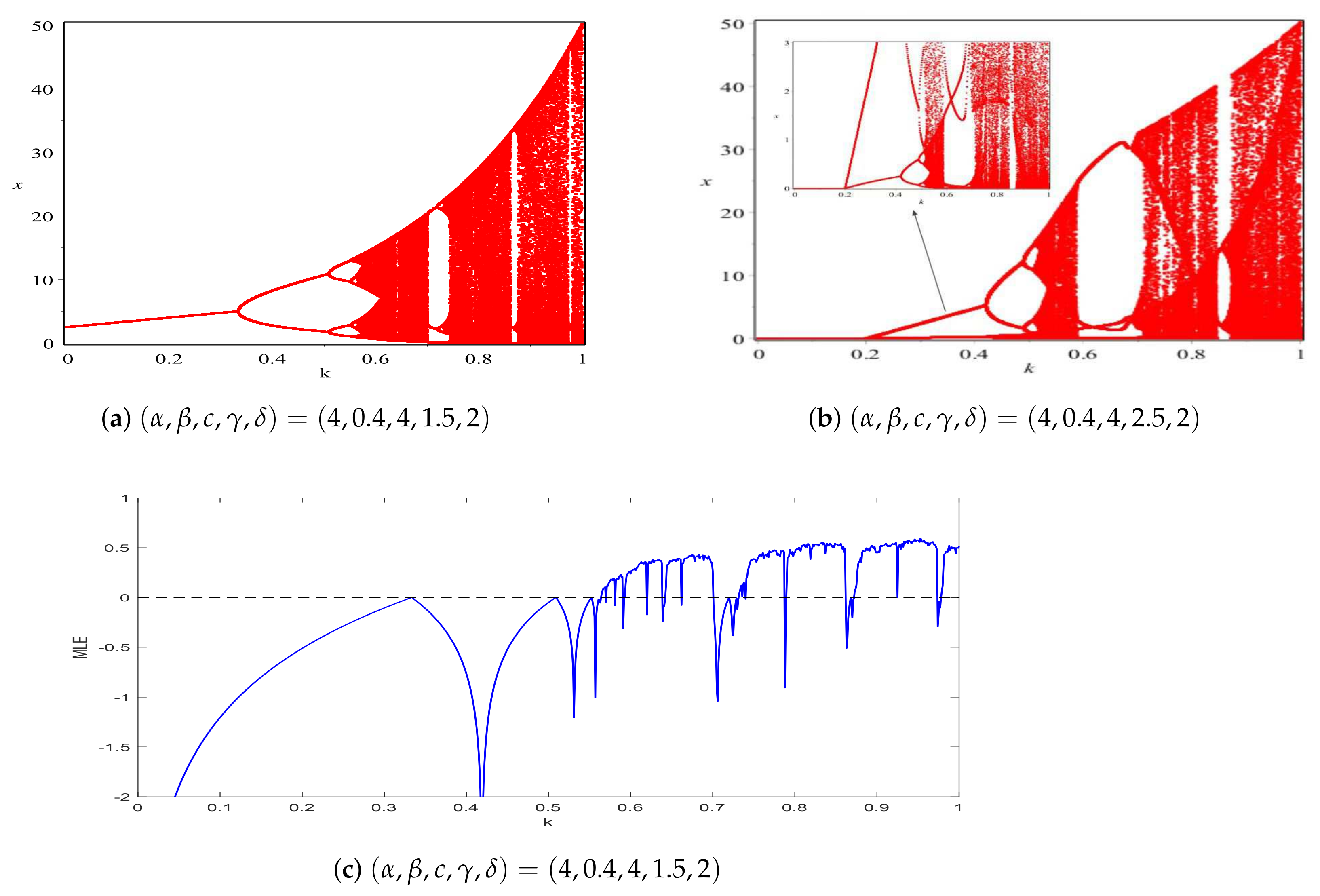
4. Numerical Examples and Discussions
- (a)
- Varying c in range , and fixing
- (b)
- Varying c in range , and fixing
- (c)
- Varying c in range , and fixing
- (d)
- Varying c in range , and fixing
- (e)
- Varying c in range , and fixing
- (f)
- Varying c in range , and fixing
- (g)
- Varying c in range , and fixing
- (h)
- Varying c in range , and fixing .
- (i)
- Fixing the parameters ;
- (j)
- Fixing the parameters .
5. Summary and Discussion
- (1)
- In system (2), Theorem 1 (2) in the Section 1 shows that if the positive equilibrium exists, it is globally stable. This means for any positive initial condition, the solution will eventually approach this equilibrium. However, for the discrete system (4), noting that for always holds, henceThat is, under more restricted conditions than that of Theorem 1 (2), we could only obtain the permanence result (see Theorem 16).
- (2)
- Since system (4) allows only one positive equilibrium, and under more restricted conditions we could only obtain the permanence result, it is natural and important to find out the conditions which guarantee the global attractivity of positive equilibrium. By developing the analysis technique of Chen [38] and Li and Chen [39], we finally obtained a set of sufficient conditions for the global attractivity of the positive equilibrium (see Theorem 18). The condition seems to be the best one, since for single species discrete modelis the best condition to ensure the global attractivity of the positive equilibrium, and with the increasing of , the system may have a period solution, and finally leads to chaos.
- (3)
- Systems (3) and (4) have three boundary fixed points and at most one interior fixed point. The topological types of their fixed points are completely classified. It seems that the local stability property of the equilibria becomes complicated. There are three cases about the stability of and . Here, the topological types of , and can be found in Theorems 4, 13, and 14, respectively. Moreover, compared with the system (2), we confirm that system (4) experiences flip bifurcation at two boundary fixed point and the positive fixed point separately.
- (I)
- We conclude that, for some fixed parameter values, the intrinsic growth rate of the second population plays a major role in the stable coexistence of two species, which is supported by numerical simulations in Examples 1 and 2. This is a novel finding compared with the previous research results [22].
- (II)
- (III)
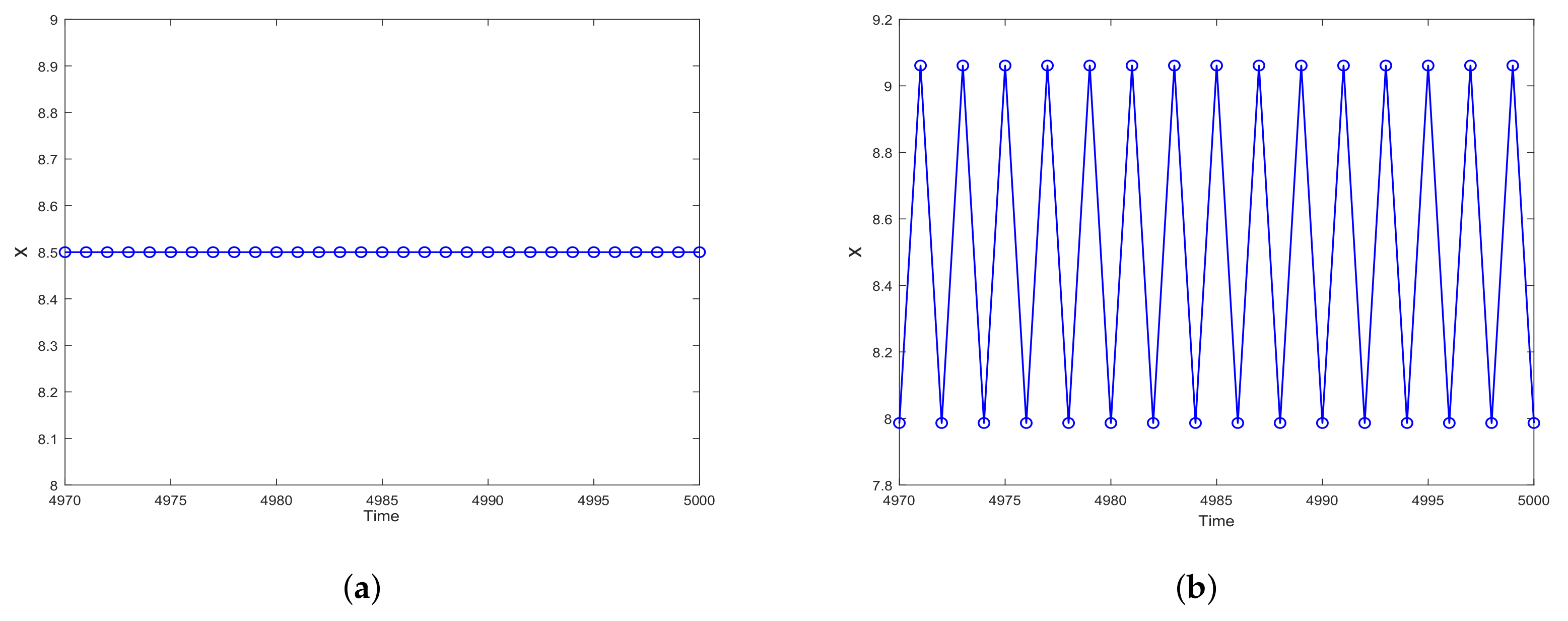
- With the change of cover intensity of the first population, system (4) experienced interesting and complex dynamic characteristics, including population stable coexistence, multiple invariant closed orbits in different chaotic regions, and the onset of chaos suddenly. According to Figure 5, one can observe that the k value is small, it is conducive to the stability of the first population. However, it may destabilize the first population causing more complex dynamical behaviors when the k value exceeds a certain threshold.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, F.D.; Zhou, Q.M.; Lin, S.J. Global stability of symbiotic model of commensalism and parasitism with harvesting in commensal populations. WSEAS Trans. Math. 2022, 21, 424–432. [Google Scholar] [CrossRef]
- Chong, Y.B.; Chen, S.M.; Chen, F.D. On the existence of positive periodic solution of an amensalism model with Beddington-DeAngelis functional response. WSEAS Trans. Math. 2022, 21, 572–579. [Google Scholar] [CrossRef]
- Deng, H.; Huang, X.Y. The influence of partial closure for the populations to a harvesting Lotka-Volterra commensalism model. Commun. Math. Biol. Neurosci. 2018, 2018, 10. [Google Scholar]
- Li, T.Y.; Wang, Q.R. Stability and hopf bifurcation analysis for a two species commensalism system with delay. Qual. Theory Dyn. Syst. 2021, 20, 83. [Google Scholar] [CrossRef]
- Wu, R.X. On the persistent and extinction property of a discrete mutualism model with time delays. Eng. Lett. 2020, 28, 192–197. [Google Scholar]
- Xu, L.L.; Xue, Y.L.; Xie, X.D.; Lin, Q.F. Dynamic behaviors of an obligate commensal symbiosis model with Crowley-Martin functional responses. Axioms 2022, 11, 298. [Google Scholar] [CrossRef]
- Xu, L.L.; Xue, Y.L.; Lin, Q.F.; Lei, C.Q. Global attractivity of symbiotic model of commensalism in four populations with Michaelis-Menten type harvesting in the first commensal populations. Axioms 2022, 11, 337. [Google Scholar] [CrossRef]
- Zhou, Q.M.; Lin, S.J.; Chen, F.D.; Wu, R.X. Positive periodic solution of a discrete Lotka-Volterra commensal symbiosis model with Michaelis–Menten type harvesting. WSEAS Trans. Math. 2022, 21, 515–523. [Google Scholar] [CrossRef]
- Dakhama, A.; Noue, J.; Lavoie, M.C. Isolation and identification of antialgal substances produced byPseudomonas aeruginosa. J. Appl. Phys. 1993, 5, 297–306. [Google Scholar] [CrossRef]
- Li, J. Ecology; Science Press: Beijing, China, 2014. [Google Scholar]
- Sun, G.C. Qualitative analysis on two populations amensalism model. J. Jiamusi Univ. 2003, 21, 283–286. [Google Scholar]
- Zhu, Z.F.; Li, Y.A.; Xu, F. Mathematical analysis on commensalism Lotka-Volterra model of populations. J. Chongqing Inst. Technol. 2008, 21, 59–62. [Google Scholar]
- Chen, B.G. Dynamic behaviors of a non-selective harvesting Lotka-Volterra amensalism model incorporating partial closure for the populations. Adv. Differ. Equ. 2018, 2018, 272. [Google Scholar] [CrossRef]
- Luo, D.M.; Wang, Q.R. Global dynamics of a Holling-II amensalism system with nonlinear growth rate and Allee effect on the first species. Int. J. Bifurc. Chaos 2021, 31, 2150050. [Google Scholar] [CrossRef]
- Chen, F.D.; He, W.X.; Han, R.Y. On discrete amensalism model of Lotka-Volterra. J. Beihua. Univ. 2015, 16, 141–144. [Google Scholar]
- Guan, X.Y.; Chen, F.D. Dynamical analysis of a two species amensalism model with Beddington–DeAngelis functional response and Allee effect on the second species. Int. J. Bifurc. Chaos 2019, 48, 71–93. [Google Scholar] [CrossRef]
- Liu, H.Y.; Yu, H.G.; Dai, C.J.; Ma, Z.; Wang, Q.; Zhao, M. Dynamical analysis of an aquatic amensalism model with non-selective harvesting and Allee effect. Math. Biosci. Eng. 2021, 18, 8857–8882. [Google Scholar] [CrossRef]
- Wei, Z.; Xia, Y.H.; Zhang, T.H. Stability and bifurcation analysis of an amensalism model with weak Allee effect. Qual. Theory Dyn. Syst. 2020, 19, 341. [Google Scholar] [CrossRef]
- Zhao, M.; Du, Y.F. Stability and bifurcation analysis of an amensalism system with Allee effect. Adv. Differ. Equ. 2020, 2020, 341. [Google Scholar] [CrossRef]
- Lei, C.Q. Dynamic behaviors of a stage structure amensalism system with a cover for the first species. Adv. Differ. Equ. 2018, 2018, 272. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, L.; Huang, X.Y.; Deng, H. Stability and bifurcation analysis of two species amensalism model with Michaelis-Menten type harvesting and a cover for the first species. Adv. Differ. Equ. 2018, 2018, 295. [Google Scholar] [CrossRef]
- Xie, X.D.; Chen, F.D.; He, M.X. Dynamic behaviors of two species amensalism model with a cover for the first species. J. Math. Comput. Sci. 2016, 16, 395–401. [Google Scholar] [CrossRef]
- Choi, H.; Kim, B.; Kim, J.; Han, M.S. Streptomyces neyagawaensis as a control for the hazardous biomass of Microcystis aeruginosa (Cyanobacteria) in eutrophic freshwaters. Biol. Control 2005, 33, 335–343. [Google Scholar] [CrossRef]
- Yang, Y.F.; Hu, X.J.; Zhang, J.; Gong, Y. Community level physiological study of algicidal bacteria in the phycospheres of Skeletonema costatum and Scrippsiella trochoidea. Harmful Algae 2013, 28, 88–96. [Google Scholar] [CrossRef]
- Banerjee, R.; Das, P.; Mukherjee, D. Stability and permanence of a discrete-time two-prey one-predator system with Holling type-III functional response. Chaos Solitons Fractals 2018, 117, 240–248. [Google Scholar]
- Din, Q. Complexity and chaos control in a discrete-time prey-predator mode. Commun. Nonlinear Sci. Numer. Simul. 2018, 49, 113–134. [Google Scholar] [CrossRef]
- Su, Q.Q.; Chen, F.D. The influence of partial closure for the populations to a non-selective harvesting Lotka-Volterra discrete amensalism model. Adv. Differ. Equ. 2019, 2019, 281. [Google Scholar] [CrossRef]
- Dubey, B.; Kumar, A.; Maiti, A.P. Global stability and Hopf-bifurcation of prey-predator system with two discrete delays including habitat complexity and prey refuge. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 528–554. [Google Scholar] [CrossRef]
- Ma, R.; Bai, Y.Z.; Wang, F. Dynamical behavior analysis of a two-dimensional discrete predator-prey model with prey refuge and fear factor. J. Appl. Anal. Comput. 2020, 10, 1683–1697. [Google Scholar] [CrossRef]
- Mahapatra, G.S.; Santra, P.K.; Bonyah, E. Dynamics on effect of prey refuge proportional to predator in discrete-time prey-predator model. Complexity 2021, 2021, 6209908. [Google Scholar] [CrossRef]
- Panigoro, H.S.; Rahmi, E.; Achmad, N.; Mahmud, S.L.; Resmawan, R.; Nuha, A.R. A discrete-time fractional-order Rosenzweig-Macarthur predator-prey model involving prey refuge. Commun. Nonlinear Sci. Numer. Simul. 2021, 2021, 77. [Google Scholar]
- Rana, S.; Bhowmick, A.R.; Bhattacharya, S. Impact of prey refuge on a discrete time predator-prey system with Allee effect. Int. J. Bifur. Chaos 2014, 24, 1450106. [Google Scholar] [CrossRef]
- Santra, P.K.; Mahapatra, G.S. Dynamical study of discrete-time prey predator model with constant prey refuge under imprecise biological parameters. J. Biol. Syst. 2020, 28, 681–699. [Google Scholar] [CrossRef]
- Zhang, N.; Kao, Y.G.; Xie, B.F. Impact of fear effect and prey refuge on a fractional order prey-predator system with Beddington-DeAngelis functional response. Chaos 2022, 32, 043125. [Google Scholar] [CrossRef]
- Shu, Q.; Xie, J.J. Stability and bifurcation analysis of discrete predator-prey model with nonlinear prey harvesting and prey refuge. Math. Methods Appl. Sci. 2022, 45, 3589–3604. [Google Scholar] [CrossRef]
- Liu, X.L.; Xiao, D.M. Complex dynamic behaviors of a discrete-time predator-prey system. Chaos Solitons Fractals 2007, 32, 80–94. [Google Scholar] [CrossRef]
- Chen, G.Y.; Teng, Z.D. On the stability in a discrete two-species competition system. J. Appl. Math. Comput. 2012, 38, 25–39. [Google Scholar] [CrossRef]
- Chen, Y.M.; Zhou, Z. Stable periodic solution of a discrete periodic Lotka-Volterra competition system. J. Math. Anal. Appl. 2003, 277, 358–366. [Google Scholar] [CrossRef]
- Li, Z.; Chen, F.D. Extinction in two dimensional discrete Lotka-Volterra competitive system with the effect of toxic substances. Dyn. Contin. Discret. Impuls. Syst. Ser. B Appl. Algorithms 2008, 15, 165–178. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Robinson, C. Dynamical Systems: Stability, Symbolic Dynamics and Chaos; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Luo, X.S.; Chen, G.; Wang, B.H.; Fang, J.Q. Hybrid control of period-doubling bifurcation and chaos in discrete nonlinear dynamical systems. Chaos Solitons Fractals 2003, 18, 775–783. [Google Scholar] [CrossRef]

| Conditions | Case | ||
|---|---|---|---|
| sink | |||
| saddle | |||
| non-hyperbolic | |||
| sink | |||
| saddle | |||
| non-hyperbolic | |||
| saddle | |||
| source | |||
| non-hyperbolic | |||
| non-hyperbolic | |||
| non-hyperbolic | |||
| non-hyperbolic | |||
| Conditions | Case | ||
|---|---|---|---|
| sink | |||
| saddle | |||
| non-hyperbolic | |||
| sink | |||
| saddle | |||
| non-hyperbolic | |||
| saddle | |||
| source | |||
| non-hyperbolic | |||
| non-hyperbolic | |||
| non-hyperbolic | |||
| is non-hyperbolic | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Chen, F.; Lin, S. Complex Dynamics Analysis of a Discrete Amensalism System with a Cover for the First Species. Axioms 2022, 11, 365. https://doi.org/10.3390/axioms11080365
Zhou Q, Chen F, Lin S. Complex Dynamics Analysis of a Discrete Amensalism System with a Cover for the First Species. Axioms. 2022; 11(8):365. https://doi.org/10.3390/axioms11080365
Chicago/Turabian StyleZhou, Qimei, Fengde Chen, and Sijia Lin. 2022. "Complex Dynamics Analysis of a Discrete Amensalism System with a Cover for the First Species" Axioms 11, no. 8: 365. https://doi.org/10.3390/axioms11080365
APA StyleZhou, Q., Chen, F., & Lin, S. (2022). Complex Dynamics Analysis of a Discrete Amensalism System with a Cover for the First Species. Axioms, 11(8), 365. https://doi.org/10.3390/axioms11080365