Stability Analysis of a Stage-Structure Predator–Prey Model with Holling III Functional Response and Cannibalism
Abstract
:1. Introduction
2. Local Stability and Hopf Bifurcation
- (i)
- If Hypothesis 4 (H4). and, thenis locally asymptotically stable;
- (ii)
- If Hypothesis 1 (H1), Hypothesis 2 (H2), Hypothesis 3 (H3), and , then there is, such that,is stable forand undergoes a Hopf bifurcation at.
3. Persistence
4. Global Stability
5. Numerical Experiments
- (A)
- Let , , , , , , , , , , , , , and. It is easy to show that System (2) has a predator-extinction equilibrium. Hence, by Theorem 1, the immature and the mature predators go into extinction.
- (B)
- Let , , , , , , , , , , , , , and. is the unique positive equilibrium of System (2). Hence, by Theorem 1, the persistence is verified by System (2). From the proof of Lemma 1, We have proved that. By the uniform boundedness theorem, ifis sufficiently small, there is a. Thus,. We know from System (2) that, if,which yields
- (1)
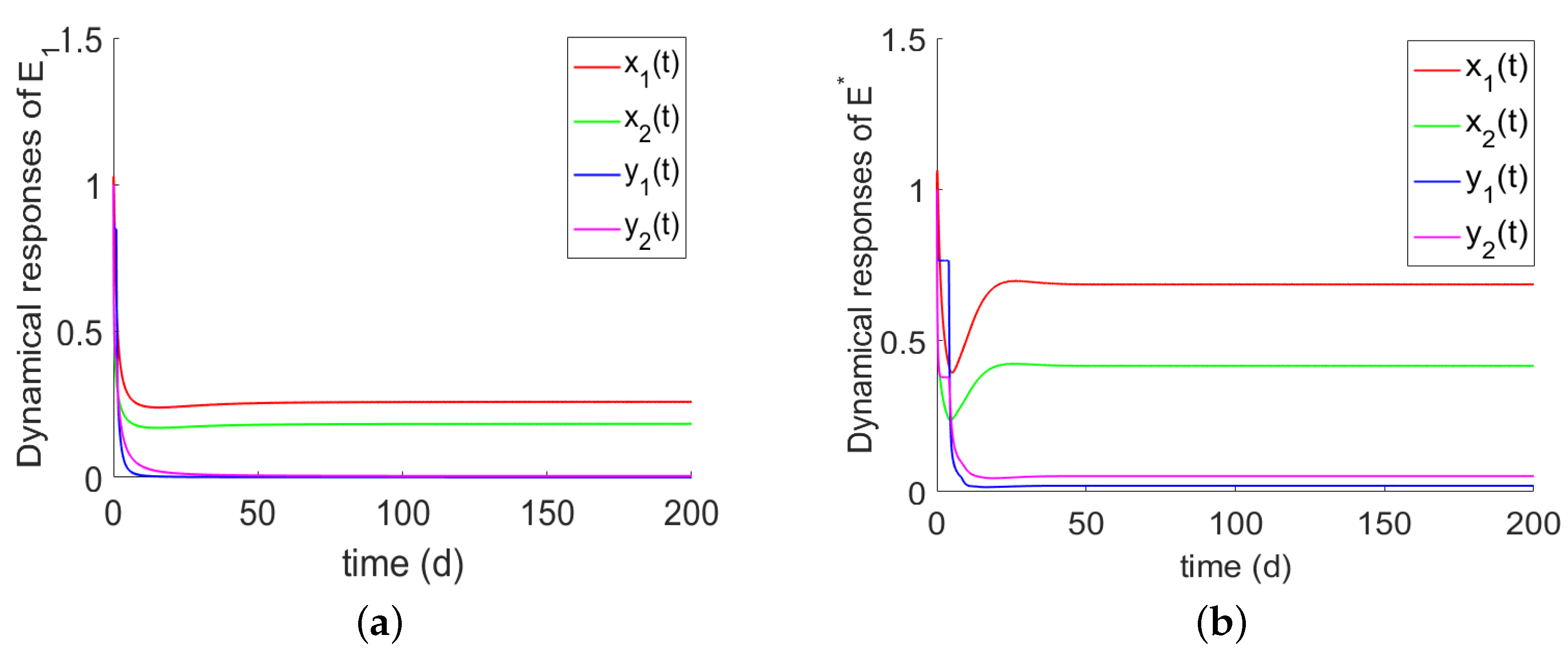
- If , the prey and the predator go into extinction. If holds, there is a predator-extinction equilibrium . From Theorem 3 and the numerical simulations Figure 4a, we can easy to see that the predator-free equilibrium (i.e., only prey) is globally asymptotically stable.
- (2)
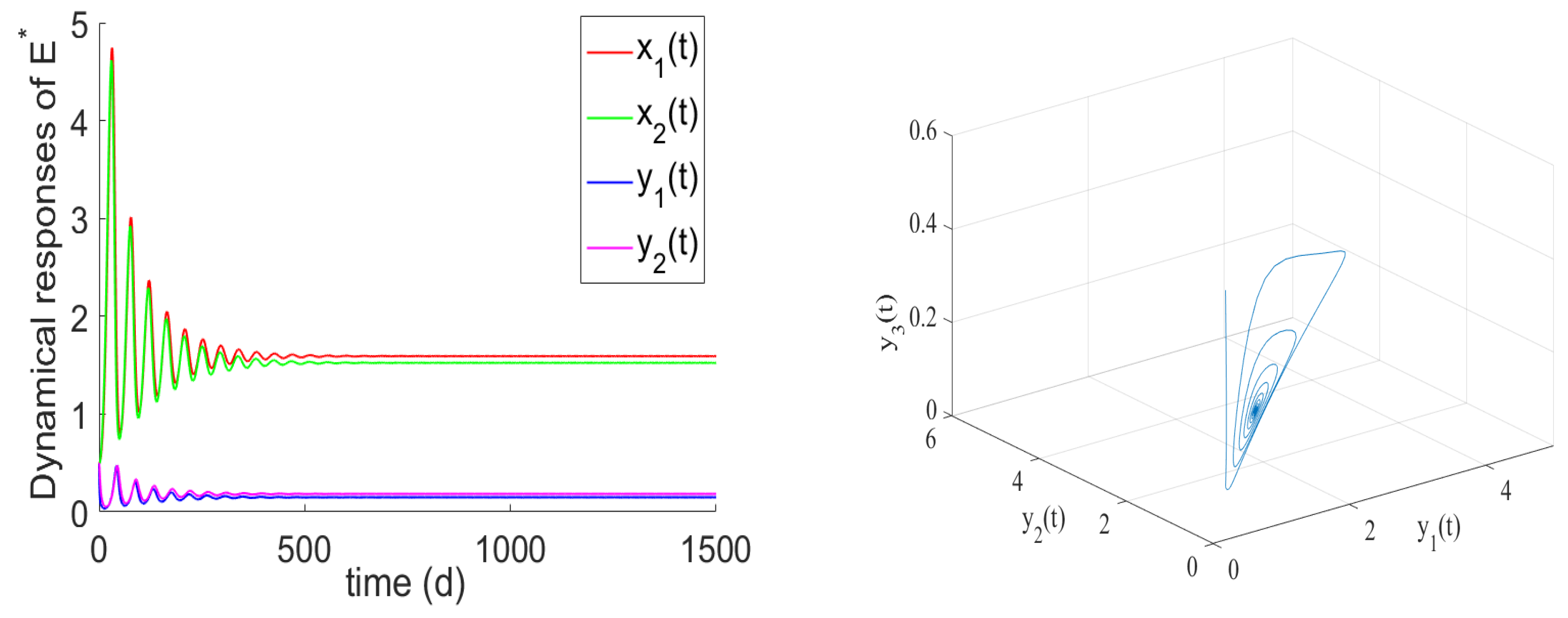
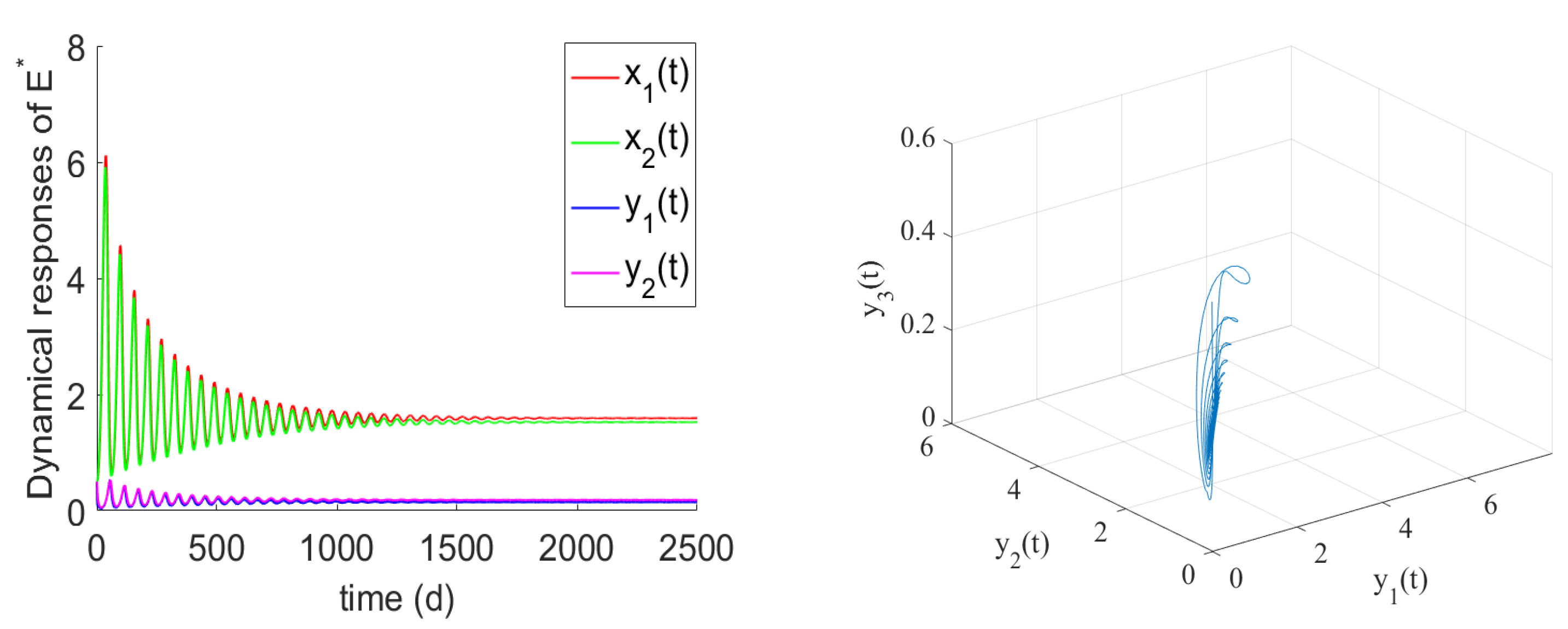
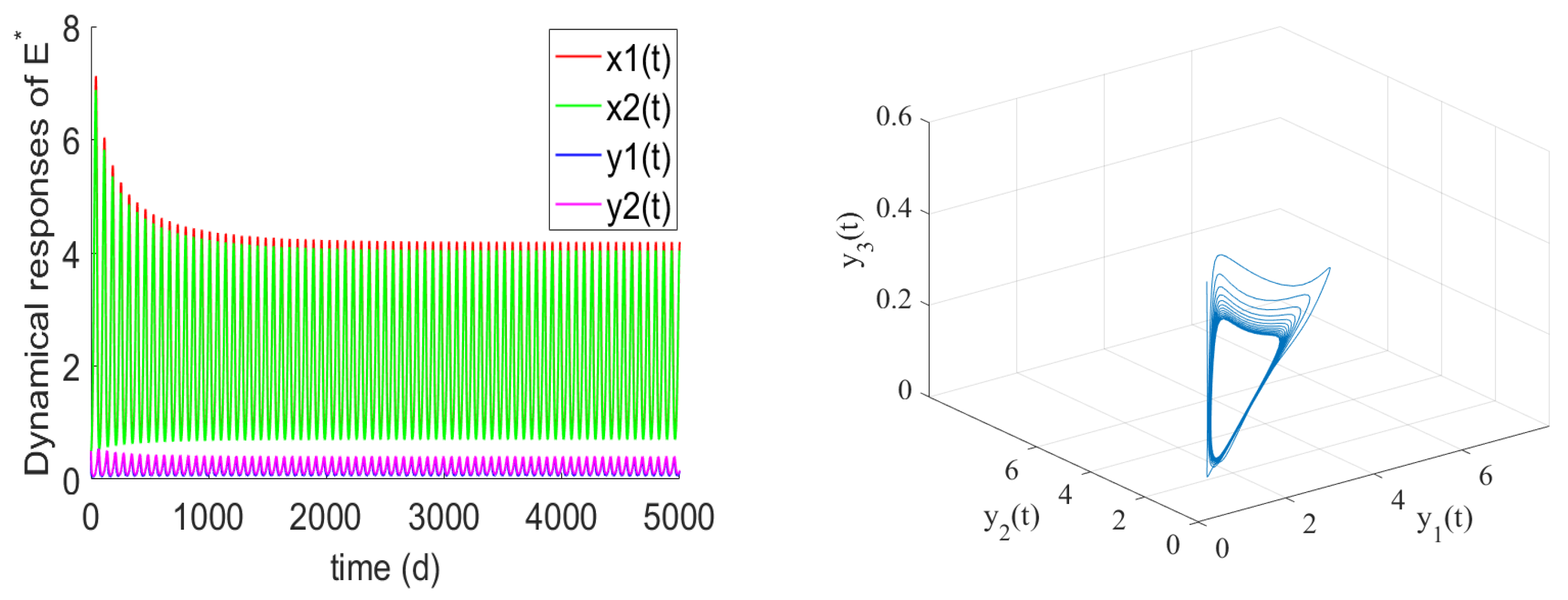
- If , the prey and predator have local stability. If , and hold, there is the positive equilibrium of System (2). is stable for and undergoes a Hopf bifurcation at . From the numerical simulations Figure 1 and Figure 2, if , , and the other parameter values remain unchanged, we can easily to see that the unique positive equilibrium is local asymptotically stable. We found that the numbers of immature prey, mature prey, immature predators, and mature predators increased with the increase of maturation delay during the same period. However, over time, their numbers tended to stabilize. Moreover, as shown in Figure 3, as increases from 9 to 12.5, the prey and predator populations may lose their stabilities and become increasingly unstable due to the enlarged amplitudes of the oscillation intervals. Biologically, this means that a shorter incubation period of mature spaces is helpful in stabilizing the system. If the incubation period is too long, the ecosystem will be unstable. If the development time is too short, the ecological interpretation shows that there are not enough mature prey for mature predators to feed on, and the predators will be subject to cannibalism, competition, natural death, etc., and immature predators will not be able to consume enough mature prey biomass.
- (3)
- If , the prey population is permanent together with the predator.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maitra, S. Dynamical behaviour of a delayed three species predator–prey model with cooperation among the prey species. Nonlinear Dyn. 2018, 92, 627–643. [Google Scholar]
- Zha, L.; Cui, J.A.; Zhou, X. Ratio-dependent predator-prey model with stage structure and time delay. Int. J. Biomath. 2012, 5, 15–37. [Google Scholar] [CrossRef]
- Biswas, S.; Saifuddin, M.; Sasmal, S.K.; Samanta, S.; Chattopadhyay, J. A delayed prey–predator system with prey subject to the strong Allee effect and disease. Nonlinear Dyn. 2016, 84, 1569–1594. [Google Scholar] [CrossRef]
- Yang, R.; Wei, J. Stability and bifurcation analysis of a diffusive prey–predator system in Holling type III with a prey refuge. Nonlinear Dyn. 2015, 79, 631–646. [Google Scholar] [CrossRef]
- Meng, X.Y.; Wang, J.G. Dynamical analysis of a delayed diffusive predator–prey model with schooling behaviour and Allee effect. J. Biol. Dyn. 2020, 84, 826–848. [Google Scholar] [CrossRef]
- Dubey, B.; Agarwal, S.; Kumar, A. Optimal harvesting policy of a prey–predator model with Crowley–Martin-type functional response and stage structure in the predator. Nonlinear Anal. Model. Control 2018, 23, 493–514. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z. Hopf bifurcation analysis in a predator-prey model with predator-age structure and predator-prey reaction time delay. Appl. Math. Model. 2021, 91, 530–548. [Google Scholar] [CrossRef]
- Yuan, Y. Stability and Hopf bifurcation in delayed prey–predator system with ratio dependent. Appl. Mech. Mater. 2014, 687–691, 655–660. [Google Scholar] [CrossRef]
- Gao, S.; Chen, L. Permanence and global stability for single-species model with three life stages and time delay. Acta Math. Sci. 2006, 26, 527–533. [Google Scholar]
- Liang, Z.; Li, B.; Jin, S. Stability and travelling waves for a time-delayed population system with stage structure. Nonlinear Anal. Real World Appl. 2012, 13, 1429–1440. [Google Scholar]
- Han, L. Data processing for cynamic consequences of prey refuge in a prey–predator system with stage structure and time delay. Adv. Mater. Res. 2014, 978, 88–93. [Google Scholar] [CrossRef]
- Xia, Y.H.; Romanovski, V.G. Bifurcation analysis of a population dynamics in a critical state. Bull. Malays. Math. Soc. Ser. 2015, 38, 499–527. [Google Scholar] [CrossRef]
- Bhattacharyya, J.; Piiroinen, P.T.; Banerjee, S. Dynamics of a Filippov prey–predator system with stage-specific intermittent harvesting. Nonlinear Dynam. 2021, 105, 1019–1043. [Google Scholar] [CrossRef]
- Morozov, A.Y.; Banerjee, M.; Petrovskii, S.V. Long-term transients and complex dynamics of a stage-structured population with time delay and the Allee effect. J. Theor. Biol. 2016, 396, 116–124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, H.T.; Li, L. Traveling wave fronts of a single species model with cannibalism and nonlocal effect. Chaos Solitons Fractals 2018, 108, 148–153. [Google Scholar] [CrossRef]
- Xu, D. Global dynamics and Hopf bifurcation of a structured population model. Nonlinear Anal.-Real. 2005, 6, 461–476. [Google Scholar] [CrossRef]
- Yu, X.; Zhu, Z.; Chen, F. Dynamic behaviors of a single species stage structure model with Michaelis-Menten-type juvenile population harvesting. Mathematics 2020, 8, 1281. [Google Scholar] [CrossRef]
- Rayungsari, M.; Suryanto, A.; Kusumawinahyu, W.M.; Darti, I. Dynamical analysis of a predator-prey model incorporating predator cannibalism and refuge. Axioms 2022, 11, 116. [Google Scholar] [CrossRef]
- Wang, L.; Xu, R. Global dynamics of a prey–predator model with stage structure and delayed predator response. Discret. Dyn. Nat. Soc. 2013, 2013, 724325. [Google Scholar] [CrossRef]
- Wang, L.; Feng, G. Global stability and Hopf bifurcation of a prey–predator model with time delay and stage structure. Chin. J. Eng. Math. 2014, 2014, 431671. [Google Scholar] [CrossRef]
- Wang, L.; Feng, G. Stability and Hopf bifurcation for a ratio-dependent prey–predator system with stage structure and time delay. Adv. Differ. Equ. 2015, 2015, 255. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Xu, R.; Feng, G. Global dynamics of a delayed predator–prey model with stage structure and holling type II functional response. J. Appl. Math. Comput. 2015, 47, 73–89. [Google Scholar] [CrossRef]
- Wang, L.; Feng, G. Global dynamics of a delayed prey–predator model with stage structure for the predator and the prey. Math. Methods Appl. Sci. 2015, 38, 3937–3949. [Google Scholar] [CrossRef]
- Zhu, H.; Gao, D. Stability and Hopf bifurcation in a time-delayed predator-prey system with stage structures for both predator and prey. Chin. J. Eng. Math. 2020, 36, 693–707. [Google Scholar]
- Wei, Y.; Zhu, H. Stability and Hopf bifurcation in a predator-prey system with Holling-III functional response and stage structure. J. Nat. Sci. Heilongjiang Univ. 2019, 36, 39–46. [Google Scholar]
- Sajjadi, S.S.; Baleanu, D.; Jajarmi, A.; Pirouz, H.M. A new adaptive synchronization and hyperchaos control of a biological snap oscillator. Chaos Solitons Fractals 2020, 138, 109919. [Google Scholar] [CrossRef]
- Srivastava, H.; Khader, M. Numerical simulation for the treatment of nonlinear predator-prey equations by using the finite element optimization method. Fractal Fract. 2021, 5, 56. [Google Scholar] [CrossRef]
- Djilali, S.; Mezouaghi, A.; Belhamiti, O. Bifurcation analysis of a diffusive predator-prey model with schooling behaviour and cannibalism in prey. Appl. Math. Inf. Sci. 2021, 11, 209. [Google Scholar] [CrossRef]
- Nishikawa, M.; Ferrero, N.; Cheves, S.; Lopez, R.; Kawamura, S.; Fedigan, L.M.; Melin, A.D.; Jack, K.M. Infant cannibalism in wild white-faced capuchin monkeys. Ecol. Evol. 2020, 10, 12679–12684. [Google Scholar] [CrossRef]
- Kang, Y.; Rodriguez-Rodriguez, M.; Evilsizor, S. Ecological and evolutionary dynamics of two-stage models of social insects with egg cannibalism. J. Math. Anal. Appl. 2015, 430, 324–353. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, Y.; Li, J. Dynamical analysis of a stage-structured predator-prey model with cannibalism. Math. Biosci. 2019, 307, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Chen, F.; Zhu, Z.; Li, Z. Dynamic behaviors of Lotka-Volterra predator-prey model incorporating predator cannibalism. Adv. Differ. Equ. 2019, 2019, 359. [Google Scholar] [CrossRef]
- Ma, Z.E.; Zhou, Y.C. Qualitative and Stable Methods for Ordinary Differential Equations; Science Press: Beijing, China, 2001. [Google Scholar]
- Chen, M.; Yang, X.; Fu, S. Global behavior of solutions in a prey–predator cross-diffusion model with cannibalism. Complexity 2020, 2020, 1265798. [Google Scholar] [CrossRef]
- Hale, J.K.; Waltman, P. Persistence in infinite-dimensional systems. J. Math. Anal. 1989, 20, 388–395. [Google Scholar] [CrossRef]
| Indicating: List the sufficient conditions for the main conclusion | |
|---|---|
| 1 | Give the sufficient conditions for the system to be uniformly bounded |
| and | |
| 2 | The necessary conditions for persistent existence remain to be proved |
| 3 | Give the sufficient conditions for to be locally asymptotically stable |
| Hypothesis 4 (H4), and | |
| 4 | The necessary conditions for being locally asymptotically stable remain to be proved |
| 5 | Give the sufficient conditions for to be globally asymptotically stable |
| Hypothesis 4 (H4), and | |
| 6 | The necessary conditions for being globally asymptotically stable remain to be proved |
| 7 | Give the sufficient conditions for to be locally asymptotically stable |
| . | |
| 8 | The necessary conditions for being globally asymptotically stable remain to be proved |
| 9 | Give the sufficient conditions for to be globally asymptotically stable |
| 10 | The necessary conditions for being globally asymptotically stable remain to be proved |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Li, Y. Stability Analysis of a Stage-Structure Predator–Prey Model with Holling III Functional Response and Cannibalism. Axioms 2022, 11, 421. https://doi.org/10.3390/axioms11080421
Wei Y, Li Y. Stability Analysis of a Stage-Structure Predator–Prey Model with Holling III Functional Response and Cannibalism. Axioms. 2022; 11(8):421. https://doi.org/10.3390/axioms11080421
Chicago/Turabian StyleWei, Yufen, and Yu Li. 2022. "Stability Analysis of a Stage-Structure Predator–Prey Model with Holling III Functional Response and Cannibalism" Axioms 11, no. 8: 421. https://doi.org/10.3390/axioms11080421
APA StyleWei, Y., & Li, Y. (2022). Stability Analysis of a Stage-Structure Predator–Prey Model with Holling III Functional Response and Cannibalism. Axioms, 11(8), 421. https://doi.org/10.3390/axioms11080421






