Inferences of a Mixture Bivariate Alpha Power Exponential Model with Engineering Application
Abstract
:1. Introduction
- (i)
- In the first case, we start with two independent and univariate APE with parameters and with . Further, we assume that , are random variables. Then, using the methodology of compounding, we develop the bivariate APE distribution, and, for the sake of notational simplicity, call it the BMAPE (type-I) distribution.
- (ii)
- In the second scenario, we consider a copula-based construction approach. We consider a bivariate Gaussian copula in which the margins are two univariate and independent APE distributions with the coupling parameter . For notational simplicity, we call this the BMAPE (type-II) distribution, for more details of copula based on construction and associated properties, see [25].
2. The APE Model with a Bivariate Mixture
- (i)
- We consider and are random and is fixed, and each are independent for fixed choices of and . Likewise, where and are random and is fixed.
- (ii)
- Next, we further assume that are independent but are correlated through their bivariate generalized Bernoulli distribution with the shape parameter , assuming the following probability matrix.where P is the mixing component with the condition .
- (i)
- and .
- (ii)
- .
- (iii)
- .
3. Structural Properties
- (1)
- A real-life data set (or sets) can assume a variety of shapes. A study such as this can help determine the adaptability of this bivariate distribution.
- (2)
- When working with bivariate distributions, it is essential to examine the joint PDF’s tails as well as the point of inflection. This study is useful in the context of data fitting, as data sets having heavier tails and/or which are small can be adequately modeled by a distribution exhibiting one of these features, as appropriate. Critical-point(s) knowledge will aid in a better understanding of these features, as will be illustrated in Appendix A.
4. Inference
5. BMAPE (Type-II) Model Gaussian Copula Distribution
5.1. BMAPE (Type-II) Distribution Based on a Gaussian Copula
5.2. Gaussian Copula and the EM Algorithm
5.3. Maximum Likelihood Estimation
5.4. Estimation via Semiparametric Methods
5.5. Moments Method
5.6. Copula Fit Tests
6. Bayesian Estimation
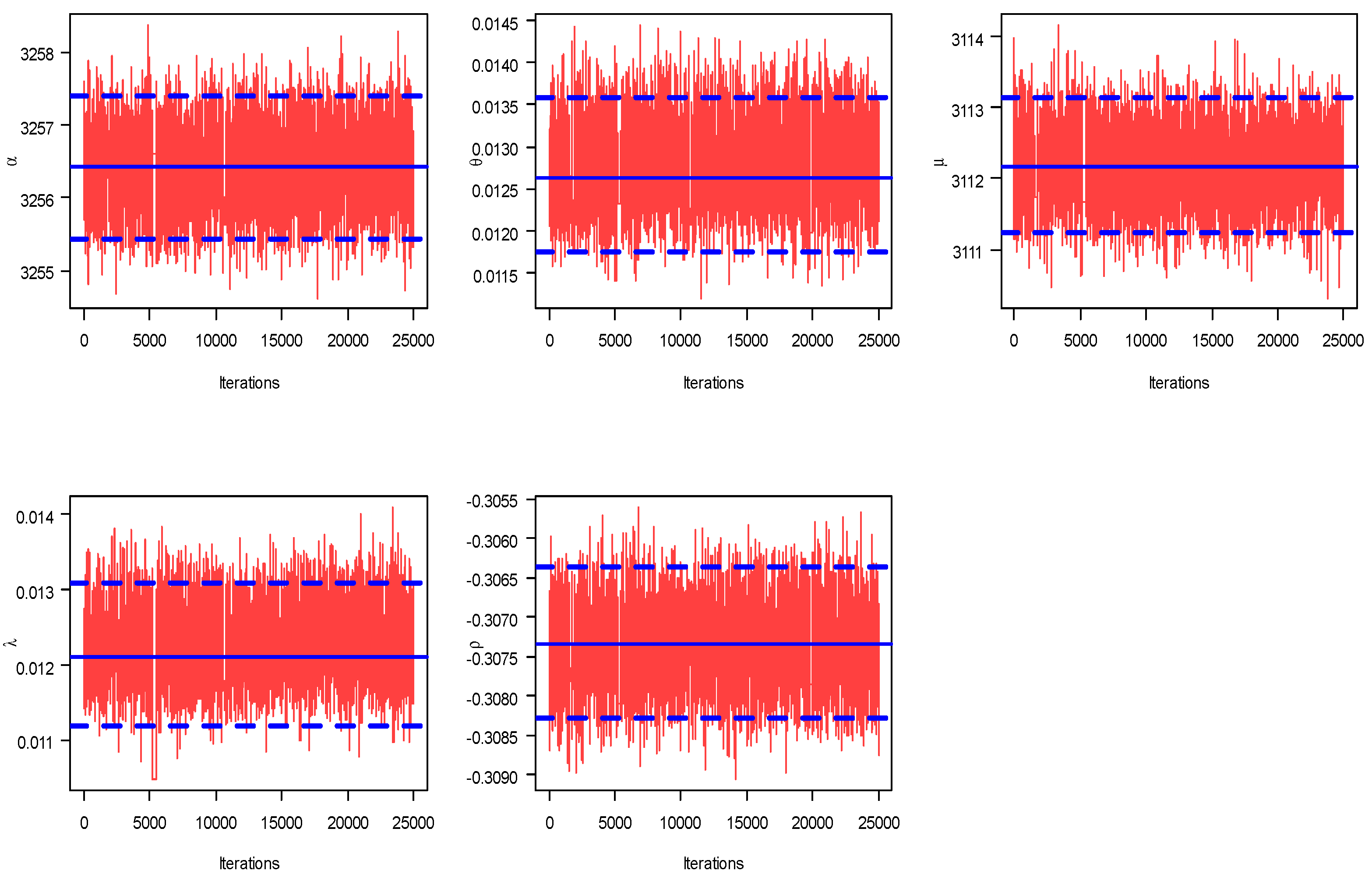
6.1. Bayes MCMC Estimates
6.2. Bayes Credible Intervals
7. Monte-Carlo Simulation
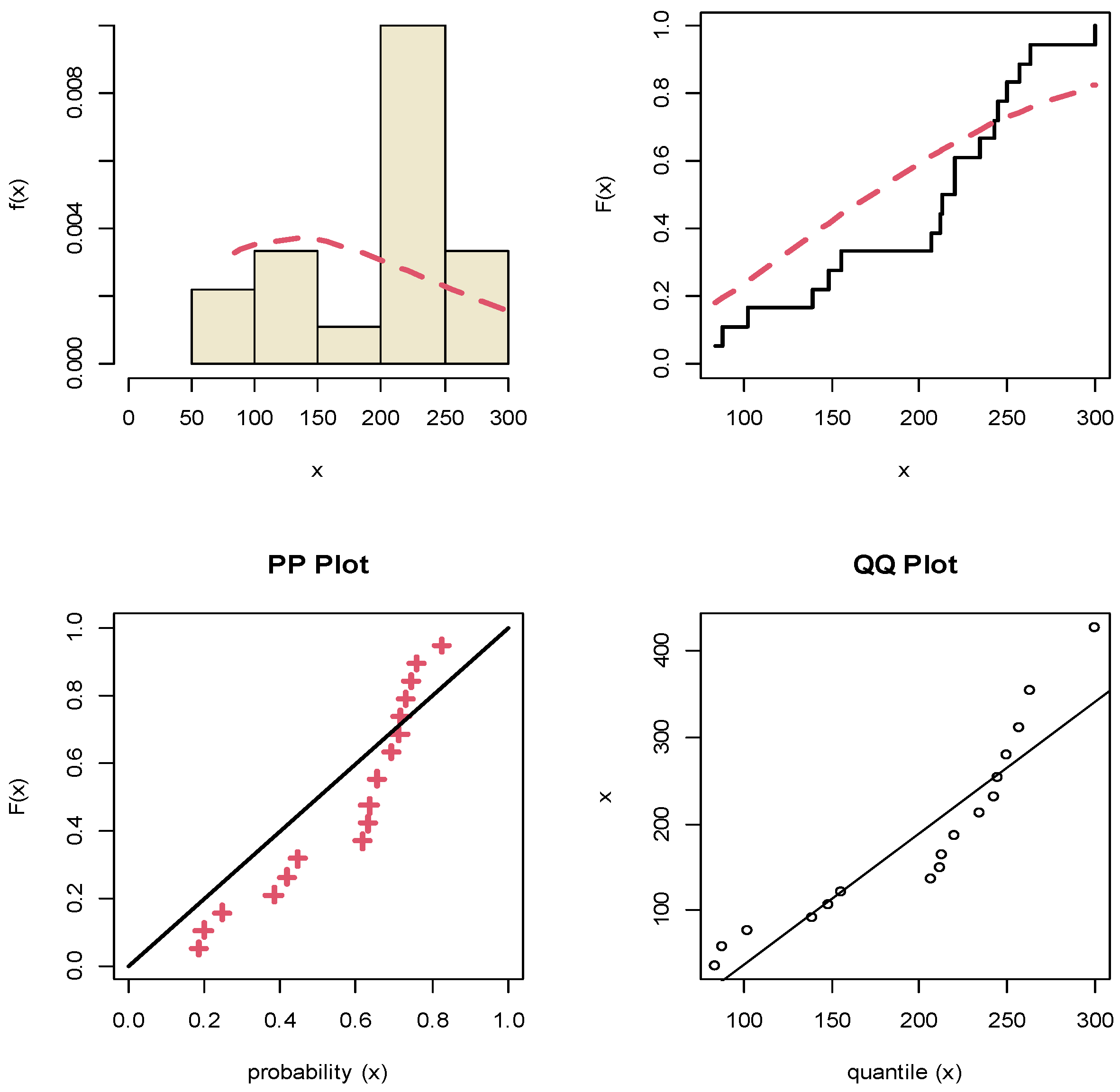
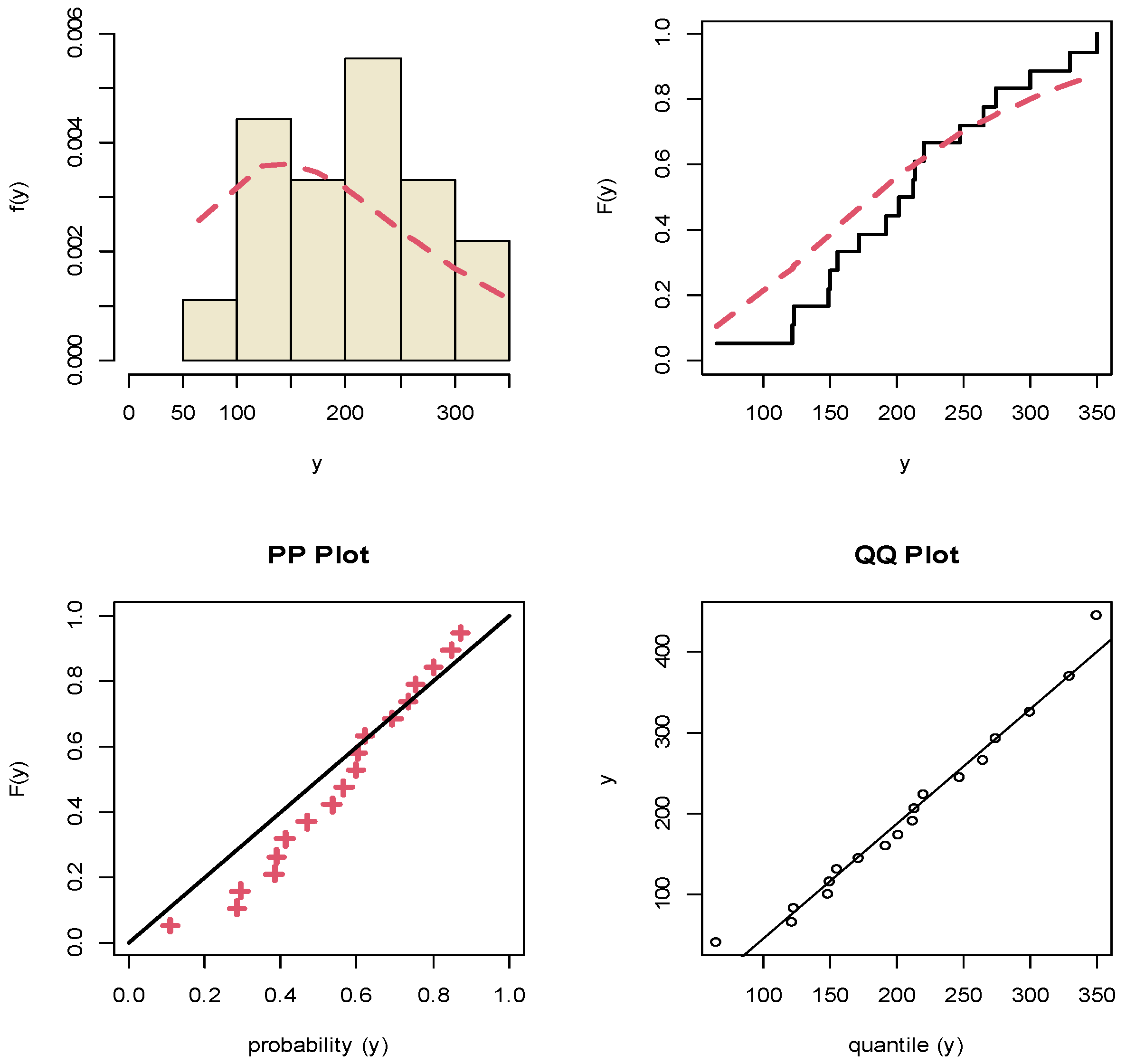
8. Motor Data Analysis
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Mahdavi, A.; Kundu, D. A new method for generating distributions with an application to exponential distribution. Commun. Stat.-Theory Methods 2017, 46, 6543–6557. [Google Scholar] [CrossRef]
- McLachlan, G.J.; Krishnan, T. The EM Algorithm and Extensions; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Mead, M.E.; Cordeiro, G.M.; Afify, A.Z.; Al Mofleh, H. The alpha power transformation family: Properties and applications. Pak. J. Stat. Oper. Res. 2019, 15, 525–545. [Google Scholar] [CrossRef]
- Newcomb, S. A generalized theory of the combination of observations so as to obtain the best result. Am. J. Math. 1886, 8, 343–366. [Google Scholar] [CrossRef]
- Pearson, K. Contributions to the Mathematical Theory of Evolution. Philos. Trans. A 1894, 185, 71–110. [Google Scholar]
- Titterington, D.M.; Smith, A.F.M.; Makov, U.E. Statistical Analysis of Finite Mixture Distributions; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Everitt, B.S.; Hand, D.J. Finite Mixture Distributions; John Wiley & Sons, Ltd.: The Netherlands, 1981. [Google Scholar]
- McLachlan, G.J.; Basford, K.E. Mixture Models Inferences and Applications to Clustering; Marcel Dekker: New York, NY, USA, 1988. [Google Scholar]
- Al-Hussaini, E.K.; Sultan, K.S. Reliability and hazard based on finite mixture Models. In Handbook of Statistics; Balakrishnan, N., Rao, C.R., Eds.; Handbook of Statistics: Amsterdam, The Netherlands, 2001; Volume 20, pp. 139–183. [Google Scholar]
- AL-Moisheer, A.S.; Alotaibi, R.M.; Alomani, G.A.; Rezk, H.R. Bivariate Mixture of Inverse Weibull Distribution: Properties and Estimation. Math. Probl. Eng. 2020, 2020, 5234601. [Google Scholar] [CrossRef]
- Nassar, M.; Alzaatreh, A.; Mead, M.; Abo-Kasem, O. Alpha power Weibull distribution: Properties and applications. Commun. Stat.-Theory Methods 2017, 46, 10236–10252. [Google Scholar] [CrossRef]
- Dey, A.; Alzaatreh, A.; Zhang, C.; Kumar, D. A new extension of generalized exponential distribution with application to ozone data. Ozone Sci. Eng. 2017, 39, 273–285. [Google Scholar] [CrossRef]
- Nadarajah, S.; Okorie, I.E. On the moments of the alpha power transformed generalized exponential distribution. Ozone Sci. Eng. 2018, 40, 330–335. [Google Scholar] [CrossRef]
- Nassar, M.; Afify, A.Z.; Dey, S.; Kumar, D. A new extension of Weibull distribution: Properties and different methods of estimation. J. Comput. Appl. Math. 2018, 336, 439–457. [Google Scholar] [CrossRef]
- Nassar, M.; Kumar, D.; Dey, S.; Cordeiro, G.M.; Afify, A.Z. The Marshall–Olkin alpha power family of distributions with applications. J. Comput. Appl. Math. 2019, 351, 41–53. [Google Scholar] [CrossRef]
- Nassar, M.; Afify, A.; Shakhatreh, M. Estimation Methods of Alpha Power Exponential Distribution with Applications to Engineering and Medical Data. Pak. J. Stat. Oper. Res. 2020, 16, 149–166. [Google Scholar] [CrossRef]
- Jaheen, Z. On record statistics from a mixture of two exponential distributions. J. Stat. Comput. Simul. 2005, 75, 1–11. [Google Scholar] [CrossRef]
- Al-Hussaini, E.K.; Hussein, M. Estimation under a Finite Mixture of Exponentiated Exponential Components Model and Balanced Square Error Loss. Open J. Stat. 2012, 2, 28–38. [Google Scholar] [CrossRef]
- Tahir, M.; Aslam, M.; Hussain, Z.; Khan, A. On finite 3-component mixture of exponential distributions: Properties and estimation. Cogent Math. 2016, 3, 1275414. [Google Scholar] [CrossRef]
- Diawara, N.; Carpenter, M. Mixture of bivariate exponential distributions. Commun. Stat.-Theory Methods 2010, 39, 2711–2720. [Google Scholar] [CrossRef]
- Rafiei, M.; Iranmanesh, A.; Nagar, D. A bivariate gamma distribution whose marginals are finite mixtures of gamma distributions. Stat. Optim. Inf. Comput. 2020, 8, 950–971. [Google Scholar] [CrossRef]
- Mardia, K.V. Measures of multivariate skewness and kurtosis with applications. Biometrika 1970, 57, 519–530. [Google Scholar] [CrossRef]
- Kotz, S.; Balakrishnan, N.; Johnson, N. Continuous Multivariate Distributions: Models and Applications, 2nd ed.; Wiley: New York, NY, USA, 2000; Volume 1. [Google Scholar]
- Balakrishnan, N.; Lai, C. Cotinuous Bivariate Distributions, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Nelson, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Dellaert, F. The Expectation Maximization Algorithm; CiteSeerX 10.1.1.9.9735. gives an easier explanation of EM algorithm as to lowerbound maximization 2002; Georgia Institute of Technology: Atlanta, GA, USA, 2002. [Google Scholar]
- Kundu, D. Bivariate sinh-normal distribution and a related model. Braz. J. Probab. Stat. 2015, 29, 590–607. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Alhussain, Z.A.; Atta, D.; Almetwally, E.M.; Eliwa, M.S. Bivariate Burr X Generator of Distributions: Properties and Estimation Methods with Applications to Complete and Type-II Censored Samples. Mathematics 2020, 8, 264. [Google Scholar] [CrossRef]
- Alotaibi, R.; Rezk, H.; Ghosh, I.; Dey, S. Bivariate exponentiated half logistic distribution: Properties and application. Commun. Stat.-Theory Methods 2020, 50, 6099–6121. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de Répartition à n Dimensions et Leurs Marges; Publications de l’Institut Statistique de l’Université de Paris: Paris, France, 1959; Volume 8, pp. 229–231. [Google Scholar]
- Kosmidis, I.; Karlis, D. Model-based clustering using copulas with applications. Stat. Comput. 2016, 26, 1079–1099. [Google Scholar] [CrossRef]
- Joe, H.; Xu, J. The Estimation Method of Inference Functions for Margins for Multivariate Models; Technical Report No. 166; Department of Statistics, University of British Columbia: Vancouver, BC, Canada, 1996. [Google Scholar]
- Kojadinovic, I.; Yan, J. Comparison of three semiparametric methods for estimating dependence parameters in copula models. Insur. Math. Econ. 2010, 47, 52–63. [Google Scholar] [CrossRef]
- Fermanian, J.D. Goodness-of-fit tests for copulas. J. Multivar. Anal. 2005, 95, 119–152. [Google Scholar] [CrossRef]
- Dobric, J.; Schmid, F. A goodness of fit test for copulas based on Rosenblatt’s transformation. Comput. Stat. Data Anal. 2007, 51, 4633–4642. [Google Scholar] [CrossRef]
- Genest, C.; Remillard, B. Validity of the parametric bootstrap for goodness-of-fit testing in semiparametric models. Ann. L’institut Henri Poincare (B) Probab. Stat. 2008, 44, 1096–1127. [Google Scholar] [CrossRef]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar] [CrossRef]
- Kojadinovic, I.; Yan, J.; Holmes, M. Fast large-sample goodness-of-fit tests for copulas. Stat. Sin. 2011, 21, 841–871. [Google Scholar] [CrossRef]
- Meintanis, S.G. Test of fit for Marshall–Olkin distributions with applications. J. Stat. Plan. Inference 2007, 137, 3954–3963. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1091. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Plummer, M.; Best, N.; Cowles, K.; Vines, K. Convergence diagnosis and output analysis for MCMC. R News 2006, 6, 7–11. [Google Scholar]
- Henningsen, A.; Toomet, O. maxLik: A package for maximum likelihood estimation in R. Comput. Stat. 2011, 26, 443–458. [Google Scholar] [CrossRef]
- Gilks, W.R.; Best, N.G.; Tan, K.K.C. Adaptive Rejection Metropolis Sampling within Gibbs Sampling. Appl. Stat. 1995, 44, 455–472. [Google Scholar] [CrossRef]
- Martino, L.; Yang, H.; Luengo, D.; Kanniainen, J.; Corander, J. A Fast Universal Self-Tuned Sampler Within Gibbs Sampling. Digit. Signal Process. 2015, 47, 68–83. [Google Scholar] [CrossRef]
- Fitzgerald, W.J. Markov chain Monte Carlo methods with applications to signal processing. Signal Process. 2001, 81, 3–18. [Google Scholar] [CrossRef]
- Alotaibi, R.; Khalifa, M.; Almetwally, E.; Ghosh, I.; Rezk, H. Classical and Bayesian Inference of a Mixture of Bivariate Exponentiated Exponential Model. J. Math. 2021, 2021, 5200979. [Google Scholar] [CrossRef]

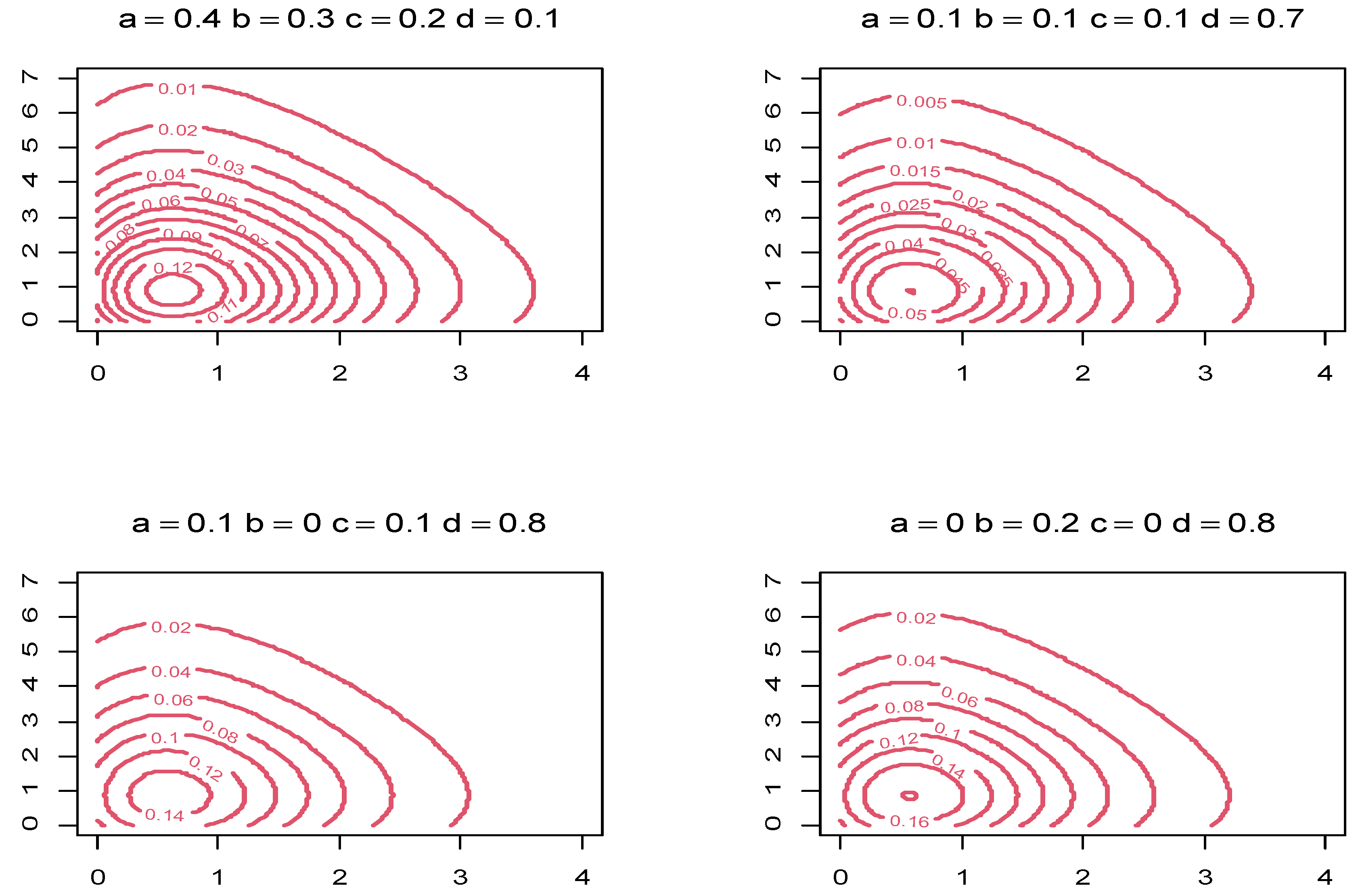

| Parameter | True Value | Prior 1 | Prior 2 | True Value | Prior 1 | Prior 2 | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| I | II | |||||||||
| 0.4 | 0.8 | 2 | 2.0 | 5 | 0.8 | 1.6 | 2 | 4.0 | 5 | |
| 0.5 | 1.0 | 2 | 2.5 | 5 | 1.5 | 3.0 | 2 | 7.5 | 5 | |
| 0.2 | 0.4 | 2 | 1.0 | 5 | 0.4 | 2.0 | 2 | 2.0 | 5 | |
| 0.8 | 1.6 | 2 | 4.0 | 5 | 1.2 | 2.4 | 2 | 6.0 | 5 | |
| 0.3 | 0.6 | 2 | 1.5 | 5 | 0.5 | 1.0 | 2 | 5.0 | 5 | |
| III | IV | |||||||||
| 0.1 | 0.2 | 2 | 0.5 | 5 | 0.3 | 0.6 | 2 | 1.5 | 5 | |
| 0.3 | 0.6 | 2 | 1.5 | 5 | 0.5 | 1.0 | 2 | 2.5 | 5 | |
| 0.5 | 1.0 | 2 | 2.5 | 5 | 1.5 | 3.0 | 2 | 7.5 | 5 | |
| 0.1 | 0.2 | 2 | 0.5 | 5 | 0.2 | 0.4 | 2 | 1.0 | 5 | |
| 0.1 | 0.2 | 2 | 0.5 | 5 | 0.2 | 0.4 | 2 | 1.0 | 5 | |
| 0.8 | 1.6 | 2 | 4.0 | 5 | 1.2 | 2.4 | 2 | 5.0 | 5 | |
| Set | Par. | MLE | MCMC.1 | MCMC.2 | ACI | BCI.1 | BCI.2 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MAB | RMSE | MAB | RMSE | MAB | RMSE | ||||||
| I | 50 | 0.618 | 1.106 | 0.143 | 0.199 | 0.037 | 0.064 | 3.056 | 0.348 | 0.092 | |
| 0.171 | 0.217 | 0.108 | 0.154 | 0.039 | 0.059 | 0.727 | 0.300 | 0.099 | |||
| 0.401 | 0.764 | 0.179 | 0.205 | 0.102 | 0.177 | 2.040 | 0.296 | 0.250 | |||
| 0.314 | 0.409 | 0.262 | 0.395 | 0.203 | 0.343 | 1.402 | 0.658 | 0.492 | |||
| 0.304 | 0.363 | 0.261 | 0.335 | 0.166 | 0.290 | 0.636 | 0.525 | 0.392 | |||
| 100 | 0.351 | 0.527 | 0.127 | 0.187 | 0.036 | 0.058 | 1.771 | 0.346 | 0.089 | ||
| 0.118 | 0.155 | 0.096 | 0.125 | 0.037 | 0.056 | 0.552 | 0.250 | 0.093 | |||
| 0.246 | 0.388 | 0.153 | 0.198 | 0.097 | 0.165 | 1.226 | 0.274 | 0.242 | |||
| 0.242 | 0.375 | 0.240 | 0.350 | 0.200 | 0.301 | 1.110 | 0.648 | 0.474 | |||
| 0.302 | 0.317 | 0.231 | 0.291 | 0.164 | 0.279 | 0.575 | 0.405 | 0.390 | |||
| 150 | 0.263 | 0.377 | 0.122 | 0.181 | 0.034 | 0.055 | 1.338 | 0.286 | 0.087 | ||
| 0.097 | 0.151 | 0.079 | 0.101 | 0.036 | 0.051 | 0.458 | 0.249 | 0.086 | |||
| 0.186 | 0.277 | 0.103 | 0.163 | 0.096 | 0.141 | 0.918 | 0.266 | 0.236 | |||
| 0.202 | 0.340 | 0.198 | 0.258 | 0.152 | 0.226 | 0.975 | 0.480 | 0.352 | |||
| 0.301 | 0.311 | 0.225 | 0.285 | 0.162 | 0.277 | 0.555 | 0.399 | 0.319 | |||
| 200 | 0.224 | 0.314 | 0.116 | 0.155 | 0.032 | 0.054 | 1.121 | 0.282 | 0.084 | ||
| 0.084 | 0.109 | 0.038 | 0.061 | 0.032 | 0.045 | 0.398 | 0.113 | 0.076 | |||
| 0.177 | 0.221 | 0.099 | 0.153 | 0.095 | 0.140 | 0.751 | 0.259 | 0.230 | |||
| 0.192 | 0.335 | 0.179 | 0.226 | 0.150 | 0.220 | 0.847 | 0.464 | 0.347 | |||
| 0.300 | 0.306 | 0.211 | 0.280 | 0.160 | 0.267 | 0.503 | 0.392 | 0.276 | |||
| II | 50 | 0.907 | 1.583 | 0.272 | 0.443 | 0.107 | 0.183 | 4.988 | 0.676 | 0.265 | |
| 0.373 | 0.482 | 0.276 | 0.437 | 0.223 | 0.396 | 1.815 | 0.726 | 0.550 | |||
| 0.591 | 1.046 | 0.368 | 0.628 | 0.360 | 0.621 | 3.161 | 1.062 | 0.867 | |||
| 0.395 | 0.562 | 0.311 | 0.461 | 0.266 | 0.453 | 1.794 | 0.883 | 0.644 | |||
| 0.503 | 0.551 | 0.470 | 0.505 | 0.236 | 0.412 | 1.057 | 0.573 | 0.551 | |||
| 100 | 0.546 | 0.819 | 0.268 | 0.404 | 0.105 | 0.177 | 2.866 | 0.640 | 0.258 | ||
| 0.293 | 0.452 | 0.262 | 0.387 | 0.221 | 0.392 | 1.295 | 0.698 | 0.544 | |||
| 0.423 | 0.693 | 0.355 | 0.621 | 0.354 | 0.568 | 1.810 | 1.033 | 0.857 | |||
| 0.346 | 0.509 | 0.288 | 0.451 | 0.255 | 0.372 | 1.328 | 0.799 | 0.630 | |||
| 0.502 | 0.525 | 0.348 | 0.476 | 0.233 | 0.400 | 0.836 | 0.571 | 0.392 | |||
| 150 | 0.427 | 0.610 | 0.254 | 0.398 | 0.101 | 0.173 | 2.179 | 0.609 | 0.248 | ||
| 0.268 | 0.437 | 0.226 | 0.378 | 0.216 | 0.338 | 1.069 | 0.695 | 0.542 | |||
| 0.407 | 0.672 | 0.351 | 0.618 | 0.270 | 0.392 | 1.326 | 1.030 | 0.851 | |||
| 0.315 | 0.487 | 0.258 | 0.444 | 0.234 | 0.299 | 1.103 | 0.764 | 0.626 | |||
| 0.501 | 0.512 | 0.339 | 0.401 | 0.230 | 0.399 | 0.789 | 0.558 | 0.319 | |||
| 200 | 0.365 | 0.514 | 0.218 | 0.320 | 0.098 | 0.169 | 1.827 | 0.521 | 0.243 | ||
| 0.244 | 0.392 | 0.223 | 0.277 | 0.184 | 0.233 | 0.914 | 0.614 | 0.539 | |||
| 0.400 | 0.648 | 0.326 | 0.558 | 0.225 | 0.313 | 1.124 | 0.862 | 0.832 | |||
| 0.307 | 0.453 | 0.255 | 0.442 | 0.200 | 0.257 | 0.959 | 0.624 | 0.619 | |||
| 0.500 | 0.509 | 0.317 | 0.399 | 0.229 | 0.381 | 0.764 | 0.552 | 0.277 | |||
| Par. | MLE | MCMC.1 | MCMC.2 | ACI | BCI.P1 | BCI.P2 | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAB | RMSE | MAB | RMSE | MAB | RMSE | |||||
| 50 | 0.085 | 0.113 | 0.058 | 0.061 | 0.039 | 0.044 | 0.606 | 0.085 | 0.074 | |
| 0.274 | 0.295 | 0.073 | 0.081 | 0.029 | 0.031 | 0.630 | 0.143 | 0.077 | ||
| 0.273 | 0.263 | 0.228 | 0.062 | 0.208 | 0.060 | 0.779 | 0.099 | 0.056 | ||
| 0.087 | 0.123 | 0.061 | 0.063 | 0.049 | 0.053 | 0.455 | 0.133 | 0.055 | ||
| 0.099 | 0.106 | 0.087 | 0.104 | 0.045 | 0.046 | 0.528 | 0.116 | 0.068 | ||
| 0.323 | 0.359 | 0.053 | 0.063 | 0.018 | 0.019 | 1.814 | 0.129 | 0.041 | ||
| 0.388 | 0.411 | 0.224 | 0.234 | 0.172 | 0.178 | 0.514 | 0.247 | 0.195 | ||
| 0.428 | 0.447 | 0.184 | 0.194 | 0.141 | 0.144 | 0.554 | 0.228 | 0.162 | ||
| 0.409 | 0.442 | 0.166 | 0.176 | 0.112 | 0.115 | 0.602 | 0.180 | 0.156 | ||
| 0.427 | 0.451 | 0.166 | 0.180 | 0.163 | 0.171 | 0.678 | 0.254 | 0.154 | ||
| 100 | 0.084 | 0.101 | 0.048 | 0.051 | 0.023 | 0.025 | 0.206 | 0.083 | 0.070 | |
| 0.268 | 0.287 | 0.041 | 0.053 | 0.024 | 0.024 | 0.549 | 0.105 | 0.067 | ||
| 0.239 | 0.260 | 0.220 | 0.035 | 0.176 | 0.015 | 0.557 | 0.079 | 0.038 | ||
| 0.086 | 0.108 | 0.050 | 0.058 | 0.045 | 0.051 | 0.388 | 0.104 | 0.053 | ||
| 0.085 | 0.101 | 0.035 | 0.044 | 0.025 | 0.030 | 0.321 | 0.101 | 0.061 | ||
| 0.322 | 0.358 | 0.047 | 0.058 | 0.015 | 0.016 | 1.045 | 0.117 | 0.040 | ||
| 0.364 | 0.391 | 0.173 | 0.181 | 0.145 | 0.158 | 0.394 | 0.192 | 0.139 | ||
| 0.420 | 0.445 | 0.157 | 0.172 | 0.109 | 0.119 | 0.381 | 0.201 | 0.117 | ||
| 0.407 | 0.439 | 0.127 | 0.136 | 0.050 | 0.059 | 0.451 | 0.161 | 0.097 | ||
| 0.422 | 0.450 | 0.113 | 0.119 | 0.053 | 0.061 | 0.449 | 0.130 | 0.128 | ||
| 150 | 0.083 | 0.096 | 0.025 | 0.028 | 0.022 | 0.022 | 0.201 | 0.069 | 0.066 | |
| 0.267 | 0.273 | 0.040 | 0.045 | 0.018 | 0.022 | 0.539 | 0.092 | 0.040 | ||
| 0.235 | 0.257 | 0.212 | 0.034 | 0.170 | 0.013 | 0.519 | 0.076 | 0.037 | ||
| 0.086 | 0.104 | 0.043 | 0.046 | 0.012 | 0.015 | 0.321 | 0.099 | 0.052 | ||
| 0.083 | 0.097 | 0.026 | 0.031 | 0.019 | 0.024 | 0.244 | 0.078 | 0.037 | ||
| 0.319 | 0.356 | 0.038 | 0.041 | 0.014 | 0.015 | 0.821 | 0.069 | 0.037 | ||
| 0.365 | 0.388 | 0.087 | 0.089 | 0.061 | 0.062 | 0.348 | 0.074 | 0.040 | ||
| 0.419 | 0.435 | 0.129 | 0.130 | 0.068 | 0.078 | 0.350 | 0.139 | 0.060 | ||
| 0.401 | 0.429 | 0.059 | 0.067 | 0.041 | 0.044 | 0.364 | 0.094 | 0.076 | ||
| 0.409 | 0.440 | 0.075 | 0.080 | 0.017 | 0.018 | 0.410 | 0.121 | 0.026 | ||
| 200 | 0.079 | 0.086 | 0.021 | 0.025 | 0.019 | 0.021 | 0.163 | 0.050 | 0.016 | |
| 0.258 | 0.269 | 0.035 | 0.040 | 0.014 | 0.018 | 0.347 | 0.080 | 0.019 | ||
| 0.232 | 0.247 | 0.171 | 0.024 | 0.167 | 0.010 | 0.413 | 0.070 | 0.013 | ||
| 0.084 | 0.099 | 0.039 | 0.045 | 0.005 | 0.006 | 0.265 | 0.068 | 0.015 | ||
| 0.081 | 0.091 | 0.022 | 0.023 | 0.011 | 0.013 | 0.201 | 0.049 | 0.020 | ||
| 0.299 | 0.343 | 0.022 | 0.028 | 0.009 | 0.011 | 0.801 | 0.057 | 0.013 | ||
| 0.358 | 0.382 | 0.030 | 0.031 | 0.018 | 0.023 | 0.298 | 0.063 | 0.011 | ||
| 0.415 | 0.434 | 0.034 | 0.038 | 0.010 | 0.011 | 0.304 | 0.054 | 0.019 | ||
| 0.392 | 0.425 | 0.050 | 0.050 | 0.040 | 0.042 | 0.361 | 0.057 | 0.008 | ||
| 0.408 | 0.438 | 0.043 | 0.059 | 0.014 | 0.015 | 0.375 | 0.095 | 0.008 | ||
| Par. | MLE | MCMC.1 | MCMC.2 | ACI | BCI.P1 | BCI.P2 | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAB | RMSE | MAB | RMSE | MAB | RMSE | |||||
| 50 | 0.095 | 0.144 | 0.065 | 0.067 | 0.045 | 0.056 | 0.807 | 0.129 | 0.083 | |
| 0.253 | 0.394 | 0.070 | 0.073 | 0.033 | 0.035 | 1.565 | 0.143 | 0.090 | ||
| 0.212 | 0.182 | 0.174 | 0.087 | 0.143 | 0.022 | 1.232 | 0.154 | 0.042 | ||
| 0.091 | 0.124 | 0.053 | 0.054 | 0.041 | 0.049 | 0.971 | 0.122 | 0.058 | ||
| 0.084 | 0.125 | 0.056 | 0.064 | 0.032 | 0.037 | 0.786 | 0.094 | 0.068 | ||
| 0.232 | 0.277 | 0.112 | 0.115 | 0.046 | 0.048 | 2.056 | 0.126 | 0.067 | ||
| 0.153 | 0.189 | 0.098 | 0.107 | 0.053 | 0.056 | 0.516 | 0.182 | 0.097 | ||
| 0.230 | 0.252 | 0.198 | 0.214 | 0.063 | 0.072 | 0.534 | 0.260 | 0.124 | ||
| 0.335 | 0.348 | 0.112 | 0.120 | 0.032 | 0.036 | 0.620 | 0.138 | 0.093 | ||
| 0.268 | 0.286 | 0.217 | 0.232 | 0.035 | 0.040 | 0.645 | 0.235 | 0.122 | ||
| 100 | 0.078 | 0.133 | 0.060 | 0.063 | 0.043 | 0.054 | 0.696 | 0.115 | 0.077 | |
| 0.220 | 0.238 | 0.059 | 0.066 | 0.030 | 0.032 | 0.787 | 0.120 | 0.079 | ||
| 0.210 | 0.177 | 0.170 | 0.049 | 0.137 | 0.011 | 1.030 | 0.117 | 0.039 | ||
| 0.077 | 0.091 | 0.047 | 0.052 | 0.034 | 0.038 | 0.758 | 0.101 | 0.054 | ||
| 0.079 | 0.101 | 0.039 | 0.042 | 0.019 | 0.023 | 0.695 | 0.092 | 0.061 | ||
| 0.216 | 0.255 | 0.068 | 0.072 | 0.027 | 0.032 | 1.752 | 0.091 | 0.052 | ||
| 0.142 | 0.171 | 0.082 | 0.102 | 0.042 | 0.047 | 0.482 | 0.146 | 0.066 | ||
| 0.227 | 0.244 | 0.102 | 0.111 | 0.038 | 0.040 | 0.524 | 0.170 | 0.070 | ||
| 0.333 | 0.346 | 0.099 | 0.105 | 0.031 | 0.033 | 0.576 | 0.133 | 0.073 | ||
| 0.266 | 0.283 | 0.106 | 0.119 | 0.029 | 0.034 | 0.602 | 0.182 | 0.087 | ||
| 150 | 0.067 | 0.087 | 0.057 | 0.062 | 0.036 | 0.041 | 0.562 | 0.113 | 0.068 | |
| 0.219 | 0.236 | 0.037 | 0.047 | 0.027 | 0.030 | 0.716 | 0.111 | 0.060 | ||
| 0.207 | 0.165 | 0.152 | 0.046 | 0.131 | 0.010 | 0.831 | 0.080 | 0.024 | ||
| 0.075 | 0.089 | 0.045 | 0.050 | 0.013 | 0.014 | 0.708 | 0.100 | 0.034 | ||
| 0.078 | 0.098 | 0.033 | 0.038 | 0.012 | 0.014 | 0.549 | 0.079 | 0.054 | ||
| 0.205 | 0.249 | 0.059 | 0.070 | 0.020 | 0.021 | 1.692 | 0.090 | 0.040 | ||
| 0.135 | 0.167 | 0.045 | 0.053 | 0.036 | 0.044 | 0.452 | 0.100 | 0.065 | ||
| 0.215 | 0.242 | 0.086 | 0.094 | 0.017 | 0.022 | 0.418 | 0.154 | 0.068 | ||
| 0.332 | 0.345 | 0.060 | 0.069 | 0.023 | 0.024 | 0.530 | 0.124 | 0.039 | ||
| 0.257 | 0.281 | 0.100 | 0.111 | 0.021 | 0.032 | 0.527 | 0.178 | 0.083 | ||
| 200 | 0.066 | 0.074 | 0.032 | 0.039 | 0.031 | 0.037 | 0.494 | 0.085 | 0.052 | |
| 0.217 | 0.233 | 0.025 | 0.031 | 0.023 | 0.028 | 0.547 | 0.090 | 0.043 | ||
| 0.180 | 0.158 | 0.147 | 0.025 | 0.130 | 0.008 | 0.804 | 0.068 | 0.022 | ||
| 0.068 | 0.081 | 0.035 | 0.041 | 0.009 | 0.012 | 0.691 | 0.092 | 0.032 | ||
| 0.067 | 0.076 | 0.029 | 0.032 | 0.011 | 0.011 | 0.544 | 0.076 | 0.052 | ||
| 0.202 | 0.243 | 0.046 | 0.048 | 0.019 | 0.020 | 1.510 | 0.052 | 0.038 | ||
| 0.133 | 0.163 | 0.042 | 0.047 | 0.022 | 0.027 | 0.390 | 0.084 | 0.062 | ||
| 0.214 | 0.233 | 0.065 | 0.076 | 0.015 | 0.020 | 0.388 | 0.117 | 0.043 | ||
| 0.330 | 0.344 | 0.036 | 0.043 | 0.020 | 0.022 | 0.528 | 0.099 | 0.035 | ||
| 0.249 | 0.260 | 0.045 | 0.056 | 0.019 | 0.030 | 0.510 | 0.150 | 0.060 | ||
| 𝒏 | Par. | MLE | MCMC.1 | MCMC.2 | ACI | BCI.P1 | BCI.P2 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| MAB | RMSE | MAB | RMSE | MAB | RMSE | |||||
| 50 | 0.235 | 0.307 | 0.065 | 0.070 | 0.038 | 0.044 | 2.610 | 0.109 | 0.084 | |
| 0.349 | 0.432 | 0.070 | 0.078 | 0.056 | 0.020 | 2.926 | 0.141 | 0.079 | ||
| 0.974 | 0.456 | 0.383 | 0.062 | 0.070 | 0.027 | 3.167 | 0.104 | 0.060 | ||
| 0.160 | 0.213 | 0.076 | 0.078 | 0.061 | 0.068 | 1.758 | 0.191 | 0.073 | ||
| 0.179 | 0.250 | 0.097 | 0.103 | 0.049 | 0.053 | 2.360 | 0.113 | 0.110 | ||
| 0.338 | 0.394 | 0.075 | 0.083 | 0.023 | 0.029 | 2.843 | 0.151 | 0.048 | ||
| 0.427 | 0.448 | 0.229 | 0.240 | 0.171 | 0.180 | 0.507 | 0.253 | 0.199 | ||
| 0.475 | 0.492 | 0.186 | 0.197 | 0.147 | 0.150 | 0.541 | 0.228 | 0.163 | ||
| 0.524 | 0.538 | 0.167 | 0.177 | 0.112 | 0.115 | 0.696 | 0.182 | 0.159 | ||
| 0.495 | 0.508 | 0.164 | 0.181 | 0.162 | 0.166 | 0.677 | 0.252 | 0.147 | ||
| 100 | 0.198 | 0.229 | 0.049 | 0.053 | 0.032 | 0.039 | 1.388 | 0.099 | 0.081 | |
| 0.338 | 0.379 | 0.042 | 0.055 | 0.029 | 0.029 | 2.324 | 0.102 | 0.078 | ||
| 0.944 | 0.445 | 0.348 | 0.057 | 0.021 | 0.019 | 2.478 | 0.100 | 0.044 | ||
| 0.144 | 0.175 | 0.062 | 0.065 | 0.057 | 0.063 | 1.410 | 0.104 | 0.066 | ||
| 0.152 | 0.196 | 0.044 | 0.049 | 0.029 | 0.034 | 1.261 | 0.099 | 0.065 | ||
| 0.305 | 0.373 | 0.065 | 0.079 | 0.014 | 0.017 | 1.982 | 0.122 | 0.036 | ||
| 0.417 | 0.427 | 0.180 | 0.185 | 0.146 | 0.160 | 0.471 | 0.192 | 0.147 | ||
| 0.473 | 0.483 | 0.154 | 0.169 | 0.111 | 0.122 | 0.435 | 0.218 | 0.140 | ||
| 0.508 | 0.520 | 0.128 | 0.138 | 0.046 | 0.058 | 0.576 | 0.163 | 0.100 | ||
| 0.481 | 0.493 | 0.113 | 0.120 | 0.054 | 0.062 | 0.535 | 0.131 | 0.130 | ||
| 150 | 0.183 | 0.244 | 0.039 | 0.045 | 0.022 | 0.027 | 1.280 | 0.076 | 0.069 | |
| 0.320 | 0.353 | 0.040 | 0.045 | 0.027 | 0.031 | 1.816 | 0.087 | 0.044 | ||
| 0.873 | 0.428 | 0.266 | 0.041 | 0.007 | 0.013 | 2.199 | 0.082 | 0.038 | ||
| 0.138 | 0.173 | 0.039 | 0.046 | 0.013 | 0.015 | 1.004 | 0.100 | 0.053 | ||
| 0.147 | 0.186 | 0.037 | 0.048 | 0.017 | 0.020 | 1.105 | 0.061 | 0.056 | ||
| 0.301 | 0.362 | 0.047 | 0.057 | 0.013 | 0.015 | 1.860 | 0.112 | 0.034 | ||
| 0.407 | 0.420 | 0.090 | 0.092 | 0.064 | 0.065 | 0.441 | 0.078 | 0.067 | ||
| 0.467 | 0.481 | 0.141 | 0.143 | 0.070 | 0.080 | 0.427 | 0.119 | 0.098 | ||
| 0.507 | 0.517 | 0.057 | 0.065 | 0.040 | 0.042 | 0.543 | 0.093 | 0.089 | ||
| 0.479 | 0.492 | 0.075 | 0.081 | 0.046 | 0.052 | 0.525 | 0.125 | 0.096 | ||
| 200 | 0.182 | 0.236 | 0.028 | 0.028 | 0.019 | 0.021 | 1.016 | 0.042 | 0.019 | |
| 0.318 | 0.352 | 0.031 | 0.036 | 0.016 | 0.056 | 1.757 | 0.084 | 0.034 | ||
| 0.382 | 0.399 | 0.038 | 0.026 | 0.003 | 0.011 | 1.866 | 0.077 | 0.025 | ||
| 0.128 | 0.150 | 0.028 | 0.033 | 0.010 | 0.011 | 0.857 | 0.061 | 0.026 | ||
| 0.132 | 0.153 | 0.013 | 0.018 | 0.012 | 0.013 | 0.920 | 0.050 | 0.025 | ||
| 0.285 | 0.354 | 0.028 | 0.030 | 0.012 | 0.014 | 1.625 | 0.070 | 0.032 | ||
| 0.402 | 0.412 | 0.061 | 0.063 | 0.019 | 0.026 | 0.439 | 0.044 | 0.038 | ||
| 0.464 | 0.474 | 0.036 | 0.040 | 0.005 | 0.006 | 0.386 | 0.055 | 0.021 | ||
| 0.506 | 0.516 | 0.049 | 0.049 | 0.038 | 0.041 | 0.511 | 0.059 | 0.010 | ||
| 0.466 | 0.476 | 0.071 | 0.073 | 0.022 | 0.025 | 0.510 | 0.056 | 0.051 | ||
| 𝒏 | Par. | MLE | MCMC.1 | MCMC.2 | ACI | BCI.P1 | BCI.P2 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| MAB | RMSE | MAB | RMSE | MAB | RMSE | |||||
| 50 | 0.250 | 0.412 | 0.072 | 0.077 | 0.056 | 0.071 | 2.545 | 0.157 | 0.087 | |
| 0.374 | 0.553 | 0.085 | 0.093 | 0.078 | 0.081 | 3.738 | 0.143 | 0.077 | ||
| 0.996 | 0.352 | 0.277 | 0.059 | 0.085 | 0.051 | 2.793 | 0.104 | 0.060 | ||
| 0.207 | 0.312 | 0.078 | 0.083 | 0.074 | 0.080 | 2.369 | 0.205 | 0.071 | ||
| 0.219 | 0.347 | 0.093 | 0.099 | 0.077 | 0.090 | 2.621 | 0.139 | 0.108 | ||
| 0.281 | 0.354 | 0.060 | 0.072 | 0.022 | 0.027 | 2.786 | 0.132 | 0.068 | ||
| 0.175 | 0.211 | 0.160 | 0.168 | 0.060 | 0.072 | 0.648 | 0.236 | 0.113 | ||
| 0.218 | 0.247 | 0.099 | 0.101 | 0.049 | 0.061 | 0.541 | 0.137 | 0.120 | ||
| 0.345 | 0.363 | 0.169 | 0.176 | 0.081 | 0.093 | 0.758 | 0.191 | 0.130 | ||
| 0.261 | 0.280 | 0.234 | 0.247 | 0.032 | 0.043 | 0.679 | 0.241 | 0.107 | ||
| 100 | 0.247 | 0.347 | 0.060 | 0.064 | 0.040 | 0.045 | 1.836 | 0.104 | 0.085 | |
| 0.326 | 0.407 | 0.050 | 0.056 | 0.034 | 0.037 | 2.958 | 0.117 | 0.074 | ||
| 0.985 | 0.327 | 0.260 | 0.050 | 0.050 | 0.021 | 2.195 | 0.098 | 0.055 | ||
| 0.201 | 0.284 | 0.065 | 0.076 | 0.043 | 0.050 | 1.818 | 0.154 | 0.063 | ||
| 0.211 | 0.330 | 0.062 | 0.069 | 0.031 | 0.037 | 2.247 | 0.110 | 0.066 | ||
| 0.246 | 0.314 | 0.050 | 0.060 | 0.018 | 0.025 | 2.147 | 0.125 | 0.043 | ||
| 0.159 | 0.190 | 0.144 | 0.159 | 0.031 | 0.041 | 0.460 | 0.163 | 0.096 | ||
| 0.214 | 0.230 | 0.061 | 0.070 | 0.020 | 0.024 | 0.459 | 0.130 | 0.064 | ||
| 0.344 | 0.361 | 0.137 | 0.148 | 0.038 | 0.046 | 0.527 | 0.180 | 0.125 | ||
| 0.258 | 0.276 | 0.136 | 0.146 | 0.031 | 0.037 | 0.575 | 0.208 | 0.097 | ||
| 150 | 0.218 | 0.329 | 0.046 | 0.047 | 0.025 | 0.029 | 1.701 | 0.101 | 0.083 | |
| 0.311 | 0.414 | 0.036 | 0.045 | 0.019 | 0.023 | 2.623 | 0.089 | 0.070 | ||
| 0.974 | 0.304 | 0.241 | 0.041 | 0.013 | 0.012 | 1.872 | 0.094 | 0.039 | ||
| 0.172 | 0.227 | 0.063 | 0.067 | 0.013 | 0.016 | 1.167 | 0.098 | 0.057 | ||
| 0.203 | 0.295 | 0.040 | 0.045 | 0.016 | 0.019 | 1.628 | 0.094 | 0.058 | ||
| 0.236 | 0.301 | 0.037 | 0.041 | 0.013 | 0.014 | 1.600 | 0.096 | 0.041 | ||
| 0.157 | 0.187 | 0.086 | 0.089 | 0.029 | 0.033 | 0.430 | 0.100 | 0.082 | ||
| 0.209 | 0.225 | 0.034 | 0.042 | 0.012 | 0.016 | 0.423 | 0.066 | 0.054 | ||
| 0.337 | 0.351 | 0.110 | 0.117 | 0.024 | 0.028 | 0.487 | 0.140 | 0.058 | ||
| 0.254 | 0.268 | 0.103 | 0.116 | 0.030 | 0.032 | 0.490 | 0.179 | 0.081 | ||
| 200 | 0.159 | 0.201 | 0.038 | 0.045 | 0.010 | 0.012 | 1.233 | 0.048 | 0.039 | |
| 0.268 | 0.314 | 0.031 | 0.037 | 0.014 | 0.019 | 2.081 | 0.084 | 0.042 | ||
| 0.922 | 0.271 | 0.184 | 0.029 | 0.010 | 0.010 | 1.570 | 0.080 | 0.036 | ||
| 0.148 | 0.202 | 0.029 | 0.034 | 0.011 | 0.012 | 1.089 | 0.065 | 0.050 | ||
| 0.156 | 0.209 | 0.022 | 0.025 | 0.011 | 0.014 | 1.269 | 0.049 | 0.041 | ||
| 0.226 | 0.281 | 0.029 | 0.033 | 0.011 | 0.012 | 1.571 | 0.071 | 0.037 | ||
| 0.149 | 0.175 | 0.048 | 0.055 | 0.023 | 0.029 | 0.363 | 0.092 | 0.052 | ||
| 0.200 | 0.219 | 0.029 | 0.035 | 0.011 | 0.015 | 0.371 | 0.061 | 0.044 | ||
| 0.333 | 0.343 | 0.084 | 0.094 | 0.018 | 0.020 | 0.429 | 0.132 | 0.034 | ||
| 0.252 | 0.265 | 0.074 | 0.082 | 0.018 | 0.024 | 0.449 | 0.176 | 0.042 | ||
| Motor | Failure Times | MLE(SE) | KS | ||
|---|---|---|---|---|---|
| Statistic | -Value | ||||
| X | 84, 88, 102, 139, 148, 156, 207, 212, 213, 220, 220, 235, 243, 245, 250, 257, 263, 300 | 39.044 (29.274) | 0.0099 (0.0016) | 0.2829 | 0.112 |
| Y | 65, 121, 123, 148, 150, 156, 172, 192, 202, 212, 214, 220, 248, 265, 275, 300, 330, 350 | 47.906 (38.493) | 0.0096 (0.0015) | 0.2289 | 0.260 |
| Method | |||||
|---|---|---|---|---|---|
| MLE (SE) | 3256.43 (0.0056) | 0.01312 (0.0014) | 3112.19 (8.3910) | 0.01262 (0.0014) | −0.30736 (0.2181) |
| Bayes (SE) | 3256.41 (0.0032) | 0.01263 (0.0001) | 3112.17 (0.0031) | 0.01212 (0.0001) | −0.30733 (0.0001) |
| Method | |||||
|---|---|---|---|---|---|
| ACI (length) | (3256.4,3256.4) (0.0218) | (0.0103,0.0160) (0.0057) | (3095.8,3128.6) (32.894) | (0.0099,0.0154) (0.0055) | (−0.7347,0.1200) (0.8547) |
| BCI (length) | (3255.4,3257.4) (1.9753) | (0.0118,0.0136) (0.0018) | (3111.2,3113.2) (1.9131) | (0.0112,0.0131) (0.0019) | (−0.3083,−0.3064) (0.0019) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alotaibi, R.; Nassar, M.; Ghosh, I.; Rezk, H.; Elshahhat, A. Inferences of a Mixture Bivariate Alpha Power Exponential Model with Engineering Application. Axioms 2022, 11, 459. https://doi.org/10.3390/axioms11090459
Alotaibi R, Nassar M, Ghosh I, Rezk H, Elshahhat A. Inferences of a Mixture Bivariate Alpha Power Exponential Model with Engineering Application. Axioms. 2022; 11(9):459. https://doi.org/10.3390/axioms11090459
Chicago/Turabian StyleAlotaibi, Refah, Mazen Nassar, Indranil Ghosh, Hoda Rezk, and Ahmed Elshahhat. 2022. "Inferences of a Mixture Bivariate Alpha Power Exponential Model with Engineering Application" Axioms 11, no. 9: 459. https://doi.org/10.3390/axioms11090459
APA StyleAlotaibi, R., Nassar, M., Ghosh, I., Rezk, H., & Elshahhat, A. (2022). Inferences of a Mixture Bivariate Alpha Power Exponential Model with Engineering Application. Axioms, 11(9), 459. https://doi.org/10.3390/axioms11090459







