Dynamical Analysis and Generalized Synchronization of a Novel Fractional-Order Hyperchaotic System with Hidden Attractor
Abstract
:1. Introduction
2. Dynamic Analysis of Fractional-Order Hyperchaotic System with Non-Equilibrium
2.1. System Description
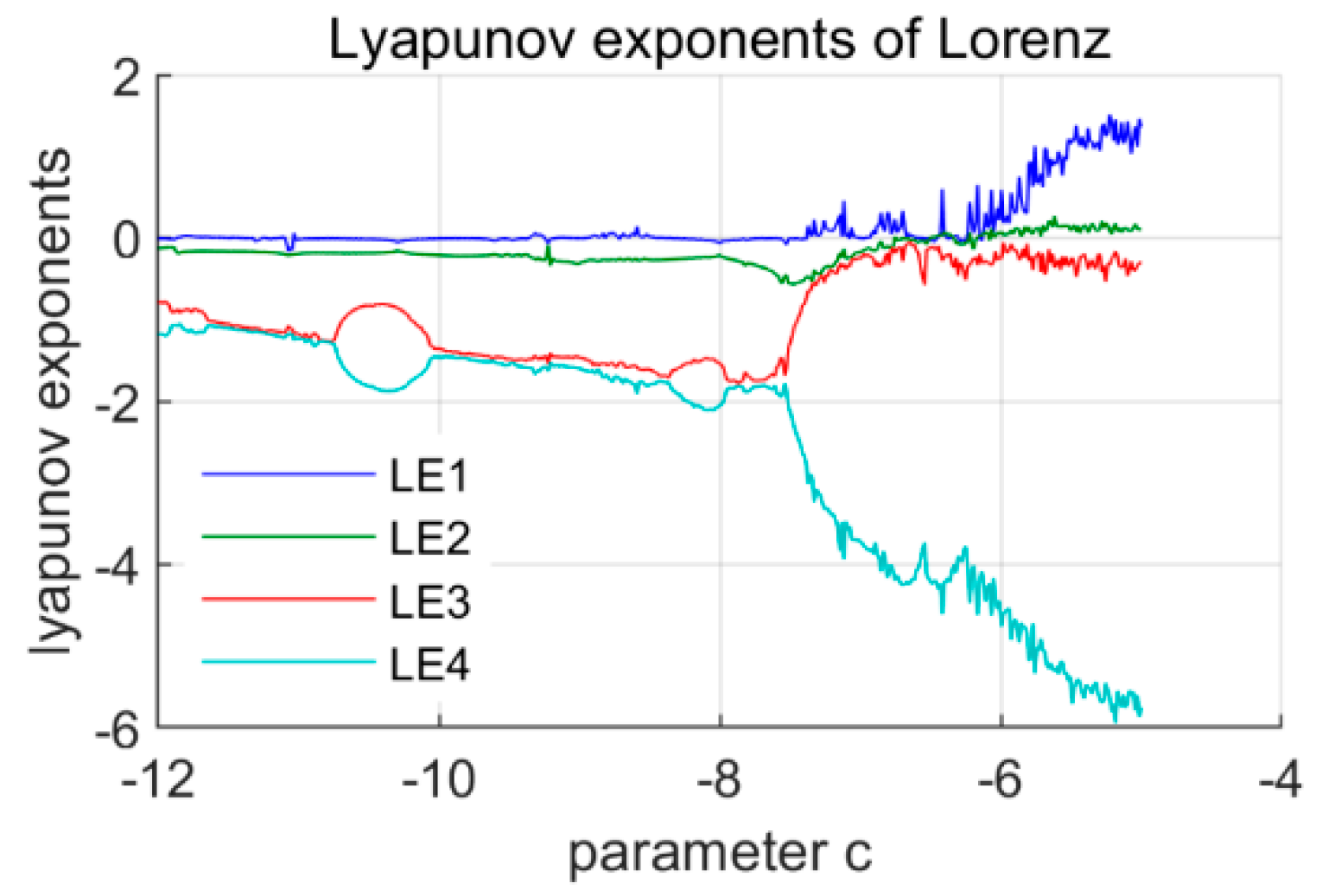
2.2. Dynamics of Non-Equilibrium Fractional-Order Hyperchaotic System
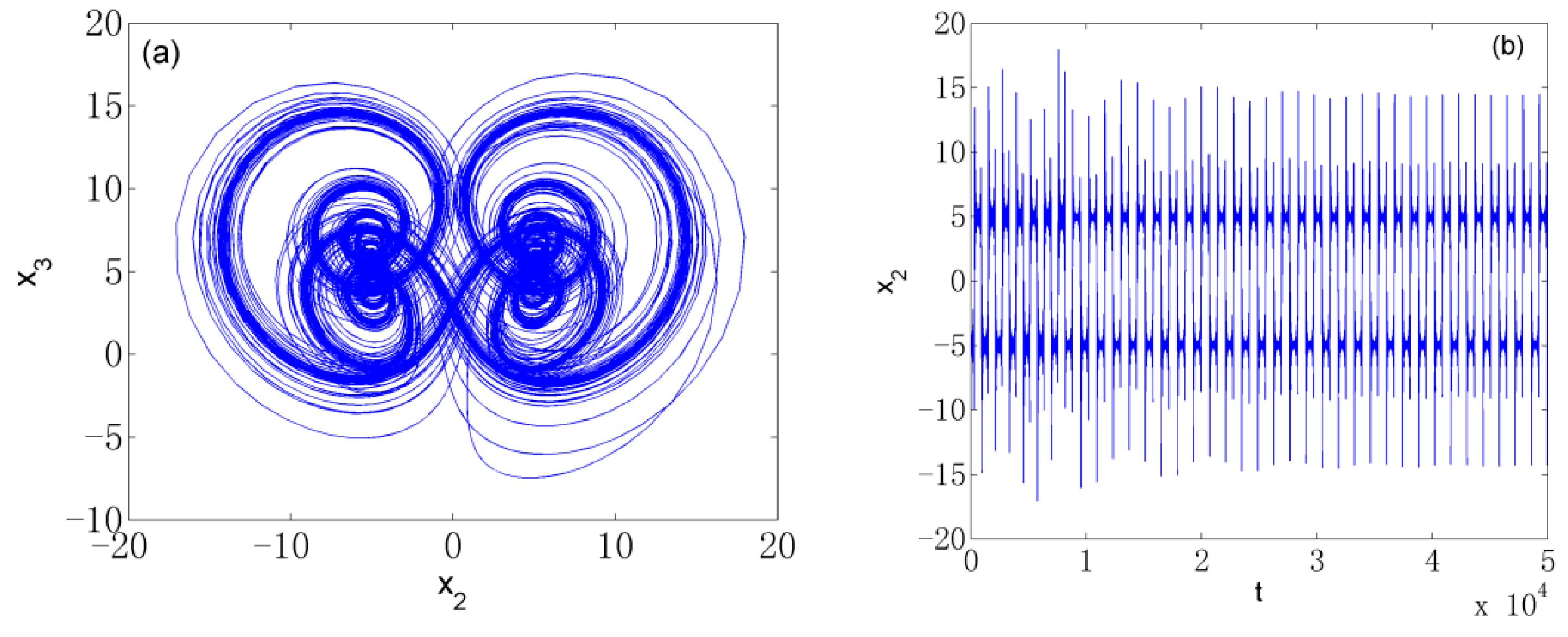
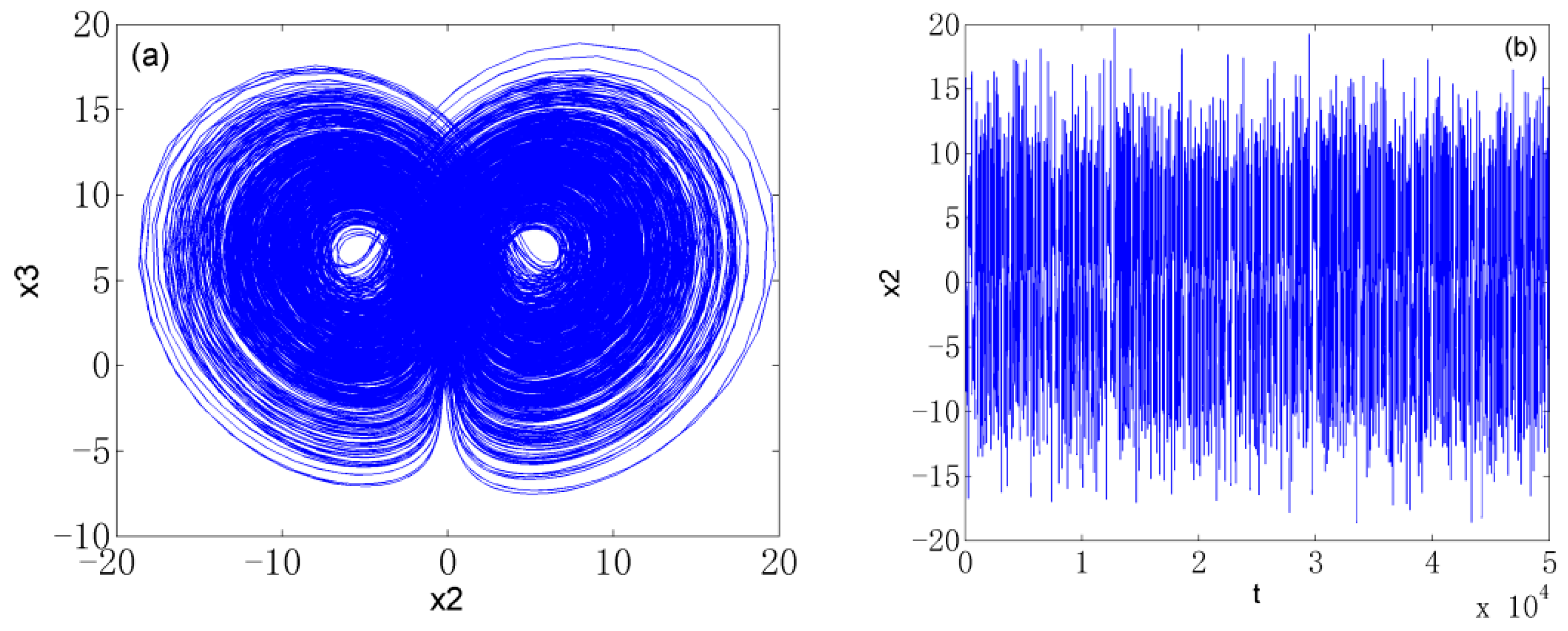
2.2.1. Hyperchaotic Attractor
2.2.2. Chaotic Attractor
2.2.3. Limit Cycle
3. Generalized Synchronization of Fractional-Order System
3.1. Generalized Synchronization Scheme
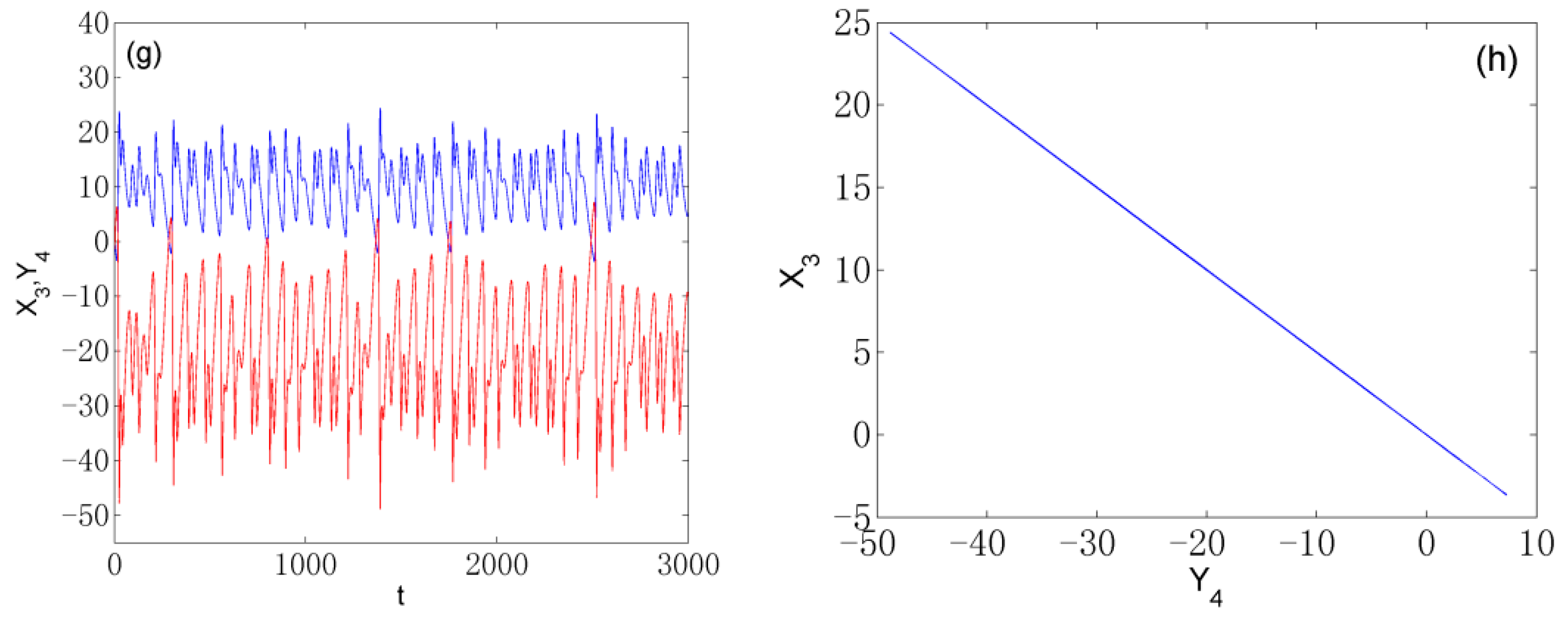
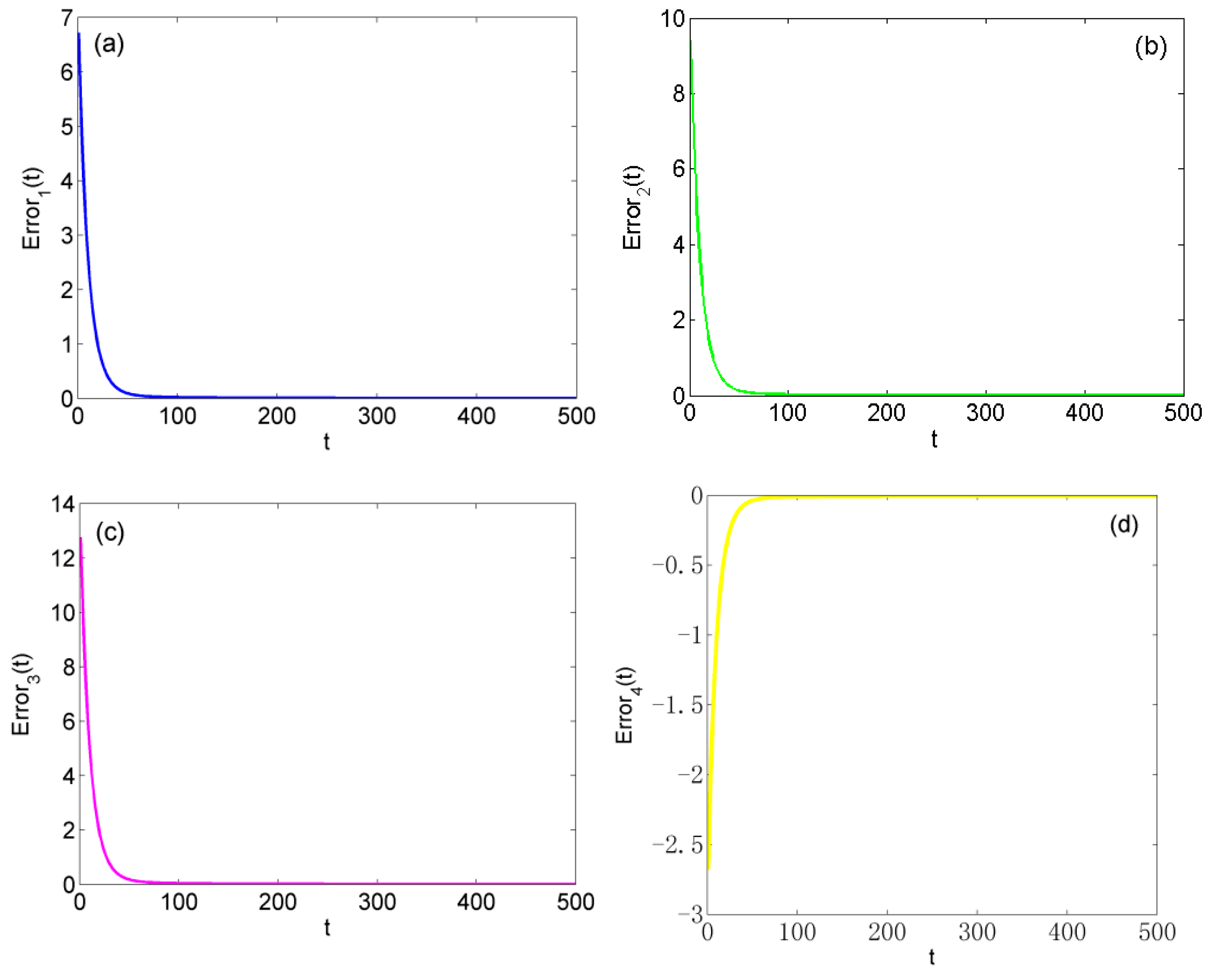
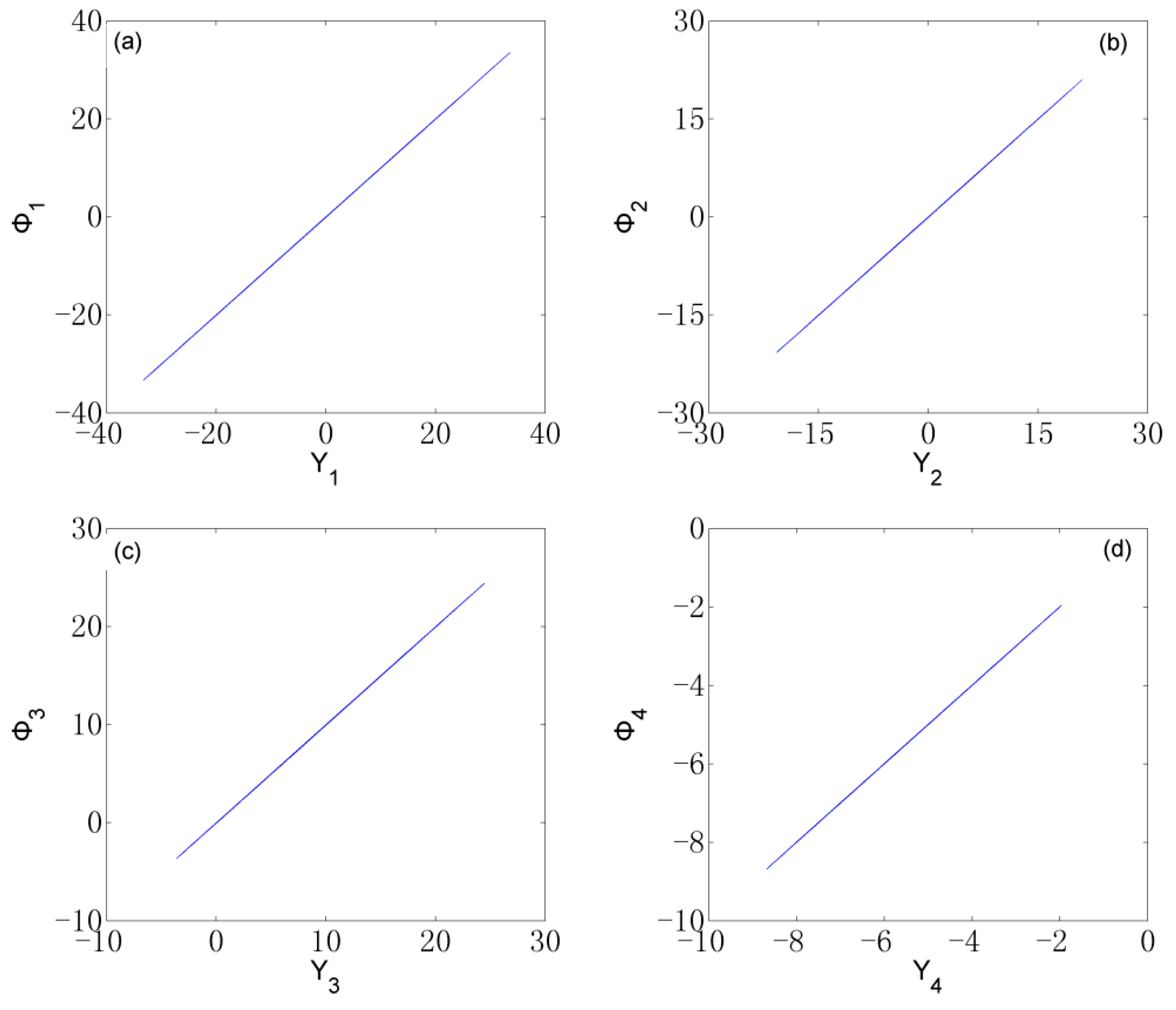
3.2. Generalized Synchronization Simulation
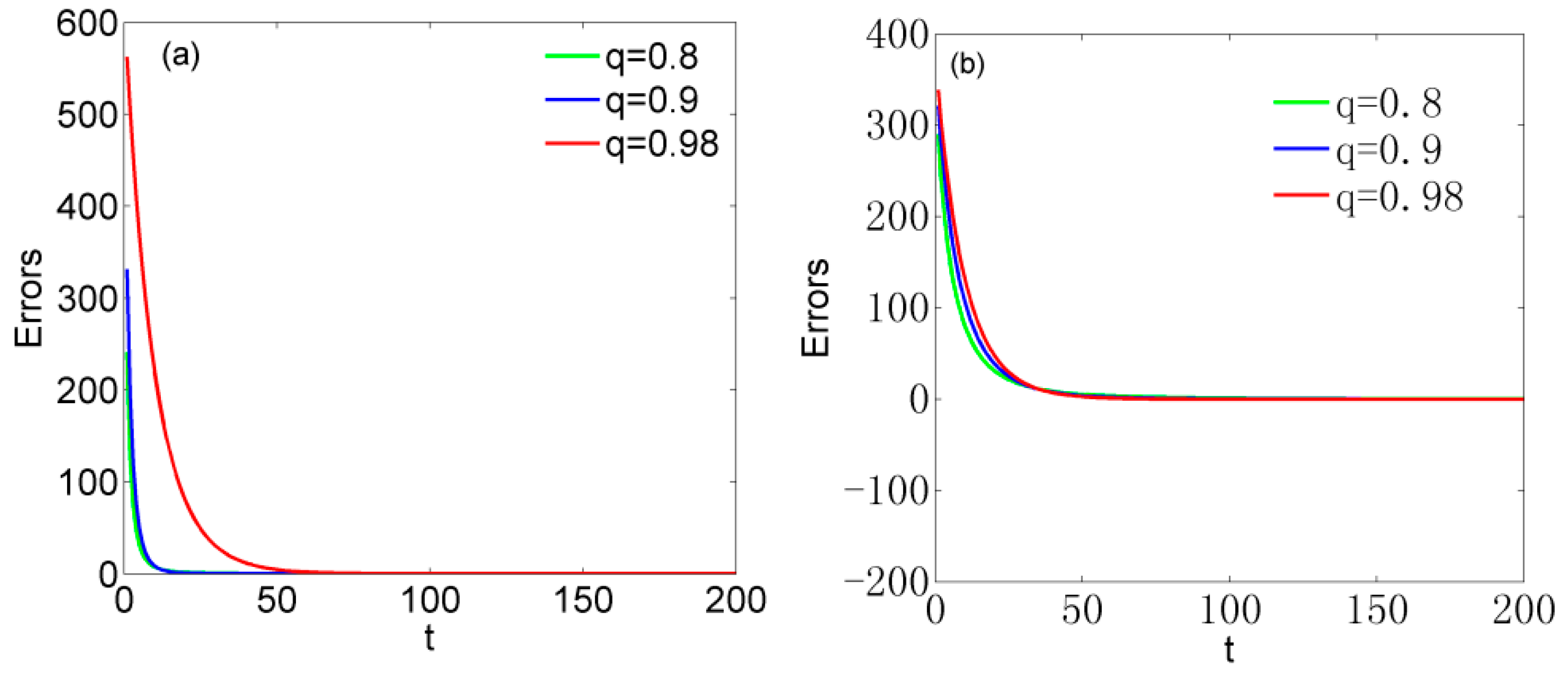
3.3. Performance Analysis of Generalized Synchronization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, Y.; Sun, K.; He, S.; Zhang, L. Dynamics of a fractional-order simplified unified system based on the Adomian decomposition method. Eur. Phys. J. Plus 2016, 131, 186. [Google Scholar] [CrossRef]
- Lan, R.; He, J.; Wang, S. Integrated chaotic systems for image encryption. Signal Process 2018, 147, 133–145. [Google Scholar] [CrossRef]
- Sun, J.; Li, C.; Lu, T.; Akgul, A.; Min, F. A memristive chaotic system with hypermultistability and its application in image encryption. IEEE Access 2020, 8, f89–f98. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Yang, F.; Yan, H. A fractional-order hopfield neural network chaotic system and its circuit realization. Eur. Phys. J. Plus 2020, 135, 100. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Inc, M.; Yusuf, A. On three-dimensional variable order time fractional chaotic system with nonsingular kernel. Chaos Solitons Fractals 2020, 133, 109628. [Google Scholar] [CrossRef]
- Grigorenko, I.; Grigorenko, E. Chaotic dynamics of the fractional Lorenz system. Phys. Rev. Lett. 2003, 91, 34101. [Google Scholar] [CrossRef]
- Cafagna, D.; Grassi, G. Bifurcation and chaos in the fractional-order Chen system via a time-domain approach. Int. J. Bifurc. Chaos 2008, 18, 1845–1863. [Google Scholar] [CrossRef]
- Cafagna, D.; Grassi, G. Hyperchaos in the fractional-order Rössler system with lowest-order. Int. J. Bifurc. Chaos 2009, 19, 339–347. [Google Scholar] [CrossRef]
- Deng, W.H.; Li, C.P. Chaos synchronization of the fractional Lü system. Phys. A 2005, 353, 61–72. [Google Scholar] [CrossRef]
- Gao, Y.; Liang, C.; Wu, Q.; Yuan, H. A new fractional-order hyperchaotic system and its modified projective synchronization. Chaos Solitons Fractals Interdiscip. J. Nonlinear Sci. Nonequilibrium Complex Phenom. 2015, 76, 190–204. [Google Scholar] [CrossRef]
- Rahman, Z.A.S.A.; Jasim, B.H.; Al-Yasir, Y.I.A.; Hu, Y.F.; Abd-Alhameed, R.A.; Alhasnawi, B.N. A new fractional-order chaotic system with its analysis, synchronization, and circuit realization for secure communication applications. Mathematics 2021, 9, 2593. [Google Scholar] [CrossRef]
- Makhlouf, A.B. Partial practical stability for fractional-order nonlinear systems. Math. Methods Appl. Sci. 2022, 45, 5135–5148. [Google Scholar] [CrossRef]
- Ji’E, M.; Yan, D.; Wang, L.; Duan, S. Hidden attractor and multistability in a novel memristor-based system without symmetry. Int. J. Bifurc. Chaos 2021, 31, 2150168. [Google Scholar] [CrossRef]
- Natiq, H.; Said, M.R.M.; Ariffin, M.R.K.; He, S.; Rondoni, L.; Banerjee, S. Self-excited and hidden attractors in a novel chaotic system with complicated multistability. Eur. Phys. J. Plus 2018, 133, 557. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V.; Mokaev, T.N. Homoclinic orbits, and self-excited and hidden attractors in a lorenz-like system describing convective fluid motion. Eur. Phys. J. Spec. Top. 2015, 224, 1421–1458. [Google Scholar] [CrossRef] [Green Version]
- Vaidyanathan, S.; Sambas, A.; Azar, A.T.; Rana, K.; Kumar, V. A new 5-d hyperchaotic four-wing system with multistability and hidden attractor, its backstepping control, and circuit simulation. Backstepping Control. Nonlinear Dyn. Syst. 2021, Chapter 6, 115–138. [Google Scholar]
- Jia, H.; Shi, W.; Wang, L.; Qi, G. Energy analysis of sprott-a system and generation of a new hamiltonian conservative chaotic system with coexisting hidden attractors. Chaos Solitons Fractals 2020, 133, 109635. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Zhang, F.; Leng, S. Hidden chaotic attractors and synchronization for a new fractional-order chaotic system. J. Comput. Nonlinear Dyn. 2019, 14, 081010. [Google Scholar] [CrossRef]
- Sprott, J.C. A proposed standard for the publication of new chaotic systems. Int. J. Bifurc. Chaos 2011, 21, 2391. [Google Scholar] [CrossRef] [Green Version]
- Cafagna, D.; Grassi, G. Fractional-order systems without equilibria: The first example of hyperchaos and its application to synchronization. Chin. Phys. B 2015, 24, 224–232. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.; Li, Z.; Wang, M.; Le, X. Generating one to four-wing hidden attractors in a novel 4d no-equilibrium chaotic system with extreme multistability. Chaos 2018, 28, 013113. [Google Scholar] [CrossRef]
- Zhou, P.; Huang, K. A new 4-D non-equilibrium fractional-order chaotic system and its circuit implementation. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2005–2011. [Google Scholar] [CrossRef]
- Liu, L.; Du, C.; Zhang, X.; Li, J.; Shi, S. Dynamics and entropy analysis for a new 4-d hyperchaotic system with coexisting hidden attractors. Entropy 2019, 21, 287. [Google Scholar] [CrossRef] [Green Version]
- Zhou, P.; Bai, R.J. The adaptive synchronization of fractional-order chaotic system with fractional-order (1 < q < 2) via linear parameter update law. Nonlinear Dyn. 2015, 80, 753–765. [Google Scholar]
- Agrawal, S.K.; Das, S. Projective synchronization between different fractional-order hyperchaotic systems with uncertain parameters using proposed modified adaptive projective synchronization technique. Math. Methods Appl. Sci. 2014, 37, 1232–1239. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E. Lag synchronization of hyperchaotic complex nonlinear systems. Nonlinear Dyn. 2012, 67, 1613–1622. [Google Scholar] [CrossRef]
- Yadav, V.K.; Shukla, V.K.; Das, S. Exponential synchronization of fractional-order complex chaotic systems and its application. Chaos Solitons Fractals 2021, 147, 110937. [Google Scholar] [CrossRef]
- Bhalekar, S.; Daftardar-Gejji, V. Synchronization of different fractional order chaotic systems using active control. Commun. Nonlinear Sci. Numer. Simul. 2013, 15, 3536–3546. [Google Scholar] [CrossRef]
- Taheri, M.; Zhang, C.; Berardehi, Z.R.; Chen, Y.; Roohi, M. No-chatter model-free sliding mode control for synchronization of chaotic fractional-order systems with application in image encryption. Multimed. Tools Appl. 2022, 81, 24167–24197. [Google Scholar] [CrossRef]
- Gammoudi, I.E.; Feki, M. Synchronization of integer order and fractional order Chua’s systems using robust observer. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 625–638. [Google Scholar] [CrossRef]
- Jin-Man, H.; Fang-Qi, C. A new fractional order hyperchaotic rabinovich system and its dynamical behaviors. Int. J. Non-Linear Mech. 2017, 95, 73–81. [Google Scholar]
- El-Sayed, A.; Nour, H.M.; Elsaid, A.; Matouk, A.E.; Elsonbaty, A. Dynamical behaviors, circuit realization, chaos control and synchronization of a new fractional order hyperchaotic system. Appl. Math. Model. 2016, 40, 3516–3534. [Google Scholar] [CrossRef]
- Li, K.; Cao, J.; He, J.M. Hidden hyperchaotic attractors in a new 4d fractional order system and its synchronization. Chaos 2020, 30, 033129. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.C.; Liu, C.X.; Yan, W. Dynamic analysis and finite time synchronization of a fractional-order chaotic system with hidden attractors. Acta Phys. Sin.-Chin. Ed. 2018, 67, 050502. [Google Scholar] [CrossRef]
- Wei, Z.C.; Wang, R.R.; Liu, A.P. A new finding of the existence of hidden hyperchaotic attractors with no equilibria. Math. Comput. Simul. 2014, 100, 13–23. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, L.; Shi, X.; Xu, M. Dynamical Analysis and Generalized Synchronization of a Novel Fractional-Order Hyperchaotic System with Hidden Attractor. Axioms 2023, 12, 6. https://doi.org/10.3390/axioms12010006
Xin L, Shi X, Xu M. Dynamical Analysis and Generalized Synchronization of a Novel Fractional-Order Hyperchaotic System with Hidden Attractor. Axioms. 2023; 12(1):6. https://doi.org/10.3390/axioms12010006
Chicago/Turabian StyleXin, Li, Xuerong Shi, and Mingjie Xu. 2023. "Dynamical Analysis and Generalized Synchronization of a Novel Fractional-Order Hyperchaotic System with Hidden Attractor" Axioms 12, no. 1: 6. https://doi.org/10.3390/axioms12010006
APA StyleXin, L., Shi, X., & Xu, M. (2023). Dynamical Analysis and Generalized Synchronization of a Novel Fractional-Order Hyperchaotic System with Hidden Attractor. Axioms, 12(1), 6. https://doi.org/10.3390/axioms12010006





