Nonlinear Dynamic Behaviors of the (3+1)-Dimensional B-Type Kadomtsev—Petviashvili Equation in Fluid Mechanics
Abstract
:1. Introduction
2. Cole—Hopf Transform and the Exact Solutions
2.1. The Multi-Waves Complexiton Solutions
- Case 1:
- Case 2:
- Case 3:
- Case 4:
- Case 5:
- Case 6:
2.2. The Multi-Wave Solutions
- Case 1:
- Case 2:
2.3. The Periodic Lump Solutions
- Case 1:
- Case 2:
3. The Traveling Wave Solutions
- Case 1:
- Case 2:
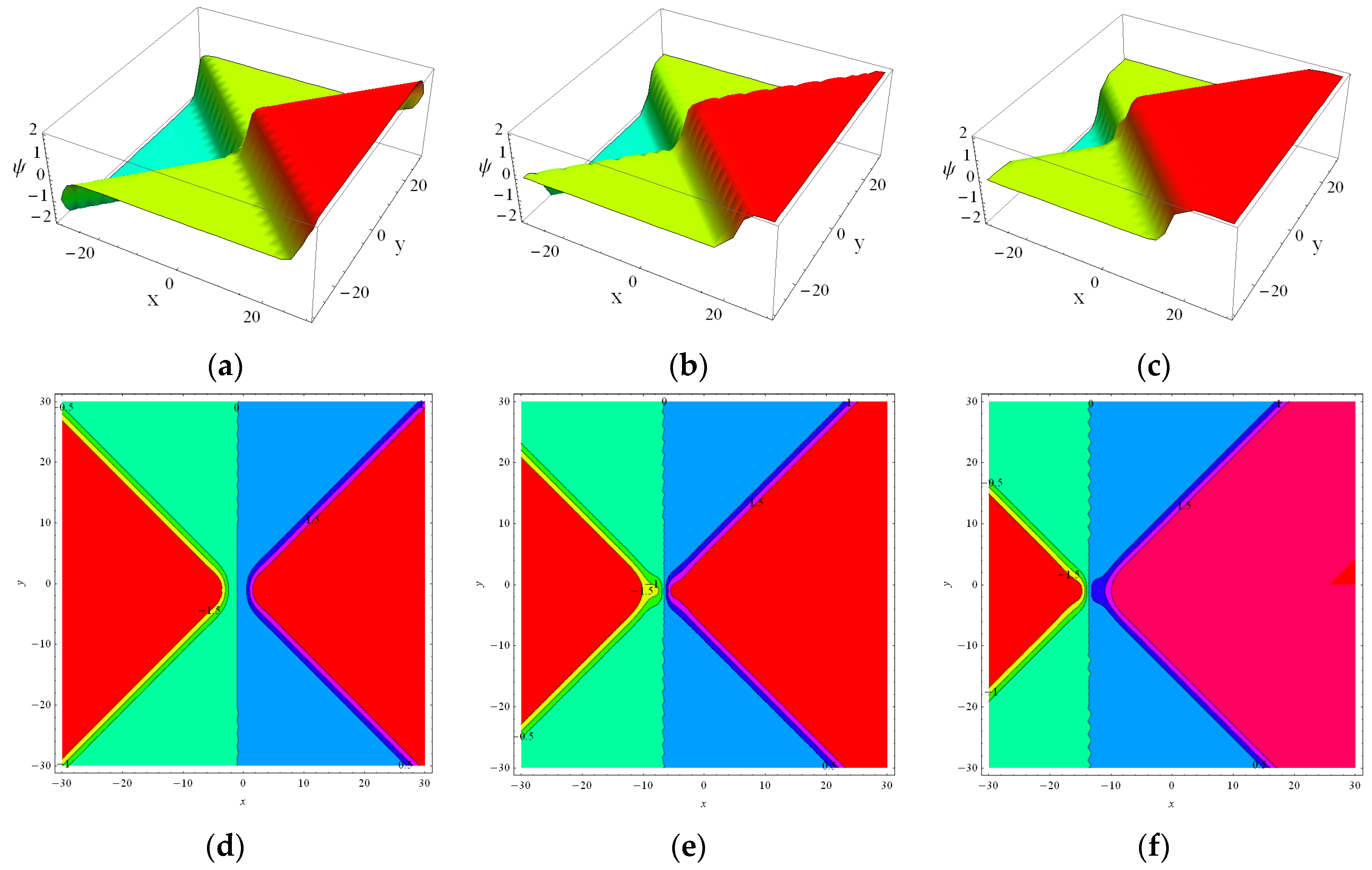
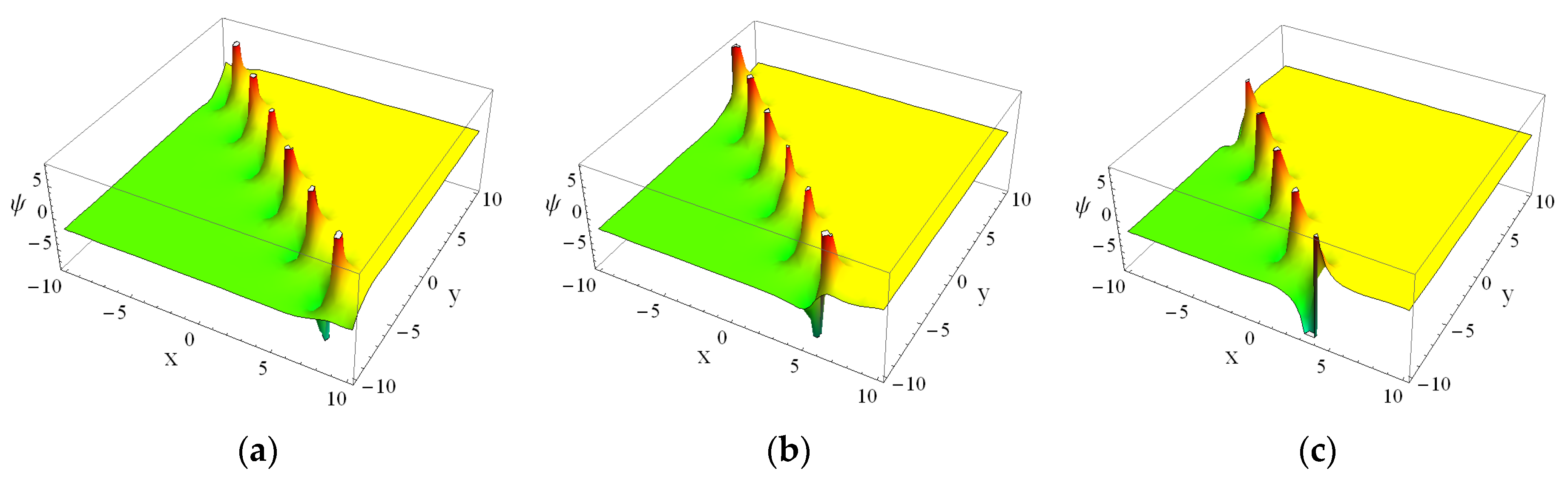
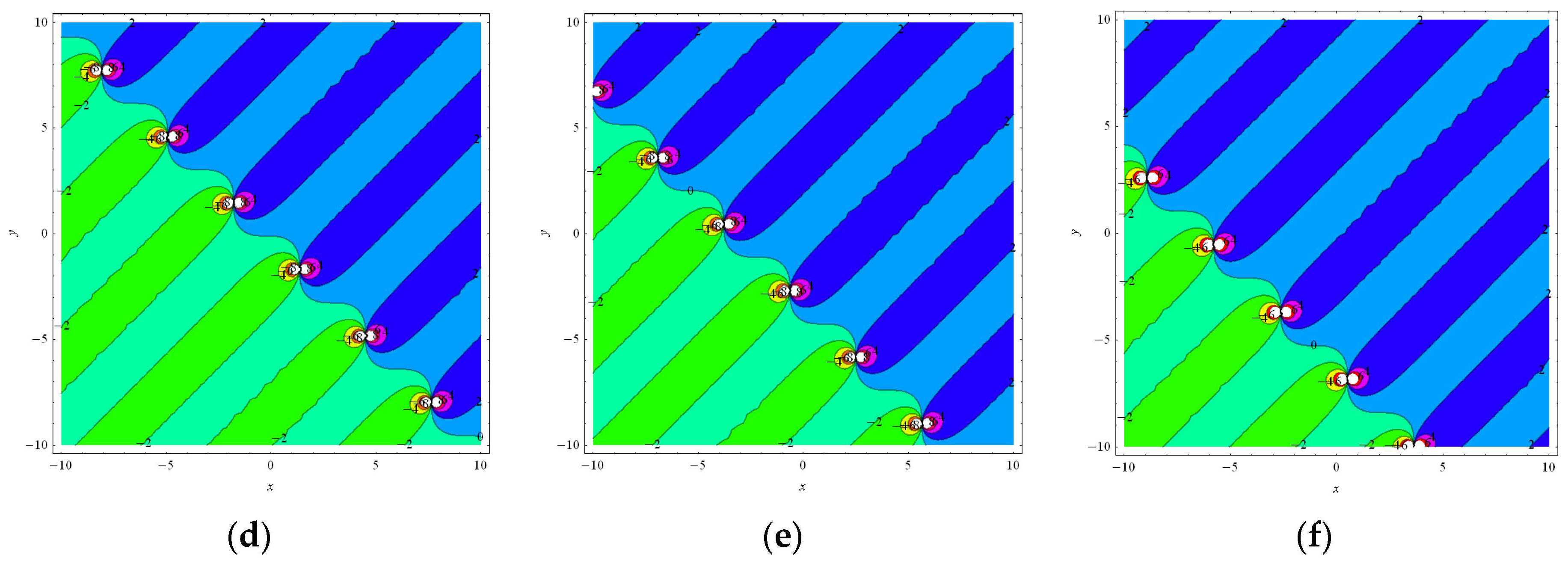
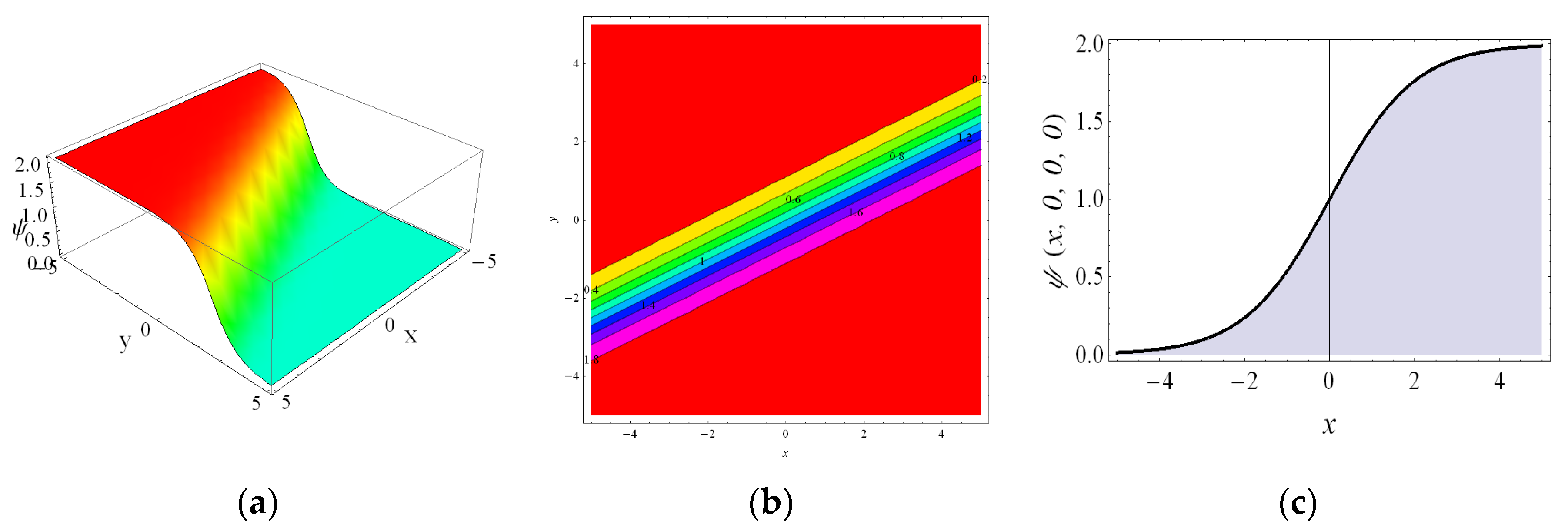
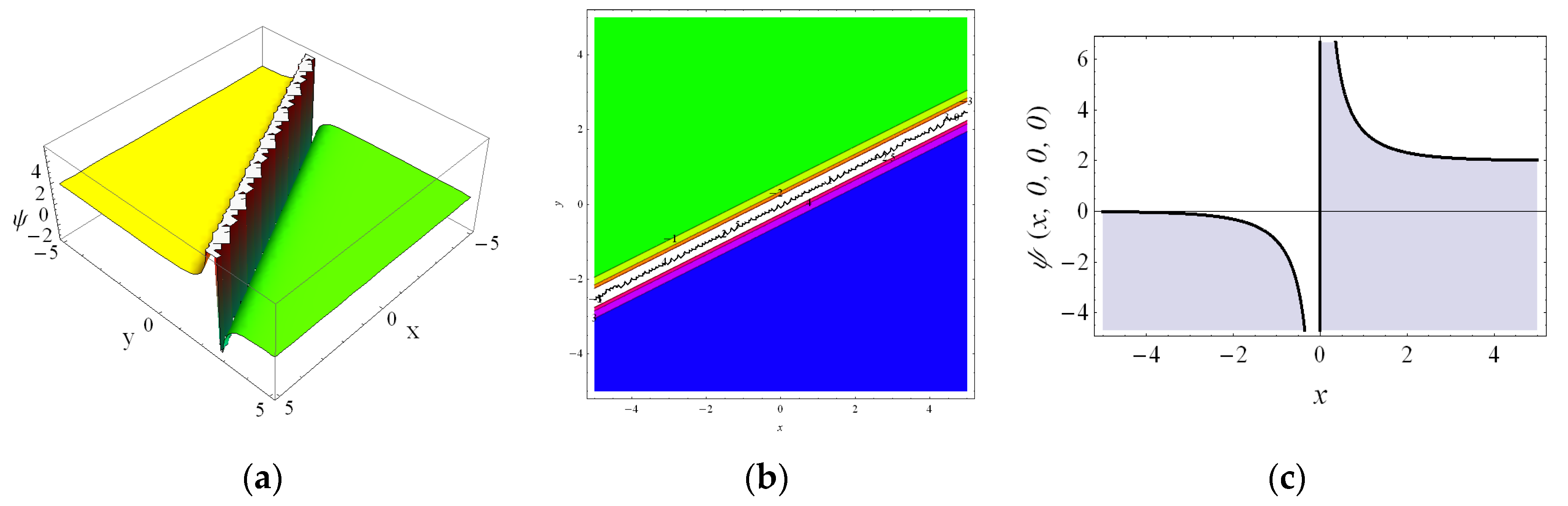
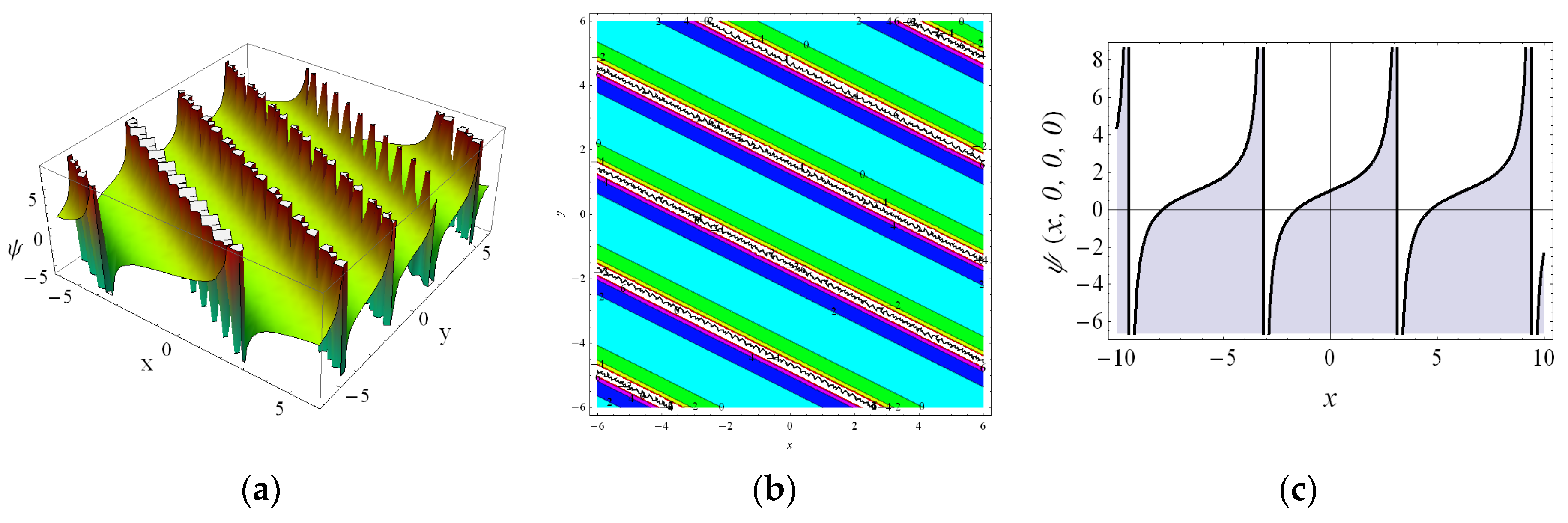
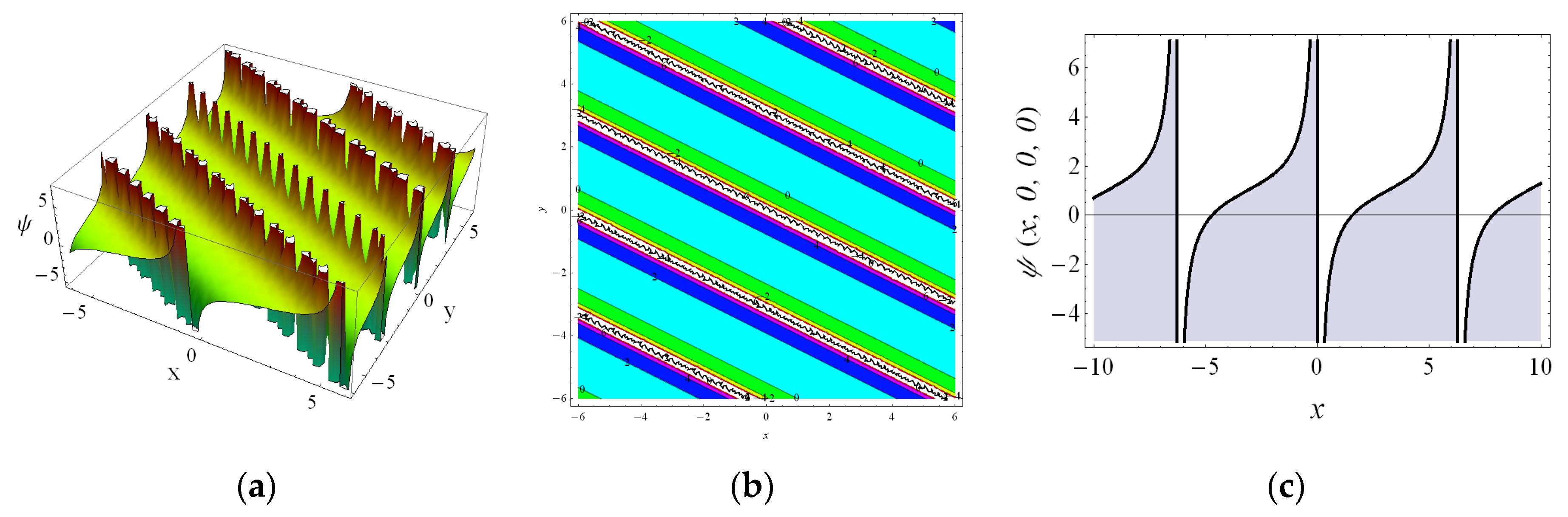
4. The Numerical Results and Physical Interpretations
5. Conclusions and Future Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jhangeer, A.; Hussain, A.; Junaid-U-Rehman, M.; Baleanu, D.; Riaz, M.B. Quasi-periodic, chaotic and travelling wave structures of modified Gardner equation. Chaos Solitons Fractals 2021, 143, 110578. [Google Scholar] [CrossRef]
- Wang, K.L. New perspective to the fractal Konopelchenko-Dubrovsky equations with M-truncated fractional derivative. Int. J. Geom. Methods Mod. Phys. 2023, 2023, 2350072. [Google Scholar] [CrossRef]
- Wang, K.J.; Si, J. On the non-differentiable exact solutions of the (2+1)-dimensional local fractional breaking soliton equation on Cantor sets. Math. Methods Appl. Sci. 2023, 46, 1456–1465. [Google Scholar] [CrossRef]
- Wang, K.L. Exact travelling wave solution for the local fractional Camassa-Holm-Kadomtsev-Petviashvili equation. Alex. Eng. J. 2022, 63, 371–376. [Google Scholar] [CrossRef]
- Yang, Z.; Cheng, D.; Cong, G.; Jin, D.; Borjalilou, V. Dual-phase-lag thermoelastic damping in nonlocal rectangular nanoplates. Waves Random Complex Media 2021, 1–20. [Google Scholar] [CrossRef]
- Wang, K.J.; Jing, S. Dynamic properties of the attachment oscillator arising in the nanophysics. Open Phys. 2023. [Google Scholar] [CrossRef]
- Ma, Y.X.; Tian, B.; Qu, Q.X.; Yang, D.-Y.; Chen, Y.-Q. Painlevé analysis, Bäcklund transformations and traveling-wave solutions for a (3+1)-dimensional generalized Kadomtsev-Petviashvili equation in a fluid. Int. J. Mod. Phys. B 2021, 35, 2150108. [Google Scholar] [CrossRef]
- Yin, Y.H.; Lü, X.; Ma, W.X. Bäcklund transformation, exact solutions and diverse interaction phenomena to a (3+1)-dimensional nonlinear evolution equation. Nonlinear Dyn. 2022, 108, 4181–4194. [Google Scholar] [CrossRef]
- Wang, K.J. Bäcklund transformation and diverse exact explicit solutions of the fractal combined KdV-mKdV equation. Fractals 2022, 30, 2250189. [Google Scholar] [CrossRef]
- Du, Z.; Tian, B.; Xie, X.Y.; Jun, C.; Wu, X.Y. Bäcklund transformation and soliton solutions in terms of the Wronskian for the Kadomtsev–Petviashvili-based system in fluid dynamics. Pramana 2018, 90, 45. [Google Scholar] [CrossRef]
- Ma, W.X. Lump solutions to the Kadomtsev-Petviashvili equation. Phys. Lett. A 2015, 379, 1975–1978. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.-H. Diverse optical soliton solutions to the Kundu-Mukherjee-Naskar equation via two novel techniques. Optik 2023, 273, 170403. [Google Scholar] [CrossRef]
- Wang, K.J. Diverse soliton solutions to the Fokas system via the Cole-Hopf transformation. Optik 2023, 272, 170250. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; Chen, J.; Guo, Q. Construction of higher-order smooth positons and breather positons via Hirota’s bilinear method. Nonlinear Dyn. 2021, 105, 2611–2618. [Google Scholar] [CrossRef]
- Wang, K.J. Variational principle and diverse wave structures of the modified Benjamin-Bona-Mahony equation arising in the optical illusions field. Axioms 2022, 11, 445. [Google Scholar] [CrossRef]
- Wang, K.J.; Shi, F.; Wang, G.D. Periodic wave structure of the fractal generalized fourth order Boussinesq equation travelling along the non-smooth boundary. Fractals 2022, 30, 2250168. [Google Scholar] [CrossRef]
- Mahak, N.; Akram, G. Extension of rational sine-cosine and rational sinh-cosh techniques to extract solutions for the perturbed NLSE with Kerr law nonlinearity. Eur. Phys. J. Plus 2019, 134, 1–10. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.-H.; Wu, J. Soliton solutions to the Fokas system arising in monomode optical fibers. Optik 2022, 251, 168319. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Inc, M.; Baleanu, D. New solitary wave solutions for variants of (3+1)-dimensional Wazwaz-Benjamin-Bona-Mahony equations. Front. Phys. 2020, 8, 332. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.H. On abundant wave structures of the unsteady korteweg-de vries equation arising in shallow water. J. Ocean. Eng. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Kudryashov, N.A. One method for finding exact solutions of nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar] [CrossRef] [Green Version]
- Alharbi, A.R.; Almatrafi, M.B.; Seadawy, A.R. Construction of the numerical and analytical wave solutions of the Joseph-Egri dynamical equation for the long waves in nonlinear dispersive systems. Int. J. Mod. Phys. B 2020, 34, 2050289. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Kumar, D.; Chakrabarty, A.K. Dispersive optical soliton solutions for the hyperbolic and cubic-quintic nonlinear Schrödinger equations via the extended sinh-Gordon equation expansion method. Eur. Phys. J. Plus 2018, 133, 182. [Google Scholar] [CrossRef]
- Raza, N.; Arshed, S.; Sial, S. Optical solitons for coupled Fokas-Lenells equation in birefringence fibers. Mod. Phys. Lett. B 2019, 33, 1950317. [Google Scholar] [CrossRef]
- Afzal, U.; Raza, N.; Murtaza, I.G. On soliton solutions of time fractional form of Sawada-Kotera equation. Nonlinear Dyn. 2019, 95, 391–405. [Google Scholar] [CrossRef]
- Raza, N.; Javid, A. Optical dark and dark-singular soliton solutions of (1+ 2)-dimensional chiral nonlinear Schrodinger’s equation. Waves Random Complex Media 2019, 29, 496–508. [Google Scholar] [CrossRef]
- Wang, K.J.; Si, J. Optical solitons to the Radhakrishnan-Kundu-Lakshmanan equation by two effective approaches. Eur. Phys. J. Plus 2022, 137, 1016. [Google Scholar] [CrossRef]
- Zheng, B.; Wen, C. Exact solutions for fractional partial differential equations by a new fractional sub-equation method. Adv. Differ. Equ. 2013, 2013, 199. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.J. A fractal modification of the unsteady korteweg-de vries model and its generalized fractal variational principle and diverse exact solutions. Fractals 2022, 30, 2250192. [Google Scholar] [CrossRef]
- Wang, K.J. A fast insight into the optical solitons of the generalized third-order nonlinear Schrödinger’s equation. Results Phys. 2022, 40, 105872. [Google Scholar] [CrossRef]
- Sağlam Özkan, Y.; Seadawy, A.R.; Yaşar, E. Multi-wave, breather and interaction solutions to (3+1) dimensional Vakhnenko-Parkes equation arising at propagation of high-frequency waves in a relaxing medium. J. Taibah Univ. Sci. 2021, 15, 666–678. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Bilal, M.; Younis, M.; Rizvi, S.T.R.; Althobaiti, S.; Makhlouf, M.M. Analytical mathematical approaches for the double-chain model of DNA by a novel computational technique. Chaos Solitons Fractals 2021, 144, 110669. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Albalahi, A.M.; Albadrani, S.; Aly, E.S.; Sidaoui, R.; Matouk, A.E. The Analytical Solutions of the Stochastic Fractional Kuramoto-Sivashinsky Equation by Using the Riccati Equation Method. Math. Probl. Eng. 2022, 2022, 5083784. [Google Scholar] [CrossRef]
- Al-Askar, F.M.; Mohammed, W.W.; Alshammari, M. Impact of brownian motion on the analytical solutions of the space-fractional stochastic approximate long water wave equation. Symmetry 2022, 14, 740. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Seadawy, A.R.; Ali, I.; Bibi, I.; Younis, M. Chirp-free optical dromions for the presence of higher order spatio-temporal dispersions and absence of self-phase modulation in birefringent fibers. Mod. Phys. Lett. B 2020, 34, 2050399. [Google Scholar] [CrossRef]
- Ding, C.C.; Gao, Y.T.; Deng, G.F. Breather and hybrid solutions for a generalized (3+1)-dimensional B-type Kadomtsev-Petviashvili equation for the water waves. Nonlinear Dyn. 2019, 97, 2023–2040. [Google Scholar] [CrossRef]
- Abudiab, M.; Khalique, C.M. Exact solutions and conservation laws of a (3+ 1)-dimensional B-type Kadomtsev-Petviashvili equation. Adv. Differ. Equ. 2013, 2013, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.R.; Tian, B.; Zhen, H.L.; Jiang, Y.; Wang, Y.P.; Sun, Y. Bäcklund transformations and soliton solutions for a (3+1)-dimensional B-type Kadomtsev-Petviashvili equation in fluid dynamics. Nonlinear Dyn. 2015, 80, 1–7. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, H.; Dai, Z. Kink degeneracy and rogue potential solution for the (3+1)-dimensional B-type Kadomtsev-Petviashvili equation. Pramana 2016, 87, 31. [Google Scholar] [CrossRef]
- Cui, W.; Liu, Y.; Li, Z. Multiwave interaction solutions for a (3+1)-dimensional B-type Kadomtsev-Petviashvili equation in fluid dynamics. Int. J. Nonlinear Sci. Numer. Simul. 2021. [Google Scholar] [CrossRef]
- Ma, H.; Huang, H.; Deng, A. Soliton molecules and some novel hybrid solutions for (3+1)-dimensional B-type Kadomtsev-Petviashvili equation. Mod. Phys. Lett. B 2021, 35, 2150388. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Najafi, M.; Arbabi, S.; Kavitha, L. Exact propagating multi-anti-kink soliton solutions of a (3+1)-dimensional B-type Kadomtsev-Petviashvili equation. Nonlinear Dyn. 2016, 83, 1453–1462. [Google Scholar] [CrossRef]
- Liu, J.G.; Zhu, W.H.; Osman, M.S.; Ma, W.-X. An explicit plethora of different classes of interactive lump solutions for an extension form of 3D-Jimbo-Miwa model. Eur. Phys. J. Plus 2020, 135, 412. [Google Scholar] [CrossRef]
- Lü, X.; Chen, S.-J. Interaction solutions to nonlinear partial differential equations via Hirota bilinear forms: One-lump-multi-stripe and one-lump-multi-soliton types. Nonlinear Dyn. 2021, 103, 947–977. [Google Scholar] [CrossRef]
- Lü, X.; Chen, S.-J. New general interaction solutions to the KPI equation via an optional decoupling condition approach. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 105939. [Google Scholar] [CrossRef]
- Ma, W.X. N-soliton solution and the Hirota condition of a (2+1)-dimensional combined equation. Math. Comput. Simul. 2021, 190, 270–279. [Google Scholar] [CrossRef]
- Akinyemi, L.; Şenol, M.; Iyiola, O.S. Exact solutions of the generalized multidimensional mathematical physics models via sub-equation method. Math. Comput. Simul. 2021, 182, 211–233. [Google Scholar] [CrossRef]
- Bekir, A.; Aksoy, E.; Cevikel, A.C. Exact solutions of nonlinear time fractional partial differential equations by sub-equation method. Math. Methods Appl. Sci. 2015, 38, 2779–2784. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.H. Periodic solution of the time-space fractional Sasa-Satsuma equation in the monomode optical fibers by the energy balance theory. EPL 2022, 138, 25002. [Google Scholar] [CrossRef]
- He, J.H.; He, C.H.; Saeed, T. A fractal modification of Chen-Lee-Liu equation and its fractal variational principle. Int. J. Mod. Phys. B 2021, 35, 2150214. [Google Scholar] [CrossRef]
- Wang, K.J.; Liu, J.H.; Si, J.; Shi, F. A new perspective on the exact solutions of the local fractional modified Benjamin-Bona-Mahony equation on Cantor sets. Fractal Fract. 2023, 7, 72. [Google Scholar] [CrossRef]
- He, J.H. Fractal calculus and its geometrical explanation. Results Phys. 2018, 10, 272–276. [Google Scholar] [CrossRef]
- Wang, K.J.; Zhu, H.W. Periodic wave solution of the Kundu-Mukherjee-Naskar equation in birefringent fibers via the Hamiltonian-based algorithm. EPL 2022, 139, 35002. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.A.T.; Cattani, C.; Gao, F. On a fractal LC-electric circuit modeled by local fract, On a fractal LC electric circuit modeled by local fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 200–206. [Google Scholar] [CrossRef]
- Wang, K.L. A novel variational approach to fractal Swift-Hohenberg model arising in fluid dynamics. Fractals 2022, 30, 2250156. [Google Scholar] [CrossRef]
- Baleanu, D.; Mohammadi, H.; Rezapour, S. Analysis of the model of HIV-1 infection of CD4+ T-cell with a new approach of fractional derivative. Adv. Differ. Equ. 2020, 2020, 71. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.J. Exact traveling wave solutions to the local fractional (3+1)-dimensional Jimbo-Miwa equation on Cantor sets. Fractals 2022, 30, 2250102. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.-J.; Liu, J.-H.; Si, J.; Wang, G.-D. Nonlinear Dynamic Behaviors of the (3+1)-Dimensional B-Type Kadomtsev—Petviashvili Equation in Fluid Mechanics. Axioms 2023, 12, 95. https://doi.org/10.3390/axioms12010095
Wang K-J, Liu J-H, Si J, Wang G-D. Nonlinear Dynamic Behaviors of the (3+1)-Dimensional B-Type Kadomtsev—Petviashvili Equation in Fluid Mechanics. Axioms. 2023; 12(1):95. https://doi.org/10.3390/axioms12010095
Chicago/Turabian StyleWang, Kang-Jia, Jing-Hua Liu, Jing Si, and Guo-Dong Wang. 2023. "Nonlinear Dynamic Behaviors of the (3+1)-Dimensional B-Type Kadomtsev—Petviashvili Equation in Fluid Mechanics" Axioms 12, no. 1: 95. https://doi.org/10.3390/axioms12010095
APA StyleWang, K. -J., Liu, J. -H., Si, J., & Wang, G. -D. (2023). Nonlinear Dynamic Behaviors of the (3+1)-Dimensional B-Type Kadomtsev—Petviashvili Equation in Fluid Mechanics. Axioms, 12(1), 95. https://doi.org/10.3390/axioms12010095







