A Visualization in GeoGebra of Leibniz’s Argument on the Fundamental Theorem of Calculus

Abstract

In the literature, it is usually assumed that Leibniz described proof for the Fundamental Theorem of Calculus (FTC) in 1693. However, did he really prove it? If the answer is no from today’s perspective, are there works in which Leibniz introduced arguments that can be understood as formulations and justifications of the FTC? In order to answer this question, we used a historiographic methodology with expert triangulation. From the study of Leibniz’s manuscripts describing the inverse problem of tangents and its relationship with the quadrature problem, we found evidence of a geometrical argument from which the FTC can be inferred. We present this argument using technological resources and modern notation. This result can be used to teach the FTC due to the existence of dynamic and geometrical software, which makes it suitable for the classroom. Moreover, it provides another interpretation of the FTC complementary to the interpretation using Riemann sums.

1. Introduction

Discussing analysis in Leibniz’s work is not an easy task. Enrico Pasini wrote that “The concept of analysis is notorious, for its part, a polycephalous monster and nearly all its meanings are spread through Leibniz’s multifarious works, where the philosophical, epistemological, logical, and mathematical receptions of the term seem to be inextricably interwoven” [1] (p. 1). Therefore, this concept of analysis was introduced by Leibniz under diverse conditions and with different purposes, but even for several such uses, there is some common ground and univocal significance: “analysis is for Leibniz… the resolution of something complex into simpler elements” [1] (p. 1).

Likewise, Leibniz was looking for algorithms to resolve some kinds of problems, e.g., to find quadratures or solve the inverse problem of tangents. Even more, for him, (mathematical) calculus was just one successful example of the power of algorithmic thinking [2].

It is in this context that Leibniz invented his calculus, from which it is known that “the fundamental theorem is a fitting capstone to any rigorous development of calculus” [3] (p. 90). Usually, the literature assumes that Leibniz proved the FTC in 1693. However, he did not [4]. Leibniz worked in mathematics for more than twenty years. However, at the present time, there is no evidence of a proposition or a theorem in Leibniz’s manuscripts that could be considered an analog of the current FTC. The following question naturally arises: are there works in which Leibniz introduced arguments that can be understood as formulations and justifications of the FTC?

Supported by Riemann sums, the common presentation of this theorem is as follows:

The Fundamental Theorem of Calculus: Suppose $f$ is continuous on $[a,b]$:

• If $g\left(x\right)={\int }_a^{x}f\left(t\right)dt,$ then $g^{\prime }\left(x\right)=f\left(x\right).$
• ${\int }_a^{b}f\left(x\right)dx=F\left(b\right)-F(a)$ where $F$ is an antiderivate of $f$; that is, $F^{\prime }\left(x\right)=f\left(x\right)$ [5] (p. 326).

Hence, the purpose of this article is to introduce a Leibnizian geometrical argument that is part of the FTC in order to offer another way of explaining it.

This Leibnizian argument can be used to teach the FTC in another manner. There are numerous problems regarding the comprehension of the FTC, e.g., the understanding of some mathematical objects such as differentiability, continuity, range of change, etc. [6,7,8]. These subjects appear complex for students. Furthermore, “the problem arises from the fact that this theorem assumes that the definite integral has been defined as a limit of Riemann sums” [9] (p. 99).

This paper has five sections. In Section 2, we describe how we used historiography to find the geometrical argument of the FTC from Leibniz manuscripts. In Section 3, we show the results of applying this argument to approximate the area under a curve without Riemann sums. In addition, it suggests a new form with which to view the definite integral. The final Section 4 and Section 5 deal with the pedagogical implications and conclusions of this research.

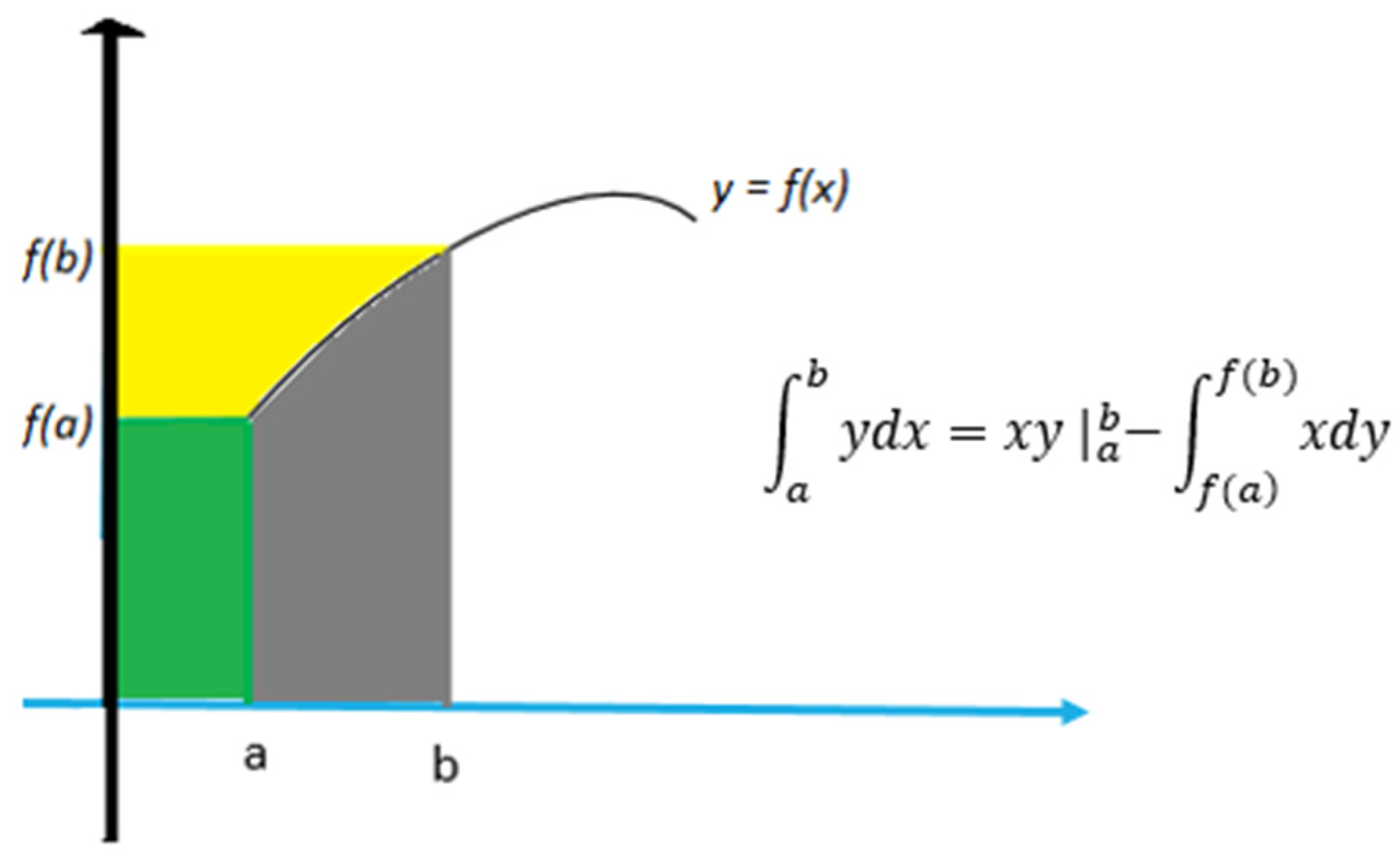
2. Methods

The methodology of historiography, that is, a method that allows mathematics to be approached from the point of view of what has been performed as a human activity that constitutes a history, rather than viewing mathematics as studied from the union of properties of objects created by that activity [10], was used to identify a historical argument; this provided an alternative partial meaning for the definite integral in addition to those currently considered in textbooks for the teaching of calculus.

The main argument for this version of the FTC is approaching it as the relationship between the inverse tangent problem and the quadrature problem. This argument is presented from the correspondence between Newton and Leibniz, and some examples are given for each of them in [11]. This geometrical argument allows us to see the common points between the works of Newton and Leibniz, in that both recognized the relationship between areas, tangents, normal, and subnormal to a curve as a necessary factor to study solutions for the emerging problems for the mathematics of their time. However, in this article, examples that are not usually referenced or explained in the selected bibliography are shown. We also discuss the Transmutation Theorem (Proposition VII) and Proposition VI of Leibniz’s book De Quadratura arithmetica circuli ellipseos et hyperbolae.

As far as Leibniz’s writings are concerned, it is possible to rely on the manuscripts restored in the Gottfried Wilhelm Leibniz Bibliothek, partly by Siegmund Probst and his team. There are writings from certain periods, for example, between the years 1674 and 1676 [12], and also the article of the year 1693 published in the journal Acta Eruditorum [13]. Complementarily, there are as-accredited sources, to cite just a few: the writings of former experts in Leibniz’s mathematical works, such as David Rabouin [14] and Davide Crippa [15], Eberhard Knobloch [16], and the Mathesis group, who were in charge of editing Leibniz’s mathematical material [17]. Indeed, the expert triangulation was made with Dr. Rabouin, and as a result, one author of this article made a presentation in the Workshop Mathesis 2021–2022 (http://www.sphere.univ-paris-diderot.fr/spip.php?article2755&lang=en) (accessed on 22 April 2021).

This study using a historiographic approach allowed us to assume that Leibniz faced problems similar to those solved by Newton, e.g., the search for the quadrature of certain curves. It was verified at this point that there is no single proposition that can be taken as the FTC given the absence of evidence and a demonstration in Leibniz’s manuscripts, which have so far been unveiled. The arguments were studied on the basis of the study of accredited and primary sources and linked to what is called the FTC.

Leibniz applied a geometrical argument for comparing a curve with a polygon. This method to compare figures was used also by Kepler in his book Nova stereometria doliorum vinariorum in 1615. Basically, what Kepler did was to identify the arc EB with a straight line (see Figure 1).

Leibniz used this argument and called it equipollence. In 1684, he wrote that other methods used at that time could be deduced from it, i.e., one can consider a curvilinear figure equipollent to a polygon with an infinite number of sides [16] (p. 303):

“Sentio autem et hanc (methodum) et alias hactenus adhibitas omnes deduci posse ex generali quodam meo dimetiendorum curvilineorum principio, quod figura curvilinea censenda sit aequipollere polygono infinitorum laterum”.

Therefore, thanks to this equipollence, Leibniz identified that one can make an approximation of the area under a curve through the addition of adequate polygons. He also applied the equipollence argument in Proposition 7 of his book De quadratura arithmetica circuli ellipseos et hyperbolae. We can read the following on its pages:

“Mihi vero feliciter accidit, ut theorema prop. 7. hujus traditum curvam daret rationalem simplicis admodum expressionis; circulo aequipollentem; unde nata est quadratura circuli arithmetica, et vera expressio analytica arcus ex tangente, cujus gratia ista conscripsimus. Inde porro investigans methodum reperi generalem admodum et pulchram ac diu quaesitam, cujus ope datae cuilibet curvae analyticae, exhiberi potest curva analytica rationalis aequipollens, re ad puram analysin reducta”.

[18] (p. 98)

An approximate translation of this paragraph follows: fortunately, it occurred to me that the theorem stated in Proposition 7 gives a rational curve of a very simple and equipollent expression to the circle; this is what gave birth to the arithmetic quadrature of the circle and to the true analytical expression of an arc from its tangent for which we wrote these things. Consequently, pushing my research further, I found a very general and beautiful method and sought it for a long time. Using this method, an analytical curve rational can be exhibited, which is equipollent to a given analytical curve after having reduced the problem to pure analysis. This Proposition 7 is his famous Transmutation Theorem:

“PROPOSITIO VII.

Si a quolibet curvae cujusdam puncto ad unum anguli recti in eodem plano positi latus ducantur ordinatae normales, ad alterum tangentes, et ex punctis occursus tangentium ducantur perpendiculares ad earum ordinatas, si opus est productas; et curva alia per intersectiones harum perpendicularium et ordinatarum transeat; erit spatium inter axem (ad quem ductae sunt ordinatae) duas ordinatas extremas, et curvam secundam comprehensum, spatii inter curvam primam et rectas duas ejus extrema cum anguli recti propositi centro jungentes, comprehensi duplum”.

[16] (p. 32)

Essentially, Leibniz’s Transmutation Theorem allows us to relate the area that lies beneath the curve $y=f(x)$ and two segment lines, which start on the origin $O$ and finish at $f(a)$ and $f(b)$, and the area under another curve $z=g(x)$ on $\left[a,b\right];$ see Figure 2. In fact, Proposition 7 gives the assumption that two curves are equipollent if they have the same area or if one is a multiple of the other. In this particular case, $f$ and $g$ are equipollent because $2·Area[Of\left(a\right)f\left(b\right)]={\int }_a^{b}zdx$.

To see the original figure and demonstration Leibniz made, we refer the reader to [19]. Leibniz showed that the way to find $z$ is to resolve the differential equation $z=y-x\frac{dy}{dx}$; see [20]. Thus, one question emerges: what is the relationship between ${\int }_a^{b}zdx$ and the area under the curve $y=f(x)$ on $\left[a,b\right]$?

In order to obtain the answer, it can be observed that the area ${\int }_a^{b}ydx$ is the sum of three curvilinear triangles, so it is easy to show the geometrical relations in Figure 3:

From Figure 3, it is also simple to verify that $∆Obf\left(b\right)=\frac{bf(b)}{2}$ and $∆Oaf\left(a\right)=\frac{af(a)}{2}$. Additionally, by applying the equation $z=y-x\frac{dy}{dx}$ we obtain the following:

$$\underset{a}{\overset{b}{\int }}ydx=\frac{1}{2}\underset{a}{\overset{b}{\int }}\left(y-x\frac{dy}{dx}\right)dx+\frac{bf(b)}{2}-\frac{af(a)}{2}$$

If we multiply this last equation by 2, we obtain

$$2\underset{a}{\overset{b}{\int }}ydx=\underset{a}{\overset{b}{\int }}ydx-\underset{f(a)}{\overset{f(b)}{\int }}xdy+xy{|}_a^b$$

Thus,

$$\underset{a}{\overset{b}{\int }}ydx=xy{|}_a^b-\underset{f(a)}{\overset{f(b)}{\int }}xdy$$

This final equation is just another way to introduce the integration by parts formula, as shown in Figure 4.

From this theorem, one can also see a slow approximation of $\pi$ [21], which is the quadrature of a circle.

The use of GeoGebra is justified in this research for the following reasons:

• The first reason is that, like most dynamical software, it allows to manipulation of geometric or graphical representation almost at the same level as symbolic representation. In particular, in this study, GeoGebra allowed us to manipulate the geometric representations of Leibniz’s FTC, which was not possible before the use of this type of software.
• The second reason is that GeoGebra has characteristics of the ISO-9126 standard (https://www.arisa.se/compendium/node6.html) (accessed on 19 October 2023).
• Since it is an open software, teachers who want to incorporate this geometrical approach to teach the FTC can do so easily.

3. Results

At this point, the main conclusion is that one can use the history of mathematics to search for other procedures and introduce mathematical objects. In the last example, we explain the transmutation geometrical argument of Leibniz in order to introduce the definite integral via the integration by parts formula. Nevertheless, Leibniz’s manuscripts and papers are sources to find this kind of argument. Notably, we introduce an application of Proposition 6 made by Leibniz in his book De Quadratura arithmetica circuli ellipseos et hyperbolae to offer another way of making an approximation of the area under a curve, i.e., another form to understand the definite integral. The original statement, figure, and proof appear in [22,23].

We considered the function $f\left(x\right)=2\sqrt{x}$ on $\left[\mathrm{0,9}\right]$. It is the curve transmuted. A polygon can be constructed, which has an area as close as possible to the area under the transformed curve. If the chosen function is increasing and continuous, the argument works exactly the same.

The first step is to draw tangents on some points of the chosen curve, namely, $f\left(x\right)=2\sqrt{x}$. In this case, we made four tangent lines. We drew them alongside the respective points of intersection with the y-axis. The original notation for these points was kept, i.e., ₁T, ₂T, ₃T, and ₄T. The second step was to draw parallel line segments to the y-axis from the points chosen for the tangents and parallel segments to the x-axis from ₁T⋯₄T; see Figure 5.

The third step is to construct the transmuted curve. This new curve was drawn from the intersection points of the segments constructed in the previous step, and we denote them B, C, D, E. Using GeoGebra Classic 5 software, the curve $g\left(x\right)=\sqrt{x}$ was obtained; see Figure 6.

The next step is to construct an equipollent polygon to $g(x)$ on $\left[\mathrm{1,9}\right]$ (from x = 1 because it is the first point of tangency chosen). To obtain this, Leibniz used the points F, G, H, and I (the initial tangency points) and took the secant lines between them. That is, we now traced the secants between F and G, G and H, and H and I, and proceeded as in Step 1, i.e., we found the points of intersection with the y-axis and constructed segments parallel to the x-axis. In this case, the intersection points are denoted as P, O, T, and S; see Figure 7.

The fifth and final step is to calculate the area under the transmuted curve $g(x)$ and the newly constructed polygon PQRSTNOMP. Again, using GeoGebra, it was found that

$$\underset{1}{\overset{9}{\int }}\sqrt{x}dx\approx 17.33$$

while the area of the polygon was $Area(PQRSTNOMP)=16.48$. Clearly, as more tangent points were taken, the approximation of the area for this equipollent polygon improved; see Figure 8.

It is clear that the relationship between the original area of $f\left(x\right)$ and $g\left(x\right)$ on $\left[\mathrm{1,9}\right]$ is given by the coefficient of transmutation, i.e., we utilized $f\left(x\right)=\frac{1}{2}g(x)$; hence,

$$\underset{1}{\overset{9}{\int }}f\left(x\right)dx=\underset{1}{\overset{9}{\int }}2\sqrt{x}dx\approx \left(17.33\right)\ast 2$$

4. Discussion

In this paper, we offer a different way to explain the definite integral from a historical study of Leibniz’s manuscripts. We started with the assumption that there are other forms of the FTC, and thanks to this historiographic study, we were able to achieve this goal. In this paper, we have introduced the geometrical perspective of Leibniz regarding what is currently known, such as the FTC, and used its visualization in GeoGebra.

This historical argument explained by Leibniz’s Proposition VI could be a new partial meaning of the definite integral. Indeed, in [24], four types of meaning for the definite integral are proposed from the perspective of the processes of mathematical instruction at the university. They are as follows:

“(1) Quantity of magnitude bounded between two sequences of convergent quantities. The magnitude can be geometric, physical, length, area, volume, distance, work, density, etc.

(2) Limit of Riemann Sums ${\int }_a^{x}f\left(t\right)dt={\sum }_{i=1}^{n}f\left(x_i^{\ast }\right)∆x$

(3) Cumulative function $G\left(x\right)={\int }_a^{x}f\left(t\right)dt$

(4) Incremental difference of the cumulative function ${\int }_a^{b}f\left(x\right)dx=G\left(b\right)-G(a)$ if $G^{\prime }\left(x\right)=f(x)$”.

[24] (p. 14)

5. Conclusions

From Leibniz’s geometrical argument of the FTC, it can be concluded that, although it seems that this meaning is similar to that of approximating the area under a curve as the sum of the area of polygons, Leibniz relates two curves and then obtains a polygon equipollent to one of them, while Riemann approximates the area under the curve with a polygon constructed from that same curve. It is evident that the Riemannian process is simpler in its geometrical construction than the one presented in Proposition VI by Leibniz.

The methodology used to find this Leibniz geometrical argument was historiography, and it produced another partial meaning of the definite integral. To confirm this concept, one can use the ontosemiotic approach (OSA).

The articulation of arguments resulting from historiographical research on the development of the Fundamental Theorem of Calculus, with manipulation processes of these arguments in software, provides a source for the identification of alternative partial meanings in order to teach FTC and consolidates the existence of a relationship between the history of mathematics and the education of mathematics.

In particular, the results of this paper can be oriented as an alternative representation for teaching the FTC to university students. Indeed, this approach [25] offers tools that enable the identification of the complexity of mathematical objects and the connection of the units in which this complexity is manifested through multiple meanings (partial meanings), which are described in terms of practices and epistemic configurations of the primary objects activated in these practices [26].