Some Variants of Integer Multiplication

Abstract

In this paper, we will explore alternative varieties of integer multiplication by modifying the product axiom of Dedekind–Peano arithmetic (PA). In addition to studying the elementary properties of the new models of arithmetic that arise, we will see that the truth or falseness of some classical conjectures will be equivalently in the new ones, even though these models have non-commutative and non-associative product operations. To pursue this goal, we will generalize the divisor and prime number concepts in the new models. Additionally, we will explore various general number properties and project them onto each of these new structures. This fact will enable us to demonstrate that indistinguishable properties on PA project different properties within a particular model. Finally, we will generalize the main idea and explain how each integer sequence gives rise to a unique arithmetic structure within the integers.

1. Introduction

In this paper, we assume the axioms of Dedekind–Peano arithmetic (PA) formulated as a first-order language (see [1], p. 154), and we will modify the multiplication one. For each modification of the axiom, we will obtain a new arithmetic, and our purpose will be to see the similarities and differences between the standard model of PA and the newly modified ones. Other attempts to modify PA consist of eliminating some axioms. For instance, Presburger arithmetic [2] contains only the addition operation and equality, omitting the multiplication operation entirely. On the other hand, Skolem arithmetic [3] contains only the multiplication operation and equality. Both are decidable theories; however, Robinson arithmetic [4] eliminates the axiom schema of mathematical induction and is undecidable.

Suppose the set of natural numbers is $\mathbb{N}=\{0,1,2,\dots \}$, the symbols «·,+» are for multiplication and addition, respectively, and the apostrophe symbol «${}^{\prime }$» is for the successor operation. We can write the two multiplication axioms in PA as follows:

(M1)

$a·0=0$ for all $a\in \mathbb{N}$.

(M2)

$a·b^{\prime }=a+(a·b)$ for all $a,b\in \mathbb{N}$.

We now replace (M1) and (M2) by (M1*) and (M2*). Given a natural number $t\in \mathbb{N}$, we substitute the usual multiplication operation above by a new one, denoted by «${\odot }_{{}_t}$».

(M1*)

$a{\odot }_{{}_t}0=0$ for all $a\in \mathbb{N}$.

(M2*)

$a{\odot }_{{}_t}{b}^{\prime }=a+\left((a+t){\odot }_{{}_t}b\right)$ for all $a,b\in \mathbb{N}$.

Therefore, it is natural to wonder about the arithmetic generated by these new axioms. If $t=0$, we have PA, and for each $t\ne 0$, we will have a new arithmetic that is a theory of first-order language with equality (see [1], p. 93). Let us take a closer look at the new multiplication operation:

$$\begin{array}{cc}\hfill a{\odot }_{{}_t}b& =a{\odot }_{{}_t}{(b-1)}^{\prime }=a+\left((a+t){\odot }_{{}_t}(b-1)\right)=a+\left((a+t){\odot }_{{}_t}{(b-2)}^{\prime }\right)\hfill \\ \hfill & =a+(a+t)+\left((a+t+t){\odot }_{{}_t}(b-2)\right)=a+(a+t)+\left((a+t+t){\odot }_{{}_t}{(b-3)}^{\prime }\right)\hfill \\ \hfill & =\dots =a+(a+t)+(a+t+t)+\dots +(a+t+\stackrel{(b-1)}{\dots }+t).\hfill \end{array}$$

(1)

As we can see, «${\odot }_{{}_t}$» is the sum of b terms, starting in a, whose difference between consecutive terms is t. For a better understanding of the new multiplication operation, from now on, we will work outside the formal theory, and we will use the usual product to better handle (M2*). For instance, we can write (1) as follows:

$$a{\odot }_{{}_t}b=a+(a+t)+(a+2t)+\dots +(a+(b-1)t)=a·b+\frac{b·(b-1)·t}{2}.$$

(2)

With (2), we can easily extend «${\odot }_{{}_t}$» to $\mathbb{Z}$ and we can consider $a,b,t\in \mathbb{Z}$. In addition, we can define the usual order relation and the subtraction operation in a normal way (see [1], p. 162).

Notation 1.

Let $t\in \mathbb{Z}$. We use the notation ${\displaystyle {\mathcal{Z}}_t=\{\mathbb{Z},+,{\odot }_{{}_t},<\}}$ to indicate that we are going to work with the set of integers, the usual order, the addition, and the new multiplication operation.

Clearly, ${\mathcal{Z}}_0$ will be the standard model of PA extended to the integers. Now, it is natural to ask about the structure of ${\mathcal{Z}}_t$: if $t\ne 0$, what numbers are primes? Is there any relation between the properties of PA and ${\mathcal{Z}}_t$? We can advance that ${\odot }_{{}_t}$ is neither commutative nor associative; however, we will see that if t is even, denoted by $t\in \mathrm{E}=\{\dots ,-4,-2,0,2,4,6,\dots \}$, then the primes on ${\mathcal{Z}}_t$ will be the usual primes, and if t is odd, denoted by $t\in \mathrm{O}=\{\dots ,-3,-1,1,3,\dots \}$, then the primes will be the powers of two. Therefore, the veracity of many of the classical results and conjectures of number theory will be equivalent in ${\mathcal{Z}}_t$, $t\in \mathrm{E}$ and hence, this fact will point out that the associativity and commutativity laws of the usual product are not necessary to prove these results.

In Section 2, we will study the basic algebraic properties of ${\odot }_{{}_t}$ (see Proposition 1). We will define the multiples on the right (see Definition 1) and on the left (see Definition 2), leading to an unusual representation of the number line (see Theorem 1). Finally, we propose an alternative approach to reach to ${\mathcal{Z}}_t$ without modifying the multiplication axiom (see Theorem 2).

In Section 3, we will generalize the concept of the divisor of a number (see Lemma 1) and primes in ${\mathcal{Z}}_t$ (see Theorem 3). This fact allows us to explore the relations between the different properties in the different arithmetics.

In Section 4, we will explore Bertrand’s postulate (see Definition 9), the Goldbach conjecture (see Definitions 10 and 11 and Corollary 5), the Twin Prime conjecture (see Definition 12 and Corollary 6), the odd perfect number conjecture (see Definitions 13 and 14, Proposition 2, and Corollary 7), the Sophie Germain conjecture (see Definition 15 and Corollary 8) and the Euclid primes conjecture (see Definitions 16 and 17 and Corollaries 9–13).

Finally, in Section 5, we propose a modification of the main idea (see Definition 18). This fact allows us to consider the arithmetic generated by any integer sequence. In particular, we will study the arithmetic generated by the arithmetic progression ${(t_1+t_2·x)}_{x\ge 0}$ (see Example 5).

This manuscript deals with typical themes of the Pythagorean mathematical heritage. We recommend to the interested reader in this topic to investigate the bibliography contained in [5,6].

2. Basic Properties

As indicated in the introduction, we will work outside the formal theory. However, we are going to study properties that could be proven axiomatically.

Proposition 1.

Given $a,b,c,t\in \mathbb{Z}$, the following properties are satisfied:

1. 

For all a, $a{\odot }_{{}_t}1=a$ and $a{\odot }_{{}_t}0=0$.

2. 

If $t\ne 0$ and $c\notin \{0,1\}$, then $\left(a{\odot }_{{}_t}b\right){\odot }_{{}_t}c\ne a{\odot }_{{}_t}\left(b{\odot }_{{}_t}c\right)$.

3. 

$a{\odot }_{{}_t}b=b{\odot }_{{}_t}a+\frac{t·(b-a)·(a+b-1)}{2}$.

4. 

$a{\odot }_{{}_t}(b+c)=a{\odot }_{{}_t}b+a{\odot }_{{}_t}c+t·b·c$.

5. 

$(a+b){\odot }_{{}_t}c=a{\odot }_{{}_t}c+b·c$.

6. 

$a{\odot }_{{}_t}(-b)=(t-a){\odot }_{{}_t}b$.

7. 

$(a-b)·(c+d)=a{\odot }_{{}_t}c+a{\odot }_{{}_t}d-b{\odot }_{{}_t}c-b{\odot }_{{}_t}d$.

Proof. 

We have only to use (2). □

Point 1 shows us that 1 and 0 are the right identity and the right null, respectively. Points 2 and 3 indicate the non-associativity and the non-commutativity, respectively. However, by 3, we can remark that $a{\odot }_{{}_t}(1-a)=(1-a){\odot }_{{}_t}a$. Points 4 and 5 study the distributive law, and Point 6 will help us to study the divisors of a positive integer later. As we can observe, the ring structure is far from ${\mathcal{Z}}_t$; nevertheless, we can appreciate interesting properties like Point 7. We leave the more detailed study of this algebraic structure for another time, and we move on to study the set of the multiples of an integer on ${\mathcal{Z}}_t$.

Definition 1.

Let $a,t\in \mathbb{Z}$. The multiples on the right of a on ${\mathcal{Z}}_t$ are the set $\{a{\odot }_{{}_t}x:x\in \mathbb{Z}\}$.

As $a{\odot }_{{}_t}x=a·x+x·(x-1)·t/2=(t·x^2+(2a-t)·x)/2$, if $t\ne 0$, then the multiples on the right of a are contained in a parabola. Therefore, solving the equation $a{\odot }_{{}_t}x=0$, we obtain two right null elements.

Remark 1.

Let $a,t\in \mathbb{Z}$ and $t\ne 0$, if $t|2a$ then $\exists c_1,c_2$ such that $a{\odot }_{{}_t}{c}_1=a{\odot }_{{}_t}{c}_2=0$.

Proof. 

The solutions to the equation $a{\odot }_{{}_t}x=0$ are $c_1=0$ and $c_2=1-2a/t$. Hence, we will have two right null elements if $t|2a$. □

Corollary 1.

Let $a,t\in \mathbb{Z}$, $t\ne 0$, and $t|2a$. For all integers n, $a{\odot }_{{}_t}n=a{\odot }_{{}_t}(c_2-n)$. Therefore, the set of the multiples on the right of a on ${\mathcal{Z}}_t$ has a maximum or minimum value in $a{\odot }_{{}_t}(c_2/2)$.

Let us now study the multiples on the left of an integer on ${\mathcal{Z}}_t$.

Definition 2.

Let $a,t\in \mathbb{Z}$. The multiples on the left of a on ${\mathcal{Z}}_t$ are the set $\{x{\odot }_{{}_t}a:x\in \mathbb{Z}\}$.

As $x{\odot }_{{}_t}a=a·x+a·(a-1)·t/2$, the multiples on the left of a are contained in a line with a-slope.

Remark 2.

Let $a,t\in \mathbb{Z}$ and $a\ne 0$; if $a\in \mathrm{O}$ or $t\in \mathrm{E}$, then $\exists n_1$ such that $n_1{\odot }_{{}_t}a=0$.

Proof. 

The solution to the equation $x{\odot }_{{}_t}a=0$ is $n_1=(1-a)·t/2$. □

Corollary 2.

Let $a,t\in \mathbb{Z}$ such that $a\in \mathrm{O}$ or $t\in \mathrm{E}$. For all integers n, $(n_1-n){\odot }_{{}_t}a=-\left((n_1+n){\odot }_{{}_t}a\right)$.

As we can see, the multiples on the left of a on ${\mathcal{Z}}_t$ behave in the usual way.

Suppose $a>0$, $t>0$, and $t<2a$. We can summarize the above information as follows.

• Multiples on the right of a on ${\mathcal{Z}}_t$:

  

  (3)
• Multiples on the left of a on ${\mathcal{Z}}_t$:

  

  (4)

Example 1.

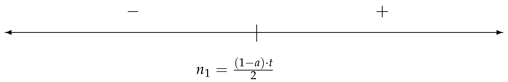
Table 1 and Table 2 evaluate the multiples on the right and left of 3 on ${\mathcal{Z}}_1$.

Table 1. Multiples on the right of 3 on ${\mathcal{Z}}_1$.

x	$-8$	$-7$	$-6$	$-5$	$-4$	$-3$	$-2$	$-1$	0	1	2	3	4
$\mathbf{3}{\odot }_{{}_{\mathbf{1}}}\mathit{x}$	12	7	3	0	$-2$	$-3$	$-3$	$-2$	0	3	7	12	18

Table 2. Multiples on the left of 3 on ${\mathcal{Z}}_1$.

x	$-8$	$-7$	$-6$	$-5$	$-4$	$-3$	$-2$	$-1$	0	1	2	3	4
$\mathit{x}{\odot }_{{}_{\mathbf{1}}}\mathbf{3}$	$-21$	$-18$	$-15$	$-12$	$-9$	$-6$	$-3$	0	3	6	9	12	15

As we can see from Table 1, $c_1=0$, $c_2=-5$, and from Table 2, it is clear that $n_1=-1$.

Based on the previous results, we could consider product mappings on the set of the real numbers. That is, given $t\in \mathbb{R}$, we could consider «${\odot }_{{}_t}$» as a product mapping of two real numbers. Once this operator is defined, we could restrict it to the integers, rounding each product to the nearest integer using the round function, denoted by «$\left[{\odot }_{{}_t}\right]$». With this, we could consider a new interpretation of the number line theorem. Let us see it.

We consider the usual representation of the set of integers $\mathbb{Z}$ in the number line as the set $\{1{\odot }_{{}_0}x:x\in \mathbb{Z}\}$. We can see this representation in (6). Now, if we see t as a real variable, we can study the set $\{1{\odot }_{{}_t}x:x\in \mathbb{Z}\}$ when t tends to 0. For instance, if $t\to 0^{+}$, by Remark 1, we have two values $c_1$, $c_2$ such that $1{\odot }_{{}_t}{c}_1=1{\odot }_{{}_t}{c}_2=0$. Nevertheless, by Remark 1, if $t\to 0^{+}$, then $c_2\to -\infty$. The situation we are trying to describe would be as if, in Table 1, $-5$ were replaced by $-N$, where N is an arbitrarily large number. With this argument, we can state the following result.

Theorem 1.

A valid and equivalent representation of the set of integers $\mathbb{Z}$ in the number line is

(5)

Proof. 

Let $a=1$. The multiples on the left of 1 on ${\mathcal{Z}}_0$ can be represented as the usual number line:

(6)

However, these multiples must coincide with the multiples on the right of 1 when $t\to 0^{+}$. If $t\to 0^{+}$, then $c_2\to -\infty$. Using Remark 1 and Corollary 1, the set $\{\left[1{\odot }_{{}_t}x\right]:x\in \mathbb{Z},t\to 0^{+}\}$ can be represented as the following Table 3 where N and L are positive and arbitrarily large numbers.

Table 3. Multiples on the right of 1 on ${\mathcal{Z}}_t$ when $t\to 0^{+}$.

x

$c_2-1$

$c_2$

$c_2+1$

…

$\frac{c_2}{2}-1$

$\frac{c_2}{2}$

$\frac{c_2}{2}+1$

…

$-1$

0

1

2

…

L

$\mathbf{1}{\odot }_{{}_{\mathbf{t}}}\mathit{x}$

1

0

$-1$

…

$-N+1$

$-N$

$-N+1$

…

$-1$

0

1

2

…

L

We can represent Table 3 as follows.

(7)

In the previous representation, if $t\to 0^{+}$, then $-N\to -\infty$. Hence, our usual negative semi-axis coincides with the unusual negative one because the multiples on the right and left of 1 coincide on ${\mathcal{Z}}_0$.

(8)

(9)

Using the same argument, the multiples on the right of 1 when $t\to 0^{-}$ must coincide with the usual ones represented in (6). But now, if $t\to 0^{-}$, then $c_2\to +\infty$. Hence, the positive semi-axis represented in (5) coincides with the usual one, and the result follows. □

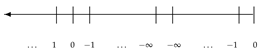
With this result, we justify, in a certain way, Wallis’s paradox about negative numbers ([7], p. 253): “In his Arithmetica Infinitorum (1655), he argued that since the ratio $a/0$, when a is positive, is infinite, then, when the denominator is changed to a negative number, as in $a/b$ with b negative, the ratio must be greater than infinity”. However, we would obtain other paradoxes, such as the appearance of the “transposed infinity” in (5) and the interpretation of Hilbert’s hotel [8] in this version of the number line.

We have considered $t\in \mathbb{R}$ to elaborate on this result. We now return to view $t\in \mathbb{Z}$. Still, we can build multiplication operations using functions of two real variables and restricting the product to the integers.

As we have seen, we have generalized the multiplication operation axiomatically. The following result, however, would have allowed us to find ${\mathcal{Z}}_t$ in a different way.

Theorem 2.

The product $n{\odot }_{{}_t}n$ is the nth $(t+4)$-gonal number.

Proof. 

The formula of the nth l-gonal is $\left((l-2)n-(l-4)\right)/2$. We have, by hypothesis, $t+4=l$; hence, $n\left((l-2)n-(l-4)\right)/2=n\left((t+2)n-t\right)/2=n^2+n(n-1)t/2=n{\odot }_{{}_t}n$. □

This theorem proposes a generalization of the arithmetic in the following way: the square of a number is a square (polygon) in the usual arithmetic (${\mathcal{Z}}_{{}_0}$) but is a pentagon in ${\mathcal{Z}}_{{}_1}$, a hexagon in ${\mathcal{Z}}_{{}_2}$, a triangle in ${\mathcal{Z}}_{{}_{-1}}$, etc. That is, $5{\odot }_{{}_0}5=25$ is the fifth square, whereas $5{\odot }_{{}_1}5=35$ is the fifth pentagonal number, etc.

In the following section, we will generalize the concept of the divisor of a number, and we will study the primes on ${\mathcal{Z}}_t$.

3. Divisors and Primes

As we have seen, the product is not commutative. Therefore, given a positive integer a, we will define the right and left divisors of a. The right divisor corresponds with the usual notion of a divisor on PA; therefore, we call it a divisor of a on ${\mathcal{Z}}_t$. The left divisor indicates where the summation starts in the new multiplication operation. We will call it a position divisor of a.

Definition 3.

Let $t\in \mathbb{Z}$; an integer $d>0$ is called a divisor of a on ${\mathcal{Z}}_t$, denoted by $d{\mid }_{{}_t}a$, if there exists some integer b such that $a=b{\odot }_{{}_t}d$. We denote the set of divisors of a on ${\mathcal{Z}}_t$ as ${\mathrm{Div}}_{{}_t}\left(a\right)$.

In other words, d is the number of terms of the summation representing the new product. This definition corresponds with the right divisor of a on ${\mathcal{Z}}_t$.

Definition 4.

Let $t\in \mathbb{Z}$; an integer b is called a position divisor of a on ${\mathcal{Z}}_t$ if there exists some integer $c>0$ such that $a=b{\odot }_{{}_t}c$. We denote the set of position divisors of a on ${\mathcal{Z}}_t$ as ${\mathrm{Divpos}}_{{}_t}\left(a\right)$.

Example 2.

$-2{\odot }_{{}_3}4=-2+1+4+7=10$. The number of terms is 4, hence $4{\mid }_{{}_3}10$ and the sum starts in $-2$, then $-2\in {\mathrm{Divpos}}_3\left(10\right)$.

Each divisor d of a on ${\mathcal{Z}}_t$ has a position divisor assigned (let us call it b). In addition, d and b have an element assigned close to their definitions. This fact is due to Point 6 of Proposition 1. For instance, in the previous example, $10=-2{\odot }_{{}_3}4=(3-(-2)){\odot }_{{}_3}(-4)=5{\odot }_{{}_3}(-4)$. However, we can not obtain the number 10 by adding $-4$ elements or starting the summation on 5, adding $+3$ to the new addend. Then, we do not consider $-4$ as a divisor of 10 on ${\mathcal{Z}}_3$, denoted by $-4{\nmid }_{3}10$ and $5\notin {\mathrm{Divpos}}_3\left(10\right)$.

Let us now define the left and right quotient to characterize the set of divisors. The first one will be similar to the usual one defined on PA. We will use the symbol «${\oslash }_{{}_t}$ » for it.

Definition 5.

Let $a,b,t\in \mathbb{Z}$, $b\ne 0$. An integer c is called a quotient of a divided by b on ${\mathcal{Z}}_t$ if and only if $c{\odot }_{{}_t}b=a$. We write: $a{\oslash }_{{}_t}b=c\iff c{\odot }_{{}_t}b=a$.

We can use (2) and write the new quotient as follows:

$$a{\oslash }_{{}_t}b=\frac{a}{b}-\frac{(b-1)t}{2}.$$

(10)

For instance, if we want to write 93 as the sum of 6 terms of an arithmetic progression- whose difference is 5, then the quotient indicates to us the first term of the solution: $93{\oslash }_{{}_5}6=93/6-5·5/2=3$. Then, $93=3{\odot }_{{}_5}6=3+8+13+18+23+28$.

The following result will allow us to study the divisors of an integer a on ${\mathcal{Z}}_t$.

Corollary 3.

Let $d>0$, d is a divisor of a on ${\mathcal{Z}}_t$ ⇔ $a{\oslash }_{{}_t}d$ is an integer.

Now, we will study the right quotient. We will see that it yields two values. These values indicate the number of terms representing the product on ${\mathcal{Z}}_t$. Therefore, in our future study, we will consider only the positive values.

Definition 6.

Let $a,b,t\in \mathbb{Z}$, $t\ne 0$. An integer c is called a position quotient of a divided by b on ${\mathcal{Z}}_t$ if and only if $b{\odot }_{{}_t}c=a$.

We can use (2) in the previous equation obtaining $t{c}^2+(2b-t)c-2a=0$. The two possible values for c, denoted by ${\mathrm{qp}}_1$ and ${\mathrm{qp}}_2$, are $(1/2t)·(t-2b\pm \sqrt{{(t-2b)}^2+8at})$.

For instance, the position quotient of 10 divided by 4 on ${\mathcal{Z}}_{-1}$ returns ${\mathrm{qp}}_1=4$ and ${\mathrm{qp}}_2=5$. Hence, $10=4{\odot }_{{}_{-1}}4=4+3+2+1$ and $10=4{\odot }_{{}_{-1}}5=4+3+2+1+0$.

As we have indicated, the position quotient shows us the number of terms representing the new product; therefore, we will only consider the positive values. On the other hand, we are interested in studying the divisors of a positive integer a on ${\mathcal{Z}}_t$ with $t>0$. In this situation, only ${\mathrm{qp}}_1$ will be positive, so we will use the following notation:

Notation 2.

Let a,t be positive integers and $b\in \mathbb{Z}$. We denote by ${\mathit{Qpos}}_{{}_t}(a,b)$ the positive value $\frac{1}{2t}(t-2b+\sqrt{{(t-2b)}^2+8at})$.

Similarly to Corollary 3, we can deduce the following result.

Corollary 4.

Let $b,t\in Z$, $t>0$; b is a position divisor of a positive integer a on ${\mathcal{Z}}_t$ ⇔ ${\mathit{Qpos}}_{{}_t}(a,b)$ is an integer.

The following lemma, which also appears in [9], characterizes the divisors of a positive integer a on ${\mathcal{Z}}_t$. Once the set ${\mathrm{Div}}_{{}_t}\left(a\right)$ is obtained, we use (10) to calculate the set ${\mathrm{Divpos}}_{{}_t}\left(a\right)$.

Lemma 1.

Let $t,a\in \mathbb{Z}$. The divisors of a on ${\mathcal{Z}}_t$ are:

1. 

The usual divisors of a if $t\in \mathrm{E}$.

2. 

The usual divisors of 2$a$ except the even usual divisors of a if $t\in \mathrm{O}$.

Proof. 

1. We use Corollary 1. If $d\mid a$, then $a/d-(d-1)t/2$ is an integer because $t\in \mathrm{E}$. The reciprocal is also trivial; hence, if $t\in \mathrm{E}$, then $d\mid a\iff d{\mid }_{{}_t}a$.

2. Let $\mathrm{Div}\left(a\right)$ be the set of the usual divisors of a. It is clear that ${\mathrm{Div}}_t\left(a\right)\subseteq \mathrm{Div}\left(2a\right)$. Indeed, $d{\mid }_{{}_t}a\iff \exists b$ such that $b{\odot }_{{}_t}d=a\iff 2a/d=b+(d-1)t\in \mathbb{Z}$. Therefore, we have two cases:

• $d\mid a$: if $d\in \mathrm{Div}\left(a\right)$ and $t\in \mathrm{O}$, then $a{\oslash }_{{}_t}d\in \mathbb{Z}\iff a/d-(d-1)t/2\in \mathbb{Z}\iff d\in \mathrm{O}$.
• $d\mid 2a$ and $d\nmid a$: we can suppose that $\exists h\in \mathbb{Z}$ such that $a/d=h/2$ with $h\equiv 1$ (mod 2). Hence, if $t\in \mathrm{O}$, then $a{\oslash }_{{}_t}d\in \mathbb{Z}$, which is equivalent to

$a/d-(d-1)t/2\in \mathbb{Z}\iff h/2-(d-1)t/2\in \mathbb{Z}\iff \left(1-(d-1)t\right)/2\in \mathbb{Z}\iff d\in \mathrm{E}.$ □

Example 3.

Calculate the sets ${\mathrm{Div}}_{{}_3}\left(30\right)$ and ${\mathrm{Divpos}}_{{}_3}\left(30\right)$.

Solution. By Point 2, the divisors of 30 on ${\mathcal{Z}}_3$ are the usual divisors of 60 except the even usual divisors of 30. Hence ${\mathrm{Div}}_{{}_3}\left(30\right)=\{1,3,4,5,12,15,20,60\}$. Now, we apply (10) to obtain ${\mathrm{Divpos}}_{{}_3}\left(30\right)=\{30,7,3,0,-14,-19,-27,-88\}$. We have placed the elements of the set ${\mathrm{Divpos}}_{{}_3}\left(30\right)$ in decreasing order to view the associated divisor of 30 on ${\mathcal{Z}}_3$. For instance, $30=7{\odot }_{{}_3}3=7+10+13$ or $30=-14{\odot }_{{}_3}12=-14-11-\dots +16+19$.

With this example, we can study the representation of a number as a sum of integer sequences in arithmetic progression or the partitions of a number into arithmetic progressions. See [9].

Let us now consider the primes. We start with the position primes associated the position divisors.

Definition 7.

Let $t\in \mathbb{Z}$, $t>0$. An integer $p>1$ is a position prime on ${\mathcal{Z}}_t$ if and only if p does not have a position divisor d with $0<d<p$.

In the previous example, 30 is not a position prime on ${\mathcal{Z}}_3$ because $3\in {\mathrm{Divpos}}_3\left(30\right)$ and $0<3<30$.

It is easy to see that a number $p>1$ will be a position prime on ${\mathcal{Z}}_t$ if and only if p does not have a partition into arithmetic progression whose difference is t.

Example 4.

In Table 4, we compute the first position primes on ${\mathcal{Z}}_t$.

Table 4. Position primes on ${\mathcal{Z}}_t$.

t	Position Primes on ${\mathcal{Z}}_{\mathit{t}}$	OEIS [10]
1	$2,4,8,16,32,64,128,256,512,1024,2048,4096,\dots$	A000079
2	$2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,\dots$	A000040
3	$2,3,4,6,8,10,14,16,20,28,32,44,52,56,64,68,76,88,\dots$	A243225
4	$2,3,4,5,7,9,11,13,17,19,23,25,29,31,35,37,41,43,47,49,\dots$
5	$2,3,4,5,6,8,10,12,14,16,20,22,26,28,32,40,44,52,56,64,\dots$
6	$2,3,4,5,6,7,9,11,13,15,17,19,23,25,29,31,35,37,41,43,47,\dots$

As we can see, the consecutive numbers $2,3,\dots ,t+1$ are position primes on ${\mathcal{Z}}_t$. This is easy to see: as $1{\odot }_{{}_t}2=t+2$, then $t+2$ is the first composite of position on ${\mathcal{Z}}_t$. Each file in this example represents the numbers that cannot be expressed as the sum of positive integers in an arithmetic progression with a common difference t. When $t=4$, the position primes on ${\mathcal{Z}}_4$ coincides with the numbers n that cannot be written as a sum of two or more distinct parts with the largest part dividing n. See A327782 in The On-line Encyclopedia of Integer Sequences (OEIS) [10]. The computations carried out in this example are based on the classical calculation of prime numbers, substituting the usual quotient by (10). In fact, all the computations in this work are obtained by modifying the definition of the product between two integers.

We now define the prime numbers on ${\mathcal{Z}}_t$. Based on Lemma 1, an integer $a>1$ always has two divisors on ${\mathcal{Z}}_t$. Indeed: if $t\in \mathrm{E}$, 1 and a are divisors of a on ${\mathcal{Z}}_t$ and if $t\in \mathrm{O}$, then 1 and $2a$ are divisors of a on ${\mathcal{Z}}_t$. Thus, we can write the following definition.

Definition 8.

An integer $p>1$ is called a prime on ${\mathcal{Z}}_t$ if it has only two divisors on ${\mathcal{Z}}_t$. An integer greater than 1 that is not a prime on ${\mathcal{Z}}_t$ is termed a composite on ${\mathcal{Z}}_t$.

We use Lemma 1 to characterize the primes on ${\mathcal{Z}}_t$.

Theorem 3.

Let $t\in \mathbb{Z}$. The primes on ${\mathcal{Z}}_t$ are:

1. 

The usual primes if $t\in \mathrm{E}$.

2. 

The powers of two if $t\in \mathrm{O}$.

Proof. 

1. Let $t\in \mathrm{E}$. By Lemma 1, if $a>1$ then $d\mid a\iff d{\mid }_{{}_t}a$ and the result holds.

2. Let $t\in \mathrm{O}$. If $a>1$ is not a power of two, then $a=2^s·b$, b is odd, and s∈$\{0,1,2,\dots \}$. By Lemma 1, $b{\mid }_{{}_t}a$. In conclusion, 1, $2a$, and b are divisors of a on ${\mathcal{Z}}_t$; hence, a is not prime on ${\mathcal{Z}}_t$.

If $a>1$ is a power of two, then $a=2^s$, $s\in \{1,2,\dots \}$. By Lemma 1, the divisors of a on ${\mathcal{Z}}_t$ are the usual divisors of $2a$ except the even usual divisors of a. Hence, the divisors of a on ${\mathcal{Z}}_t$ are: $\{1,2·2^s\}$; 1 and $2^{s+1}$ are the unique divisors of a on ${\mathcal{Z}}_t$; thus, a is prime on ${\mathcal{Z}}_t$. □

We could ask if it is possible to adapt Euclid’s proof of the infinitude of primes on ${\mathcal{Z}}_t$ and the answer is no: if $t=1$, by Theorem 3, the primes on ${\mathcal{Z}}_1$ are 2, 4, 8, …. However, the classic argument does not work. For instance, $\left(8{\odot }_{{}_1}4\right){\odot }_{{}_1}2+1=78$ and $78=18{\odot }_{{}_1}4$. Is there a universal argument to prove the infinity of primes on ${\mathcal{Z}}_t$? The answer is yes: Furstenberg’s proof of the infinitude of primes can be adapted on ${\mathcal{Z}}_t$. This fact has been studied in [11].

We have now come to the most exciting part of this work. We will state specific properties of the numbers on ${\mathcal{Z}}_t$ and see how the truth or falsity behaves depending on t. This fact will remind us of what happens in geometry with the postulate of parallels and the space chosen to study it.

4. Number’s Properties on ${\mathcal{Z}}_{\mathit{t}}$

Let us begin by analyzing Bertrand’s postulate (for every integer $n>1$, there is always at least one prime p such that $n<p<2n$). In principle, we will state this property on ${\mathcal{Z}}_t$ and then, given a concrete integer $t_{{}_0}$, we will consider the interpretation of the property on ${\mathcal{Z}}_{t_{{}_0}}$. We can write Bertrand’s postulate in at least two different ways.

Definition 9.

Let B ($B^{*}$) have the following property: for every integer $n>1$, there is always at least one prime p on ${\mathcal{Z}}_t$ such that $n<p<n{\odot }_{{}_t}2$ ($n<p<n+n$).

If we consider the property B on ${\mathcal{Z}}_{t_0}$, denoted by ${\Pi }_{t_0}\left(B\right)$, the “projection” of the property on ${\mathcal{Z}}_{t_0}$ can be true or false depending on $t_0$. In the same way, given $t_0,t_1\in \mathbb{Z}$, every property P on ${\mathcal{Z}}_{t_0}$ can be considered on ${\mathcal{Z}}_{t_1}$. We write this fact as ${\Pi }_{t_1}\left(P\right)$. In principle, the property P we are considering can be written in a first-order language.

Returning to the example at hand, if we consider ${\Pi }_1\left(B\right)$ (we can denoted it by $B_1$), we can use Theorem 3 to see that ${\Pi }_1\left(B\right)$ is true. Indeed, $n{\odot }_{1}2=2n+1$ and for every $n>1$, there is always a power of two between n and $2n+1$; therefore $B_1$ is true. Now, we examine ${\Pi }_1\left(B^{*}\right)$, and then $B_1^{*}$ is false on ${\mathcal{Z}}_1$. Indeed, if n is a power of two, then there is not a new power of two between n and $n+n$; since the primes on ${\mathcal{Z}}_1$ are the powers of two, $B_1^{*}$ is false. Thus, we have a paradoxical outcome: if we consider ${\Pi }_0\left(B_1\right)$ and ${\Pi }_0\left(B_1^{*}\right)$, in both cases, we would have Bertrand’s original postulate, hence, as we have seen, the properties: “there is always at least one prime p such that $n<p<n·2$”, and “there is always at least one prime p such that $n<p<n+n$”, although indistinguishable on PA, would be different properties since one of them would be the projection of a true property and the other would be the projection of a false one.

The most common situation will be described in the following examples when we study the classical conjectures.

Definition 10.

Let $H=\{6,8,10,\dots \}$ and let G have the following property: for all $h\in H$, there exist $p_1$, $p_2$ primes on ${\mathcal{Z}}_t$ such that $p_1+p_2=h$.

Based on Theorem 3, it is clear that if $l\in \mathrm{O}$, then ${\Pi }_l\left(G\right)$ is false on ${\mathcal{Z}}_l$. Indeed, 30 is not the sum of two powers of two, and if $s\in \mathrm{E}$, then ${\Pi }_s\left(G\right)$ is true if and only if ${\Pi }_0\left(G\right)$ is true. That is, if the classical Goldbach conjecture is true, then the conjecture must be true on ${\mathcal{Z}}_s$, $s\in \mathrm{E}$. This result points to this fact: the truth or falsity of the Goldbach conjecture does not depend on the associative or commutative property of the usual product because we have variants of PA where the conjecture is well-defined and is equivalent to the classical one. Nevertheless, the product defined in these variants is neither commutative nor associative.

Let us try to define the Goldbach conjecture in another way:

Definition 11.

Let $G^{*}$ have the following property: for all integers $a{\odot }_{t}2>4$, there exist $p_1$, $p_2$ primes on ${\mathcal{Z}}_t$ such that $p_1+p_2=a{\odot }_{t}2$.

Now, we have the same situation that occurred with Definition 10, however, for a different reason: if $s\in \mathrm{E}$, then the conjecture is equivalent to the classical one on ${\mathcal{Z}}_s$ and if $l\in \mathrm{O}$, then ${\Pi }_l\left(G^{*}\right)$ is false on ${\mathcal{Z}}_l$, but now the reason is that $a{\odot }_{l}2\in \mathrm{O}$ for all integers a, and, then, it is impossible to obtain an odd number adding two powers of two. The situation that we have and that will be repeated with more conjectures could be denoted as follows:

Corollary 5.

If $l\in \mathrm{O}$, then ${\mathcal{Z}}_l\vDash \neg {\Pi }_l\left(G\right)$. If $s\in \mathrm{E}$, then ${\mathcal{Z}}_0\vDash {\Pi }_0\left(G\right)\iff {\mathcal{Z}}_s\vDash {\Pi }_s\left(G\right)$.

We use the notation ${\mathcal{Z}}_t\vDash P$ to indicate that the property P is satisfied on ${\mathcal{Z}}_t$.

Let us look at some more examples.

Definition 12.

Let $TP$ have the following property: there are infinitely many primes p on ${\mathcal{Z}}_t$ such that $p+2$ is also prime on ${\mathcal{Z}}_t$.

Using Theorem 3, it is easy to see that we have the same situation with the twin prime conjecture as in the previous example. That is:

Corollary 6.

If $l\in \mathrm{O}$, then ${\mathcal{Z}}_l\vDash \neg {\Pi }_l\left(TP\right)$. If $s\in \mathrm{E}$, then ${\mathcal{Z}}_0\vDash {\Pi }_0\left(TP\right)\iff {\mathcal{Z}}_s\vDash {\Pi }_s\left(TP\right)$.

Additionally, we have the same situation with the extended twin prime conjecture (for all integers $a{\odot }_{{}_t}2\ge 2$, there are infinitely many primes p on ${\mathcal{Z}}_t$ such that $p+a{\odot }_{{}_t}2$ is also prime on ${\mathcal{Z}}_t$).

Let us study more cases.

Definition 13.

Let $t\in \mathbb{Z}$. A perfect number on ${\mathcal{Z}}_t$ is a positive integer n that is equal to the sum of its divisors d on ${\mathcal{Z}}_t$ less than itself.

Definition 14.

Let $OPN$ have the following property: there are no odd perfect numbers on ${\mathcal{Z}}_t$.

Based on Lemma 1, we have to study two cases: $t\in \mathrm{E}$ and $t\in \mathrm{O}$. The first one is equivalent to the classic problem of perfect numbers. For the second one, we use Point 2 of the lemma.

Proposition 2.

Let $l\in \mathrm{O}$. The unique $n>0$ such that $n\in \mathrm{O}$ and n is perfect on ${\mathcal{Z}}_l$ is $n=3$.

Proof. 

If $n\in \mathrm{O}$, then n and $2n$ are divisors of n on ${\mathcal{Z}}_t$. Based on Point 2 of Lemma 1, if the usual factorization in primes of n is $n=p_1^{a_1}·\dots ·p_r^{a_r}$, then the sum of the divisors less than n on ${\mathcal{Z}}_l$ are:

$$(1+2)·(1+p_1+p_1^2+\dots +p_1^{a_1})·\dots ·(1+p_r+p_r^2+\dots +p_r^{a_r})-2n-n.$$

Hence, we have to study the following equation.

$$3·\frac{p_1^{a_1+1}-1}{p_1-1}·\dots ·\frac{p_r^{a_r+1}-1}{p_r-1}-2n-n=n\iff 3·\frac{p_1^{a_1+1}-1}{p_1-1}·\dots ·\frac{p_r^{a_r+1}-1}{p_r-1}=4·p_1^{a_1}·\dots ·p_r^{a_r}.$$

(11)

Dividing by 3 into both sides of (11), we can deduce that 3 must be a prime of n. Without loss of generality, we can rewrite (11):

$$\frac{3^{a_1+1}-1}{2}·\frac{p_2^{a_2+1}-1}{p_2-1}·\dots ·\frac{p_r^{a_r+1}-1}{p_r-1}=4·3^{a_1-1}·p_2^{a_2}·\dots ·p_r^{a_r}.$$

(12)

As $(3^{a_1+1}-1)/2\ge 4·3^{a_1-1}$, and we get the equality when $a_1=1$, we can deduce that $a_1=1$ and $a_2=a_3=\dots =a_r=0$. □

If $l\in \mathrm{O}$, then the first even perfect numbers on ${\mathcal{Z}}_l$ are: 10, 12, 408, 528, 14560, 90816. We do not know if the even perfect numbers on ${\mathcal{Z}}_l$ are infinite. Similarly to the previous examples, we can write the following result.

Corollary 7.

If $l\in \mathrm{O}$, then ${\mathcal{Z}}_l\vDash \neg {\Pi }_l\left(OPN\right)$. If $s\in \mathrm{E}$, then ${\mathcal{Z}}_0\vDash {\Pi }_0\left(OPN\right)\iff {\mathcal{Z}}_s\vDash {\Pi }_s\left(OPN\right)$.

We emphasize once again the significance of definitions. If we had defined a perfect number n on ${\mathcal{Z}}_t$ as “… the sum of all its divisors on ${\mathcal{Z}}_t$ excluding the largest one is equal to n”, this property would translate to ${\mathcal{Z}}_s$, $s\in \mathrm{E}$ in a conventional manner. However, 3 would not be considered perfect on ${\mathcal{Z}}_l$, $l\in \mathrm{O}$, as the sum of its divisors minus the largest would be $1+2+3=6\ne 3$.

In the following two cases, we encounter distinct scenarios.

Definition 15.

Let $SG$ have the following property: there are infinitely many primes p on ${\mathcal{Z}}_t$ such that $p{\odot }_{{}_t}2+1$ is also prime on ${\mathcal{Z}}_t$.

Using Theorem 3, we can study the Sophie Germain conjecture on ${\mathcal{Z}}_t$. Let n be a positive integer. If $l\in \mathrm{O}$, then

$$p{\odot }_{{}_l}2+1=2^n·2+\frac{2·1·l}{2}+1=2^{n+1}+l+1.$$

(13)

Expression (13) is prime on ${\mathcal{Z}}_l$ if and only if $l=-1$ or $l+1=(2^a-1)·2^{n+1}$, $a\in \{-n,-n+1,\dots \}$. For instance: if $n=1$, then $l=2^{a+2}-5$, $a\in \{-1,0,1,2,3,\dots \}$; hence $l=-3,-1,3,11,\dots$. That is, 2 is a Sophie Germain prime on ${\mathcal{Z}}_l$, $l\in \{-3,-1,3,11,\dots \}$. In the same way, $2^n$ will be a Sophie Germain prime on ${\mathcal{Z}}_l$,

$$l=2^{a+n+1}-2^{n+1}-1,a\in \{-n,-n+1,\dots \}.$$

(14)

All the powers of two are Sophie Germain primes on ${\mathcal{Z}}_{-1}$ and for each l value of (14), $l\ne -1$, $2^n$ will be the unique Sophie Germain prime on ${\mathcal{Z}}_l$. To see this fact, if we suppose that $2^n$ and $2^s$ are Sophie Germain primes on ${\mathcal{Z}}_l$, then

$$l=2^{a+n+1}-2^{n+1}-1=2^{b+s+1}-2^{s+1}-1;a\in \{-n,-n+1,\dots \},b\in \{-s,-s+1,\dots \}.$$

(15)

If $a=0$, using the previous equation, then $l=-1$ and $b=0$. Similarly, $b=0\Rightarrow l=-1\Rightarrow a=0$. If $a\ne b$, we have the following cases.

• $a>0$, $b>0$: without loss of generality, we can suppose that $n\ge s$. From (15), we obtain

  $$2^{n-s}=\frac{2^b-1}{2^a-1}.$$

  (16)
  Hence, we can deduce that $n=s$.
• $a>0$, $b<0$: using (15), $2^{n-s}·(2^a-1)=2^b-1$. This expression is contradictory because the left side of the equation is positive, and the right side is negative. Similarly, we can rule out the case $a<0$, $b>0$.

Hence, we can resume the situation as follows:

Corollary 8.

If $l\in \mathrm{O}$, $l\ne -1$ then ${\mathcal{Z}}_l\vDash \neg {\Pi }_l\left(SG\right)$. If $l=-1$, then ${\mathcal{Z}}_{-1}\vDash {\Pi }_{-1}\left(SG\right)$.

Now, it is not trivial that if $s\in \mathrm{E}$, then ${\mathcal{Z}}_0\vDash {\Pi }_0\left(SG\right)\iff {\mathcal{Z}}_s\vDash {\Pi }_s\left(SG\right)$. The proofs with the computer point us that there are infinite Sophie Germain primes p on ${\mathcal{Z}}_s$, $s\in \mathrm{E}$.

Before moving on to the following example, we note that if we define the property ${\mathrm{SG}}^{*}$ as “there are infinitely many primes p on ${\mathcal{Z}}_t$ such that $p+p+1$ is also prime on ${\mathcal{Z}}_t$”, then ${\Pi }_{-1}\left({\mathrm{SG}}^{*}\right)$, denoted by $S{G}_{-1}^{*}$, would be false. Therefore, we would have the paradoxical result that the usual conjecture on PA can be the projection of either a true (${\Pi }_0\left({\mathrm{SG}}_{-1}\right)$) or a false (${\Pi }_0\left({\mathrm{SG}}_{-1}^{*}\right)$) property.

We finish this section by studying Euclid primes.

Definition 16.

Let $EP$ have the following property: there are infinitely many primes p on ${\mathcal{Z}}_t$ of the form $p_{n,t}^{\#}+1$ where

$$p_{n,t}^{\#}=\left(\left(\left(p_1{\odot }_{{}_t}{p}_2\right){\odot }_{{}_t}{p}_3\right){\odot }_{{}_t}\dots \right){\odot }_{{}_t}{p}_n,$$

and $p_i$$(i=1,\dots ,n)$ is the ith prime on ${\mathcal{Z}}_t$.

If $t\in \mathrm{O}$, it is easy to prove that there are no Euclid primes on ${\mathcal{Z}}_t$: the product $p_{n,t}^{\#}+1=\left(\left(2{\odot }_{{}_t}4\right){\odot }_{{}_t}8\right){\odot }_{{}_t}\dots ){\odot }_{{}_t}{2}^n$ has the form $2^s+1+e·t$, where s and e are positive integers and e is even. Hence the equation $2^s+1+e·t=2^l$, $l>0$, does not produce an integer value on t. Therefore:

Corollary 9.

If $l\in \mathrm{O}$, then ${\mathcal{Z}}_l\vDash \neg {\Pi }_l\left(EP\right)$.

If $s\in \mathrm{E}$, similarly to the previous example, it is not trivial that ${\mathcal{Z}}_0\vDash {\Pi }_0\left(EP\right)\iff {\mathcal{Z}}_s\vDash {\Pi }_s\left(EP\right)$. For instance, $2{\odot }_{{}_s}3+1=s+7$ is not prime on ${\mathcal{Z}}_s$ if $s\in \{2+6·i:i\ge 0\}$ because $2{\odot }_{{}_s}3+1$ will be a multiple of 3. The problem when $t\in \mathrm{E}$ seems just as difficult as the original. For instance, 200560490131 is the greatest primorial prime on PA, but we can find the primorial prime.

$$p_{14,2}^{\#}+1=38202330012536761\mathrm{on}{\mathcal{Z}}_2$$

or

$$p_{22,4}^{\#}+1=15573728727717884729475991628131\mathrm{on}{\mathcal{Z}}_4$$

There are several ways to define $p_{n,t}^{\#}$. The definition would vary based on the placement of parentheses. Although they may appear similar, the definitions can lead to significant differences. Let us take a look.

Definition 17.

Let $E{P}^{*}$ have the following property: there are infinitely many primes p on ${\mathcal{Z}}_t$ of the form $p_{n,t}^{\#*}+1$ where

$$p_{n,t}^{\#*}=\left(\left(\left(p_n{\odot }_{{}_t}{p}_{n-1}\right){\odot }_{{}_t}{p}_{n-2}\right){\odot }_{{}_t}\dots \right){\odot }_{{}_t}{p}_1.$$

and $p_i$$(i=1,\dots ,n)$ is the ith prime on ${\mathcal{Z}}_t$.

Suppose $s\in \mathrm{E}$, $s=2·a$. As the product of two odd primes on ${\mathcal{Z}}_s$ and the product of an odd number by an odd prime is also odd, we can suppose that

$$p_{n,s}^{\#*}+1=\left((2k+1){\odot }_{{}_{2a}}3\right){\odot }_{{}_{2a}}2+1=12k+14a+7\equiv 2a+1\left(\mathrm{mod}3\right).$$

(17)

We can deduce at least that if $a\in \{1+3·i:i\in \mathbb{Z}\}$, then $p_{n,s}^{\#*}+1$ is a multiple of 3 ($n\ge 3$). Hence:

Corollary 10.

If $s\in \{2+6·i:i\in \mathbb{Z}\}$ then ${\mathcal{Z}}_s\vDash \neg {\Pi }_s\left(E{P}^{*}\right)$.

It appears that we can prove that ${\Pi }_s\left({\mathit{EP}}^{*}\right)$ will be false on ${\mathcal{Z}}_s$. For instance, if $s=4$, it is easy to prove that $p_{n,4}^{\#*}+1$ is a multiple of 17 when $n\ge 7$:

$$\left(\left(\left((2k+1){\odot }_{{}_4}17\right){\odot }_{{}_4}13\right){\odot }_{{}_4}\dots \right){\odot }_{{}_t}2+1=1021020t+17616539,$$

(18)

and gcd$(1021020,17616539)=17$. In the same way, we can see that $p_{n,6}^{\#*}+1$ is a multiple of 29 when $n\ge 10$, and $p_{n,10}^{\#*}+1$ is a multiple of 59 when $n\ge 17$. Although it is easy to prove a specific case, we have not found a general method to prove all cases where $s\in \mathrm{E}$.

The stydy of ${\Pi }_l\left(E{P}^{*}\right),l\in \mathrm{O}$, is a little bit more difficult than ${\Pi }_l\left(EP\right),l\in \mathrm{O}$. Suppose $l=2l_1+1,l\in \mathbb{Z}$. As $2^n{\odot }_{{}_l}{2}^{n-1}$, $n\ge 3$, is an even number, and the product of an even number for $2^n$ is also an even number, we can write $p_{n,l}^{\#*}+1$ as follows:

$$p_{n,l}^{\#*}+1=\left(\left(2k{\odot }_{{}_l}4\right){\odot }_{{}_l}2\right)+1=16k+26l_1+14.$$

(19)

Now, if $l_1$ = 0, then $16k+26l_1+14=16k+14=2·(2·(4k+3)+1)$. As we have the usual product of 2 by an odd number, we will never get a power of two. Therefore:

Corollary 11.

${\mathcal{Z}}_1\vDash \neg {\Pi }_1\left(E{P}^{*}\right)$.

If $l_1$ is even, say, $l_1=2l_2$, then $16k+26l_1+14=2·(2·(4k+13l_2+3)+1)$ is not a power of two. Hence:

Corollary 12.

${\mathcal{Z}}_i\vDash \neg {\Pi }_i\left(E{P}^{*}\right)$, $i\in \{1+4j:j\in \mathbb{Z}\}$.

If $l_1$ is odd, say, $l_1=2l_2+1$, then $16k+26l_1+14=16k+52l_2+40=4(2(2k+6l_2+5)+l_2)$. And now, if $l_2$ is odd, say, $l_2=2l_3+1$, the result holds. Hence:

Corollary 13.

${\mathcal{Z}}_i\vDash \neg {\Pi }_i\left(E{P}^{*}\right)$, $i\in \{7+8j:j\in \mathbb{Z}\}$.

If $l_2$ is even, say, $l_2=2l_3$, we continue this process, and it is easy to see that $p_{n,l}^{\#*}+1$, $n\ge 3$, is the product of a power of two by an odd number.

We finish analyzing the product $\left(4{\odot }_{{}_l}2\right)+1=l+9$. Then, we must study the equation $l+9=2^n$, $n\ge 1$. We conclude that if $l=2^n-9$, then $2^n$ will be the unique Euclid prime on ${\mathcal{Z}}_l$.

We can keep analyzing other well-known problems. For instance, [11] studies the Collatz conjecture and finds that if $l\in \mathrm{O}$, it is false. If $s\in \mathrm{E}$, computer tests show that every cycle converges on ${\mathcal{Z}}_s$.

Many of these unsolved problems are equivalent to problems in arithmetic with a non-commutative and non-associative product. The situation reminds us of geometry: in specific spaces, property P can be true, and in others, it is false. This suggestion is the most interesting of this article.

To finish, we generalize the main idea of this work and see that any integer sequence generates an arithmetic on the integers. Therefore, the possibilities to define the set of prime numbers are many.

5. New Ways of Integer Multiplication

We have studied that, given an integer t, the sequence $\left(a_n\right)=t,t,t,\dots$ generates an arithmetic similar to the usual one. With the same idea, we can define the following operators. For the following definitions, let be $m,n,a,b,d\in \mathbb{Z}$, and let be $\left(a_n\right)$ an integer sequence.

Definition 18.

Let $n>0$. We define the product generated by $\left(a_n\right)$ as follows:

$$m{\odot }_{a_n}n=m+(m+a_1)+\dots +(m+a_1+\dots +a_{n-1}).$$

Clearly, $m{\odot }_{a_n}n=m·n+(n-1)a_1+(n-2)a_2+\dots +1·a_{n-1}$. Thus, we can write:

$$m{\odot }_{a_n}n=m·n+\sum _{i=1}^{n-1}(n-i)·a_i.$$

(20)

We can extend the definition for all integers by calculating a formula for ${\sum }_{i=1}^{n-1}(n-i)·a_i$.

Definition 19.

Let $d>0$. We say that d is a divisor of a on ${\mathcal{Z}}_{a_n}$, denoted by $d{\mid }_{{}_{a_n}}a$, if and only if $\exists b\in \mathbb{Z}$ such that $b{\odot }_{a_n}d=a$.

Definition 20.

Let $b\ne 0$, we define the quotient c of a divided by b on ${\mathcal{Z}}_{a_n}$, denoted by $a{\oslash }_{a_n}b=c$, if and only if $c{\odot }_{a_n}b=a$.

Similarly to (10), we have

$$a{\oslash }_{a_n}b=\frac{1}{b}·(a-\sum _{i=1}^{b-1}(b-i)a_i).$$

(21)

Additionally, similarly to Corollary 1:

Corollary 14.

$d>0$, d is a divisor of a on ${\mathcal{Z}}_{a_n}\iff a{\oslash }_{a_n}b$ is an integer.

To end this part of the definitions, we will say that p is prime on ${\mathcal{Z}}_{a_n}$ if it has only two divisors on ${\mathcal{Z}}_{a_n}$.

For a clear notation, if we work on ${\mathcal{Z}}_{a_n}$, we will use the symbols «⊙» and «⊘» for multiplication and division, respectively.

In [11], various examples of arithmetic defined by series are computationally analyzed. From [9], we can take the following example.

Example 5.

Let $\left(a_n\right)$ be an arithmetic progression with first term $t_1\in \mathbb{Z}$ and common difference $t_2\in \mathbb{Z}$. Let $s,l\in \mathbb{Z}$, $s,l>0$ and p usual prime, $p\equiv 1$ (mod 3). The set of primes on ${\mathcal{Z}}_{a_n}$ can be seen in Table 5. In this case, we can use the notation ${\mathcal{Z}}_{t_1,t_2}$ to indicate that we are working on ${\mathcal{Z}}_{a_n}$.

Table 5. Primes on ${\mathcal{Z}}_{{}_{t_1,t_2}}$.

	${\mathit{t}}_2\equiv 1$ (Mod 3)	${\mathit{t}}_2\equiv 2$ (Mod 3)	${\mathit{t}}_2\equiv 0$ (Mod 3)
${\mathbf{t}}_{\mathbf{1}}$ ∈ E	$3^s$	$3^{s-1}·p$	Usual primes
${\mathbf{t}}_{\mathbf{1}}$ ∈ O	$2^{2l-1}·3^{s-1}$	∅	$2^l$

We comment only that if $t_1\in$ O and $t_2\equiv 2$ (mod 3), then all numbers $a>1$ have at least three divisors: if $a=2^{l-1}·h$, h odd, then 1, $2^l$, and $6a$ are divisors of a. Hence, a is not prime. It can be proved that the set of numbers with exactly three divisors is the following: $\{2^{2l-2}·3^{s-1}>1:s,l\in \mathbb{N}\}$.

We have also used in this example that we can write the product and the quotient as follows. Let $m,n,a,b\in \mathbb{Z}$, $b\ne 0$, then

$$m\odot n=m·n+\frac{(n-1)·n·t_1}{2}+\frac{(n-2)·(n-1)·n·t_2}{6}.$$

(22)

$$a\oslash b=\frac{a}{b}-(b-1)·(\frac{t_1}{2}+\frac{(b-2)·t_2}{6}).$$

(23)

6. Conclusions

In this paper, we have modified the multiplication axiom of PA, thus creating new models of arithmetic that are very close to the usual one. The study of ${\mathcal{Z}}_t$ is interesting and deserves further research. The connection of the classical conjectures in one or another arithmetic and the extension of the notion of prime number treated in this paper is a subject that should be carefully studied.

Another noteworthy aspect deserving further investigation is the following. There exist properties concerning numbers P and $P^{*}$, indistinguishable on PA, such that their projections ${\Pi }_t\left(P\right)$ and ${\Pi }_t\left(P^{*}\right)$ differ on ${\mathcal{Z}}_t$ for a certain integer t. The following conjecture would also encompass many unsolved classical conjectures, such as Goldbach or Twin Prime conjectures.

Conjecture 1.

Let P be a property about numbers verifying the following two points.

1. 

If $l\in \mathrm{O}$, then ${\mathcal{Z}}_l\vDash \neg {\Pi }_l\left(P\right)$.

2. 

If $s\in \mathrm{E}$, then ${\mathcal{Z}}_0\vDash {\Pi }_0\left(P\right)\iff {\mathcal{Z}}_s\vDash {\Pi }_s\left(P\right)$.

Then, ${\mathcal{Z}}_0\vDash {\Pi }_0\left(P\right)$.

One exciting application that arises when studying these arithmetics is their connection to combinatorics. For example, problems of integer partitions can be solved by studying the set of divisors in certain arithmetics (see [9]) or by considering the set of squares. For instance, if $\left(a_n\right)$ is an arithmetic progression whose first term $t_1=1$ and whose common difference is $t_2=1$, then the set of squares $\{n{\odot }_{{}_{a_n}}n:n\in \mathbb{Z},n>0\}=\{1,5,13,26,45,\dots \}$ represents the number of n-dimensional partitions of 4 (see A008778).

Another attempt is to apply analysis tools like convolutions when we study an arithmetic generated by an integer sequence. For instance, we can express the product on ${\mathcal{Z}}_{{}_{a_n}}$ as follows:

$$m{\odot }_{{}_{a_n}}n={[m\ast n]}_n=\sum _{i=0}^n{m}_{{}_i}\ast n_{{}_{n-i}},\mathrm{where}{m}_0=m,m_1=a_1,\dots ,m_n=a_n\mathrm{and}{n}_i=i.$$

(24)

Furthermore, in (20), we can try to calculate ${\sum }_{i=1}^{n-1}(n-i)·a_i$ using the Euler–Maclaurin summation formula.

Considering this, the topic developed here deserves a more in-depth and comprehensive study.