Bayesian Estimation Using Product of Spacing for Modified Kies Exponential Progressively Censored Data
Abstract
:1. Introduction
2. Maximum Likelihood Estimation
3. Maximum Product of Spacing Estimation
4. LF-Based Bayesian Estimation
4.1. Lindley’s Approximation
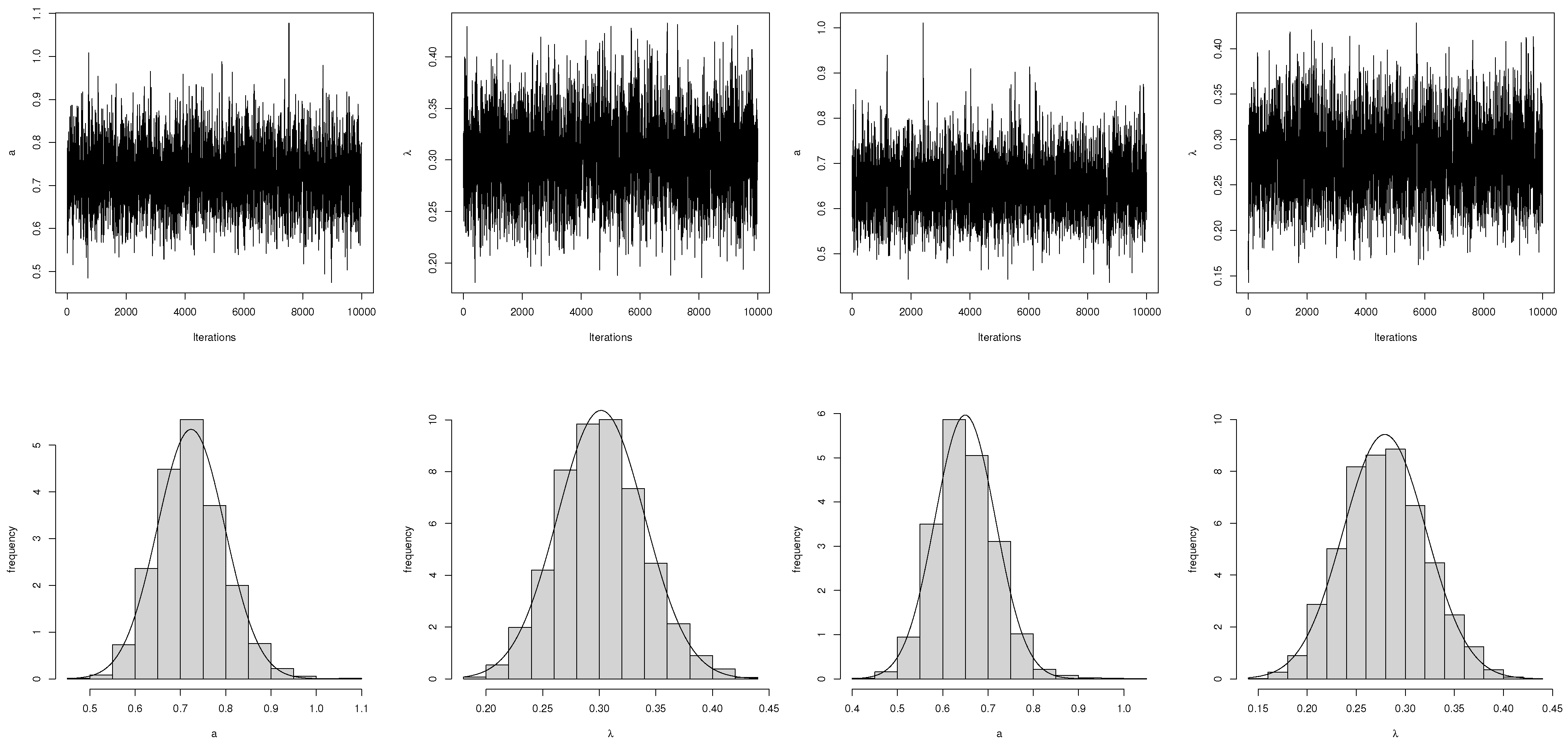
4.2. MCMC Technique
- Step 1
- Set initial guess points for as .
- Step 2
- Set .
- Step 3
- Generate a* from .
- Step 4
- Calculate .
- Step 5
- Generate a sample u from .
- Step 6
- If , accept the generated value and set ; otherwise, reject the proposed distribution and set .
- Step 7
- Follow the same line as in steps in 3–6 to generate from (29).
- Step 8
- Obtain and .
- Step 9
- Set .
- Step 10
- Repeat steps 3–9 M times and obtain M random samples of a,, and as , ,and , respectively.
- Step 11
- The LF-based Bayes estimates using a, , , and (say, ) under SELF are provided bywhere Q is the burn-in period.
- Step 12
- Follow the approach suggested by Chen and Shao [28] to obtain the HPD credible interval of the parameter , as follows:
- Arrange the MCMC chain of after the burn-in period to obtain .
- In this case, the two-sided HPD credible interval of can be found as follows:where is selected such that
5. PSF-Based Bayesian Estimation
5.1. Lindley’s Approximation
5.2. MCMC Technique
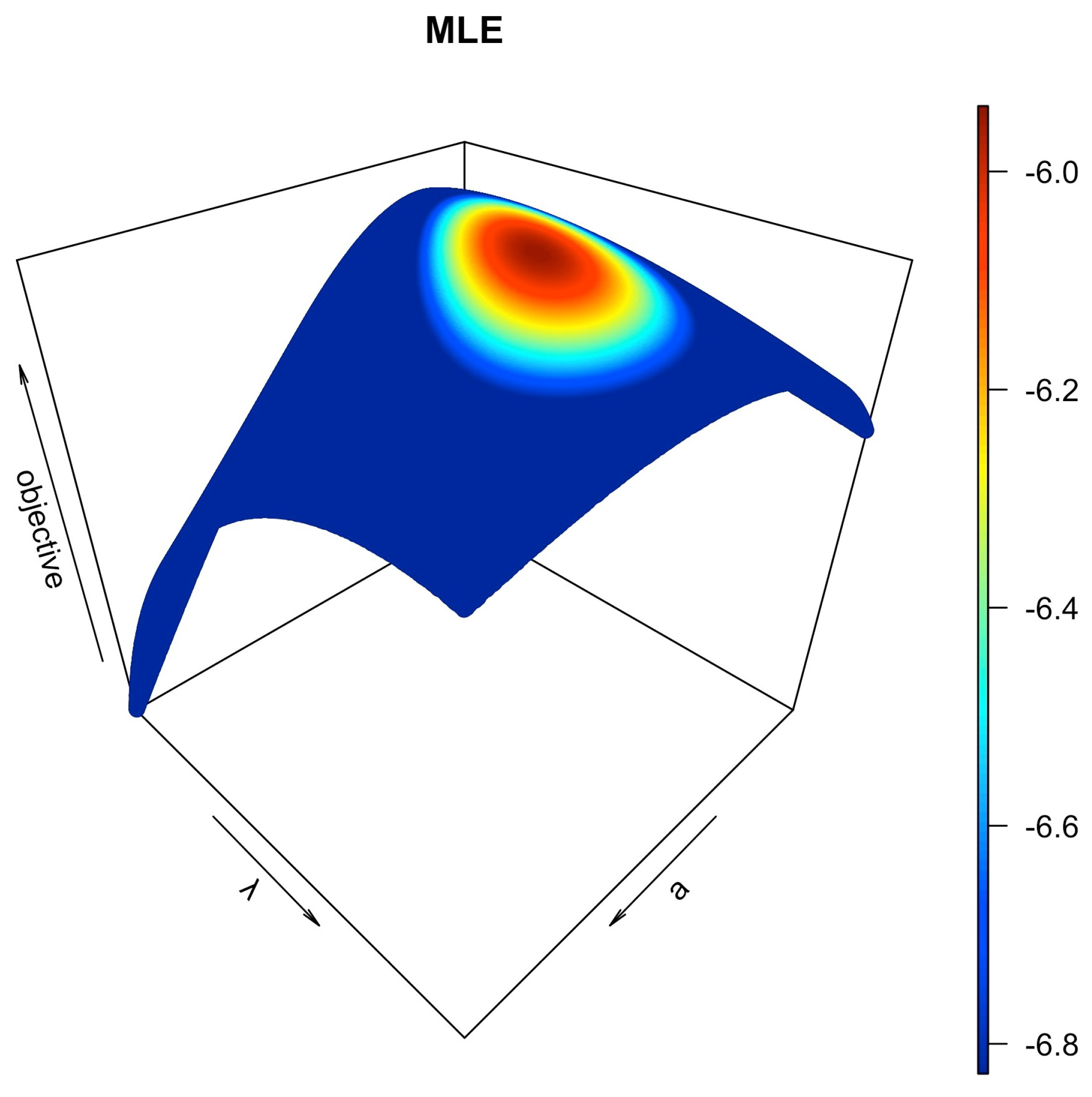
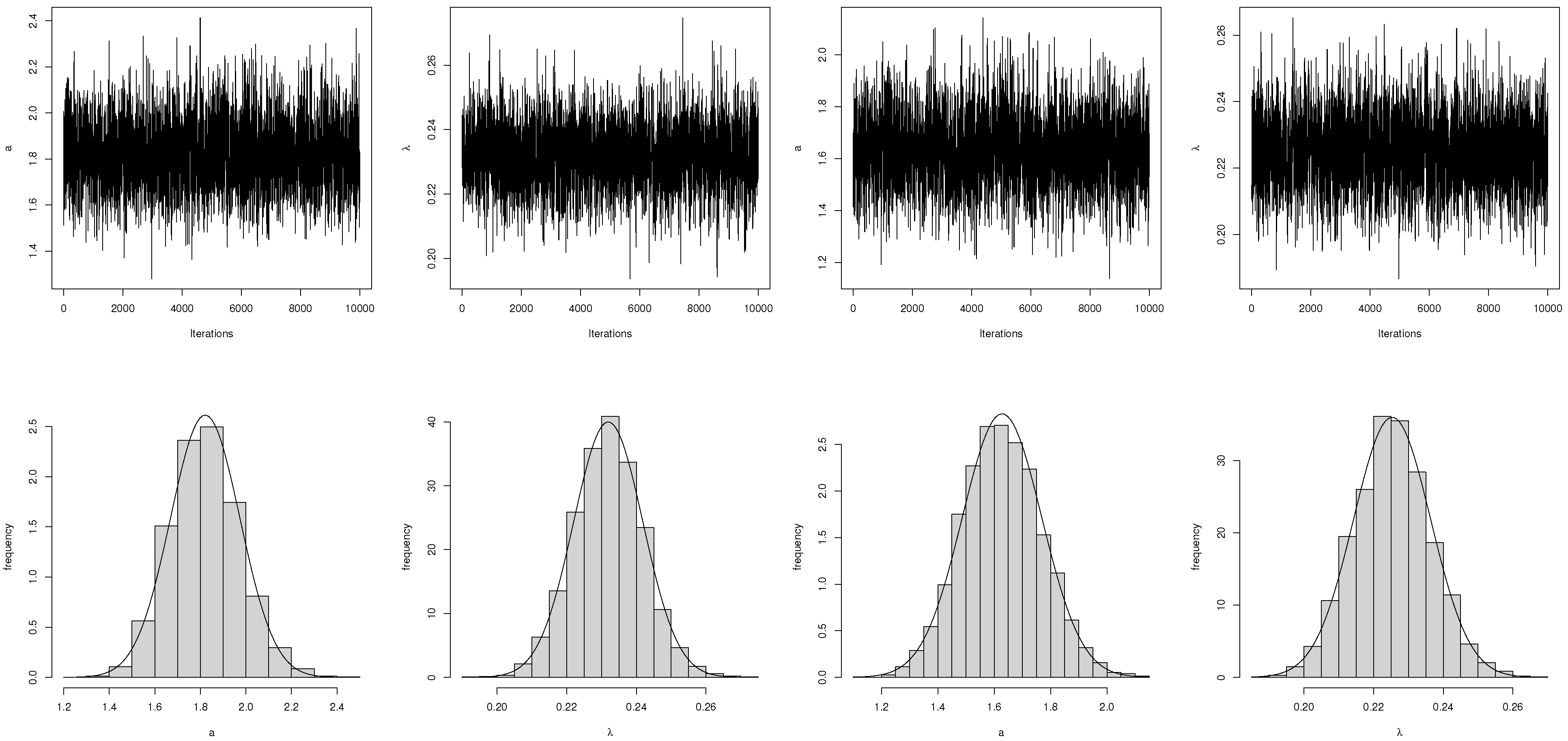
6. Simulation Study
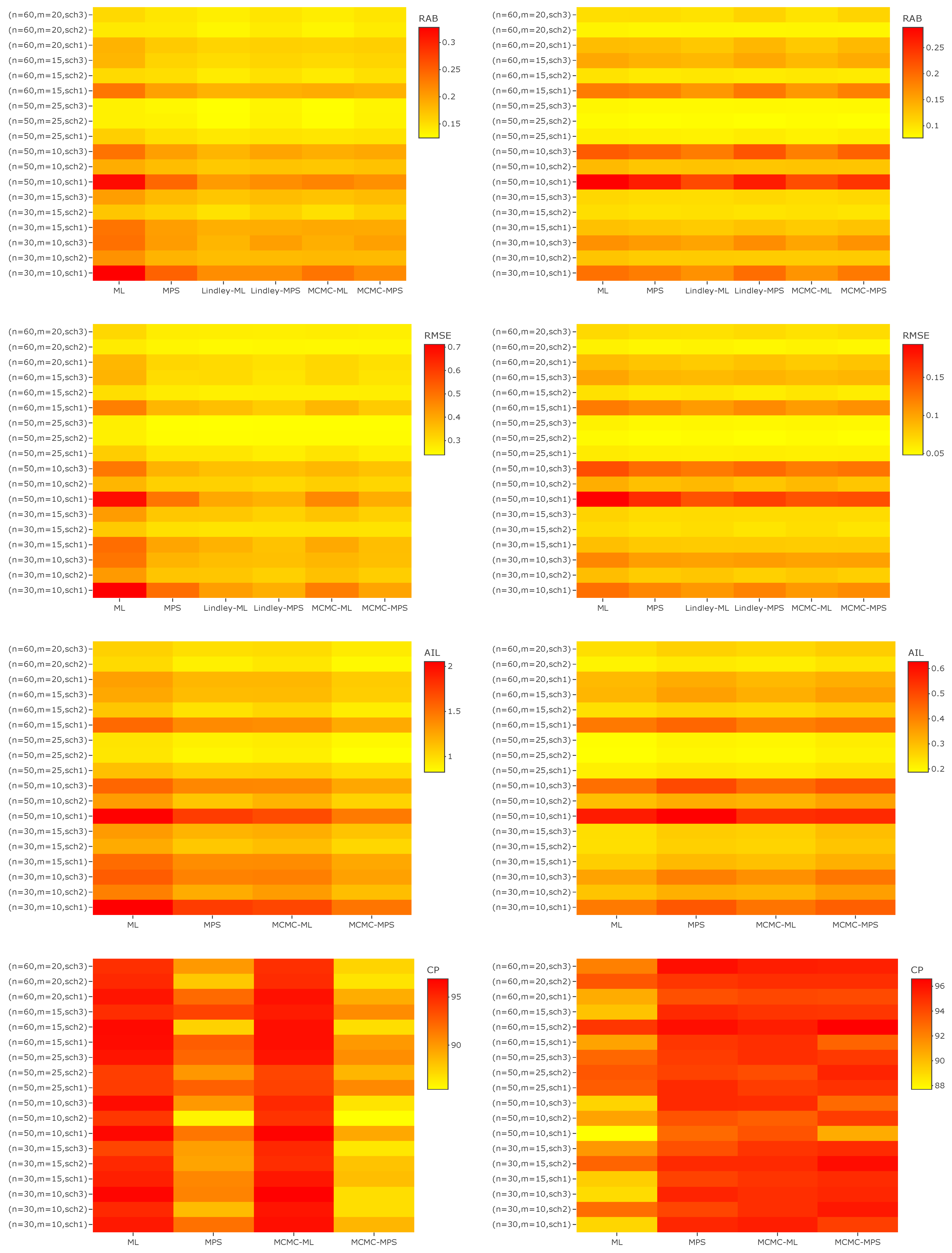
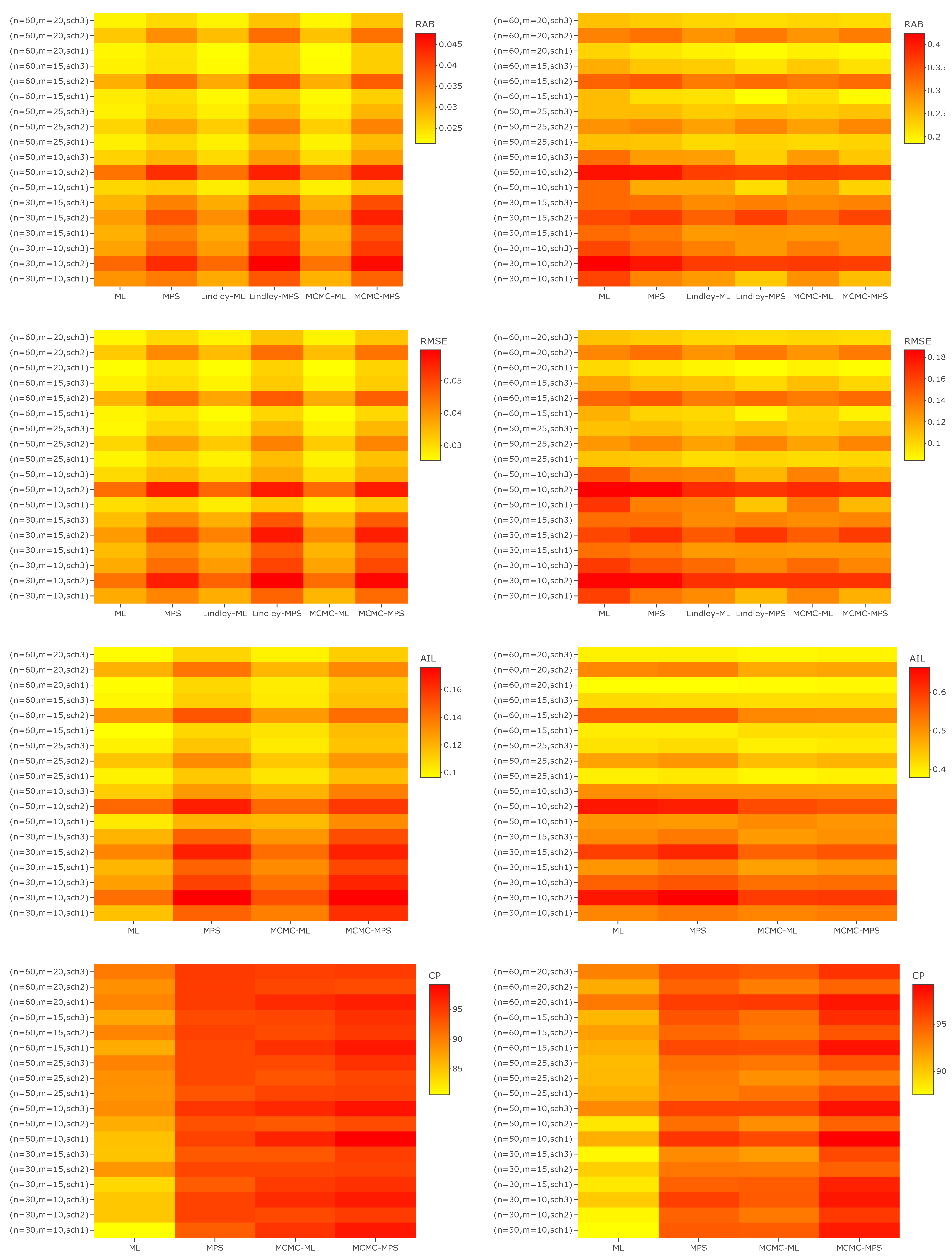
- In most cases, the MPS method performs better in terms of RAB and RMSE than the ML method for a, , and , especially in the case of small m.
- When n is fixed, the values of RAB, RMSE and AIL become smaller and smaller as m increases for each censoring scheme.
- In most cases, when n and m are fixed, Scheme 2 performs better than the other schemes in terms of RAB, RMSE, and AIL.
- In the majority of cases, LF-based Bayesian estimation using the MCMC technique and Lindley’s approximation performs better than the other approaches for all parameters in terms of RAB.
- In most cases, when comparing the RMSE of a for different approaches, PSF-based Bayesian estimation using Lindley’s approximation performs better than the others, while LF-based Bayesian estimation usually performs better than the other methods for , , and in terms of RMSE.
- For the parameter a, it is observed that PSF-based Bayesian estimation usually provides better estimates than other methods in terms of AIL, while for the parameters and the ML performs better than the other methods in terms of AIL in most cases. The AILs of when using the LF-based Bayesian method are usually shorter than the AILs using other methods.
- In terms of CP, the PSF-based Bayesian method usually performs better other approaches for , , and . On the other hand, for a the LF-based Bayesian method always surpasses the other methods in terms of CP.
- It can be concluded that the different estimates have asymptotical behaviour with large m. It is observed that the RABs, RMSEs, and AILs all tend to zero as m increases. In the case of small m, it is noted that the MLEs have larger values of RABs, RMSEs, and AILs in most of the cases when compared with the MPSEs and Bayes estimates. On the other hand, it can be seen that the various Bayes estimates perform well with both small and large m when compared with the classical estimates.
- Overall, it can be noted that the MPS method is more accurate than the ML method in the case of a small number of observed failures. On the other hand, the Bayesian estimation methods perform better than the classical methods when there is prior information about the unknown parameters. The Bayesian method requires more computational time than the classical methods. Therefore, in the case of limited time the classical methods are to be preferred over the Bayesian methods. Finally, when no information is available about the unknown parameters and the decision is taken to use non-informative priors, it is advised to use the classical methods in this case, as the acquired estimates can be expected to approximately coincide.
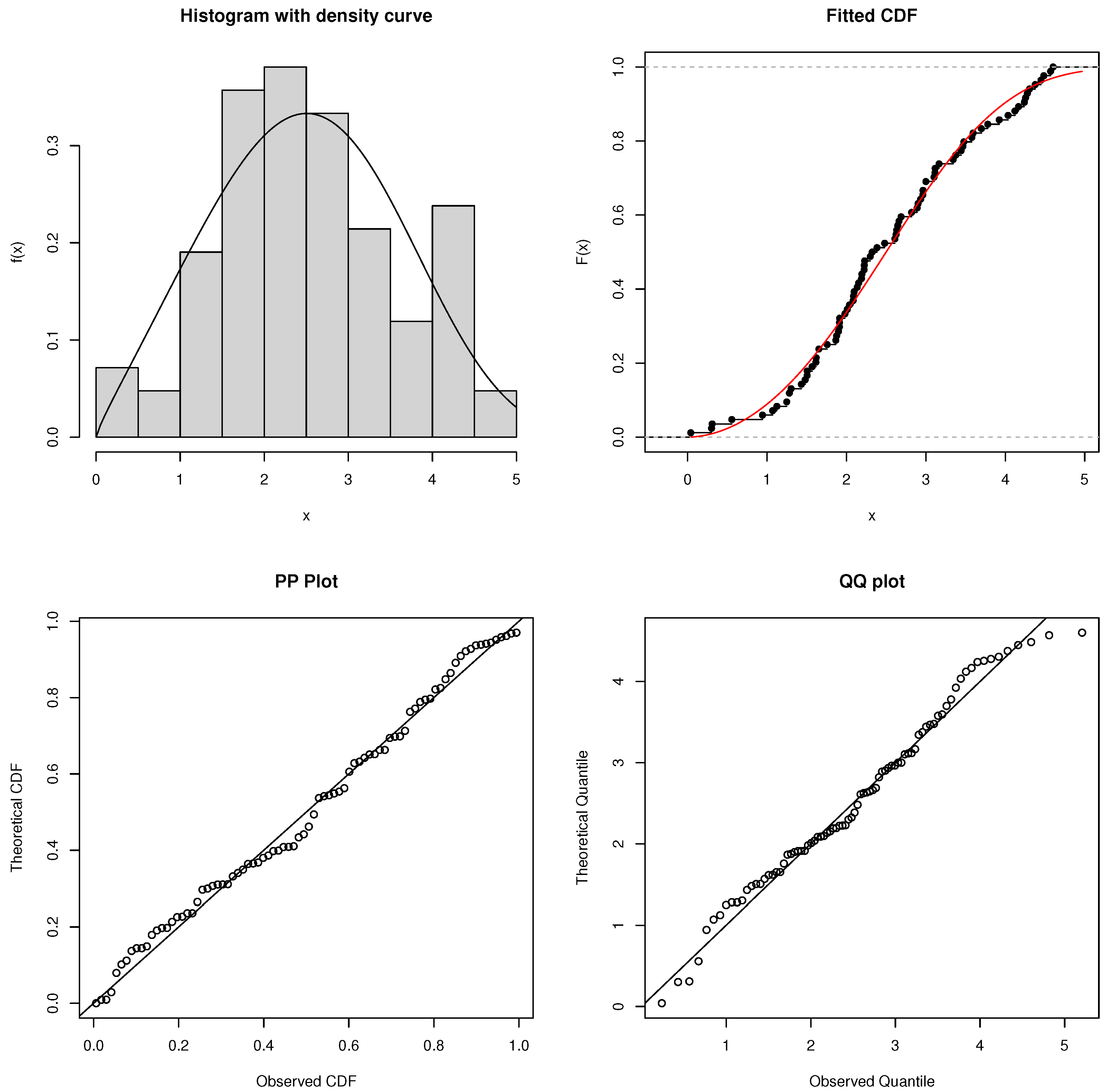
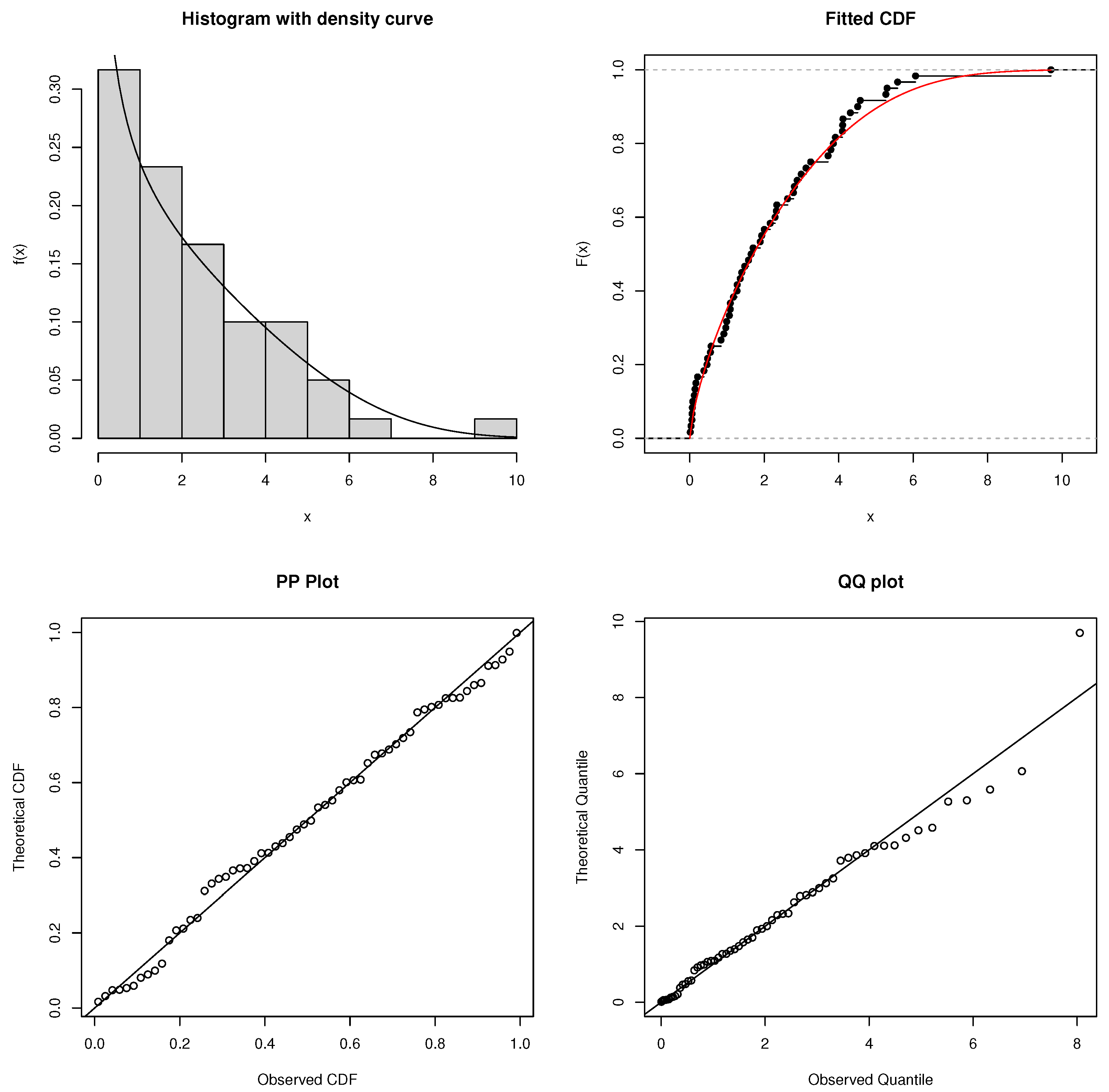
7. Real Data Analysis
7.1. Failure Times of Aircraft Windshields
7.2. Number of 1000s of Cycles to Failure for Electrical Appliances
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Second Derivatives of log-LF
Appendix B. The Second Derivatives of log-PSF
- where ,
- ,
- and .
Appendix C. The Derivatives in Lindley’s Approximation Using LF
Appendix D. The Derivatives in Lindley’s Approximation Using PSF
References
- Al-Babtain, A.A.; Shakhatreh, M.K.; Nassar, M.; Afify, A.Z. A new modified Kies family: Properties, estimation under complete and type-II censored samples, and engineering applications. Mathematics 2020, 8, 1345. [Google Scholar] [CrossRef]
- Aljohani, H.M.; Almetwally, E.M.; Alghamdi, A.S.; Hafez, E. Ranked set sampling with application of modified Kies exponential distribution. Alex. Eng. J. 2021, 60, 4041–4046. [Google Scholar] [CrossRef]
- Nassar, M.; Alam, F.M.A. Analysis of Modified Kies Exponential Distribution with Constant Stress Partially Accelerated Life Tests under Type-II Censoring. Mathematics 2022, 10, 819. [Google Scholar] [CrossRef]
- El-Raheem, A.M.A.; Almetwally, E.M.; Mohamed, M.S.; Hafez, E.H. Accelerated life tests for modified Kies exponential lifetime distribution: Binomial removal, transformers turn insulation application and numerical results. AIMS Math. 2021, 6, 5222–5255. [Google Scholar] [CrossRef]
- Ng, H.K.; Luo, L.; Hu, Y.; Duan, F. Parameter estimation of three-parameter weibull distribution based on progressively type-II censored samples. J. Stat. Comput. Simul. 2012, 82, 1661–1678. [Google Scholar] [CrossRef]
- Singh, R.; Kumar Singh, S.; Singh, U. Maximum product spacings method for the estimation of parameters of generalized inverted exponential distribution under progressive type II censoring. J. Stat. Manag. Syst. 2016, 19, 219–245. [Google Scholar] [CrossRef]
- Alshenawy, R.; Al-Alwan, A.; Almetwally, E.M.; Afify, A.Z.; Almongy, H.M. Progressive type-II censoring schemes of extended odd weibull exponential distribution with applications in medicine and engineering. Mathematics 2020, 8, 1679. [Google Scholar] [CrossRef]
- Lin, Y.J.; Okasha, H.M.; Basheer, A.M.; Lio, Y.L. Bayesian estimation of Marshall Olkin extended inverse Weibull under progressive type II censoring. Qual. Reliab. Eng. Int. 2023, 39, 931–957. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Cramer, E. The Art of Progressive Censoring: Applications to Reliability and Quality; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Cheng, R.C.; Amin, N.A. Estimating parameters in continuous univariate distributions with a shifted origin. J. R. Stat. Soc. Ser. B (Methodol.) 1983, 45, 394–403. [Google Scholar] [CrossRef]
- Ranneby, B. The Maximum Spacing Method. An Estimation Method Related to the Maximum Likelihood Method. Scand. J. Stat. 1984, 11, 93–112. [Google Scholar]
- Rahman, M.; Pearson, L.M. Estimation in two-parameter exponential distributions. J. Stat. Comput. Simul. 2001, 70, 371–386. [Google Scholar] [CrossRef]
- Singh, U.; Singh, S.K.; Singh, R.K. A comparative study of traditional estimation methods and maximum product spacings method in generalized inverted exponential distribution. J. Stat. Appl. Probab. 2014, 3, 153–169. [Google Scholar] [CrossRef]
- Rahman, M.; An, D.; Patwary, M.S. Method of product spacings parameter estimation for beta inverse weibull distribution. Far East J. Theor. Stat. 2016, 52, 1–15. [Google Scholar] [CrossRef]
- Aruna, C.V. Estimation of Parameters of Lomax Distribution by Using Maximum Product Spacings Method. Int. J. Res. Appl. Sci. Eng. Technol. 2022, 10, 1316–1322. [Google Scholar] [CrossRef]
- Teimouri, M.; Nadarajah, S. MPS: An R package for modelling shifted families of distributions. Aust. N. Z. J. Stat. 2022, 64, 86–108. [Google Scholar] [CrossRef]
- Almetwally, E.M.; Jawa, T.M.; Sayed-Ahmed, N.; Park, C.; Zakarya, M.; Dey, S. Analysis of unit-Weibull based on progressive type-II censored with optimal scheme. Alex. Eng. J. 2023, 63, 321–338. [Google Scholar] [CrossRef]
- Tashkandy, Y.A.; Almetwally, E.M.; Ragab, R.; Gemeay, A.M.; El-Raouf, M.A.; Khosa, S.K.; Hussam, E.; Bakr, M. Statistical inferences for the extended inverse Weibull distribution under progressive type-II censored sample with applications. Alex. Eng. J. 2023, 65, 493–502. [Google Scholar] [CrossRef]
- DeGroot, M.H.; Schervish, M.J. Probability and Statistics; Pearson Education, Inc.: London, UK, 2019. [Google Scholar]
- Cohen, A.C. Maximum Likelihood Estimation in the Weibull Distribution Based on Complete and on Censored Samples. Technometrics 1965, 7, 579–588. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference; Cengage Learning: Duxbury, CA, USA, 2002. [Google Scholar]
- Greene, W.H. Econometric Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 2000. [Google Scholar]
- Fathi, A.; Farghal, A.W.A.; Soliman, A.A. Bayesian and Non-Bayesian inference for Weibull inverted exponential model under progressive first-failure censoring data. Mathematics 2022, 10, 1648. [Google Scholar] [CrossRef]
- Eliwa, M.S.; EL-Sagheer, R.M.; El-Essawy, S.H.; Almohaimeed, B.; Alshammari, F.S.; El-Morshedy, M. General entropy with Bayes techniques under Lindley and MCMC for estimating the new Weibull–Pareto parameters: Theory and application. Symmetry 2022, 14, 2395. [Google Scholar] [CrossRef]
- Dey, S.; Elshahhat, A.; Nassar, M. Analysis of progressive type-II censored gamma distribution. Comput. Stat. 2022, 38, 481–508. [Google Scholar] [CrossRef]
- Lindley, D.V. Approximate Bayesian methods. Trab. Estad. Y Investig. Oper. 1980, 31, 223–245. [Google Scholar] [CrossRef]
- Chen, M.H.; Shao, Q.M. Monte Carlo Estimation of Bayesian Credible and HPD Intervals. J. Comput. Graph. Stat. 1998, 8, 69–92. [Google Scholar] [CrossRef]
- Coolen, F.; Newby, M. A note on the use of the product of spacings in Bayesian inference. KM 1991, 37, 19–32. [Google Scholar]
- Cohen, A.C.; Whitten, B.J. Parameter Estimation in Reliability and Life SPAN Models; Dekker: Nottingham, UK, 1988. [Google Scholar]
- Basu, S.; Singh, S.K.; Singh, U. Bayesian inference using product of spacings function for Progressive Hybrid Type-I censoring scheme. Statistics 2017, 52, 345–363. [Google Scholar] [CrossRef]
- Nassar, M.; Elshahhat, A. Statistical Analysis of Inverse Weibull Constant-Stress Partially Accelerated Life Tests with Adaptive Progressively Type I Censored Data. Mathematics 2023, 11, 370. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Sandhu, R.A. A Simple Simulational Algorithm for Generating Progressive Type-II Censored Samples. Am. Stat. 1995, 49, 229–230. [Google Scholar] [CrossRef]
- Kundu, D. Bayesian Inference and Life Testing Plan for the Weibull Distribution in Presence of Progressive Censoring. Technometrics 2008, 50, 144–154. [Google Scholar] [CrossRef]
- Kundu, D.; Howlader, H. Bayesian inference and prediction of the inverse Weibull distribution for Type-II censored data. Comput. Stat. Data Anal. 2010, 54, 1547–1558. [Google Scholar] [CrossRef]
- Kundu, D.; Raqab, M.Z. Bayesian inference and prediction of order statistics for a Type-II censored Weibull distribution. J. Stat. Plan. Inference 2012, 142, 41–47. [Google Scholar] [CrossRef]
- Basu, S.; Singh, S.K.; Singh, U. Estimation of inverse Lindley distribution using product of spacings function for hybrid censored data. Methodol. Comput. Appl. Probab. 2019, 21, 1377–1394. [Google Scholar] [CrossRef]
- Dey, S.; Dey, T.; Luckett, D.J. Statistical inference for the generalized inverted exponential distribution based on upper record values. Math. Comput. Simul. 2016, 120, 64–78. [Google Scholar] [CrossRef]
- Ijaz, M.; Mashwani, W.K.; Belhaouari, S.B. A novel family of lifetime distribution with applications to real and simulated data. PLoS ONE 2020, 15, e0238746. [Google Scholar] [CrossRef]
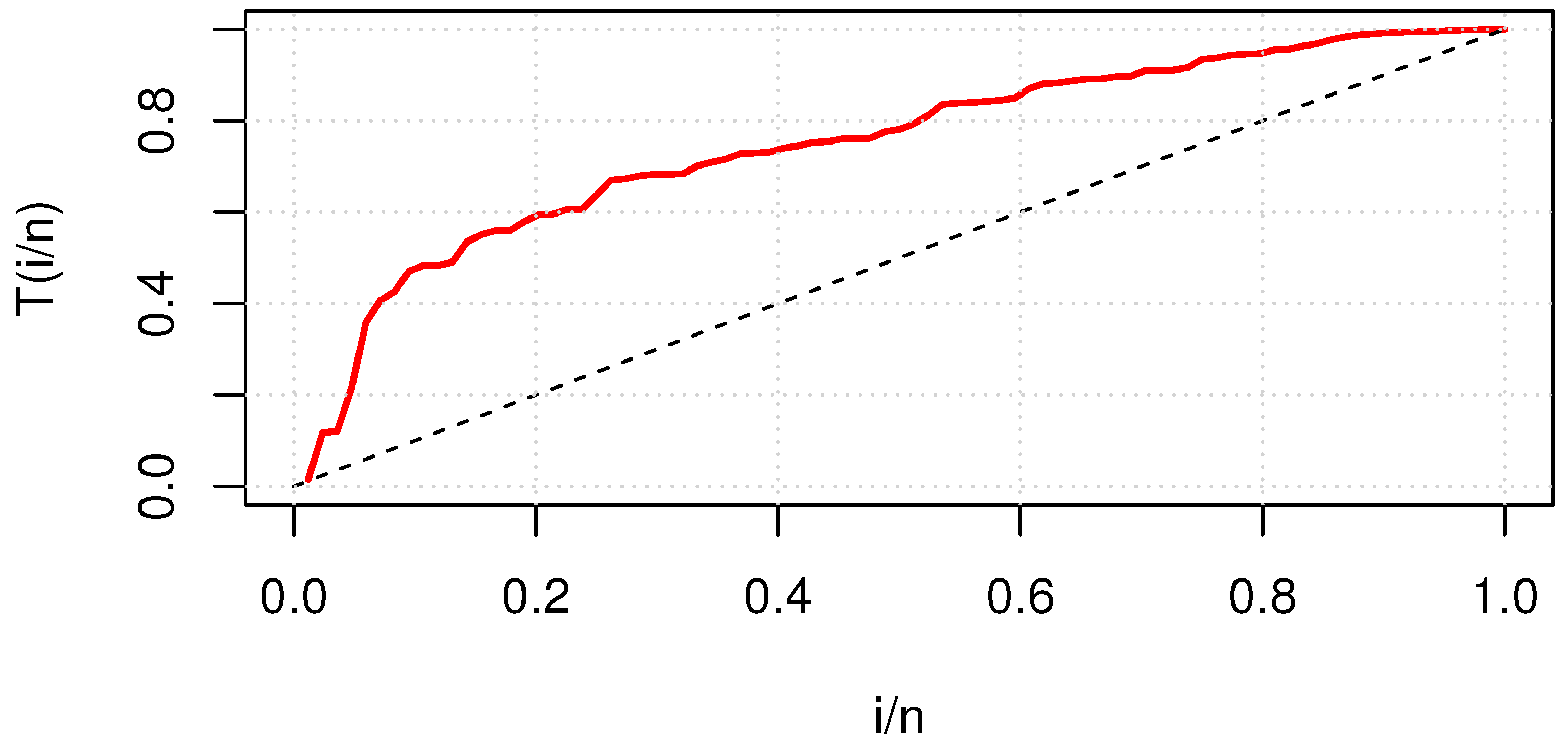
- Barlow, R.E.; Campo, R.A. Total Time on Test Processes and Applications to Failure Data Analysis; Technical Report; California Univ. Berkeley Operations Research Center: Berkeley, CA, USA, 1975. [Google Scholar]



| m | Censoring Scheme | Generated Samples |
|---|---|---|
| 10 | sch1: (2 × 9, 56) | 0.040, 0.301, 0.309, 0.557, 0.943, 1.124, 1.248, 1.281, 1.303, 1.432 |
| 30 | sch2: (2 × 27, 0 × 3) | 0.040, 0.301, 0.309, 0.557, 0.943, 1.070, 1.124, 1.248, 1.281, 1.303, 1.480, 1.615, 1.619, 1.757, 1.866, 1.876, 1.899, 1.912, 2.085, 2.097, 2.154, 2.223, 2.224, 2.324, 2.934, 3.000, 3.117, 3.166, 3.595, 4.305 |
| 42 | sch3: (1 × 42) | 0.040, 0.301, 0.309, 0.557, 1.070, 1.124, 1.248, 1.281, 1.303, 1.432, 1.480, 1.505, 1.568, 1.619, 1.652, 1.757, 1.866, 1.876, 1.899, 1.911, 1.912, 1.981, 2.010, 2.038, 2.135, 2.154, 2.190, 2.223, 2.229, 2.300, 2.324, 2.385, 2.481, 2.625, 2.632, 2.962, 3.117, 3.166, 3.344, 3.443, 3.699, 4.121 |
| sch | ML | MPS | Lindley-ML | Lindley-MPS | MCMC-ML | MCMC-MPS | |
|---|---|---|---|---|---|---|---|
| 1 | a | 1.2206 | 0.9658 | 1.4325 | 0.8454 | 1.3504 | 0.9426 |
| (0.3466) | (0.2977) | (0.2744) | (0.2723) | (0.2387) | (0.1940) | ||
| 0.1294 | 0.0853 | 0.1639 | 0.0623 | 0.1502 | 0.0821 | ||
| (0.0629) | (0.0585) | (0.0525) | (0.0538) | (0.0391) | (0.0363) | ||
| 0.9808 | 0.9710 | 0.9833 | 0.9627 | 0.9819 | 0.9669 | ||
| (0.0126) | (0.0164) | (0.0123) | (0.0141) | (0.0105) | (0.0169) | ||
| 0.0805 | 0.0958 | 0.0710 | 0.0977 | 0.0773 | 0.0992 | ||
| (0.0341) | (0.0337) | (0.0328) | (0.0336) | (0.0328) | (0.0365) | ||
| 2 | a | 1.7523 | 1.5726 | 1.8108 | 1.4385 | 1.7857 | 1.5176 |
| (0.2382) | (0.2218) | (0.2309) | (0.1767) | (0.1638) | (0.1437) | ||
| 0.2243 | 0.2143 | 0.2271 | 0.2031 | 0.2253 | 0.2110 | ||
| (0.0185) | (0.0204) | (0.0183) | (0.0170) | (0.0130) | (0.0138) | ||
| 0.9907 | 0.9860 | 0.9902 | 0.9800 | 0.9906 | 0.9830 | ||
| (0.0056) | (0.0078) | (0.0056) | (0.0050) | (0.0042) | (0.0066) | ||
| 0.0566 | 0.0761 | 0.0569 | 0.0969 | 0.0561 | 0.0863 | ||
| (0.0268) | (0.0326) | (0.0268) | (0.0251) | (0.0195) | (0.0257) | ||
| 3 | a | 1.7968 | 1.6612 | 1.8294 | 1.5703 | 1.8196 | 1.6282 |
| (0.2145) | (0.2041) | (0.212) | (0.1827) | (0.1569) | (0.1354) | ||
| 0.2309 | 0.2262 | 0.2318 | 0.2216 | 0.2317 | 0.2256 | ||
| (0.0146) | (0.0157) | (0.0146) | (0.015) | (0.0106) | (0.0111) | ||
| 0.9913 | 0.9879 | 0.9906 | 0.9838 | 0.991 | 0.9861 | ||
| (0.0049) | (0.0064) | (0.0049) | (0.0049) | (0.0037) | (0.0051) | ||
| 0.0545 | 0.0695 | 0.0562 | 0.0854 | 0.0549 | 0.0766 | ||
| (0.0244) | (0.0290) | (0.0243) | (0.0243) | (0.0180) | (0.0217) |
| sch | ML | MPS | MCMC-ML | MCMC-MPS | |
|---|---|---|---|---|---|
| 1 | a | (0.5412, 1.9000) | (0.3823, 1.5494) | (0.9035, 1.8212) | (0.5824, 1.3149) |
| [1.3588] | [1.1671] | [0.9177] | [0.7325] | ||
| (0.0062, 0.2526) | (0.0000, 0.2000) | (0.0749, 0.2225) | (0.0209, 0.1550) | ||
| [0.2464] | [0.2000] | [0.1476] | [0.1341] | ||
| (0.9561, 1.0000) | (0.9389, 1.0000) | (0.962, 0.9976) | (0.935, 0.9946) | ||
| [0.0439] | [0.0611] | [0.0356] | [0.0596] | ||
| (0.0137, 0.1474) | (0.0298, 0.1618) | (0.0215, 0.142) | (0.0346, 0.1733) | ||
| [0.1337] | [0.1320] | [0.1205] | [0.1388] | ||
| 2 | a | (1.2854, 2.2191) | (1.1379, 2.0073) | (1.4706, 2.1054) | (1.2526, 1.8175) |
| [0.9337] | [0.8693] | [0.6348] | [0.5649] | ||
| (0.188, 0.2606) | (0.1743, 0.2543) | (0.1999, 0.2505) | (0.1853, 0.2385) | ||
| [0.0726] | [0.0800] | [0.0506] | [0.0533] | ||
| (0.9797, 1.0000) | (0.9707, 1.0000) | (0.982, 0.9971) | (0.9698, 0.9939) | ||
| [0.0203] | [0.0293] | [0.0151] | [0.0241] | ||
| (0.0040, 0.1092) | (0.0121, 0.1400) | (0.0228, 0.0960) | (0.0391, 0.1367) | ||
| [0.1052] | [0.1279] | [0.0731] | [0.0976] | ||
| 3 | a | (1.3765, 2.2172) | (1.2612, 2.0612) | (1.5198, 2.1271) | (1.3551, 1.8802) |
| [0.8407] | [0.8000] | [0.6074] | [0.5251] | ||
| (0.2023, 0.2595) | (0.1955, 0.2569) | (0.2126, 0.2542) | (0.2026, 0.2459) | ||
| [0.0572] | [0.0614] | [0.0416] | [0.0432] | ||
| (0.9816, 1.0000) | (0.9753, 1.0000) | (0.9836, 0.9971) | (0.9757, 0.9945) | ||
| [0.0184] | [0.0247] | [0.0135] | [0.0188] | ||
| (0.0067, 0.1023) | (0.0126, 0.1263) | (0.0239, 0.0908) | (0.038, 0.1195) | ||
| [0.0956] | [0.1138] | [0.0670] | [0.0815] |
| m | Censoring Scheme | Generated Samples |
|---|---|---|
| 10 | sch1: (2 × 9, 32) | 0.014, 0.034, 0.059, 0.069, 0.080, 0.123, 0.142, 0.210, 0.464, 0.556 |
| 20 | sch2: (1 × 19, 21) | 0.014, 0.034, 0.059, 0.061, 0.069, 0.080, 0.123, 0.142, 0.165, 0.210, 0.464, 0.556, 0.574, 0.839, 0.991, 1.064, 1.088, 1.270, 1.275, 1.355 |
| 30 | sch3: (1 × 30) | 0.014, 0.034, 0.059, 0.061, 0.069, 0.080, 0.123, 0.142, 0.165, 0.210, 0.381, 0.464, 0.479, 0.556, 0.574, 0.839, 0.969, 0.991, 1.064, 1.270, 1.275, 1.397, 1.578, 1.702, 1.932, 2.292, 2.628, 3.248, 3.912, 4.116 |
| sch | ML | MPS | Lindley-ML | Lindley-MPS | MCMC-ML | MCMC-MPS | |
|---|---|---|---|---|---|---|---|
| 1 | a | 0.6877 | 0.5762 | 0.7767 | 0.5267 | 0.7271 | 0.5653 |
| (0.1876) | (0.1688) | (0.1651) | (0.1614) | (0.1387) | (0.1115) | ||
| 0.2084 | 0.1311 | 0.2935 | 0.1199 | 0.2423 | 0.1379 | ||
| (0.1543) | (0.1270) | (0.1287) | (0.1265) | (0.1186) | (0.0892) | ||
| 0.8591 | 0.8549 | 0.8569 | 0.8521 | 0.8590 | 0.8508 | ||
| (0.0421) | (0.0428) | (0.0420) | (0.0427) | (0.0432) | (0.0462) | ||
| 0.3591 | 0.3070 | 0.4131 | 0.2851 | 0.3779 | 0.3075 | ||
| (0.1367) | (0.1238) | (0.1256) | (0.1218) | (0.1257) | (0.1041) | ||
| 2 | a | 0.7036 | 0.6391 | 0.7479 | 0.5894 | 0.7226 | 0.6323 |
| (0.1314) | (0.1228) | (0.1237) | (0.1123) | (0.0970) | (0.0857) | ||
| 0.2547 | 0.2243 | 0.2816 | 0.1976 | 0.2675 | 0.2262 | ||
| (0.0828) | (0.0841) | (0.0783) | (0.0797) | (0.0603) | (0.0606) | ||
| 0.8452 | 0.8335 | 0.8472 | 0.8233 | 0.8447 | 0.8287 | ||
| (0.0408) | (0.0418) | (0.0407) | (0.0406) | (0.0358) | (0.0374) | ||
| 0.4098 | 0.4012 | 0.4194 | 0.3846 | 0.4149 | 0.4029 | ||
| (0.0865) | (0.0859) | (0.0860) | (0.0843) | (0.0749) | (0.0731) | ||
| 3 | a | 0.7150 | 0.6651 | 0.7300 | 0.6258 | 0.7227 | 0.6528 |
| (0.1004) | (0.0952) | (0.0993) | (0.0867) | (0.0698) | (0.0654) | ||
| 0.2967 | 0.2809 | 0.3055 | 0.2748 | 0.3022 | 0.2790 | ||
| (0.0533) | (0.0555) | (0.0526) | (0.0551) | (0.0396) | (0.0408) | ||
| 0.8327 | 0.8200 | 0.8318 | 0.8043 | 0.8320 | 0.8146 | ||
| (0.0419) | (0.0429) | (0.0419) | (0.0400) | (0.0291) | (0.0309) | ||
| 0.4561 | 0.4588 | 0.4573 | 0.4644 | 0.4581 | 0.4596 | ||
| (0.0791) | (0.0765) | (0.0791) | (0.0763) | (0.0569) | (0.0550) |
| sch | ML | MPS | MCMC-ML | MCMC-MPS | |
|---|---|---|---|---|---|
| 1 | a | (0.3200, 1.0554) | (0.2453, 0.9070) | (0.4783, 1.0092) | (0.3570, 0.7898) |
| [0.7354] | [0.6617] | [0.5308] | [0.4329] | ||
| (0.0000, 0.5108) | (0.0000, 0.3799) | (0.0365, 0.4687) | (0.0058, 0.3122) | ||
| [0.5108] | [0.3799] | [0.4322] | [0.3063] | ||
| (0.7767, 0.9416) | (0.7711, 0.9388) | (0.7739, 0.9404) | (0.7587, 0.9364) | ||
| [0.1649] | [0.1677] | [0.1666] | [0.1777] | ||
| (0.0910, 0.6271) | (0.0644, 0.5496) | (0.1447, 0.6213) | (0.1249, 0.5134) | ||
| [0.5360] | [0.4852] | [0.4766] | [0.3885] | ||
| 2 | a | (0.4461, 0.9611) | (0.3985, 0.8798) | (0.5417, 0.9116) | (0.4696, 0.7958) |
| [0.5150] | [0.4813] | [0.3698] | [0.3262] | ||
| (0.0924, 0.4169) | (0.0596, 0.3891) | (0.1491, 0.3818) | (0.1105, 0.3443) | ||
| [0.3245] | [0.3295] | [0.2327] | [0.2338] | ||
| (0.7652, 0.9251) | (0.7515, 0.9155) | (0.7721, 0.9099) | (0.7533, 0.8976) | ||
| [0.1599] | [0.1640] | [0.1378] | [0.1444] | ||
| (0.2403, 0.5794) | (0.2329, 0.5695) | (0.2672, 0.5588) | (0.2639, 0.5485) | ||
| [0.3391] | [0.3366] | [0.2916] | [0.2846] | ||
| 3 | a | (0.5183, 0.9118) | (0.4786, 0.8517) | (0.5887, 0.8609) | (0.5292, 0.7851) |
| [0.3935] | [0.3732] | [0.2721] | [0.2559] | ||
| (0.1921, 0.4012) | (0.1722, 0.3896) | (0.2291, 0.3843) | (0.2001, 0.3586) | ||
| [0.2091] | [0.2174] | [0.1552] | [0.1586] | ||
| (0.7506, 0.9148) | (0.7359, 0.9042) | (0.7757, 0.8896) | (0.75, 0.8706) | ||
| [0.1642] | [0.1683] | [0.1139] | [0.1206] | ||
| (0.3011, 0.6112) | (0.3089, 0.6086) | (0.3443, 0.5681) | (0.3534, 0.5665) | ||
| [0.3101] | [0.2997] | [0.2238] | [0.2131] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurdi, T.; Nassar, M.; Alam, F.M.A. Bayesian Estimation Using Product of Spacing for Modified Kies Exponential Progressively Censored Data. Axioms 2023, 12, 917. https://doi.org/10.3390/axioms12100917
Kurdi T, Nassar M, Alam FMA. Bayesian Estimation Using Product of Spacing for Modified Kies Exponential Progressively Censored Data. Axioms. 2023; 12(10):917. https://doi.org/10.3390/axioms12100917
Chicago/Turabian StyleKurdi, Talal, Mazen Nassar, and Farouq Mohammad A. Alam. 2023. "Bayesian Estimation Using Product of Spacing for Modified Kies Exponential Progressively Censored Data" Axioms 12, no. 10: 917. https://doi.org/10.3390/axioms12100917









