Quadratic Phase Multiresolution Analysis and the Construction of Orthonormal Wavelets in L²(ℝ)

Abstract

The multi-resolution analysis (MRA) associated with quadratic phase Fourier transform (QPFT) serves as a tool to construct orthogonal bases of the $L^2\left(\mathbb{R}\right)$. Consequently, it assumes a pivotal role in facilitating potential applications of QPFT. Inspired by the sampling theorem applicable to band-limited signals in the QPFT domain, this paper formulates the development of the MRA linked with QPFT. Subsequently, we develop a method for constructing orthogonal bases for $L^2\left(\mathbb{R}\right)$, followed by some examples.

1. Introduction

The Fourier transform (FT) is a remarkable discovery in the field of mathematical sciences, which has had a profound impact on many branches of science and engineering [1,2]. Over time, the domain of Fourier analysis has witnessed numerous mathematical breakthroughs, leading to significant advancements and profound implications of the classical Fourier transform. Notable developments that stem from the conventional Fourier transform include the fractional Fourier transform [3,4], linear canonical transform [5], special affine Fourier transform [6], and the relatively recent quadratic-phase Fourier transform [7]. The quadratic-phase Fourier transform (QPFT) extends the classical Fourier transform, incorporating quadratic phase factors into its kernel. In the QPFT, the signal’s time-domain representation is multiplied by a quadratic phase term before computing its frequency-domain representation. This additional quadratic phase term allows for a more flexible analysis of signals with time-varying frequency content. The QPFT provides a unified framework for handling transient and non-transient signals, making it particularly useful for analyzing signals with time-varying properties. It has found applications in various fields, including signal processing, time-frequency analysis, and communication systems. The mathematical expression for the QPFT involves five real parameters $(A,B,C,D,E)$ that control characteristics of the quadratic phase term. Adjusting these parameters can tailor the QPFT to suit specific signal processing requirements. Overall, the quadratic-phase Fourier transform enhances the traditional Fourier transform’s capabilities, enabling a more versatile and powerful analysis of signals in the time-frequency domain. Shah et al. studied short-time quadratic-phase Fourier transform as well as quadratic-phase wavelet transform (QPWT) with many applications in [8,9]. Also, the quadratic phase Fourier wavelet transform was explored by Prasad and Sharma in [10]. Over the past decades, various integral transforms, including the Fourier, fractional Fourier, and linear canonical transforms, have been extensively explored in time-frequency analysis.

On the other hand, multiresolution analysis (MRA) is a powerful mathematical framework used in signal and image processing introduced by Mallat [11], particularly in the field of wavelet analysis. It provides a systematic and hierarchical approach to analyzing signals or images at different levels of detail or resolution. The concept of MRA is rooted in the idea of representing a signal or an image in terms of a series of subspaces, each capturing different levels of frequency or scale information. Madych [12] established elementary properties of MRA in $L^2\left({\mathbb{R}}^n\right)$ with scaling functions represented as characteristic functions. Subsequently, Zhang [13] explored scaling functions and wavelets in standard MRA, providing a characterization of the support of the Fourier transform of these scaling functions. Malhotra and Vashisht [14] contributed to understanding scaling functions on Euclidean spaces. The MRA associated with FrWT was also introduced in [15], where FrWT analyzes signals in the time-frequency-FrFD domain. Ahmad [16] studied fractional MRA and associated scaling functions in $L^2\left(\mathbb{R}\right).$ Dai et al. [17] proposed a novel fractional wavelet transform (FRWT) and studied MRA associated with the developed FRWT, together with the construction of the orthogonal fractional wavelets. Shah and Lone [18,19] studied special affine MRA and the construction of orthonormal wavelets in $L^2\left(\mathbb{R}\right)$ and studied Shannon’s sampling theorem for the quadratic-phase Fourier transform, which serves as a comprehensive sampling theorem applicable to a broad range of integral transforms. Shah and Tantary [20] formulated the sampling theorem for the QPFT and developed a novel convolution structure for efficient filtering in the quadratic-phase Fourier domain and also gave the advantages of the proposed convolution structure and its integration with the Wigner distribution to filter out undesired signal components. As a generalization of FT, QPFT can represent adaptively signals in both time and FT domains. Therefore, QPFT not only breaks through the limitation of FT in time-Fourier domain analysis but also overcomes the limitation of FT in indicating the signal’s characteristics. QPFT successfully inherits the advantages of MRA for FT. The MRA and the construction of orthogonal wavelets associated with QPFT are crucial in its perspective applications. Thus, detecting the MRA and the construction of the orthogonal wavelets related to QPFT is necessary. Therefore, our primary concern is introducing the notion of quadratic phase MRA, which allows a smoother construction of orthonormal bases simply and insightfully.

The main contributions of this article are as follows:

• To give an alternative proof of Shannon’s sampling theorem associated with the quadratic phase Fourier transform.
• Inspired by the sampling theorem of band-limited signals in the QPFT domain, the MRA associated with quadratic phase wavelet transform is developed.
• Discuss the construction of the orthonormal basis of $L^2\left(\mathbb{R}\right)$ starting from a given scaling function.
• To give examples of quadratic phase wavelets from given scaling functions.

The rest of the article follows this structure: in Section 2, we offer a comprehensive introduction to the basics, covering the QPFT and also obtain some of its fundamental properties that are new in the literature. Moving on to Section 3, we give an alternative proof of the sampling theorem for the band-limited theorem in the QPFT domain. Based on this sampling theorem, we define a novel MRA and discuss constructing an orthonormal basis for $L^2\left(\mathbb{R}\right)$, followed by some examples in Section 4. Finally, in Section 5, we conclude our paper.

2. Preliminaries

In time-frequency analysis, a recent signal processing tool that has garnered attention is the quadratic-phase Fourier transform (QPFT), introduced by Castro et al. [21]. This transformative tool offers a unified approach to handling transient and non-transient signals.

Definition 1.

Given a parameter set $\mathsf{\Lambda }=(A,B,C,D,E)$, the QPFT of $f\in L^2\left(\mathbb{R}\right)$ is denoted as $Q^{\mathsf{\Lambda }}f$ and is defined by

$$\begin{array}{c}\hfill \left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)=\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}f\left(\mathit{t}\right)K_{\mathsf{\Lambda }}(\mathit{t},\xi )d\mathit{t},\end{array}$$

where $K_{\mathsf{\Lambda }}(\mathit{t},\xi )$ is a quadratic-phase kernel and is given by

$$\begin{array}{c}\hfill K_{\mathsf{\Lambda }}(\mathit{t},\xi )=e^{i(A{\mathit{t}}^2-B\mathit{t}\xi +C{\xi }^2+D\mathit{t}+E\xi )}\end{array}$$

and the corresponding inversion formula and Parseval’s formula for the QPFT reads

$$\begin{array}{cc}\hfill f\left(\mathit{t}\right)& ={\int }_{\mathbb{R}}\left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)\overline{K_{\mathsf{\Lambda }}(\mathit{t},\xi )}d\xi ,\hfill \end{array}$$

and

$$\langle f,g\rangle =\left|B\right|\langle Q^{\mathsf{\Lambda }}f,Q^{\mathsf{\Lambda }}g\rangle \forall f,g\in L^2\left(\mathbb{R}\right),$$

where $A,B,C,D,E\in \mathbb{R},B\ne 0.$

Some Properties Associated with the Quadratic Phase Fourier Transform

The lemma below gives some formula for the QPFT, that will be used later in this paper.

Lemma 1.

Let $f\in L^2\left(\mathbb{R}\right),$ $a\ne 0$, then the following holds:

(1) 

$\left(Q^{\mathsf{\Lambda }}\left\{f\left(a\mathit{t}\right)\right\}\right)\left(\xi \right)=\frac{1}{\left|a\right|}{e}^{i\left\{C\left({\xi }^2-{\left(\frac{\xi }{a}\right)}^2\right)+E\left(\xi -\frac{\xi }{a}\right)\right\}}\left(Q^{\mathsf{\Lambda }}\left\{e^{i\left\{A{\left(\frac{\mathit{t}}{a}\right)}^2-A{\mathit{t}}^2+D\left(\frac{\mathit{t}}{a}\right)-D\mathit{t}\right\}}f\left(\mathit{t}\right)\right\}\right)\left(\frac{\xi }{a}\right).$

(2) 

$\left(Q^{\mathsf{\Lambda }}\left\{e^{i\left\{A{\left(a\mathit{t}\right)}^2-A{\mathit{t}}^2+D\left(a\mathit{t}\right)-D\mathit{t}\right\}}f\left(a\mathit{t}\right)\right\}\right)\left(\xi \right)=\frac{1}{\left|a\right|}{e}^{i\left\{C\left({\xi }^2-{\left(\frac{\xi }{a}\right)}^2\right)+E\left(\xi -\frac{\xi }{a}\right)\right\}}\left(Q^{\mathsf{\Lambda }}f\left(\mathit{t}\right)\right)\left(\frac{\xi }{a}\right).$

Proof. 

Using the definition of the quadratic phase Fourier transform, we have

$$\begin{array}{cc}\hfill & \left(Q^{\mathsf{\Lambda }}\left\{f\left(a\mathit{t}\right)\right\}\right)\left(\xi \right)\hfill \\ \hfill & =\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}f\left(a\mathit{t}\right)e^{i(A{\mathit{t}}^2-B\mathit{t}\xi +C{\xi }^2+D\mathit{t}+E\xi )}d\mathit{t}\hfill \\ \hfill & =\frac{1}{\sqrt{2\pi }\left|a\right|}{\int }_{\mathbb{R}}f\left(\mathit{t}\right)e^{i\{A{\left(\frac{\mathit{t}}{a}\right)}^2-\frac{B}{a}\mathit{t}\xi +C{\xi }^2+\frac{D}{a}\mathit{t}+E\xi \}}d\mathit{t}\hfill \\ \hfill & =\frac{1}{\sqrt{2\pi }\left|a\right|}{\int }_{\mathbb{R}}{e}^{i\left\{A{\left(\frac{\mathit{t}}{a}\right)}^2-A{\mathit{t}}^2+D\left(\frac{\mathit{t}}{a}\right)-D\mathit{t}\right\}}f\left(\mathit{t}\right)e^{i\left\{A{\mathit{t}}^2-B\mathit{t}\left(\frac{\xi }{a}\right)+C{\left(\frac{\xi }{a}\right)}^2+D\mathit{t}+E\left(\frac{\xi }{a}\right)\right\}}\hfill \\ \hfill & \times e^{i\left\{C\left({\xi }^2-{\left(\frac{\xi }{a}\right)}^2\right)+E\left(\xi -\frac{\xi }{a}\right)\right\}}d\mathit{t}\hfill \\ \hfill & =\frac{1}{\left|a\right|}{e}^{i\left\{C\left({\xi }^2-{\left(\frac{\xi }{a}\right)}^2\right)+E\left(\xi -\frac{\xi }{a}\right)\right\}}{\int }_{\mathbb{R}}{e}^{i\left\{A{\left(\frac{\mathit{t}}{a}\right)}^2-A{\mathit{t}}^2+D\left(\frac{\mathit{t}}{a}\right)-D\mathit{t}\right\}}f\left(\mathit{t}\right)\hfill \\ \hfill & \times \frac{1}{\sqrt{2\pi }}{e}^{i\left\{A{\mathit{t}}^2-B\mathit{t}\left(\frac{\xi }{a}\right)+C{\left(\frac{\xi }{a}\right)}^2+D\mathit{t}+E\left(\frac{\xi }{a}\right)\right\}}d\mathit{t}\hfill \\ \hfill & =\frac{1}{\left|a\right|}{e}^{i\left\{C\left({\xi }^2-{\left(\frac{\xi }{a}\right)}^2\right)+E\left(\xi -\frac{\xi }{a}\right)\right\}}\left(Q^{\mathsf{\Lambda }}\left\{e^{i\left\{A{\left(\frac{\mathit{t}}{a}\right)}^2-A{\mathit{t}}^2+D\left(\frac{\mathit{t}}{a}\right)-D\mathit{t}\right\}}f\left(\mathit{t}\right)\right\}\right)\left(\frac{\xi }{a}\right),\hfill \end{array}$$

i.e.,

$$\begin{array}{c}\hfill \left(Q^{\mathsf{\Lambda }}\left\{f\left(a\mathit{t}\right)\right\}\right)\left(\xi \right)=\frac{1}{\left|a\right|}{e}^{i\left\{C\left({\xi }^2-{\left(\frac{\xi }{a}\right)}^2\right)+E\left(\xi -\frac{\xi }{a}\right)\right\}}\left(Q^{\mathsf{\Lambda }}\left\{e^{i\left\{A{\left(\frac{\mathit{t}}{a}\right)}^2-A{\mathit{t}}^2+D\left(\frac{T}{a}\right)-D\mathit{t}\right\}}f\left(\mathit{t}\right)\right\}\right)\left(\frac{\xi }{a}\right).\end{array}$$

Now,

$$\begin{array}{cc}\hfill & \left(Q^{\mathsf{\Lambda }}\left\{\varphi \left(\mathit{t}\right)f\left(a\mathit{t}\right)\right\}\right)\left(\xi \right)\hfill \\ \hfill & =\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}\varphi \left(\mathit{t}\right)f\left(a\mathit{t}\right)e^{i(A{\mathit{t}}^2-B\mathit{t}\xi +C{\xi }^2+D\mathit{t}+E\xi )}d\mathit{t}\hfill \\ \hfill & =\frac{1}{\sqrt{2\pi }\left|a\right|}{\int }_{\mathbb{R}}\varphi \left(\frac{\mathit{t}}{a}\right)f\left(\mathit{t}\right)e^{i\left\{A{\left(\frac{\mathit{t}}{a}\right)}^2-B\frac{\mathit{t}}{a}\xi +C{\xi }^2+D\frac{\mathit{t}}{a}+E\xi \right\}}d\mathit{t}\hfill \\ \hfill & =\frac{1}{\left|a\right|}{e}^{i\left\{C\left({\xi }^2-{\left(\frac{\xi }{a}\right)}^2\right)+E\left(\xi -\frac{\xi }{a}\right)\right\}}\left(Q^{\mathsf{\Lambda }}\left\{e^{i\left\{A{\left(\frac{\mathit{t}}{a}\right)}^2-A{\mathit{t}}^2+D\left(\frac{\mathit{t}}{a}\right)-D\mathit{t}\right\}}\varphi \left(\frac{\mathit{t}}{a}\right)f\left(\mathit{t}\right)\right\}\right)\left(\frac{\xi }{a}\right).\hfill \end{array}$$

If we take $\varphi \left(\mathit{t}\right)=e^{-i\left\{A{\mathit{t}}^2-A{\left(a\mathit{t}\right)}^2+D\mathit{t}-D\left(a\mathit{t}\right)\right\}},$ then

$$\begin{array}{c}\hfill \left(Q^{\mathsf{\Lambda }}\left\{e^{-i\left\{A{\mathit{t}}^2-A{\left(a\mathit{t}\right)}^2+D\mathit{t}-D\left(a\mathit{t}\right)\right\}}\right\}\right)\left(\xi \right)=\frac{1}{\left|a\right|}{e}^{i\left\{C\left({\xi }^2-{\left(\frac{\xi }{a}\right)}^2\right)+E\left(\xi -\frac{\xi }{a}\right)\right\}}\left(Q^{\mathsf{\Lambda }}f\left(\mathit{t}\right)\right)\left(\frac{\xi }{a}\right),\end{array}$$

i.e.,

$$\begin{array}{c}\hfill \left(Q^{\mathsf{\Lambda }}\left\{e^{i\left\{A{\left(a\mathit{t}\right)}^2-A{\mathit{t}}^2+D\left(a\mathit{t}\right)-D\mathit{t}\right\}}f\left(a\mathit{t}\right)\right\}\right)\left(\xi \right)=\frac{1}{\left|a\right|}{e}^{i\left\{C\left({\xi }^2-{\left(\frac{\xi }{a}\right)}^2\right)+E\left(\xi -\frac{\xi }{a}\right)\right\}}\left(Q^{\mathsf{\Lambda }}f\left(\mathit{t}\right)\right)\left(\frac{\xi }{a}\right).\end{array}$$

(1)

This finishes the proof. □

The following lemma is an important tool in proving the Shannon’s sampling theorem in the QPFT domain. It says that if a function f is band-limited in the quadratic phase Fourier transform domain, then there is a function g depending on f such that it is band-limited in the Fourier domain. Note that, from here on, we take the value B in $\mathsf{\Lambda }$ as positive.

Lemma 2.

Assume a signal $f\left(\mathit{t}\right)$ is band limited to ${\mathsf{\Omega }}_{\mathsf{\Lambda }}$ in quadratic phase Fourier domain with parameter $\mathsf{\Lambda }=(A,B,C,D,E)$ and $B>0.$ Let

$$\begin{array}{c}\hfill g\left(\mathit{t}\right)={\int }_{-\infty }^{\infty }\left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)e^{-i[-B\xi \mathit{t}+C{\xi }^2+E\xi ]}d\xi ,\end{array}$$

(2)

then $g\left(\mathit{t}\right)$ is a signal band-limited in $(-B{\mathsf{\Omega }}_{\mathsf{\Lambda }},B{\mathsf{\Omega }}_{\mathsf{\Lambda }})$ in the Fourier domain.

Proof. 

Given,

$$\begin{array}{cc}\hfill g\left(\mathit{t}\right)& ={\int }_{-\infty }^{\infty }\left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)e^{-i[-B\xi \mathit{t}+C{\xi }^2+E\xi ]}d\xi .\hfill \end{array}$$

Taking the Fourier transform, we have

$$\begin{array}{cc}\hfill \left(\mathfrak{F}\left\{g\right(\mathit{t}\left)\right\}\right)\left(\omega \right)& ={\int }_{-\infty }^{\infty }\left\{{\int }_{-\infty }^{\infty }\left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)e^{-i[-B\xi \mathit{t}+C{\xi }^2+E\xi ]}d\xi \right\}\frac{e^{-i\mathit{t}\omega }}{\sqrt{2\pi }}d\mathit{t}\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }\left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)e^{-i[C{\xi }^2+E\xi ]}\left\{{\int }_{-\infty }^{\infty }{e}^{-i[-B\xi \mathit{t}]}\frac{e^{-i\mathit{t}\omega }}{\sqrt{2\pi }}d\mathit{t}\right\}d\xi \hfill \\ \hfill & ={\int }_{-\infty }^{\infty }\left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)e^{-i[C{\xi }^2+E\xi ]}\left\{\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }{e}^{i(B\xi -\omega )\mathit{t}}d\mathit{t}\right\}d\xi \hfill \\ \hfill & ={\int }_{-\infty }^{\infty }\left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)e^{-i\left(C{\xi }^2+E\xi \right)}\sqrt{2\pi }\delta (B\xi -\omega )d\xi \hfill \\ \hfill & ={\int }_{-\infty }^{-\infty }\left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)e^{-i(C{\xi }^2+E\xi )}\sqrt{2\pi }\delta (B\xi -\omega )d\xi \hfill \\ \hfill & =\frac{\sqrt{2\pi }}{B}{\int }_{-\infty }^{-\infty }\left(Q^{\mathsf{\Lambda }}f\right)\left(\frac{\xi }{B}\right)e^{-i\left(C\frac{{\xi }^2}{B^2}+E\frac{\xi }{B}\right)}\sqrt{2\pi }\delta (\xi -\omega )d\xi \hfill \\ \hfill & =\frac{\sqrt{2\pi }}{B}\left(Q^{\mathsf{\Lambda }}f\right)\left(\frac{\omega }{B}\right)e^{-i\left(C\frac{{\omega }^2}{B^2}+E\frac{\omega }{B}\right)},\hfill \\ \hfill \mathrm{i}.\mathrm{e}.,\left(\mathfrak{F}\left\{g\right(\mathit{t}\left)\right\}\right)\left(\omega \right)& =\frac{\sqrt{2\pi }}{B}\left(Q^{\mathsf{\Lambda }}f\right)\left(\frac{\omega }{B}\right)e^{-i(C\frac{{\omega }^2}{B^2}+E\frac{\omega }{B})}.\hfill \end{array}$$

Since $\left(Q^{\mathsf{\Lambda }}f\right)\left(\omega \right)$ is band-limited to ${\mathsf{\Omega }}_{\mathsf{\Lambda }},$ so $\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\left(Q^{\mathsf{\Lambda }}f\right)\subset [-{\mathsf{\Omega }}_{\mathsf{\Lambda }},{\mathsf{\Omega }}_{\mathsf{\Lambda }}]$, i.e.,

$$\begin{array}{cc}\hfill \left(Q^{\mathsf{\Lambda }}f\right)\left(\omega \right)& \ne 0\mathrm{a}.\mathrm{e}.,\left|\omega \right|>{\mathsf{\Omega }}_{\mathsf{\Lambda }}\hfill \\ \hfill \Rightarrow \left(Q^{\mathsf{\Lambda }}f\right)\left(\frac{\omega }{B}\right)& \ne 0\mathrm{a}.\mathrm{e}.,\left|\frac{\omega }{B}\right|>{\mathsf{\Omega }}_{\mathsf{\Lambda }}\hfill \\ \hfill \Rightarrow \left(Q^{\mathsf{\Lambda }}f\right)\left(\frac{\omega }{B}\right)& \ne 0\mathrm{a}.\mathrm{e}.,\left|\omega \right|>B{\mathsf{\Omega }}_{\mathsf{\Lambda }},\hfill \end{array}$$

i.e., supp $\left(\mathfrak{F}\left\{g\left(\mathit{t}\right)\right\}\right)\subset [-B{\mathsf{\Omega }}_{\mathsf{\Lambda }},B{\mathsf{\Omega }}_{\mathsf{\Lambda }}]$ Thus, $\left(\mathfrak{F}\left\{g\left(\mathit{t}\right)\right\}\right)\left(\omega \right)\ne 0\mathrm{a}.\mathrm{e}.,\left|\omega \right|>B{\mathsf{\Omega }}_{\mathsf{\Lambda }}.$ Therefore, $g\left(\mathit{t}\right)$ is band-limited to $B{\mathsf{\Omega }}_{\mathsf{\Lambda }}$ in the Fourier domain. □

3. Sampling Theorem for Band Limited Signal in QPFT Domain

The sampling theorem, also known as the Nyquist–Shannon sampling theorem, is a fundamental principle in signal processing and digital signal theory. It provides guidance on how to accurately reconstruct a continuous-time analog signal from its discrete samples. The theorem states that, to avoid aliasing and to perfectly reconstruct the original signal, the sampling rate (i.e., the number of samples taken per second) must be at least twice the highest frequency in the analog signal. Mathematically, if a band-limited signal contains a range of k frequencies, it can be accurately reconstructed by taking $2k$ evenly spaced samples. Taking additional samples would prove redundant, whereas fewer samples would lead to a loss in signal quality. The sampling theorem can be expressed as follows: If a continuous-time signal is band-limited, meaning it contains no frequencies higher than a certain maximum frequency (known as the Nyquist frequency), then the signal can be completely reconstructed from its samples if the sampling rate is greater than or equal to twice the Nyquist frequency.

Inspired by the sampling theorem of band-limited signal in QPFT domain, in this section, the MRA associated with QPFT is established in the next section. The sampling theorem of a band-limited signal associated with QPFT is given by the following theorem.

Theorem 1.

Let signal $f\left(\mathit{t}\right)$ be band-limited to ${\mathsf{\Omega }}_{\mathsf{\Lambda }}$ in QPFT-domain having parameter $\mathsf{\Lambda }=(A,B,C,D,E),B>0.$ Then, the following sampling theorem expansion for $f\left(\mathit{t}\right)$ holds:

$$\begin{array}{c}\hfill f\left(t\right)=e^{i(A{\mathit{t}}^2+D\mathit{t})}\sum _{n\in \mathbb{Z}}f\left(nT\right)e^{iA{\left(nT\right)}^2+D\left(nT\right)}sinc\left(\frac{B{\mathsf{\Omega }}_{\mathsf{\Lambda }}(\mathit{t}-nT)}{\pi }\right),\end{array}$$

(3)

where T is the sampling period and satisfies $T=\frac{\pi }{B{\mathsf{\Omega }}_{\mathsf{\Lambda }}}$ and is called as the Nyquist rate of sampling theorem associated with the quadratic phase Fourier transform.

Proof. 

We have

$$\begin{array}{cc}\hfill f\left(\mathit{t}\right)& =\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}\left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)e^{-i(A{\mathit{t}}^2-B\mathit{t}\xi +C{\xi }^2+D\mathit{t}+E\xi )}d\xi \hfill \\ \hfill & =\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}\left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)e^{-i(-B\mathit{t}\xi +C{\xi }^2+E\xi )}{e}^{-i(A{\mathit{t}}^2+D\mathit{t})}d\xi \hfill \\ \hfill & =\left\{{\int }_{\mathbb{R}}\left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)e^{-i(-B\mathit{t}\xi +C{\xi }^2+E\xi )}d\xi \right\}\frac{1}{\sqrt{2\pi }}{e}^{-i(A{\mathit{t}}^2+D\mathit{t})}\hfill \\ \hfill & =\frac{1}{\sqrt{2\pi }}{e}^{-i(A{\mathit{t}}^2+D\mathit{t})}g\left(\mathit{t}\right).\hfill \end{array}$$

Since $g\left(\mathit{t}\right)$ is band-limited to $(-B{\mathsf{\Omega }}_{\mathsf{\Lambda }},B{\mathsf{\Omega }}_{\mathsf{\Lambda }})$ in the Fourier domain, by applying the classical Shannon’s sampling theorem, we get

$$\begin{array}{c}\hfill g\left(\mathit{t}\right)=\sum _{n\in \mathbb{Z}}g\left(nT\right)sinc\left(\frac{B{\mathsf{\Omega }}_{\mathsf{\Lambda }}(\mathit{t}-nT)}{\pi }\right),\end{array}$$

where $T=\frac{\pi }{B{\mathsf{\Omega }}_{\mathsf{\Lambda }}}$ is the sample period. Therefore,

$$\begin{array}{cc}\hfill f\left(\mathit{t}\right)=& \frac{1}{\sqrt{2\pi }}{e}^{-i(A{\mathit{t}}^2+D\mathit{t})}\sum _{n\in \mathbb{Z}}g\left(nT\right)sinc\left(\frac{B{\mathsf{\Omega }}_{\mathsf{\Lambda }}(\mathit{t}-nT)}{\pi }\right)\hfill \\ \hfill =& e^{-i(A{\mathit{t}}^2+D\mathit{t})}\sum _{n\in \mathbb{Z}}{e}^{i\{A{\left(n\mathit{t}\right)}^2+D\left(n\mathit{t}\right)\}}f\left(nT\right)sinc\left(\frac{B{\mathsf{\Omega }}_{\mathsf{\Lambda }}(\mathit{t}-nT)}{\pi }\right),\hfill \end{array}$$

i.e.,

$$\begin{array}{c}\hfill f\left(\mathit{t}\right)=e^{-i(A{\mathit{t}}^2+D\mathit{t})}\sum _{n\in \mathbb{Z}}f\left(nT\right)e^{i\{A{\left(n\mathit{t}\right)}^2+D\left(n\mathit{t}\right)\}}sinc\left(\frac{B{\mathsf{\Omega }}_{\mathsf{\Lambda }}(\mathit{t}-nT)}{\pi }\right).\end{array}$$

This finishes the proof. □

4. Multiresolution Analysis Associated with QPFT

This section is devoted to the MRA associated with the QPFT. To introduce the definition, we first start with the following discussion, which has mainly to do with the Shannon’s sampling theorem discussed before. It motivated us to define an MRA associated with the QPFT. In what follows, the results also show the existence of the so-developed MRA.

When ${\mathsf{\Omega }}_{\mathsf{\Lambda }}=\frac{\pi }{B},$ the set of band-limited signals in QPFT domain is denoted by $V_0^{\mathsf{\Lambda }},$ i.e.,

$$V_0^{\mathsf{\Lambda }}=\left\{f\in L^2\left(\mathbb{R}\right):\left(Q^{\mathsf{\Lambda }}f\right)\left(u\right)=0,\left|u\right|\ge {\mathsf{\Omega }}_{\mathsf{\Lambda }}=\frac{\pi }{B}\right\},$$

where sampling period $T=1.$ Therefore, from the sampling theorem, for all $f\left(\mathit{t}\right)\in V_0^{\mathsf{\Lambda }},$ we get

$$\begin{array}{cc}\hfill f\left(\mathit{t}\right)& =\sum _{n\in \mathbb{Z}}{e}^{-i(A{\mathit{t}}^2+D\mathit{t})}f\left(n\right)e^{i\{A{n}^2+Dn\}}sinc\left(\frac{B{\mathsf{\Omega }}_{\mathsf{\Lambda }}(\mathit{t}-n)}{\pi }\right).\hfill \end{array}$$

Since ${\mathsf{\Omega }}_{\mathsf{\Lambda }}=\frac{\pi }{B},$ we have

$$\begin{array}{c}\hfill f\left(\mathit{t}\right)=\sum _{n\in \mathbb{Z}}{e}^{-i\{A({\mathit{t}}^2-n^2)+D(\mathit{t}-n)\}}f\left(n\right)sinc(\mathit{t}-n),\end{array}$$

i.e.,

$$\begin{array}{c}\hfill f\left(\mathit{t}\right)=\sum _{n\in \mathbb{Z}}f\left(n\right){\varphi }_{\mathsf{\Lambda },0,n}\left(\mathit{t}\right),\end{array}$$

where ${\varphi }_{\mathsf{\Lambda },0,n}\left(\mathit{t}\right)=e^{-i\{A({\mathit{t}}^2-n^2)+D(\mathit{t}-n)\}}sinc(\mathit{t}-n).$

Combining with the orthogonality of ${\left\{{\varphi }_{\mathsf{\Lambda },0,n}\right\}}_{n\in \mathbb{Z}},$ we can further obtain that ${\{{\varphi }_{\mathsf{\Lambda },0,n}=e^{-i\{A({\mathit{t}}^2-n^2)+D(\mathit{t}-n)\}}sinc(\mathit{t}-n)\}}_{n\in \mathbb{Z}}$ forms an orthonormal basis of $V_0^{\mathsf{\Lambda }}.$

When ${\mathsf{\Omega }}_{\mathsf{\Lambda }}=\frac{2\pi }{B},T=\frac{1}{2},$ the set of band-limited signal in the QPFT domain is denoted by $V_1^{\mathsf{\Lambda }},$ i.e.,

$$\begin{array}{c}\hfill V_1^{\mathsf{\Lambda }}=\left\{f\in L^2\left(\mathbb{R}\right):\left(Q^{\mathsf{\Lambda }}f\right)\left(u\right)=0,\left|u\right|\ge {\mathsf{\Omega }}_{\mathsf{\Lambda }}=\frac{2\pi }{B}\right\}.\end{array}$$

Therefore, according to sampling theorem Equation (3),

$$\begin{array}{cc}\hfill g\in V_0^{\mathsf{\Lambda }}& \Rightarrow \left(Q^{\mathsf{\Lambda }}f\right)\left(u\right)=0,\left|u\right|\ge \frac{\pi }{B}\hfill \\ \hfill & \Rightarrow \left(Q^{\mathsf{\Lambda }}f\right)\left(u\right)=0,\left|u\right|\ge \frac{2\pi }{B}\hfill \\ \hfill & \Rightarrow g\in V_1^{\mathsf{\Lambda }},\hfill \end{array}$$

i.e., $V_0^{\mathsf{\Lambda }}\subset V_1^{\mathsf{\Lambda }}.$ Also for $T=\frac{1}{2},{\mathsf{\Omega }}_{\mathsf{\Lambda }}=\frac{2\pi }{B},f\in V_1^{\mathsf{\Lambda }}$ can be written as

$$\begin{array}{cc}\hfill f\left(\mathit{t}\right)=& e^{-i(A{\mathit{t}}^2+D\mathit{t})}\sum _{n\in \mathbb{Z}}f\left(\frac{n}{2}\right)e^{i\left\{A{\left(\frac{n}{2}\right)}^2-D\left(\frac{n}{2}\right)\right\}}sinc\left(2\left(\mathit{t}-\frac{n}{2}\right)\right)\hfill \\ \hfill =& \sum _{n\in \mathbb{Z}}f\left(\frac{n}{2}\right)e^{-i\left\{A\left({\mathit{t}}^2-{\left(\frac{n}{2}\right)}^2\right)+D\left(\mathit{t}-\frac{n}{2}\right)\right\}}sinc\left(2\mathit{t}-n\right)\hfill \\ \hfill =& \sum _{n\in \mathbb{Z}}\frac{1}{\sqrt{2}}f\left(\frac{n}{2}\right){\varphi }_{\mathsf{\Lambda },1,n}\left(\mathit{t}\right),\hfill \end{array}$$

where ${\varphi }_{\mathsf{\Lambda },1,n}\left(\mathit{t}\right)=2^{\frac{1}{2}}{e}^{-i\left\{A\left({\mathit{t}}^2-{\left(\frac{n}{2}\right)}^2\right)+D\left(\mathit{t}-\frac{n}{2}\right)\right\}}sinc(2\mathit{t}-n).$

It can be further obtained that ${\{{\varphi }_{\mathsf{\Lambda },1,n}=2^{\frac{1}{2}}{e}^{-i\left\{A\left({\mathit{t}}^2-{\left(\frac{n}{2}\right)}^2\right)+D\left(\mathit{t}-\frac{n}{2}\right)\right\}}sinc(2\mathit{t}-n)\}}_{n\in \mathbb{Z}}$ forms an orthonormal basis of $V_1^{\mathsf{\Lambda }}.$ For $a=2,$ Equation (1) can be written as

$$\begin{array}{c}\hfill \left(Q^{\mathsf{\Lambda }}\left\{e^{i\left\{A{\left(2\mathit{t}\right)}^2-A{\mathit{t}}^2+D\left(2\mathit{t}\right)-D\mathit{t}\right\}}f\left(2\mathit{t}\right)\right\}\right)\left(\xi \right)=\frac{1}{2}{e}^{i\left\{C\left({\xi }^2-{\left(\frac{\xi }{2}\right)}^2\right)+E\left(\xi -\frac{\xi }{2}\right)\right\}}\left(Q^{\mathsf{\Lambda }}f\right)\left(\frac{\xi }{2}\right).\end{array}$$

This implies that $f\in V_0^{\mathsf{\Lambda }}$ if and only if $e^{i\left\{A{\left(2\mathit{t}\right)}^2-A{\mathit{t}}^2+D\left(2\mathit{t}\right)-D\mathit{t}\right\}}f\left(2\mathit{t}\right)\in V_1^{\mathsf{\Lambda }}.$ This is because

$$\begin{array}{cc}\hfill f\in V_0^{\mathsf{\Lambda }}& \iff \left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)=0,\left|\xi \right|\ge {\mathsf{\Omega }}_{\mathsf{\Lambda }}=\frac{\pi }{B}\hfill \\ \hfill & \iff \left(Q^{\mathsf{\Lambda }}f\right)\left(\frac{\xi }{2}\right)=0,\left|\frac{\xi }{2}\right|\ge \frac{\pi }{B}\hfill \\ \hfill & \iff \left(Q^{\mathsf{\Lambda }}f\right)\left(\frac{\xi }{2}\right)=0,\left|\xi \right|\ge \frac{2\pi }{B}\hfill \\ \hfill & \iff \frac{1}{2}{e}^{i\left\{C\left({\xi }^2-{\left(\frac{\xi }{2}\right)}^2\right)+E\left(\xi -\frac{\xi }{2}\right)\right\}}\left(Q^{\mathsf{\Lambda }}f\left(\mathit{t}\right)\right)\left(\frac{\xi }{2}\right)=0,\left|\xi \right|\ge \frac{2\pi }{B}\hfill \\ \hfill & \iff \left(Q^{\mathsf{\Lambda }}\left\{e^{i\left\{A{\left(2\mathit{t}\right)}^2-A{\mathit{t}}^2+D\left(2\mathit{t}\right)-D\mathit{t}\right\}}f\left(2\mathit{t}\right)\right\}\right)\left(\xi \right)=0,\left|\xi \right|\ge \frac{2\pi }{B}\hfill \\ \hfill & \iff e^{i\left\{A{\left(2\mathit{t}\right)}^2-A{\mathit{t}}^2+D\left(2\mathit{t}\right)-D\mathit{t}\right\}}f\left(2\mathit{t}\right)\in V_1^{\mathsf{\Lambda }},\hfill \end{array}$$

i.e., $f\in V_0^{\mathsf{\Lambda }}\iff e^{i\left\{A{\left(2\mathit{t}\right)}^2-A{\mathit{t}}^2+D\left(2\mathit{t}\right)-D\mathit{t}\right\}}f\left(2\mathit{t}\right)\in V_1^{\mathsf{\Lambda }}.$

Generally, let ${\mathsf{\Omega }}_{\mathsf{\Lambda }}=2^k\frac{\pi }{B},T=\frac{1}{2^k},$

$$\begin{array}{c}\hfill V_k^{\mathsf{\Lambda }}=\{f\in L^2\left(\mathbb{R}\right):\left(Q^{\mathsf{\Lambda }}f\right)\left(\xi \right)=0,\left|u\right|\ge 2^k\frac{\pi }{B}\}.\end{array}$$

Now, $\forall f\in V_k^{\mathsf{\Lambda }},$ we have

$$\begin{array}{cc}\hfill f\left(\mathit{t}\right)& =\sum _{n\in \mathbb{Z}}f\left(\frac{n}{2^k}\right)e^{-i\left\{A\left({\mathit{t}}^2-{\left(\frac{n}{2^k}\right)}^2\right)+D\left(\mathit{t}-\frac{n}{2^k}\right)\right\}}sinc\left(2^k\mathit{t}-n\right)\hfill \\ \hfill & =\sum _{n\in \mathbb{Z}}\frac{1}{2^{\frac{k}{2}}}f\left(\frac{n}{2^k}\right){\varphi }_{\mathsf{\Lambda },k,n}\left(\mathit{t}\right),\hfill \end{array}$$

where ${\varphi }_{\mathsf{\Lambda },k,n}\left(\mathit{t}\right)=2^{\frac{k}{2}}{e}^{-i\left\{A\left({\mathit{t}}^2-{\left(\frac{n}{2^k}\right)}^2\right)+D\left(\mathit{t}-\frac{n}{2^k}\right)\right\}}sinc\left(2^k\mathit{t}-n\right).$ Thus, ${\left\{{\varphi }_{\mathsf{\Lambda },k,n}\left(\mathit{t}\right)\right\}}_{n\in \mathbb{Z}}$ forms an orthonormal basis of $V_k^{\mathsf{\Lambda }}.$

Thus, $\forall k\in \mathbb{Z},$ we have

(a)

$V_k^{\mathsf{\Lambda }}\subset V_{k+1}^{\mathsf{\Lambda }};$

(b)

$f\left(\mathit{t}\right)\in V_k^{\mathsf{\Lambda }}\iff e^{i\left\{A{\left(2\mathit{t}\right)}^2-A{\mathit{t}}^2+D\left(2\mathit{t}\right)-D\mathit{t}\right\}}f\left(2\mathit{t}\right)\in V_{k+1}^{\mathsf{\Lambda }};$

(c)

${\cap }_{k\in \mathbb{Z}}{V}_k^{\mathsf{\Lambda }}=\left\{0\right\}$ and $\overline{{\cup }_{k\in \mathbb{Z}}{V}_k^{\mathsf{\Lambda }}}=L^2\left(\mathbb{R}\right).$

To put it briefly, the sampling theorem for band-limited signals in the QPFT domain serves as the inspiration to establish an orthonormal MRA associated with QPFT.

In this section, our focus lies on introducing the concept of a quadratic phase MRA within the space $L^2\left(\mathbb{R}\right)$. This MRA will hold significant importance in developing the quadratic phase orthonormal wavelet basis for $L^2\left(\mathbb{R}\right)$. Initially, we present the formal definition of a special affine MRA in $L^2\left(\mathbb{R}\right)$.

Definition 2.

An orthogonal MRA associated with QPFT is defined as a sequence of closed subspace $V_k^{\mathsf{\Lambda }},k\in \mathbb{Z}$ such that

(A) 

$V_k^{\mathsf{\Lambda }}\subset V_{k+1}^{\mathsf{\Lambda }},\forall k\in \mathbb{Z}.$

(B) 

$f\left(\mathit{t}\right)\in V_k^{\mathsf{\Lambda }}\iff e^{i\left\{A{\left(2\mathit{t}\right)}^2-A{\mathit{t}}^2+D\left(2\mathit{t}\right)-D\mathit{t}\right\}}f\left(2\mathit{t}\right)\in V_{k+1}^{\mathsf{\Lambda }}\forall k\in \mathbb{Z}.$

(C) 

${\cap }_{k\in \mathbb{Z}}{V}_k^{\mathsf{\Lambda }}=\left\{0\right\}$ and $\overline{{\cup }_{k\in \mathbb{Z}}{V}_k^{\mathsf{\Lambda }}}=L^2\left(\mathbb{R}\right).$

(D) 

There exist a function $\varphi \in L^2\left(\mathbb{R}\right)$ such that ${\{{\varphi }_{\mathsf{\Lambda },0,n}\left(\mathit{t}\right)=e^{-i\{A({\mathit{t}}^2-n^2)+D(\mathit{t}-n)\}}sinc(\mathit{t}-n)\}}_{n\in \mathbb{Z}}$ is an orthonormal basis of the subspace $V_0^{\mathsf{\Lambda }},$ where ϕ is called the scaling function of the given MRA.

Lemma 3.

The family $\{{\varphi }_{\mathsf{\Lambda },0,n}:n\in \mathbb{Z}\}$, given by the above, constitute an orthonormal system in $L^2\left(\mathbb{R}\right)$ iff

$$\begin{array}{c}\hfill \sum _{k\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)(\xi +2k\pi )\right|}^2=\frac{1}{2\pi }.\end{array}$$

Proof. 

We have

$$\begin{array}{cc}\hfill \left(Q^{\mathsf{\Lambda }}\left\{{\varphi }_{\mathsf{\Lambda },0,n}\right\}\right)\left(\xi \right)& ={\int }_{\mathbb{R}}\varphi (\mathit{t}-n)e^{-i\{A({\mathit{t}}^2-n^2)+D(\mathit{t}-n)\}}\frac{1}{\sqrt{2\pi }}{e}^{i(A{\mathit{t}}^2-B\mathit{t}\xi +C{\xi }^2+D\mathit{t}+E\xi )}d\mathit{t}\hfill \\ \hfill & ={\int }_{\mathbb{R}}\varphi (\mathit{t}-n)e^{-i\{A(-n^2)+D(-n)\}}\frac{1}{\sqrt{2\pi }}{e}^{i(-B\mathit{t}\xi +C{\xi }^2+E\xi )}d\mathit{t}\hfill \\ \hfill & =\frac{1}{\sqrt{2\pi }}{e}^{i\{A{n}^2+Dn-Bn\xi +C{\xi }^2+E\xi \}}{\int }_{\mathbb{R}}\varphi \left(\mathit{t}\right)e^{-i\mathit{t}\left(B\xi \right)}d\mathit{t},\hfill \end{array}$$

i.e., $\left(Q^{\mathsf{\Lambda }}\left\{{\varphi }_{\mathsf{\Lambda },0,n}\right\}\right)\left(\xi \right)=e^{i\{A{n}^2+Dn-Bn\xi +C{\xi }^2+E\xi \}}\left(\mathfrak{F}\varphi \right)\left(B\xi \right).$ Now since,

$$\begin{array}{cc}\hfill \langle {\varphi }_{\mathsf{\Lambda },0,n},{\varphi }_{\mathsf{\Lambda },0,l}\rangle & =B\langle Q^{\mathsf{\Lambda }}\left\{{\varphi }_{\mathsf{\Lambda },0,n}\right\},Q^{\mathsf{\Lambda }}\left\{{\varphi }_{\mathsf{\Lambda },0,l}\right\}\rangle \hfill \\ \hfill & =B{\int }_{\mathbb{R}}\left(Q^{\mathsf{\Lambda }}\left\{{\varphi }_{\mathsf{\Lambda },0,n}\right\}\right)\left(\xi \right)\overline{\left(Q^{\mathsf{\Lambda }}\left\{{\varphi }_{\mathsf{\Lambda },0,l}\right\}\right)\left(\xi \right)}d\xi \hfill \\ \hfill & =B{\int }_{\mathbb{R}}{e}^{i(A{n}^2+Dn-Bn\xi +C{\xi }^2+E\xi )}{e}^{-i(A{l}^2+Dl-Bl\xi +C{\xi }^2+E\xi )}{\left|\left(\mathfrak{F}\varphi \right)\left(B\xi \right)\right|}^{2}d\xi \hfill \\ \hfill & =B{\int }_{\mathbb{R}}{e}^{i(A(n^2-l^2)+D(n-l)-B(n-l)\xi )}{\left|\left(\mathfrak{F}\varphi \right)\left(B\xi \right)\right|}^{2}d\xi \hfill \\ \hfill & =B{e}^{i(A(n^2-l^2)+D(n-l)}{\int }_{\mathbb{R}}{e}^{-iB(n-l)\xi )}{\left|\left(\mathfrak{F}\varphi \right)\left(B\xi \right)\right|}^{2}d\xi \hfill \\ \hfill & =e^{i(A(n^2-l^2)+D(n-l)}{\int }_{\mathbb{R}}{e}^{-i(n-l)\xi )}{\left|\left(\mathfrak{F}\varphi \right)\left(\xi \right)\right|}^{2}d\xi .\hfill \end{array}$$

Since ${\left\{{\varphi }_{\mathsf{\Lambda },0,n}\right\}}_{n\in \mathbb{Z}}$ forms an orthonormal basis of $V_0^{\mathsf{\Lambda }},$ we have

$$\langle {\varphi }_{\mathsf{\Lambda },0,n},{\varphi }_{\mathsf{\Lambda },0,l}\rangle ={\delta }_{n,l}\forall k,l\in \mathbb{R}.$$

This implies $e^{i(A(n^2-l^2)+D(n-l)}{\int }_{\mathbb{R}}{e}^{-i(n-l)\xi )}{\left|\left(\mathfrak{F}\varphi \right)\left(\xi \right)\right|}^{2}d\xi ={\delta }_{n,l}.$ Set $n-l=q$ then

$$\begin{array}{cc}\hfill & e^{i[A{(q+l)}^2-l^2]+Dq}{\int }_{\mathbb{R}}{e}^{-iq\xi }{\left|\left(\mathfrak{F}\varphi \right)\left(\xi \right)\right|}^{2}d\xi ={\delta }_{q+l,l}\hfill \\ \hfill & \Rightarrow {\int }_{\mathbb{R}}{e}^{-iq\xi }{\left|\left(\mathfrak{F}\varphi \right)\left(\xi \right)\right|}^{2}d\xi ={\delta }_{q,0},q\in \mathbb{Z}\hfill \\ \hfill & \Rightarrow \sum _{k\in \mathbb{Z}}{\int }_{2k\pi }^{2(k+1)\pi }{e}^{-iq\xi }{\left|\left(\mathfrak{F}\varphi \right)\left(\xi \right)\right|}^{2}d\xi ={\delta }_{q,0}\hfill \\ \hfill & \Rightarrow \sum _{k\in \mathbb{Z}}{\int }_0^{2\pi }{e}^{-iq(\eta +2k\pi )}{\left|\left(\mathfrak{F}\varphi \right)(\eta +2k\pi )\right|}^{2}d\eta ={\delta }_{q,0}\hfill \\ \hfill & \Rightarrow \sum _{k\in \mathbb{Z}}{\int }_0^{2\pi }{e}^{-iq\eta }{\left|\left(\mathfrak{F}\varphi \right)(\eta +2k\pi )\right|}^{2}d\eta ={\delta }_{q,0},\hfill \\ \hfill & \mathrm{i}.\mathrm{e}.,{\int }_0^{2\pi }{e}^{-iq\eta }\sum _{k\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)(\eta +2k\pi )\right|}^{2}d\eta ={\delta }_{q,0}.\hfill \end{array}$$

Let $F\left(u\right)={\sum }_{k\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)(\eta +2k\pi )\right|}^2.$ Then

$$\begin{array}{cc}\hfill F(u+2\pi )=& \sum _{u\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)(u+2\pi +2k\pi )\right|}^2\hfill \\ \hfill =& \sum _{u\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)(u+2(k+1\left)\pi \right)\right|}^2\hfill \\ \hfill =& \sum _{r\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)(u+2r\pi )\right|}^2\hfill \\ \hfill =& F\left(u\right),\hfill \end{array}$$

i.e., $F\left(u\right)$ is $2\pi$ periodic. Therefore,

$$\begin{array}{cc}\hfill {\int }_0^{2\pi }{e}^{-iq\eta }F\left(\eta \right)d\eta & ={\delta }_{q,0}\hfill \\ \hfill \Rightarrow \frac{1}{2\pi }{\int }_0^{2\pi }{e}^{-iq\eta }F\left(\eta \right)d\eta & =\frac{1}{2\pi }{\delta }_{q,0}\hfill \\ \hfill F\left(\eta \right)=\frac{1}{2\pi },\end{array}$$

i.e., ${\sum }_{k\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)(\xi +2k\pi )\right|}^2=\frac{1}{2\pi }.$

Conversely, let ${\sum }_{k\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)(\xi +2k\pi )\right|}^2=\frac{1}{2\pi },$ then

$$\begin{array}{cc}\hfill \langle {\varphi }_{\mathsf{\Lambda },0,n},{\varphi }_{\mathsf{\Lambda },0,l}\rangle & =e^{i(A(n^2-l^2)+D(n-l)}{\int }_{\mathbb{R}}{e}^{-i(n-l)\xi )}{\left|\left(\mathfrak{F}\varphi \right)\left(\xi \right)\right|}^{2}d\xi \hfill \\ \hfill & =e^{i(A(n^2-l^2)+D(n-l)}\sum _{k\in \mathbb{Z}}{\int }_{2k\pi }^{2(k+1)\pi }{e}^{-i(n-l)\xi }{\left|\left(\mathfrak{F}\varphi \right)\left(\xi \right)\right|}^{2}d\xi \hfill \\ \hfill & =e^{i(A(n^2-l^2)+D(n-l)}\sum _{k\in \mathbb{Z}}{\int }_0^{2\pi }{e}^{-i(n-l)\xi }{\left|\left(\mathfrak{F}\varphi \right)(\xi +2k\pi )\right|}^{2}d\xi \hfill \\ \hfill & =e^{i(A(n^2-l^2)+D(n-l)}{\int }_0^{2\pi }{e}^{-i(n-l)\xi }\sum _{k\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)(\xi +2k\pi )\right|}^{2}d\xi \hfill \\ \hfill & =e^{i(A(n^2-l^2)+D(n-l)}\frac{1}{2\pi }{\int }_0^{2\pi }{e}^{-i(n-l)\xi }d\xi \hfill \\ \hfill & =\left\{\begin{array}{cc}1,\hfill & n=l\hfill \\ 0,\hfill & n\ne l\hfill \end{array}\right.\hfill \\ \hfill & ={\delta }_{n,l},\hfill \end{array}$$

i.e., the system is orthonormal. Hence the conclusion follows. □

Let ${\left\{V_k^{\mathsf{\Lambda }}\right\}}_{k\in \mathbb{Z}}$ be an orthonormal MRA of $L^2\left(\mathbb{R}\right).$ Since ${\varphi }_{\mathsf{\Lambda },0,0}\left(\mathit{t}\right)\in V_0^{\mathsf{\Lambda }}\subset V_1^{\mathsf{\Lambda }},$ and ${\left\{{\varphi }_{\mathsf{\Lambda },1,n}\right\}}_{n\in \mathbb{Z}}$ forms an orthonormal basis of $V_1^{\mathsf{\Lambda }},$ so there exists ${\left\{h_n\right\}}_{n\in \mathbb{Z}}$ such that

$$\begin{array}{cc}\hfill {\varphi }_{\mathsf{\Lambda },0,0}\left(\mathit{t}\right)& =\sum _{n\in \mathbb{Z}}{h}_n{\varphi }_{\mathsf{\Lambda },1,n}\left(\mathit{t}\right)\hfill \\ \hfill & =\sum _{n\in \mathbb{Z}}{h}_n\sqrt{2}\varphi (2\mathit{t}-n)e^{-i\left\{A\left({\mathit{t}}^2-{\left(\frac{n}{2}\right)}^2\right)+D(\mathit{t}-\frac{n}{2})\right\}}.\hfill \end{array}$$

(4)

Equation (4) is called the quadratic phase refinement equation. Here,

$$\begin{array}{cc}\hfill h_n& =\sqrt{2}{\int }_{\mathbb{R}}{\varphi }_{\mathsf{\Lambda },0,0}\left(\mathit{t}\right)\overline{\varphi (2\mathit{t}-n)}{e}^{i\left\{A\left({\mathit{t}}^2-{\left(\frac{n}{2}\right)}^2\right)+D(\mathit{t}-\frac{n}{2})\right\}}d\mathit{t}\hfill \\ \hfill & =\sqrt{2}{\int }_{\mathbb{R}}\varphi \left(\mathit{t}\right)\overline{\varphi (2\mathit{t}-n)}{e}^{-i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}d\mathit{t}.\hfill \end{array}$$

Now, from Equation (4), we have

$$\begin{array}{c}\hfill \varphi \left(\mathit{t}\right)e^{-i(A{\mathit{t}}^2+D\mathit{t})}=\sqrt{2}\sum _{n\in \mathbb{Z}}{h}_n\varphi (2\mathit{t}-n)e^{-i\left\{A\left({\mathit{t}}^2-{\left(\frac{n}{2}\right)}^2\right)+D(\mathit{t}-\frac{n}{2})\right\}}.\end{array}$$

Taking QPFT on both sides we get

$$\begin{array}{cc}\hfill & {\int }_{\mathbb{R}}\varphi \left(\mathit{t}\right)e^{-i(A{\mathit{t}}^2+D\mathit{t})}{e}^{i(A{\mathit{t}}^2-B\mathit{t}\xi +C{\xi }^2+D\mathit{t}+E\xi )}d\mathit{t}\hfill \\ \hfill & =\sqrt{2}{\int }_{\mathbb{R}}\sum _{n\in \mathbb{Z}}{h}_n\varphi (2\mathit{t}-n)e^{-i\left\{A\left({\mathit{t}}^2-{\left(\frac{n}{2}\right)}^2\right)+D(\mathit{t}-\frac{n}{2})\right\}}{e}^{i(A{\mathit{t}}^2-B\mathit{t}\xi +C{\xi }^2+D\mathit{t}+E\xi )}d\mathit{t}.\hfill \end{array}$$

This gives

$$\begin{array}{cc}\hfill {\int }_{\mathbb{R}}\varphi \left(\mathit{t}\right)e^{i(-B\mathit{t}\xi +C{\xi }^2+E\xi )}d\mathit{t}& =\sqrt{2}\sum _{n\in \mathbb{Z}}{h}_n{\int }_{\mathbb{R}}\varphi (2\mathit{t}-n)e^{-i\left\{-A{\left(\frac{n}{2}\right)}^2-D\left(\frac{n}{2}\right)\right\}}{e}^{i(-B\mathit{t}\xi +C{\xi }^2+E\xi )}d\mathit{t}\hfill \\ \hfill \mathrm{i}.\mathrm{e}.,e^{i(C{\xi }^2+E\xi )}{\int }_{\mathbb{R}}\varphi \left(\mathit{t}\right)e^{-iB\mathit{t}\xi }d\mathit{t}& =e^{i(C{\xi }^2+E\xi )}\sqrt{2}\sum _{n\in \mathbb{Z}}{h}_n{\int }_{\mathbb{R}}\varphi (2\mathit{t}-n)e^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{e}^{-iB\mathit{t}\xi }d\mathit{t}.\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill {\int }_{\mathbb{R}}\varphi \left(\mathit{t}\right)e^{-i\mathit{t}\left(B\xi \right)}d\mathit{t}& =\sqrt{2}\sum _{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{\int }_{\mathbb{R}}\varphi (2\mathit{t}-n)e^{-i\mathit{t}\left(B\xi \right)}d\mathit{t}\hfill \\ \hfill & =\sum _{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{\int }_{\mathbb{R}}\sqrt{2}\varphi (2\mathit{t}-n)e^{-i\mathit{t}\left(B\xi \right)}d\mathit{t}\hfill \\ \hfill & =\sum _{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{\int }_{\mathbb{R}}\frac{1}{\sqrt{2}}\varphi (\mathit{t}-n)e^{-i\mathit{t}\left(\frac{B\xi }{2}\right)}d\mathit{t}\hfill \\ \hfill & =\sum _{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{\int }_{\mathbb{R}}\frac{1}{\sqrt{2}}\varphi \left(\mathit{t}\right)e^{-i(\mathit{t}+n)\left(\frac{B\xi }{2}\right)}d\mathit{t}\hfill \\ \hfill & =\sum _{n\in \mathbb{Z}}\frac{1}{\sqrt{2}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\left(\frac{B\xi }{2}\right)\right\}}{\int }_{\mathbb{R}}\varphi \left(\mathit{t}\right)e^{-i\mathit{t}\left(\frac{B\xi }{2}\right)}d\mathit{t},\hfill \end{array}$$

i.e., $\left(\mathfrak{F}\varphi \right)\left(B\xi \right)={\mathsf{\Lambda }}_0\left(\frac{B\xi }{2}\right)\left(\mathfrak{F}\varphi \right)\left(\frac{B\xi }{2}\right),$ where ${\mathsf{\Lambda }}_0\left(\frac{B\xi }{2}\right)=\frac{1}{\sqrt{2}}{\sum }_{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\left(\frac{B\xi }{2}\right)\right\}}.$

Equivalently,

$$\begin{array}{c}\hfill \left(\mathfrak{F}\varphi \right)\left(\xi \right)={\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}\right),\end{array}$$

(5)

where ${\mathsf{\Lambda }}_0\left(\xi \right)=\frac{1}{\sqrt{2}}{\sum }_{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\xi \right\}}.$

Since ${\left\{{\varphi }_{\mathsf{\Lambda },0,n}\right\}}_{n\in \mathbb{Z}}$ is an orthonormal basis or orthonormal system of $V_0^{\mathsf{\Lambda }},$ so by Lemma 3, we have

$$\begin{array}{c}\hfill \sum _{k\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)(\xi +2k\pi )\right|}^2=\frac{1}{2\pi }.\end{array}$$

(6)

Hence, we can write

$$\begin{array}{cc}\hfill \frac{1}{2\pi }& =\sum _{k\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)(\xi +2k\pi )\right|}^2\hfill \\ \hfill & =\sum _{k\in \mathbb{Z}}{\left|{\mathsf{\Lambda }}_0\left(\frac{\xi +2k\pi }{2}\right)\left(\mathfrak{F}\varphi \right)\left(\frac{\xi +2k\pi }{2}\right)\right|}^2\hfill \\ \hfill & =\sum _{k\in \mathbb{Z}}{\left|{\mathsf{\Lambda }}_0\left(\frac{\xi +2k\pi }{2}\right)\right|}^2{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi +2k\pi }{2}\right)\right|}^2\hfill \\ \hfill & =\sum _{k\in \mathbb{Z}}{\left|{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+2k\pi \right)\right|}^2{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+2k\pi \right)\right|}^2\hfill \\ \hfill & +\sum _{k\in \mathbb{Z}}{\left|{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+(2k+1)\pi \right)\right|}^2{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+(2k+1)\pi \right)\right|}^2.\hfill \end{array}$$

(7)

Observe that

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_0\left(\xi \right)& =\frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\xi \right\}}\hfill \\ \hfill {\mathsf{\Lambda }}_0\left(\xi +2\pi \right)& =\frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n(\xi +2\pi )\right\}}\hfill \\ \hfill & =\frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\xi \right\}}{e}^{-2in\pi }\hfill \\ & =\frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\xi \right\}}\hfill \\ \hfill \mathrm{i}.\mathrm{e}.,{\mathsf{\Lambda }}_0(\xi +2\pi )& ={\mathsf{\Lambda }}_0\left(\xi \right).\hfill \end{array}$$

Also,

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_0(\xi +2k\pi )=& {\mathsf{\Lambda }}_0\left(\xi \right).\hfill \end{array}$$

(8)

Hence, from (7)

$$\begin{array}{cc}\hfill \frac{1}{2\pi }& =\sum _{k\in \mathbb{Z}}{\left|{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+2k\pi \right)\right|}^2{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+2k\pi \right)\right|}^2+\sum _{k\in \mathbb{Z}}{\left|{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+(2k+1)\pi \right)\right|}^2{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+(2k+1)\pi \right)\right|}^2\hfill \\ \hfill & ={\left|{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\right|}^2\sum _{k\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+2k\pi \right)\right|}^2+{\left|{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+\pi \right)\right|}^2\sum _{k\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+(2k+1)\pi \right)\right|}^2.\hfill \end{array}$$

Now using Equation (6), we have

$$\begin{array}{cc}\hfill {\left|{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\right|}^2·\frac{1}{2\pi }+{\left|{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+\pi \right)\right|}^2·\frac{1}{2\pi }& =\frac{1}{2\pi }\hfill \\ \hfill \Rightarrow {\left|{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\right|}^2+{\left|{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+\pi \right)\right|}^2& =1.\hfill \end{array}$$

Given an orthogonal MRA ${\left\{V_n^{\mathsf{\Lambda }}\right\}}_{n\in \mathbb{Z}}$, we define another sequence ${\left\{W_n^{\mathsf{\Lambda }}\right\}}_{n\in \mathbb{Z}}$, of closed subspaces of $L^2\left(\mathbb{R}\right)$ by $V_{j+1}^{\mathsf{\Lambda }}=V_j^{\mathsf{\Lambda }}\oplus W_j^{\mathsf{\Lambda }},j\in \mathbb{Z}$. Followed by a definition, these subspace inherit the scaling property of $\{V_j^{\mathsf{\Lambda }}{\}}_{j\in \mathbb{Z}}$, namely

$$\begin{array}{c}\hfill f\left(\mathit{t}\right)\in W_j^{\mathsf{\Lambda }}\iff f\left(2\mathit{t}\right)e^{i[A\{{\left(2\mathit{t}\right)}^2-{\mathit{t}}^2\}+D(2\mathit{t}-\mathit{t})]}\in W_{j+1}^{\mathsf{\Lambda }},j\in \mathbb{Z}.\end{array}$$

(9)

Moreover, the subspaces $W_j^{\mathsf{\Lambda }}$ are mutually orthogonal with the following decomposition formula

$$\begin{array}{c}\hfill L^2\left(\mathbb{R}\right)={\oplus }_{j\in \mathbb{Z}}{W}_j^{\mathsf{\Lambda }}.\end{array}$$

(10)

Note that condition (10) means that any orthonormal basis for $L^2\left(\mathbb{R}\right)$ can be constructed by finding out an orthonormal basis for the subspace $W_j^{\mathsf{\Lambda }}$. On the other hand, condition (9) implies that the quadratic phase basis can be constructed as long as the orthonormal basis for $W_0^{\mathsf{\Lambda }}$ is found. Therefore, our main concern is to construct a mother function ${\psi }_{\mathsf{\Lambda },0,0}$ in $W_0^{\mathsf{\Lambda }}$ such that $\{{\psi }_{\mathsf{\Lambda },0,k}:k\in \mathbb{Z}\}$ forms an orthonormal basis of $W_0^{\mathsf{\Lambda }}$.

Suppose ${\psi }_{\mathsf{\Lambda },0,0}(t)\in W_0^{\mathsf{\Lambda }}\subset V_1^{\mathsf{\Lambda }}$, there exists $\{d_k{\}}_{k\in \mathbb{Z}}$ such that

$$\begin{array}{c}\hfill {\psi }_{\mathsf{\Lambda },0,0}\left(\mathit{t}\right)=\sqrt{2}\sum _{k\in \mathbb{Z}}{d}_k\varphi (2\mathit{t}-k)e^{i\left\{A\left({\mathit{t}}^2-{\left(\frac{k}{2}\right)}^2\right)+D\left(\mathit{t}-\frac{k}{2}\right)\right\}}.\end{array}$$

(11)

Equation (11) is called quadratic phase wavelet equation. Taking QPFT on both sides, we get

$$\begin{array}{cc}\hfill \left(\mathfrak{F}\psi \right)\left(B\xi \right)=& {\mathsf{\Lambda }}_1\left(\frac{B\xi }{2}\right)\left(\mathfrak{F}\varphi \right)\left(\frac{B\xi }{2}\right),\hfill \\ \hfill \mathrm{i}.\mathrm{e}.,\left(\mathfrak{F}\psi \right)\left(\xi \right)=& {\mathsf{\Lambda }}_1\left(\frac{\xi }{2}\right)\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}\right),\hfill \end{array}$$

(12)

where

$$\begin{array}{c}\hfill {\mathsf{\Lambda }}_1\left(\xi \right)=\frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{d}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\xi \right\}}.\end{array}$$

(13)

Since $W_0^{\mathsf{\Lambda }}$ and $V_0^{\mathsf{\Lambda }},$ are orthogonal in $V_1^{\mathsf{\Lambda }},$ we have

$$\begin{array}{cc}\hfill 0& =\langle {\varphi }_{\mathsf{\Lambda },0,k},{\varphi }_{\mathsf{\Lambda },0,l}\rangle \hfill \\ \hfill & =B\langle Q^{\mathsf{\Lambda }}\left\{{\varphi }_{\mathsf{\Lambda },0,k}\right\},Q^{\mathsf{\Lambda }}\left\{{\varphi }_{\mathsf{\Lambda },0,l}\right\}\rangle .\hfill \end{array}$$

(14)

Observe that

$$\begin{array}{cc}\hfill \left(Q^{\mathsf{\Lambda }}\left\{{\varphi }_{\mathsf{\Lambda },0,k}\right\}\right)\left(\xi \right)=& \frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}{\varphi }_{\mathsf{\Lambda },0,k}\left(\mathit{t}\right)e^{i(A{\mathit{t}}^2-B\mathit{t}\xi +C{\xi }^2+D\mathit{t}+E\xi )}d\mathit{t}\hfill \\ \hfill =& \frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}\varphi (\mathit{t}-k)e^{i\{A{k}^2+Dk\}}{e}^{i(-B\mathit{t}\xi +C{\xi }^2+E\xi )}d\mathit{t}\hfill \\ \hfill =& \frac{1}{\sqrt{2\pi }}{e}^{i\{A{k}^2+Dk\}}{e}^{i(C{\xi }^2+E\xi )}{\int }_{\mathbb{R}}\varphi (\mathit{t}-k)e^{-i\mathit{t}\left(B\xi \right)}d\mathit{t}\hfill \\ \hfill =& \frac{1}{\sqrt{2\pi }}{e}^{i\{A{k}^2+Dk\}}{e}^{i(C{\xi }^2+E\xi )}{\int }_{\mathbb{R}}\varphi \left(\mathit{t}\right)e^{-i(\mathit{t}+k)B\xi }d\mathit{t}\hfill \\ \hfill =& e^{i\{A{k}^2+Dk\}}{e}^{i(C{\xi }^2+E\xi )}{e}^{-ik\left(B\xi \right)}\frac{1}{\sqrt{2\pi }}{\int }_{\mathbb{R}}\varphi \left(\mathit{t}\right)e^{-i\mathit{t}\left(B\xi \right)}d\mathit{t}\hfill \\ \hfill \mathrm{i}.\mathrm{e}.,Q^{\mathsf{\Lambda }}\left({\varphi }_{\mathsf{\Lambda },0,k}\right)\left(\xi \right)=& e^{i\{A{k}^2+Dk+C{\xi }^2+E\xi -kB\xi \}}\left(\mathfrak{F}\varphi \right)\left(B\xi \right).\hfill \end{array}$$

(15)

Similarly,

$$\begin{array}{cc}\hfill Q^{\mathsf{\Lambda }}\left({\psi }_{\mathsf{\Lambda },0,l}\right)\left(\xi \right)=& e^{i\{A{l}^2+Dl+C{\xi }^2+E\xi -lB\xi }\}\left(\mathfrak{F}\psi \right)\left(B\xi \right).\hfill \end{array}$$

(16)

Therefore, using Equations (15) and (16) in (14), we get

$$\begin{array}{cc}\hfill 0=& {\int }_{\mathbb{R}}{e}^{i\{A{k}^2+Dk+C{\xi }^2+E\xi -kB\xi }\left\}\left(\mathfrak{F}\varphi \right)\left(B\xi \right)e^{-i\{Al+Dl+C{\xi }^2+E\xi -lB\xi }\right\}\overline{\left(\mathfrak{F}\psi \right)\left(B\xi \right)}d\xi \hfill \\ \hfill =& e^{i\{A(k^2-l^2)+D(k-l)\}}{\int }_{\mathbb{R}}{e}^{-i(k-l)B\xi }\left(\mathfrak{F}\varphi \right)\left(B\xi \right)\overline{\left(\mathfrak{F}\psi \right)\left(B\xi \right)}d\xi \hfill \\ \hfill =& \frac{1}{B}{e}^{i\{A(k^2-l^2)+D(k-l)\}}{\int }_{\mathbb{R}}{e}^{i(l-k)\xi }\left(\mathfrak{F}\varphi \right)\left(\xi \right)\overline{\left(\mathfrak{F}\psi \right)\left(\xi \right)}d\xi \hfill \\ \hfill =& \frac{1}{B}{e}^{i\{A(k^2-l^2)+D(k-l)\}}{\int }_{\mathbb{R}}{e}^{i(l-k)\xi }{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}\right)}{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}\right)\right|}^{2}d\xi \hfill \\ \hfill =& \frac{1}{B}{e}^{i\{A(k^2-l^2)+D(k-l)\}}\sum _{m\in \mathbb{Z}}{\int }_{4m\pi }^{4(m+1)\pi }{e}^{i(l-k)\xi }{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}\right)}{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}\right)\right|}^{2}d\xi \hfill \\ \hfill =& \frac{1}{B}{e}^{i\{A(k^2-l^2)+D(k-l)\}}\sum _{m\in \mathbb{Z}}{\int }_0^{4\pi }{e}^{i(l-k)(\xi +4m\pi )}{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+2m\pi \right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}+2m\pi \right)}\hfill \\ \hfill & \times {\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+2m\pi \right)\right|}^{2}d\xi \hfill \\ \hfill =& \frac{1}{B}{e}^{i\{A(k^2-l^2)+D(k-l)\}}\sum _{m\in \mathbb{Z}}{\int }_0^{4\pi }{e}^{i(l-k)\xi }{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}\right)}{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+2m\pi \right)\right|}^{2}d\xi \hfill \\ \hfill =& \frac{1}{B}{e}^{i\{A(k^2-l^2)+D(k-l)\}}\sum _{m\in \mathbb{Z}}[{\int }_0^{2\pi }{e}^{i(l-k)\xi }{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}\right)}{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+2m\pi \right)\right|}^{2}d\xi \hfill \\ \hfill & +{\int }_{2\pi }^{4\pi }{e}^{i(l-k)\xi }{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}\right)}{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+2m\pi \right)\right|}^{2}d\xi ]\hfill \\ \hfill =& \frac{1}{B}{e}^{i\{A(k^2-l^2)+D(k-l)\}}\sum _{m\in \mathbb{Z}}[{\int }_0^{2\pi }{e}^{i(l-k)\xi }{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}\right)}{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+2m\pi \right)\right|}^{2}d\xi \hfill \\ \hfill & +{\int }_0^{2\pi }{e}^{i(l-k)(\xi +2\pi )}{\mathsf{\Lambda }}_0\left(\frac{\xi +2\pi }{2}\right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi +2\pi }{2}\right)}{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi +2\pi }{2}+2m\pi \right)\right|}^{2}d\xi ]\hfill \\ \hfill =& \frac{1}{B}{e}^{i\{A(k^2-l^2)+D(k-l)\}}[{\int }_0^{2\pi }{e}^{i(l-k)\xi }{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}\right)}\sum _{m\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+2m\pi \right)\right|}^{2}d\xi \hfill \\ \hfill & +{\int }_0^{2\pi }{e}^{i(l-k)(\xi +2\pi )}{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+\pi \right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}+\pi \right)}\sum _{m\in \mathbb{Z}}{\left|\left(\mathfrak{F}\varphi \right)\left(\frac{\xi }{2}+(2m+1)\pi \right)\right|}^{2}d\xi ]\hfill \\ \hfill =& \frac{1}{B}{e}^{i\{A(k^2-l^2)+D(k-l)\}}[{\int }_0^{2\pi }{e}^{i(l-k)\xi }{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}\right)}d\xi \hfill \\ \hfill & +{\int }_0^{2\pi }{e}^{i(l-k)(\xi +2\pi )}{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+\pi \right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}+\pi \right)}d\xi ]\hfill \\ \hfill =& \frac{1}{B}{e}^{i\{A(k^2-l^2)+D(k-l)\}}{\int }_0^{2\pi }{e}^{i(l-k)\xi }\left\{{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}\right)}+{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+\pi \right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}+\pi \right)}\right\}d\xi .\hfill \end{array}$$

Therefore,

$$\begin{array}{c}\hfill {\int }_0^{2\pi }{e}^{i(l-k)\xi }\left\{{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}\right)}+{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+\pi \right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}+\pi \right)}\right\}d\xi =0.\end{array}$$

(17)

From Equation (17), we conclude that

$$\begin{array}{c}\hfill {\mathsf{\Lambda }}_0\left(\frac{\xi }{2}\right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}\right)}+{\mathsf{\Lambda }}_0\left(\frac{\xi }{2}+\pi \right)\overline{{\mathsf{\Lambda }}_1\left(\frac{\xi }{2}+\pi \right)}=0.\end{array}$$

This implies

$$\begin{array}{c}\hfill {\mathsf{\Lambda }}_0\left(\xi \right)\overline{{\mathsf{\Lambda }}_1\left(\xi \right)}+{\mathsf{\Lambda }}_0\left(\xi +\pi \right)\overline{{\mathsf{\Lambda }}_1\left(\xi +\pi \right)}=0.\end{array}$$

(18)

Equation (18) can be written in the matrix form as

$$\begin{array}{c}\hfill M{M}^{*}=I_{2\times 2},\end{array}$$

where $M^{*}$ denotes the conjugate transpose of M, $I_{2\times 2}$ is the identity matrix, and

$$\begin{array}{c}\hfill M=\left[\begin{array}{cc}{\mathsf{\Lambda }}_0\left(\xi \right)& {\mathsf{\Lambda }}_0(\xi +\pi )\\ {\mathsf{\Lambda }}_1\left(\xi \right)& {\mathsf{\Lambda }}_1(\xi +\pi )\end{array}\right].\end{array}$$

Since ${\mathsf{\Lambda }}_0\left(\xi \right)$ and ${\mathsf{\Lambda }}_0(\xi +\pi )$ cannot vanish together on a set of non-zero measures due to the orthogonal property, there exists a $2\pi$- periodic function $\lambda \left(\xi \right)$ such that

$$\begin{array}{c}\hfill \left({\mathsf{\Lambda }}_1\left(\xi \right),{\mathsf{\Lambda }}_1(\xi +\pi )\right)=\left(\lambda \left(\xi \right)\overline{{\mathsf{\Lambda }}_0(\xi +\pi )},-\lambda \left(\xi \right)\overline{{\mathsf{\Lambda }}_0\left(\xi \right)}\right).\end{array}$$

(19)

Since,

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_1\left(\xi \right)=& \lambda \left(\xi \right)\overline{{\mathsf{\Lambda }}_0(\xi +\pi )}\hfill \\ \hfill {\mathsf{\Lambda }}_1(\xi +\pi )=& \lambda (\xi +\pi )\overline{{\mathsf{\Lambda }}_0(\xi +2\pi )}.\hfill \end{array}$$

(20)

Using Equation (8),

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_1(\xi +\pi )=& \lambda (\xi +\pi )\overline{{\mathsf{\Lambda }}_0\left(\xi \right)}.\hfill \end{array}$$

Therefore, we have

$$\begin{array}{cc}\hfill -\lambda \left(\xi \right)\overline{{\mathsf{\Lambda }}_0\left(\xi \right)}& =\lambda (\xi +\pi )\overline{{\mathsf{\Lambda }}_0\left(\xi \right)}\hfill \\ \hfill \{\lambda (\xi +\pi )+\lambda \left(\xi \right)\}\overline{{\mathsf{\Lambda }}_0\left(\xi \right)}& =0\hfill \\ \hfill \lambda (\xi +\pi )+\lambda \left(\xi \right)& =0.\hfill \end{array}$$

Therefore, $\lambda \left(\xi \right)$ is $2\pi$- periodic, it can be expressed as

$$\begin{array}{c}\hfill \lambda \left(\xi \right)=\sum _{k\in \mathbb{Z}}{c}_k{e}^{-ik\xi },\end{array}$$

where

$$\begin{array}{cc}\hfill c_k=& \frac{1}{2\pi }{\int }_0^{2\pi }\lambda \left(\xi \right)e^{ik\xi }d\xi \hfill \\ \hfill =& \frac{1}{2\pi }\left[{\int }_0^{\pi }\lambda \left(\xi \right)e^{ik\xi }d\xi +{\int }_{\pi }^{2\pi }\lambda \left(\xi \right)e^{ik\xi }d\xi \right]\hfill \\ \hfill =& \frac{1}{2\pi }\left[{\int }_0^{\pi }\lambda \left(\xi \right)e^{ik\xi }d\xi +{\int }_0^{\pi }\lambda (\xi +\pi )e^{ik(\xi +\pi )}d\xi \right]\hfill \\ \hfill =& \frac{1}{2\pi }\left[{\int }_0^{\pi }\lambda \left(\xi \right)e^{ik\xi }d\xi +{\int }_0^{\pi }{(-1)}^k\lambda (\xi +\pi )e^{ik\xi }d\xi \right]\hfill \\ \hfill =& \frac{1}{2\pi }\left[{\int }_0^{\pi }\lambda \left(\xi \right)e^{ik\xi }d\xi +{(-1)}^k{\int }_0^{\pi }-\lambda \left(\xi \right)e^{ik\xi }d\xi \right]\hfill \\ \hfill =& \frac{1}{2\pi }\{1-{(-1)}^k\}{\int }_0^{\pi }\lambda \left(\xi \right)e^{ik\xi }d\xi .\hfill \end{array}$$

Therefore, $\lambda \left(\xi \right)={\sum }_{k\in \mathbb{Z}}{c}_k{e}^{-ik\xi },$ where

$$\begin{array}{cc}\hfill c_k=& \frac{1}{2\pi }\{1-{(-1)}^k\}{\int }_0^{\pi }\lambda \left(\xi \right)e^{ik\xi }d\xi \hfill \\ \hfill \Rightarrow c_k=& 0\forall k=2m,m\in \mathbb{Z}.\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill \lambda \left(\xi \right)=& \sum _{l\in \mathbb{Z}}{c}_{2l+1}{e}^{-i(2l+1)\xi }\hfill \\ \hfill =& \sum _{l\in \mathbb{Z}}{c}_{2l+1}{e}^{-2il\xi }{e}^{-i\xi }\hfill \\ \hfill =& e^{-i\xi }\sum _{l\in \mathbb{Z}}{c}_{2l+1}{e}^{-2il\xi }\hfill \\ \hfill =& e^{-i\xi }\gamma \left(2\xi \right),\hfill \end{array}$$

where $\gamma \left(\xi \right)={\sum }_{l\in \mathbb{Z}}{c}_{2l+1}{e}^{-2il\xi }.$ Now,

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_0\left(\xi \right)& =\frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\xi \right\}}\hfill \\ \hfill \Rightarrow {\mathsf{\Lambda }}_0(\xi +\pi )& =\frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n(\xi +\pi )\right\}}\hfill \\ \hfill & =\frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n(\xi +\pi )\right\}}\hfill \\ \hfill & =\frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\xi \right\}}{e}^{-in\xi }\hfill \\ \hfill & =\frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{(-1)}^n{h}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\xi \right\}}.\hfill \end{array}$$

Therefore,

$$\begin{array}{c}\hfill \overline{{\mathsf{\Lambda }}_0(\xi +\pi )}=\frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{(-1)}^n\overline{h_n}{e}^{-i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\xi \right\}}.\end{array}$$

Thus, from (20)

$$\begin{array}{cc}\hfill {\mathsf{\Lambda }}_1\left(\xi \right)=& \lambda \left(\xi \right)\overline{{\mathsf{\Lambda }}_0(\xi +\pi )}\hfill \\ \hfill =& e^{-i\xi }\gamma \left(2\xi \right)\overline{{\mathsf{\Lambda }}_0(\xi +\pi )}.\hfill \end{array}$$

In particular, for $\gamma \left(2\xi \right)=1,$ using (13), we have

$${\mathsf{\Lambda }}_1\left(\xi \right)=e^{-i\xi }\gamma \left(2\xi \right)\overline{{\mathsf{\Lambda }}_0(\xi +\pi )}.$$

This implies

$$\begin{array}{cc}\hfill \frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{d}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\xi \right\}}& =e^{-i\xi }\frac{1}{\sqrt{2}}\sum _{n\in \mathbb{Z}}{(-1)}^n\overline{h_n}{e}^{-i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)-n\xi \right\}}\hfill \\ \hfill \mathrm{i}.\mathrm{e}.,\sum _{n\in \mathbb{Z}}{d}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{e}^{-in\xi }& =\sum _{n\in \mathbb{Z}}{(-1)}^n\overline{h_n}{e}^{-i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{e}^{i(n-1)\xi }\hfill \\ \hfill \mathrm{i}.\mathrm{e}.,\sum _{n\in \mathbb{Z}}{d}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{e}^{-in\xi }{e}^{ik\xi }& =\sum _{n\in \mathbb{Z}}{(-1)}^n\overline{h_n}{e}^{-i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{e}^{i(n-1)\xi }{e}^{ik\xi }.\hfill \end{array}$$

Integrating both sides, we get

$$\begin{array}{cc}\hfill & \sum _{n\in \mathbb{Z}}{d}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{\int }_{\mathbb{R}}{e}^{-i(n-k)\xi }d\xi =\sum _{n\in \mathbb{Z}}{(-1)}^n\overline{h_n}{e}^{-i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{\int }_{\mathbb{R}}{e}^{-i(1-n-k)\xi }d\xi \hfill \\ \hfill & \Rightarrow \sum _{n\in \mathbb{Z}}{d}_n{e}^{i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{\delta }_{n-k}=\sum _{n\in \mathbb{Z}}{(-1)}^n\overline{h_n}{e}^{-i\left\{A{\left(\frac{n}{2}\right)}^2+D\left(\frac{n}{2}\right)\right\}}{\delta }_{1-n-k}\hfill \\ \hfill & \Rightarrow \sum _{k\in \mathbb{Z}}{d}_k{e}^{i\left\{A{\left(\frac{k}{2}\right)}^2+D\left(\frac{k}{2}\right)\right\}}={(-1)}^{1-k}\overline{h_{1-k}}{e}^{-i\left\{A{\left(\frac{1-k}{2}\right)}^2+D\left(\frac{1-k}{2}\right)\right\}}\hfill \\ \hfill & \Rightarrow d_k={(-1)}^{1-k}\overline{h_{1-k}}{e}^{-i\left\{A{\left(\frac{1-k}{2}\right)}^2+D\left(\frac{1-k}{2}\right)+A{\left(\frac{k}{2}\right)}^2+D\left(\frac{k}{2}\right)\right\}}\hfill \\ \hfill & \Rightarrow d_k={(-1)}^{1-k}\overline{h_{1-k}}{e}^{-i\left\{A\left(\frac{{(1-k)}^2+k^2}{4}\right)+\frac{D}{2}\right\}}.\hfill \end{array}$$

Therefore, equivalently, we can write the wavelet coefficients $d_k$ of Equation (11) as

$$\begin{array}{cc}\hfill d_k& ={(-1)}^{1-k}\overline{h_{1-k}}{e}^{-i\left\{A\left(\frac{{(1-k)}^2+k^2}{4}\right)+\frac{D}{2}\right\}},k\in \mathbb{Z}.\hfill \end{array}$$

(21)

The above discussion can be summarized in the following theorem.

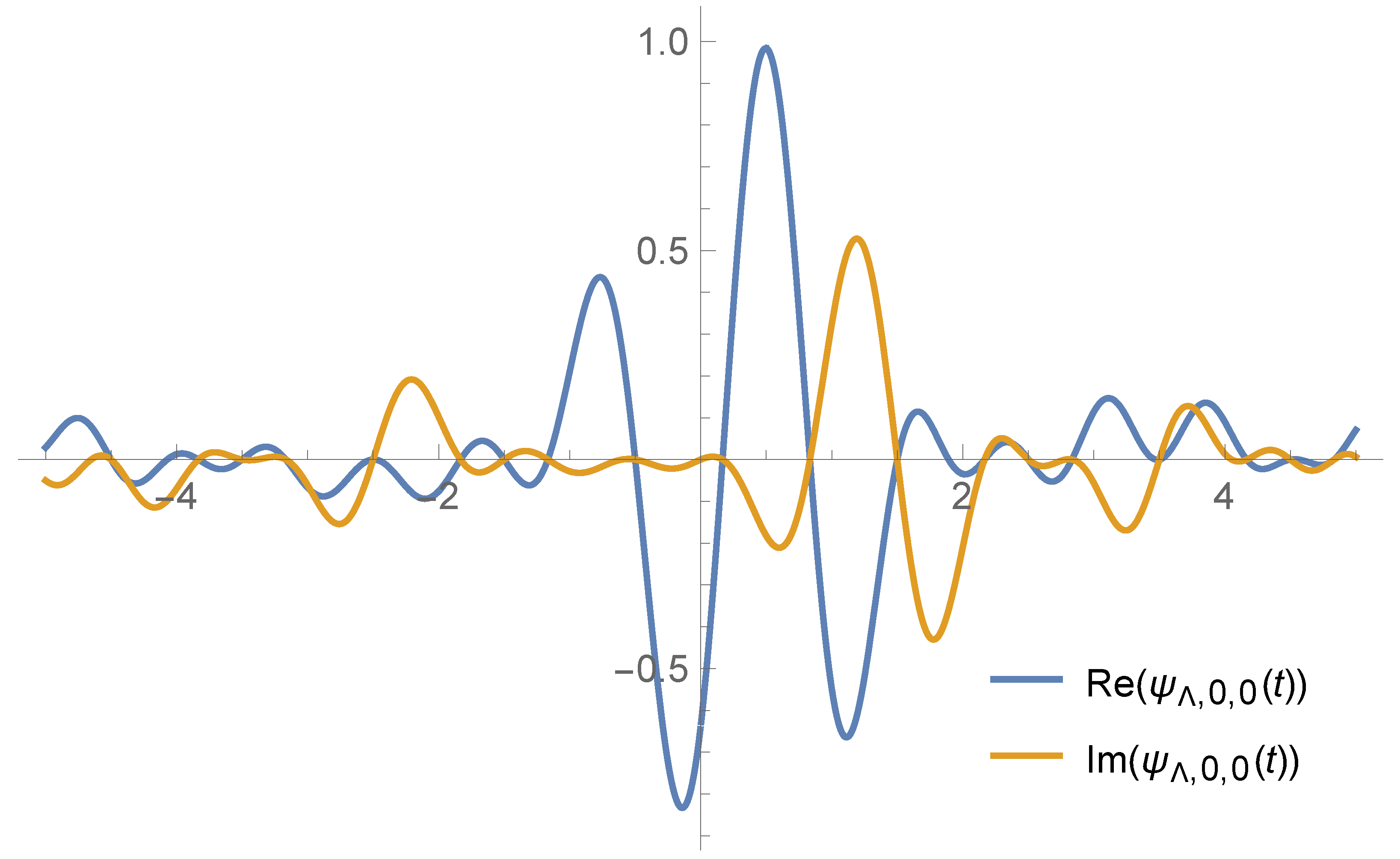
Theorem 2.

If ${\left\{V_n^{\mathsf{\Lambda }}\right\}}_{n\in \mathbb{Z}}$ is the quadratic phase MRA associated with the scaling function $\varphi ,$ then there exists a function ψ such that

$$\begin{array}{c}\hfill {\psi }_{\mathsf{\Lambda },0,0}\left(\mathit{t}\right)=\sqrt{2}\sum _{k\in \mathbb{Z}}{d}_k\varphi (2\mathit{t}-k)e^{-i\left\{A\left({\mathit{t}}^2-{\left(\frac{k}{2}\right)}^2\right)+D\left(\mathit{t}-\frac{k}{2}\right)\right\}},\end{array}$$

(22)

where $d_k$ is given by (21) with $h_k=\sqrt{2}{e}^{-i\left\{A{\left(\frac{k}{2}\right)}^2+D\left(\frac{k}{2}\right)\right\}}{\int }_{\mathbb{R}}\varphi \left(\mathit{t}\right)\overline{\varphi (2\mathit{t}-k)}d\mathit{t}$, i.e., the system $\left\{{\psi }_{\mathsf{\Lambda },k,n},k,n\in \mathbb{Z}\right\}$ is an orthonormal basis of $L^2\left(\mathbb{R}\right).$

Example 1.

It is observed in the earlier discussion that the function $sinc\left(\mathit{t}\right)=\frac{sin\left(\pi \mathit{t}\right)}{\pi \mathit{t}}$ is a scaling function for the quadratic phase MRA ${\left\{V_n^{\mathsf{\Lambda }}\right\}}_{n\in \mathbb{Z}},$ where ${\{{\varphi }_{\mathsf{\Lambda },0,n}\left(\mathit{t}\right)=e^{-i\{A({\mathit{t}}^2-n^2)+D(\mathit{t}-n))\}}sinc(\mathit{t}-n)\}}_{n\in \mathbb{Z}}$ is an orthonormal basis of the subspace $V_0^{\mathsf{\Lambda }}.$ Hence,

$$h_n=\left\{\begin{array}{cc}\frac{1}{\sqrt{2}},\hfill & n=0\hfill \\ \frac{\sqrt{2}sin\left(\frac{\pi n}{2}\right)e^{-i\left(\frac{A{n}^2}{4}+\frac{Dn}{2}\right)}}{\pi n},\hfill & n\ne 0,\hfill \end{array}\right.$$

which results in

$$d_n=\left\{\begin{array}{cc}\frac{1}{\sqrt{2}}{e}^{-i\left(\frac{A}{4}+\frac{D}{2}\right)},\hfill & n=1\hfill \\ \frac{\sqrt{2}{(-1)}^{-n}cos\left(\frac{\pi n}{2}\right)e^{-\frac{1}{4}in(An+2D)}}{\pi (n-1)},\hfill & n\ne 1.\hfill \end{array}\right.$$

Thus, the quadratic phase wavelet corresponding to the scaling function $sinc\left(\mathit{t}\right)$ is given by

$$\begin{array}{cc}\hfill {\psi }_{\mathsf{\Lambda },0,0}\left(\mathit{t}\right)=& \sqrt{2}{d}_1{e}^{-i\left\{A\left({\mathit{t}}^2-{\left(\frac{1}{2}\right)}^2\right)+D\left(\mathit{t}-\frac{1}{2}\right)\right\}}\varphi (2\mathit{t}-1)\hfill \\ \hfill & +\sqrt{2}\sum _{n\in \mathbb{Z},n\ne 1}{d}_n\varphi (2\mathit{t}-n)e^{-i\left\{A\left({\mathit{t}}^2-{\left(\frac{n}{2}\right)}^2\right)+D\left(\mathit{t}-\frac{n}{2}\right)\right\}}\hfill \\ \hfill & =e^{-i\mathit{t}(A\mathit{t}+D)}\varphi (2\mathit{t}-1)+\sqrt{2}\sum _{n\in \mathbb{Z},n\ne 1}\frac{\sqrt{2}{(-1)}^{-n}cos\left(\frac{\pi n}{2}\right)e^{-i\mathit{t}(A\mathit{t}+D)}}{\pi (n-1)}\varphi (2\mathit{t}-n)\hfill \\ \hfill & =e^{-i\mathit{t}(A\mathit{t}+D)}\frac{sin\left(\right(2\mathit{t}-1\left)\pi \right)}{(2\mathit{t}-1)\pi }\hfill \\ \hfill & +\sqrt{2}\sum _{n\in \mathbb{Z},n\ne 1}\frac{\sqrt{2}{(-1)}^{-n}cos\left(\frac{\pi n}{2}\right)e^{-i\mathit{t}(A\mathit{t}+D)}}{\pi (n-1)}\frac{sin\left(\right(2\mathit{t}-n\left)\pi \right)}{(2\mathit{t}-n)\pi }.\hfill \end{array}$$

The plots of the real and imaginary part of ${\psi }_{\mathsf{\Lambda },0,0}$ are given below for the particular choice of the parameter $\mathsf{\Lambda }=(0,1,0,0,0)$ and $\mathsf{\Lambda }=(\frac{1}{3},1,0,\frac{1}{5},0)$

Example 2.

Let $\varphi \left(\mathit{t}\right)={\chi }_{[0,1)}\left(\mathit{t}\right),$ where ${\chi }_{[0,1)}\left(\mathit{t}\right)$ is a characteristic function on $[0,1).$ It is a matter of simple verification that the set $\left\{{\varphi }_{\mathsf{\Lambda },0,n}\left(\mathit{t}\right):n\in \mathbb{Z}\right\}$ forms an orthonormal system. Hence it forms an orthonormal basis of the set $V_0^{\mathsf{\Lambda }},$ thus is a scaling function associated with the MRA ${\left\{V_n^{\mathsf{\Lambda }}\right\}}_{n\in \mathbb{Z}}.$ Thus,

$$h_n=\left\{\begin{array}{cc}\frac{1}{\sqrt{2}},\hfill & n=0\hfill \\ \frac{1}{\sqrt{2}}{e}^{-i\left\{A{\left(\frac{1}{2}\right)}^2+D\left(\frac{1}{2}\right)\right\}},\hfill & n=1\hfill \\ 0,\hfill & otherwise\hfill \end{array}\right.$$

resulting in

$$d_n=\left\{\begin{array}{cc}-\frac{1}{\sqrt{2}},\hfill & n=0\hfill \\ \frac{1}{\sqrt{2}}{e}^{-i\left\{A{\left(\frac{1}{2}\right)}^2+D\left(\frac{1}{2}\right)\right\}},\hfill & n=1\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

Thus, the quadratic phase wavelet corresponding to the scaling function ${\chi }_{[0,1)}\left(\mathit{t}\right)$ is given by

$${\psi }_{\mathsf{\Lambda },0,0}\left(\mathit{t}\right)=\left\{\begin{array}{cc}-e^{-i\mathit{t}(A\mathit{t}+D)},\hfill & 0\le \mathit{t}<\frac{1}{2}\hfill \\ e^{-i\mathit{t}(A\mathit{t}+D)},\hfill & \frac{1}{2}\le \mathit{t}<1.\hfill \end{array}\right.$$

The plots of the real and imaginary parts of ${\psi }_{\mathsf{\Lambda },0,0}$ are given below for the particular choice of the parameter $\mathsf{\Lambda }=(0,1,0,0,0)$ and $\mathsf{\Lambda }=(\frac{1}{3},1,0,\frac{1}{5},0)$

Remark 1.

By virtue of Lemma 3 and the Definition 2 of MRA we can say that any function that serves as a scaling function in the classical MRA will also serve as a scaling function for the MRA given by Definition 2. But, depending on the choice of parameters Λ, we can have different quadratic phase wavelets and thus different families of orthonormal bases of $L^2\left(\mathbb{R}\right)$. In particular, for the choice of the parameter $\mathsf{\Lambda }=(0,1,0,0,0),$ we get the classical wavelets and the quadratic phase wavelets for $\mathsf{\Lambda }=(\frac{1}{3},1,0,\frac{1}{5},0)$ (see Figure 1, Figure 2, Figure 3 and Figure 4). The flexibility in the choice of the parameters results in the development of some novel families of orthonormal bases of $L^2\left(\mathbb{R}\right)$ corresponding to the same scaling function.

5. Conclusions

The MRA and the construction of orthogonal wavelets for QPFT play a vital role in facilitating prospective applications of QPFT. In this paper, we gave an alternative proof of the Shannon’s sampling theorem applicable to the band-limited signal in the QPFT. Inspired by the theorem, we developed an MRA associated with QPFT. Subsequently, we discussed the construction of the quadratic phase wavelets for a given scaling function, followed by some of its examples.