Analysis of the Stress–Strength Model Using Uniform Truncated Negative Binomial Distribution under Progressive Type-II Censoring
Abstract
:1. Introduction
2. Maximum Likelihood Estimation
Asymptotic Confidence Interval
3. Parametric Bootstrap
3.1. Percentile Bootstrap
- Create random sample sets and from and with and , respectively. Determine the MLEs of and .
- Use and to generate independent bootstrap samples and from and with and , respectively. Compute the MLEs of unknown parameters based on the bootstrap samples, represented by and .
- Determine the bootstrap estimate of R in (10), then denote it with the symbol .
- Repeat Steps 2 and 3 N times and obtain the ordered value .
- The BP confidence interval of R is given by
3.2. Bootstrap-t
- 1–3.
- Similar to the BP algorithm mentioned above.
- 4.
- Determine the forthcoming statistics:
- 5.
- Repeat Steps (2) through (4) N times.
- 6.
- Assume that is the CDF of . Define . The approximate BT confidence interval of R is given by
4. Bayesian Estimation Using MCMC
- Start with an initial guess indicated by and set .
- Generate from gamma .
- Generate from gamma .
- Using the M–H algorithm, generate from with the proposal distribution , where is a variance of .
- Compute .
- Set .
- Repeat Steps 2–6 M times.
- The Bayesian estimate of R can be obtained usingwhere is the burn-in period.
5. Numerical Explorations
- It is clear that the MSEs and AWs decrease with increasing sample size and effective sample size for both Bayesian and non-Bayesian (ML, BP, and BT) estimation methods. This verifies the consistency characteristics of every estimation technique.
- Because the related MSEs are relatively small, all point estimates are generally fully accurate. With rising and , MSEs tend to zero out.
- The MSEs and AWs are dropping in tandem with a rise in the real value of R.
- When sample sizes are fixed and there are observed failures, the first scheme (I,I) performs the best in terms of reduced MSEs and AWs.
- With schemes (I,II), (I,III), and (II,III), neither MSEs nor AWs exhibit regular behavior (increasing or decreasing).
- When removals are postponed, MSEs and AWs both rise.
- In terms of MSEs and AWs, bootstrap approaches outperform the ML method of R. Additionally, BT outperforms BP in terms of MSEs and AWs.
- In addition to having ACIs with high CPs (about 0.95), the estimates generated by the ML, bootstrap, and Bayesian techniques are quite similar.
- The simulation findings demonstrate that all point and interval estimators approaches are effective, despite the fact that the Bayes estimators outperform all other estimators. If one has sufficient prior knowledge, they may choose for the Bayes approach. Using bootstrap approaches, which largely rely on MLEs, is preferable if prior knowledge about the subject under study is not accessible.
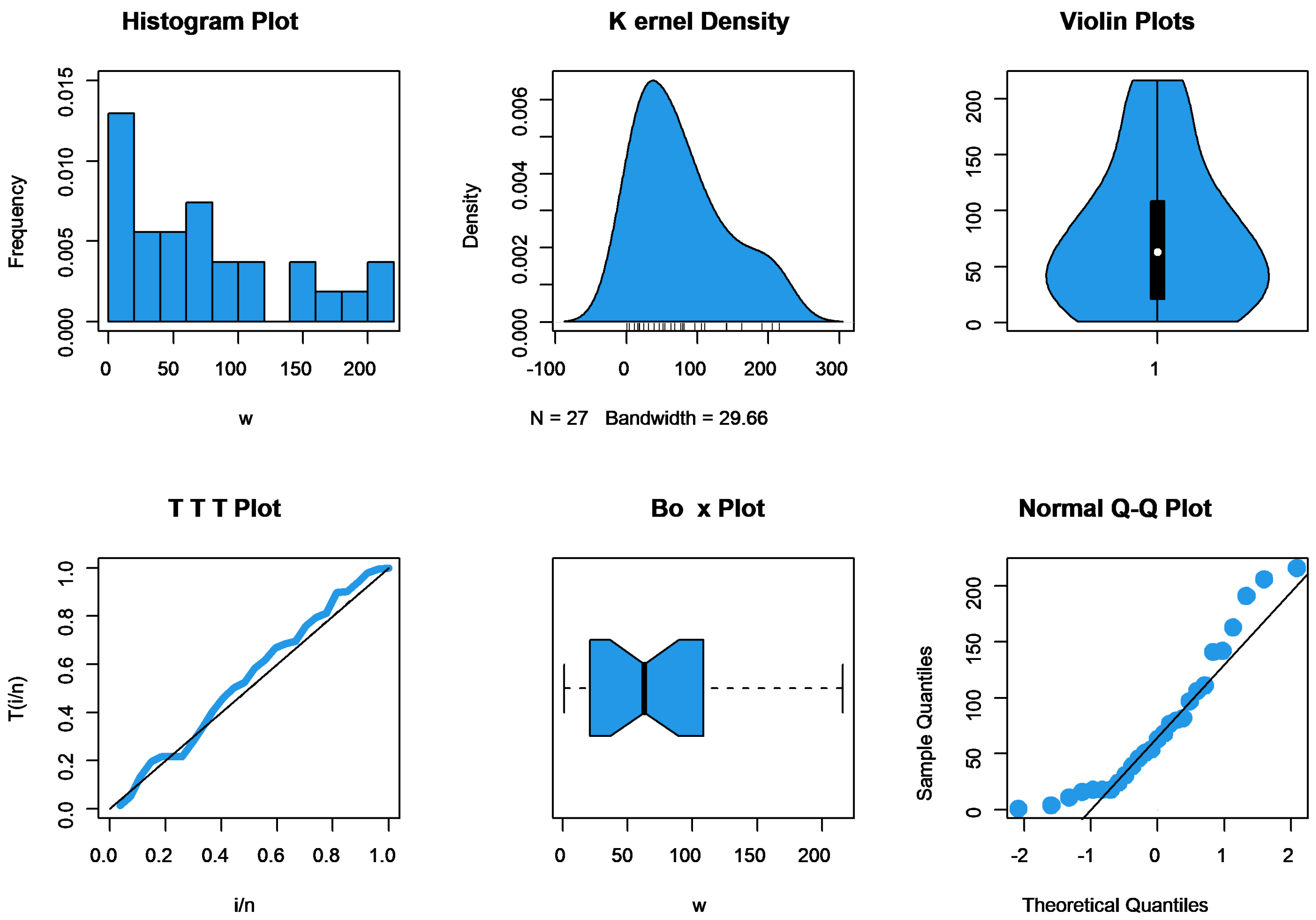
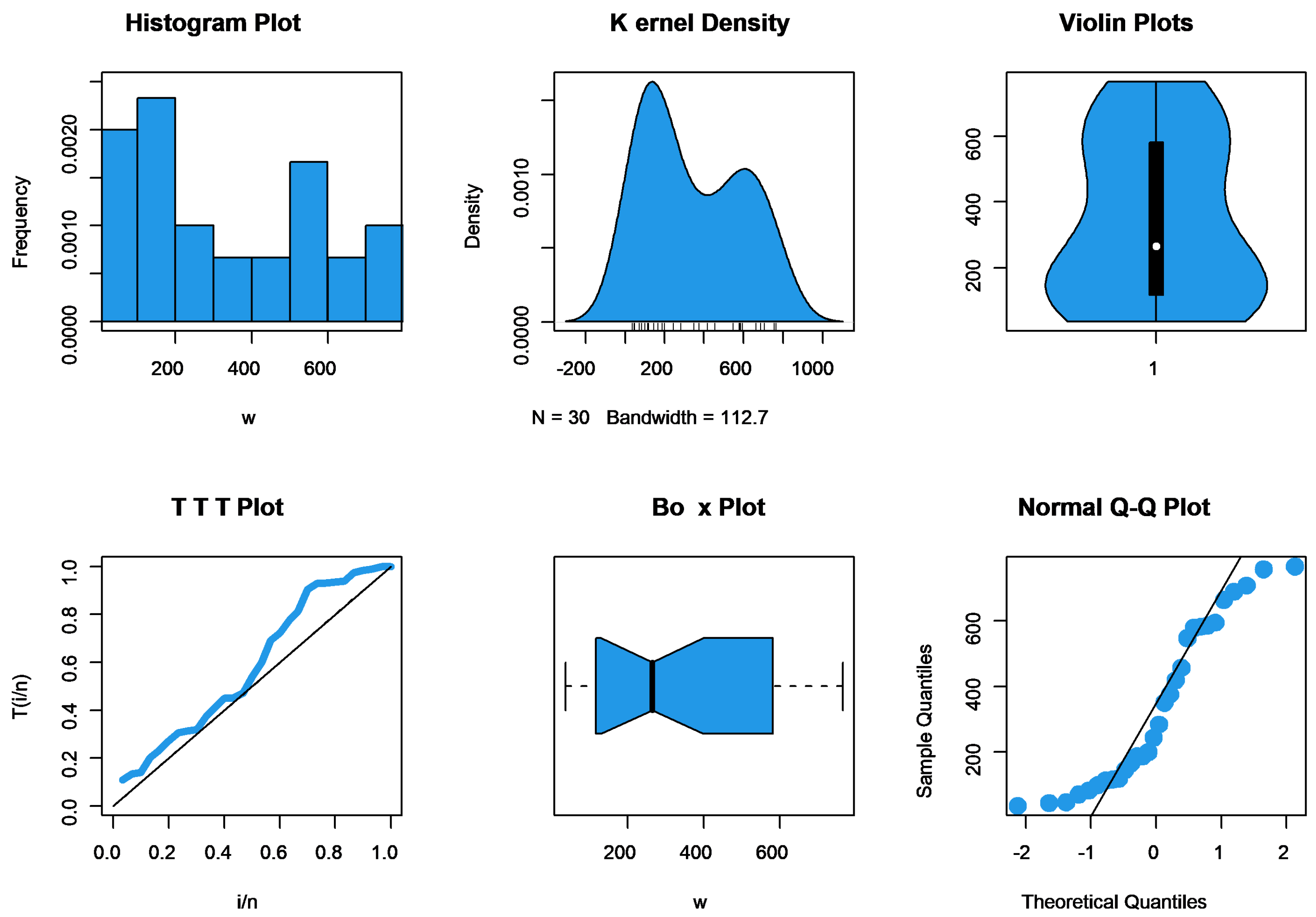
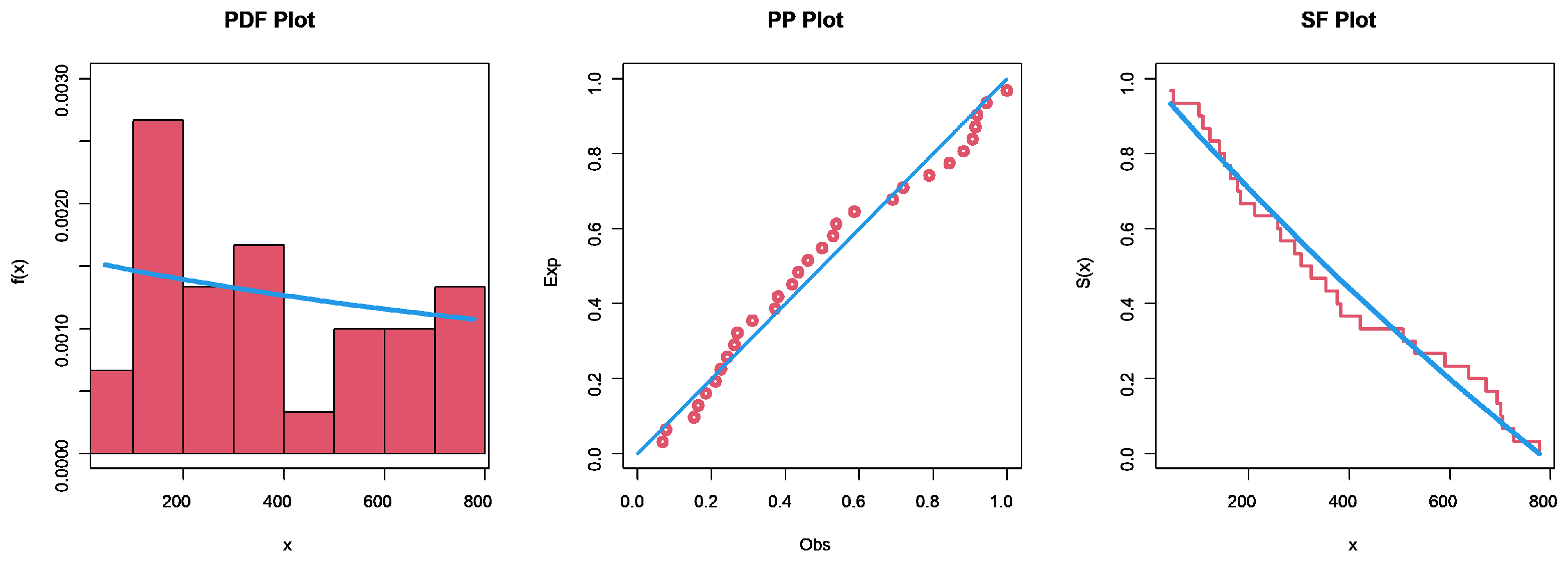
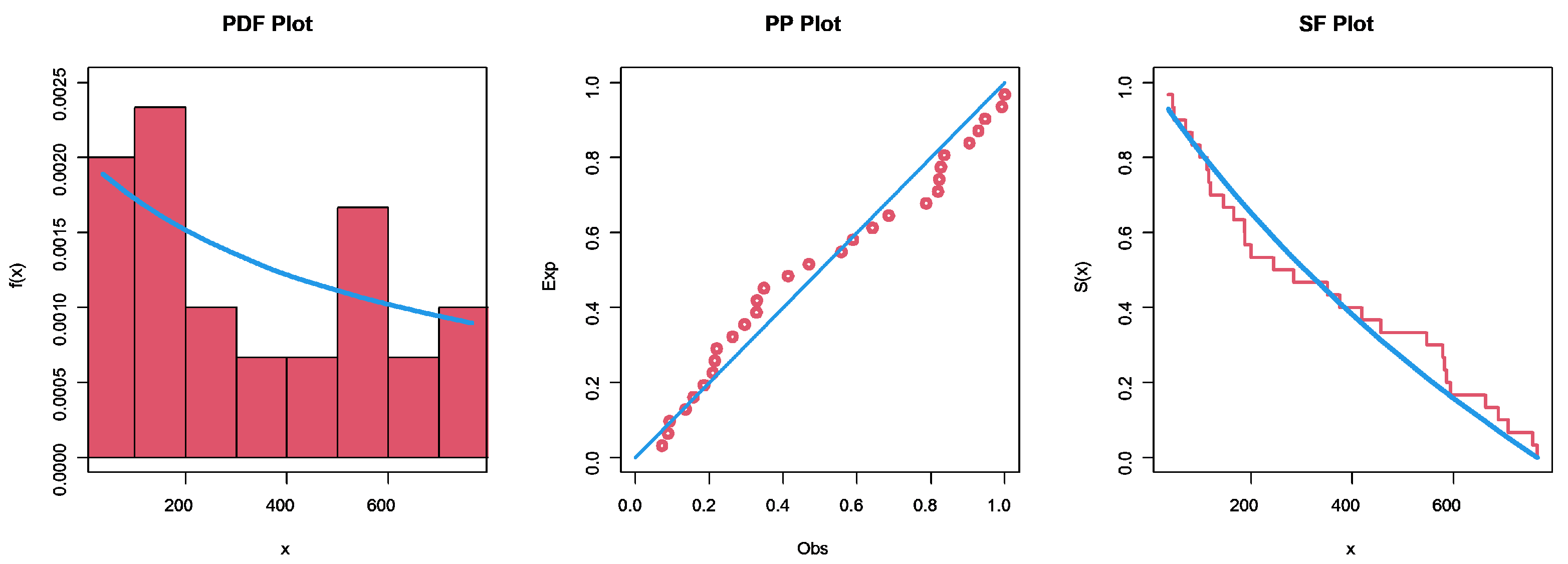
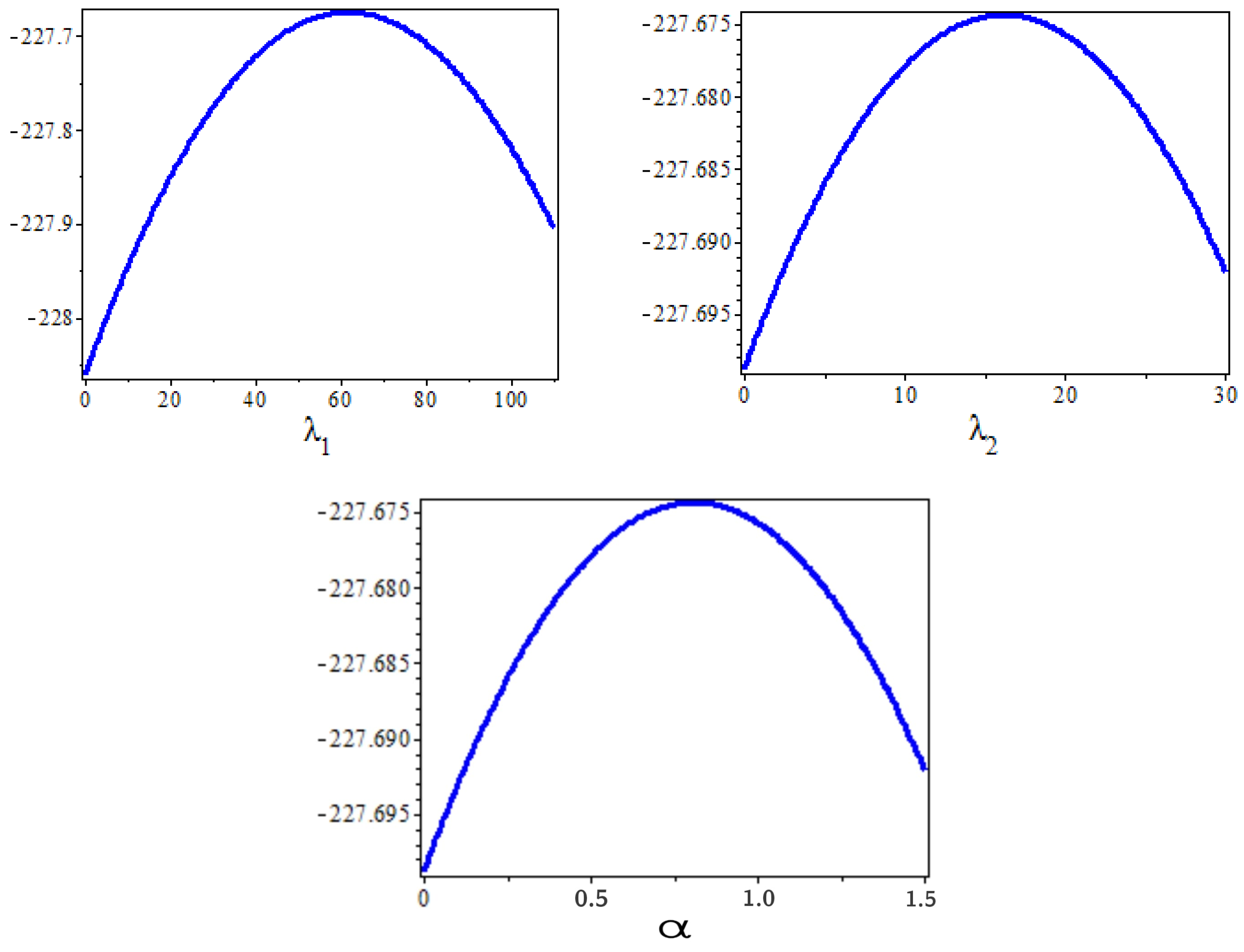
6. Application to Jute Fiber
7. Summary Findings
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kotz, S.; Lumelskii, Y.; Pensky, M. The Stress-Strength Model and Its Generalization: Theory and Applications; World Scientific: Singapore, 2003. [Google Scholar]
- Church, J.D.; Harris, B. The estimation of the reliability from stress–strength relationships. Technometrics 1970, 12, 49–54. [Google Scholar] [CrossRef]
- Surles, J.G.; Padgett, W.J. Inference for P(Y < X) in the Burr Type X model. J. Appl. Stat. Sci. 1998, 7, 225–238. [Google Scholar]
- Surles, J.G.; Padgett, W.J. Inference for reliability and stress–strength for a scaled Burr-Type X distribution. Lifetime Data Anal. 2001, 7, 187–200. [Google Scholar] [CrossRef]
- Kundu, D.; Gupta, R.D. Estimation of P(Y < X) for generalized exponential distribution. Metrika 2005, 61, 291–308. [Google Scholar]
- Raqab, M.Z.; Kundu, D. Comparison of different estimators of P(Y < X) for a scaled Burr type X distribution. Commun. Stat. Simul. Comput. 2005, 34, 465–483. [Google Scholar]
- Kundu, D.; Gupta, R.D. Estimation of P(Y < X) for Weibull Distribution, IEEE Trans. Reliab. 2006, 55, 270–280. [Google Scholar]
- Nadar, M.; Kizilaslan, F.; Papadopoulos, A. Classical and Bayesian estimation of P(Y < X) for Kumaraswamy distribution. Stat. Comput. Simul. 2014, 84, 1505–1529. [Google Scholar]
- Sharma, V.K.; Singh, S.K.; Singh, U.; Agiwal, V. The inverse Lindley distribution: A stress-strength reliability model with application to head and neck cancer data. J. Ind. Prod. 2015, 32, 162–173. [Google Scholar] [CrossRef]
- Ahmed, A.; Batah, F. On the estimation of stress-strength model reliability parameter of power rayleigh distribution. Iraqi J. Sci. 2023, 64, 809–822. [Google Scholar] [CrossRef]
- Baklizi, A. Estimation of P(Y < X) using record values in the one and two parameter exponential distributions. Valiollahi 2008, 37, 692–698. [Google Scholar]
- Nadar, M.; Kizilaslan, F. Classical and Bayesian estimation of P[Y < X] using upper record values from Kumaraswamy distribution. Stat. Pap. 2014, 55, 751–783. [Google Scholar]
- Mahmoud, A.W.M.; EL-Sagheer, R.M.; Soliman, A.A.; Abd Ellah, A.H. Bayesian estimation of P[Y < X] based on record values from the Lomax distribution and MCMC technique. J. Mod. Appl. Stat. 2016, 15, 488–510. [Google Scholar]
- Hasan, A.S.; Abd-Allah, M.; Nagy, H.F. Estimation of P(Y < X) using record values from the generalized inverted exponential distribution. Pak. J. Stat. Oper. Res. 2018, XIV, 645–660. [Google Scholar]
- Balakrishnan, N.; Sandhu, R.A. A simple simulation algorithm for generating progressive type-II censored samples. Am. Assoc. 1995, 49, 229–230. [Google Scholar]
- Yu, Y.; Wang, L.; Dey, S.; Liu, J. Estimation of stress-strength reliability from unit-Burr III distribution under records data. Math. Biosci. Eng. 2023, 20, 12360–12379. [Google Scholar] [CrossRef]
- Koul, S.; Chaturvedi, A. Estimation and testing procedures for the reliability functions of one parameter generalized exponential distribution. Thail. Stat. 2023, 21, 268–290. [Google Scholar]
- Saracoglu, B.; Kinaci, I.; Kundu, D. On estimation of R = P(Y < X) for exponential distribution under progressive type II censoring. Stat. Comput. Simul. 2012, 82, 729–744. [Google Scholar]
- Valiollahi, R.; Asgharzadeh, A.; Raqab, M.Z. Estimation of P(Y < X) for Weibull distribution under progressive type II censoring. Commun. Stat. Theory Methods 2013, 42, 4476–4498. [Google Scholar]
- Kumar, K.; Krishna, H.; Garg, R. Estimation of P(Y < X) in Lindley distribution using progressively first failure censoring. Int. J. Syst. Assur. Eng. Manag. 2015, 6, 330–341. [Google Scholar]
- Krishna, H.; Dube, M.; Garg, R. Estimation of P(Y < X) for progressively first failure censored generalized inverted exponential distribution. Stat. Comput. Simul. 2017, 87, 2274–2289. [Google Scholar]
- EL-Sagheer, R.M.; Mansour, M.M.M. The efficacy measurement of treatment methods: An application to stress-strength model. Appl. Math. Inf. Sci. 2020, 14, 487–492. [Google Scholar]
- Kamel, B.I.; Abo Youssef, S.E.; Sief, M.G. The Uniform truncated negative binomial distribution and its properties. J. Math. Stat. 2016, 12, 290–301. [Google Scholar] [CrossRef]
- EL-Sagheer, R.M. Estimation of parameters of Weibull-Gamma distribution based on progressively censored data. Stat. Pap. 2018, 59, 725–757. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference, 2nd ed.; Duxbury Press: Pacific Grove, CA, USA, 2002. [Google Scholar]
- Xu, J.; Long, J.S. Using the delta method to construct confidence intervals for predicted probabilities, rates, and discrete changes. Stata J. 2005, 5, 537–559. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 27, 1–26. [Google Scholar] [CrossRef]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- DiCiccio, T.J.; Efron, B. Bootstrap confidence intervals. Stat. Sci. 1996, 11, 189–212. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; Chapman & Hall: New York, NY, USA, 1994. [Google Scholar]
- Arnold, B.C.; Press, S.J. Bayesian inference for Pareto populations. Econometrics 1983, 21, 287–306. [Google Scholar] [CrossRef]
- Upadhyay, S.K.; Vasistha, N.; Smith, A.F.M. Bayes inference in life testing and reliability via Markov chain Monte Carlo simulation. Sankhya A 2001, 63, 15–40. [Google Scholar]
- Kundu, D.; Howlader, H. Bayesian inference and prediction of the inverse Weibull distribution for Type-II censored data. Comput. Stat. Data Anal. 2010, 54, 1547–1558. [Google Scholar] [CrossRef]
- Chen, M.-H.; Shao, Q.-M. Monte Carlo estimation of Bayesian credible and HPD intervals. J. Comput. Graph. 1999, 8, 69–92. [Google Scholar]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Xia, Z.P.; Yu, J.Y.; Cheng, L.D.; Liu, L.F.; Wang, W.M. Study on the breaking strength of jute fibres using modified Weibull distribution. Compos. Part Appl. Sci. Manuf. 2009, 40, 54–59. [Google Scholar] [CrossRef]
| BP | BT | Bayes | |||
|---|---|---|---|---|---|
| (I, I) | 0.00854 | 0.00815 | 0.00795 | 0.00772 | |
| (II, II) | 0.00923 | 0.00964 | 0.00836 | 0.00795 | |
| (III, III) | 0.00976 | 0.00996 | 0.00943 | 0.00837 | |
| (I, II) | 0.00867 | 0.00835 | 0.00815 | 0.00784 | |
| (I, III) | 0.00884 | 0.00854 | 0.00834 | 0.00805 | |
| (II, I) | 0.00859 | 0.00847 | 0.00826 | 0.00799 | |
| (II, III) | 0.00896 | 0.00879 | 0.00844 | 0.00816 | |
| (III, I) | 0.00887 | 0.00879 | 0.00857 | 0.00825 | |
| (III, II) | 0.00896 | 0.00878 | 0.00849 | 0.00820 | |
| (I, I) | 0.00747 | 0.00715 | 0.00688 | 0.00657 | |
| (II, II) | 0.00796 | 0.00778 | 0.00745 | 0.00698 | |
| (III, III) | 0.00839 | 0.00805 | 0.00776 | 0.00729 | |
| (I, II) | 0.00765 | 0.00748 | 0.00724 | 0.00678 | |
| (I, III) | 0.00779 | 0.00766 | 0.00741 | 0.00696 | |
| (II, I) | 0.00766 | 0.00758 | 0.00739 | 0.00711 | |
| (II, III) | 0.00822 | 0.00805 | 0.00773 | 0.00732 | |
| (III, I) | 0.00785 | 0.00774 | 0.00756 | 0.00718 | |
| (III, II) | 0.00819 | 0.00798 | 0.00778 | 0.00745 | |
| (I, I) | 0.00667 | 0.00655 | 0.00612 | 0.00589 | |
| (II, II) | 0.00697 | 0.00673 | 0.00639 | 0.00605 | |
| (III, III) | 0.00733 | 0.00707 | 0.00669 | 0.00634 | |
| (I, II) | 0.00678 | 0.00667 | 0.00647 | 0.00618 | |
| (I, III) | 0.00715 | 0.00699 | 0.00656 | 0.00627 | |
| (II, I) | 0.00680 | 0.00677 | 0.00654 | 0.00639 | |
| (II, III) | 0.00704 | 0.00698 | 0.00687 | 0.00644 | |
| (III, I) | 0.00717 | 0.00692 | 0.00666 | 0.00632 | |
| (III, II) | 0.00724 | 0.00708 | 0.00687 | 0.00644 | |
| (I, I) | 0.00557 | 0.00539 | 0.00515 | 0.00489 | |
| (II, II) | 0.00596 | 0.00578 | 0.00559 | 0.00526 | |
| (III, III) | 0.00622 | 0.00606 | 0.00586 | 0.00553 | |
| (I, II) | 0.00568 | 0.00547 | 0.00524 | 0.00501 | |
| (I, III) | 0.00576 | 0.00568 | 0.00543 | 0.00512 | |
| (II, I) | 0.00603 | 0.00589 | 0.00564 | 0.00519 | |
| (II, III) | 0.00619 | 0.00599 | 0.00587 | 0.00537 | |
| (III, I) | 0.00586 | 0.00578 | 0.00553 | 0.00522 | |
| (III, II) | 0.00618 | 0.00597 | 0.00577 | 0.00535 |
| BP | BT | Bayes | |||
|---|---|---|---|---|---|
| (I, I) | 0.00469 | 0.00427 | 0.00399 | 0.00368 | |
| (II, II) | 0.00496 | 0.00458 | 0.00427 | 0.00395 | |
| (III, III) | 0.00523 | 0.00496 | 0.00468 | 0.00437 | |
| (I, II) | 0.00475 | 0.00446 | 0.00415 | 0.00379 | |
| (I, III) | 0.00485 | 0.00469 | 0.00438 | 0.00415 | |
| (II, I) | 0.00479 | 0.00456 | 0.00425 | 0.00389 | |
| (II, III) | 0.00499 | 0.00478 | 0.00465 | 0.00428 | |
| (III, I) | 0.00487 | 0.00468 | 0.00434 | 0.00417 | |
| (III, II) | 0.00498 | 0.00488 | 0.00475 | 0.00438 | |
| (I, I) | 0.00364 | 0.00325 | 0.00296 | 0.00258 | |
| (II, II) | 0.00398 | 0.00368 | 0.00335 | 0.00287 | |
| (III, III) | 0.00425 | 0.00398 | 0.00378 | 0.00329 | |
| (I, II) | 0.00378 | 0.00336 | 0.00315 | 0.00268 | |
| (I, III) | 0.00387 | 0.00344 | 0.00326 | 0.00278 | |
| (II, I) | 0.00369 | 0.00347 | 0.00325 | 0.00285 | |
| (II, III) | 0.00396 | 0.00356 | 0.00338 | 0.00301 | |
| (III, I) | 0.00385 | 0.00345 | 0.00327 | 0.00279 | |
| (III, II) | 0.00399 | 0.00357 | 0.00348 | 0.00311 | |
| (I, I) | 0.00295 | 0.00278 | 0.00246 | 0.00199 | |
| (II, II) | 0.00325 | 0.00318 | 0.00289 | 0.00235 | |
| (III, III) | 0.00356 | 0.00338 | 0.00318 | 0.00274 | |
| (I, II) | 0.00301 | 0.00289 | 0.00257 | 0.00208 | |
| (I, III) | 0.00325 | 0.00297 | 0.00271 | 0.00229 | |
| (II, I) | 0.00304 | 0.00288 | 0.00267 | 0.00218 | |
| (II, III) | 0.00335 | 0.00328 | 0.00299 | 0.00245 | |
| (III, I) | 0.00326 | 0.00298 | 0.00275 | 0.00231 | |
| (III, II) | 0.00338 | 0.00329 | 0.00298 | 0.00264 | |
| (I, I) | 0.00235 | 0.00215 | 0.00196 | 0.00152 | |
| (II, II) | 0.00258 | 0.00236 | 0.00214 | 0.00178 | |
| (III, III) | 0.00293 | 0.00279 | 0.00258 | 0.00213 | |
| (I, II) | 0.00245 | 0.00225 | 0.00206 | 0.00162 | |
| (I, III) | 0.00255 | 0.00234 | 0.00211 | 0.00173 | |
| (II, I) | 0.00243 | 0.00222 | 0.00204 | 0.00165 | |
| (II, III) | 0.00283 | 0.00269 | 0.00248 | 0.00203 | |
| (III, I) | 0.00257 | 0.00238 | 0.00221 | 0.00183 | |
| (III, II) | 0.00287 | 0.00257 | 0.00251 | 0.00212 |
| ML | BP | BT | Bayes | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (n1,m1), (n2,m2) | (Si, Ti) | AWs | CPs | AWs | CPs | AWs | CPs | AWs | CPs |
| (I, I) | 0.5278 | 0.925 | 0.4934 | 0.929 | 0.4256 | 0.941 | 0.3745 | 0.947 | |
| (II, II) | 0.5568 | 0.924 | 0.5179 | 0.927 | 0.4568 | 0.942 | 0.3974 | 0.951 | |
| (III, III) | 0.6124 | 0.919 | 0.5534 | 0.937 | 0.4967 | 0.941 | 0.4378 | 0.954 | |
| (I, II) | 0.5378 | 0.918 | 0.5034 | 0.934 | 0.4356 | 0.939 | 0.3846 | 0.961 | |
| (I, III) | 0.5667 | 0.915 | 0.5278 | 0.941 | 0.4669 | 0.938 | 0.4173 | 0.962 | |
| (II, I) | 0.5397 | 0.920 | 0.5045 | 0.926 | 0.4358 | 0.937 | 0.3844 | 0.957 | |
| (II, III) | 0.6025 | 0.925 | 0.5336 | 0.927 | 0.4868 | 0.941 | 0.4279 | 0.949 | |
| (III, I) | 0.5699 | 0.927 | 0.5258 | 0.929 | 0.4643 | 0.951 | 0.4167 | 0.948 | |
| (III, II) | 0.6126 | 0.924 | 0.5437 | 0.923 | 0.49687 | 0.942 | 0.4478 | 0.955 | |
| (I, I) | 0.4465 | 0.931 | 0.4175 | 0.941 | 0.3987 | 0.938 | 0.3345 | 0.960 | |
| (II, II) | 0.4763 | 0.934 | 0.4457 | 0.939 | 0.4365 | 0.954 | 0.3647 | 0.962 | |
| (III, III) | 0.5136 | 0.929 | 0.4768 | 0.938 | 0.4567 | 0.947 | 0.3899 | 0.957 | |
| (I, II) | 0.4565 | 0.927 | 0.4275 | 0.937 | 0.4078 | 0.938 | 0.3448 | 0.958 | |
| (I, III) | 0.4863 | 0.931 | 0.4557 | 0.937 | 0.4465 | 0.937 | 0.3748 | 0.956 | |
| (II, I) | 0.4567 | 0.940 | 0.4279 | 0.927 | 0.4179 | 0.941 | 0.3547 | 0.952 | |
| (II, III) | 0.5037 | 0.928 | 0.4667 | 0.929 | 0.4468 | 0.947 | 0.3798 | 0.960 | |
| (III, I) | 0.4865 | 0.923 | 0.4558 | 0.926 | 0.4564 | 0.938 | 0.3847 | 0.962 | |
| (III, II) | 0.5136 | 0.919 | 0.4765 | 0.925 | 0.4668 | 0.937 | 0.3997 | 0.957 | |
| (I, I) | 0.3547 | 0.941 | 0.3285 | 0.951 | 0.2997 | 0.951 | 0.2658 | 0.958 | |
| (II, II) | 0.3745 | 0.939 | 0.3489 | 0.949 | 0.3258 | 0.952 | 0.2974 | 0.956 | |
| (III, III) | 0.3997 | 0.938 | 0.3658 | 0.954 | 0.3457 | 0.949 | 0.3178 | 0.952 | |
| (I, II) | 0.3647 | 0.938 | 0.3385 | 0.948 | 0.3199 | 0.939 | 0.2759 | 0.960 | |
| (I, III) | 0.3846 | 0.937 | 0.3587 | 0.949 | 0.3359 | 0.937 | 0.3075 | 0.962 | |
| (II, I) | 0.3648 | 0.927 | 0.3389 | 0.939 | 0.3187 | 0.936 | 0.2768 | 0.957 | |
| (II, III) | 0.3897 | 0.926 | 0.3558 | 0.939 | 0.3357 | 0.941 | 0.3078 | 0.970 | |
| (III, I) | 0.3847 | 0.934 | 0.3555 | 0.927 | 0.3367 | 0.940 | 0.3087 | 0.952 | |
| (III, II) | 0.3899 | 0.928 | 0.3658 | 0.929 | 0.3455 | 0.938 | 0.3177 | 0.951 | |
| (I, I) | 0.3257 | 0.951 | 0.2978 | 0.950 | 0.2689 | 0.952 | 0.2147 | 0.971 | |
| (II, II) | 0.3465 | 0.950 | 0.3125 | 0.949 | 0.2867 | 0.951 | 0.2346 | 0.969 | |
| (III, III) | 0.3599 | 0.949 | 0.3346 | 0.951 | 0.3022 | 0.949 | 0.2647 | 0.958 | |
| (I, II) | 0.3357 | 0.948 | 0.3178 | 0.939 | 0.2789 | 0.938 | 0.2245 | 0.957 | |
| (I, III) | 0.3564 | 0.949 | 0.3226 | 0.941 | 0.2968 | 0.936 | 0.2447 | 0.949 | |
| (II, I) | 0.3359 | 0.934 | 0.3169 | 0.940 | 0.2787 | 0.941 | 0.2346 | 0.947 | |
| (II, III) | 0.3499 | 0.928 | 0.3246 | 0.928 | 0.2922 | 0.939 | 0.2548 | 0.952 | |
| (III, I) | 0.3568 | 0.935 | 0.3227 | 0.939 | 0.2969 | 0.938 | 0.2449 | 0.954 | |
| (III, II) | 0.3498 | 0.927 | 0.3247 | 0.931 | 0.3025 | 0.935 | 0.2549 | 0.953 | |
| ML | BP | BT | Bayes | ||||||
|---|---|---|---|---|---|---|---|---|---|
| (n1,m1), (n2,m2) | (Si, Ti) | AWs | CPs | AWs | CPs | AWs | CPs | AWs | CPs |
| (I, I) | 0.4377 | 0.929 | 0.4157 | 0.939 | 0.3769 | 0.941 | 0.2857 | 0.960 | |
| (II, II) | 0.4562 | 0.924 | 0.4368 | 0.937 | 0.3974 | 0.942 | 0.3145 | 0.962 | |
| (III, III) | 0.4936 | 0.919 | 0.4697 | 0.941 | 0.4478 | 0.940 | 0.3567 | 0.957 | |
| (I, II) | 0.4474 | 0.915 | 0.4256 | 0.929 | 0.3867 | 0.939 | 0.2955 | 0.958 | |
| (I, III) | 0.4663 | 0.932 | 0.4469 | 0.927 | 0.4095 | 0.951 | 0.3246 | 0.956 | |
| (II, I) | 0.4475 | 0.918 | 0.4258 | 0.928 | 0.3868 | 0.950 | 0.2959 | 0.952 | |
| (II, III) | 0.4762 | 0.917 | 0.4568 | 0.926 | 0.4174 | 0.948 | 0.3345 | 0.960 | |
| (III, I) | 0.4664 | 0.916 | 0.4468 | 0.925 | 0.4096 | 0.946 | 0.3247 | 0.962 | |
| (III, II) | 0.4761 | 0.922 | 0.4569 | 0.919 | 0.4175 | 0.945 | 0.3343 | 0.957 | |
| (I, I) | 0.3174 | 0.939 | 0.2658 | 0.938 | 0.2267 | 0.939 | 0.1855 | 0.954 | |
| (II, II) | 0.3561 | 0.934 | 0.2954 | 0.928 | 0.2543 | 0.941 | 0.2146 | 0.961 | |
| (III, III) | 0.3798 | 0.925 | 0.3456 | 0.918 | 0.2867 | 0.946 | 0.2574 | 0.971 | |
| (I, II) | 0.3274 | 0.931 | 0.2758 | 0.917 | 0.2367 | 0.948 | 0.1955 | 0.969 | |
| (I, III) | 0.3371 | 0.927 | 0.2857 | 0.928 | 0.2465 | 0.936 | 0.2056 | 0.962 | |
| (II, I) | 0.3257 | 0.926 | 0.2766 | 0.925 | 0.2347 | 0.938 | 0.1957 | 0.957 | |
| (II, III) | 0.3694 | 0.921 | 0.3352 | 0.924 | 0.2765 | 0.954 | 0.2475 | 0.952 | |
| (III, I) | 0.3372 | 0.924 | 0.2858 | 0.923 | 0.2466 | 0.951 | 0.2157 | 0.955 | |
| (III, II) | 0.3595 | 0.910 | 0.3351 | 0.933 | 0.2664 | 0.947 | 0.2373 | 0.960 | |
| (I, I) | 0.2475 | 0.938 | 0.2257 | 0.940 | 0.1969 | 0.951 | 0.1553 | 0.947 | |
| (II, II) | 0.2784 | 0.934 | 0.2578 | 0.939 | 0.2236 | 0.949 | 0.1874 | 0.951 | |
| (III, III) | 0.2978 | 0.932 | 0.2863 | 0.937 | 0.2647 | 0.947 | 0.2089 | 0.954 | |
| (I, II) | 0.2575 | 0.929 | 0.2357 | 0.929 | 0.2069 | 0.944 | 0.1654 | 0.961 | |
| (I, III) | 0.2684 | 0.930 | 0.2478 | 0.931 | 0.2137 | 0.950 | 0.1775 | 0.962 | |
| (II, I) | 0.2576 | 0.924 | 0.2358 | 0.930 | 0.2067 | 0.936 | 0.1653 | 0.957 | |
| (II, III) | 0.2871 | 0.921 | 0.2764 | 0.928 | 0.2546 | 0.939 | 0.1988 | 0.949 | |
| (III, I) | 0.2685 | 0.920 | 0.2479 | 0.918 | 0.2138 | 0.938 | 0.1776 | 0.948 | |
| (III, II) | 0.2875 | 0.923 | 0.2669 | 0.921 | 0.2448 | 0.941 | 0.1984 | 0.955 | |
| (I, I) | 0.1978 | 0.941 | 0.1752 | 0.940 | 0.1564 | 0.951 | 0.1256 | 0.958 | |
| (II, II) | 0.2178 | 0.940 | 0.1968 | 0.939 | 0.1745 | 0.951 | 0.1466 | 0.956 | |
| (III, III) | 0.2465 | 0.941 | 0.2255 | 0.938 | 0.2014 | 0.950 | 0.1748 | 0.952 | |
| (I, II) | 0.2078 | 0.939 | 0.1852 | 0.928 | 0.1664 | 0.949 | 0.1355 | 0.960 | |
| (I, III) | 0.2177 | 0.938 | 0.1969 | 0.919 | 0.1746 | 0.948 | 0.1465 | 0.962 | |
| (II, I) | 0.2075 | 0.924 | 0.1851 | 0.923 | 0.1661 | 0.939 | 0.1353 | 0.957 | |
| (II, III) | 0.2365 | 0.926 | 0.2155 | 0.922 | 0.1914 | 0.939 | 0.1648 | 0.960 | |
| (III, I) | 0.2176 | 0.920 | 0.1993 | 0.934 | 0.1741 | 0.934 | 0.1463 | 0.962 | |
| (III, II) | 0.2265 | 0.918 | 0.2156 | 0.927 | 0.1999 | 0.935 | 0.1715 | 0.967 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
EL-Sagheer, R.M.; Eliwa, M.S.; El-Morshedy, M.; Al-Essa, L.A.; Al-Bossly, A.; Abd-El-Monem, A. Analysis of the Stress–Strength Model Using Uniform Truncated Negative Binomial Distribution under Progressive Type-II Censoring. Axioms 2023, 12, 949. https://doi.org/10.3390/axioms12100949
EL-Sagheer RM, Eliwa MS, El-Morshedy M, Al-Essa LA, Al-Bossly A, Abd-El-Monem A. Analysis of the Stress–Strength Model Using Uniform Truncated Negative Binomial Distribution under Progressive Type-II Censoring. Axioms. 2023; 12(10):949. https://doi.org/10.3390/axioms12100949
Chicago/Turabian StyleEL-Sagheer, Rashad M., Mohamed S. Eliwa, Mahmoud El-Morshedy, Laila A. Al-Essa, Afrah Al-Bossly, and Amel Abd-El-Monem. 2023. "Analysis of the Stress–Strength Model Using Uniform Truncated Negative Binomial Distribution under Progressive Type-II Censoring" Axioms 12, no. 10: 949. https://doi.org/10.3390/axioms12100949






