An Improved Intuitionistic Fuzzy Decision-Theoretic Rough Set Model and Its Application
Abstract
:1. Introduction
Motivation for This Study
- i
- We will generalize the concept of a three-way decision based on a decision-theoretic rough set for intuitionistic fuzzy numbers.
- ii
- We will employ similarity classes instead of equivalence classes, which expands the scope of the approach.
- iii
- iv
- We will use our proposed approach to show the validity and effectiveness of solving real-life issues. For this purpose, we will discuss the model of an electronic device for the special person and use the proposed approach for taking decisions.
- v
- We will deeply discuss the comparative analysis of the developed model and some existing techniques and show our preference for the mentioned approach.
2. Preliminaries
2.1. IFSs: A Brief Overview
- (1)
- ;
- (2)
- (3)
- ; where is a scalar.
- (4)
- .
2.2. 3WD Based on Rough Set-Theory and DTRS Model
- (1)
- If and then
- (2)
- If and , then
- (3)
- If and then
3. 3WD Based on DTRS Model with IFNs: Existing Model
- (1)
- If and , then
- (2)
- If and then
- (3)
- If and then
- (4)
- If and , then
- (5)
- If and then
- (6)
- If and then
- (7)
- If , then take
- (8)
- If , then take
- (9)
- If , then take .
4. Generalized Intuitionistic Fuzzy-Based DTRS (GI-DTRS) Model
4.1. Some Concerns in the Existing IF-Based DTRS Model
- i
- The clustering of elements via equivalence classes is a restrictive condition. Stating differently, for two elements to be in the same cluster, their feature values in all the features should be exactly similar. Even when all other feature values are the same, a slight variation in one feature value may cause two components to be in distinct clusters. Relaxing this restriction, we introduce similarity classes in the DTRS model. The threshold is determined by how much similarity between the elements is required.
- ii
- The essence of DTRS lies in defining the conditional probabilities of elements for the given concept. In [22], these conditional probabilities have been replaced with intuitionistic fuzzy degrees. Probabilities and fuzzy degrees are totally different concepts that cannot be interchanged. Probability describes how likely an event is to occur, while fuzzy and IF degrees are linguistic information-based concepts used to manage partial truths. To retain the true essence of DTRS theory, we use conditional probabilities defined by Yao in [22]. These probabilities are a generalization of the equivalence-class-based conditional probabilities.
- iii
- The classical DTRS starts with the set of states that are to be approximated. These states are actually subsets of the universe. In [50], these states are considered external components that have no link with the universe. As a result, the theory outlined in [22] significantly deviates from the fundamental idea of DTRS. On the other hand, we nevertheless adhere to the classical approach’s interpretation of the concept of states. This makes our model more reliable.
4.2. Generalized DTRS Based on IFNs
- (10)
- If and , then
- (11)
- If and then
- (12)
- If and then
- (13)
- If and , then
- (14)
- If and then
- (15)
- If and then
- (16)
- If , then take
- (17)
- If , then take
- (18)
- If , then take ,
5. Case Study
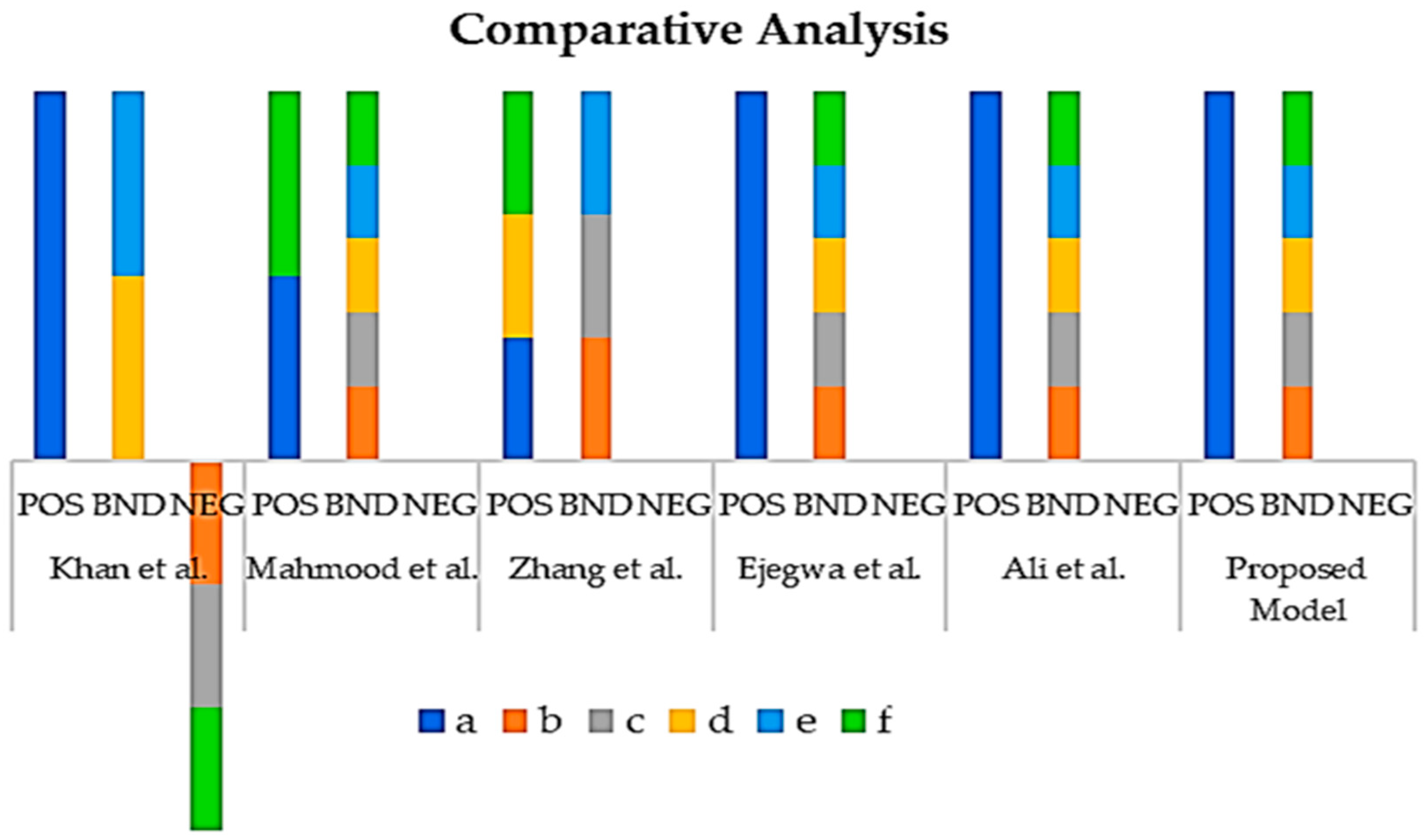
Comparative Analysis
- i
- When it comes to analyzing different approaches to solving a problem, it is important to consider their effectiveness, feasibility, and scalability. In this case, we compared an established approach with an existing approach, focusing on how they satisfy results and their benefits.
- ii
- The established approach typically refers to a well-known and widely used method for solving a problem. This approach is based on a proven methodology that has been tested and validated over time, and it often has a track record of delivering reliable results. The existing approach, on the other hand, refers to a method that has been developed but may not be as widely known or tested. For example, all the existing approaches based on similarity measures give the majority of elements of the acceptance region the same, such as , similarly to the negative and boundary zones.
- iii
- One advantage of the established approach is that it is often easier to solve. This is because the methodology has been refined and improved over time, and there are typically more resources available to help people understand and apply it.
- iv
- Another advantage of the established approach is that it is often more general. This means that it can be applied to a wider range of problems or scenarios. For example, if we were comparing an established statistical model with a newer one, the established model may have been designed to handle a wider range of data types or distributions, making it more versatile.
- v
- In addition, the established approach often uses well-defined similarity measures and similarity classes. These measures and classes help to ensure that the results are consistent and meaningful.
- vi
- However, it is important to note that the existing approach may have benefits as well. For example, it may be more specialized, meaning that it is designed specifically for a particular problem or scenario. This can make it more effective than the established approach in certain contexts.
- vii
- In conclusion, when comparing an established approach with an existing approach, it is important to consider factors such as ease of implementation, generalizability, and the use of well-defined similarity measures and similarity classes. While the established approach has advantages in these areas, the existing approach may be more effective in certain contexts due to its specialization. Ultimately, the choice of approach will depend on the specific problem being solved and the resources available.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bourahla, M. Using Rough Set Theory for Reasoning on Vague Ontologies. Int. J. Intell. Syst. Appl. 2022, 13, 21. [Google Scholar] [CrossRef]
- Ardil, C. Vague Multiple Criteria Decision-Making Analysis Method for Fighter Aircraft Selection. Int. J. Aerosp. Mech. Eng. 2022, 16, 133–142. [Google Scholar]
- Zadeh, L.A.; Klir, G.J.; Yuan, B. Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers; World Scientific: Singapore, 1996; Volume 6. [Google Scholar]
- Zhang, L.; Zhang, B. The quotient space theory of problem solving. Fundam. Inform. 2004, 59, 287–298. [Google Scholar]
- Pawlak, Z. Rough set theory and its applications to data analysis. Cybern. Syst. 1998, 29, 661–688. [Google Scholar] [CrossRef]
- Yao, Y. Three-way decisions and cognitive computing. Cogn. Comput. 2016, 8, 543–554. [Google Scholar] [CrossRef]
- Yao, Y. An outline of a theory of three-way decisions. In Proceedings of the International Conference on Rough Sets and Current Trends in Computing, Chengdu, China, 17–20 August 2012; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Yao, Y. Tri-level thinking: Models of three-way decision. Int. J. Mach. Learn. Cybern. 2020, 11, 947–959. [Google Scholar] [CrossRef]
- Yao, Y. The geometry of three-way decision. Appl. Intell. 2021, 51, 6298–6325. [Google Scholar] [CrossRef]
- Mehmood, A.; Ali, A. Application of Deep Reinforcement Learning for Tracking Control of 3WD Omnidirectional Mobile Robot. Inf. Technol. Control 2021, 50, 507–521. [Google Scholar] [CrossRef]
- Anwar, M.Z.; Bashir, S.; Shabir, M.; Alharbi, M.G. Multigranulation roughness of intuitionistic fuzzy sets by soft relations and their appli-cations in decision making. Mathematics 2021, 9, 2587. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, J.; Li, D.; Zhan, J. A novel multi-granularity three-way decision-making approach in q-rung orthopair fuzzy information systems. Int. J. Approx. Reason. 2021, 138, 161–187. [Google Scholar] [CrossRef]
- Zhu, J.; Ma, X.; Zhan, J.; Yao, Y. A three-way multi-attribute decision making method based on regret theory and its application to medical data in fuzzy environments. Appl. Soft Comput. 2022, 123, 108975. [Google Scholar] [CrossRef]
- Dada, E.G.; Bassi, J.S.; Chiroma, H.; Abdulhamid, S.M.; Adetunmbi, A.O.; Ajibuwa, O.E. Machine learning for email spam filtering: Review, approaches and open research problems. Heliyon 2019, 5, e01802. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.-H.; Min, F.; Chen, G.S.; Shen, S.P.; Wen, Z.C.; Zhou, X.B. Tri-partition state alphabet-based sequential pattern for multivariate time series. Cogn. Comput. 2021, 14, 1881–1899. [Google Scholar] [CrossRef]
- Wang, W.; Zhan, J.; Mi, J. A three-way decision approach with probabilistic dominance relations under intuitionistic fuzzy information. Inf. Sci. 2022, 582, 114–145. [Google Scholar] [CrossRef]
- Yang, M.-S.; Ali, Z.; Mahmood, T. Three-way decisions based on q-rung orthopair fuzzy 2-tuple linguistic sets with generalized Maclaurin symmetric mean operators. Mathematics 2021, 9, 1387. [Google Scholar] [CrossRef]
- Ali, W.; Shaheen, T.; Haq, I.U.; Toor, H.G.; Akram, F.; Jafari, S.; Uddin, M.Z.; Hassan, M.M. Multiple-Attribute Decision Making Based on Intuitionistic Hesitant Fuzzy Connection Set Environment. Symmetry 2023, 15, 778. [Google Scholar] [CrossRef]
- Tao, L.; Wang, C.; Jia, Y.; Zhou, R.; Zhang, T.; Chen, Y.; Lu, C.; Suo, M. Simultaneous-Fault Diagnosis of Satellite Power System Based on Fuzzy Neighborhood ζ-Decision-Theoretic Rough Set. Mathematics 2022, 10, 3414. [Google Scholar] [CrossRef]
- Liu, D.; Yao, Y.; Li, T. Three-way investment decisions with decision-theoretic rough sets. Int. J. Comput. Intell. Syst. 2011, 4, 66–74. [Google Scholar]
- Dağıstanlı, H.A. An integrated fuzzy MCDM and trend analysis approach for financial performance evaluation of energy companies in Borsa Istanbul sustainability index. J. Soft Comput. Decis. Anal. 2023, 1, 39–49. [Google Scholar] [CrossRef]
- Yao, Y.; Deng, X. Sequential three-way decisions with probabilistic rough sets. In Proceedings of the IEEE 10th International Con-ference on Cognitive Informatics and Cognitive Computing (ICCI-CC’11), Banff, AB, Canada, 18–20 August 2011; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Wagh, M.; Nanda, P.K. Decision-Theoretic Rough Sets based automated scheme for object and back-ground classification in unevenly illuminated images. Appl. Soft Comput. 2022, 119, 108596. [Google Scholar] [CrossRef]
- Ali, W.; Shaheen, T.; Haq, I.U.; Alballa, T.; Alburaikan, A.; El-Wahed Khalifa, H.A. A Novel Generalization of Q-Rung Orthopair Fuzzy Aczel Alsina Aggregation Operators and Their Application in Wireless Sensor Networks. Sensors 2023, 23, 8105. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.R.; Hu, B.Q. Three-way decisions with decision-theoretic rough sets in multiset-valued information tables. Inf. Sci. 2020, 507, 684–699. [Google Scholar] [CrossRef]
- Qian, Y.; Zhang, H.; Sang, Y.; Liang, J. Multigranulation decision-theoretic rough sets. Int. J. Approx. Reason. 2014, 55, 225–237. [Google Scholar] [CrossRef]
- Liang, D.; Xu, Z.; Liu, D. Three-way decisions based on decision-theoretic rough sets with dual hesitant fuzzy information. Inf. Sci. 2017, 396, 127–143. [Google Scholar] [CrossRef]
- Liu, F.; Liu, Y.; Abdullah, S. Three-way decisions with decision-theoretic rough sets based on covering-based q-rung orthopair fuzzy rough set model. J. Intell. Fuzzy Syst. 2021, 40, 9765–9785. [Google Scholar] [CrossRef]
- Liu, D.; Li, T.; Ruan, D. Probabilistic model criteria with decision-theoretic rough sets. Inf. Sci. 2011, 181, 3709–3722. [Google Scholar] [CrossRef]
- Liu, J.; Huang, B.; Li, H.; Bu, X.; Zhou, X. Optimization-Based Three-Way Decisions with Interval-Valued Intuitionistic Fuzzy Information. IEEE Trans. Cybern. 2022, 53, 3829–3843. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy sets, probability and measurement. Eur. J. Oper. Res. 1989, 40, 135–154. [Google Scholar] [CrossRef]
- Shaheen, T.; Ali, M.I.; Shabir, M. Generalized hesitant fuzzy rough sets (GHFRS) and their application in risk analysis. Soft Comput. 2020, 24, 14005–14017. [Google Scholar] [CrossRef]
- Shabir, M.; Ali, M.I.; Shaheen, T. Another approach to soft, rough sets. Knowl.-Based Syst. 2013, 40, 72–80. [Google Scholar] [CrossRef]
- Khan, M.R.; Ullah, K.; Pamucar, D.; Bari, M. Performance measure using a multi-attribute decision making approach based on Complex T-spherical fuzzy power aggregation operators. J. Comput. Cogn. Eng. 2022, 1, 138–146. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets. Intuitionistic Fuzzy Sets; Physica: Heidelberg, Germany, 1999; pp. 1–137. [Google Scholar]
- Atanassov, K.T. New topological operator over intuitionistic fuzzy sets. J. Comput. Cogn. Eng. 2022, 1, 94–102. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, J.; Niu, B.; Liu, L.; He, X. A novel hybrid multi-criteria group decision-making approach with intuitionistic fuzzy sets to design reverse supply chains for COVID-19 medical waste recycling channels. Comput. Ind. Eng. 2022, 169, 108228. [Google Scholar] [CrossRef] [PubMed]
- Sharma, B.; Suman; Saini, N.; Gandotra, N. Multi criteria decision making under the fuzzy and intuitionistic fuzzy environment: A review. In AIP Conference Proceedings; AIP Publishing LLC: Long Island, NY, USA, 2022; Volume 2357. [Google Scholar] [CrossRef]
- Mahmood, T.; Ali, W.; Ali, Z.; Chinram, R. Power aggregation operators and similarity measures based on improved intuitionistic hesitant fuzzy sets and their applications to multiple attribute decision making. Comput. Model. Eng. Sci. 2021, 126, 1165–1187. [Google Scholar] [CrossRef]
- Senapati, T.; Chen, G.; Yager, R.R. Aczel–Alsina aggregation operators and their application to intui-tionistic fuzzy multiple attribute decision making. Int. J. Intell. Syst. 2022, 37, 1529–1551. [Google Scholar] [CrossRef]
- Gohain, B.; Chutia, R.; Dutta, P.; Gogoi, S. Two new similarity measures for intuitionistic fuzzy sets and its various applications. Int. J. Intell. Syst. 2022, 37, 5557–5596. [Google Scholar] [CrossRef]
- Singh, S.; Som, T. Intuitionistic Fuzzy Rough Sets: Theory to Practice. In Mathematics in Computational Science and Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 91–133. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/9781119777557.ch (accessed on 1 September 2023).
- Liang, D.; Liu, D. Deriving three-way decisions from intuitionistic fuzzy decision-theoretic rough sets. Inf. Sci. 2015, 300, 28–48. [Google Scholar] [CrossRef]
- Liang, D.; Xu, Z.; Liu, D. Three-way decisions with intuitionistic fuzzy decision-theoretic rough sets based on point operators. Inf. Sci. 2017, 375, 183–201. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, J. Measurement, modeling, reduction of decision-theoretic multigranulation fuzzy rough sets based on three-way decisions. Inf. Sci. 2022, 607, 1550–1582. [Google Scholar] [CrossRef]
- Ali, W.; Shaheen, T.; Haq, I.U.; Toor, H.G.; Alballa, T.; Khalifa, H.A.E.-W. A Novel Interval-Valued Decision Theoretic Rough Set Model with Intuitionistic Fuzzy Numbers Based on Power Aggregation Operators and Their Application in Medical Diagnosis. Mathematics 2023, 11, 4153. [Google Scholar] [CrossRef]
- Xue, Z.; Sun, B.; Hou, H.; Pang, W.; Zhang, Y. Three-way decision models based on multi-granulation rough intuitionistic hesitant fuzzy sets. Cogn. Comput. 2022, 14, 1859–1880. [Google Scholar] [CrossRef]
- Huang, X.; Zhan, J.; Sun, B. A three-way decision method with pre-order relations. Inf. Sci. 2022, 595, 231–256. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, C.; Wang, G. A sequential three-way decision model with intuitionistic fuzzy numbers. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 2640–2652. [Google Scholar] [CrossRef]
- Ye, J. Cosine similarity measures for intuitionistic fuzzy sets and their applications. Math. Comput. Model. 2011, 53, 91–97. [Google Scholar] [CrossRef]
- Ejegwa, P.A.; Agbetayo, J.M. Similarity-distance decision-making technique and its applications via intuitionistic fuzzy pairs. J. Comput. Cogn. Eng. 2023, 2, 68–74. [Google Scholar] [CrossRef]
- Ali, W.; Shaheen, T.; Toor, H.G.; Akram, F.; Uddin, M.Z.; Hassan, M.M. Selection of Investment Policy Using a Novel Three-Way Group Decision Model under Intuitionistic Hesitant Fuzzy Sets. Appl. Sci. 2023, 13, 4416. [Google Scholar] [CrossRef]
- Haq, I.U.; Shaheen, T.; Ali, W.; Toor, H.; Senapati, T.; Pilla, F.; Moslem, S. Novel Fermatean Fuzzy Aczel–Alsina Model for Investment Strategy Selection. Mathematics 2023, 11, 3211. [Google Scholar] [CrossRef]
- Ali, W.; Shaheen, T.; Haq, I.U.; Toor, H.; Akram, F.; Garg, H.; Uddin, M.Z.; Hassan, M.M. Aczel-Alsina-based aggregation operators for intuitionistic hesitant fuzzy set environment and their application to multiple attribute decision-making process. AIMS Math. 2023, 8, 18021–18039. [Google Scholar] [CrossRef]
- Nazir, N.; Shaheen, T.; Jin, L.; Senapati, T. An Improved Algorithm for Identification of Dominating Vertex Set in Intuitionistic Fuzzy Graphs. Axioms 2023, 12, 289. [Google Scholar] [CrossRef]
- Radenovic, S.; Ali, W.; Shaheen, T.; Haq, I.U.; Akram, F.; Toor, H. Multiple attribute decision-making based on bonferroni mean operators under square root fuzzy set environment. J. Comput. Cogn. Eng. 2023, 2, 236–248. [Google Scholar] [CrossRef]
- Ibrahim, H.Z.; Alshammari, I. n, m-Rung Orthopair Fuzzy Sets With Applications to Multicriteria Decision Making. IEEE Access 2022, 10, 99562–99572. [Google Scholar] [CrossRef]
| Symbols | Description | Symbols | Description |
|---|---|---|---|
| IFSs | Intuitionistic Fuzzy Sets | DTRS | Decision-Theoretic Rough Sets |
| IFNs | Intuitionistic Fuzzy Numbers | DRs | Decision Rules |
| 3WD | Three-Way Decision | TWDM | Three-Way Decision Making |
| Actions\States | ||
|---|---|---|
| Actions\States | ||
|---|---|---|
| Yes | |||||
| No | |||||
| No | |||||
| Yes | |||||
| Yes | |||||
| Yes |
| Similarity of Alternatives | ||||||
|---|---|---|---|---|---|---|
| 1 | ||||||
| 1 | 0.827 | |||||
| Alternatives | Probability Values | Complement of Probability | Error Values |
|---|---|---|---|
| Alternatives | |||
|---|---|---|---|
| a | 0.359 | 0.201 | 0.124 |
| 0.423 | 0.237 | 0.146 | |
| 0.599 | 0.335 | 0.206 | |
| 0.631 | 0.353 | 0.217 | |
| 0.599 | 0.335 | 0.206 | |
| 0.599 | 0.335 | 0.206 |
| Classification | |||
|---|---|---|---|
| Participants | , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, W.; Shaheen, T.; Toor, H.G.; Alballa, T.; Alburaikan, A.; Khalifa, H.A.E.-W. An Improved Intuitionistic Fuzzy Decision-Theoretic Rough Set Model and Its Application. Axioms 2023, 12, 1003. https://doi.org/10.3390/axioms12111003
Ali W, Shaheen T, Toor HG, Alballa T, Alburaikan A, Khalifa HAE-W. An Improved Intuitionistic Fuzzy Decision-Theoretic Rough Set Model and Its Application. Axioms. 2023; 12(11):1003. https://doi.org/10.3390/axioms12111003
Chicago/Turabian StyleAli, Wajid, Tanzeela Shaheen, Hamza Ghazanfar Toor, Tmader Alballa, Alhanouf Alburaikan, and Hamiden Abd El-Wahed Khalifa. 2023. "An Improved Intuitionistic Fuzzy Decision-Theoretic Rough Set Model and Its Application" Axioms 12, no. 11: 1003. https://doi.org/10.3390/axioms12111003
APA StyleAli, W., Shaheen, T., Toor, H. G., Alballa, T., Alburaikan, A., & Khalifa, H. A. E.-W. (2023). An Improved Intuitionistic Fuzzy Decision-Theoretic Rough Set Model and Its Application. Axioms, 12(11), 1003. https://doi.org/10.3390/axioms12111003