A Supplier Selection Decision-Making Approach for Complex Product Development Based on Hesitant Fuzzy Information

Abstract

During the development process of complex products, selecting the best desirable alternative supplier is a challenge since an improperly selected alternative may cause losing capacity and increasing the cycle time and cost of development for a company. For this multiple-attribute decision-making problem of supplier selection, in this paper, a supplier selection problem in which the decision data are hesitant fuzzy information and the attribute weight is unknown in complex product development is investigated, and a supplier selection decision-making approach based on hesitant fuzzy information is proposed. Firstly, a bidirectional projection based on hesitant fuzzy information is established, and then the measurement equation for the degree of closeness is improved. Further, an attribute weight determination model which minimizes the projection total deviation for the hesitant fuzzy elements is constructed. By solving this model, scientific and reasonable attribute weights are provided. Subsequently, an illustrative example is employed to not only give the ranking result of alternative suppliers but also demonstrate the validity and feasibility of the developed approach. Meanwhile, sensitivity analysis and comparative analysis are put forward to illustrate the stability of the given final ranking result and the advantages and reliability of the constructed method. For alternative or strategy selection, this proposed approach can be used as a decision-making means when uncertainties are inherent.

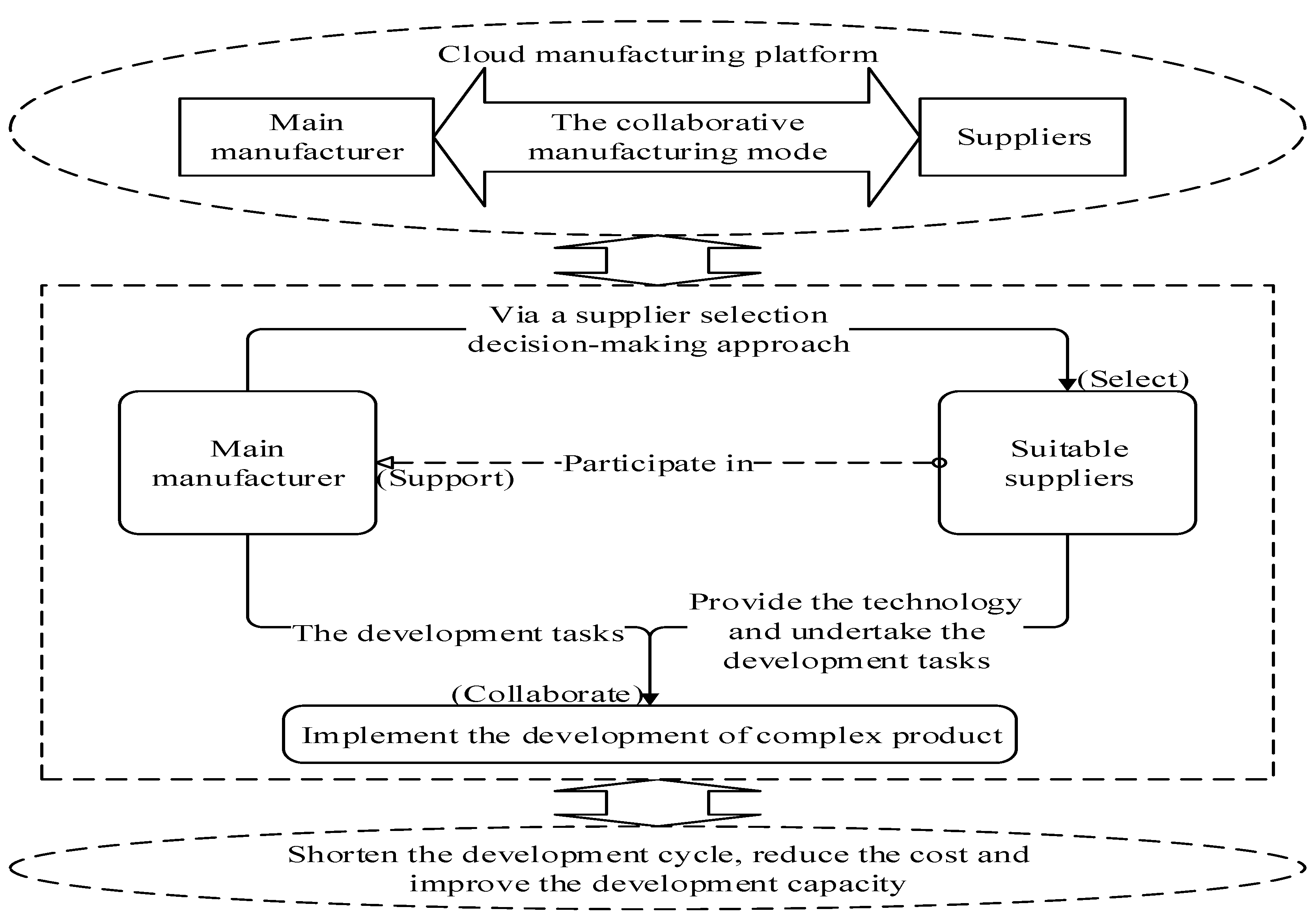
1. Introduction

A core component of the manufacturing industry in China is the equipment manufacturing industry, in which most of the products are complex products [1]. The same is true in other countries or regions. Further, complex products are large-scale products, systems, or infrastructure with high R&D costs, large-scale, high-technology, individual or small-batch customization, and high integration. As is well known, large airliners and ships are typical complex products. Distinctly, the complex product development process involves many disciplines such as machinery, electronics, materials, and automation. Simultaneously, various subsystems and functional modules exist in the development process, which contains as many as millions of parts and components. Consequently, undertaking and completing these development tasks independently will be a great challenge to some enterprises given that their own resources are deficient. Confronting this background, in order to accomplish complex product development, multi-disciplinary, cross-organizational, multi-agent collaborative development should be considered [2]. Accordingly, complex product development needs support from other suppliers [3], where suppliers which participate in the complex product development provide certain technology and undertake the corresponding development tasks, which will contribute to shortening the development cycle, reducing the cost, and improving the development capacity. Sequentially, for the process of supplier selection, a cloud manufacturing platform which is based on the sharing and utilization of socialized resources and large-scale cooperation can be introduced, which will provide a market resource platform support for manufacturers to implement complex product development [4,5]. In summary, complex product development tasks can use the cloud manufacturing platform to select suitable outsourcing suppliers by applying decision-making approaches or other methods, and then the collaborative manufacturing mode of “main manufacturer + suppliers” is adopted. Accordingly, through collaborative manufacturing, complex product development can be completed, which is depicted in Figure 1.

As shown in Figure 1, selecting and implementing the supplier selection decision-making approach will be a significant portion of this process. In recent years, most research on supplier selection has focused on the evaluation indexes and constructing models [6,7,8]. Further, Mafakheri et al. [9] and Khoshfetrat et al. [10] used the analytic hierarchy process to evaluate suppliers. Cebi and Otay [11] adopted a fuzzy multi-objective optimization technique to evaluate and select suppliers in the supplier selection stage. Mohammed et al. [12] proposed a method integrating AHP, TOPSIS, and multi-objective planning to solve the problem of sustainable supplier selection. Suprasongsin et al. [13] integrated supplier selection decision-making into a fuzzy multi-objective programming model to optimize the fuzzy requirements. Simultaneously, Liu and Hua [14] constructed a supplier selection model using the VIKOR method within a single-valued neutrosophic environment for solving the problem of supplier optimization with completely unknown attribute weight information. Zhu and Qiu [15] built a risk evaluation system of suppliers, and then used the model of entropy weight and TOPSIS to evaluate the risk in suppliers for an air subcontracting production project to select the optimal supplier. Wang et al. [16] developed an integrated fuzzy two-stage multi-period optimization model based on risk mean analysis for the supplier selection and order allocation problem with different supply contracts in an uncertain environment. Dong and Li [17] established a hybrid method to solve the problem of sustainable supplier selection considering the complexity of sustainable supplier selection and the uncertainty of standards. Liang and Zou [18] put forward a sustainable supplier index system for emerging industries for the multi-attribute decision-making problem of sustainable supplier selection in strategic emerging industries. Zhang [19] constructed a supplier selection and evaluation model based on the gray correlation degree and it was applied to the competitive negotiation pricing process, which provides a reference for supplier selection and the evaluation of the same type of enterprises. Lu and Zhang [20] proposed a multi-attribute group decision-making method for addressing the studied supplier selection. Gu et al. [21] proposed and designed a supplier evaluation method based on a backpropagation neural network, a weak classifier, and a technique for order preference by similarity to create an ideal solution in order to improve the applicability and accuracy of the evaluation criteria for aviation equipment suppliers. Wang et al. [22] developed a VIKOR multi-attribute decision-making method based on grey group clustering and improved criteria importance using intercriteria correlation combination weighting to solve the problem of weapon equipment supplier selection.

Along with the deepening of the research in this field, it can be found that the essence of the supplier selection problem is a multiple-attribute decision-making process [23,24,25,26]. Multiple-attribute decision-making has been widely applied in the process of socio-economic management, but with the rapid development of modern society, the realistic decision-making environment faced by decision-makers is becoming more and more complex [27]. Due to a lack of knowledge and experience, decision-makers often hesitate to evaluate complex decision-making problems in reality [28]. Thus, some research literature on fuzzy information has emerged [29,30,31,32]. Specifically, Yücenur et al. [33] integrated the analytic hierarchy process and the analytic network process and took service quality, cost, risk factors, and supplier characteristics as the main indicators within logistics supplier selection in order to compare and analyze the results of logistics supplier selection. Kar [34] designed a mixed-group decision support system based on AHP, fuzzy set theory, and a neural network for supplier selection research. Mehmet and Haluk [35] proposed a hybrid method based on fuzzy TOPSIS and a fuzzy analytic hierarchy process in order to identify a suitable supplier. Govindan at al. [36] constructed a sustainable third-party reverse logistics supplier selection approach based on the ELECTRE I method. Meanwhile, Wang and Wu [37] constructed a COPRAS model for supplier selection based on an intuitionistic fuzzy weight-determined method, and the priority of each supplier was obtained according to the utility of each supplier. As a result, the best supplier selection scheme was obtained. You et al. [38] transformed customers’ linguistic requirements into the criteria for supplier selection based on a fuzzy mathematics method and quality function deployment. Wang et al. [39] presented an integrated approach of fuzzy AHP and fuzzy goal programming and considered the carbon emission of suppliers as one important criterion to deal with the supplier selection problem. Weng et al. [40] used an intuitionistic fuzzy analytic hierarchy process to decide the index weight based on the fuzzy preference relationship of experts combined with the decision membership function, and the optimal selection scheme of cold chain logistics suppliers was discussed according to the assignment optimization calculation for multiple indexes according to the weighted arithmetic average operator. Yao and Ma [41] established an equipment supplier evaluation index system and proposed the equipment supplier selection based on an intuitionistic fuzzy TOPSIS method. Lin et al. [42] proposed an expert weight determination method that comprehensively considered the hesitancy degree and similarity of the evaluation information to deal with the problem of supplier selection decision-making with the attribute evaluation value as linguistic variables and unknown expert weights. Xu et al. [43] put forward a method of optimizing a green supplier selection model with a combination of fuzzy C-means (GW-FCM) and VIKOR based on a genetic heuristic attribute weight search strategy. Guo et al. [44] offered an intuitionistic fuzzy multiple-attribute decision-making approach for reverse logistics supplier selection based on intuitionistic fuzzy entropy. Liang et al. [45] improved the fuzzy multi-criteria decision method and used the best-worst method to establish a supplier selection model considering the risk factors to initially select suppliers.

Further, in order to better deal with addressing these problems in management decision-making activities, a hesitant fuzzy set, which is an effective means to describe the decision-making information in the case of hesitation, is introduced, which is often used to express hesitant fuzzy information [46]. As a consequence, multiple-attribute decision-making problems [47,48] with hesitant fuzzy information have also paid attention to the process of socio-economic management. Nevertheless, the determination of attribute weights which affects the decision-making process is a significant influence factor [49,50,51], which plays an important role in scientific and reasonable decision-making. To dig into this problem deeply, for instance, Wang [52] investigated a weighting method based on the entropy principle. Wang et al. [53] proposed a linear programming method to solve the weights of multiple-attribute decision-making. Wei [54] constructed an optimization method of an IFN ideal decision-making matrix from a similarity point. Yuan et al. [55] proposed a nonlinear method for solving the weights, which was applied to multiple-attribute decision-making problems. Liao and Xu [56] discussed the multiple-attribute decision-making problem of partially knowing the weight information, and then an optimization model was constructed for solving the weights. Rezaei [57] proposed a best-worst method for multiple-attribute decision-making, and a maximin approach was designed and solved to determine the attribute weights. The literature [58,59,60] established a projection method to rank alternative schemes. The above research methods have achieved good results. However, there are still some shortcomings, such as the linear programming method being limited by prior weights and the distance measurement method ignoring the information on the hesitation degree, as well as the compared relationship between the alternatives and the negative ideal direction being neglected in the projection method, the reliability analysis of the method being deficient, and so on.

To sum up, in this paper, hesitant fuzzy information is introduced. For the supplier selection problem in complex product development, research on multiple-attribute decision-making with unknown weights will be further discussed. Therefore, the multiple-attribute decision-making problem of supplier selection in complex product development with hesitant fuzzy decision-making data is deeply investigated and explored. Specifically, in the case of fuzzy information with unknown attribute weights, projection technology is introduced into multiple-attribute decision-making, and then the relationships between the positive and negative ideal hesitant fuzzy elements and alternative hesitant fuzzy elements are fully considered in order to propose the bidirectional projection. Simultaneously, an improved measurement equation for degree of closeness is developed to retain more information. Further, an attribute weight determination model is established to obtain the attribute weights scientifically. Hence, alternative suppliers can be ranked for selecting the best one. Moreover, through an example, the validity of the proposed approach is verified. Subsequently, the sensitivity analysis and the comparative analysis are introduced to further illustrate the applicability and reliability of this proposed approach. Consequently, the proposed decision-making approach in this paper provides a novel method for selecting a reasonable supplier to involve in complex product development, which will better meet the real requirements of engineering.

The remainder of the present paper is set out as follows. Section 2 briefly describes the definition and characteristics of the hesitant fuzzy element. In Section 3, the bidirectional projection is proposed to calculate the projection values and the improved closeness degree equation is given, and the attribute weight determination model is established for solving the attribute weights. Additionally, the decision-making procedure is elaborated. In Section 4, the illustrative example of complex product development is employed to demonstrate the validity and feasibility of the proposed approach in this paper. In Section 5, through sensitivity analysis and comparative analysis, the superiority of this proposed approach is discussed, analyzed, and summarized. The conclusion and future research are presented in Section 6.

2. Preliminaries

As an extended form of a fuzzy set [61], Torra proposed a hesitant fuzzy set [62]. He points out that a set of possible values constructs the membership function of the hesitant fuzzy set, which indicates that the membership degree of an element belonging to a set can consist of several possible values. The decision-makers can obtain more decision-making information by applying the hesitant fuzzy set to fully and comprehensively understand certain objectivities [63]. When the decision-makers are in a hesitant state, or there is important fuzzy information, utilizing the hesitant fuzzy set will extract the valuable decision-making information, which provides important evidence for the decision-makers to make an accurate judgment. For dealing with hesitant fuzzy information, the hesitant fuzzy set is a very effective technical means [63,64], which is defined as follows.

Definition 1 

[62]. Let $X$ be a set, which is not empty, and $D=\left\{〈x,f_D(x)〉,x\in X\right\}$ denote a hesitant fuzzy set (HFS) $D$ on $X$. Where $f(x):X\to D\left[0,1\right]$ represents a set of all $x\in X$ possible membership degrees. For convenience, $D$ is described as a hesitant fuzzy element (HFE) $D=\left\{f_D(x)\right\}$, which is abbreviated as $D=\left\{f\right\}$.

As mentioned above, for the supplier selection process, applying the hesitant fuzzy elements obtains and evaluates the hesitant fuzzy information for the alternative suppliers. Then, the alternative hesitant fuzzy elements of alternative suppliers can be given. Further, a decision-making matrix of alternative suppliers is constructed.

Most often, there are some characteristics in the hesitant fuzzy elements. That is, in the hesitant fuzzy element $D=\left\{f_D(x)\right\}$, the order of the contained elements may be disordered and the number of elements may be also different. Consequently, the hesitant fuzzy elements need to be normalized and the processing process is introduced below.

In the set $f_D(x_i)$, when there is a disordered element order, the elements of the set should be reordered [65]. Accordingly, we sort the elements in the set according to $f^{{}_{\delta (s)}}(x)\le f^{{}_{\delta (s+1)}}(x)$, where $\delta :(1,2,\cdots ,m)$$\to (1,2,\cdots ,m)$ denotes a permutation for $s=1,2,\cdots ,m-1$.

Additionally, in different hesitant fuzzy elements, the number of elements in the sets $f_D(x_i)$ and $f_F(x_i)$ may be inconsistent. Subsequently, let $l(f_D(x_i))$ and $l(f_F(x_i))$ denote the number of the sets $f_D(x_i)$ and $f_F(x_i)$, where $l_i=max\{l(f_D(x_i)),l(f_F(x_i))\}$. In order to achieve the same number of elements in different sets, the extension principle is used to deal with the sets with fewer elements. Namely, the elements will be added to the sets for the sake of $l(f_D(x_i))=l(f_F(x_i))$.

Generally, the principle of adding elements will reflect the risk preference of the decision-makers [66]. Therefore, under an optimistic criterion, the largest element in the set is usually added, which indicates that the decision-makers love risks. Contrary, under a pessimistic one, the smallest element in the set is generally added, which indicates that the decision-makers are risk-averse. In this paper, the optimistic criterion is applied to extend the length of the sets.

3. Supplier Selection Decision-Making Approach with Hesitant Fuzzy Information

This section will systematically discuss the process of constructing the proposed supplier selection decision-making approach with hesitant fuzzy information. On the one hand, the bidirectional projection under hesitant fuzzy information is constructed and the improved closeness degree is developed in order to process information more efficiently. On the other hand, the attribute weight determination model is established for calculating the attribute weights scientifically. Subsequently, the decision-making procedure is proposed.

3.1. Bidirectional Projection

In order to construct the bidirectional projection, the module, correlation coefficient [67], and projection of the hesitant fuzzy element [68,69] are defined below. The bidirectional projection values of the hesitant fuzzy elements are calculated by applying the bidirectional projection equations, and the projection value matrices are aggregated with the weights to obtain the weighted projection of the alternative suppliers. Further, the closeness degree equation is improved to effectively rank the alternative suppliers.

Definition 2. 

Let  $f(x)$ represent a hesitant fuzzy element, satisfying the condition  $f^{{}_{\delta (s)}}(x)\le f^{{}_{\delta (s+1)}}(x)$, where $\delta$ is a permutation, and then the module of a hesitant fuzzy element is described as:

$$\left|f(x)\right|=\sqrt{{\left(f^{{}_{\delta (1)}}(x)\right)}^2+{\left(f^{{}_{\delta (2)}}(x)\right)}^2+\cdots +{\left(f^{{}_{\delta (s+1)}}(x)\right)}^2}$$

(1)

Definition 3. 

Let $f_1(x)=\left\{f_1^{{}_{\delta (1)}}(x),f_1^{{}_{\delta (2)}}(x),\right.$$\left.\cdots ,f_1^{{}_{\delta (m)}}(x)\right\}$ and $f_2(x)=\left\{f_2^{{}_{\delta (1)}}(x),f_2^{{}_{\delta (2)}}(x),\cdots ,\right.$$\left.f_2^{{}_{\delta (m)}}(x)\right\}$ be two hesitant fuzzy elements, and then the correlation coefficient between $f_1(x)$ and $f_2(x)$ is described by:

$$\begin{array}{cc}\rho \left(f_1(x),f_2(x)\right)\hfill & =\cos \left(f_1(x),f_2(x)\right)\hfill \\ & =\frac{{\displaystyle \sum _{i=1}^m{f}_1^{{}_{\delta (i)}}(x)f_2^{{}_{\delta (i)}}(x)}}{\left|f_1(x)\right|\left|f_2(x)\right|}\hfill \end{array}$$

(2)

The above Definitions 2 and 3 give the calculating equations of the module and correlation coefficient for the hesitant fuzzy element. On this basis, the definition and equation of projection are as follows.

Definition 4. 

Let $f_1(x)$ and $f_2(x)$ be two hesitant fuzzy elements, then the projection of $f_1(x)$ on $f_2(x)$ is defined as:

$$\begin{array}{c}P{r}_{f_2(x)}^{f_1(x)}=\left|f_1(x)\right|\rho \left(f_1(x),f_2(x)\right)\\ =\frac{{\displaystyle \sum _{i=1}^m{f}_1^{{}_{\delta (i)}}(x)f_2^{{}_{\delta (i)}}(x)}}{\left|f_2(x)\right|}\end{array}$$

(3)

$P{r}_{f_2(x)}^{f_1(x)}$ represents the projection value of $f_1(x)$ on $f_2(x)$. Generally, the higher the value of $P{r}_{f_2(x)}^{f_1(x)}$, the closer $f_1(x)$ is to $f_2(x)$. On the contrary, the relationship is not close.

In order to fully investigate this relationship, the formed vector between two hesitant fuzzy elements is proposed. Simultaneously, the positive and negative ideal hesitant fuzzy elements are introduced for constructing the bidirectional projection.

Definition 5. 

For two hesitant fuzzy elements  $f_1(x)=\left\{f_1^{{}_{\delta (1)}}(x),f_1^{{}_{\delta (2)}}(x),\cdots ,f_1^{{}_{\delta (n)}}(x)\right\}$ and $f_2(x)=$ $\left\{f_2^{{}_{\delta (1)}}(x),f_2^{{}_{\delta (2)}}(x),\cdots ,f_2^{{}_{\delta (n)}}(x)\right\}$, let $f_1(x)f_2(x)=\left\{f_2^{{}_{\delta (1)}}(x)-f_1^{{}_{\delta (1)}}(x),f_2^{{}_{\delta (2)}}(x)-f_1^{{}_{\delta (2)}}(x),\right.$ $\cdots ,\left.f_2^{{}_{\delta (n)}}(x)-f_1^{{}_{\delta (n)}}(x)\right\}$ be the formed vector between two hesitant fuzzy elements $f_1(x)$ and $f_2(x)$.

Definition 6. 

Let $F={\left[f_{ij}\right]}_{m\times n}$ be the normalized hesitant fuzzy decision-making matrix, where  $i\in \left\{1,2\cdot \cdot \cdot ,m\right\}$ $j\in \left\{1,2\cdot \cdot \cdot ,n\right\}$.  Also, $F^{+}=\left(f_1^{+},f_2^{+},\cdots ,f_n^{+}\right)$ denotes the positive ideal hesitant fuzzy element of $F$, and $F^{-}=\left(f_1^{-},f_2^{-},\cdots ,f_n^{-}\right)$ denotes the negative ideal hesitant fuzzy element of $F$, where $f_j{}^{+}=\underset{1\le i\le m}{max}\left(f_{ij}^{{}^{\delta (S)}}\right)$  and  $f_j{}^{-}=\underset{1\le i\le m}{min}\left(f_{ij}^{{}^{\delta (S)}}\right)$.

In combination with Definitions 5 and 6, suppose $F_i=\left(f_{i1},f_{i2},\cdots ,f_{in}\right)$ is the alternative hesitant fuzzy element. Meanwhile, the positive and negative ideal hesitant fuzzy elements $F^{+}=\left(f_1^{+},f_2^{+},\cdots ,f_n^{+}\right)$ and $F^{-}=\left(f_1^{-},f_2^{-},\cdots ,f_n^{-}\right)$ are given. Accordingly, the formed vectors between the positive ideal hesitant fuzzy element, the negative ideal hesitant fuzzy element, and the alternative hesitant fuzzy element can be described as follows:

$$F^{-}{F}^{+}=\left(f_1^{+}-f_1^{-},f_2^{+}-f_2^{-},\cdots ,f_n^{+}-f_n^{-}\right)$$

(4)

$$F^{-}{F}_i=\left(f_{i1}-f_1^{-},f_{i2}-f_2^{-},\cdots ,f_{in}-f_n^{-}\right)$$

(5)

Based on the above analysis, the projection relationships of the formed vectors between the positive ideal hesitant fuzzy element $F^{+}=\left(f_1^{+},f_2^{+},\cdots ,f_n^{+}\right)$, the negative ideal hesitant fuzzy element $F^{-}=\left(f_1^{-},f_2^{-},\cdots ,f_n^{-}\right)$, and the alternative hesitant fuzzy element $F_i=\left(f_{i1},f_{i2},\cdots ,f_{in}\right)$ are as follows, respectively:

(1) The projection of the formed vectors between the negative ideal hesitant fuzzy element and the alternative hesitant fuzzy element onto the formed vectors between the positive and negative ideal hesitant fuzzy element is expressed by:

$$\begin{array}{c}P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}=\left|F^{-}{F}_i\right|\rho \left(F^{-}{F}_i,F^{-}{F}^{+}\right)\\ =\frac{{\displaystyle \sum _{j=1}^n(f_j^{+}-f_j^{-})(f_{ij}-f_j^{-})}}{\left|F^{-}{F}^{+}\right|}\end{array}$$

(6)

(2) The projection of the formed vectors between the positive and negative ideal hesitant fuzzy elements onto the formed vectors between the alternative hesitant fuzzy element and the positive ideal hesitant fuzzy element is expressed by:

$$\begin{array}{c}P{r}_{F_i{F}^{+}}^{F^{-}{F}^{+}}=\left|F^{-}{F}_i\right|\rho \left(F^{-}{F}^{+},F_i{F}^{+}\right)\\ =\frac{{\displaystyle \sum _{j=1}^n(f_j^{+}-f_j^{-})(f_j^{+}-f_{ij})}}{\left|F_i{F}^{+}\right|}\end{array}$$

(7)

It can be seen from Equation (6) that the higher the value of $P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}$, the closer the alternative hesitant fuzzy element $F_i$ is to the positive ideal hesitant fuzzy element $F^{+}$. Similarly, for Equation (7), the higher the value of $P{r}_{F_i{F}^{+}}^{F^{-}{F}^{+}}$, the closer alternative hesitant fuzzy element $F_i$ is to the negative ideal hesitant fuzzy element $F^{-}$.

As mentioned above, the equations of bidirectional projection measurement have been given to obtain projection value matrices in the positive and negative directions. However, in order to extract and integrate hesitant fuzzy information more effectively in both directions, the closeness degree based on the TOPSIS method [70,71] is introduced as follows:

$$D\left(F_i\right)=\frac{P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}}{P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}+P{r}_{F_i{F}^{+}}^{F^{-}{F}^{+}}}$$

(8)

Nevertheless, for the supplier selection problem with hesitant fuzzy multiple attributes, the equation of closeness degree can be preliminarily improved using the attribute weights.

Accordingly, let $S_i=\left\{S_1,S_2,\cdot \cdot \cdot S_m\right\}$ be the set of alternative suppliers, and $G_j=\left\{G_1,G_2,\cdot \cdot \cdot G_n\right\}$ denote the set of attributes. Simultaneously, in the normalized hesitant fuzzy decision-making matrix $F={\left[f_{ij}\right]}_{m\times n}$, $f_{ij}$ indicates the evaluate information for the alternative supplier $S_i$ under the attribute $G_j$. Furthermore, ${\alpha }_j=\left\{{\alpha }_1,{\alpha }_2,\cdot \cdot \cdot {\alpha }_n\right\}$ represents the projected attribute weights of the formed vectors between the negative ideal hesitant fuzzy element and the alternative hesitant fuzzy element onto the formed vectors between the positive and negative ideal hesitant fuzzy element. ${\beta }_j=\left\{{\beta }_1,{\beta }_2,\cdot \cdot \cdot {\beta }_n\right\}$ represents the projected attribute weights of the formed vectors between the positive and negative ideal hesitant fuzzy elements onto the formed vectors between the alternative hesitant fuzzy element and the positive ideal hesitant fuzzy element, where, ${\alpha }_j\in \left[0,1\right]$, ${\displaystyle \sum _{j=1}^n{\alpha }_j}=1$, ${\beta }_j\in \left[0,1\right]$, and ${\displaystyle \sum _{j=1}^n{\beta }_j}=1$. As previously noted, the projection matrices based on the hesitant fuzzy information can be aggregated with the attribute weights, and then the weighted projection of suppliers $S_i$ under the attribute $G_j$ will be obtained as follows.

(1)

The weighted projection of alternative supplier $S_i$ under the attribute $G_j$ of the positive ideal direction is described by:

$$P{r}^{+}={\alpha }_j\times P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}$$

(9)

(2)

The weighted projection of alternative supplier $S$ under the attribute $G$ of the negative ideal direction is described by:

$$P{r}^{-}={\beta }_j\times P{r}_{F_i{F}^{+}}^{F^{-}{F}^{+}}$$

(10)

Moreover, in order to retain enough information and make the proposed approach more applicable and effective, the parameter $\theta \in \left(0,1\right)$ is introduced in this paper, which represents the risk preferences of the decision-makers. Generally, $\theta >0.5$ indicates that the decision-makers are optimists, and the smaller the distance between the alternative and the positive ideal solution, the better the choice; on the contrary, $\theta <0.5$. Thereby, the equation of closeness degree can be further improved, and the equation of closeness degree under the attribute weights becomes the below:

$$D\left(S_i\right)=\frac{\theta P{r}^{+}}{\theta P{r}^{+}+\left(1-\theta \right)P{r}^{-}}$$

(11)

As aforementioned, using the value $D\left(S_i\right)$, the alternative suppliers can be ranked. Equation (11) shows that the higher the value $D\left(S_i\right)$, the better the alternative supplier $S_i$.

However, in the background of complex decision-making, the determination of attribute weights is difficult. As a consequence, on the basis of the above-mentioned research and analysis, this paper designs a model for determining the attribute weights when the attribute weights are completely unknown.

3.2. Attribute Weight Determination Model

In order to determine the attribute weights, an attribute weight determination model which minimizes the projected total deviation of the hesitant fuzzy elements is established.

On the one hand, the deviation between the hesitant fuzzy elements $F_i$ under alternative suppliers $S_i$ and the positive ideal hesitant fuzzy element $F^{+}$ is denoted as $\left(1-P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}\right)$. On the other hand, considering the attribute weights ${\alpha }_j$ under all the attributes $G_j$, the deviation $\left(1-P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}\right)$ is multiplied by the attribute weight ${\alpha }_j$ to obtain the expression ${\alpha }_j\left(1-P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}\right)$. In order to remove the influence of the symbol, the square of the expression ${\alpha }_j\left(1-P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}\right)$ is constructed. Thereby, the equation under all attributes is proposed below.

$$d_i={\displaystyle \sum _{j=1}^n{\left[{\alpha }_j\left(1-P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}\right)\right]}^2}$$

(12)

Further, the sum of $d_i$ for alternative suppliers $S$ is described by:

$$d={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{\left[{\alpha }_j\left(1-P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}\right)\right]}^2}}$$

(13)

Since the final obtained attribute weight vector should minimize $d$, the following objective function can be established:

$$\begin{array}{c}minG\left(\alpha \right)={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{\left[{\alpha }_j\left(1-P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}\right)\right]}^2}}\\ S.T.\left\{\begin{array}{l}{\displaystyle \sum _{j=1}^n{\alpha }_j}=1\\ 0\le {\alpha }_j^L\le {\alpha }_j\le {\alpha }_j^U\le 1\end{array}\right.\end{array}$$

(14)

According to the Lagrange multiplier method, the Lagrange multiplier $\eta$ is introduced to convert Equation (14) into Equation (15), which is expressed by:

$$L\left(\alpha ,\eta \right)={\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{\left[{\alpha }_j\left(1-P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}\right)\right]}^2}}+2\eta \left({\displaystyle \sum _{j=1}^n{\alpha }_j}-1\right)$$

(15)

Subsequently, applying Equation (15) gives the derivatives of ${\alpha }_j$ and $\eta$, respectively. Using the calculation, the solution to ${\alpha }_j$ can be solved. Similarly, ${\beta }_j$ is also obtained.

As aforementioned, the bidirectional projection and attribute weight determination model are constructed. Accordingly, a supplier selection decision-making approach with unknown attribute weights under hesitant fuzzy information is put forward.

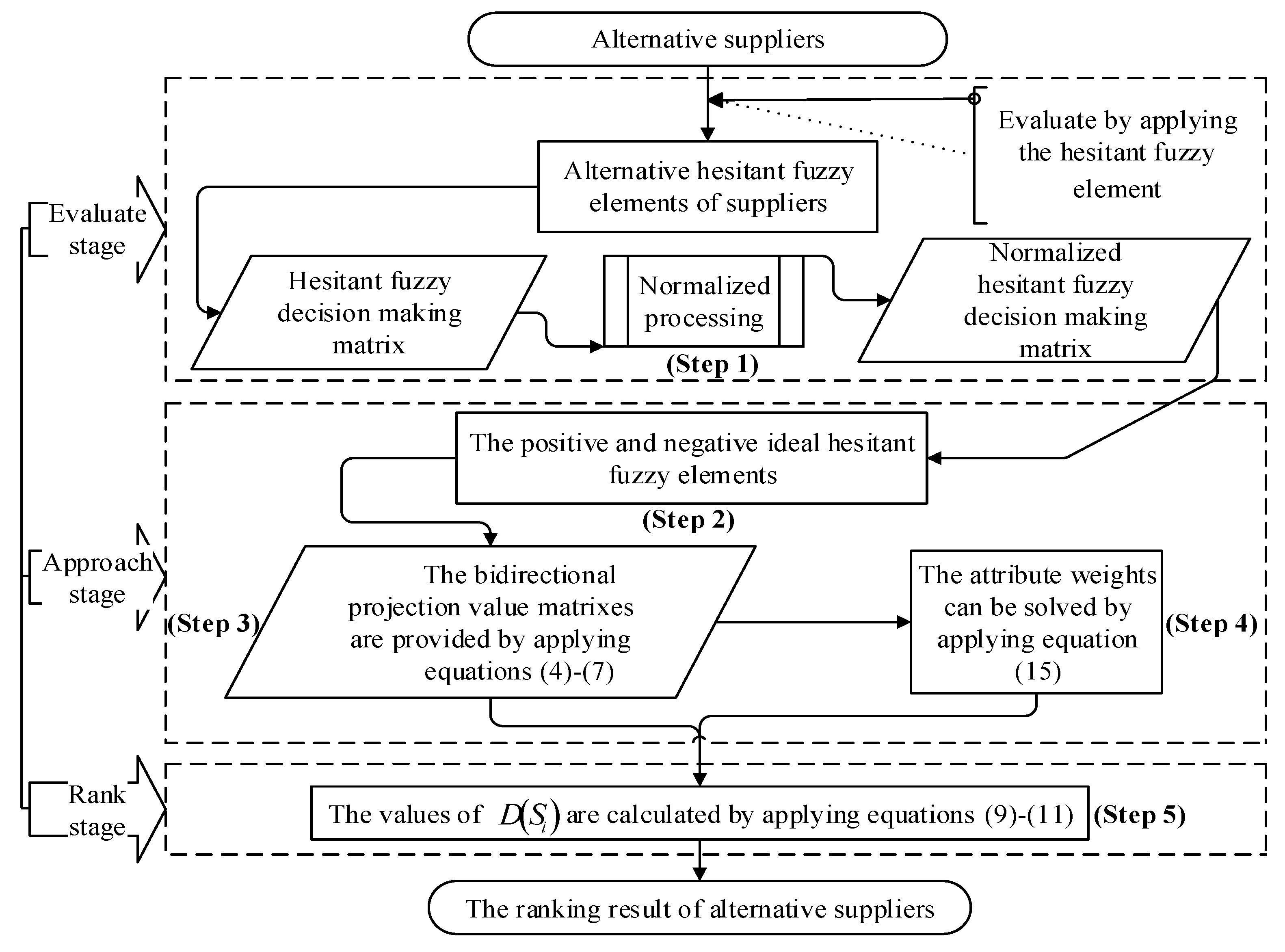
3.3. Decision-Making Procedure

To elaborate on this process, the decision-making procedure of the supplier selection decision-making approach with unknown attribute weights under hesitant fuzzy information is provided, which is shown in Figure 2.

Step 1

The hesitant fuzzy decision-making matrix of alternative suppliers is given. After normalized processing, the normalized hesitant fuzzy decision-making matrix $F={\left[f_{ij}\right]}_{m\times n}$ is obtained.

Step 2

According to Definition 6, in the matrix $F={\left[f_{ij}\right]}_{m\times n}$, the positive ideal hesitant fuzzy element and negative ideal hesitant fuzzy element are given.

Step 3

By applying Equations (4)–(7), the bidirectional projection value matrices are provided.

Step 4

By applying Equation (15), the attribute weights ${\alpha }_j=\left\{{\alpha }_1,{\alpha }_2,\cdot \cdot \cdot {\alpha }_n\right\}$ and ${\beta }_j=\left\{{\beta }_1,{\beta }_2,\cdot \cdot \cdot {\beta }_n\right\}$ can be solved.

Step 5

By using Equations (9)–(11), the values of $D\left(S_i\right)$ are calculated, and then the alternative suppliers are ranked according to the values of $D\left(S_i\right)$.

As mention above, this section discusses the construction of the supplier selection decision-making approach with unknown attribute weights under hesitant fuzzy information. In the next section, the feasibility of the proposed approach to supplier selection will be demonstrated using an example of complex product development.

4. Illustrative Example

It is well known that a large ship is a complex product. Due to the complexity of its technology and functions, the development of a ship has always been a focus of research in the manufacturing industry. DSIC is one of the ship manufacturing enterprises in China that has achieved great success. In order to further adapt to the rapid changes in market demand and enhance development capacity and market competitiveness, according to the research and analysis in this paper, the collaborative manufacturing mode of “main manufacturer + suppliers” can be considered in the development of a ship. The suppliers participate in the development and undertake certain development tasks to shorten the development cycle, reduce the cost, and improve the quality of complex products.

At present, DSIC is planning to develop the $M$ type of ship, and the collaborative manufacturing mode of “main manufacturer + suppliers” will be adopted. In the development process for the $M$ type of ship, the development tasks of its power systems need to be outsourced to the corresponding suppliers. After screening using the cloud manufacturing platform, five alternative suppliers are found to be able to provide these kinds of development task resources (the development resources provided by each supplier are homogeneous).

In addition, in this study, supplier selection for the complex product development is a multiple-attribute decision-making problem. Therefore, it is challenge for DSIC to determine the assessable supplier’s attribute indexes. In order to overcome this difficulty and determine the required attribute indexes scientifically and reasonably, this paper will elaborate the solution and approach to proposing the attribute indexes selected by the supplier in the illustrative example. Further, in DSIC, a mature and well-run industrial internet platform for supplier selection has been established. The construction purpose of this platform is a comprehensive and systematic understanding of the basic attribute information of suppliers, so as to help DSIC compare, analyze, evaluate, and select the best supplier according to its needs. On the one hand, based on this platform, the basic attribute information of different alternative suppliers can be obtained. On the other hand, different enterprise experts can state their degree of concern and requirements for the basic attribute information of suppliers. Further, the data crawler technology is used to extract and calculate the degree of concern about these suppliers’ basic attribute information. Meanwhile, using the suppliers’ basic attribute information summary and induction, according to the specific situation, the attribute indexes of supplier selection at different stages can be given.

It should be noted that the results of the data crawler technology are obtained by executing the relevant code on the PyCharm software (Pycharm Professional Edition 2019.3.3), parts of which are as follows:

#Regular rectangular word clouds. #Introduction of jieba and wordcloud libraries. import jieba import wordcloud #Open the document in which the extracted comment is located. f = open(“F:\list_attribute.txt”, “r”, encoding=“utf-8”) t = f.read() f.close() #Word. ls = jieba.lcut(t) txt = “ ”.join(ls) #Draw word clouds. w = wordcloud.WordCloud(width = 1000, height = 700, background_color = “white”, font_path = “msyh.ttf”) w.generate(txt) w.to_file(“word cloud.png”) # Statistical word frequency. counts = {} for word in ls:  if len(word) == 1:   continue  else:   counts[word] = counts.get(word,0) + 1 items = list(counts.items()) items.sort(key=lambda x:x[1], reverse=True) #Output the words and their corresponding word frequency, meanwhile, the form of “words-> word frequency” is written to the txt document. for i in range(20):  word, count = items[i]  with open(‘F:// word frequency.txt’,‘a’,encoding=‘utf-8’) as f:    f.write(word+‘->’+str(count)+‘\n’) #print (“{0:<10}{1:>5}”.format(word, count)).

Specifically, DSIC randomly selects 100 experts’ opinions on the supplier attribute information using this constructed industrial internet platform. Sequentially, a ranking of the current supplier attribute information concern degree is obtained using the data crawler technology. That is, it includes enterprise reputation, product quality, technical ability, service level, product price, supply capacity, machinery equipment, management standard, management level, information technology, etc. Simultaneously, according to the statistics, the basic attribute information of suppliers is visualized and quantified, which is depicted and listed in Figure 3 and Figure 4. Further, using the comprehensive analysis of enterprise experts, enterprise reputation, product quality, technical ability, and service level are classified as the attribute indexes for supplier selection. For supplier selection, these four attribute indicators are also important elements for judging a supplier’s ability [44,45].

Subsequently, to address this supplier selection problem, let $S_i=\left\{S_1,S_2,S_3,S_4,S_5\right\}$ represent the set of alternative suppliers, and $G_j=\left\{G_1,G_2,G_3,G_4\right\}$ denote the set of attributes, where $G_1$ represents the enterprise reputation; $G_2$ stands for the product quality; $G_3$ denotes the technical ability; and $G_4$ indicates the service level. Through the above four attribute indexes, the main manufacturer evaluates the alternative supplier $S_m$. Nevertheless, due to the complexity and uncertainty of the socio-economic environment and the cognitive diversity of decision-makers, it is difficult to give accurate preference information. As a consequence, the hesitant fuzzy set is used to evaluate alternative suppliers. Using an expert vote and statistical analysis, the hesitant fuzzy decision-making matrix is given, which is listed in

Table 1. Hesitant fuzzy decision-making matrix.

	${\mathit{S}}_1$	${\mathit{S}}_2$	${\mathit{S}}_3$	${\mathit{S}}_4$	${\mathit{S}}_5$
$G_1$	$\left\{0.2,0.3,0.7\right\}$	$\{0.2,0.4,0.5\}$	$\left\{0.4,0.5,0.6\right\}$	$\left\{0.3,0.4\right\}$	$\left\{0.3,0.8\right\}$
$G_2$	$\left\{0.6,0.7\right\}$	$\left\{0.3,0.7\right\}$	$\left\{0.3,0.6\right\}$	$\left\{0.6\right\}$	$\left\{0.4,0.5,0.8\right\}$
$G_3$	$\left\{0.4,0.6\right\}$	$\left\{0.3,0.7\right\}$	$\left\{0.4,0.5\right\}$	$\left\{0.2,0.8\right\}$	$\left\{0.6\right\}$
$G_4$	$\{0.4,0.4,0.7\}$	$\left\{0.4,0.4\right\}$	$\left\{0.3,0.7\right\}$	$\left\{0.2,0.6\right\}$	$\left\{0.1,0.4,0.6\right\}$

.

First of all, the optimistic criterion is adopted, and then the largest element is added to the sets. After normalized processing, the normalized hesitant fuzzy decision-making matrix $F={\left[f_{ij}\right]}_{m\times n}$ is obtained as listed in

Table 2. Normalized hesitant fuzzy decision-making matrix.

	${\mathit{S}}_1$	${\mathit{S}}_2$	${\mathit{S}}_3$	${\mathit{S}}_4$	${\mathit{S}}_5$
$G_1$	$\left\{0.2,0.3,0.7\right\}$	$\{0.2,0.4,0.5\}$	$\left\{0.4,0.5,0.6\right\}$	$\left\{0.3,0.4,0.4\right\}$	$\left\{0.3,0.8,0.8\right\}$
$G_2$	$\left\{0.6,0.7,0.7\right\}$	$\left\{0.3,0.7,0.7\right\}$	$\left\{0.3,0.6,0.6\right\}$	$\left\{0.6,0.6,0.6\right\}$	$\left\{0.4,0.5,0.8\right\}$
$G_3$	$\left\{0.4,0.6\right\}$	$\left\{0.3,0.7\right\}$	$\left\{0.4,0.5\right\}$	$\left\{0.2,0.8\right\}$	$\left\{0.6,0.6\right\}$
$G_4$	$\{0.4,0.4,0.7\}$	$\left\{0.4,0.4,0.4\right\}$	$\left\{0.3,0.7,0.7\right\}$	$\left\{0.2,0.6,0.6\right\}$	$\left\{0.1,0.4,0.6\right\}$

.

Then, according to Definition 6 and Table 2, the positive and negative ideal hesitant fuzzy elements $F^{+}$ and $F^{-}$ in the normalized hesitant fuzzy decision-making matrix are given as follows.

$$F^{+}=\left(\begin{array}{l}\left\{0.4,0.8,0.8\right\},\left\{0.6,0.7,0.8\right\}\\ \left\{0.6,0.8\right\},\left\{0.4,0.7,0.7\right\}\end{array}\right), F^{-}=\left(\begin{array}{l}\left\{0.2,0.3,0.4\right\},\left\{0.3,0.5,0.6\right\}\\ \left\{0.2,0.5\right\},\left\{0.1,0.4,0.4\right\}\end{array}\right)$$

In addition, the bidirectional projection values are calculated using Equations (4)–(7), and the bidirectional projection value matrices are obtained.

$$P{r}_{F^{-}{F}^{+}}^{F^{-}{F}_i}=\left[\begin{array}{ccccc}0.18& 0.13& 0.33& 0.10& 0.64\\ 0.36& 0.15& 0.05& 0.27& 0.17\\ 0.22& 0.20& 0.16& 0.16& 0.38\\ 0.35& 0.17& 0.46& 0.29& 0.12\end{array}\right],P{r}_{F_i{F}^{+}}^{F^{-}{F}^{+}}=\left[\begin{array}{ccccc}0.60& 0.67& 0.64& 0.66& 0.20\\ 0.20& 0.35& 0.40& 0.27& 0.35\\ 0.49& 0.47& 0.47& 0.40& 0.30\\ 0.30& 0.42& 0.30& 0.49& 0.48\end{array}\right]$$

Furthermore, in this example, suppose that the weight information from the decision-makers is given: $\mathrm{\Omega }=\left\{{\alpha }_1\ge 0.2,{\alpha }_2\ge 0.15,{\alpha }_3\ge 0.2,{\alpha }_4\ge 0.15;\right.$ $\left.{\beta }_1\ge 0.2,{\beta }_2\ge 0.15,{\beta }_3\ge 0.2,{\beta }_4\ge 0.1\right\}$. Then, according to Equation (15), the attribute weights ${\alpha }_j$ and ${\beta }_j$ are given.

$${\alpha }_j=\left\{0.26,0.23,0.24,0.27\right\}, {\beta }_j=\left\{0.36,0.17,0.25,0.22\right\}$$

Also, by applying Equations (9) and (10), the weighted projections are calculated, respectively.

(1) The weighted projection of supplier $S_i$ under the attribute $G_j$ in the positive ideal direction is provided below:

$$P{r}^{+}=\left\{0.28,0.16,0.26,0.20,0.33\right\}$$

(2) The weighted projection of supplier $S_i$ under the attribute $G_j$ in the negative ideal direction is provided below:

$$P{r}^{-}=\left\{0.44,0.51,0.48,0.49,0.31\right\}$$

Subsequently, in Equation (11), let the parameter $\theta$ be $0.6$. Based on Equation (11), the values of $D\left(S_i\right)$ can be solved and the alternative suppliers are ranked according to the values of $D\left(S_i\right)$.

$$D\left(S_1\right)=0.49, D\left(S_2\right)=0.32, D\left(S_3\right)=0.45, D\left(S_4\right)=0.38, D\left(S_5\right)=0.61$$

Based on these values, it can be known that:

$$D\left(S_5\right)>D\left(S_1\right)>D\left(S_3\right)>D\left(S_4\right)>D\left(S_2\right)$$

Further, the ranking result of alternative suppliers is given as follows: $S_5\succ S_1\succ S_3\succ S_4\succ S_2$, where, “$\succ$“ indicates “is prior to”. That is, $S_5$ will be selected as the best supplier to participate in the development tasks for the $M$ type of ship.

As aforementioned, on the one hand, the proposed approach of this paper provides a novel supplier selection method for development tasks for the $M$ type of ship, which is effective and feasible. On the other hand, this kind of “main manufacturer + suppliers” mode can be implemented using the proposed approach in this paper, which contributes to collaborative manufacturing in complex product development.

5. Discussions

From the above illustrative example and calculations, discussions will be further provided. Primarily, the sensitivity analysis is given to illustrate the stability of the proposed ranking result. Additionally, the comparative analysis is performed to demonstrate the advantages and reliability of the proposed approach.

5.1. Sensitivity Analysis

In this method, the equation of the degree of closeness has been further improved by introducing the parameter $\theta$. Nevertheless, does the variation in the parameter $\theta$ affect the ranking results? Accordingly, the sensitivity analysis is designed according to the variation of the parameter $\theta$. Sequentially, several different coefficients of the parameter $\theta$ are applied in this illustrative example. Simultaneously, the values of $D\left(S_i\right)$ and the ranking result are calculated and given by using the proposed approach, which are listed in

Table 3. The sensitivity analysis of the ranking.

Parameter $\mathit{\theta }$	$\mathbf{The} \mathbf{Values} \mathbf{of} \mathit{D}\left({\mathit{S}}_{\mathit{i}}\right),\mathit{i}=1,2,3,4,5$.	The Ranking Result of Alternative Suppliers
$0.2$	$D(S_1)=0.14$ $D(S_2)=0.07$ $D(S_3)=0.12$ $D(S_4)=0.09$ $D(S_5)=0.21$	$S_5\succ S_1\succ S_3\succ S_4\succ S_2$
$0.4$	$D(S_1)=0.30$ $D(S_2)=0.17$ $D(S_3)=0.26$ $D(S_4)=0.22$ $D(S_5)=0.41$	$S_5\succ S_1\succ S_3\succ S_4\succ S_2$
$0.5$	$D(S_1)=0.39$ $D(S_2)=0.24$ $D(S_3)=0.35$ $D(S_4)=0.29$ $D(S_5)=0.51$	$S_5\succ S_1\succ S_3\succ S_4\succ S_2$
$0.6$	$D(S_1)=0.49$ $D(S_2)=0.32$ $D(S_3)=0.45$ $D(S_4)=0.38$ $D(S_5)=0.61$	$S_5\succ S_1\succ S_3\succ S_4\succ S_2$
$0.8$	$D(S_1)=0.72$ $D(S_2)=0.56$ $D(S_3)=0.68$ $D(S_4)=0.63$ $D(S_5)=0.81$	$S_5\succ S_1\succ S_3\succ S_4\succ S_2$

.

It can be found from Table 3 the values of $D\left(S_i\right)$ change with the variation of the parameter $\theta$. However, the ranking result is invariable. This illustrates the stability of the proposed ranking result: $S_5$ is the best supplier to participate in the development tasks of the $M$ type of ship. Further, for the supplier selection, the stable ranking result can be obtained by applying the proposed approach in this paper.

5.2. Comparative Analysis

In addition, during the solving process of the proposed approach, it can be observed that the ranking result of alternative suppliers may change with the variation of the attribute weights ${\alpha }_j$ and ${\beta }_j$. In this example, when the hesitant fuzzy decision-making matrix has been given, the proposed attribute weight determination model in this paper can solve the unique attribute weights ${\alpha }_j$ and ${\beta }_j$. Subsequently, several attribute weight determination models from the existing literature [56,72,73] are introduced and applied in this example. Through comparative analysis, the applicability and reliability of the proposed approach will be further discussed and demonstrated.

Consequently, based on the example in this paper, the attribute weight determination models from the above three literature examples are, respectively, employed to calculate the attribute weights ${\alpha }_j$ and ${\beta }_j$. Meanwhile, the ranking result of alternative suppliers can be given.

(1) In the literature [56], according to the proposed method, the model of calculating the attribute weights ${\alpha }_j$ is expressed by:

$$\begin{array}{cc}\hfill max=& \frac{0.108{\alpha }_1+0.216{\alpha }_2+0.132{\alpha }_3+0.21{\alpha }_4}{0.436{\alpha }_1+0.472{\alpha }_2+0.444{\alpha }_3+0.47{\alpha }_4}+\frac{0.078{\alpha }_1+0.09{\alpha }_2+0.12{\alpha }_3+0.102{\alpha }_4}{0.426{\alpha }_1+0.43{\alpha }_2+0.44{\alpha }_3+0.434{\alpha }_4}\hfill \\ & +\frac{0.198{\alpha }_1+0.03{\alpha }_2+0.096{\alpha }_3+0.276{\alpha }_4}{0.466{\alpha }_1+0.41{\alpha }_2+0.432{\alpha }_3+0.492{\alpha }_4}+\frac{0.06{\alpha }_1+0.162{\alpha }_2+0.096{\alpha }_3+0.174{\alpha }_4}{0.42{\alpha }_1+0.454{\alpha }_2+0.432{\alpha }_3+0.458{\alpha }_4}\hfill \\ & +\frac{0.384{\alpha }_1+0.102{\alpha }_2+0.228{\alpha }_3+0.072{\alpha }_4}{0.528{\alpha }_1+0.434{\alpha }_2+0.476{\alpha }_3+0.424{\alpha }_4}\hfill \end{array}$$

where, ${\alpha }_j\in \left[0,1\right]$, ${\displaystyle \sum _{j=1}^n{\alpha }_j}=1$. This model can be solved using the Matlab or Lingo software, and the attribute weights ${\alpha }_j=\left\{0.20,0.15,0.20,0.45\right\}$ will be obtained. Similarly, the attribute weights ${\beta }_j$ can be obtained as follows: ${\beta }_j=\left\{0.20,0.50,0.20,0.10\right\}$.

(2) In the literature [72], based on the developed approach, the model of determining the attribute weights ${\alpha }_j$ is denoted by:

$$\begin{array}{c}min=\frac{\left(2.8178{\alpha }_1^2+3.2564{\alpha }_2^2+3.044{\alpha }_3^2+2.6815{\alpha }_4^2\right)}{2}\\ +\frac{\left({\alpha }_1\ln {\alpha }_1+{\alpha }_2\ln {\alpha }_2+{\alpha }_3\ln {\alpha }_3+{\alpha }_4\ln {\alpha }_4\right)}{2}\end{array}$$

where, ${\alpha }_j\in \left[0,1\right]$, ${\displaystyle \sum _{j=1}^n{\alpha }_j}=1$. By solving this model, the attribute weights ${\alpha }_j=\left\{0.26,0.24,0.24,0.26\right\}$ can be obtained. Likewise, we also obtain the attribute weights ${\beta }_j=\left\{0.30,0.21,0.25,0.24\right\}$.

(3) In the literature [73], using the presented method, the model of solving the attribute weights ${\alpha }_j$ is described by:

$$\begin{array}{c}min=\frac{\left(2.8178{\alpha }_1^2+3.2564{\alpha }_2^2+3.044{\alpha }_3^2+2.6815{\alpha }_4^2\right)}{2}\\ -\frac{\left({\alpha }_1\ln {\alpha }_1+{\alpha }_2\ln {\alpha }_2+{\alpha }_3\ln {\alpha }_3+{\alpha }_4\ln {\alpha }_4\right)}{2}\end{array}$$

where ${\alpha }_j\in \left[0,1\right]$, ${\displaystyle \sum _{j=1}^n{\alpha }_j}=1$. Through solving the above model, the attribute weights ${\alpha }_j=\left\{0.29,0.15,0.23,0.33\right\}$ are obtained. In like manner, the attribute weights ${\beta }_j$ can be acquired as follows: ${\beta }_j=\left\{0.55,0.15,0.20,0.10\right\}$.

As aforementioned, the attribute weights ${\alpha }_i$ and ${\beta }_j$ have been obtained using the above three different methods. Consequently, according to Equations (9)–(11), the values of $D\left(S_i\right)$ and the ranking result of alternative suppliers can be calculated and obtained correspondingly, and the comparative analysis between the proposed approach of this paper and the above three methods is shown in

Table 4. The comparative analysis of the methods.

Methods	Attribute Weights ${\mathit{\alpha }}_{\mathit{i}}$	Attribute Weights ${\mathit{\beta }}_{\mathit{j}}$	$\mathbf{The} \mathbf{Values} \mathbf{of} \mathit{D}\left({\mathit{S}}_{\mathit{i}}\right),\mathit{i}=1,2,3,4,5$.	The Ranking Result of Alternative Suppliers
The proposed method of this paper	$\left\{0.26,0.23,0.24,0.27\right\}$	$\left\{0.36,0.17,0.25,0.22\right\}$	$D(S_1)=0.49$ $D(S_2)=0.32$ $D(S_3)=0.45$ $D(S_4)=0.38$ $D(S_5)=0.61$	$S_5\succ S_1\succ S_3\succ S_4\succ S_2$
The existing model of the literature [56]	$\left\{0.20,0.15,0.20,0.45\right\}$	$\left\{0.20,0.50,0.20,0.10\right\}$	$D(S_1)=0.56$ $D(S_2)=0.36$ $D(S_3)=0.51$ $D(S_4)=0.46$ $D(S_5)=0.57$	$S_5\succ S_1\succ S_3\succ S_4\succ S_2$
The existing model of the literature [72]	$\left\{0.26,0.24,0.24,0.26\right\}$	$\left\{0.30,0.21,0.25,0.24\right\}$	$D(S_1)=0.50$ $D(S_2)=0.33$ $D(S_3)=0.45$ $D(S_4)=0.39$ $D(S_5)=0.60$	$S_5\succ S_1\succ S_3\succ S_4\succ S_2$
The existing model of the literature [73]	$\left\{0.29,0.15,0.23,0.33\right\}$	$\left\{0.55,0.15,0.20,0.10\right\}$	$D(S_1)=0.46$ $D(S_2)=0.30$ $D(S_3)=0.45$ $D(S_4)=0.36$ $D(S_5)=0.65$	$S_5\succ S_1\succ S_3\succ S_4\succ S_2$

.

It can be seen from Table 4, in this example, using the above four methods, the attribute weights ${\alpha }_j$ and ${\beta }_j$ are solved respectively. Simultaneously, the values of $D\left(S_i\right)$ and the ranking result of alternative suppliers have been listed in Table 4. Further, the attribute weights ${\alpha }_j$ and ${\beta }_j$ and the values of $D\left(S_i\right)$ are different between the methods of the proposed approach of this paper and the existing literature. Subsequently, the ranking result of alternative suppliers is consistent according to the comparison for the values of $D\left(S_i\right)$ among alternative suppliers. This indirectly proves that the attribute weight determination model proposed in this paper is reasonable and feasible. Moreover, compared with these literature approaches, the advantage of the method proposed in this paper is that it comprehensively considers the uncertainty of the degree of closeness and the attribute weight information when using hesitant fuzzy information. It makes the alternative supplier values obtained more reliable and more in line with reality. Accordingly, this will lay the foundation for decision-makers to make accurate decisions.

Moreover, the discussion should be further elaborated upon. As described above, supplier selection in complex product development is a multiple attribute decision-making problem. Thus, in the constructed method of this paper, the hesitant fuzzy set is adopted to extract the preference information for alternative suppliers. Sequentially, a supplier selection decision-making approach with hesitant fuzzy information is proposed. Subsequently, for the sake of further illustrating the characteristics or merits of this proposed model, a comparison between this proposed model and the existing approach [74] is designed.

As far as we know, a multi-objective weighted grey target decision model based on the grey system theory has been widely used to solve various decision target selection problems [75,76,77,78]. Where the grey system theory was founded by professor Deng [79], later, a multi-objective weighted grey target decision model was proposed by Liu et al. [80]. It can help decision-makers choose the optimal decision goal from multiple decision goals in the absence of data and information. The multi-objective weighted grey target decision model is very suitable to help enterprises make choices when suppliers provide limited information. This method directly selects the evaluation indicator information to determine the bullseye and bullseye distance, and uses the bullseye distance to sort the suppliers. The advantage of this method is that it can avoid the errors caused by the evaluation method allowing the suppliers to exploit loopholes, thus increasing the accuracy of the evaluation [74].

Specifically, based on the existing approach of the literature [74], in the study, we treat the alternative supplier selection decision as event $a_1$, and the event set is given as $A=\left\{a_i\right\}=\left\{a_1\right\}$. The countermeasures $s_1,s_2,s_3,s_4,s_5$ correspond to alternative supplier 1, alternative supplier 2, alternative supplier 3, alternative supplier 4, and alternative supplier 5. In addition, the countermeasure set $S=\left\{s_j\right\}=\left\{s_1,s_2,s_3,s_4,s_5\right\}$ is put forward. Simultaneously, the decision scheme $C=\left\{\left.c_{ij}=(a_i,s_j)\right|a_i\in A,s_j\in S,i=1,j=1,2,3,4,5\right\}=\left\{c_{11},c_{12},c_{13},c_{14},c_{15}\right\}$ is constructed using the event set and the countermeasure set.

According to the above research, in complex product development, enterprise reputation, product quality, technical ability, and service level are still selected for the five alternative suppliers to select the evaluation content, that is, the decision attributes. After argumentation, the types of four decision attributes are determined, as shown in

Table 5. The decision attribute types of the suppliers.

Attributes	Unit of Measurement	Attribute Types
Enterprise reputation	Score	Benefit attribute
Product quality	Score	Benefit attribute
Technical ability	Score	Benefit attribute
Service level	Score	Benefit attribute

.

Subsequently, the analytic hierarchy process [81] is used to construct the judgment matrix $u$, and the attribute weights ${\eta }_t$ of the four decision attributes can be calculated, where $t=1,2,3,4$. These are listed and shown in the judgment matrix $u$ and

Table 6. The attribute weights.

Attributes	$\mathbf{Attribute} \mathbf{Weights} {\mathit{\eta }}_{\mathit{t}}$
Enterprise reputation	0.33
Product quality	0.28
Technical ability	0.26
Service level	0.13

, respectively. Where ${\lambda }_{max}=4.1171$, meanwhile, the random consistency ratio $CR=0.0439<0.1$. This reveals that satisfactory consistency of the judgment matrix is existent.

$$u=\left[\begin{array}{cccc}1& 1& 2& 2\\ 1& 1& 1& 2\\ 1/2& 1& 1& 3\\ 1/2& 1/2& 1/3& 1\end{array}\right]$$

Based on the data provided by the five alternative suppliers, the rating experts give the score of the four attributes, including enterprise reputation, product quality, technical ability, and service level. Specifically, a 100 mark system is proposed [74,82], where 90–100 indicates optimal, 80–90 indicates excellent, 70–80 indicates good, 60–70 indicates average, and below 60 indicates poor. Furthermore, the arithmetic average method is used to address the scores of the 10 experts to obtain the score value of each attribute. After sorting them, the attribute effect statistics are listed in

Table 7. The attribute effect statistics.

Attributes	Alternative Supplier 1	Alternative Supplier 2	Alternative Supplier 3	Alternative Supplier 4	Alternative Supplier 5
Enterprise reputation	100	90	100	100	100
Product quality	75	70	70	60	80
Technical ability	75	90	75	90	75
Service level	100	100	95	90	95

.

Accordingly, the attribute effect matrix $r$ is constructed.

$$r=(r_{ij}^{(t)})=\left[\begin{array}{ccccc}100& 90& 100& 100& 100\\ 75& 70& 70& 60& 80\\ 75& 90& 75& 90& 75\\ 100& 100& 95& 90& 95\end{array}\right]$$

Simultaneously, let $r_{i_o{j}_o}^{(t)}=\left[\begin{array}{cccc}90& 70& 80& 90\end{array}\right]$ be the attribute effect threshold. Consequently, by applying $d_{ij}^{(t)}=\frac{r_{ij}^{(t)}-r_{i_o{j}_o}^{(t)}}{\underset{i}{max}\underset{j}{max}\left\{r_{ij}^{(t)}\right\}-r_{i_o{j}_o}^{(t)}}$, the uniform effect measure matrix $d$ is obtained below.

$$d=[d_{ij}^{(t)}]=\left[\begin{array}{ccccc}1& 0& 1& 1& 1\\ 0.5& 0& 0& -1& 1\\ -0.5& 1& -0.5& 1& -0.5\\ 1& 1& 0.5& 0& 0.5\end{array}\right]$$

Meanwhile, according to $c_{ij}={\displaystyle \sum _{t=1}^4{\eta }_t\cdot d_{ij}^{(t)}}={({\eta }_t)}^T\cdot d$, the comprehensive effect measure matrix $c_{ij}=\left[\begin{array}{ccccc}0.47& 0.39& 0.27& 0.31& 0.54\end{array}\right]$ of the alternative suppliers is calculated. Since all of them $c_{11},c_{12},c_{13},c_{14},c_{15}$ are greater than 0 and all of the five alternative suppliers have an ash rake, this indicates that it is reasonable to select these five alternative suppliers for the final selection decision. Equally, because $c_{15}>c_{11}>c_{12}>c_{14}>c_{13}$, the $\underset{1\le j\le 5}{max}\left\{c_{1j}\right\}=c_{15}=0.54$ be discovered. Further, the ranking result of alternative suppliers is $S_5\succ S_1\succ S_2\succ S_4\succ S_3$. Thus, the fifth alternative supplier should be selected as the final priority for negotiation and cooperation to discuss involvement in development of the complex product.

As aforementioned, the analysis of the ranking results between the developed model and the existing model in the literature [74] is listed in

Table 8. The analysis of the ranking results.

Model	The Optimal Ranking Value	The Ranking Result of Alternative Suppliers
The developed model of this paper	0.61	$S_5\succ S_1\succ S_3\succ S_4\succ S_2$
The existing model of the literature [74]	0.54	$S_5\succ S_1\succ S_2\succ S_4\succ S_3$

.

Table 4 reveals that the ranking result of alternative suppliers when using these two models is different, where the optimal ranking value in the developed model of this paper is better than that of the existing model in the literature, that is, 0.61 > 0.54; also, the fifth alternative supplier is the final priority in these two models. Furthermore, in reality, the selection information is fuzzy and uncertain. However, in the existing method in the literature, the selection information is given directly. This maybe omits some of the decision information, which makes the ranking values and result imprecise. Meanwhile, in this method, the attribute weights are given using the analytic hierarchy process approach, which will affect the reliability of the attribute weights. On the contrary, in the developed approach of this paper, the hesitant fuzzy set is applied to extract the selection information in order to avoid the loss of selection information for making a reasonable and effective selection. Simultaneously, the attribute weight determination model is introduced and constructed to give a scientific and accurate attribute weight. This not only makes full use of selection information but also well reflects the fuzziness and hesitant degree of selection preference within an uncertain environment. As a consequence, the comparison between the proposed model and the existing model demonstrates the advantages of this proposed model, and the approach proposed in this paper is effective and feasible.

As aforementioned, the innovative contributions of this paper can be summarized as follows:

(1) In terms of preference information, the hesitant fuzzy set [70,83] is introduced to extract the hesitant fuzzy information of alternative suppliers as selection preference information. This well reflects the fuzziness and hesitance degree [71,84] of the selection preference within an uncertain environment.

(2) In terms of the projection technology, the existing literature [59,85,86] has only considered the relationship between alternatives and the ideal direction, while this paper discusses the relationship between alternative suppliers and positive and negative ideal directions, and the bidirectional projection is given, which can better reflect the reliability.

(3) In terms of determining the attribute weights, in the literature [73,87,88], the grey correlation analysis method was adopted to obtain the attribute weights, and the effect of hesitation on the evaluation results was neglected. However, in this paper, the attribute weights are given based on the attribute weight determination model, which minimizes the projected total deviation of the hesitant fuzzy [89] elements, and the hesitation degree of the evaluation information is considered, which has certain rationality to some extent.

(4) In terms of solution reliability, in the literature [90,91], the obtained results by using the model could change with a change in the parameter $\theta$, which will cause some confusion to the decision-makers in the decision-making process. Meanwhile, in this paper, since the obtained attribute weights are stable, a unique ranking result can be obtained. Simultaneously, a sensitivity analysis and a comparative analysis have been put forward to illustrate the stability of the proposed ranking result and the reliability of the proposed approach. Further, the attribute weights can be obtained easily by using the proposed approach when the attribute weights are unknown, and the schemes can be ranked effectively when there are many schemes.

6. Conclusions

This paper focuses on the selection of suppliers involved in complex product development, and a hesitant fuzzy multiple-attribute decision-making problem with unknown attribute weights is investigated. Accordingly, the formed vector equations of the alternative suppliers’ hesitant fuzzy element, positive ideal hesitant fuzzy element, and negative ideal hesitant fuzzy element are given. Further, a hesitant fuzzy projection equation based on two different directions is proposed for the bidirectional projection, and an improved equation for the degree of closeness is presented. And then, the attribute weight determination model is constructed, and, through the introduction of the Lagrange multiplier method, the corresponding attribute weights can be obtained by solving the model. By utilizing the aggregation of the hesitant fuzzy information projection matrix and the attribute weights, a weighted projection of the suppliers according to the given attributes is obtained, and the improved equation for the degree of closeness is used to obtain a ranking of the alternative suppliers. The feasibility of the proposed approach is verified using a case study of ship development. Simultaneously, discussions from a sensitivity analysis and a comparative analysis are provided, which show that the given final ranking result is stable and the proposed approach of this paper is applicable and reliable.

In the development process of a complex product, this paper proposes the collaborative manufacturing mode of “main manufacturer + suppliers” and discusses the supplier selection problem with unknown attribute weights under hesitant fuzzy information, which will develop and enrich complex product development research and supplier selection strategy theory. It should be emphasized that the proposed approach can provide more choices in the methods for the cloud manufacturing platform or the decision-makers to solve the supplier selection problem when using hesitant fuzzy information and unknown attribute weights. However, with the increasing complexity and uncertainty of the decision-making process, heterogeneous multiple-attribute decision-making has become one of the important bodies of research in modern decision-making science. Therefore, the future focus of discussion will be the multiple-attribute decision-making problem under heterogeneous decision-making information and its extensive application in supplier selection in complex product development.

Further, when there are more complex product development tasks, the proposed model in this paper will be limited. Thus, it is necessary to investigate how to match suitable suppliers to different tasks, and the one-to-one two-sided matching problem or one-to-many two-sided matching problem between tasks and suppliers in complex product development should be researched by applying the two-sided matching theory. Simultaneously, the differences in the psychological behavior characteristics among the matching agents will have an impact on the matching process. Therefore, the focus of the future also will be to further expand and apply research on the psychological behavior of matching agents when using hesitant fuzzy preference information in the development of complex products. Moreover, we can also focus on two-sided matching with multi-type agent expectations and multi-form preference information.