Is Technical Analysis Profitable on Renewable Energy Stocks? Evidence from Trend-Reinforcing, Mean-Reverting and Hybrid Fractal Trading Systems

Abstract

Demand for power sources is gradually shifting from ozone-depleting-substances towards renewable and sustainable energy resources. The growth prospects of the renewable energy industry coupled with improved cost efficiency means that renewable energy companies offer potential returns for traders in stock markets. Nonetheless, there have been no studies investigating technical trading rules in renewable energy stocks by amalgamating fractal geometry with technical indicators that focus on different market phases. In this paper, we explore the profitability of technical analysis using a portfolio of 20 component stocks from the NASDAQ OMX Renewable Energy Generation Index using fractal dimension together with trend-reinforcing and mean-reverting (contrarian) indicators. Using daily prices for the period 1 July 2012 to 30 June 2022, we apply several tests to measure trading performance and risk-return dynamics of each form of technical trading system—both in isolation and simultaneously. Overall, trend (contrarian) trading system outperforms (underperforms) the naïve buy-and-hold policy on a risk-adjusted basis, while the outcome is further enhanced (reduced) by the fractal-reinforced strategy. Simultaneous use of both trend-reinforcing and mean-reverting indicators strengthened by fractal geometry generates the best risk-return trade-off, significantly outperforming the benchmark. Our findings suggest that renewable energy stock prices do not fully capture historical price patterns, allowing traders to earn significant profits from the weak form market inefficiency.

1. Introduction

In recent years, global warming due to increased concentrations of greenhouse gases has triggered unusual weather conditions and rising sea levels in different parts of the world. One of the biggest emitters of greenhouse gases in the world is the United States (US), which contributed about 12% of the greenhouse gas, second only after China. The main culprit of the greenhouse gas is carbon dioxide which according to the US Environmental Protection Agency, accounted for about 80% of all gases contributed by the country. The gas is mostly emitted from fossil fuel and industrial processes and traps heat on earth. The unabsorbed gas will remain in the air for thousands of years.

The alarming amount of gas pollution has motivated governments and non-profit organizations to intervene in the operations of corporations. For example, various measures were introduced to promote renewable energy from solar, wind, hydropower, and other alternative sources with lucrative financial incentives to corporations and users. The financial factors together with the increased importance and demand for sustainable business practices have seen a growing trend of companies moving towards renewable energy ventures [1,2]. Likewise, in the capital markets of advanced nations such as the US, China and the United Kingdom, individual investors and mutual funds have started undertaking socially responsible investment practices. A recent report published by the Centre for Climate Finance and Investment [3] indicates that the performance of clean energy portfolios in financial markets for 2016–2020 has significantly surpassed fossil fuel companies in terms of returns and volatility. It also reported that the strength of the renewable power portfolios continues even with the advent and the recovery period of the COVID-19 crisis. The positive performance of renewable power portfolios is also documented in several academic research studies, such as those of Chang et al. [4] and Chang et al. [5]. These studies employed technical analysis and found superior returns for renewable energy stocks against fossil energy markets in the US and Europe.

As one of the investment strategies dominating the stock market, technical analysis has a long history where ancient societies began using historical prices to forecast future profits. One of the earliest forms of this strategy was used by the ancient Babylonians in the 7th century BC for the purpose of predicting the prices of commodities. The 20th century has seen a proliferation of technical analysis techniques due to technological advancements. In academia, studies such as those of [6,7,8,9,10] have explored different markets and/or financial instruments. By comparison, studies devoted to exploring technical rules in the energy markets, particularly renewable energy, remain scarce.

A limited number of studies have investigated energy markets using different tools for predictions, such as those of [11,12,13,14]. Chen et al. [11] found that combining information content of oil price ranges and graphical information of time series provides more accurate predictions of oil price movements than traditional models. Based on 168 energy stocks included in the NYSE Energy Index, Thomakos and Papailias [14] observed a strong presence of the momentum effect in the energy sector of which risk-reward characteristics can be exploited through various momentum trading strategies. Lin et al. [13] tested the predictive ability of technical trading rules proposed by Sullivan et al. [15] based on daily returns for thirteen energy market indices. Results show that the profitability of trading rules exists even after considering non-synchronous trading bias but disappears when transaction costs are considered, which implies that developed energy markets are efficient. More recently, Gurrib et al. [12] investigated the performance of charting using Ichimoku Cloud on the top ten stocks listed in the S&P Composite 1500 Energy Index. Using data from 2012 to 2019, they found that technical charts can offer speculators positive returns and outperform the buy-and-hold (B&H) strategy.

The profitability of technical analysis has significant implications for investment practice and efficient market hypothesis (EMH) at the weak form level. Although recent studies have investigated some forms of trading strategies using fractals to detect persistence (anti-persistence) by going long (short) in the financial markets, they are explored in isolation from technical trading rules. For example, Batten et al. [16] built trading rules by utilizing the Hurst coefficient for the gold-silver spread and showed that these rules can beat the B&H strategies and moving average rules across diverse holding periods. Auer [17] later used return-based ratio, but technical analysis was still ignored. Using a different approach, Paluch and Jackowska-Strumiłło [18] integrated fractal moving averages into technical indicators, which were then used as inputs to neural networks to forecast next-day closing prices. However, the study made no attempt to distinguish between market phases for utilizing appropriate indicators. In exploring different market states, Mahata and Nurujjaman [19] observed randomness in the short-term, while the long-term investment horizon displayed a correlation with firm fundamentals in some Indian and US companies. Nonetheless, the authors did not explore the combination trading rule.

Since some technical indicators perform better in certain conditions but show poor performance in other conditions, investors can benefit during trending or mean-reverting phases as identified from fractals (or Hurst exponents). Nonetheless, our bibliometric survey from the Scopus database using keywords such as “fractal”, “Hurst”, “exponent”, “technical analysis”, “trading rule” and “trading strategy”, reveals that this research area in econophysics and investment is still not well explored. Indeed, prior studies in technical analysis such as those by [8,9,10,16,20], among others, showed considerable evidence that might compromise EMH for yielding abnormal returns in various markets. More recently, Ni et al. [21] found that the Korean and Shanghai stock markets are not fully efficient, favouring contrarian (momentum) strategies for the former (latter). These findings reinforce the idea of augmenting fractals with the right technical analysis during the right market conditions in emitting trading signals, particularly in renewable energy firms which can be promising for investors due to the growth prospects of this industry. Hence, this study seeks to address the research question of whether technical analysis can provide economically significant returns and outperforms the passive B&H strategy using a portfolio of clean energy firms. In doing so, we computerize several trading rules and incorporate different market phases as identified by fractals to investigate if these enhanced trading strategies yield better performance.

Our research makes several contributions to the literature. First, we explore the profitability of technical trading in renewable energy stocks, which remains understudied in the literature despite its potential. Second, we merge fractal geometry with technical indicators that focus on different states of the market, which is also not well explored. Following from these two, to our knowledge, our study is the first to explore technical trading rules using this fractal-technical hybrid approach. Third, we utilize realistic constraints (budget, trading costs and long-only rule), as well as money (anti-Martingale) and risk (trailing stop) management policies to allow for valid empirical tests. Despite the significant importance of these practical constraints and policies, they are often ignored in the existing literature (see, for instance [22,23]). Hence, their inclusion in this paper would further contribute to the research in this area. Finally, for robustness purposes, we employ several performance metrics to allow for an in-depth analysis of the trading performance across several dimensions of return, risk, and their trade-off.

The remainder of this paper proceeds as follows. Section 2 explains the data and trading strategies. In Section 3, we provide the results and discussion. Section 4 concludes.

2. Research Methods

2.1. Data

Daily data for 20 component stocks from the NASDAQ OMX Renewable Energy Generation Index (GNREG) were obtained from the Yahoo Finance database. The sample companies are derived from the published list and filtered to include only companies with at least 10 years of data to allow for sufficient analysis over time. These companies are involved in fuel cells, solar and wind energy businesses, among others. Historical prices span the period 1 July 2012 through 30 June 2022. This period captures different economic episodes and the recent COVID-19 pandemic. In total, the sample period has 50,093 daily observations.

Table 1. Sample companies and statistics for 10-day nonoverlapping returns.

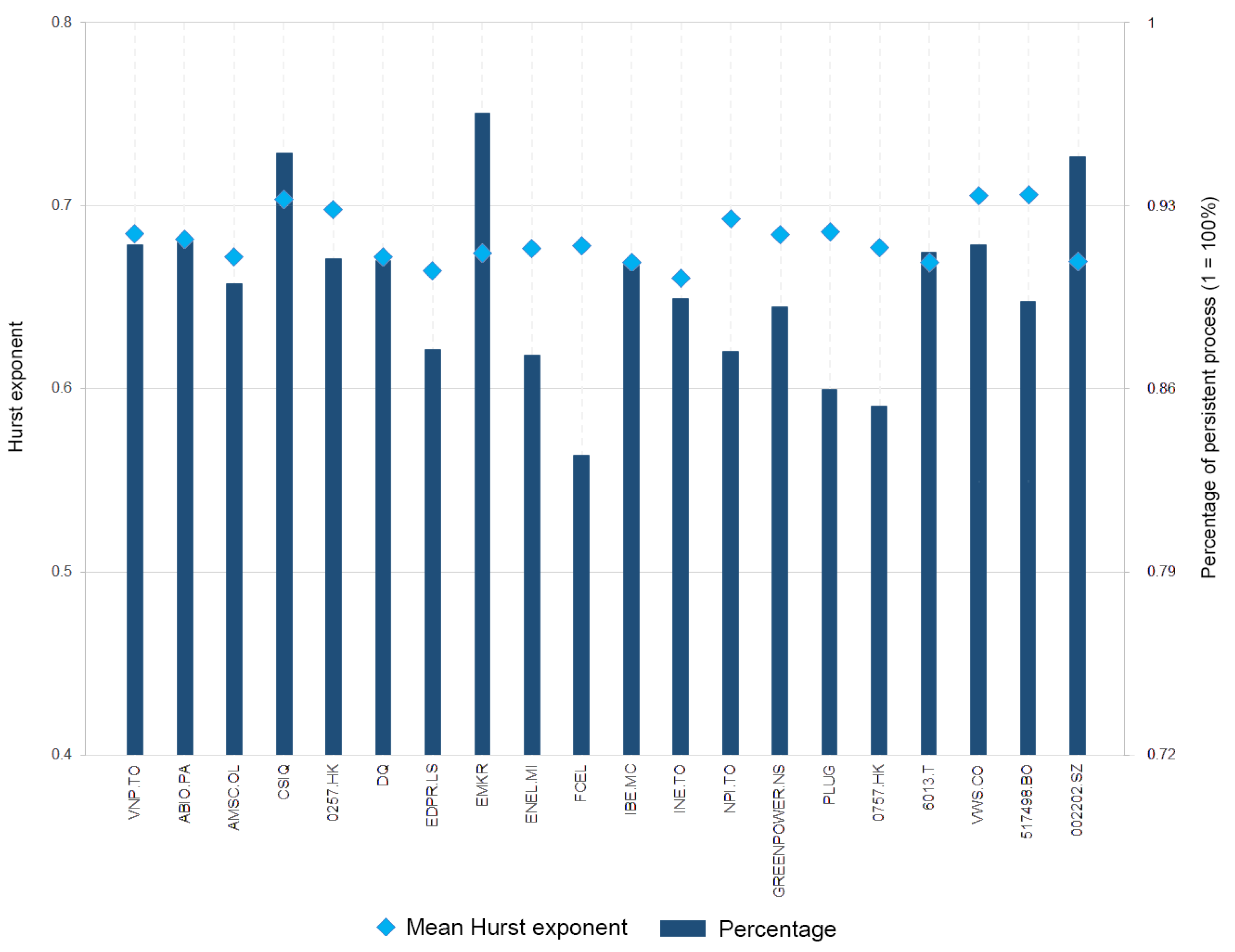
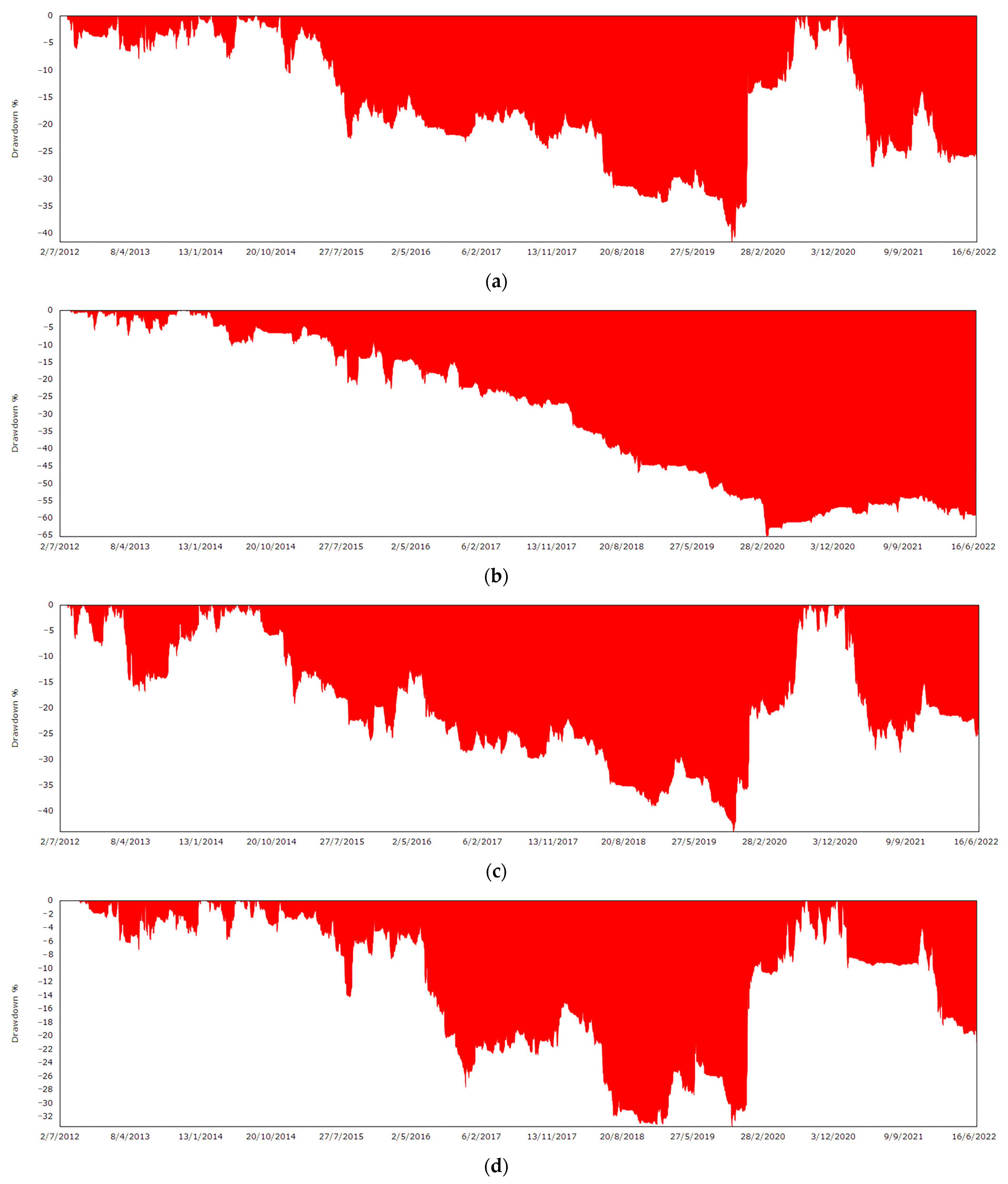
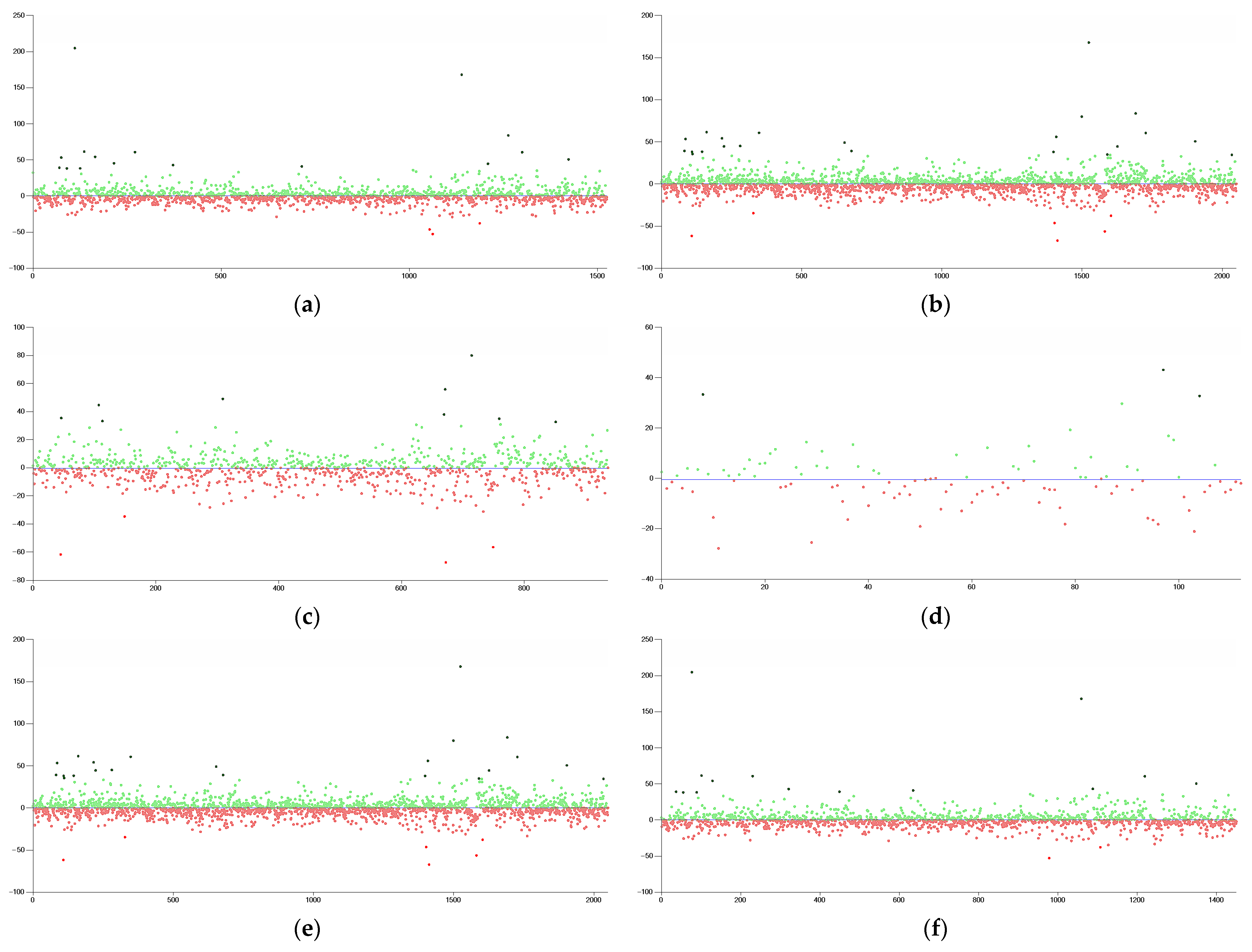
	Company	Stock Code	Mean	Min	Max	SD	Skew	Kurt
1	5N Plus	VNP.TO	0.333	−41.63	39.81	10.187	0.09	2.992
2	Albioma	ABIO.PA	0.643	−31.18	15.4	5.251	−0.555	4.944
3	American Shipping Company	AMSC.OL	1.746	−32.55	160.32	14.73	6.176	58.177
4	Canadian Solar	CSIQ	1.566	−34.54	68.13	12.289	0.686	3.583
5	China Everbright Environment Group	0257.HK	0.524	−30.39	24.87	6.802	0.308	2.864
6	Daqo New Energy	DQ	2.696	−44.98	94.14	18.129	1.379	5.042
7	EDP Renováveis	EDPR.LS	0.918	−22.56	21.44	5.146	0.26	3.269
8	EMCORE Corporation	EMKR	0.61	−33.56	47.95	10.036	0.814	4.562
9	Enel	ENEL.MI	0.568	−26.45	18.38	4.741	−0.475	4.225
10	FuelCell Energy	FCEL	0.903	−60.26	147.62	22.772	2.617	13.883
11	Iberdrola	IBE.MC	0.499	−19.05	10.82	4.053	−0.875	3.209
12	Innergex Renewable Energy	INE.TO	0.191	−19	15.81	4.242	−0.024	3.037
13	Northland Power	NPI.TO	0.406	−17.69	11.06	3.772	−0.591	2.848
14	Orient Green Power Company	GREENPOWER.NS	0.894	−29.65	52.76	12.909	1.078	2.593
15	Plug Power	PLUG	2.758	−67.5	212.12	23.778	3.689	26.705
16	Solargiga Energy Holdings	0757.HK	0.783	−35.44	108.33	13.133	3.586	22.751
17	Takuma	6013.T	0.645	−19.34	23.49	6.394	0.021	0.581
18	Vestas Wind Systems	VWS.CO	1.576	−26.39	38.17	8.286	0.244	1.781
19	Websol Energy System	517498.BO	2.238	−30.24	84.97	17.373	1.556	3.728
20	Xinjiang Goldwind Science & Technology	002202.SZ	0.813	−23	30.64	8.568	0.591	1.309

Note: The table provides descriptive statistics of 10-day nonoverlapping returns (%) for the sample portfolio during the period 1 July 2012 to 30 June 2022. These returns are reported for statistical purposes and are thus computed without deducting trading costs.

reports the list of companies and their sample statistics based on 10-day nonoverlapping holding period returns.

In Table 1, we observe that the companies offer positive 10-day mean returns during the sample period. Nonetheless, the mean returns vary quite considerably among the 20 stocks. Notably, Plug Power (PLUG)’s return ranges from −67.5% to 212.12% and recorded the highest mean return of 2.76%. The variation in PLUG’s returns during the period is also high as indicated by the standard deviation (23.78). Innergex Renewable Energy (INE.TO) offered the lowest mean return of 0.19% and its return ranges from −19% to 15.81%, with an associated standard deviation of 4.24. With respect to the distribution of stock returns, most sample stocks are positively skewed. We note that several stocks are highly skewed and leptokurtic, namely, American Shipping Company (AMSC.OL), Daqo New Energy (DQ), FuelCell Energy (FCEL), PLUG, Solargiga Energy Holdings (0757.HK), and Websol Energy System (517498.BO). Overall, the mean, ranges and volatilities of returns suggest that there are possibilities of generating profitable trades, provided that a trading strategy can identify proper entry and exit points to exploit any predictable patterns in the time series.

2.2. Fractal Analysis and Technical Indicators

Empirical tests of this study focus on trend-following (momentum) and contrarian (mean-reverting) indicators, both of which are among the most central financial anomalies [24]. We generate the automated trading signals using two of the most frequently applied technical indicators, namely moving average convergence divergence (MACD) [25] and Bollinger bands (BB) [26], and a hybrid strategy that reinforces these two with fractal dimension (D) [27]. Academic studies have widely investigated the performance of MACD and BB as technical trading strategies, either as a single indicator or combined indicators [9,28,29,30,31]. For example, Xie et al. [31] found that MACD performs better than other trend-following indicators, such as dual moving average (MA) crossover and average directional index (ADX). Lento and Gradojevic [29] showed that, out of a set of technical indicators tested, BB appears as the only technical indicator that is profitable during the market crash. In detecting market phases, there are variations or more sophisticated techniques that utilize fractals or the Hurst exponent, such as multifractal detrended fluctuation analysis (MF-DFA) by Kantelhardt et al. [32]. Nonetheless, they are well explored in academic literature (as opposed to being implemented by real-world traders) and thus D is more relevant from the perspective of an investor.

One of the main advantages of D is its ability to analyse the fractality in the time series, allowing one to measure the level of (anti)persistence and efficiency in financial markets. As such, MACD (BB) is expected to perform better during the trending (mean-reverting) market stage as identified by the Hurst exponents from the D. In other words, our research approach utilizes the well-known trend-following and contrarian indicators, while fractal geometry serves as the market mode sensor.

MACD is a momentum indicator built upon the difference between the long and short-term exponential moving averages (EMA), which can be formulated as

$${\mathrm{EMA}}_t=\left[\frac{2}{n}\times \left(P_t-{\mathrm{EMA}}_{t-1}\right)\right]+{\mathrm{EMA}}_{t-1}$$

(1)

where n represents the number of periods for the EMA and P_t is the closing stock price at time (day) t. A signal line constructed from a 9-day EMA is often used together with the MACD to generate buy and sell signals. Briefly stated, a long signal occurs if the MACD crosses above the signal line, and vice versa. This is one of the most popular approaches used by traders and it is also utilized in this study.

Unlike MACD, BB is a price envelope formulated from standard deviations and reflects the volatility of a security. It can be used to exploit the mean-reverting phase. The lower band (LB) of the BB is formulated as

$$\mathrm{LB}=\mathrm{MB}-m\times \sqrt{\frac{{\displaystyle {{\displaystyle \sum }}_{t=1}^n}{\left(P_t-\mathrm{MB}\right)}^2}{n}}$$

(2)

where MB is the middle band, m is a constant (number of standard deviations, typically 2), while n is the number of periods in the moving average (usually 20 days). Contrarians believe that trend reversal approaches when stock price pierces the lower band, which emits a buy signal [9].

As a market mode sensor inspired by Mandelbrot’s [33] fractal geometry, D allows a trading system to spot whether the market is trending or cycling, and this enables a trader to employ an appropriate strategy for that particular market condition. Using the formulation in [18,27,34], D can be represented mathematically as

$$\mathrm{D}=\frac{\log \left(\frac{{\mathrm{N}}_{1\mathrm{T}}+{\mathrm{N}}_{2\mathrm{T}}}{{\mathrm{N}}_{\left(0-2\right)\mathrm{T}}}\right)}{\log \left(\frac{2\mathrm{T}}{\mathrm{T}}\right)}=\frac{\log \left({\mathrm{N}}_{1\mathrm{T}}+{\mathrm{N}}_{2\mathrm{T}}\right)-\log \left({\mathrm{N}}_{\left(0-2\right)\mathrm{T}}\right)}{\log \left(2\right)}$$

(3)

where N_1T (N_2T) refers to the differences between highest and lowest stock prices in the first (second) subperiod T (T to 2T) over the first subperiod T, while N_0−2T are based on the highest and lowest prices over the whole subperiod 2T. Because the financial time-series are assumed to be self-similar, the Hurst exponent (H) can be presented as H = 2 − D. Random walk is represented by D = 1.5 (or H = 0.5). The market is considered persistent (i.e., trend-reinforcing) when 1 < D < 1.5 (or 0.5 < H < 1.0) and anti-persistent (i.e., mean-reverting, cycling or contrarian) when 1.5 < D ≤ 2 (or 0 ≤ H < 0.5). See [35] for a brief description of fractal taxonomy in time series.

In total, we explore the following six technical trading strategies (the buy signals for the first two strategies as described earlier):

• MACD (trading occurs when signals are generated, regardless of market phases);
• BB (trading occurs when signals are generated, regardless of market phases);
• MACD-BB (trading occurs based on signals from MACD and BB, regardless of market phases);
• D-MACD (trading occurs based on signals triggered by MACD but only when D shows the market is in the trending mode);
• D-BB (trading using BB signals is only executed when the market is in the mean-reversion phase);
• D-MACD-BB (trading is done using signals from MACD when the market is trending and BB when the market is mean-reverting).

Where buy trading signals are emitted at time t, trading occurs at t + 1 (the next day), hence allaying look-ahead bias. Following this signal, a 10-day holding period return is computed, which is in line with prior research [36,37,38]. Consistent with existing studies, the unconditional B&H rule serves as the benchmark policy, and coherently the returns are measured based on a 10-day nonoverlapping holding period.

2.3. Robustness—Experimental Design and Performance Evaluation

One of the most serious errors when inferring profitability of trading rules is data snooping bias, where researchers exhaustively mine for patterns from the dataset that may not be exploitable after the fact. Typically, there are two approaches to deal with this bias. The first is through corrections via bootstrap approach introduced by White [39] (reality check) and later improvements to it by Hansen [40] (superior predictive ability). The second approach is via optimization, using methods such as genetic algorithm or programming of the parameters and testing the strategies within the out-of-sample context, as explored by [41,42,43,44], among others.

Nonetheless, by utilizing MACD, BB and D as described by [25,26,27,34], in which the indicators were already in existence prior to the sample period, our approach does not violate the protocol for testing market efficiency as outlined by Timmermann and Granger [45]. Stated differently, using standard indicators and parameters can inherently alleviate data snooping since they were drawn from the population space of indicators that were already available (and widely known) to market participants during that point in time.

To mimic the realistic investment setting and to allow for valid empirical tests, we consider both money and risk management rules [46,47]. The incorporation of these rules with technical indicators in making trading decisions is classified as a technical trading system [46]. For simulation purposes, we restrict the initial capital to USD 100,000. We employ anti-Martingale strategy as described by [47,48,49]. This approach considers winning (losing) streaks by increasing (decreasing) subsequent trade sizes based on the performance of the previous trades. Using 2% per trade [50] as a starting point, a profitable (losing) trade will increase (reduce) the consequent trade size by 2% (1%). This strategy also alleviates the dangers associated with the gambler’s fallacy [49].

As a fail-safe risk management strategy, a stop loss rule liquidates the stocks mechanically when the loss reaches a certain threshold. Practitioners may utilize different stops, including limits based on certain prices or percentages such as 7% or 8% below the buying price [51] or even a wider stop [52]. Hence, the choice of arbitrary levels of stops may differ according to factors such as risk aversion level and market fluctuations, but such choice may also impose dangers of it being attributed to subjective interpretation and data snooping. Alternatively, a more scientific (and popular) approach is the application of trailing stop by using the average true range (ATR) indicator, as investigated in [53]. This rule facilitates a trader to reduce losses (increase threshold) when the position becomes non-favourable (favourable) based on the ATR. As such, this paper employs the ATR method since it is both systematic and practical within the trading context.

Finally, to evaluate the performance of technical trading rules against B&H policy in the renewable energy stocks and to provide a more rigorous analysis of risk-return trade-off, we report several core metrics such as maximum drawdown, recovery factor, MAR ratio, tail ratio, ulcer index, ulcer performance index, Sharpe ratio and Sortino ratio. In line with existing literature, t-test (one-tailed) is used to see if our technical trading systems (TS) produce significant positive returns (µ_TS > 0) and outperform the benchmark (µ_TS > µ_B&H). As for the risk-return trade-off, the Sharpe ratio is typically considered as one of the most (if not the most) popular measures among traders and academicians. In this study, we employ the approach in Opdyke [54] to test whether the Sharpe ratios of the trading systems are significantly greater than zero (SR_TS > 0) and whether they significantly surpass the ratio produced by the B&H (SR_TS > SR_B&H).

Our simulation is based on long-only transactions (because of short-selling restrictions) and a brokerage fee of 2% round-trip (or 1% one-way) to replicate the real-world trading environment.

3. Results and Discussion

3.1. Performance of Trend-Reinforcing, Mean-Reverting and Hybrid Fractal Trading Systems

In

Table 2. Profitability and risk of the technical trading systems and the benchmark.

	Benchmark	Non-Fractal Systems			Hybrid Fractal Systems
Performance Measures	B&H	MACD	BB	MACD-BB	D-MACD	D-BB	D-MACD-BB
Net Profit (%)	46.74	45.68	−56.00	64.52	78.85	−8.88	112.69
Annualized Return (%)	3.91	3.84	−7.89	5.11	5.99	−0.93	7.84
Mean Return (USD)	9.65	29.94	−59.77	31.46	58.76	−78.58	77.66
µTS > 0	-	0.2045	0.9945	0.0805 *	0.1810	0.8775	0.0080 ***
µTS > µB&H	-	0.2030	0.9880	0.2045	0.0670 *	0.8440	0.0102 **
Ulcer Index	35.68	18.88	36.40	21.72	15.62	9.24	8.14
Max Drawdown (%)	−71.67	−41.56	−65.32	−43.99	−33.45	−18.65	−27.87
Max Drawdown Date	23 March 2020	29 October 2019	18 March 2020	29 October 2019	29 October 2019	20 March 2020	7 November 2019

Note: The table summarizes the performance of the benchmark policy, non-fractal trading systems and fractal-based trading systems during the period 1 July 2012 to 30 June 2022 after deducting trading costs. µ_TS refers to the mean returns per trade of the trading system in that column, while µ_B&H means mean returns for the B&H rule. The µ_TS > 0 and µ_TS > µ_B&H rows report the p-values. *, ** and *** indicate statistical significance at 10%, 5% and 1% levels, respectively. Bold figures highlight superior performance over the benchmark.

, we show that the after-cost trading performance of the trending, countertrending, and hybrid strategies as well as that of the unconditional B&H policy. Few remarks are in order. Trend-based trading rule produces a positive net return (45.68%) and an annualized return of 3.84%. This strategy slightly underperforms the passive B&H rule (46.74% and 3.91%, respectively) when trading signals are executed without considering market states. To the extent where trading occurs only during the trending phase, the fractal-enhanced D-MACD produced superior results with greater net and annualized gains (78.85% and 5.99%, respectively). Contrarian-based rule, however, suffers losses of over half the original capital (BB with −56%), but this is significantly reduced when trading signals are emitted during the correct phase (D-BB with −8.88%). This highlights the importance of incorporating the market state to use the correct indicator. One possible explanation for the loss is that the counter-trending periods are relatively brief to allow the trading rule to capture profit opportunities, before it moves to the next (trending) phase.

Figure 1 provides support for the preceding argument. On average, the daily Hurst exponents of each company lie between 0.66 and 0.71, indicating a persistent process. Throughout the sample period, the stock prices of each company mostly fall within the trend-reinforcing phase (from 83% to 97% of the daily observations). Hence, the limited and short mean-reverting periods lend credence to the poor performance of the contrarian-based rule, due to abrupt changes in the market phase towards momentum. In general, this also raises the importance of using different strategies during different market phases. As seen in Table 2, the dual-rule MACD-BB can produce higher returns than the naïve B&H strategy, and the outcome is more pronounced in the fractal-based D-MACD-BB where the net profit (annualized return) is 112.69% (7.84%). In short, entering the renewable energy market using MACD (BB) when D shows the market is trending (countertrending) yields over double the net and annualized profits of the elementary B&H.

The mean returns of MACD-BB and D-MACD-BB are significantly greater than zero at the 10% and 1% levels, respectively. With the exception of BB and D-BB, the mean returns of all trading systems are greater than those of the naïve policy, ranging from 3.1 (MACD) to 8 (D-MACD-BB) times that of the B&H. The hybrid fractal-based momentum-contrarian and momentum-only trading systems enjoy statistically significantly better returns than those from the unconditional B&H. Note that using a parametric t-test relies on the sample returns that follow the Gaussian distribution. While this may not always be the case, the sample sizes of our analysis (number of trades) are sufficiently large to invoke the central limit theorem, supporting the use of parametric statistics. Indeed, as pointed out by Wilmott [55], the assumption of normality is vital to the advancements in finance. Moreover, using t-tests also allows for consistency and comparability with the bulk of literature in technical analysis, such as [10,36,37,56]. Nonetheless, for information purposes, we also performed the nonparametric Mann-Whitney U test (MW) to see if the median return is significantly greater than zero and the Kolmogorov-Smirnov test (KS) to compare the technical trading returns against those of the B&H policy. In both cases, the hybrid fractal-based momentum-contrarian strategy remains statistically significant (MW, p < 0.10 and KS, p < 0.01). Also note that although several stocks have different statistics (see Table 1), there are no qualitative differences in the trading system performances between the subset portfolios of different groups (results are available upon request).

The technical-based strategies (except for BB) experienced a smaller ulcer index against the B&H, indicating lower downside risk. In other words, all technical rules had lower volatilities as compared to the B&H policy (35.68), while D-MACD-BB (8.14) came on top. Based on the maximum drawdowns, all trading systems faced lower drawdowns as compared to the one suffered by the naïve policy.

Figure 2 shows the drawdowns during the whole period and displays the maximum drawdowns for all technical trading systems. Not surprisingly, maximum drawdowns for all trading systems occurred between the end of 2019 and early 2020, which can be attributed to the global health emergency caused by the COVID-19 outbreak. The unconditional B&H policy saw its peak-to-valley declined by 71.67% shortly after the World Health Organization declared the novel coronavirus as a pandemic.

Note that the findings so far only explain the one-dimensional return (net profit, annualized and mean) or risk (drawdown) factor of the trading systems. Since investments must be gauged by both risk and return, higher (lower) trading return does not indicate better (worse) performance if it is gauged in isolation from the relevant risk. As such, it remains to be seen if these trading systems can also dominate the B&H based on their risk-return trade-off measures. The trading metrics which capture both risk and return elements are vital to ensure the robustness of the findings and are discussed below.

3.2. Robustness

Table 3. Risk-return metrics of the technical trading systems and the benchmark.

	Benchmark	Non-Fractal Systems			Hybrid Fractal Systems
Performance Measures	B&H	MACD	BB	MACD-BB	D-MACD	D-BB	D-MACD-BB
Sharpe Ratio	0.32	0.29	−0.73	0.40	0.48	−0.33	0.73
SRTS > 0	-	0.1626	0.9925	0.1118	0.0474 **	0.8671	0.0049 ***
SRTS > SRB&H	-	0.5232	0.9993	0.3927	0.2813	0.9240	0.0804 *
Sortino Ratio	0.62	0.63	−0.89	0.87	1.07	−0.27	1.56
Recovery Factor	0.28	0.81	0	1.03	1.54	0	2.56
MAR Ratio	0.05	0.09	0	0.12	0.18	0	0.28
Tail Ratio	1.11	1.00	0.92	1.08	1.19	0.88	1.24
Ulcer Performance Index	0.11	0.20	−0.22	0.24	0.38	−0.10	0.96

Note: The table summarizes the performance of the benchmark policy, non-fractal trading systems and fractal-based trading systems during the period 1 July 2012 to 30 June 2022 after deducting trading costs. SR_TS refers to the Sharpe ratio of the trading system in that column, while SR_B&H means the Sharpe ratio for B&H rule. The SR_TS > 0 and SR_TS > SR_B&H rows report the p-values. *, ** and *** indicate statistical significance at the 10%, 5% and 1% levels, respectively. Bold figures highlight superior performance over the benchmark.

details several key metrics which measure the risk-return performance of the technical trading systems versus the unconditional B&H strategy. Except for contrarian-based rules, trend-reinforcing (MACD and D-MACD) and combined (MACD-BB and D-MACD-BB) trading rules outperform B&H in overcoming the effects of drawdown, as reflected by the recovery factors and the MAR ratio. This result is superior among hybrid fractal strategies, particularly D-MACD-BB. Both performance measures tell the same story, where the hybrid rules produced better performance against drawdowns, apart from mean-reverting based technical strategy in isolation.

Figure 3 exhibits the profits and losses (after costs) of each trading position in chronological sequence for each trading system. Over time, winning (losing) trades were generally centred without extreme profits or losses, with small exceptions of outliers. As shown in Table 3, the tail ratios were slightly higher than one (except for contrarian-only strategy), suggesting that extreme gains were marginally better than extreme losses. The hybrid D-MACD-BB again appears as the best performer, with a tail ratio of 1.24, indicating that the magnitude of the largest average profit (95th percentile) gained from using the strategy is greater than the largest losses (5th percentile). Note the visible lack of BB trades in Panel (c), which is more pronounced in Panel (d) with D-BB, when trading occurs only during the countertrending market state, supporting our earlier argument about the possibility of a shorter phase that generated limited trading signals.

Figure 4 shows the heatmaps of mean returns for each trading system by focusing on each component stock. Larger squares indicate more trades, and vice versa. It can be seen that the number of trades is roughly consistent among different constituent stocks and across different trading systems. Similarly, the returns appear to spread evenly, with only one or two companies in each strategy that result in higher profits or losses, as compared to the other components. Accordingly, the figure suggests that the performance of our trading systems is consistent across the renewable energy portfolio and is not peculiar to any stocks.

The risk-return trade-off shown Table 3 tells us several stories. With the enhanced D-MACD-BB obtaining the highest ulcer performance index of 0.96, the result suggests that it yields better returns against risk as characterized by the ulcer index by entering the market during the appropriate trend or mean-reverting phase. Evidently, different metrics may favour different trading systems, but the overall result clearly tilts towards D-MACD-BB.

Ultimately, it is acknowledged that Sharpe and Sortino ratios are the essential metrics. The main limitation of the Sharpe ratio is that it evenly punishes upside and downside volatilities. However, investors are more worried about the risk of losing money, while the upside is desired. Sortino ratio addresses this weakness by penalizing bad volatility. As seen in Table 3, the Sharpe values of three trading systems (MACD-BB, D-MACD and D-MACD-BB) are higher than that of the benchmark and range from 0.4 to 0.73 against 0.32 produced by B&H. Both Sharpe ratios of D-MACD and D-MACD-BB are significantly greater than zero, while the latter also significantly outperforms the unconditional B&H strategy.

Our findings offer compelling evidence that using fractals with both trend-following and countertrending technical signals producing the best performance, both in economic and statistical senses. To the extent that Hurst exponents capture different market phases, trending and contrarian technical indicators can produce greater returns by emitting entry and exit signals at optimal points. This is similarly reflected in the Sortino ratios, where MACD-BB (D-BB) earned a better return per risk of 1.07 (−0.27) as compared to MACD (BB) with a return per risk of 0.63 (−0.89) in isolation. Even though BB-based indicators were making losses, the results were less severe when the market phase was considered. The main strategy combining both trend-reinforcing and mean-reverting indicators, D-MACD-BB, produces the highest Sortino ratio of 1.56. This result confirms that the fractal-enhanced trading system dominates the passive policy by producing greater returns per unit of downside risk. Further, D-MACD-BB also outperforms each technical strategy in isolation (MACD and BB), as well as hybrid rules based either on persistent (D-MACD) or anti-persistent (D-BB) market phase.

Our results are robust in several ways. First, as described earlier, we use only strategies which were already available (known to investors) during the testing period. This may seem straightforward, although ironically, many studies often overlooked this aspect. For example, in a highly cited study, Wong et al. [10] explored MACD and the relative strength index in the Singapore stock market during the period 1974 to 1994. The main weakness of their study is that it ignored the fact that these indicators were only developed in the late 1970s, hence it is impossible to make a conclusion about the profitability of their strategies because they were non-existent during their early sample period. This is not the case in our research. Second, our research design, which uses well-known indicators and lagged trading rules, alleviates data snooping and look-ahead biases. Third, we utilize money management (anti-Martingale) and risk management (trailing stop loss) policies, and consider practical constraints namely budget limitation, long-only transactions, and a brokerage fee of 2% round-trip (or 1% one-way) to simulate a realistic trading environment. Finally, we employed several performance measures.

By considering risk-return dynamics, we can determine the economic significance of each trading rule and its relative performance based on several dimensions. This is crucial because if the market is efficient, superior returns (after trading costs) should be associated with higher risk [57]. Our findings, however, reveal that trading using a popular trend indicator in combination with the contrarian indicator driven by fractal geometry yields the highest returns per risk and dominates the B&H policy, both in economic and statistical significance senses. The economic interpretation of this outcome is that market participants do not price renewable energy companies efficiently. Because renewable energy is a relatively new and niche area compared to other sectors such as banking and finance, construction, healthcare, and technology, several costs and benefits associated with its business nature cannot be expressed in monetary terms [58]. Thus, fundamental valuation using techniques such as the Gordon growth model can be a difficult task, supporting the use of technical trading. Furthermore, limited market participation among traders and investment funds may lead to potential mispricing and thus allows for profitable trades. As noted earlier, research focusing on trading rules in renewable energy markets is still underdeveloped, as indicated by the Scopus survey. As such, this lack of coverage in academic research also provides support for technical trading profitability in this green energy sector, and this argument is consistent with [59]. In an economic sense, our empirical findings contradict the risk-based explanation of technical trading returns. The fractal-based momentum-contrarian system outperforms the naïve B&H rule by generating higher returns per risk based on all the key metrics, most importantly, the Sharpe and Sortino ratios.

In this study, we focus on two of the most popular technical indicators and variation of the parameters (long EMA, short EMA, signal line, period and the number of standard deviations). This approach (i.e., using default or popular parameters for empirical analysis) is in line with many studies in technical analysis such as [12,36,60], and allows us to mitigate the bias associated with data snooping. For information purposes only, we also run the test 101,160 times using 5058 variations of the technical parameters. The results are provided in Appendix A, showing the best and worst parameters for each non-fractal trading system (

Table A1. Trading performance of non-fractal trading systems using different parameters.

	Parameters	NP (%)	MD (%)	MAR	RF	SR	SOR
Panel A. MACD
T1	MACD (11,19,5)	164.41	−30.56	0.33	3.77	0.59	1.92
T2	MACD (14,63,5)	165.70	−24.96	0.40	4.10	0.78	1.90
T3	MACD (9,49,7)	164.89	−36.04	0.28	2.43	0.63	1.89
B3	MACD (17,72,15)	−36.14	−53.73	0	0	−0.34	−0.49
B2	MACD (19,67,15)	−46.66	−67.73	0	0	−0.41	−0.57
B1	MACD (20,79,11)	−41.56	−59.76	0	0	−0.42	−0.61
Panel B. BB
T1 *	BB (59,2.5)	0.002	−10.30	0	0.03	0.02	0.02
T2	BB (50,2.5)	−8.68	−29.25	0	0	−0.12	−0.12
T3	BB (56,2.5)	−5.76	−15.44	0	0	−0.16	−0.16
B3	BB (30,2.5)	−52.19	−52.95	0	0	−1.25	−1.35
B2	BB (50,2)	−62.03	−64.45	0	0	−1.29	−1.36
B1	BB (25,1)	−72.80	−76.06	0	0	−0.89	−1.40
Panel C. MACD-BB
T1	MACD (10,25,7), BB (47,2.5)	231.18	−36.63	0.35	3.14	0.70	2.31
T2	MACD (14,37,9), BB (60,2.5)	214.46	−24.07	0.50	4.70	0.83	2.15
T3	MACD (9,29,7), BB (60,2.5)	235.17	−28.23	0.46	3.18	0.59	2.05
B3	MACD (18,90,15), BB (25,1)	−70.38	−74.12	0	0	−0.70	−0.95
B2	MACD (20,90,14), BB (28,1)	−60.05	−69.02	0	0	−0.76	−1.00
B1	MACD (16,34,14), BB (38,1)	−61.47	−66.56	0	0	−0.67	−1.02

Note: The table summarizes the best and worst performance of each non-fractal trading system based on different parameters during the period 1 July 2012 to 30 June 2022. Trading is executed using signals from MACD and/or BB, regardless of the market phases. The ranking of parameters is sorted according to their Sortino ratios. T1, T2 and T3 denote the top, second and third best results, while B1, B2 and B3 indicate the worst, second worst and third worst outcomes, respectively. The parameters are described as MACD (short EMA, long EMA, signal period) and BB (period, number of standard deviations). NP (%), MD (%), MAR, RF, SR and SOR denote net profit (%), maximum drawdown (%), MAR ratio, recovery factor, Sharpe ratio and Sortino ratio, respectively. * For BB, only T1 generates profit and thus positive Sortino ratio.

) and hybrid fractal trading system (

Table A2. Trading performance of hybrid fractal trading systems using different parameters.

	Parameters	NP (%)	MD (%)	MAR	RF	SR	SOR
Panel A. D-MACD
T1	MACD (20,28,6)	292.18	−22.83	0.57	5.70	0.67	2.55
T2	MACD (15,20,12)	183.05	−30.37	0.35	3.23	0.57	2.54
T3	MACD (20,52,5)	220.31	−37.13	0.36	2.99	0.73	2.52
B3	MACD (16,90,12)	−42.27	−58.27	0	0	−0.51	−0.67
B2	MACD (20,27,11)	−40.11	−60.62	0	0	−0.43	−0.71
B1	MACD (18,88,7)	−49.32	−61.24	0	0	−0.56	−0.80
Panel B. D-BB
T1	BB (56,1)	15.82	−5.20	0.21	2.11	0.50	0.79
T2	BB (32,2.5)	4.14	−1.08	0.19	1.77	0.37	0.69
T3	BB (58,1)	15.40	−5.90	0.22	2.18	0.50	0.66
B3	BB (29,1)	−19.30	−20.83	0	0	−0.65	−0.60
B2	BB (23,1)	−22.77	−24.57	0	0	−0.63	−0.66
B1	BB (24,1)	−29.37	−30.85	0	0	−0.76	−0.80
Panel C. D-MACD-BB
T1	MACD (20,47,5), BB (10,1)	264.31	−24.60	0.56	3.98	0.77	2.94
T2	MACD (8,66,7), BB (52,1)	255.63	−21.94	0.62	4.66	1.02	2.92
T3	MACD (13,30,5), BB (10,2)	278.74	−26.90	0.53	3.80	0.71	2.82
B3	MACD (20,90,11), BB (23,1)	−43.40	−59.99	0	0	−0.48	−0.72
B2	MACD (18,82,8), BB (60,2)	−51.41	−59.54	0	0	−0.55	−0.78
B1	MACD (20,81,13), BB (31,1.5)	−59.79	−67.94	0	0	−0.81	−0.89

Note: The table summarizes the best and worst performance of each hybrid fractal trading systems based on different parameters during the period 1 July 2012 to 30 June 2022. Trading is executed using signals from MACD when the market is trending and/or BB when the market is mean-reverting. The ranking of parameters is sorted according to their Sortino ratios. T1, T2 and T3 denote the top, second and third best results, while B1, B2 and B3 indicate the worst, second worst and third worst outcomes, respectively. The parameters are described as MACD (short EMA, long EMA, signal period) and BB (period, number of standard deviations). NP (%), MD (%), MAR, RF, SR and SOR denote net profit (%), maximum drawdown (%), MAR ratio, recovery factor, Sharpe ratio and Sortino ratio, respectively.

). While there can be a limitless combination of trading indicators, rules, and parameters, our findings support the economic significance of the hybrid fractal trend-countertrend trading system using publicly known parameters advocated by practitioners. Overall, the results are in line with [12] who found profitable trading opportunities in the broader group of US energy stocks, as well as [61] who documented superior risk-return performance of technical trading rules over the B&H in the portfolio of international integrated oil and gas firms.

4. Conclusions and Implications

Renewable energy companies have the potential to offer attractive returns on investments for individual and institutional investors. As well, the nature of their businesses is typically in line with socially responsible investing. In this study, we computerized trend-reinforcing (MACD), contrarian (BB) and their combination (MACD-BB), as well as hybrid fractal trading systems (D-MACD, D-BB, and D-MACD-BB) that wield appropriate signals during different market phases. We explore these trading systems on a sample of 20 NASDAQ OMX Renewable Energy Generation Index constituents. Our results show that using both trend- and contrarian-based technical indicators in combination with fractal geometry in a trading system outperforms the unconditional B&H policy, supporting the use of historical patterns to forecast future returns. Further, D-MACD (D-BB) produces better results than MACD (BB), and D-MACD-BB dominates all other trading rules. These findings confirm the capability of D as a sensor for different market modes. Augmenting fractal geometry with technical signals by trading based on MACD when the market is persistent and BB during the anti-persistent phase produces a better risk-return outcome, as opposed to its constituent indicator separately.

In view of the above, our results indicate that stock prices of companies involved in the business of inexhaustible sources of energy do not move randomly. Such an outcome implies that these stock prices do not adjust instantaneously to historical price information, and this pattern is consistent with weak form inefficiency. Thus, investors might be able to capitalize on these price patterns optimally by using fractals to establish the right technical tools at the right time. Nonetheless, given the small sample used, caution must be applied before our findings can be extrapolated to all companies in other industries and markets.

Further research can investigate different markets, industries and sample periods using similar experimental setups. For example, the performance of fractal-based trading systems can be explored during different periods (and subperiods) over time, to capture different macroeconomic events, significant technological developments, and crisis episodes, among others. Focusing on a shorter subsample may allow for a specific evaluation of performance, but this comes at the expense of limited trading signals and sacrificing the stability of the trading parameters. The recent COVID-19 pandemic, for instance, has serious implications for stock returns [62] and can affect mutual funds’ performance [63,64,65]. Another area for research is exploring different variants of the trading rules (e.g., using different short- and long-term moving averages, standard deviations and holding periods) using machine learning to discern optimal trading parameters and to capture the relationship between various technical indicators, fractals and even fundamental factors to extend prior research, such as those of [66,67,68,69,70,71,72,73,74,75].