On the Application of the Block Hybrid Methods to Solve Linear and Non-Linear First Order Differential Equations
Abstract
:1. Introduction
2. The Solution Method
Local Truncation Error
3. Applications
3.1. Numerical Linear Examples
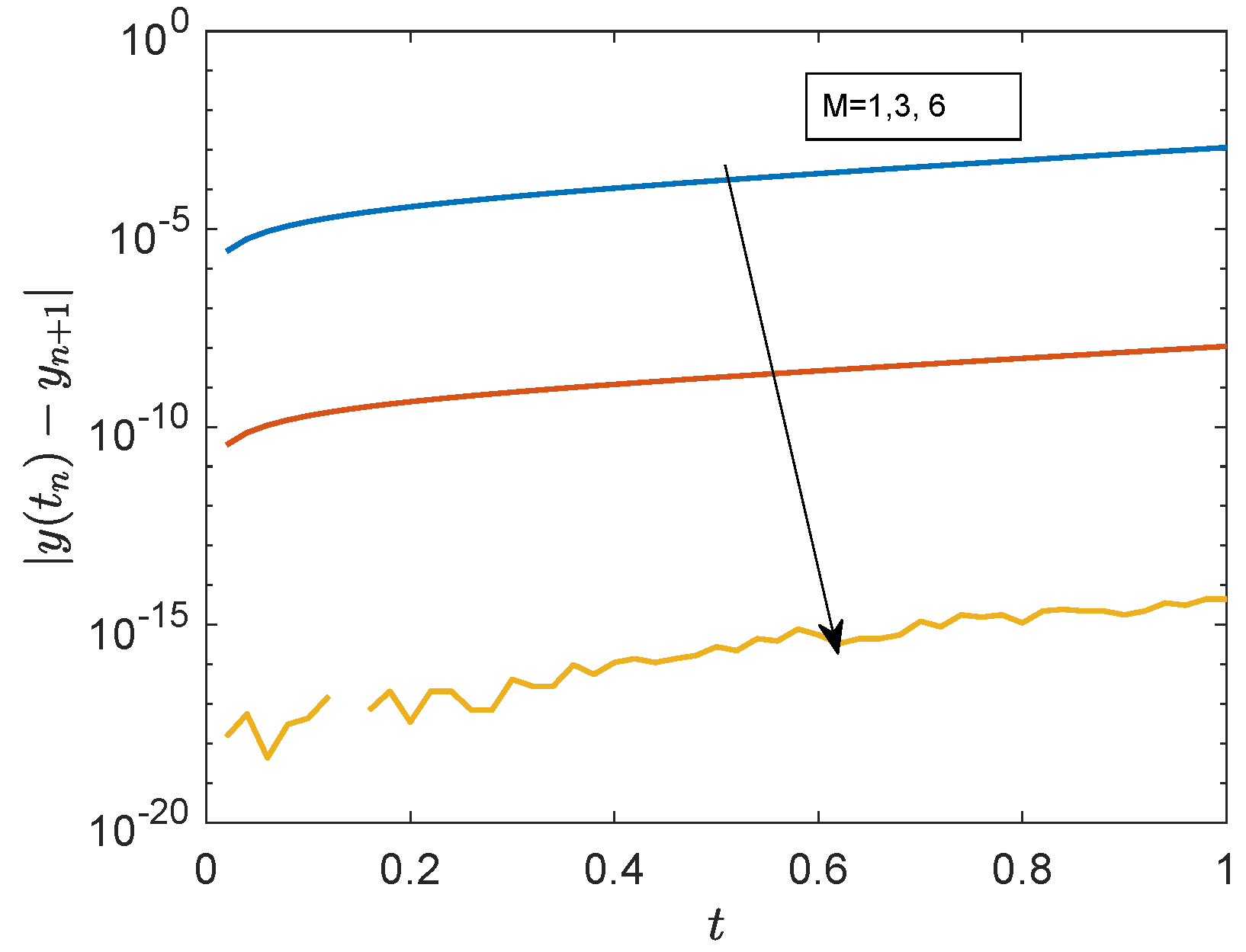
3.1.1. Linear Example 1
3.1.2. Linear Example 2
3.1.3. Linear Example 3
3.1.4. Linear Example 4
3.2. Numerical Nonlinear First Order Differential Equations
3.2.1. Nonlinear Example 1 (Riccati Equation)
3.2.2. Nonlinear Example 2
3.3. Nonlinear Systems of First Order Equations
3.3.1. Nonlinear Systems, Example 1
3.3.2. Nonlinear Systems, Example 2
3.3.3. Nonlinear Systems Example 3
3.3.4. Nonlinear Systems Example 4
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shampine, L.F.; Watts, H.A. Block Implicit One-Step Methods. Math. Comput. 1969, 23, 731–740. [Google Scholar] [CrossRef]
- Brugnano, L.; Trigiante, D. Solving Differential Problems by Multistep Initial and Boundary Value Methods; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Ramos, H.; Kalogiratou, Z.; Monovasilis, T.H.; Simos, T.E. An optimized two-step hybrid block method for solving general second order initial-value problems. Numer. Algorithms 2016, 72, 1089–1102. [Google Scholar] [CrossRef]
- Yap, L.K.; Ismail, F.; Senu, N. An Accurate Block Hybrid Collocation Method for Third Order Ordinary Differential Equations. J. Appl. Math. 2014, 2014, 549597. [Google Scholar] [CrossRef]
- Yap, L.K.; Ismail, F. Block Hybrid Collocation Method with Application to Fourth Order Differential Equations. Math. Probl. Eng. 2015, 2015, 561489. [Google Scholar] [CrossRef]
- Awari, Y.S. Some generalized two-step block hybrid Numerov method for solving general second order ordinary differential equations without predictors. Sci. World J. 2015, 12, 12–18. [Google Scholar]
- Albarbi, A.R.; Almatrafi, M.B. Exact and Numerical SolitaryWave Structures to the Variant Boussinesq System. Symmetry 2020, 12, 1473. [Google Scholar] [CrossRef]
- Xia, S. Existence of a weak solution to a generalized Riemanntype hydrodynamical equation. In Applicable Analysis; Taylor & Francis: Abingdon, UK, 2022. [Google Scholar] [CrossRef]
- Albarbi, A.R.; Almatrafi, M.B. Exact solitary wave and numerical solutions for geophysical KdV equation. J. King Saud Univ. Sci. 2022, 34, 102087. [Google Scholar] [CrossRef]
- Ononogbo, C.B.; Airemen, I.E.; Ezurike, U.J. Numerical Algorithm for One and Two-Step Hybrid Block Methods for the Solution of First Order Initial Value Problems in Ordinary Differential Equations. Appl. Eng. 2022, 6, 13–23. [Google Scholar] [CrossRef]
- Gear, C.N. Hybrid methods for initial value problems in Ordinary Differential Equations. SIAM J. Numer. Anal. 1964, 2, 69–86. [Google Scholar] [CrossRef]
- Motsa, S.S. Block hybrid methods. In Proceedings of the 13th Annual Workshop on Computational Mathematics and Modelling, University of KwaZulu-Natal, Pietermaritzburg Campus, Durban, South Africa, 5–9 July 1964. [Google Scholar]
- Yakubu, D.G.; Shokri, A.; Kumleng, G.M.; Marian, D. Second Derivative Block Hybrid Methods for the Numerical Integration of Differential Systems. Fractal Fract. 2022, 6, 386. [Google Scholar] [CrossRef]
- Ramos, H.; Rufai, M.A. A two-step hybrid block method with fourth derivatives for solving third-order boundary value problems. J. Comput. Appl. Math. 2022, 404, 113419. [Google Scholar] [CrossRef]
- Motsa, S. Overlapping Grid-Based Optimized Single-Step Hybrid Block Method for Solving First-Order Initial Value Problems. Algorithms 2022, 15, 427. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, J.D. Numerical Analysis, 9th ed.; Brooks/Cole, Cengage Learning: San Francisco, CA, USA, 2011; pp. 302–314. [Google Scholar]
- Motsa, S.S. Hybrid block methods for IVPs using Mathematica. In Proceedings of the 14th Annual Workshop on Computational Mathematics and Modelling, University of KwaZulu-Natal, Pietermaritzburg Campus, Durban, South Africa, 4–8 July 2022. [Google Scholar]
- Bellman, R.E.; Kalaba, R.E. Quasilinearization and Nonlinear Boundary-Value Problems; Elsevier: New York, NY, USA, 1965. [Google Scholar]
- Fang, H.P.; Hao, B.L. Symbolic dynamics of the Lorenz equations. Chaos Solitons Fractals 1966, 7, 217–246. [Google Scholar] [CrossRef]
- Hao, B.; Liu, J.; Zheng, W. Symbolic dynamics analysis of the Lorenz equations. Phys. Rev. 1998, 57, 5378. [Google Scholar] [CrossRef]
- Garashchuk, I.R.; Kudryashov, N.A.; Sinelshchikov, D.I. On the analytical properties and some exact solutions of the Glukhovsky-Dolzhansky system. J. Phys. Conf. Ser. 2017, 788, 012013. [Google Scholar] [CrossRef]
- Brogliato, B.; Lozano, R.; Maschke, B.; Egeland, O. Dissipative Systems Analysis and Control, 2nd ed.; Theory and Applications; Springer: London, UK, 2007. [Google Scholar]





















































| t | Exact Solution | BHM-Errors | RK4-Errors |
|---|---|---|---|
| 0 | 0.5 | 0 | 0 |
| 0.2 | 0.829298620919917 | ||
| 0.4 | 1.214087651179369 | ||
| 0.6 | 1.648940599804753 | ||
| 0.8 | 2.127229535753778 | ||
| 1.0 | 2.640859085770495 | ||
| 1.2 | 3.179941538631752 | ||
| 1.4 | 3.732400016577701 | ||
| 1.6 | 4.283483787802496 | ||
| 1.8 | 4.815176267793600 | ||
| 2.0 | 5.305471950534773 |
| Exact | BHM | Error | Adams Order Predictor-Corrector Method | Error (Burden and Faires [16]) | |
|---|---|---|---|---|---|
| 0.0 | 0.5000000 | 0.5000000 | 0 | 0.5000000 | 0 |
| 0.2 | 0.8292986 | 0.8292986 | 0 | 0.8292933 | 0.0000053 |
| 0.4 | 1.2140877 | 1.2140877 | 0 | 1.21407762 | 0.0000114 |
| 0.6 | 1.6489406 | 1.6489406 | 0 | 1.6489220 | 0.0000186 |
| 0.8 | 2.1272295 | 2.1272295 | 0 | 2.1272056 | 0.0000239 |
| 1.0 | 2.6408591 | 2.6408591 | 0 | 2.6408286 | 0.0000305 |
| 1.2 | 3.1799415 | 3.1799415 | 0 | 3.1799026 | 0.0000389 |
| 1.4 | 3.7324000 | 3.7324000 | 0 | 3.7323505 | 0.0000495 |
| 1.6 | 4.2834838 | 4.2834838 | 0 | 4.2834208 | 0.0000630 |
| 1.8 | 4.8151763 | 4.8151763 | 0 | 4.8150964 | 0.0000799 |
| 2.0 | 5.3054720 | 5.3054720 | 0 | 5.3053707 | 0.0001013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shateyi, S. On the Application of the Block Hybrid Methods to Solve Linear and Non-Linear First Order Differential Equations. Axioms 2023, 12, 189. https://doi.org/10.3390/axioms12020189
Shateyi S. On the Application of the Block Hybrid Methods to Solve Linear and Non-Linear First Order Differential Equations. Axioms. 2023; 12(2):189. https://doi.org/10.3390/axioms12020189
Chicago/Turabian StyleShateyi, Stanford. 2023. "On the Application of the Block Hybrid Methods to Solve Linear and Non-Linear First Order Differential Equations" Axioms 12, no. 2: 189. https://doi.org/10.3390/axioms12020189





