1. Introduction
Organisations such as the OECD and the World Bank classify a geographic area based on some characteristics such as the population size, population density, and movement of inhabitants from area to area. The OECD classifies an area as rural if it consists mostly of low-density grid cells (two inhabitants per km
) [
1]. Unfortunately, the inhabitants of rural areas have the lowest access to the Internet, as well as the lowest access to bank services, independent of the country’s income level (see [
2]). In addition, evidence suggests that the more people are connected to the internet, the greater the benefits to society. Broadband Internet has proven over the years to generate significant social and economic benefits in developing areas and to improve the educational, financial, and health systems [
3], e.g., the unemployment rate is lower by 0.26 percent in countries with high-speed connections [
4], and the economy grows about 1.5 percent when the telecommunication penetration is increased by 1.38 percent [
5] in low- and middle-income economies.
In rural areas where the Internet network has been deployed, the impact reaches all the activities of farm and non-farming small businesses including personal activities such as health, basic communication, and education [
6,
7].
One of the main activities in rural areas is related to agriculture. Broadband Internet has mitigated the risk associated with it by delivering useful information about crop care, fertilisers, etc. Thus, the productivity in those areas impacts the whole of society. Another remarkable example is the reduction of poverty by 2% in Kenya by implementing the mobile money strategy [
8]. Moreover, some studies have shown that, in rural areas where Internet networks have been deployed, they have experienced larger levels of growth in employment, in the number of businesses, and in IT-intensive sector business, i.e., economic growth for people living in these areas [
9].
Even though there is evidence of social and economic benefits, there are technical and non-technical issues that make it difficult to deploy optic fibre in rural communities. In relation to the non-technical issues, the demand volume and cost of the infrastructure are key issues that policy-makers take into account.
The problem in urban areas has been studied extensively. In [
10], a robust model was proposed to optimise a Fibre-To-The-x (FTTx) architecture using wired and wireless technology. The network topology included central offices, Steiner nodes, facilities, and final users. The authors modelled the design problem as a Mixed-Integer Linear Programming Model (MILPM) with a cost objective function; for large instances, the authors relaxed the MILPM and found the binary solution by means of a metaheuristic-based algorithm. The authors tested their model using a 450-pixel area of the metropolitan area of Rome (Italy). A network based on optical fibre and cooper with Free Space Optical communication (FSO) was modelled as an MILPM. The first part of their solution algorithm minimised the cost of connecting a user; then, the capacity solution was tested for feasibility. To test the model, the authors solved a 100-location instance in the City of Milano [
11].
In [
12], a theoretical FFTx network was solved to minimise the costs, such as site survey and devices’ installation/extraction. Another approach based on cost optimisation was presented in [
13]. The FTTx network was designed by interactively solving problems such as connectivity and the central office problem, signal splitting problems, node installation problems, and cable and duct installation problems. The authors based their approach on two very well-known problems in combinatorial optimisation: the Steiner tree and the capacitated facility location. Another example of designing an FFTx network was reported in [
14]. In this case, the authors minimised the capital expenditure associated with implementing an FTTHome optical access network. A detailed study of the effect of governmental regulation in a next-generation network on the final customer was presented in [
15]. The study, specifically in Spain, clearly stated that the cabling cost could be up to 22% of the deployment cost in buildings.
The above approaches were applied to an urban area. In our case, we propose to connect communities in rural areas. Moreover, we used a Geographic Information System (GIS) to model the network and compute a driving distance matrix.
As in urban areas [
10,
12,
13,
14,
15], one important element of the infrastructure cost in rural areas is the civil construction work, which includes trench excavation, pipe installation, warning tape installation, and backfilling (see [
16] for a detailed description). Therefore, the longer the optic fibre network, the higher the infrastructure and optic fibre costs. Thus, the network topology is a paramount design characteristic not only in the costing methodology, but also in the performance of the network [
17,
18].
In the combinatorial optimisation literature, the problem of finding the network topology that connects all the nodes (in our case, rural communities) with the minimum length (in our case, the minimum length of the optic fibre) is the spanning tree problem [
19]. Some related works included the network design in a rural area in Turkey and Nigeria, as well as the redesign of a copper-based network [
20,
21].
The proposed approach assumes that the only technology to provide Internet service is optical fibre, which is deployed alongside paths, roads, and highways.
Although satellite Internet is an alternative solution to provide Internet service in rural communities because of its speed, the independence of the cable, quick installation, and security, the solution is neither reliable nor affordable because of the dependency on weather conditions, the price of fast service, specialised installation, and transfer delay. [
22]. Therefore, to have a tangible impact on rural communities, it is necessary to deploy optic fibre to manage users’ high demand for downloading and uploading data.
On the other hand, aerial and underground deployments are two strategies for setting up optical fibre cables. The aerial strategy depends on installing utility poles as the ones used to deploy electrical cable, and in the underground strategy, the optical fibre is directly buried or passes through a duct in a trench [
23]. Independent of which strategy is used, the utility poles or the trench are placed alongside the actual highways and road due to the cost savings from co-deployment, compared to a separate deployment; see [
16,
24]. The work in [
24] used the actual roads to compute the distance to compute the topology of the broadband network access to end-customers, known as passive optical networks.
In our work, we used the actual highways and roads because this is a common practice in companies that deploy optic fibre because of the savings; see [
24]. Moreover, we computed the shortest distance among all the communities using OpenStreetMap based on the actual roads.
The work in [
20] computed real distances from the ArcGIS roadmap, while the Euclidean distances (not real ones) were used in [
21]. In both cases, the solved instances were small: 74 nodes in the first case and 88 in the second one. One issue in the previous works is that they built a spanning tree to connect all possible nodes (communities) for small instances; even though, if the deployment company cannot connect all the communities at once (i.e., it cannot invest all the required monetary resources to build the infrastructure or buy the optic fibre), they did not provide to the decision-maker a plan that states which community to connect first, and so on, i.e., a plan to prioritise the communities.
Our application provides to the policy-maker not only the minimum spanning tree to connect all the rural communities, but also a list of communities in the order in which they should be connected based on one of the three proposed criteria. Besides, our application [
25] computes the shortest driving distances given two coordinate points (similar to [
21]) and solves instances with up to 600 communities in a reasonable CPU time.
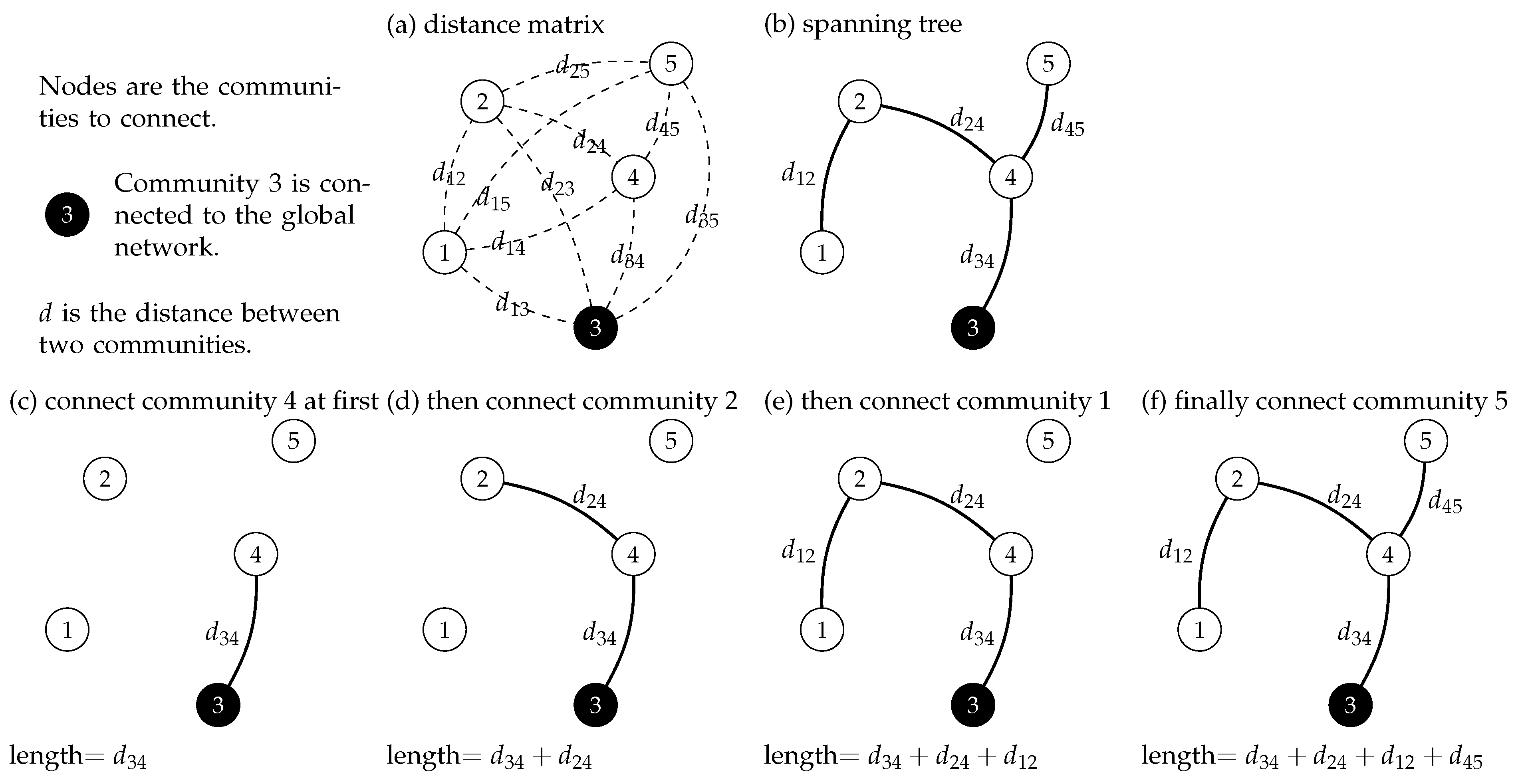
Figure 1 graphically shows the problem to solve with our application. First, the shortest distance among all the communities is computed using the GIS system OpenStreetMap; then, the spanning tree is computed by selecting the edges that minimise the network’s total length, as in
Figure 1b. After the spanning tree is computed, the decision-maker has to decide in which order the communities should be connected to the global network. In our example, Community 3 is already connected; thus, the network will be extended using that community first. The first community to connect is 4, which adds
kilometres to the total length of the network, as in
Figure 1c. In
Figure 1d, the network could be extended to Community 2 or 5 according to
Figure 1b; using a criterion (see
Section 2.2), Community 2 was selected. In
Figure 1e, Communities 1 and 5 could be connected, and the decision-maker selects one of them. Finally, Community 5 is joined to the network in
Figure 1f, and the network’s total length is the sum of the individual distances in
Figure 1c–f.
To connect a community to the network, decision-makers can use three criteria: connect the nearest community, the most-populated community, or the community that increases the ratio between the connected population and the length of the network; see a detailed description in
Section 2.2.
To test our application, we selected a rural area in southern Mexico that belongs to the State of Morelos, whose main production activity is agriculture and tourism. It contributes 1.1% to the total GDP of Mexico. The Mexican Government amended the constitution to introduce individual rights to all Mexicans to have access to communication and information technologies, as well as broadcasting and telecommunication services, including broadband and Internet access [
26].
Even with the amendment of the Mexican constitution, access to those services for all Mexicans has not been improved since 2013. Approximately 7% of the population that did not have Internet access back then do not have it now. This population lives in very small towns in Mexico, where the economic activity is so weak that private businesses and government cannot find the means to get them connected. We have been studying such communities and evaluating innovative alternatives to justify the costly infrastructure deployment that is required.
The aim of this work was to design an algorithm that not only computes the minimum length of optic fibre to connect a number of rural communities, but also returns a plan to prioritise the communities, i.e., the order in which the communities must be connected (unlike the related works in [
20,
21]). Moreover, the developed free computational application downloads a graph of the considered geographic area from OpenStreetMap to compute the real distances among the communities. Those real distances are based on the actual highways and paths inside the area under study, one assumption in our work is that the optic fibre is placed along them.
Our application finds the shortest distance among all the communities to build the driving distance matrix in which the application finds the minimum spanning tree (i.e., optic fibre topology). The minimum spanning tree guarantees the minimum length of the network. Nevertheless, one limitation is the risk of service interruption because, if one link (that connects two communities) fails, some part of the network will lose connection.
The decision-maker inputs the first connected community from which the ordered list is built. The application identifies the communities that are linked to the already-connected communities by an edge that belongs to the spanning tree. To select one community, the decision-maker selects one of the three criteria proposed in this work: the community that (i) is the nearest, (ii) is the most-populated, or (iii) increases the ratio of the connected population to the length of the optic fibre. Another objective is to create maps to represent graphically how the optic fibre network grows according to the ordered list. The reader can download the application to reproduce the results of this work and other worldwide geographic areas from [
25].
This work is organised as follows. In
Section 2, we describe the whole algorithm that is run in our computer application. In
Section 3, the algorithm is run to solve a rural geographic area in southern Mexico with 597 communities; some graphs are shown about the covered population against the number of communities, the length of the optic fibre network, and the connected people per kilometre of optic fibre. In
Section 4, we describe the significance of our application and results, and some conclusions are stated in
Section 5. The ordered list of the 150 communities is provided as an example in
Appendix A.
2. Materials and Methods
The area under study was modelled as a graph , where is the set of vertices that represent the communities and is the set of edges (or roads) that link community i and community j. We assumed that the graph G is fully connected; thus, there is a subset of edges that connect any two communities. The distance between community i and community j is , and all the distances to any two communities are stored in the matrix . Notice that .
To compute
, we assumed that the optical fibre can be deployed along driving routes between two communities, i.e., the optical fibre network is built over the road network as in [
23,
27].
To compute the minimum distance between two communities, our application downloads geodata maintained by the open collaborative project OpenStreetMap (OSM). From OSM, our application builds the road network
(as shown in
Figure 2a) by defining a geographic area within coordinate points
and
.
Every community
i has associated a geographic coordinate
defined by its latitude
and longitude
, i.e.,
. To find the driving or road distance
among two communities, their geographic points
and
are located on
, then we computed the driving shortest path using Dijkstra’s shortest path algorithm; see [
28,
29,
30].
2.1. Building the Optical Fibre Network
The problem of connecting some communities with optical fibre was modelled as the optimisation problem, called the minimum spanning tree [
19,
31]. Formally, a spanning tree, referred to as
, is a sub-graph of
G that satisfies two conditions: (i) all the vertices are connected with
edges, and (ii) cycles (loops) are not allowed as a consequence of the first condition.
There are many formulations of the problem; for simplicity, we followed the cycle elimination formulation proposed in [
32]. Therefore, the binary decision variable is defined as follows:
In other words, if two communities are connected with optical fibre, the variable . The cycle elimination formulation is presented as follows:
Equation (2a) is the objective function that minimises the length of the optical fibre network; thus, if communities
i and
j are connected, the distance
is added to the total length. Equation (2b) ensures that the spanning tree has exactly
edges to satisfy the first condition. In relation to Condition (ii), Equation (2c) guarantees that
T has no cycles by creating subsets
with
edges; the fact that each subset has exactly
edges guarantees that there are no cycles. Finally, the constraint in Equation (2d) guarantees that all the variables are binary, as defined by Equation (
1).
In this formulation, all the possible subsets must be built to ensure that all of them have exactly
edges, as stated in Equation (2c).
In the literature, there are methods proposed to solve the problem optimally, e.g., column and row generation [
33], Bender decomposition [
34], and the classical Kruskal and Prim algorithm [
35,
36]. According to the size of the instances solved in the rural communities in our test case, we decided to implement in our application the Kruskal algorithm for its easiness and low CPU time to compute the solution.
Algorithm 1 returns the minimal distance to connect all the communities, i.e., it returns the optimum value of Equation (2a) and the set of edges of the minimum spanning tree
T.
| Algorithm 1: Kruskal’s algorithm. |
![Axioms 12 00269 i001]() |
2.2. Order in Which Communities Should Be Connected
Using Algorithm 1 in
Section 2.1, the spanning tree, which represents the fibre network with the minimum length, is computed; thus, the model in Equation (2) is solved. Mathematically, the spanning tree is
, so the edges
of that fibre network that minimise the length are in
.
At this point, the decision-maker knows the topology and the length of the network, but she/he does not know in which order to connect the communities. Our application returns a set of ordered communities such as .
Usually, when a company has to deploy optical fibre to connect rural communities, the company knows two facts: (a) there is a community that has already been connected to a larger optic fibre network, and (b) it cannot connect all the rural communities at once because of the amount of the investment. Usually, the regulator gives a period of time for the company to connect all the communities.
The first fact is known by a regulator or federal agency; thus, it is a known fact. The second one is more complicated to deal with, given that the company has to decide how to extend the optimal fibre from the already connected community with the available investment. To decide which community to connect next, we propose three criteria to decide which community to link to the optical fibre as follows.
2.2.1. Connect the Nearest Community
If
k is an already-connected community, then the community
j that must be linked is the nearest to
k. The objective is to connect the community with the minimum distance
, as shown in Equation (
3).
In this case, the company will require small stretches of fibre to expand the network. Notice that the edges that belong to the spanning tree are the only ones taken into account. Therefore, we ensured that the objective of minimising the optical fibre was met.
2.2.2. Connect the Most-Populated Community
The objective of this criterion is to connect as many people as possible by selecting the most-populated community
j given that there is an edge
in the spanning tree (
k is an already-connected community). Therefore,
is the number of individuals in community
j; see Equation (
4).
2.2.3. Connect the Community That Increases Population/Network Length
This criterion aims to connect as many people as possible while the length of the network does not increase. The communities that have been connected are stored in O; thus, the connected population is the sum of the people in the communities in O, and the length of the network is the length of the links that are in the spanning tree given that the two communities that form a link are already connected; i.e., the two communities are in .
The ratio of the so-far connected communities is the cumulative population divided by the length of the network of the communities in O.
Therefore, the community to connect is selected according to Equation (
5), where
k are the already-linked communities.
2.3. Proposed Fibre Optic Deployment Algorithm
The proposed solution approach is depicted in Algorithm 2. It encompasses three parts: (a) download data from the OSM GIS system, and compute the shortest driving distance among all the communities (Lines 1 to 8); (b) compute the spanning tree that represents the fibre optic network and its minimum length (Lines 9 to 11 and Algorithm 1); (c) determine the order in which the communities should be joined to the fibre optic network; we propose three criteria for this (Lines 12 to 21).
The result of Algorithm 2 is a list of ordered rural communities to connect based on a given criterion according to
Section 2.2.
In the first part, Algorithm 2 downloads the road network from OpenStreetMap between the two coordinate points and , which define the area under study. The road network is stored in the matrix . The geographic coordinates for every community i are known, and our application locates every in the downloaded area under study.
After that, the shortest distance among all communities i and j is computed using Dijkstra’s algorithm implemented in OpenStreetMap (Lines 2 to 7). Those shortest driving distances are stored in the matrix (Line 8).
The next step in Algorithm 2 is to compute the spanning tree, which represents the optic fibre network that returns its minimum length. In Line 9, the set of vertices
V (i.e., communities) and the set of edges
E (i.e., the driving roads that connect communities with each other) are defined.
| Algorithm 2: Fibre optic deployment. |
![Axioms 12 00269 i002]() |
In Line 10, Algorithm 1 is run to solve the model in Equation (2); thus, the spanning tree
is computed. From the set of edges
E in the road network, the model returns the subset of edges
that links all the communities (see
Figure 1) with the minimum length of the fibre optic network (Line 11). Note that
.
Once the topology of the fibre optic network is computed, the next step is to define the order in which communities should be connected (Lines 12 to 21). At this point, our application knows how all the communities must be connected to minimise the network length (see
Figure 1b), but the order in which communities must be connected is unknown.
To know the order, the algorithm identifies the first connected community
k; thus,
(Lines 12 and 13). Then, the decision-maker has to select one of the three proposed criteria to link communities to the optic fibre network, as described in
Section 2.2 (Line 14). Basically, she/he has to decide if the priority is not to increase the length of the network (Equation (
3)) so fast given the investment in optic fibre, or if the priority is to connect the maximum amount of people (Equation (
4)) because the regulator states it, or if the priority is to connect the maximum number of people, but keep the length of the network as short as possible (Equation (
5)).
Once the criterion is selected, the algorithm finds all the communities k already connected (Line 15) in the ordered set O. In Line 16, the equation of the selected criterion is computed for all the , and subsequently, one is selected according to it; the selected one is stored in O (Line 17). If all the communities have been linked (Line 18), then the algorithm stops (Line 19); otherwise (Line 21), the application selects all the connected communities and selects one to add to O.
3. Results
Algorithm 2 was tested using an open database of geographic and demographic data of Mexico, retrieved from [
37]. It is maintained by The National Institute of Statistics and Geography (INEGI by its Spanish abbreviation), which collects and disseminates information about Mexico in terms of territory, resources, population, and economy. The test was carried out using a MacBook Pro (2.8 GHz Quad-Core Intel Core i7 and 16 GB of RAM Memory) and Python 3.6.6 (Spyder 4.0.1).
The area under study was within the coordinates
,
(see
Figure 2). They correspond to Mexico’s southern region, specifically the State of Morelos. There are 597 communities with a population of 454,514. In a typical rural area in Mexico, the population is distributed as shown in
Figure 3, i.e., many people live in a small number of communities. In this test case, 9% of the communities hold 80% of the population, i.e., there are 363,611 people in 50 out of 597 communities.
There are 431,890 (95%) people in 162 communities. The most-populated community is called “Emiliano Zapata” with 49,193 inhabitants, and we considered communities with 1 person given that 597 communities can be handled in a reasonable CPU time by our application.
Once the distance matrix is computed, Algorithm 1 returns the minimum spanning tree, as shown in
Figure 4d. The length of the optical fibre is about 949.09 km to connect the 597 communities (Line 10 of Algorithm 2). This is the minimum length of the optical fibre since Algorithm 1 outputs the optimal solution, i.e., the minimum length of the optical fibre.
According to the spanning tree
T, a company must decide how to build the optical fibre network, given that it cannot link the
T in a single period of time. As time passes, the company links the communities until all are connected, as in
Figure 4d.
Recall that a deployment company needs to know how to grow the network, given that one community is already linked to a global optical fibre network. To show a deployment plan, it is supposed that the community called “Puente de Ixtla” is the initial connected one. Its location is at coordinate , and it is the third-most-populated community with 21,098 inhabitants (Algorithm 2—Line 11).
The next-to-link communities are connected according to one of the criteria described in
Section 2.2 given that the community is linked to another one by an edge in the spanning tree. Thus, the only possible connections are the ones in the spanning tree to guarantee that the length of the optic fibre network is the shortest. This is the last part of Algorithm 2 (Lines 13–24); the output is the list
O of the communities that must be connected (see
Appendix A).
Figure 5 shows the relation between the cumulative covered population and the number of linked communities according to the ordered list
O. For example, if a decision-maker wants to cover 90% of the population (about 408,777 people), then she/he has to connect 450 communities assuming that the criterion to add them is
(i.e., add the community that increases the ratio of the covered population/length of the network), see
Figure 6. However, if the decision-maker wants to connect 500 communities and to cover 90% of the population, then the best criterion to add communities to the optic fibre network is
(i.e., connect the most-populated community). As shown in
Figure 5, the number of connected communities is similar for the three criteria.
Figure 7 shows the results if the decision-maker measures the ratio (
) of the cumulative covered people to km of fibre. The highest value of the ratio is
connected people per km of optical fibre. if the decision-maker wants to connect 90% of the population, the value of the ratio is
covered people per km of optic fibre. Using
,
, and with
,
. If the 454,514 people are covered with the total network length 949.09 km, then
covered people per km of optic fibre.
Table 1 shows a summary of the results for different percentages of the covered population according to the three criteria. For example, if the decision-maker wants to connect only 90% of the population and if the criterion to connect communities is the nearest community
to the one that is already connected, then 475 communities will be connected, the length of the network will be 615.9.1 km, and 651.5 people will be covered per km of optic fibre.
On the other hand, if the decision-maker knows that she/he will connect 90% of the population and she/he wants to minimise the length of the network, then the communities must be connected using the criterion.
Finally,
Figure 4 shows how the optic fibre network expands among the communities if the
criterion is used and the initial community is the one called “Puente de Ixtla”.
4. Discussion
Although practitioners and researchers have developed many approaches to connect people in urban areas (see [
10,
12,
13,
14]), there are only some about connecting rural communities, such as [
20,
21].
Rural communities have the lowest access to the Internet; thus, the benefits of the Internet in society are very limited in those communities. Nonetheless, where Internet access is available, evidence [
9,
38] suggests that rural communities experience economic growth. Despite this, decision-makers find technical and non-technical issues in extending the fibre optic network to those areas, one of the most-important issues being the cost of infrastructure and optic fibre. Thus, our work contributes to the cost reduction not only by minimising the length of the optic fibre network, but also by prioritising the communities to know the order in which the decision-maker should connect them to the network, given that she/he cannot make the entire investment. The decision-maker defines a criterion to order the communities.
To this end, the application computes the shortest driving distances among the communities by downloading the actual paths and highways inside the communities in the rural area. Then, using Dijkstra’s algorithm, all the shortest distances among the communities are computed to find the minimum spanning tree, i.e., the minimum length of the network. To build it, the application uses Kruskal’s algorithm, given that it can handle hundreds of vertices (communities). Therefore, there is no need to use another algorithm based on optimum and approximation algorithms. Unlike other approaches that only build the whole optic fibre network from unreal distances, the proposed algorithm builds the real distance of the optic fibre network and the deployment plan, which states the order in which communities must be linked, given a criterion defined by the policy-maker. Another novelty of our work is that the policy-maker chooses the criterion to build the ordered list of communities, given that one objective is to maximise the number (or percentage) of covered people. Therefore, the application shows results about how the number of communities, the length of the network, and the ratio of the covered people to the kilometres of optic fibre change as the number of covered people increases.
Different from other approaches dealing with rural communities such as [
21,
23], the optic fibre network can be deployed gradually by prioritising the communities given a criterion defined by the policy-maker. Moreover, the application returns the minimum length of the optic fibre due to the algorithms used. One of them is Kruskal’s algorithm, given that the distances between two communities are the same, i.e.,
. Using this assumption, Kruskal’s algorithm performs in polynomial time [
35] without the need to use its mathematical formulation or other solution methods [
32].
On the other hand, to the best of our knowledge, there are no attempts to provide a sorted communities list that states the order in which communities must be connected to the optic fibre network given the assumption, not taking into account in this work that the deployment company has all the monetary resources to build the network as a plot by the solution algorithms; see [
6,
7,
16,
18,
39,
40].
Another important result is the map visualisation to show how the optic fibre network grows, as shown in
Figure 4. The reader can plot any number of communities using the proposed application. In
Figure 4, 150, 300, 450, and 597 communities are plotted. These plots are an important result for the policy-maker because she/he can plan the resources and deploy them in the right location and at the right time.
As stated above, the proposed algorithm has a reasonable CPU time for hundreds of communities to connect. Even though, if an instance (i.e., rural area) has thousands of communities, then another algorithm to compute the spanning tree could be implemented, e.g., the branch-and-bound exact algorithm [
34]. In relation to the driving distance, if other more detailed map systems are used, the distances could change because our application could find the shortest path among communities using the same Dijkstra algorithm.
Therefore, future research could be to implement other algorithms to compute the spanning tree and use other map systems to run the whole algorithm. Moreover, in this work, other technologies were not considered. An extension of the proposed algorithm could be to use satellite or other means to connect rural communities.
For the instance solved in
Section 3, our algorithm generated the graphs of the ordered list using the three criteria. The decision-maker can select the desired criterion and select the order in which communities must be connected.
5. Conclusions
Rural communities have the lowest access to the Internet independent of the country’s income. Policymakers cope with the infrastructure and optic fibre costs to cover people in those communities; thus, to minimise those costs, the optic fibre network can be as short as possible. The proposed algorithm not only minimises the network length (as the reported approaches in the literature), but also sorts the communities given an initial connected one to define the order in which communities must be linked to the optic fibre network. Moreover, the policy-maker defines the criterion to sort (prioritise) the communities. These criteria connect the most-populated community, the nearest community, or the highest ratio of the covered population to the kilometres of optic fibre.
To this end, we proposed an algorithm based on OpenStreetMap to compute the shortest driving distance, the minimum length of the optic fibre network, and the ordered list of communities. The policy-maker can use this result as a planning tool because she/he knows in advance which community will be connected; thus, the necessary monetary resources are required to connect a given number of communities.
Our proposed approach relies on the OpenStreetMap GIS system, which is open-source and free. Although the system is quite reliable and accurate, the decision-maker could implement other non-free GIS systems, such as Google Maps, which are more precise, and the length of the optic fibre network could be different.
One paramount characteristic of the spanning tree is that, if a link is broken, the network is split into two separate networks. Therefore, the network in which the already-connected community k belongs is the one with Internet service. The other part of the network must wait until the broken link is repaired. We could consider more than one already-connected community to cope with this problem; thus, the problem could be to assign a community to the nearest already-connected community.
One major issue in solving the spanning tree is the number of communities to be considered. One instance cannot be solved because the area among the two coordinate points and is “big” (so downloading that amount of information is time-consuming) or because it has “many” communities such that Algorithm 1 cannot handle them. To cope with this, all the information in the GIS systems must be downloaded locally (we worked online with Algorithm 2), so instead of downloading the information from online servers, we could access local ones. In this way, our application could solve bigger instances.
Something to take into account is the modelling process of the network. Our application only takes into account the central offices; in future works, the modelled network could include Steiner nodes, facilities, and final users, i.e., to include different types of nodes.