Nonparametric Directional Dependence Estimation and Its Application to Cryptocurrency
Abstract
:1. Introduction
2. Copula and Directional Dependence
3. Nonparametric Directional Dependence and Numerical Study
- (1)
- Choose a measure-preserving function that captures the desired dependence structure.
- (2)
- Choose a parametric family of copulas (the copulas admit densities ).
- (3)
- The resulting copula density function is given as and the corresponding distribution function is given as .
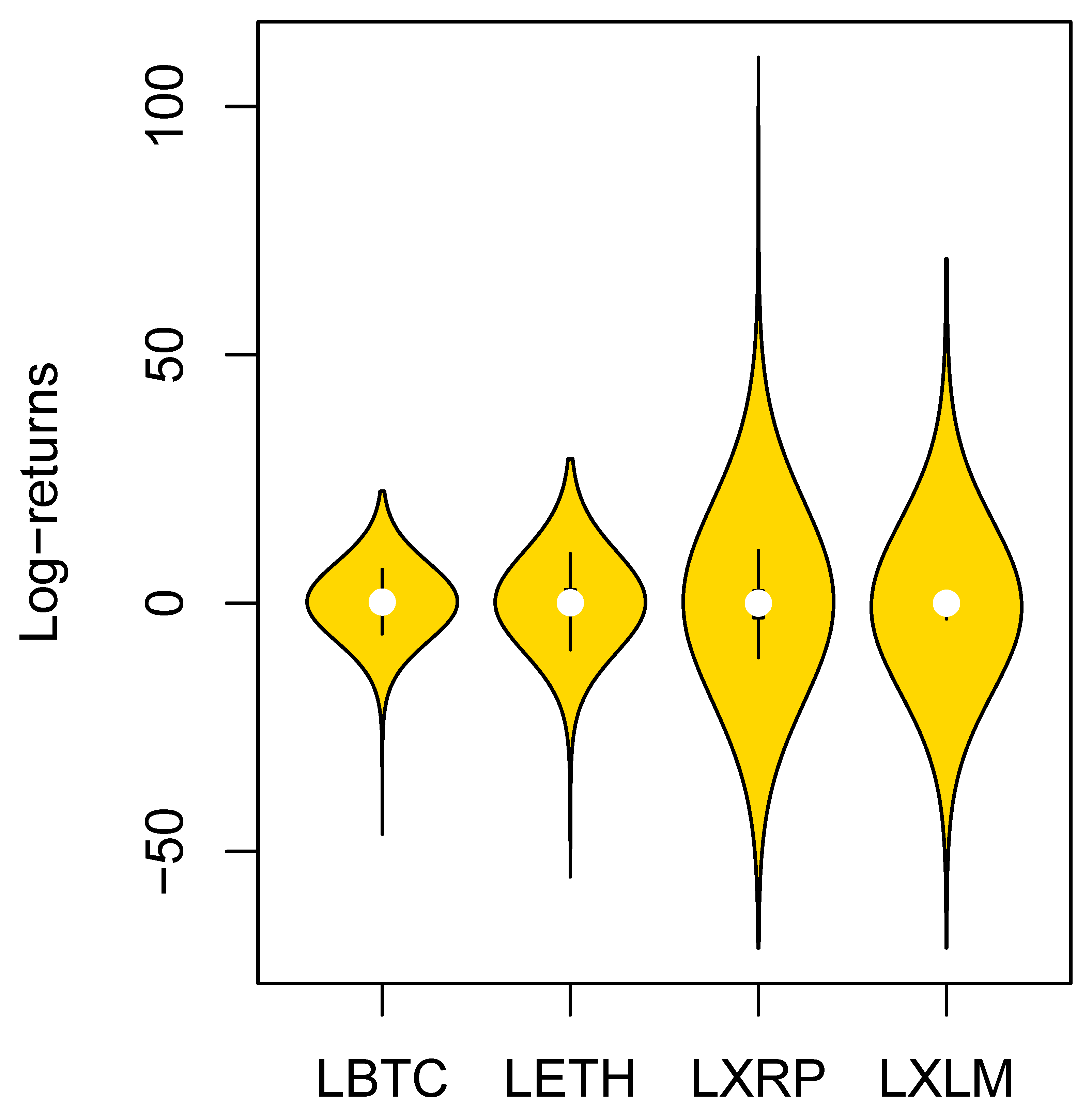
4. Real Data Illustration
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, J.-M.; Kim, S.; Kim, S.T. On the Relationship of Cryptocurrency Price with US Stock and Gold Price using Copula Models. Mathematics 2020, 8, 1859. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de repartition an dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Joe, H. Families of m-variate distributions with given margins and m (m − 1)/2 bivariate dependence parameters. In Distributions with Fixed Marginals and Related Topics; Rüschendorf, L., Schweizer, B., Taylor, M.D., Eds.; Institute of Mathematical Statistics: Washington, DC, USA, 1996; pp. 120–141. [Google Scholar]
- Bedford, T.; Cooke, R.M. Vines—A new graphical model for dependent random variables. Ann. Stat. 2002, 30, 1031–1068. [Google Scholar] [CrossRef]
- Aas, K.; Berg, D. Models for construction of multivariate dependence: A comparison study. Eur. Financ. 2009, 15, 639–659. [Google Scholar] [CrossRef]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef] [Green Version]
- Kurowicka, D.; Cooke, R.M. Distribution—Free continuous bayesian belief nets. In Proceedings of the Fourth International Conference on Mathematical Methods in Reliability Methodology and Practice, Santa Fe, NM, USA, 21–25 June 2004. [Google Scholar]
- Bauer, A.; Czado, C.; Klein, T. Pair-copula constructions for non-Gaussian DAG models. Can. J. Stat. 2012, 40, 86–109. [Google Scholar] [CrossRef] [Green Version]
- Brechmann, E.; Czado, C.; Aas, K. Truncated and simplified regular vines in high dimensions with application to financial data. Can. J. Stat. 2012, 40, 68–85. [Google Scholar] [CrossRef]
- Hobæk Haff, I.; Aas, K.; Frigessi, A. On the simplified pair-copula construction—Simply useful or too simplistic? J. Multivar. Anal. 2010, 101, 1296–1310. [Google Scholar] [CrossRef] [Green Version]
- Panagiotelis, A.; Czado, C.; Joe, H. Pair Copula Constructions for Multivariate Discrete Data. J. Am. Stat. Assoc. 2012, 107, 1063–1072. [Google Scholar] [CrossRef]
- Smith, M.; Min, A.; Almeida, C.; Czado, C. Modelling longitudinal data using a pair-copula decomposition of serial dependence. J. Am. Stat. 2010, 105, 1467–1479. [Google Scholar] [CrossRef]
- Masarotto, G.; Varin, C. Gaussian copula marginal regression. Electron. J. Stat. 2012, 6, 1517–1549. [Google Scholar] [CrossRef]
- Guolo, A.; Varin, C. Beta regression for time series analysis of bounded data, with application to Canada Google flu trends. Ann. Appl. Stat. 2014, 8, 74–88. [Google Scholar] [CrossRef]
- Kim, J.-M.; Hwang, S.Y. Directional dependence via gaussian copula beta regression model with asymmetric garch marginals. Commun. Stat. Simul. Comput. 2017, 46, 7639–7653. [Google Scholar] [CrossRef]
- Kim, J.-M.; Hwang, S.Y. The Copula Directional Dependence by Stochastic Volatility Models. Commun. Stat. Simul. Comput. 2019, 48, 1153–1175. [Google Scholar] [CrossRef]
- Hyun, S.; Lee, J.; Kim, J.M.; Jun, C. What Coins lead in the Cryptocurrency Market? Using Copula and Neural Networks Model. J. Risk Fin. Manag. 2019, 12, 132. [Google Scholar] [CrossRef] [Green Version]
- Sungur, E.A. Some observations on copula regression functions. Commun. Stat. Theory Methods 2005, 34, 1967–1978. [Google Scholar] [CrossRef]
- Doksum, K.; Samarov, A. Nonparametric Estimation of Global Functionals and a Measure of the Explanatory Power of Covariates in Regression. Ann. Stat. 1995, 23, 1443–1473. [Google Scholar] [CrossRef]
- Ferrari, S.; Cribari-Neto, F. Beta regression for modelling rates and proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Fan, J.; Gijbels, I. Local Polynomial Modelling and Its Applications; Chapman & Hall: London, UK, 1996. [Google Scholar]
- Durante, F. Construction of non-exchangeable bivariate distribution functions. Stat. Pap. 2009, 50, 383–391. [Google Scholar] [CrossRef]
- Scarsini, M.; Venetoulias, A. Bivariate distributions with nonmonotone dependence structure. J. Am. Stat. Assoc. 1993, 88, 338–344. [Google Scholar]
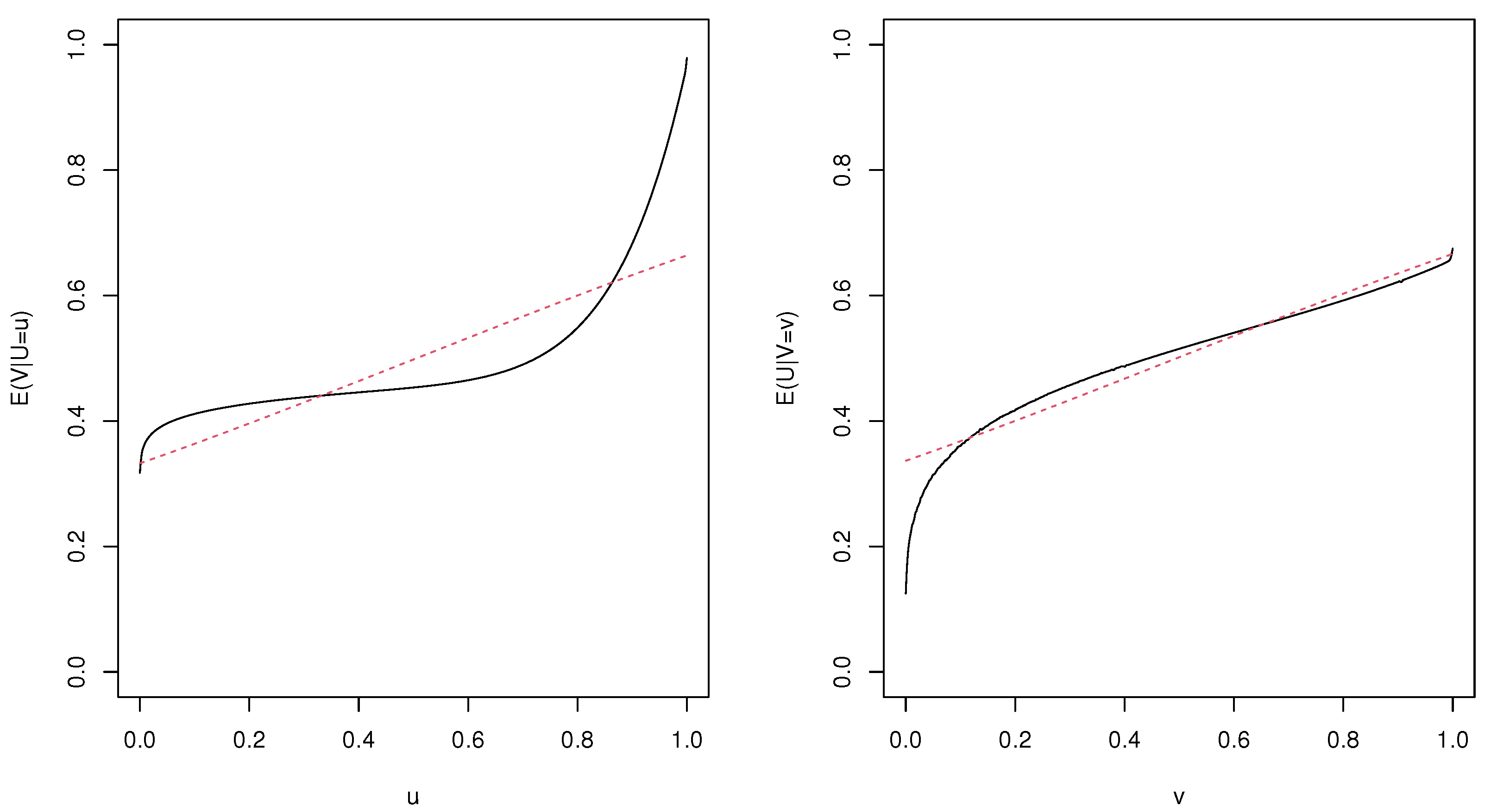
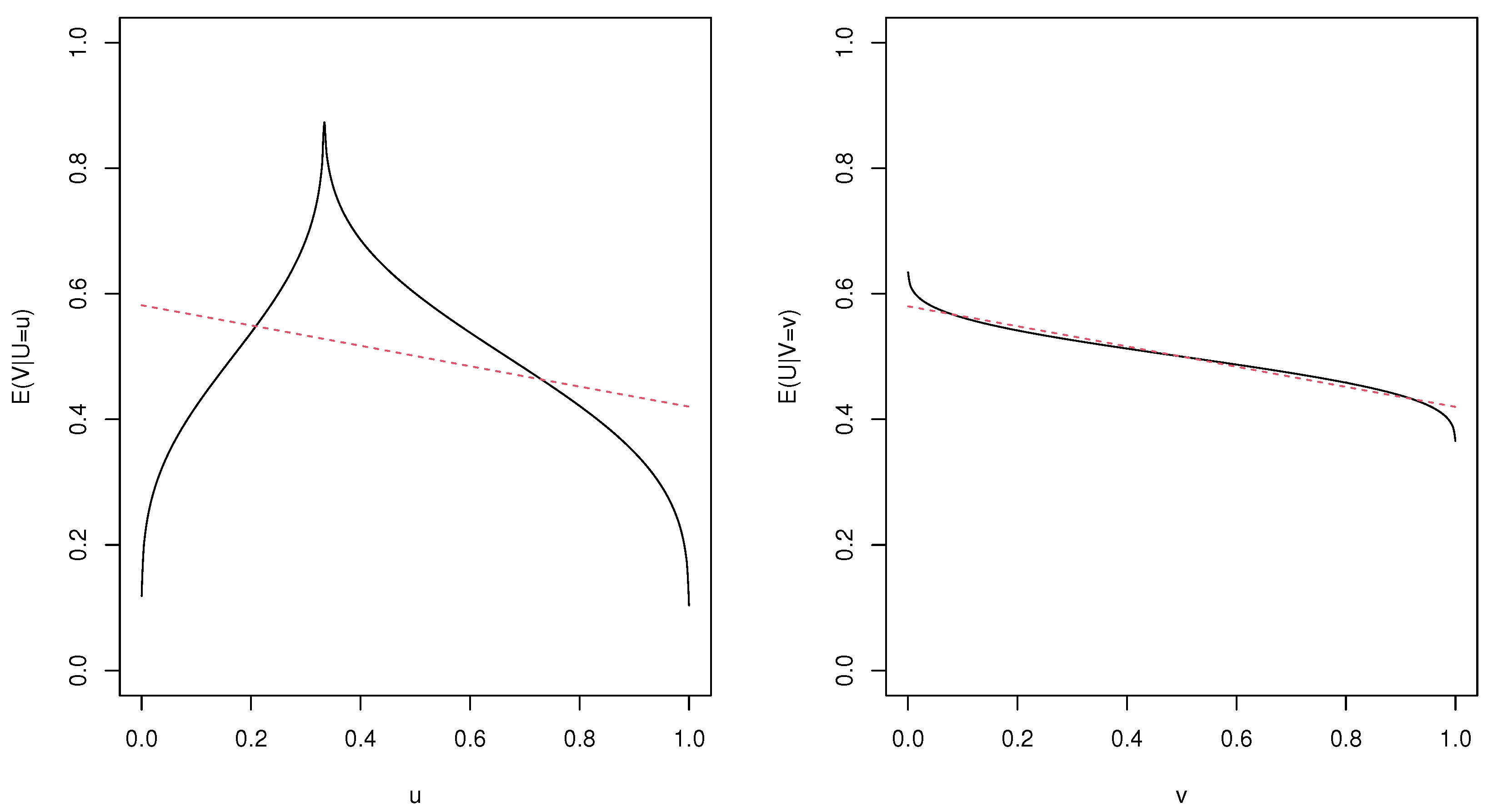
| Sample Size | ||||
|---|---|---|---|---|
| Nonparametric DD | Copula DD | Nonparametric DD | Copula DD | |
| n = 100 | 0.077 | 0.083 | 0.076 | 0.056 |
| n = 200 | 0.050 | 0.076 | 0.050 | 0.042 |
| n = 400 | 0.035 | 0.072 | 0.033 | 0.031 |
| n = 800 | 0.025 | 0.071 | 0.023 | 0.025 |
| n = 1600 | 0.018 | 0.069 | 0.016 | 0.021 |
| Sample Size | ||||
|---|---|---|---|---|
| Nonparametric DD | Copula DD | Nonparametric DD | Copula DD | |
| 0.072 | 0.208 | 0.076 | 0.034 | |
| 0.052 | 0.212 | 0.040 | 0.022 | |
| 0.038 | 0.213 | 0.025 | 0.017 | |
| 0.028 | 0.214 | 0.015 | 0.011 | |
| 0.021 | 0.214 | 0.010 | 0.008 | |
| LBTC | LETH | LXRP | LXLM | |
|---|---|---|---|---|
| Mean | 0.213 | 0.277 | 0.242 | 0.260 |
| Standard Deviation | 4.133 | 5.661 | 7.896 | 9.118 |
| Sample variance | 17.080 | 32.046 | 62.342 | 83.145 |
| Kurtosis | 11.885 | 8.674 | 34.177 | 16.897 |
| Skewness | −0.797 | −0.418 | 2.135 | 1.133 |
| Range | 68.985 | 84.084 | 179.176 | 138.629 |
| Minimum | −46.473 | −55.071 | −69.315 | −69.315 |
| Maximum | 22.512 | 29.013 | 109.861 | 69.315 |
| Sum | 387.253 | 503.490 | 439.491 | 472.758 |
| Count | 1817 | 1817 | 1817 | 1817 |
| Nonparametric DD Method | ||||
| Coin | LBTC | LETH | LXRP | LXLM |
| LBTC | 0.45 | 0.26 | 0.18 | |
| LETH | 0.44 | 0.36 | 0.21 | |
| LXRP | 0.26 | 0.35 | 0.26 | |
| LXLM | 0.18 | 0.23 | 0.27 | |
| Copula DD Method | ||||
| Coin | LBTC | LETH | LXRP | LXLM |
| LBTC | 0.39 | 0.21 | 0.14 | |
| LETH | 0.4 | 0.29 | 0.18 | |
| LXRP | 0.22 | 0.3 | 0.23 | |
| LXLM | 0.14 | 0.17 | 0.21 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, H.; Jang, H.; Kim, K.H.; Kim, J.-M. Nonparametric Directional Dependence Estimation and Its Application to Cryptocurrency. Axioms 2023, 12, 293. https://doi.org/10.3390/axioms12030293
Noh H, Jang H, Kim KH, Kim J-M. Nonparametric Directional Dependence Estimation and Its Application to Cryptocurrency. Axioms. 2023; 12(3):293. https://doi.org/10.3390/axioms12030293
Chicago/Turabian StyleNoh, Hohsuk, Hyuna Jang, Kun Ho Kim, and Jong-Min Kim. 2023. "Nonparametric Directional Dependence Estimation and Its Application to Cryptocurrency" Axioms 12, no. 3: 293. https://doi.org/10.3390/axioms12030293
APA StyleNoh, H., Jang, H., Kim, K. H., & Kim, J.-M. (2023). Nonparametric Directional Dependence Estimation and Its Application to Cryptocurrency. Axioms, 12(3), 293. https://doi.org/10.3390/axioms12030293







