An Asymmetric Model Position Dependent Mass: Quantum Mechanical Study

Abstract

We propose an asymmetric model position dependent mass and study its quantum mechanical behaviour on different potentials such as harmonic oscillator potential, double well potential, Gaussian single well potential and triangular single well model potential. It is observed from our study that the model asymmetric mass works well for weak coupling preserving the symmetric phase portrait. However, the dominance of asymmetric feature of the mass in the system clearly visible for higher values of the constant associated with the mass. Though, both position dependent mass and potential have significant role in controlling the spectral feature of the system, one may dominate over other for certain cases.

1. Introduction

The study of the problems associated with position dependent mass (PDM) have continued to attract the attention of scientific community due to their relevance in various branches of physics and allied areas of science [1,2]. Further, the identification of wave function in a complex environment could be possible by solving Schrödinger equation with PDM [3]. The majority of such studies dedicated to the problems relevance to semiconductor physics and solid state physics [4,5,6,7]. The PDM involved in various problems can either be symmetric or asymmetric in nature. Further, the asymmetric forms of PDM have successfully been explained certain features related to semiconductor physics. For example; the propagation of electron through the abrupt interface of a semiconductor heterostructure [8] as well as optomechanical features of resonator [9] can be shown to explain by the PDM of type.

$$m(x)=\frac{m}{{(1+\gamma x)}^2}$$

(1)

Further, in a recent work, da Costa et al. [10] has investigated the coherent state nature using the above PDM. El-Nabulsi has studied the system involving the PDM of the type.

$$m(x)=m{(1+\gamma x)}^k$$

(2)

And reported some of its implications to semiconductors, quantum dots, crystalline solid in the presence of impurity [4,5]. In addition, the transport of electrons in a semiconductor can be tailored by considering the PDM of the form [11].

$$m(x)=m{e}^{ax+\frac{1}{2}b{x}^2}$$

(3)

Several authors also explained different aspects of the quantum systems considering asymmetric PDM. For example; Dong et al. [12] obtained the eigenvalues and eigenfunctions of the asymmetric model singular mass oscillator with mass of the type.

$$m(x)=\frac{1}{{\tau }^{\alpha }{(x+a)}^{\alpha }}$$

(4)

Asad et al. [1] studied the phase portrait and stability of the harmonic like oscillator associated with asymmetric PDM of the type.

$$m(x)=\frac{m}{1+e^{-x-\lambda x^2}}$$

(5)

Recently, Dong et al. [3] have used an asymmetric model PDM

$$m(x)=\frac{\alpha e^{-\alpha x}}{\left(1-e^{-\alpha x}\right)}$$

(6)

And reported the exact solution of the Schrodinger equation for few typical potentials. One can extend such asymmetric PDM for understanding the properties of solid state and semiconductor physics. Further, it is worth mentioning here that the some of the properties of the semiconductor has also been studied using symmetric PDM [13]. For example; El-Nabulsi [14] has studied the dynamics of electron with PDM of type.

$$m(x)=m{e}^{-a{x}^2}$$

(7)

Silva et al. studied the electronic properties of electrons on a bilayer graphene catenoid bridge characterized by the PDM of the form [15].

$$m(x)=m\left(1+\frac{\lambda R^2}{{\left(x^2+R^2\right)}^2}\right)$$

(8)

Further, the vibrational inversion modes of NH₃ molecule has been explained by using the PDM of the form [16]

$$m(x)=m\left(\frac{1-\eta a^2{x}^2}{1-a^2{x}^2}\right)$$

(9)

In view of the importance of the PDM, several studies [17,18,19,20,21,22,23] also report different features of the systems in which the PDM varies either symmetric or asymmetric. The sgn(x) unction shows the asymmetry character which can suitably be used in formulating quantum mechanical problem involving double well [24,25].

In the present study, we designed a new type mass which varies asymmetrically with position in view of the importance of asymmetric PDM in explaining different features of semiconductor physics and study the spectral characteristics of the system by varying model parameter associated with the PDM as well as potentials. Our study thus suggested that both the PDM and potential have significant role in controlling the spectral feature of the system. Further, one may dominate over other for certain case.

2. Characteristic Features of New Asymmetric PDM

The asymmetric PDM used in this work is constructed as

$$m(x)=\frac{m}{1+\lambda \left(\mathrm{sgn}(x)\right)+{\lambda }^2{x}^2}$$

(10a)

In the above, the sign function, $\mathrm{sgn}(x)$ is defined as

$$\mathrm{sgn}(x)=\left\{\begin{array}{l}1,x\succ 0\\ 0,x=0\\ -1,x\prec 0\end{array}\right.$$

(10b)

The above PDM is very sensitive to the parameter, $\lambda$ and its behaviour changes dramatically upon the change of $\lambda$ value. Figure 1 and Figure 2 show the behaviour of the PDM with distance for $\lambda$ = 0.01 and 0.1 respectively. The nature of the graph changes dramatically for higher values of $\lambda$.

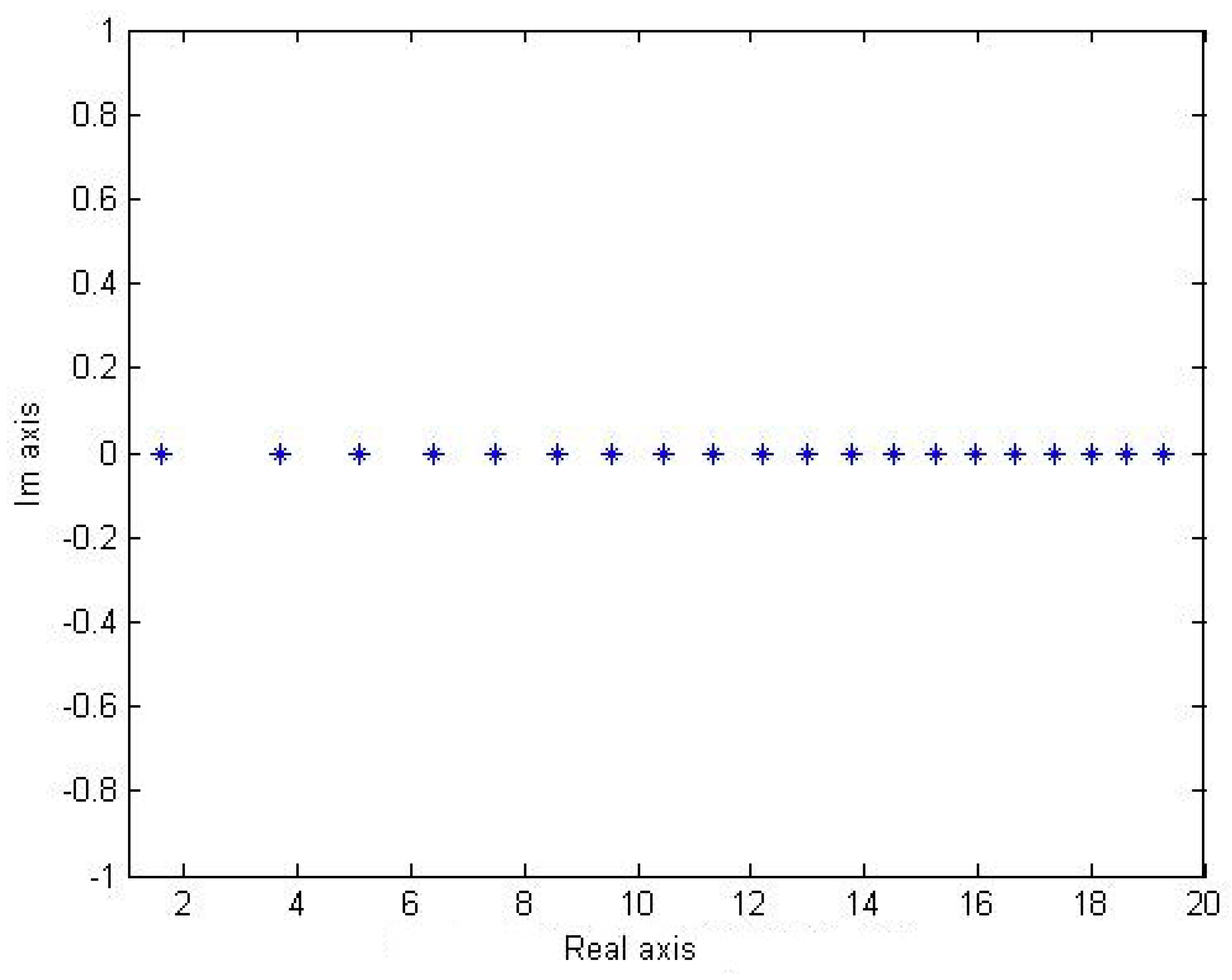
3. Quantum Mechanical Study on the New PDM Systems

Here, we solve the eigenvalue relation [26],

$$H\left|\mathsf{\Psi }\right.〉=E\left|\mathsf{\Psi }\right.〉$$

(11a)

where

$$\left|\mathsf{\Psi }\right.〉={\displaystyle \sum _n{A}_n\left|{\varphi }_n\right.〉}$$

(11b)

In the above, $\left|{\varphi }_n\right.〉$ satisfies the relation

$$H_o\left|{\varphi }_n\right.〉=\left(2n+1\right)\left|{\varphi }_n\right.〉$$

(12a)

and

$$\left|{\varphi }_n\right.〉=N_n{e}^{-\frac{x^2}{2}}{H}_n(x)$$

(12b)

where $N_n$ is the normalization constant such that

$$〈{\varphi }_n|{\varphi }_m〉={\delta }_{mn}$$

(13)

The Hamiltonian considered here is

$$H=T+m(x)V(x)$$

(14)

where,

$$T=\frac{1}{{\left[m(x)\right]}^{\frac{1}{4}}}p\frac{1}{{\left[m(x)\right]}^{\frac{1}{2}}}p\frac{1}{{\left[m(x)\right]}^{\frac{1}{4}}}$$

(15)

The above expression is considered due to the mass and the said kinetic energy is due to von Roos model operator [27,28].

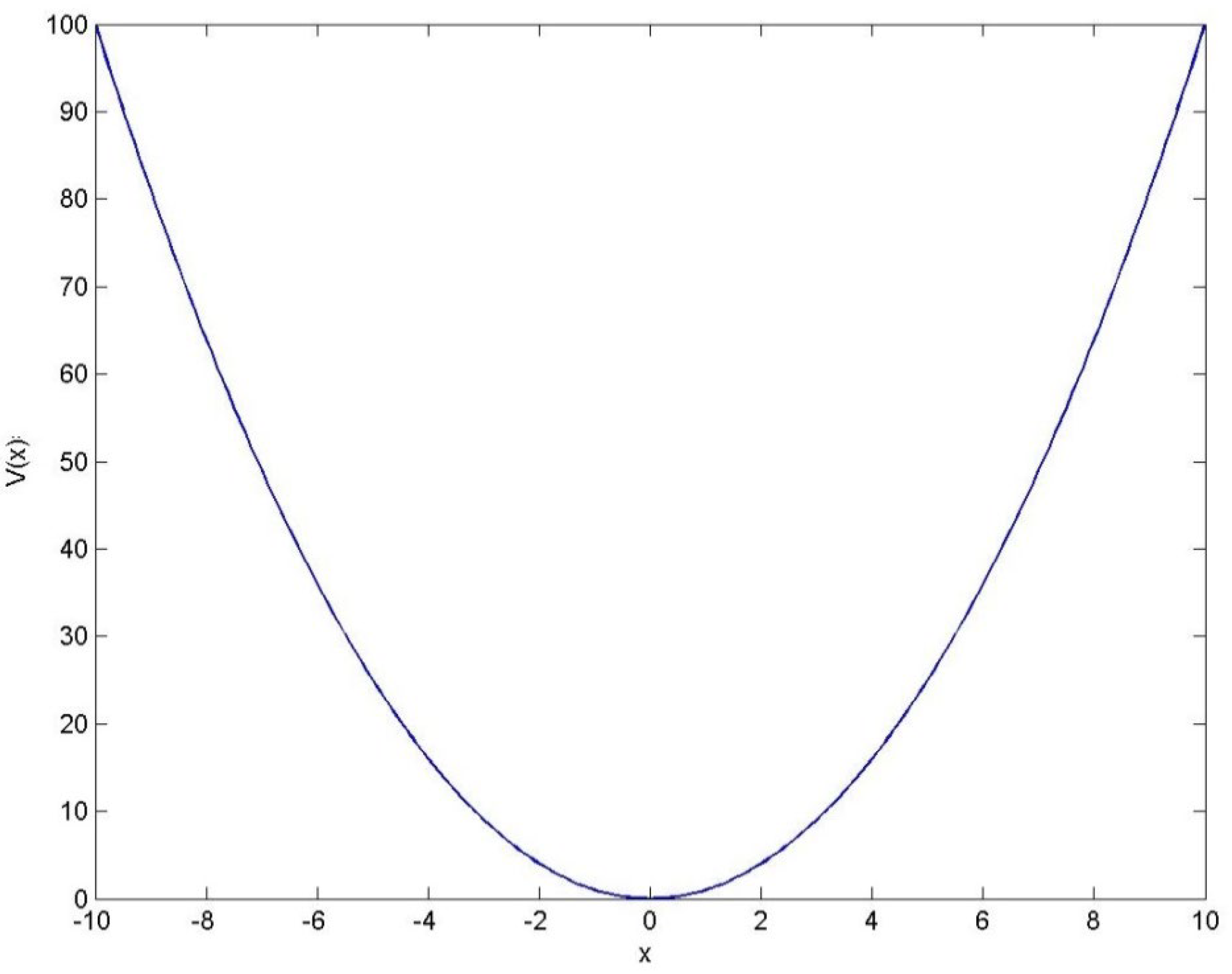
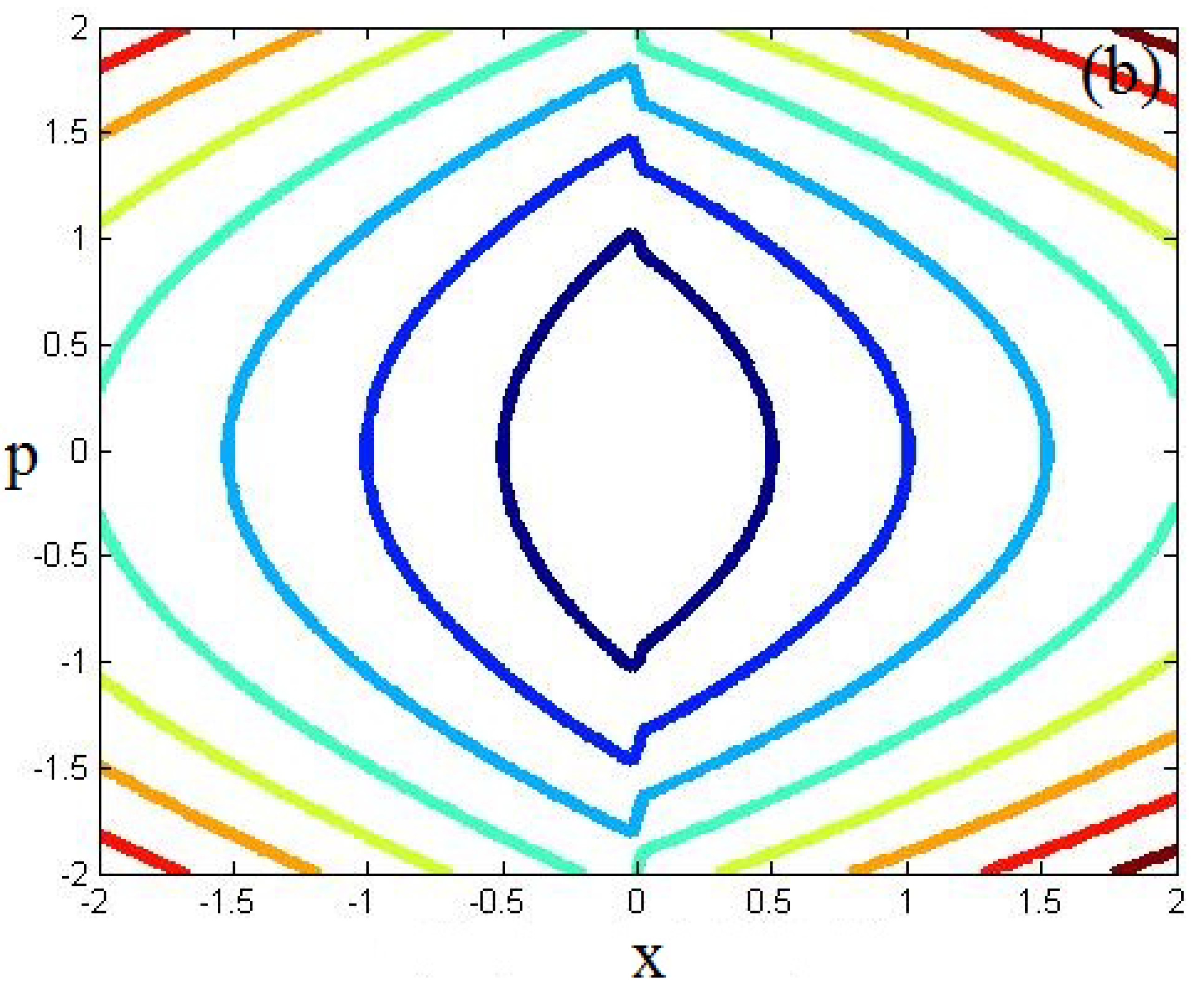
4. Effect of Potential

Here, we consider different forms of potential in order to study their effect on the energy eigenvalues of the Hamiltonian (Equation (14)) associated with PDM (Equation (10a)). We have seen that the change of potential also affect the spectral features of the Hamiltonian. The details of these studies are discussed in the followings.

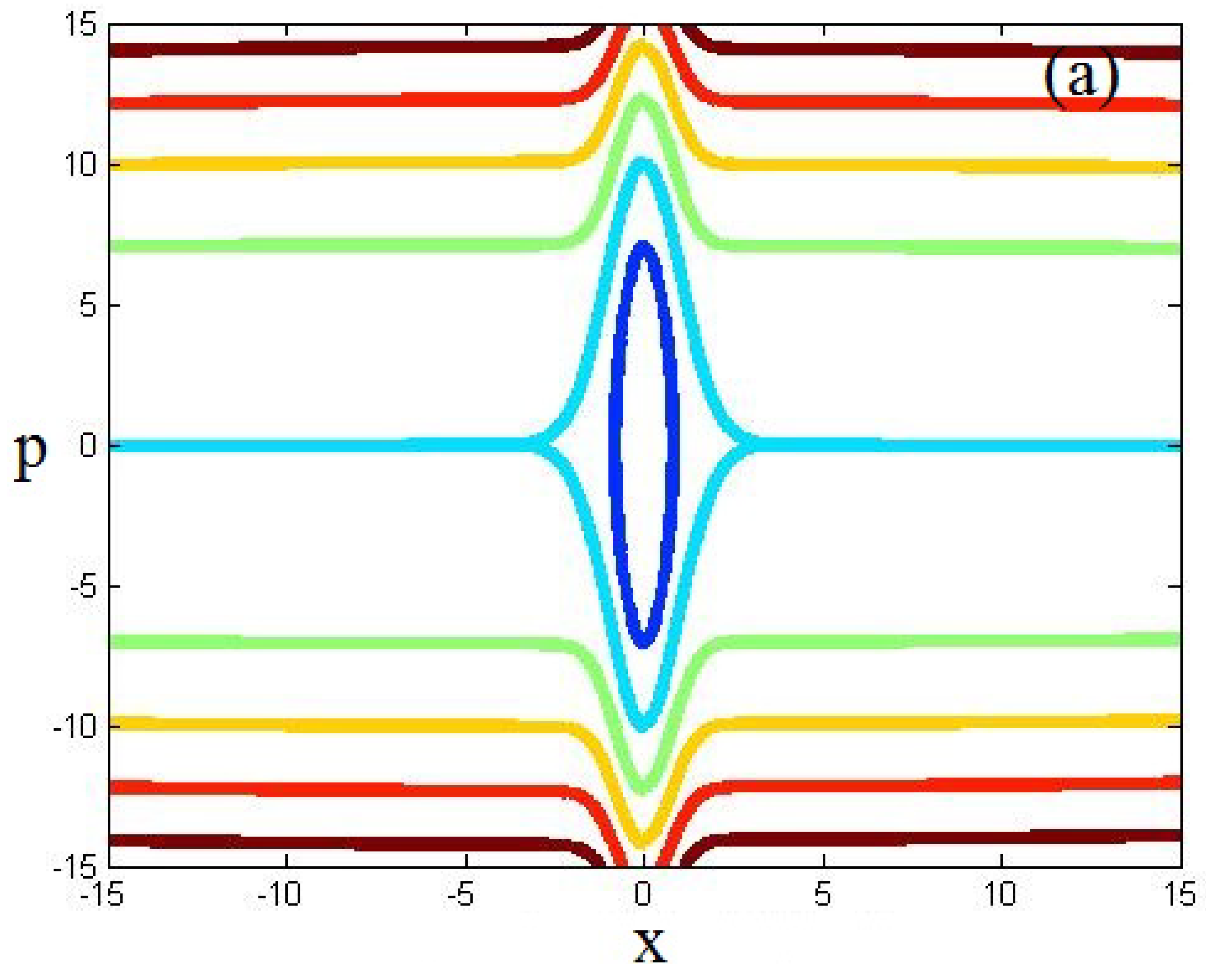
4.1. Single Well Potential

We consider the single potential as

$$V(x)=x^2$$

(16)

And study the behaviour of the PDM Hamiltonian as stated above. On solving the Hamiltonian with the potential (Equation (16), Figure 3), we obtained the closed phase portrait for $\lambda$ = 0.01 (Figure 4) and 0.1 (Figure 5) along with the stable real energy level. The representative real energy spectra for the studied system with $\lambda$ = 0.01 is shown in Figure 6. It should be noted here that the circular symmetric nature of the phase portrait is evident for $\lambda$ = 0.01 (Figure 4) and the effect of mass becomes significant at higher values of $\lambda$ i.e., $\lambda$ = 0.1. The effect of asymmetry associated with the PDM is clearly visible in the asymmetric nature of phase portrait (Figure 5).

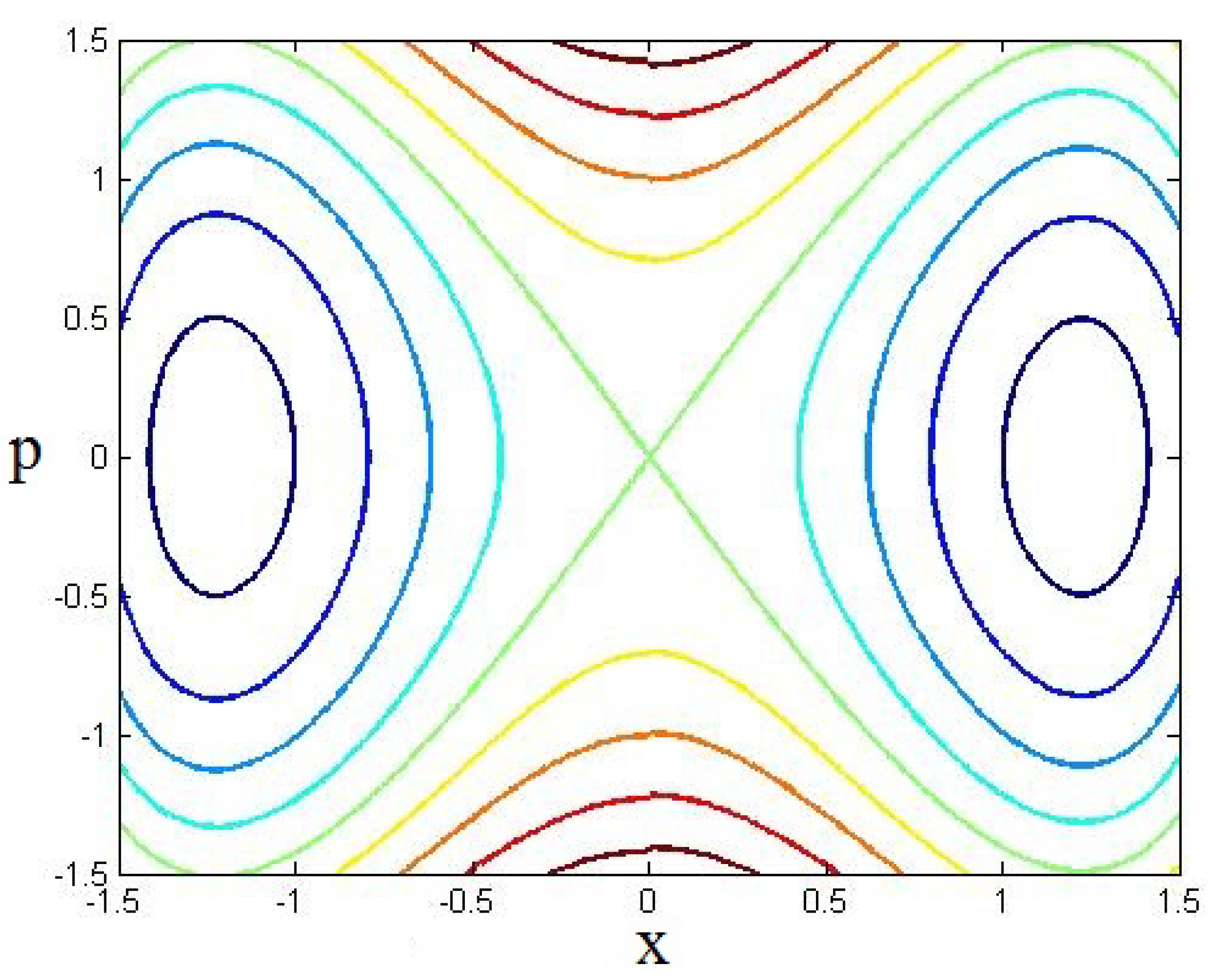
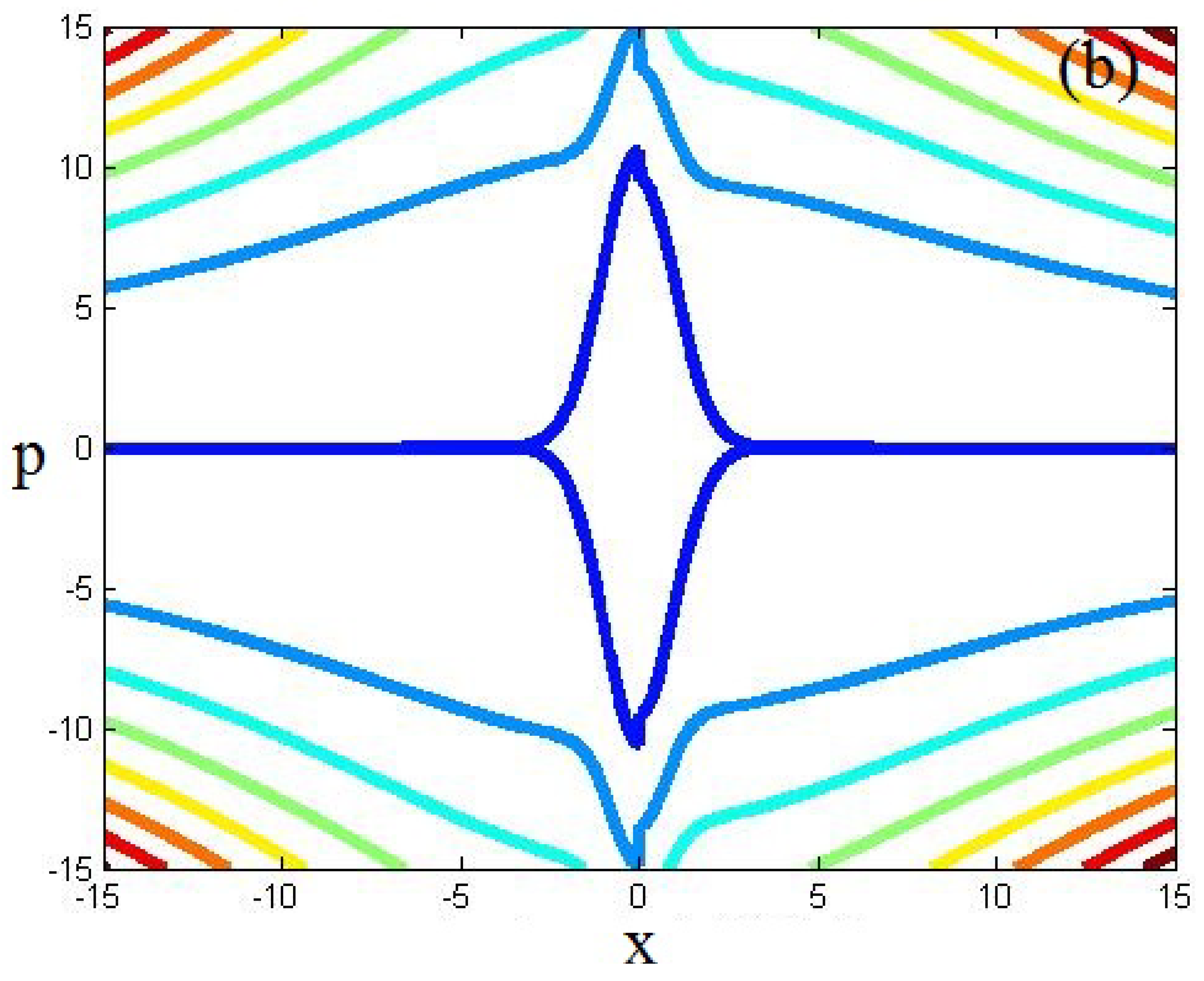
4.2. Double Well Potential

We consider the single potential as [29]

$$V(x)=x^4-3x^2$$

(17)

And study the behaviour of the PDM Hamiltonian as stated above. On solving the Hamiltonian with the potential (Equation (17), Figure 7), we obtained the closed phase portrait for $\lambda$ = 0.01 (Figure 8) and 0.1 (Figure 9) along with the stable real energy level. The representative real energy spectra for the studied system with $\lambda$ = 0.01 is shown in Figure 10. Like the single well case, the asymmetry associated with the PDM is also clearly visible in the asymmetric nature of phase portrait for $\lambda$ = 0.1 (Figure 9).

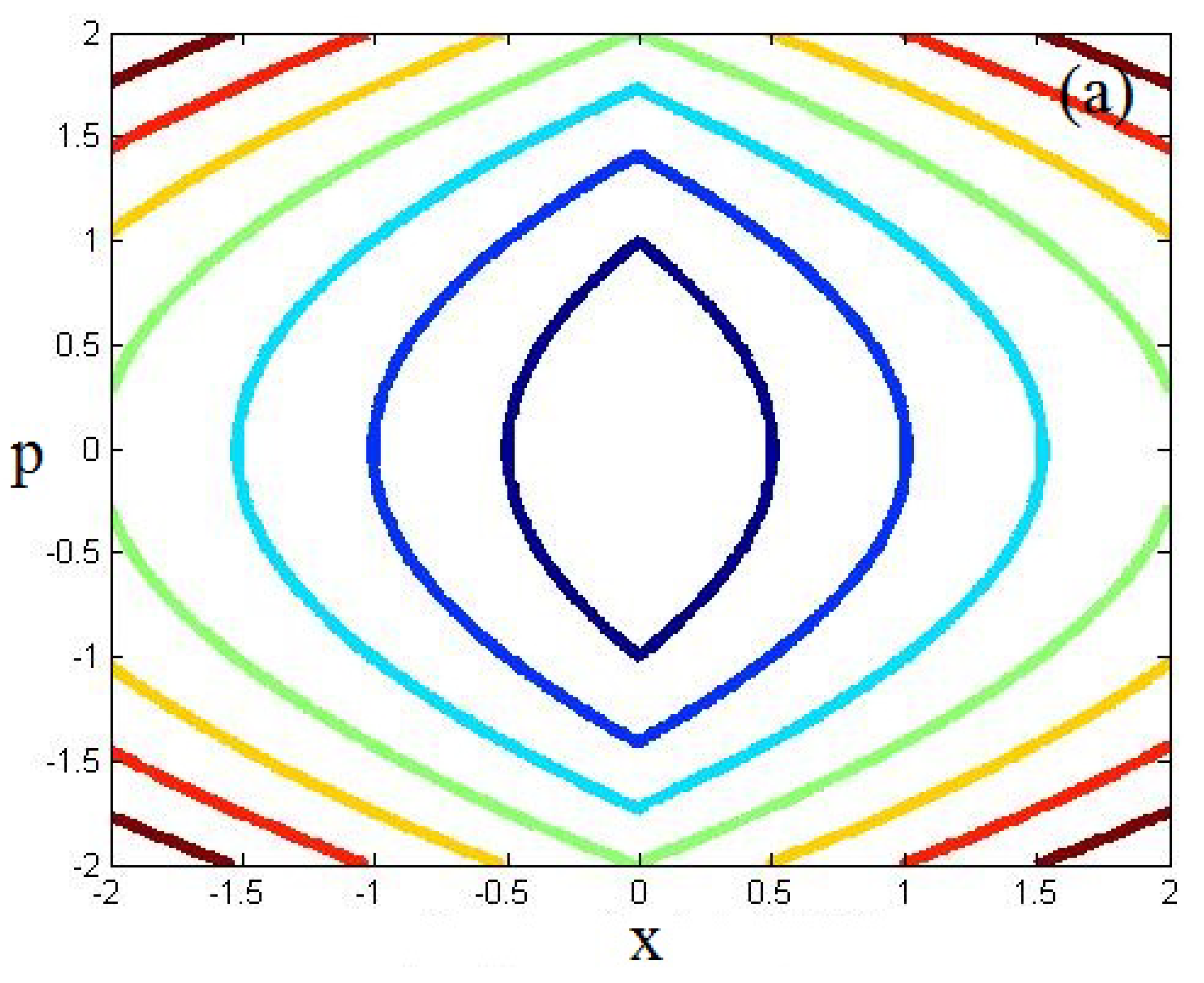
4.3. Gaussian Single Well Potential

Here, we consider the potential as [30]

$$V(x)=-100e^{-x^2}$$

(18)

To study the behaviour of the PDM Hamiltonian as stated above. On solving the Hamiltonian with the potential (Equation (18), Figure 11), we obtained the closed phase portrait for $\lambda$ = 0.01 and 0.1 (Figure 12) with the stable real energy level (Figure 13). In this case, a typical type symmetric phase portrait is seen for $\lambda$ = 0.01. However, the same showed distortion with appearance of asymmetry for $\lambda$ = 0.1 like the previous cases. This result also indicates the dominance of the potential for low values of $\lambda$ i.e., for $\lambda$ = 0.01.

4.4. Rath Triangular Potential

Here, we consider the potential as [31]

$$V(x)=100\left(1-\exp \left(-0.02\left|x\right|\right)\right)$$

(19)

To study the behaviour of the PDM Hamiltonian as stated above. On solving the Hamiltonian with the potential (Equation (19), Figure 14), we obtained the closed phase portrait for $\lambda$ = 0.01 and 0.1 (Figure 15) with the stable real energy level (Figure 16). It is to be noted here that the phase portrait still shows the symmetric loop in this case as well as for single well and double well potential cases for very low values of $\lambda$ i.e., for $\lambda$ = 0.01 due to the dominating nature of respective potentials (single well, double well and Rath triangular potentials) at low value of constant ($\lambda$ = 0.01) associated with the PDM. The symmetric nature of the phase portrait starts distorting and the asymmetry becomes clearly visible for $\lambda$ = 0.1 due to the dominating nature of asymmetric PDM. The present study thus suggests that both potential and PDM have the significant role in controlling the spectral feature of the Hamiltonian. However, one may dominate over other for certain case.

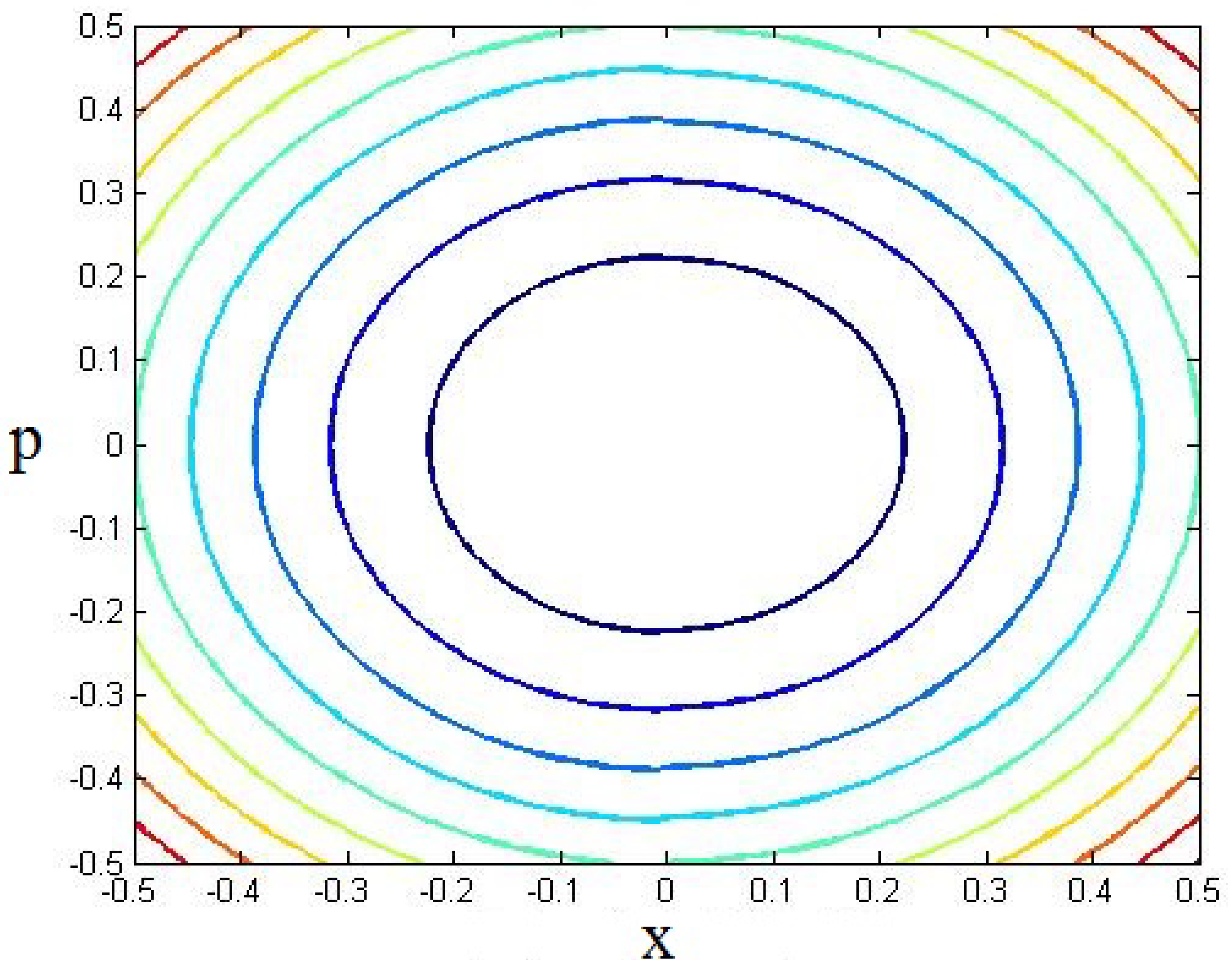
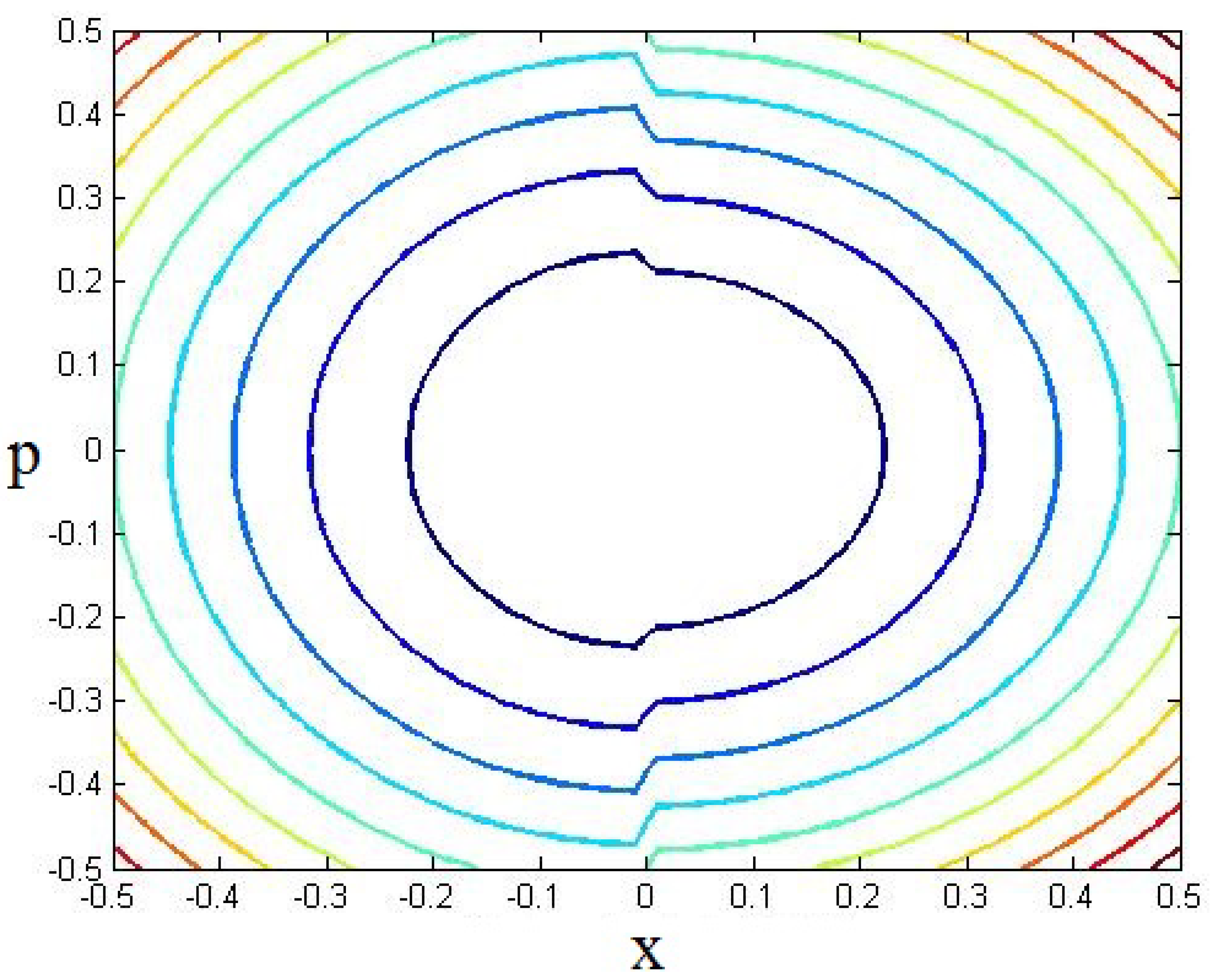
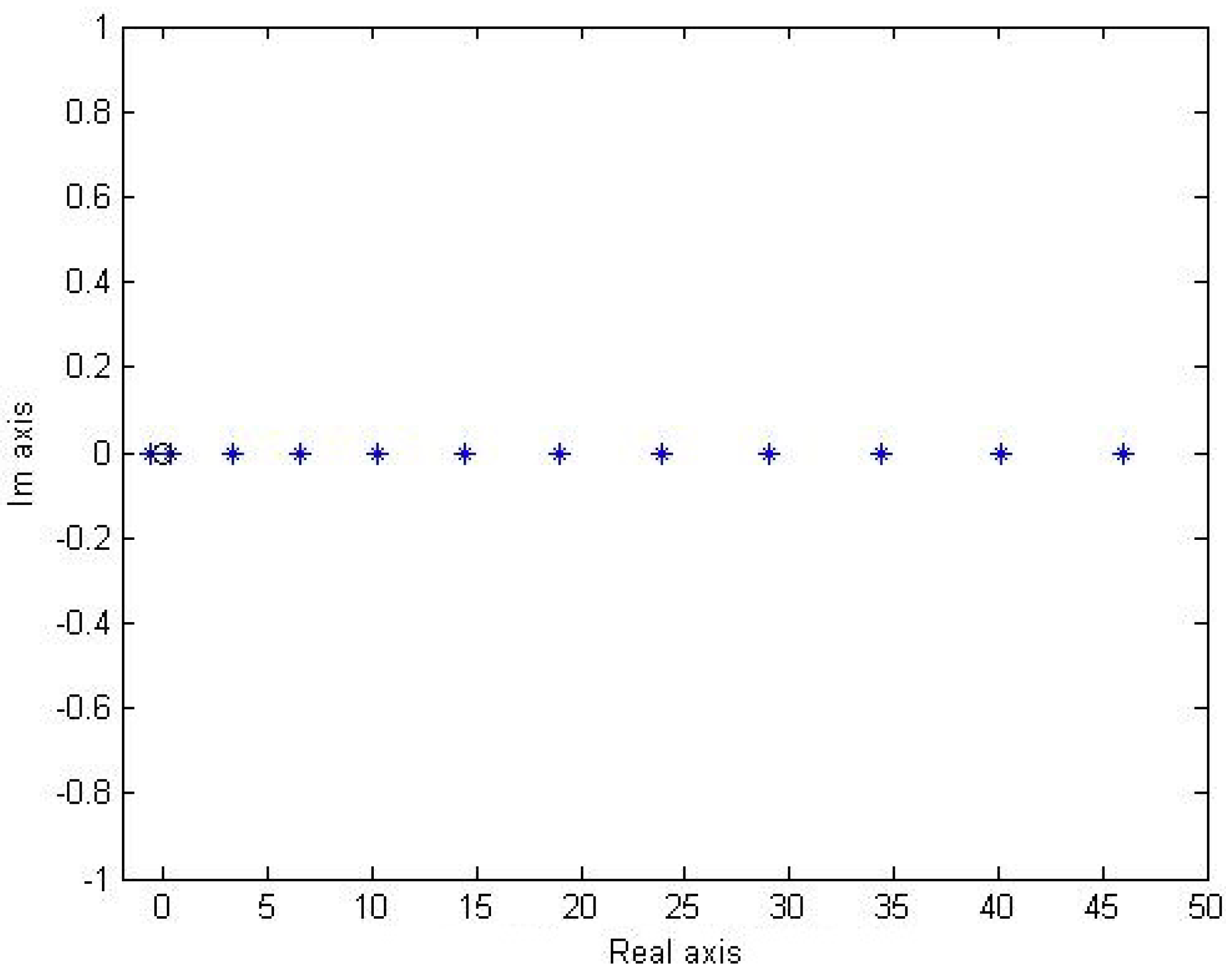
5. Validity of Uncertainty Relation

All the PDM Hamiltonian discussed above would satisfy the uncertainty relation [32]. Here, we consider a typical harmonic oscillator type potential (single well potential (16)) to calculate the uncertainty relation as follows

$$\Delta x=\sqrt{〈x^2〉-{〈x〉}^2}=0.7137$$

(20)

$$\Delta p=\sqrt{〈p^2〉-{〈p〉}^2}=0.7035$$

(21)

$$\Delta x\Delta p=0.5057$$

(22)

The above analysis indicates that the uncertainty product ($\Delta x\Delta p$) is greater than that of simple harmonic oscillator.

6. Discussion and Conclusions

We model a new PDM in view of its importance in realizing different features associated with semiconductor physics. The effect of PDM on the spectral feature of the associated Hamiltonian was studied by varying potential term and constant parameter of the PDM using the matrix diagonalization method as started above. It is worth mentioning here that the method of calculation has also been tested for other systems [1,2,26]. Further, the result of da Costa et al. [33] have successfully been reproduced and reflected in our recent work [34]. The present PDM contain a sensitive asymmetric term i.e., sgn(x) function and a symmetric function (${\lambda }^2{x}^2$). Without the sgn(x) function, the mass function remains the same as that of Mathew’s Lakshmanan [35] PDM which is quite symmetric about the origin. However, with the inclusion of sgn(x) function, we noticed that the mass function shows asymmetric character. In fact the study of sgn(x) function is crucial. The sgn(x) function has previously been used in supersymmetry [24] where the shape invariant property cannot be verified. Secondly, the sgn(x) function is also used in double well potential [25]. We therefore introduce sgn(x) function in designing a new mass and study its spectral behaviour associated with different potentials. It is worth mentioning here that the triangular model potential proposed by Rath [31] is an alternative to model scattering potential [36] for the study of spectral feature. Since the PDM used in the present study is asymmetric in nature, the phase portrait is expected to preserve the asymmetric feature. The phase portrait of different systems for different potentials show the symmetric behaviour for weak coupling limit i.e., for $\lambda$ = 0.01. The symmetric nature of the phase portrait starts distorting and the asymmetry becomes clearly visible for $\lambda$ = 0.1 due to the dominating nature of asymmetric PDM. However, the closed phase portraits of the studied systems reflect the unbroken nature of spectra irrespective of symmetric or asymmetric nature. This feature thus signifies the stability of the system. In order to study the spectral nature, we used matrix diagonalization method [26] and noticed that the spectral feature (energy levels) remains invariant for different size of the matrix. We feel that the interested readers will be motivated by the present investigation. Our study thus suggested that both PDM and potential have significant role in controlling the spectral feature of the system. Further, one may dominate over other for certain case. We believe that the results of all the PDM Hamiltonian discussed above would be within the preview of usual uncertainty relation.