Limit Cycles of Polynomially Integrable Piecewise Differential Systems
Abstract
:1. Introduction
- (i)
- If , then .
- (ii)
- If , , and there are two positive integers, p and q, such that and , then
- (iii)
- If , and and there are two positive integers p and q such that and , then
2. Proof of Theorem 1
- Subcase (I.1): . Then, , and the variables in system (12) can be separated. Thus, the first integral is
- Subcase (I.2): and . Then,
- Case (II): . Changing variables and to system (3) giveswhere , , , , and . Two subcases can be identified.
- Subcase (II.1): , which agrees with case (I) previously discussed. Therefore, the PFI exists.
- Subcase (II.1.1): , for which it is known that one PFI is
- Subcase (II.1.2): and . This subcase coincides with conditions (14) in Subcase (I.2). Therefore, in order to have a PFI , there must be a such that ,and where
3. Proof of Theorem 2
- (i)
- and in this case
- (ii)
- with and . In this case,
- (ii)
- System (27) has a PFI if and only if
- (ii.1)
- , with ; or
- (ii.2)
- where and , with
- (i)
- if p is even, for all , decreases for and increases outside, with a local minimum at and an inflexion point at ; and,
- (ii)
- if p is odd, if and only if , increases for all , with an inflexion point at and, if , another one at .
- (i)
- When p is even, it is obvious that for all and . From (34)which implies that either and , or and . Thus,andMoreover, the sign of changes at . It is negative before and positive after it, so at this point has a local minimum.Since is equivalent to , then (35) can be rewritten ashence, if and only if or, equivalently, if . This means that has an inflexion point at .
- (ii)
- When p is odd, is positive if and only if , i.e., . This implies that if and only if .In order to study the monotonicity, (34) is used:This implies that for all . Since we conclude that for all . So is an increasing function in the whole domain.Finally, we use (35) to study the convexity,As far as for all x, for and , or and . In the first case, if and , then if . In the second case, if and . However, , and since and , then there is no other solution for x where . In conclusion, if and only if . In a similar way, we conclude that if, and only if, .
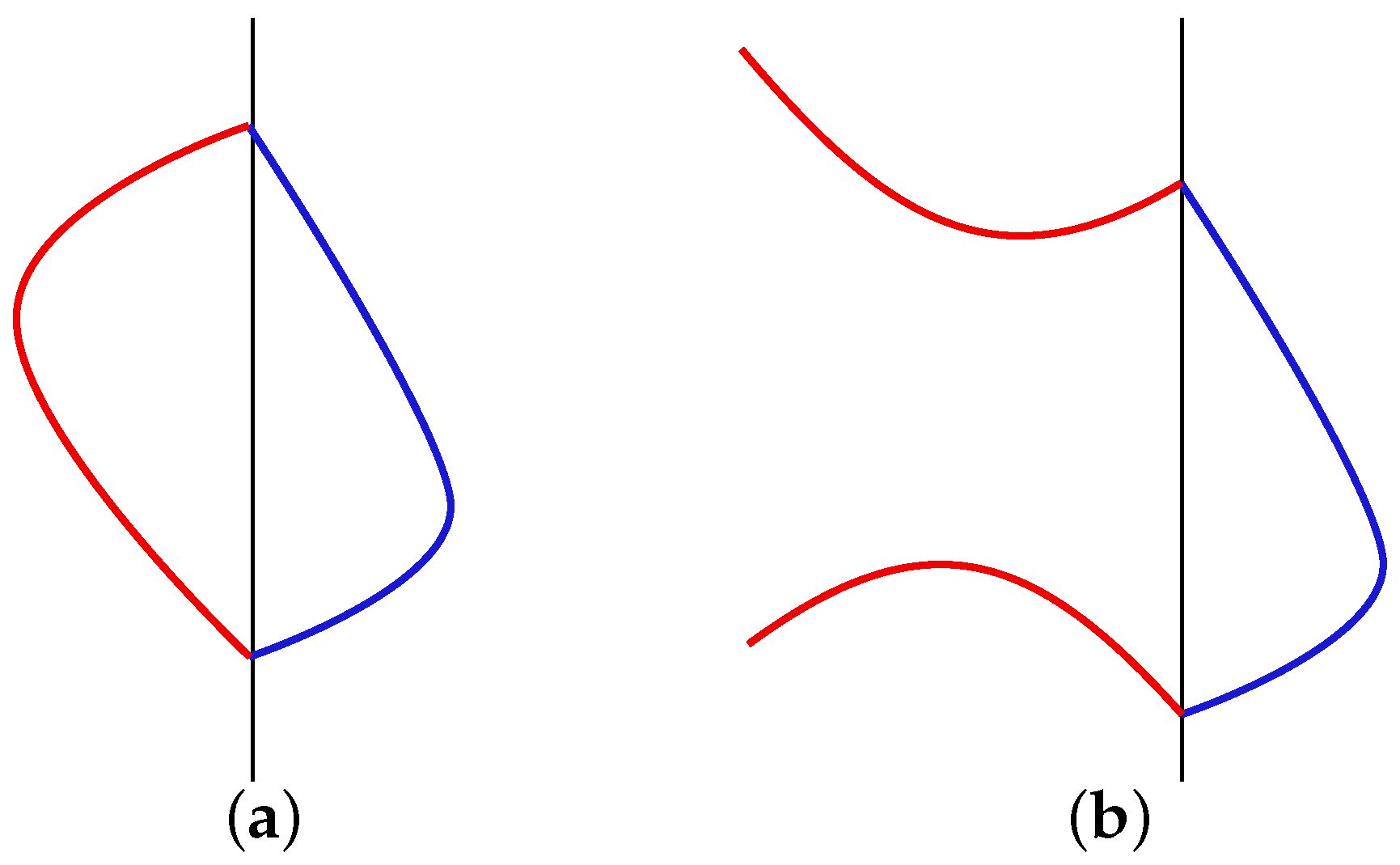
- Case 3: Only system (27) is Hamiltonian. Again, from Proposition 3, in system (27) and in system (26) and with . In this case, every limit cycle of the DPwLS (26) and (27) crosses at two different points, and , satisfying the systemSimilar arguments as the ones used in Case 2 show that DPwLS (26) and (27) have at most one limit cycle.
4. Examples
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Filippov, A.F. Differential Equations with Discontinuous Right–Hand Sides; Mathematics and Its Applications (Soviet Series); Translated from Russian; Kluwer Academic Publishers Group: Dordrecht, The Netherlands, 1988; Volume 18. [Google Scholar]
- Andronov, A.; Vitt, A.; Khaikin, S. Theory of Oscillations; Pergamon Press: Oxford, UK, 1966. [Google Scholar]
- Di Bernardo, M.; Budd, C.J.; Champneys, A.R.; Kowalczyk, P. Piecewise-Smooth Dynamical Systems: Theory and Applications; Springer: London, UK, 2008; Volume 163. [Google Scholar]
- Simpson, D.J.W. Bifurcations in Piecewise-Smooth Continuous Systems; World Scientific: Singapore, 2010. [Google Scholar]
- Makarenko, O.; Lamb, J.S.W. Dynamics and bifurcations of nonsmooth systems: A survey. Physica D 2012, 241, 1826–1844. [Google Scholar]
- Euzébio, R.D.; Llibre, J. On the number of limit cycles in discontinuous piecewise linear differential systems with two pieces separated by a straight line. J. Math. Anal. Appl. 2015, 424, 475–486. [Google Scholar] [CrossRef] [Green Version]
- Buzzi, C.; Gasull, A.; Torregrosa, J. Algebraic limit cycles in piecewise linear differential systems. Int. J. Bifurc. Chaos 2018, 28, 1850039. [Google Scholar] [CrossRef]
- Artés, J.C.; Llibre, J.; Vulpe, N. Quadratic systems with an integrable saddle: A complete classification in the coefficient space R12. Nonlinear Anal. 2012, 75, 5416–5447. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Llibre, J. Limit cycles in piecewise polynomial Hamiltonian systems allowing nonlinear switching boundaries. J. Differ. Equ. 2023, 344, 405–438. [Google Scholar] [CrossRef]
- Dieci, L.; Elia, C.; Pi, D. Limit cycles for regularized discontinuous dynamical systems with a hyperplane of discontinuity. Discret. Contin. Dyn. Syst. B 2017, 22, 3091–3112. [Google Scholar] [CrossRef] [Green Version]
- Huzak, R.; Uldall Kristiansen, K. The number of limit cycles for regularized piecewise polynomial systems is unbounded. J. Differ. Equ. 2023, 342, 34–62. [Google Scholar] [CrossRef]
- Sotomayor, J.; Teixeira, M.A. Regularization of discontinuous vector fields. In Proceedings of the International Conference on Differential Equations, Lisboa, Portugal, 24–29 July 1995; pp. 207–223. [Google Scholar]
- Freire, E.; Ponce, E.; Torres, F. Canonical Discontinuous Planar Piecewise Linear Systems. SIAM J. Appl. Dyn. Syst. 2012, 11, 181–211. [Google Scholar] [CrossRef]
- García, B.; Llibre, J.; Pérez del Río, J.S. Phase portraits of the quadratic vector fields with a polynomial first integral. Rend. Circ. Mat. Palermo 2006, 55, 420–440. [Google Scholar] [CrossRef]

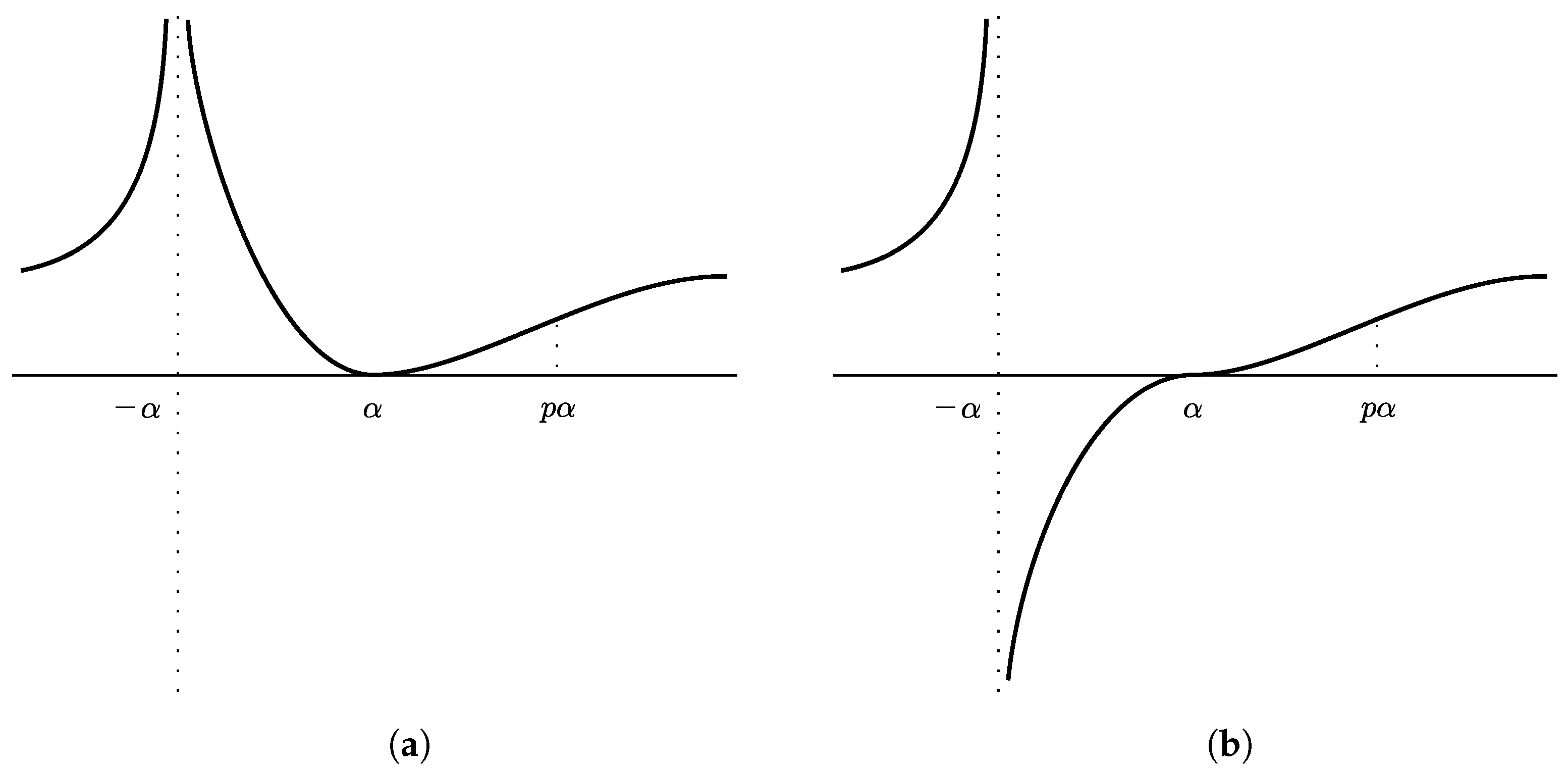


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García, B.; Llibre, J.; Pérez del Río, J.S.; Pérez-González, S. Limit Cycles of Polynomially Integrable Piecewise Differential Systems. Axioms 2023, 12, 342. https://doi.org/10.3390/axioms12040342
García B, Llibre J, Pérez del Río JS, Pérez-González S. Limit Cycles of Polynomially Integrable Piecewise Differential Systems. Axioms. 2023; 12(4):342. https://doi.org/10.3390/axioms12040342
Chicago/Turabian StyleGarcía, Belén, Jaume Llibre, Jesús S. Pérez del Río, and Set Pérez-González. 2023. "Limit Cycles of Polynomially Integrable Piecewise Differential Systems" Axioms 12, no. 4: 342. https://doi.org/10.3390/axioms12040342
APA StyleGarcía, B., Llibre, J., Pérez del Río, J. S., & Pérez-González, S. (2023). Limit Cycles of Polynomially Integrable Piecewise Differential Systems. Axioms, 12(4), 342. https://doi.org/10.3390/axioms12040342





